Abstract
This study examined the effects of passage and presentation order on progress monitoring assessments of oral reading fluency in 134 second grade students. The students were randomly assigned to read six one minute passages in one of six fixed orders over a seven week period. The passages had been developed to be comparable based on readability formulae. Estimates of oral reading fluency varied across the six stories (67.9 to 93.9), but not as a function of presentation order. These passage effects altered the shape of growth trajectories and affected estimates of linear growth rates, but were shown to be removed when forms were equated. Explicit equating is essential to the development of equivalent forms, which can vary in difficulty despite high correlations across forms and apparent equivalence through readability indices.
Fluency and Curriculum Based Measurement (CBM)
Fluency, the ability to read text aloud with speed, accuracy, and prosody is an important skill in reading development (National Reading Panel; NRP, 2000; Snow, Burns, & Griffin, 1998) It represents a directly observable analog to the automatic word recognition skills that support silent reading. While a struggling reader attends mainly to the process of decoding words in the text, a fluent reader expends less cognitive resources on decoding allowing the reader to concentrate on the meaning of the text. This relationship between fluency and comprehension has been argued theoretically (e.g., Perfetti’s verbal efficiency theory, 1985) and studied empirically, where it has been shown across a variety of settings and contexts using different measures of fluency and comprehension, that a fluent reader is more likely to have better comprehension skills (Fuchs, Fuchs, Hosp, & Jenkins, 2001; Young & Bowers, 1995; Nathan & Stanovich, 1991; LaBerge & Samuels, 1974). Because of the tight empirical and theoretical link between fluency and comprehension and the relative ease of assessing fluency over comprehension, fluency assessments are often used as proxies to monitor student growth in reading.
Curriculum-Based Measurement (CBM)
Progress monitoring assessments of fluency are often used in the classroom to provide teachers and other professionals with regular feedback on students’ rate of skill acquisition. Such assessments help to identify students needing modifications of their current instruction based on slower than expected rates of skill acquisition. There are five essential characteristics of progress monitoring assessments. One is that they are administered to students on a regular, fixed intervals. Second, they have to be brief and easy to administer in the classroom by the classroom teacher or other professional. Third, they need to provide scores on a constant metric in order to validly and reliably measure student progress. Fourth, performance on the assessment, both the final level of attainment and the rate of progress during the year, should be predictive of end of year outcomes of interest to the student, teacher, and school system. Finally, they need to be free from measurement artifacts such as practice effects and form effects which can lead to distortions in the growth trajectory from which rates of skill acquisition are estimated. Curriculum Based Measurement (CBM) has been proposed as a method of progress monitoring that has these properties (Shinn, Rosenfield, & Knutson, 1989; Deno, 1986; Fuchs & Deno, 1991; Marston, 1989).
Developed in the context of special education, in the past few years CBM has moved to the general education classroom in response to the need for regular monitoring of student progress in reading. The use of CBM has the potential to become even more widespread given recently enacted changes to the Individuals with Disabilities Act (IDEA) that will allow the use of response to intervention as a component of special education disability determination. Due to the increased use of CBM for measuring growth in student performance over time for various purposes, it is important to empirically examine factors that affect the use of CBM to assess development of oral reading fluency.
CBM has specific features that make it suitable for widespread use for educational decision making. There is a standard set of administration procedures for using CBM to monitor reading development. Most commonly, these include having the student read connected text for a fixed duration of time, typically one minute. Oral reading fluency is computed as the number of words read correctly per minute, which is then charted as a measure of growth in reading rate. A word is read correctly if the word is pronounced aloud correctly, either initially, or following self-correction. Errors include mispronunciations, substitutions, omissions, and words not read within three seconds (Shinn, 1989). The reading materials that are used for CBM range from basal readers to pre-packaged texts.
According to the authors, the Dynamic Indicators of Basic Early Literacy Skills (DIBELS; Good & Kaminiski, 2002b) was developed as a CBM assessment for monitoring student progress (Technical Report 9). DIBELS measures a variety of early reading skills using one-minute CBM probes. The DIBELS oral reading fluency (DORF) measure applies the principles of CBM and consists of one-minute probes, given as frequently as once a week. The results provide within grade evaluation of student growth as the reading passages are written such that Words Correct Per Minute (WCPM) measured with DIBELS ORF passages will correlate with performance on a middle of the year reading passage.
Scaling and Equating of Passages
A challenge to progress monitoring, whether CBM or non-curriculum based measures are used, is the large number of texts needed for continuous assessments throughout the year and across Kindergarten through Grade 3. The system of assessments needs to be comprised in such a way to yield scores on a constant metric throughout the range of intended ability because with CBM it is not the level of performance at any one time that is of greatest interest, but rather the rate of progress being made with respect to skill acquisition. To ensure proper functioning of the assessment system, passages need to be selected or constructed to have consistent properties with respect to their difficulty level as measured in terms of oral reading fluency rates. That is, forms need to function as parallel forms within the same grade level. However, as in most psychometric endeavors, precise control of the stimulus properties is difficult, and does not, in and of itself, guarantee equivalence in the distribution of raw scores. Consequently, some care must be taken to convert raw scores (i.e., in this case the measured oral reading fluency rate) into scores for reporting that are independent of the precise stimulus materials that were used to obtain them. Without a means for removing the effects of the text on the distribution of scores, it is impossible to know if someone’s true reading rate is improving, declining, or holding steady simply by examining changes in their observed oral reading fluency over time. This problem has been incorrectly construed as a problem of reliability/unreliability of the observed oral reading fluency score. In fact, the problem is unrelated to reliability. Rather it is a problem of scaling the observed scores in a consistent and coherent manner, such that fluctuations in observed scores due to differences in text difficulty across passages have been factored out of the reported score distribution.
It is in this final area that questions about the equivalence of DORF passages arises, because the test development process in DIBELS relies heavily on readability as the primary criterion for determining passage equivalence. DIBELS is not unique in this approach, which characterizes most, if not all, development of CBM passages. As such, DIBELS provides an excellent example of the scaling issue that will inevitably emerge from exclusive reliance on stimulus equating (i.e., readability) for establishing equivalence of observed scores.
Problems with Readability Equating
Readability formulae are imperfect as tools for equating passages. It is well known that the rank ordering of passages will vary depending on the readability index used. Using DORF as an example, Good and Kaminski (2002b) reported that the passages were written with a target readability of the end of the year or the beginning of the next grade year. First grade passages were written at a Spache readability of 2.0 to 2.3, second grade stories were written at a Spache readability of 2.4 to 2.7, and third grade stories were written at a Spache readability of 2.8 to 3.1. These statistics define a fairly narrow range of readability within each grade as measured by the Spache index. However, these same passages show a markedly different range of readabilities based on other indices (see Table 4, pg. 7, Good and Kaminski, 2002b). For example, the Grade 2 passages with Spache index from 2.4 to 2.7 ranged from 4.3 to 8.0 on the FOG, 3.0 to 6.6 on the Fry, 6.8 to 9.5 on the Forecast, and 2.2 to 5.3 on the Flesch.
Table 4.
Model Fit Statistics for Different Covariance Structure Models at Wave 1
| Model | AIC | BIC | −2 * Log(LR) | r | Difference χ2 (df) | p |
|---|---|---|---|---|---|---|
| Unrestricted | 2775.8 | 2834.0 | 2733.8 | 21 | 28.4 (19) | .076 |
| 1 Factor | 2769.6 | 2802.8 | 2745.6 | 12 | 17.6 (10) | .062 |
| 1 Factor – Equal ε | 2767.4 | 2786.8 | 2753.4 | 7 | 8.8 (5) | .117 |
| CSH | 2764.0 | 2783.4 | 2750.0 | 7 | 12.2 (5) | .032 |
| CS | 2766.2 | 2771.7 | 2762.2 | 2 |
Note: r = number of covariance parameters in the model. Models: Unrestricted – All variances and covariances free to vary; 1 Factor – Correlations constrained to fit one factor model with error variances free to vary across passages; 1 Factor Equal ε – Correlations constrained to fit one factor model with error variances constrained equal across passages; CSH – Heterogeneous Compound Symmetric; CS – Compound Symmetry model (equal variances and correlations across all passages). Difference χ2 is the difference between −2*Log(Likelihood Ratio) for the model in question and the CS model; df is the difference in the number of covariance parameters between the two models.
More importantly, readability indices have limited utility for predicting oral reading fluency differences across stories. Ardoin, Suldo, Witt, Aldrich, & McDonald (2005) investigated the validity of eight reliability formulas as predictors of student’s WCPM. The stories were from a reading program used in both third and fourth grade. The stories were retyped and readability estimates were calculated for 40, 100, and 150 word passages. Students were presented stories in a counterbalanced order and read the passages for one minute. Analyses were conducted using all three levels of word count to determine which, if any, of the readability formulas accurately predicted the WCPM. Two readability formulas, the Forecast and the FOG, were the top two predictors with the Spache and Dale-Chall being the worst two predictors. Even the best predictors had only modest correlation with WCPM.
The real issue is not which readability formula to use, but rather whether the equating of passages through a readability formula is sufficient to guarantee comparability in the distribution of WCPM such that passages can be considered substitutable for one another. In order to verify text equivalence with respect to WCPM performance, data are needed to demonstrate that the distribution of WCPM performance does not differ across different CBM texts. That is, one must demonstrate that individual students obtain similar WCPM scores on passages identified as being equivalent with respect to difficulty level. Thus, a complete evaluation of text difficulty requires a study design that can test for equivalence in the performance distributions across different stories and thereby empirically validate that the stories are equivalent. Because students will read from different passages at different times in the year, the lack of such data demonstrating equivalence of the score distributions for different passages threatens the validity of the CBM assessment as a measure of student growth and the utility of CBM to identify students needing additional instruction.
Individual Growth Models in Progress Monitoring
Fundamental to progress monitoring as implemented through CBM is the idea of fitting individual regression lines to students’ data. The slope of the individual’s regression line becomes the measure of progress for each student and criteria are established for judging whether the slope of the line is adequate for the student to meet end-of-year achievement objectives under the current instructional milieu. This approach to progress monitoring has been made possible by advances in statistical theory and statistical computing related to individual growth modeling, arguably one of the most important advances in statistical science as it relates to psychology and education in the last twenty years.
The foundation for current approaches to individual growth models lies in random coefficient regression models as articulated by Laird and Ware (1982). The conceptual and mathematical framework for individual growth models in the study of change was laid out for psychologists and educational researchers in seminal papers by Rogosa, Brandt, and Zimowski (1982), Rogosa and Willett (1985), Willett (1987) and Bryk and Raudenbush (1987). However, popularity for individual growth models in education and psychology exploded with the development of multi-level modeling software and the clear explication of individual growth models as special cases of multi-level models in Bryk and Raudenbush (1987). We do not review here the statistical or conceptual underpinnings of this framework that are by now well known to educational researchers. Rather we focus on the psychometric requirements of dependent measures employed in individual growth models, as these are often overlooked and can have significant implications for the validity of inferences that are based on the estimated parameters of the individual growth model. References on individual growth modeling (Bryk & Raudenbush, 1987; Burchinal & Appelbaum, 1991; Francis et al., 1991; Rogosa, Brandt, & Zimowski, 1982; Willett, 1987) routinely cite the need for a dependent measure that is expressed on a constant metric, but only a few elaborate on what it means for this requirement to be met psychometrically (Francis et al., 1996; Mehta, Neale, & Flay, 2004; Mehta & Neale, 2005). Some of the information that follows is inescapably technical in nature. We have tried to reduce the demands posed by the equations by providing the reader with verbal explanations immediately after their introduction.
As mentioned previously, the use of individual growth models to estimate learning rates requires that observed scores are expressed on a constant metric. In fact, this requirement concerns the relationship between observed scores and the latent ability the observed scores are presumed to measure. This requirement has been referred to as measurement invariance and is related to the notion of measurement invariance in the factor analytic sense. However, we will see that the measurement invariance required by individual growth curve modeling is more stringent than the measurement invariance required in factor analytic models that do not impose constraints on latent variable means. In order to discuss the measurement invariance requirement of individual growth models, it is helpful to distinguish among four related quantities: (a) observed fluency rates, (b) true fluency rates, (c) observed rates of change in observed fluency rates, and (d) true rates of change in true fluency rates. In using CBM to monitor student progress and make decisions about students who are at-risk, the quantities of interest are (b) and (d), the true fluency rate and the true rates of change in true fluency rates, respectively. However, it is the quantities (a) and (c) which are available to researchers and practitioners. Measurement invariance is a necessary precondition for (a) and (c) to provide unbiased information about (b) and (d), and the basis for this requirement is apparent in the relations among the four quantities. Because these relations are mathematical in nature, it is helpful to introduce several equations in order to make these relations explicit. We begin with Equation (1) which describes the relation between observed reading rates and true reading rates.
| (1) |
Equation (1) describes the relation between the observed reading rate (Yikt) for a particular person (subscript i) on a particular test form (subscript k) at a particular point in time (subscript t) to that person’s true reading rate (ηit) at the same point in time. In order to develop the relations of interest, we make several standard assumptions. The role of the assumptions is to help keep the mathematical relations as simple as possible, that is, the assumptions could be relaxed and our principal findings would still hold, but the mathematics for proving the relations would be more complex. Thus, we assume that the errors of measurement for each and every test form (εikt) have a mean of 0 at every time point, and that the errors of measurement are independent of the true reading rate within and across time. We further assume that error variance for any particular form is the same at all time points, V(εkt)=V(εk). This latter assumption implies that the magnitude of error variability in the observed scores is the same regardless of when a form is used. Finally, we arbitrarily scale the true reading rate such that it is expressed as a deviation from the grand mean of the true reading rates at some specific point in time of interest, which we designate as t*.
Under these standard and simplifying assumptions, the intercept term in Equation (1), αk, indicates the expected reading rate on form k for an individual whose true reading rate at time t is equal to the grand mean of the reading rates at time t*. A person whose true reading rate (ηit) at time t exceeds the average reading rate at time t* by 10 words per minute would be expected to obtain a reading rate, Yikt, on form k at time t that is equal αk + 10λk.
Equation (1) describes a simple measurement model in the factor analytic sense, where λk is the factor loading that describes the regression of observed reading rates at time t on the true reading rates at time t, whereas αk provides the intercept term in that regression equation. It may be easiest to see Equation (1) as a measurement model in the factor analytic sense if one considers measuring reading rates using multiple forms at a single point in time, The only difference between Equation (1) and a standard factor analytic measurement model is the inclusion of the intercept term, αk., which is a necessary addition to allow the model to describe the means of the measures. If we were only interested in understanding the variances of the measures, the intercept term could be ignored, but the monitoring of progress using CBM and individual growth models requires that our measurement model capture the means of the observed measures as well as their variances and covariances. In fact, the form specific terms αk and λk play very important roles in determining the mean and variance of the observed reading rates at time t for form k. Specifically, the population average in observed reading rates and the population variance in observed reading rates at time t on form k will be:
| (2) |
| (3) |
What are the implications of the foregoing specifications and assumptions with respect to measuring the true reading rate, η, at time t with a particular form k? While one might assume that the assumption that V(εkt)=V(εk) implies that form k provides an equally precise measure of true reading rates at all time points, such is not the case. In fact, when coupled with the specification that λk does not vary across time, the assumption that V(εkt)=V(εk) implies that the reliability and validity of form k will vary over time as a function of the variance in true reading rates. Following Bollen (1989), the validity coefficient for a measured variable, such as Yk in Equation (1), is a function of its direct relation to the latent variable that it measures. Similarly, we define the reliability of Yk at time t as the proportion of variance in observed scores at time t that is due to variance in the true reading rates at time t. Given these definitions, it can be seen that both the reliability and validity of inferences based on scores from form k will vary only as a function of λk, V(ηt), and V(εk). That is αk is not a factor in determining either the reliability or validity of Yk at time t. Specifically, the reliability and validity of form k for measuring the reading rate at time t are given by:
| (4) |
| (5) |
Equation (4) and Equation (5) show us that, given the specifications to this point, reliability and validity for a particular form will vary over time as the variance in true reading rates changes over time. This conclusion follows directly from the fact that the variance in true reading rates (V(ηt)) is the only quantity in Equation (4) or (5) that is assumed to vary over time. All other components of Equation (4) and Equation (5) are specified or assumed constant with respect to time, although they may differ across test forms.
While the implications of Equation (4) and Equation (5) for the reliability and validity of a particular form over time are of some interest, more important are their implications for the reliability and validity of different forms at a given point in time. Specifically, the set of Equations (2–5) make it quite clear that unless αk, λk, and V(εkt) are the same for all forms, then means and variances of observed reading rates, and the precision with which true reading rates are measured, will vary depending on the form used at any particular point in time. Clearly, if αk, λk, and V(εkt) are the same for all forms, then the forms can be substituted for one another without regard for time or form, because reliability and validity at a given point in time will be unaffected by the choice of form, and scores collected using different forms at different points in time will differ only because of changes in the mean and variance in the true reading rates over time. In contrast, if only λk, and V(εkt) are the same for all forms, then all forms will have the same reliability and validity at any given point in time, but the forms will not be strictly substitutable for one another. Specifically, scores from different forms used at the same time point will differ on average because of differences in intercept terms, αk, across forms, while the scores collected on different forms at different points in time will differ on average because of both differences in the intercept terms for different forms and because of changes in the mean of the true reading rates over time. Moreover, variability in observed reading rates will differ over time because of differences across forms in the relationship between observed scores and true reading rates (λk) and differences in error variance (V(εk)), but also because of differences over time in the variance of true reading rates (V(ηt)). In fact, if individuals differ from one another in their rates of progress (i.e., in the rate of change in their true reading rates), then the variance in true reading rates must change over time (Bryk & Raudenbush, 1987; Willett, 1987).
What is less clear from Equations (1–5) is how differences in the terms of Equation (1) across CBM forms will impact the estimation of individual rates of change in true reading rates. Recall that the goal of progress monitoring is to use serial assessments to estimate the rate of growth in the oral reading fluency of each child and to select those children whose rate of growth indicates inadequate development to achieve end of year benchmarks. While CBM assessments given at a particular moment in time are intended to estimate the true reading rate for a student at that point in time, the use of CBM assessments over time is for the express purpose of estimating individual rates of change in the true reading rates. If each term with a k subscript on the right hand side of Equation (1) is, in fact, equal for all values of k, thereby allowing the k subscript to be dropped from Equation (1), then the forms can be substituted for one another. In that case, differences in the expected values of observed scores over time for individual students will be attributable entirely to differential rates of change in children’s true reading rates (ηi). However, in the more plausible scenario that differences exist across CBM forms in the terms of Equation (1), what are the consequences for estimating individual rates of growth (πi) in reading rates?
To understand the consequences of differences across CBM forms in the right hand terms of Equation (1), we must first develop the model for change over time in ηi, and then determine its implications for models of change in observed reading rates (Yi) given Equation (1) and the relation between observed reading rates and true reading rates. The standard model for change employed in progress monitoring systems is one of linear growth. The linear growth model is the simplest model for change and is easily described mathematically. Here we employ the common notation of individual growth models employed in other multi-level modeling references (Bryk & Raudenbush, 1987; Francis et al., 1991; 1996), with the only change being that we are describing a model for linear growth in true reading rates (ηi) rather than observed reading rates (Yi).
| (6) |
Equation (6) provides a model for linear growth in reading rates that is child specific, as evidenced by the person subscripts, i, on the growth parameters, πoi and πli. The model is written in such a way that πoi represents the expected true reading rate for person i at time t*, whereas πli indicates the rate of change in the child’s true reading rate for a one unit increment in time. Time is indexed by the variable t, which is subscripted for both person and time. The value of time given by t* is chosen for ease of interpretation of πoi, such as the end of the year, while the units for time are chosen to coincide with the timing of assessments, e.g., weeks, months, or intervention sessions. The model described by Equation (6) further stipulates that true reading rates might not be perfectly described by this linear model and therefore includes an error term, Rit, which simply reflects the extent to which the true reading rates do not fall precisely on the line described by πoi + πli(tit – t*). We make the standard assumptions that the growth parameters, πoi and πli, are multivariate normally distributed with mean vector μ and variance-covariance matrix τ, while the Rit are assumed normally distributed with mean 0 at each time point and variance-covariance matrix Σ. For simplicity, we assume here that the Rit have constant variance and are not correlated over time, but what follows can be generalized to more complex variance-covariance structures for Σ.
To understand the implications of Equation (6) and Equation (1) for modeling growth in observed reading rates, we substitute Equation (6) into Equation (1) for ηit. Equation (7) provides a model for growth in observed reading rates, given that true reading rates are changing linearly over time at rates that differ from one student to another, that true reading rates are imperfectly measured by observed reading rates, and that the relation between observed reading rates and true reading rates differs across forms as reflected in Equation (1).
| (7) |
In Equation (7), we have bracketed the model parameters that relate to the intercept, the rate of growth, and the error term. It is important to keep in mind when considering Equation (7), that the terms of Equation (7) are parameters, and not estimates. While estimation introduces uncertainty into the process, we are also concerned about differences between the parameters of Equation (7) and the parameters of interest, namely those of Equation (6). In fact, the problem that confronts us is that we would like to estimate the parameters of Equation (6) directly, but the necessity to work with observed reading rates rather than true reading rates forces us to estimate the parameters of Equation (7) instead. Thus, it is instructive to consider how the parameters of Equation (7) relate to the parameters of interest in Equation (6), and in particular to consider when the two are equal.
In examining Equation (7), one can see that the form parameters αk and λk both contribute to the intercept term of the model, while the form parameter λk interacts with the rate of change in true reading rates, and with the error component from Equation (6). It is perhaps easiest to see how the presence of these form parameters distort the growth model if we consider a scenario where different students are measured on different forms, but all students use the same form each time they are tested. Under such a testing scenario, the same form parameters would contribute to each score obtained on a particular student, but different form parameters would contribute to the scores of different students. In this case, a student being tested on an easier form, i.e., one with larger αk, would have a higher expected reading rate at time t* than a student with the same true reading rate who was tested on a more difficult form. Likewise, two students with the same rate of growth in true reading rates (πl) would have different expected rates of growth in observed reading rates (λkπli) because of differences in the regression coefficients that relate observed scores to true reading rates (i.e., the λk). Specifically, the student who read the form with the smaller λk would have a lower expected rate of growth in observed reading rates even though both students’ true reading rate is progressing at the same rate of change.
While this testing scenario makes it easier to talk about the consequences of having to work with the model of Equation (7) instead of Equation (6) for estimating growth in reading rates, it is an unlikely scenario. The more likely scenario is one where students use different CBM forms on different testing occasions. Under these circumstances, the precise impact of using different forms over time on the estimation of individual rates of growth will depend on several factors. Specifically, the impact will depend on the extent to which the CBM form parameters in Equation (1) differ across forms, differences across students in when they are tested on particular forms, and whether or not all students are tested on the same form at any given point in time. In general, it is safe to say that the parameters of Equation (7) will not equal the parameters of Equation (6) for any given student when the form parameters in Equation (1) are not strictly equal across forms.
The current study was designed to test the comparability of CBM passages using DORF with second grade students in order to assess the extent to which students’ level of performance and/or rate of growth might be expected to vary as a consequence of the passages that they are asked to read at particular points in time. If WCPM is highly correlated across passages, and passages do not differ in their distribution of WCPM (mean, variances, and distribution shape), then passages can be substituted for one another without requiring adjustment to the observed WCPM. If passages differ in the distribution of WCPM, then some method must be employed to adjust out these form effects on the distribution of WCPM scores. Thus, this study was designed to examine the effects of passage (i.e., test form) and presentation order on students’ WCPM scores as measured with the DORF passages.
Method
Setting and Participants
Two schools in a large urban school district in Texas were selected to participate in this study. A total of 134 students in second grade were tested, 85 from school one and 49 from school two. Collectively, there were 69 female students and 65 male students. Both schools represented an ethnically diverse student population as well as one of relatively low socio-economic status as defined by the number of students receiving free or reduced lunch. The ethnic composition was 31% African-American, 3% Asian, 57% Hispanic, and 9% Caucasian, with 80% economically disadvantaged. All students in the general education reading classroom participated in the study regardless of special status (e.g., limited English proficiency or special education) and were receiving their literacy instruction in English.
Measures
We used DIBELS oral reading fluency (DORF) (Good & Kaminski, 2002a) to measure students’ reading rate. There are a total of 29 passages in second grade, 20 stories are read in order throughout the school year, nine stories serve as benchmarks for the beginning, middle, and end of the year. These stories are considered equivalent according to the technical manual and suitable for grade 2 students. For the purposes of this study, six passages were randomly selected from the 20 stories that are read throughout the school year. The six passages chosen for inclusion in the study were: I'm a Good Babysitter; The New Bookstore; Color of the Rainbow; Going to the Movies at Home; Going to the Swimming Pool; and Twins. These six randomly selected stories had an average Spache readability of 2.65 with three at 2.6 and three at 2.7 (Good & Kaminski, 2002b). The six DORF passages were used intact, i.e., they were not modified for the sake of the current study.
Table 1 presents a schematic of the overall research design. The six DIBELS passages were arranged into six possible orderings so that each passage appeared in each position (e.g., first, second, etc.), and students were randomly assigned to read the stories in one of these six orders (A–F) described in Table 1. Thus, each student read each passage one time, and all of the students assigned to a particular order read the passages in the same order. This design allows for tests of passage effects, order effects, and interaction of passage with order, but does not allow for tests of sequence effects. To test for sequence effects would have required that many more sequences be used, and therefore would have required many more students. Thus, we opted to design the study to test for the more common effects of passage, order, and their interaction.
Table 1.
DIBELS Passages Grouped into Sets of Three with Six Counterbalanced Orders
| Group | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| A | Twin | Color | Baby | Book | Pool | Home |
| B | Color | Baby | Book | Pool | Home | Twin |
| C | Baby | Book | Pool | Home | Twin | Color |
| D | Book | Pool | Home | Twin | Color | Baby |
| E | Pool | Home | Twin | Color | Baby | Book |
| F | Home | Twin | Color | Baby | Book | Pool |
Table Note: Passages in columns 1–3 were read in order in one sitting, while passages in columns 4, 5, and 6 were read individually on three subsequent occasions separated by 2 weeks each. Passages were read in the order indicated in the Table for all students assigned to a given group (A–F). Passages appearing in columns 1 and 4 were not both read by any group of children in Wave 1. Thus, correlations between these three pairs of passages cannot be computed from the data at Wave 1. These passages are italicized in the table for ease of identification.
Students read the six DIBELS passages over the course of seven weeks from November to December. In week one, students were given the first three DIBELS passages that appeared in the order to which they had been assigned. These passages are numbered 1, 2, and 3 in Table 1 for each group A–F. In each of the remaining six weeks (i.e., Waves 2–4), students read one additional DIBELS passage, in each case reading the passage that appeared next in the fixed order to which the student had been assigned (i.e., passages 1,2, and 3 were read on the first day, passage number 4 was read in week 3, passage number 5 in week 5, and passage number 6 in week 7). We first examine performance from the first assessment, when students read the first three of the six passages (i.e., those numbered 1, 2, and 3 in Table 1). These three passages were read in a single sitting. Thus, one can legitimately infer that there has been no true change in students’ reading ability over the span of time that took place between reading the first and third passage, a span of roughly five minutes. Rather, any significant differences in performance across passages at Wave 1 must be due to (1) passage effects, (2) order effects, and/or (3) their interaction. In contrast, it is possible that students will experience gains in true oral reading fluency over the ensuing seven weeks represented by Waves 2–4. Consequently, we also employed individual growth models to examine the effects of passages on patterns and/or rates of growth in oral reading fluency from Waves 1–4.
Procedures
Three research assistants were trained in correct administration procedures for the fluency measures. A pair-wise inter-rater reliability of .85 was established between the three research assistants and the first author. The assistants went to the schools to administer the oral reading fluency measures once every two weeks. At the first school, the assistants sat in the back of the classroom to administer the assessment to students individually. In the second school, a common testing area was used by all three assistants instead of the classroom.
The research assistant placed the passage in front of the student and stated, “Please read this out loud. If you get stuck, I will tell you the word so you can keep reading. When I say ‘stop,’ I may ask you to tell me about what you read, so do your best reading. Start here. Begin.” Students read for one minute while the research assistants noted errors on a record sheet. Words correct per minute (WCPM) was calculated using the criteria provided in the DIBELS manual. Although students were advised that they might be required to answer questions after a passage, no questions were asked as part of the study. After reading the passage numbered 1 in Table 1 for their group (A–F), the student then read the passage numbered 2 for one minute, followed by the passage numbered 3.
In addition to reading the DORF passages, students had also been administered a word reading list and a story passage from the Texas Primary Reading Inventory (TPRI: Foorman, Fletcher, & Francis, 2004) at the beginning of the school year. The TPRI uses a list of 15 words read aloud to place students into an appropriately leveled story for assessing reading comprehension and oral reading fluency. Children read from one of five TPRI passages depending on the number of words read from the word list. Approximately 75% of the students read the same story, Story 4, from the set of second grade passages, with another 10% reading Story 1, and approximately 7% reading each of stories 2 and 3. Fewer than 1% of the students read a passage from the end of Grade 1. TPRI fluencies ranged from 22 to 145 words per minute, with a mean of 59.9 and standard deviation of 26.4. Correlations between the TPRI fluency rates and DIBELS fluency rates were .88, .86, .69, .75, .82, and .84 for DIBELS stories 1–6, respectively, on the first occasion of measurement. All correlations are statistically significant at p < .0001.
Design and Analysis
Oral reading fluency scores (i.e., WCPM) from the first wave of data collection were analyzed using the mixed model approach to repeated measures analysis of variance through SAS PROC MIXED (Littell, Milliken, Stroup, & Wolfinger, 1996). Despite random assignment of students to study groups, an analysis of TPRI fluency scores indicated that the six groups differed somewhat in oral reading fluency (F(5,112)=3.05, p<.009). Consequently, fluency scores on the TPRI were used as a covariate to adjust for any between group differences in ability. Further, the model included fixed effects for passage (1–6), presentation order (1st, 2nd, or 3rd), and the interaction of passage and order. Statistically significant differences among passages in this analysis were followed up by testing pair-wise comparisons using the adaptive version of the Benjamini-Hochberg false discovery rate (FDR) with FDR = .05 (Benjamini & Hochberg, 1995; 2000).
Before examining fixed effects for passage, presentation order, and their interaction, we fit a series of models with different error structures in order to determine an appropriate covariance structure for the Wave 1 data. All models took into account the fact that observations made on the same subject are not independent of one another. Failure to account for this within-subject correlation can lead to incorrect statistical inferences about the fixed effects in the model due to bias in the estimation of the standard errors. We used Akaike’s Information Criterion (AIC), the Bayesian Information Criterion (BIC), and a comparison of likelihood ratio tests to select an appropriate covariance structure for the Wave 1 data, and then used that model to examine effects of passage, presentation order, and their interaction.
Following analysis of the Wave 1 data, we conducted an individual growth curves analysis of changes in oral reading fluencies across the four waves of data to determine if patterns and/or rates of growth differed across the six study groups. These analyses were also conducted using PROC MIXED in SAS. If the passages function equivalently, then patterns and rates of growth should not differ by study group. The individual growth models included effects for TPRI fluency, wave, and group (A–F), and the interactions of TPRI with group, and of wave with group. Wave was treated as a continuous measure centered at 2.51, and thus provided an estimate of the linear rate of change in oral reading fluency rates over the four waves, while the intercept of the growth model reflected the student’s expected fluency midway through the study. Parameterized in this way, the interaction of wave with group provided a test of differences in rates of change in oral reading fluency as a function of the order in which passages were read over the four waves of data collection. Random effects (i.e., variances and covariances) for intercepts and slopes were estimated, but constrained equal across the six study groups.
In order to complete the individual growth curve analysis, we had to first obtain a single estimate of children’s fluency at Wave 1, where the children had read three passages. To do so, we employed the commonly recommended CBM practice of selecting the student’s median oral reading fluency, and evaluated this practice in terms of the relative frequency with which each passage was selected within a study group. If passages function equivalently, then within a study group, each passage should be equally likely to be chosen as the passage yielding the median oral reading fluency. Thus, in all, we will present three sets of analyses designed to examine equivalence across the DORF passages, and the extent to which non-equivalence among passages might impact on decisions made about students’ oral reading fluency rates and progress. Rejecting the equivalence hypothesis in each of these three analyses, we then attempted to create a scale score metric in order to remove these form effects on estimates of students’ oral reading fluency rates. Specifically, we demonstrate how equipercentile equating can be used to create a scale score metric that will remove form effects from raw scores, but still yield scores on an easily interpretable metric that would be useful and familiar to teachers.
Results
Descriptive statistics for WCPM disaggregated by passage and wave are presented in Table 2. As can be seen in Table 2, fluency rates varied considerably within passage as evidenced by the magnitude of the standard deviations, as well as between passages as evidenced by the differences among means in the column labeled Total in Table 2. In fact, mean fluency rates at the first assessment ranged from 67.9 to 93.9 (M = 83.0, SD = 34.5) across the six passages, with the most difficult passage being The New Bookstore and the easiest being Going to the Movies at Home. Thus, the largest observed mean difference across passages is over 15 words correct per minute. In contrast, mean reading fluency rates ranged from 82.0 to 85.6 as a function of wave.
Table 2.
Descriptive Statistics: Observed Means and Standard Deviations
| Wave | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | Total | ||||||
| Passage | Mean1 | SD1 | Mean | SD | Mean | SD | Mean | SD | Passage Average | SD |
| BABY | 74.3 | 30.7 | 105.2 | 34.3 | 93.9 | 38.5 | 87.1 | 38.3 | 83.6 | 35.2 |
| N | 69 | 18 | 19 | 18 | 124 | |||||
| BOOK | 67.9 | 31.2 | 57.0 | 25.3 | 94.5 | 37.5 | 81.5 | 36.8 | 71.6 | 33.8 |
| N | 65 | 25 | 20 | 15 | 125 | |||||
| COLOR | 87.2 | 32.3 | 97.3 | 34.1 | 83.0 | 35.9 | 88.2 | 37.7 | 88.2 | 33.9 |
| N | 67 | 18 | 19 | 21 | 125 | |||||
| HOME | 93.9 | 36.9 | 87.8 | 33.8 | 79.3 | 29.6 | 75.6 | 27.9 | 86.7 | 34.0 |
| N | 57 | 20 | 23 | 24 | 124 | |||||
| POOL | 84.4 | 34.1 | 78.0 | 31.7 | 71.1 | 20.6 | 103.3 | 33.1 | 83.5 | 32.6 |
| N | 59 | 24 | 22 | 18 | 123 | |||||
| TWIN | 86.7 | 31.1 | 81.1 | 33.7 | 81.0 | 28.9 | 81.6 | 26.6 | 83.9 | 30.2 |
| N | 61 | 20 | 20 | 23 | 124 | |||||
| Overall | 82.0 | 32.5 | 82.5 | 35.0 | 83.4 | 32.5 | 85.6 | 33.6 | 83.1 | 31.2 |
| N | 126 | 125 | 123 | 119 | 126 | |||||
Note. BABY = I'm a Good Babysitter; BOOK = The New Bookstore; COLOR = Color of the Rainbow; HOME = Going to the Movies at Home; POOL = Going to the Swimming Pool; TWIN = Twins.
Correlations of WCPM as measured by different passages at Wave 1 are presented in Table 3. It can be seen from Table 3 that fluency tends to be highly correlated across stories, with correlation coefficients ranging from .87 to .93 (p<.0001). The magnitude of these within-time correlations suggests that the passages have high reliability and validity for assessing oral reading fluency, although these correlations are insufficient to guarantee that passages will function equivalently and provide a constant metric for estimating rates of change in oral reading fluency.
Table 3.
Estimated Correlations Among Stories at Wave 1 along with Least Squares Means and Differences
| TWIN | COLOR | BABY | BOOK | POOL | HOME | |
|---|---|---|---|---|---|---|
| TWIN | 89.0 | −1.3 | 6.3* | 17.8* | 1.6 | −1.3 |
| (2.02) | (2.4) | (2.9) | (3.2) | (2.8) | (2.4) | |
| COLOR | .93 | 90.2 | 7.5** | 19.0* | 2.9 | −0.1 |
| (.018) | (2.21) | (2.5) | (2.9) | (3.4) | (3.0) | |
| BABY | .89 | .96 | 82.7 | 11.5* | −4.6 | −7.6* |
| (.047) | (.012) | (2.59) | (2.5) | (3.1) | (3.8) | |
| BOOK | NE | .92 | .89 | 71.3 | −16.1* | −19.1* |
| (.025) | (.028) | (2.53) | (2.5) | (3.2) | ||
| POOL | .96 | NE | .88 | .90 | 87.3 | −3.0 |
| (.018) | (.040) | (.025) | (2.55) | (2.6) | ||
| HOME | .94 | .93 | NE | .87 | .92 | 90.3 |
| (.015) | (.023) | (.044) | (.021) | (2.74) |
Note. BABY = I'm a Good Babysitter; BOOK = The New Bookstore; COLOR = Color of the Rainbow; HOME = Going to the Movies at Home; POOL = Going to the Swimming Pool; TWIN = Twins. Least Squares Means rounded to first decimal and Standard Errors (in parentheses) are given on the diagonal; Differences in Least-Square Means are computed as Row Variable minus Column Variable rounded to first decimal with standard error of difference (in parentheses) are presented above the diagonal. The False Discovery Rate (FDR) of Benjamini and Hochberg (1995) was used on the least squares mean differences to control for Type I error in testing pairwise comparison across the six passages.
Significant comparison using the FDR procedure. Correlations among measures were estimated from an unrestricted correlation model without TPRI fluency as a covariate at Wave 1 and are given below the diagonal with standard errors (in parentheses); All correlations are significant at p < .0001; NE: Correlation is not estimable at Wave 1 from the design.
Mixed Model Results for Wave 1
In conducting the mixed-model repeated measures ANOVA, we first examined a variety of covariance structures using SAS PROC MIXED (Littell et al., 1996) to arrive at an appropriate covariance structure for the data prior to estimating the effects of passage, order, and their interaction. These different covariance structures have different implications for the correlations among the passages at Wave 1. The inclusion of TPRI fluency as a covariate in the model implies that the covariance structure being modeled is the residual covariance matrix after predicting performance on each passage from TPRI fluency.2
Best fit indicators (Aikake’s Information Criterion and Bayes Information Criterion) for the different covariance structures are presented in Table 4. Based on the information in Table 4, the model of heterogeneous compound symmetry (CSH) was most appropriate for the data. Although the compound symmetry (CS) model produced the lowest BIC and AIC, a comparison of the likelihood ratio statistics for the CSH and CS models shows that the CSH model’s allowance for different error variances across passages produced a statistically significant improvement in fit to the data.
The CSH covariance structure implies that the passages cannot be considered equivalent. If the passages were equivalent, i.e., substitutable, then the correlations among all pairs of passages would be equivalent and the error variances of all passages would be equivalent, which implies that the appropriate model would be one of homogeneous compound symmetry (i.e., Model CS). Rejection of the CS covariance structure indicates that the parallelism hypothesis is not supported3.
We next examine evidence for differences in mean oral reading fluencies across the six passages using the CSH model as the basis for tests of these fixed effects. Tests of significance for the fixed effects in the CSH model are presented in Table 5. Examination of Table 5 shows that the TPRI fluency measure strongly related to the DIBELS oral reading fluency measures. Nevertheless, despite controlling for fluency as measured by TPRI, significant effects of passage were found at Wave 1 (F(5,219) = 15.3, p< .0001). In contrast, presentation order was not statistically significant, and did not interact with passage effects. Least Squares Means for each of the six passages as estimated from the CSH model are presented above the diagonal of Table 3. It can be seen from the Least Squares Means that one passage is substantially more difficult than the others (viz. Book) with a mean fluency of 71 WCPM, while a second passage (viz. Baby) is somewhat more difficult than the other four with a mean WCPM of 83. The remaining four passages are quite comparable on average, with means ranging from 87 to 90 words per minute. Using the FDR (Benjamini & Hochberg, 1995), we find that, in fact, fluency rates are lower for Book than for each of the other five stories (FDR p < .00030), while fluency rates are lower for Baby than for Color (FDR p < .006). Although raw p values for comparing Baby with Twin and Home were less than .05, the FDR adjusted p values were not. In the interests of space, we present the tests of significance for fixed effects and Least Squares Means for the CSH model. However, conclusions about the fixed effects were identical across the five models for the covariance structure presented in Table 4. While the actual Least Squares Means and standard errors vary somewhat across the different models, these differences tend to be small with only minor changes in tests of significance. Thus, the conclusions presented here regarding differences across passages at Wave 1 are invariant across a wide array of assumptions about the error covariance structure of the model.
Table 5.
Analysis of Variance for Fixed Effects from CSH Model of Wave 1 Data
| Effect | Num DF | Den DF | F Value | p < |
|---|---|---|---|---|
| TPRI fluency | 1 | 116 | 225.8 | .0001 |
| Passage | 5 | 219 | 15.3 | .0001 |
| Presentation Order | 2 | 219 | 2.44 | .0899 |
| Passage X Pres. Order | 10 | 219 | 0.77 | .6566 |
Analysis of Individual Growth
While the Wave 1 results indicate that the passages cannot be considered equivalent in terms of means and variances, the question remains as to whether these differences have implications for estimation of growth in the progress monitoring context. To investigate the latter question, we fit individual growth models to the data from all four waves. In order to do so, we first had to derive an estimate of reading fluency at Wave 1 for each child based on the three passages that the student had read at that wave. Rather than take the mean fluency from the three passages, we followed the recommended CBM practice of selecting the median oral reading fluency from the three passages read by each child.
Table 6 shows the number of times that each passage was selected as the passage yielding a child’s median oral reading fluency. If the passages function equivalently, then it should be the case that each passage is equally likely to be chosen as the passage yielding the child’s median fluency. However, as can be seen in Table 6, some passages are much more likely to yield a child’s median fluency than are others. Not surprisingly, the passage Book is almost never the passage yielding the median fluency for a child, while the passage Baby is almost always chosen for group B when it is paired with a relatively easy passage (Color) and the difficult passage Book. To test if the passages are equally likely to yield a child’s median fluency we computed a chi-square statistic for the row associated with each Group as well as for the row marked Total in Table 6. The chi-square for Group B was statistically significant (χ2(2) = 10.9, p < .004), as was the chi-square for the total row. The latter statistic had to be computed by hand due to the unequal expected cell counts (i.e., the total number reading a given story divided by 3) and was found to be 11.655 with df = 5, p< .039. These results indicate that the passages are not equally likely to yield a students’ median fluency, further corroborating the conclusion that the passages are not equally difficult.
Table 6.
Number of Students in each Group who obtained their Median Oral Reading Fluency on a Particular Passage at Wave I
| Group | Twin | Color | Baby | Book | Pool | Home | Total |
|---|---|---|---|---|---|---|---|
| A | 8 | 11 | 5 | --- | --- | --- | 24 |
| B | --- | 5.5 | 15.5 | 3 | --- | --- | 24 |
| C | --- | --- | 11 | 3 | 7 | --- | 21 |
| D | --- | --- | --- | 4 | 5 | 11 | 20 |
| E | 9 | --- | --- | --- | 4.5 | 4.5 | 18 |
| F | 8.5 | 4.5 | --- | --- | --- | 6 | 19 |
| Total | 25.5 / 61 | 21 / 67 | 31.5 / 69 | 10 / 65 | 16.5 / 59 | 21.5 / 57 | 126 |
Note: Thirteen students obtained the exact same fluency score on two passages. These students are counted as contributing .5 to the number of students who obtained their median fluency on each of the two stories that yielded that fluency score. The Total row gives the number of students who obtained their median fluency on a particular passage divided by the number of students who read that passage at Wave 1.
Taking each student’s median frequency at Wave 1 as their score at that wave, we then fit an individual growth model to the four waves of data using SAS PROC MIXED. The model again included TPRI fluency as a covariate. However, in this case, the model included effects of wave, study group, and the interaction of wave with study group, and the interaction of TPRI with study group. Wave was treated as a continuous measure and thus served to estimate the constant rate of change in oral reading fluency across the seven weeks of data collection. The interaction of wave with study group thus reflects the extent to which groups are estimated to have different rates of growth in their oral reading fluency. In so far as group membership was assigned at random and simply reflects the order in which stories were read across the four waves of data collection, and in so far as we have also included the covariate of TPRI fluency in the model, there should be no interaction of group with wave unless the ordering of the stories across the four waves of assessment affects the estimation of the rate of growth. Tests of significance for fixed effects in the model are included in Table 7.
Table 7.
Analysis of Variance for Fixed Effects from Individual Growth Model
| Effect | Num DF | Den DF | F Value | p < |
| TPRI fluency | 1 | 110 | 178.25 | .0001 |
| Wave | 1 | 109 | 1.17 | .2824 |
| Group | 5 | 106 | 1.55 | .1800 |
| TPRI fluency X Group | 5 | 110 | 0.40 | .8497 |
| Wave X Group | 5 | 109 | 8.38 | .0001 |
| Random Effects for Individual Growth Model | ||||
| Effect | Estimate | Standard Error | Z – value | p |
| Intercept | 273.9 | 45.9 | 5.97 | .0001 |
| Wave | 3.45 | 11.8 | 0.29 | .3849 |
| Cov(I,W) | 6.18 | 15.5 | 0.40 | .6895 |
| Corr(I,W) | .2010 | |||
Note: Wave = slope or constant rate of change; Cov(I,W) = Covariance of Intercept and Slope parameters; Corr(I,W) = correlation of Intercept and Slope parameters.
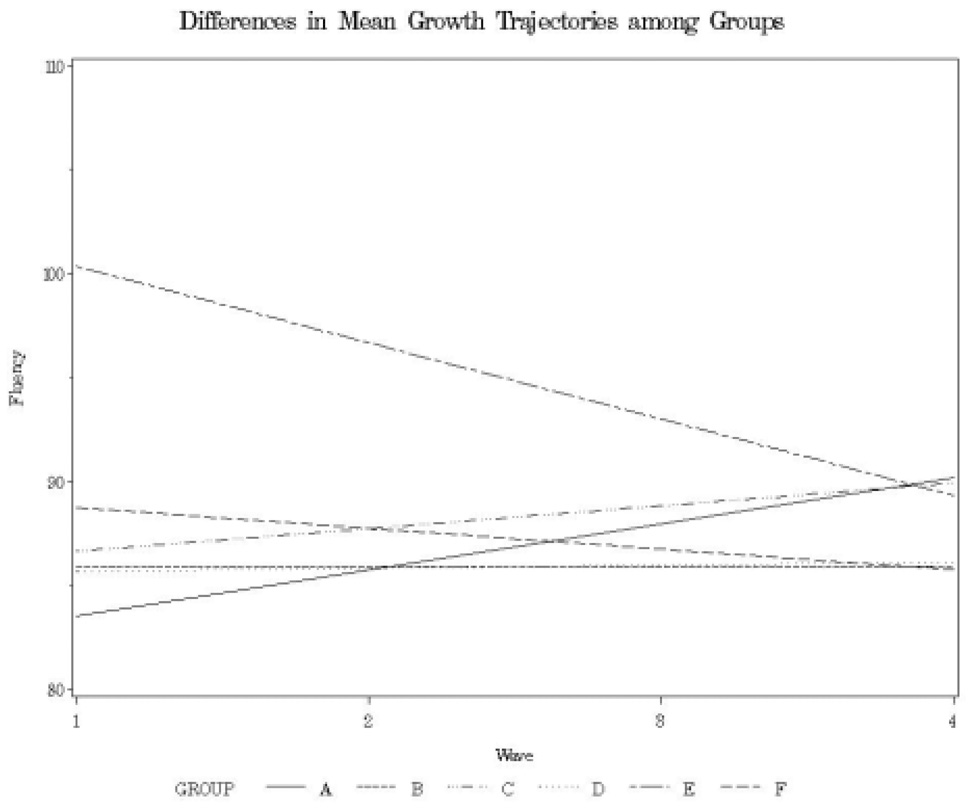
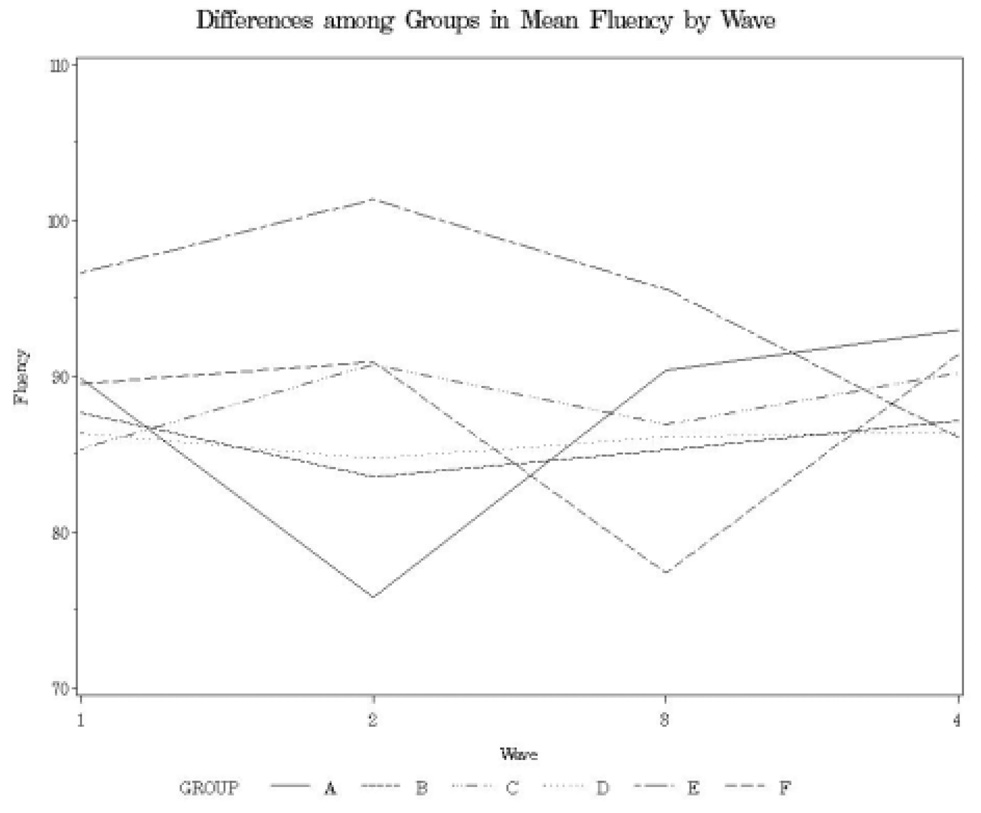
Examination of Table 7 shows that TPRI fluency did not interact with study group, nor were there significant main effects of wave or study group (F(5,110) = 0.40, p = .8497, F(1,109) = 1.17, p = .2824, and F(5,106) = 1.55, p = .1800, respectively). That is, oral reading fluency rates are not changing on average over the seven weeks of the study, nor do the groups differ on average in their oral reading fluency at the mid-point of the four waves, once TPRI fluency is controlled. However, there were significant differences across study groups in the rate of change as evidenced by the significant group by wave interaction (F(5,109)=8.38, p < .0001). To understand the Group by Wave interaction, mean growth curves are plotted for the six study groups in Figure 1. Figure 1 illustrates that groups five and six, which received Book in Waves 4 and 3, respectively, have the appearance of negative growth, while group 1, which received Book in Wave 2 has the appearance of positive growth. The impact of the placement of the more difficult stories can be seen more clearly by graphing the means for each group across the four waves (see Figure 2). Figure 2 illustrates that the slopes of the growth trajectories are significantly influenced by the placement of the more difficult stories. In Figure 2, it is easily noted that Book has little impact on groups two, three, and four. These three groups received Book in Wave 1 where students read three stories, and as we have already seen, few students obtained their median score on this passage.
Figure 1.
Differences in Mean Growth Trajectories among Groups
Figure 2.
Differences among Groups in Mean Fluency by Wave
Creating a Scale Score Metric to Equate Passages
Taken together, the three sets of analyses indicate that the six forms examined here are not substitutable without consideration of scaling differences, thus supporting the first hypothesis. Whereas scores are highly correlated across different forms, mean and variance differences across forms are not ignorable for the purpose of estimating rates of growth for individual children. These form differences should be taken into account in reporting fluency rates for individual students and classrooms, and especially in progress monitoring of student growth in fluency.
The reason for this recommendation is simple. The high correlation tells us that students’ relative standing is only minimally different when comparing one form to another. However, the substantial mean and variance differences across forms indicate that actual WCPM scores will vary on average from one passage to the next, and relative differences will vary in magnitude as well. Thus, substantial fluctuations in scores can be expected due to form differences when different forms are used from one week to the next. Without some correction for these form effects, teachers run the risk of misinterpreting gains and losses in WCPM as gains and losses in student fluency when, in fact, they are little more than expected differences resulting from the use of easier or more difficult passages from one week to the next.
One approach to removing form effects from the WCPM scores is to create a scale score metric for reporting fluency such that the reported scale scores take into account the difficulty of the specific passage that was used to assess fluency. There are numerous approaches to creating scale score metrics (Angoff, 1967; Kolen & Brennan, 1995). We develop scale scores for the six forms by adjusting all scores to coincide with expected fluency rates from the passage Home. In this way, the scaled score tells us the WCPM rate that would have been obtained if students had read Home rather than the particular passage that they actually read. Home is the easiest of the six stories. The reason for equating WCPM scores back to the easiest form has the benefit that scores will tend to be adjusted upward (i.e., increasing the reported words correct per minute), so that students and teachers are less likely to feel that the student has been penalized by reading a passage more difficult than Home, which could be the case if students’ scores were adjusted downward.
Raw score conversion
In order to equate WCPM scores across the different stories, we used an equipercentile equating method rather than linear equating. Linear equating would adjust scores for differences across forms in the mean and standard deviation, such that the resultant scale scores for different forms will have the same mean and standard deviation. However, linear equating assumes that the same adjustment should be made throughout the distribution of WCPM scores in order to equate fluency scores taken from different stories. In contrast, equipercentile equating is more general than linear equating in that it allows that the relation between the two forms may change across the range of scores on the base form, which in this case is Home. For example, it could be that Home is more difficult over one score range than the passage to be equated, but easier over another score range. Alternatively, it could be that the difference between forms is not consistent throughout the range of WCPM scores such that one adjustment is needed for the lowest scores and another adjustment is needed for scores near the center, and still another adjustment for scores at or near the top. Equipercentile equating can take these differences into account, whereas linear equating will not.
To calculate the equiperentile rank for a target score, the cumulative percentage of the scores below the target score is added to one half the percentage of cases who obtained the target score. For example, if 70% of test takers achieve a score 19 or less on a given test and 5% of individuals earn a score of 20, then the equipercentile rank of 20 is 72.5. For an explanation of why the equipercentile ranking is not equal to the cumulative percent at a given score, readers are referred to Blommers & Forsyth, 1977.
Through the conversion of raw scores to equipercentile ranks, students’ scores on nonequivalent forms can be compared. However, when comparing scores across a large number of tests it may be more useful to determine the raw scores that correspond to specific integer percentiles. These conversions utilize a similar rationale to the raw score conversions to equipercentile ranks described above, but determine the WCPM score on a given form that is associated with specific percentiles. This latter approach facilitates the creation of conversion tables that can handle multiple forms at the same time.
Table 8 provides equipercentile conversions for the six forms back to a common scale score where the scale score gives the expected WCPM if the student had been asked to read the passage Home. That is, the columns of Table 8 give scores for each of the six stories associated with a particular integer percentile rank. The column marked WCPM is the proposed scale score of words correct per minute and is identical to the column in the table for Home. To use the table, a teacher would simply locate the title of the passage that the child had been asked to read. The teacher would then read down the column until she/he found the WCPM score for the specific child or, more commonly, found the two rows that bracket the student’s score. The teacher would then read across the rows to the column marked WCPM and find the entry in the WCPM column associated with the row (or set of rows) for the student’s score. To get the most precise score, linear interpolation could be used. However, teachers could also round up or down with only slight loss of accuracy.
Table 8.
Equipercentile Conversion Table for Six DIBELS Forms
| PERCENTILE | WCPM | BABY | BOOK | COLOR | HOME | POOL | TWIN |
|---|---|---|---|---|---|---|---|
| 0 | LE 24 | LE 15 | LE 18 | LE 22 | LE 24 | LE 16 | LE 22 |
| 1 | 25.1 | 16.2 | 19.2 | 23.2 | 25.1 | 17.1 | 23.2 |
| 2 | 27.2 | 19.9 | 19.8 | 31.7 | 27.2 | 18.8 | 31.2 |
| 3 | 27.8 | 24.2 | 20.5 | 32.1 | 27.8 | 19.4 | 31.5 |
| 4 | 33.4 | 24.9 | 21.2 | 32.4 | 33.4 | 21.5 | 31.8 |
| 5 | 39.1 | 26.1 | 22.9 | 42.5 | 39.1 | 23.7 | 39.8 |
| 6 | 39.7 | 28.3 | 30.5 | 44.7 | 39.7 | 24.3 | 40.5 |
| 7 | 43.8 | 33.0 | 31.2 | 45.4 | 43.8 | 26.9 | 45.6 |
| 8 | 44.4 | 33.4 | 37.9 | 46.1 | 44.4 | 35.0 | 53.8 |
| 9 | 49.0 | 33.7 | 38.5 | 47.2 | 49.0 | 35.7 | 54.4 |
| 10 | 51.6 | 36.6 | 39.2 | 47.5 | 51.6 | 42.6 | 58.1 |
| 11 | 52.2 | 37.0 | 39.9 | 47.9 | 52.2 | 42.8 | 58.8 |
| 12 | 52.8 | 37.3 | 40.5 | 49.4 | 52.8 | 43.0 | 59.4 |
| 13 | 53.4 | 40.7 | 40.9 | 50.6 | 53.4 | 43.2 | 60.1 |
| 14 | 54.0 | 41.0 | 41.2 | 51.3 | 54.0 | 43.4 | 61.2 |
| 15 | 54.7 | 41.4 | 41.5 | 52.0 | 54.7 | 51.0 | 61.9 |
| 16 | 55.3 | 45.5 | 41.9 | 52.7 | 55.3 | 60.1 | 63.6 |
| 17 | 55.9 | 46.6 | 42.2 | 53.4 | 55.9 | 60.7 | 65.2 |
| 18 | 56.5 | 47.0 | 42.5 | 54.8 | 56.5 | 62.6 | 65.9 |
| 19 | 58.6 | 47.3 | 42.9 | 55.2 | 58.6 | 62.8 | 68.0 |
| 20 | 61.2 | 47.9 | 43.2 | 56.7 | 61.2 | 63.0 | 70.2 |
| 21 | 61.8 | 48.6 | 43.6 | 58.2 | 61.8 | 63.2 | 70.9 |
| 22 | 65.4 | 48.9 | 44.2 | 63.7 | 65.4 | 63.5 | 72.1 |
| 23 | 69.0 | 49.3 | 45.4 | 64.1 | 69.0 | 66.0 | 72.3 |
| 24 | 69.6 | 50.6 | 47.1 | 64.4 | 69.6 | 68.6 | 72.5 |
| 25 | 71.3 | 51.0 | 47.8 | 69.0 | 71.3 | 69.3 | 72.6 |
| 26 | 71.9 | 51.4 | 48.7 | 70.2 | 71.9 | 69.9 | 72.8 |
| 27 | 72.7 | 53.9 | 49.1 | 70.9 | 72.7 | 70.5 | 73.0 |
| 28 | 73.0 | 55.7 | 49.4 | 73.3 | 73.0 | 71.1 | 74.6 |
| 29 | 73.4 | 56.4 | 51.4 | 73.7 | 73.4 | 71.8 | 74.7 |
| 30 | 73.7 | 59.6 | 53.6 | 75.5 | 73.7 | 72.4 | 74.9 |
| 31 | 74.0 | 62.7 | 53.9 | 75.7 | 74.0 | 72.7 | 75.0 |
| 32 | 74.3 | 63.0 | 54.2 | 76.0 | 74.3 | 72.9 | 75.1 |
| 33 | 78.6 | 63.4 | 54.6 | 76.2 | 78.6 | 73.1 | 75.3 |
| 34 | 78.9 | 64.0 | 54.9 | 76.4 | 78.9 | 73.3 | 75.4 |
| 35 | 79.2 | 64.7 | 55.2 | 77.0 | 79.2 | 73.5 | 76.6 |
| 36 | 79.5 | 65.4 | 55.5 | 77.7 | 79.5 | 73.8 | 77.3 |
| 37 | 84.6 | 67.1 | 55.8 | 78.4 | 84.6 | 74.2 | 77.7 |
| 38 | 85.7 | 68.9 | 56.0 | 78.8 | 85.7 | 74.5 | 78.0 |
| 39 | 86.3 | 71.1 | 56.2 | 79.2 | 86.3 | 74.8 | 78.4 |
| 40 | 87.4 | 71.8 | 56.4 | 79.5 | 87.4 | 75.1 | 79.1 |
| 41 | 88.5 | 73.8 | 56.7 | 79.9 | 88.5 | 75.4 | 79.4 |
| 42 | 88.8 | 74.1 | 56.9 | 80.2 | 88.8 | 76.0 | 79.6 |
| 43 | 89.1 | 74.5 | 57.1 | 81.6 | 89.1 | 78.1 | 79.8 |
| 44 | 89.4 | 75.2 | 57.3 | 81.9 | 89.4 | 78.4 | 81.0 |
| 45 | 90.2 | 75.5 | 58.2 | 82.3 | 90.2 | 78.7 | 81.7 |
| 46 | 90.5 | 75.7 | 58.8 | 84.2 | 90.5 | 79.0 | 82.9 |
| 47 | 90.8 | 76.0 | 59.8 | 84.9 | 90.8 | 82.1 | 84.0 |
| 48 | 91.8 | 76.8 | 60.1 | 86.1 | 91.8 | 84.7 | 84.2 |
| 49 | 92.4 | 77.1 | 60.4 | 86.8 | 92.4 | 85.4 | 84.5 |
| 50 | 93.5 | 77.5 | 61.3 | 87.5 | 93.5 | 88.5 | 84.7 |
| 51 | 95.6 | 78.2 | 61.6 | 88.2 | 95.6 | 90.5 | 84.9 |
| 52 | 96.2 | 78.7 | 61.9 | 88.9 | 96.2 | 90.8 | 86.1 |
| 53 | 99.8 | 79.1 | 63.0 | 92.0 | 99.8 | 91.0 | 86.3 |
| 54 | 100.4 | 79.4 | 66.7 | 92.2 | 100.4 | 91.2 | 86.6 |
| 55 | 103.6 | 80.6 | 67.4 | 92.4 | 103.6 | 91.4 | 86.8 |
| 56 | 105.2 | 81.8 | 71.0 | 92.6 | 105.2 | 92.8 | 87.0 |
| 57 | 105.8 | 82.5 | 74.2 | 92.7 | 105.8 | 93.4 | 88.1 |
| 58 | 107.4 | 83.3 | 74.9 | 92.9 | 107.4 | 95.0 | 88.6 |
| 59 | 108.0 | 84.0 | 79.5 | 96.2 | 108.0 | 95.7 | 89.0 |
| 60 | 109.1 | 85.2 | 81.6 | 96.5 | 109.1 | 96.3 | 89.3 |
| 61 | 109.7 | 85.9 | 81.9 | 96.9 | 109.7 | 96.7 | 89.8 |
| 62 | 110.3 | 88.1 | 82.3 | 98.9 | 110.3 | 97.0 | 90.4 |
| 63 | 110.9 | 90.4 | 83.1 | 100.6 | 110.9 | 97.4 | 93.1 |
| 64 | 112.0 | 91.6 | 83.3 | 101.3 | 112.0 | 97.7 | 95.7 |
| 65 | 112.7 | 92.3 | 83.5 | 104.5 | 112.7 | 98.0 | 96.4 |
| 66 | 113.8 | 93.0 | 83.7 | 107.7 | 113.8 | 98.3 | 97.6 |
| 67 | 114.4 | 93.6 | 84.0 | 108.4 | 114.4 | 98.7 | 98.7 |
| 68 | 116.5 | 94.0 | 85.6 | 108.8 | 116.5 | 99.3 | 99.4 |
| 69 | 121.0 | 94.3 | 87.2 | 109.2 | 121.0 | 100.0 | 101.7 |
| 70 | 121.2 | 95.9 | 87.9 | 109.5 | 121.2 | 100.6 | 101.9 |
| 71 | 121.4 | 97.6 | 91.2 | 110.2 | 121.4 | 101.2 | 102.1 |
| 72 | 121.6 | 98.3 | 91.4 | 110.5 | 121.6 | 102.4 | 102.3 |
| 73 | 121.8 | 99.3 | 91.6 | 110.7 | 121.8 | 103.0 | 106.2 |
| 74 | 126.1 | 99.6 | 91.9 | 110.9 | 126.1 | 104.1 | 106.8 |
| 75 | 126.8 | 102.0 | 95.8 | 111.8 | 126.8 | 107.6 | 111.0 |
| 76 | 128.7 | 102.7 | 96.4 | 112.1 | 128.7 | 107.9 | 113.7 |
| 77 | 129.0 | 104.7 | 98.1 | 112.5 | 129.0 | 108.3 | 114.3 |
| 78 | 129.3 | 105.1 | 100.1 | 115.3 | 129.3 | 112.6 | 118.5 |
| 79 | 130.2 | 105.4 | 100.5 | 115.7 | 130.2 | 113.3 | 122.6 |
| 80 | 130.8 | 107.3 | 100.8 | 116.0 | 130.8 | 121.4 | 123.3 |
| 81 | 132.9 | 107.7 | 103.8 | 119.2 | 132.9 | 128.5 | 125.0 |
| 82 | 136.5 | 110.0 | 104.4 | 120.4 | 136.5 | 129.2 | 127.1 |
| 83 | 137.1 | 110.8 | 105.7 | 122.1 | 137.1 | 130.6 | 127.8 |
| 84 | 142.2 | 112.2 | 105.9 | 122.8 | 142.2 | 130.8 | 131.9 |
| 85 | 142.9 | 112.4 | 106.2 | 127.8 | 142.9 | 131.0 | 137.1 |
| 86 | 146.0 | 112.6 | 106.4 | 128.1 | 146.0 | 131.2 | 137.8 |
| 87 | 146.5 | 112.9 | 108.3 | 128.5 | 146.5 | 131.4 | 140.2 |
| 88 | 146.8 | 114.9 | 109.0 | 133.6 | 146.8 | 134.4 | 140.5 |
| 89 | 147.2 | 117.1 | 111.1 | 134.8 | 147.2 | 137.1 | 140.9 |
| 90 | 147.5 | 117.8 | 113.3 | 135.5 | 147.5 | 137.7 | 141.9 |
| 91 | 148.5 | 119.0 | 114.0 | 138.7 | 148.5 | 138.8 | 142.6 |
| 92 | 153.1 | 119.7 | 116.1 | 142.7 | 153.1 | 139.5 | 143.2 |
| 93 | 153.4 | 120.5 | 116.8 | 143.1 | 153.4 | 141.6 | 144.4 |
| 94 | 153.7 | 122.2 | 117.5 | 143.4 | 153.7 | 144.2 | 146.0 |
| 95 | 154.0 | 124.9 | 120.2 | 145.0 | 154.0 | 144.9 | 146.7 |
| 96 | 160.6 | 127.6 | 124.8 | 151.2 | 160.6 | 149.5 | 148.9 |
| 97 | 170.7 | 128.3 | 125.5 | 151.9 | 170.7 | 155.6 | 156.5 |
| 98 | 171.3 | 170.6 | 138.7 | 159.1 | 171.3 | 156.2 | 157.2 |
| 99 | 179.4 | 225.3 | 181.8 | 162.3 | 179.4 | 192.9 | 176.8 |
| 100 | GE 180 | GE 239 | GE 214 | GE 164 | GE 180 | GE 227 | GE 190 |
For example, suppose a student had read the passage Book and obtained a score of 53 words correct per minute. Scores for Book are found in column 4 of Table 8. Thus, the teacher would scan down column 4 until coming to 53.55, which is associated with a percentile rank of 30. Then reading across the rows to the column marked WCPM (Column 2), she/he would find that the score of 53 on Book is approximately equal to a score of 73.65 WCPM if the child had been asked to read the passage Home. In this particular instance, a score of 53 on Book is part way between a score of 51.43 and 53.55, the scores on Book associated with the 29th and 30th percentiles. Thus, to get a more precise scaled score the teacher could interpolate between the WCPM scores of 73.35 and 73.65 which are associated with the 29th and 30th percentiles, respectively. To do so, the teacher would compute 53 as a percentage of the distance from 51.43 to 53.55 by taking (53.00 – 51.43) / (53.55 - 51.43) = 1.57 / 2.12 = .741. This number is then multiplied by the difference between 73.65 and 73.35 (.741*(73.65 – 73.35) = .741*0.30 = .223) and the result added to 73.35 (73.35 + .223 = 73.573) to give the interpolated WCPM score. In this case, the difference between the 29th and 30th percentiles are sufficiently small as to make the interpolation not worth the effort of calculation (less than a quarter of a word per minute), but in some cases the difference will be substantially larger and a more precise score might be desired, in which case the interpolation method will work reasonably well. For most purposes, rounding the numbers in Table 8 to the nearest integer will not sacrifice much in the way of precision and will be substantially more accurate than current practice which ignores the rather substantial differences due to forms. These differences are apparent by simply scanning across the various rows of Table 8 which highlights the different fluency rates associated with a particular percentile rank depending on which story was read by the student.
To examine the effectiveness of the equipercentile equating method used here, we reanalyzed the data for Wave 1 and the seven week growth models using the equated scores. That is, we converted all of the raw scores to equipercentile scores and reran the mixed model at Wave 1 and the growth models across the four waves. Using the equated scores, the mixed model analysis for Wave 1 showed no differences due to story (F(5, 119) = 0.07, p < .997) or the interaction of story and order (F(10, 119) = 0.69, p < .732). Least squares means ranged from 88.1 to 89.1 across the six stories. At the same time, there were statistically significant differences due to order of testing (F(2, 119) = 3.49, p < .0337). Least squares means indicated the first story was read more slowly (Mean = 86.9, s.e. = 1.7) than either the second (Mean = 89.9, s.e. = 1.7) or third (Mean = 89.5, s.e. = 1.7).
Growth in oral reading fluency over the seven-week period was also examined using the equated scores. The model included TPRI fluency as a covariate, linear growth in oral reading fluency, group (i.e., the six groups to which students had been randomized), and differences between groups in the linear growth rates. When growth was analyzed using equipercentile equated scores, there was evidence of significant positive growth in oral reading fluency over the seven week period (F(1 115) = 7.29, p < .008). On average, oral reading fluency increased by 2.46 (s.e.= 0.94) words per wave (or roughly 1.2 words per week). Growth rates and average fluency rates varied significantly across students (Intercept Variance = 254.1, s.e. = 43.0, p < .0001; slope variance = 4.04, s.e. = 2.4, p < .0489). There were no significant differences among the groups in mean oral reading fluency (F(5 114) = 0.62, p < .684), or in average rates of growth (F(5, 115) = 2.10, p < .071). That is, the group differences in average rates of growth over the seven-week period that were found in the previous analysis were eliminated when passages were equated using equipercentile equating. In short, the failure to equate forms masked an overall positive average rate of growth across all groups and suggested that groups were growing at different rates. When passages were equated, groups were found to be comparable both in their average oral reading fluencies and in their average rates of growth across the seven-week period.
Discussion
In both special education and general education based applications of CBM-like assessments, the criterion for growth is based on the slope of the student’s charted progress, that is, the rate of change in the students’ performance. In the case of traditional CBM, this rate of growth is based on end of year instructional materials,. In the case of DIBELS the rate of growth is on leveled, grade-appropriate texts. This difference seems to be of minor consequence given the expected connection between grade appropriate texts and end-of-year instructional material, which one would expect to be high, especially in the elementary grades and in literacy instruction. In both the general and special education applications of CBM for progress monitoring, the rate of change in performance must indicate the rate of progress toward the end of the year goal in order to be of use to teachers. Given this indicator of rate of progress toward end of year goals, this growth rate also serves to signal when intervention is necessary whenever that rate of progress is inadequate to reach the end of year benchmark.
In order to accurately influence decision making for individual students, the rate of progress must be estimated with some precision, especially if decisions are to be based on estimates that involve short time series (e.g., six to eight weeks of data). Here is where scaling issues come to the fore. If point estimates of performance can differ significantly on the basis of form choice by as much as was found in the present study (26 words per minute), the potential for poorly informed decisions is high. In a data rich environment, i.e., one with many data points on which to base the estimate of the individual student’s rate of change in performance, such large fluctuations due to form effects could be reduced, but not eliminated. But in the present context, where point estimates are based on one minute of reading from a single passage, and decisions to intervene could be based on slope estimates based on four such data points, failure to adjust charted WCPM scores for form effects seems ill-advised.
Some CBM developers have recommended that students read three passages, each for one minute, and that teachers take the median performance across the three measures. While the gathering of additional data at each time point mitigates somewhat the scaling problem identified in the current study, the decision to take the median performance across the three measures works against the collection of the extra assessment data because the median will throw out two of the three WCPM measures in favor of the middle measure. Thus, the final estimate is again based on a single minute of reading from a single passage. In short, this point estimate of a student’s reading rate would also benefit from scaling the WCPM scores to take into account form effects. Of course, such rescaling of the observed WCPM scores should be completed prior to taking the median.
Given the importance of fluency in the role of learning to read and the growing role of assessment in monitoring of student growth in their reading skills, it is important to find a more accurate and reliable way to measure growth of fluency rates. This study evaluated the DIBELS Oral Reading Fluency measure for differences between passages. The developers of DORF made significant efforts to control for passage differences by using multiple readability formulas to equate passages, and by relying on the Spache readability index to make sure that all grade two stories were written to be approximately in the 2.5 range. However, the current study suggests that these efforts were not sufficient to equate the stories at a level that would make them substitutable for one another without further adjustment when estimating students’ fluency. In a multi-tiered intervention model relying on progress monitoring assessments to move students from one level to another, or to simply gauge response to instruction, the magnitude of the observed form effects has important implications for the use of CBM as a tool for identifying students who need Tier 2 and/or Tier 3 instruction. While some variability is expected in fluency rates from one assessment to the next, a 20 word difference between passages as observed in this study will be difficult for teachers to reconcile when attempting to decide whether or not to alter a given student’s instruction.
This study found evidence of significant and substantial differences among the six DORF passages. However, it should be pointed out that several of the passages displayed negligible differences, and all passages tended to correlate quite highly, although possibly not equally. Thus, while not all passages were found to be parallel, several passages appeared to be and may well function in a manner that makes them function like parallel forms. At the same time, there appeared to be little evidence of order effects in the original analysis. When forms were equated, there was some evidence of order effects, although these were not large (roughly three words per minute on average).
We proposed a solution to the scaling problem across passages that was based on equipercentile equating. While equipercentile equating offers a viable solution to the problem of passage effects, the current study is not optimal for carrying out the equating process and the equated scores in Table 8 must be used with some degree of caution. The current study only included 134 students and tested only six of the 20 non-benchmark stories found in the second grade oral reading measure, with each passage read by approximately one-third of the students. In general, a much larger sample of students would be preferred for deriving the equated scores. Future studies should include larger sample sizes and additional passages to better address the equating issue. It is important to keep in mind that future studies need not include all possible passages, or have all passages read by all students. Rather, a single passage can be selected as the base passage (e.g., Home), and all other passages equated back to that base passage. It is important that future studies employ random assignment and counter balance the order of presentation so that order effects can also be estimated on a larger sample and controlled in the equating process. Given the random selection of the six passages from the population of 20 available, the finding of one or two passages that were substantially different from the others would suggest that roughly one-third of the 20 passages may differ in their mean WCPM. Of course, the extent to which this inference is supported awaits further research. The current study simply provides a starting point from which to continue the study of passage effects on the estimation of students’ oral reading fluency and the appropriate assessment of oral reading fluency in order to monitor children’s progress toward end of year reading goals.
Finally, the current study focused only on the DORF as a representative example of CBM. There is no reason to suspect that the issues raised in the current study are unique to DIBELS. To the contrary, differences in raw scores across forms are likely the rule, not the exception. These scaling issues must be taken into account in the reporting of scores, and not just assumed to be negligible because readability estimates suggest equivalent passages and because all passages yield reliable estimates of WCPM. For passages to be treated as equivalent, parallel forms, some attention must also be paid to the development of a suitable scale score metric when raw score distributions are found to differ across passages.
Acknowledgments
This work is supported by the Inter-agency Education Research Initiative (IERI; grant R305W020001 from the U.S. Department of Education), funded by the Institute for Education Sciences (IES), the National Institute of Child Health and Human Development (NICHD), and the National Science Foundation (NSF). This article does not reflect the position or policy of these agencies, and no official endorsement should be inferred.
Footnotes
The original wave variable was scored 1, 2, 3, and 4 corresponding to the first to fourth testing session, respectively. In modeling growth, the values of wave were transformed by subtracting 2.5 from them so that the intercept value in the individual growth model represented the student’s expected oral reading fluency between waves 2 and 3, or midway through the study.
We examined five different models for the covariance structure: (1) An unrestricted model (UNR), (2) a one-factor model with unequal error variance across passages (1F), (3) a one factor model with equal error variance across passages (1FEQ), (4) a heterogeneous compound symmetry model (CSH), and (5) a compound symmetry model (CS). Model 1 is the least restrictive and allows that the correlations among measures vary freely. Models 1F and 1FEQ imply that the correlations among measures can be explained by a single underlying factor, but differ in their specifications for the error variance, with model 1FEQ constraining the error variance to be equal across measures. Neither model constrains the factor loadings to be equal. The last two models are variations of the compound symmetry model, both of which imply that the correlations among measures are constrained to be equal. The CSH model allows that the error variances differ across passages, while model (5) constrains the correlations equal across passages as well as the variances. The CS model is consistent with a single underlying factor with equal factor loadings and equal error variances across all measures. In contrast, the CSH model is consistent with a single factor model with equal standardized factor loadings, but unequal unstandardized factor loadings and unequal error variances across passages. While both covariance structures can also be produced from multi-factored data, the one factor model is the most parsimonious factor model that can produce the CS or CSH covariance structure.
Although the test of parallel forms is rejected, acceptance of the CSH model over the 1 Factor model indicates that the parallelism model failed due to non-equivalence of V(εk) of Equation (3), and that the λk of Equation (1) are equal when all measures have been standardized. Direct comparison of the CSH and 1 Factor models shows these models not to be statistically significantly different from one another (χ2(5) = 5.4, p < .37). This result implies that the hypothesis of equal standardized λk is tenable. The CSH structure indicates that the variance in reading fluency was different for different passages, whereas passage correlations could be considered equal. In the psychometric literature, the passages would be considered to be essentially tau-equivalent (Bollen, 1989) when standardized to constant variance. That is, standardized relationships to the underlying latent factor are the same for all passages. However, in their unstandardized metric, the measures are simply congeneric, meaning they have a common factor structure. True scores for a given person on passages that are essentially tau-equivalent may differ from one another because of the scaling constant (αk). As shown in the model for true scores in Equation (2), the true scores can differ even if the factor loadings of Equation (2) are equal when standardized.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Angoff WH. Scales, norms, and equivalent scores. Princeton: Educational Testing Service; 1967. [Google Scholar]
- Ardoin SP, Suldo SM, Witt J, Aldrich S, McDonald E. Accuracy of readability of estimates’ predictions of CBM performance. School Psychology Quarterly. 2005;20(1):1–22. [Google Scholar]
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. Journal of the Royal Statistical Society, Series B. 1995;57:289–300. [Google Scholar]
- Benjamini Y, Hochberg Y. Adaptive control of the false discovery rate in multiple testing with independent statistics. Journal of Educational and Behavioral Statistics. 2000;25:60–83. [Google Scholar]
- Blommers PJ, Forsyth RA. Elementary statistical methods in psychology and education. 2nd ed. Boston: Houghton Mifflin; 1977. [Google Scholar]
- Bollen KA. Structural equation modeling with latent variables. New York: Wiley; 1989. [Google Scholar]
- Bryk AS, Raudenbush SW. Application of hierarchical linear models to assessing change. Psychological Bulletin. 1987;101:147–158. [Google Scholar]
- Burchinal M, Applebaum MI. Estimating individual developmental functions: Methods and their assumptions. Child Development. 1991;62:23–43. [Google Scholar]
- Deno SL. Formative evaluation of individual programs: A new role for school psychologist. School Psychology Review. 1986;15:358–374. [Google Scholar]
- Francis DJ, Fletcher JM, Stuebing KK, Davidson KC, Thompson NR. Analysis of change: Modeling individual growth. Journal of Consulting and Clinical Psychology. 1991;59:27–37. doi: 10.1037//0022-006x.59.1.27. [DOI] [PubMed] [Google Scholar]
- Francis DJ, Shaywitz SE, Stuebing KK, Shaywitz BA, Fletcher JM. Developmental lag versus deficit models of reading disability: A longitudinal, individual growth curve analysis. Journal of Educational Psychology. 1996;88(1):151–170. [Google Scholar]
- Fuchs LS, Fuchs DF, Hosp MK, Jenkins JR. Oral reading fluency as an indicator of reading competence: A theoretical, empirical, and historical analysis. Scientific Studies of Reading. 2001;5:239–256. [Google Scholar]
- Fuchs LS, Deno SL. Paradigmatic distinctions between instructionally relevant measurement models. Exceptional Children. 1991;57:488–500. [Google Scholar]
- Good RH, Kaminski RA. [Retrieved October, 2002];Dynamic Indicators of Basic Early Literacy Skills (2000–2003) 2002a from http://dibels.uoregon.edu/
- Good RH, Kaminski RA. Eugene, OR: University of Oregon; DIBELS Oral Reading Fluency Passages for First through Third Grades (Technical Report No. 10) 2002b
- Kolen MJ, Brennan RL. Test equating methods and practices. New York, NY: Springer-Verlag; 1995. [Google Scholar]
- La Berge D, Samuels SJ. Toward a theory of automatic information processing in reading. Cognitive Psychology. 1974;6:293–323. [Google Scholar]
- Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38:963–974. [PubMed] [Google Scholar]
- Littell RC, Milliken GA, Stroup WW, Wolfinger RD. SAS Systems for Mixed Models. Cary, NC: SAS Institute Inc.; 1996. [Google Scholar]
- Marston DB. Curriculum based measurement. In: Shinn MR, editor. Curriculum-based measurement: Assessing special children. New York: Guilford Press; 1989. pp. 18–78. [Google Scholar]
- Mehta PD, Neale MC, Flay BR. Squeezing interval change from ordinal panel data: Latent growth curves with ordinal outcomes. Psychological Methods. 2004;9(3):301–333. doi: 10.1037/1082-989X.9.3.301. [DOI] [PubMed] [Google Scholar]
- Mehta PD, Neale MC. People are variables too: Multilevel structural equations modeling. Psychological Methods. 2005;10(3):259–284. doi: 10.1037/1082-989X.10.3.259. [DOI] [PubMed] [Google Scholar]
- National Reading Panel. Teaching children to read: An evidence-based assessment of the scientific research literature on reading and its implications for reading instruction. Washington, D.C.: National Institute of Child Health and Human Development; 2000. [Google Scholar]
- Nathan RG, Stanovich KE. The causes and consequences of difference in reading fluency. Theory into Practice. 1991;30:76–184. [Google Scholar]
- Perfetti CA. Reading ability. New York: Oxford University Press; 1985. [Google Scholar]
- Rogosa DR, Brandt D, Zimowski M. A growth curve approach to the measurement of change. Psychological Bulletin. 1982;90:726–748. [Google Scholar]
- Rogosa DR, Willet JB. Understanding correlates of change by modeling individual differences in growth. Psychometrika. 1985;50:203–228. [Google Scholar]
- Shinn MR, editor. Curriculum-based measurement: Assessing special children. New York: Guilford Press; 1989. [Google Scholar]
- Shinn MR, Rosenfield S, Knutson N. Curriculum-based assessment: A comparison and integration of models. School Psychology Review. 1989;18:299–316. [Google Scholar]
- Snow CE, Burns MS, Griffin P, editors. Preventing reading difficulties in young children. Washington, D C: National Academy Press; 1998. [Google Scholar]
- Willett JB. Questions and answers in the measurement of change. In: Rothkopf EZ, editor. Review of Research in Education. Vol. 15. 1987. pp. 345–422. [Google Scholar]
- Young A, Bowers PG. Individual difference and text difficulty determinants of reading fluency and expressiveness. Journal of Experimental Child Psychology. 1995;60:428–454. [Google Scholar]