Salt-Mediated Electrostatics in the Association of TATA Binding Proteins to DNA: A Combined Molecular Mechanics/Poisson-Boltzmann Study

Abstract

The TATA-binding protein (TBP) is a key component of the archaea ternary preinitiation transcription assembly. The archaeon TBP, from the halophile/hyperthermophile organism Pyrococcus woesei, is adapted to high concentrations of salt and high-temperature environments. Although most eukaryotic TBPs are mesophilic and adapted to physiological conditions of temperature and salt, they are very similar to their halophilic counterparts in sequence and fold. However, whereas the binding affinity to DNA of halophilic TBPs increases with increasing salt concentration, the opposite is observed for mesophilic TBPs. We investigated these differences in nonspecific salt-dependent DNA-binding behavior of halophilic and mesophilic TBPs by using a combined molecular mechanics/Poisson-Boltzmann approach. Our results are qualitatively in good agreement with experimentally observed salt-dependent DNA-binding for mesophilic and halophilic TBPs, and suggest that the distribution and the total number of charged residues may be the main underlying contributor in the association process. Therefore, the difference in the salt-dependent binding behavior of mesophilic and halophilic TBPs to DNA may be due to the very unique charge and electrostatic potential distribution of these TBPs, which consequently alters the number of repulsive and attractive electrostatic interactions.

INTRODUCTION

TATA-binding proteins (TBP) (1) are involved in the transcription machinery, where they recognize and bind to a consensus eight-basepair site, 5′-TATAXAXX-3′, (where X is either adenine (A) or thymine (T)) named TATA box or TATA element, located ∼25 basepairs upstream relative to the Pol I-III initiation transcription binding site (2). Due to its seminal role in the early transcription initiation stage, the TBP is—with very few exceptions—present in various organisms that have adapted to live in a diverse set of environments (3,4). One of these organisms, the archaeon Pyrococcus woesi (Pw) grows in highly saline solutions (∼1 M concentration) and at high temperatures (close to the boiling point of water) and falls in the category of hyperthermophilic and halophilic organisms. On the other hand, species sharing TBP-involved biological mechanisms that are adapted to physiological pH, salt concentrations (∼0.2 M), and room temperatures are classified as mesophilic organisms.

Previous sequence analysis of the TBPs revealed 36–41% of sequence identity between different classes of organisms (5). The known three-dimensional crystal structures of TBPs show that the tertiary fold of these proteins are very similar (5–10); built of ∼180 residues with a saddle-shaped, β-α-β-α (TBP-like) fold. When in complex with DNA, the central region of the DNA moiety bends ∼180° due to two conserved DNA-intercalating Phe residues (Fig. 1), whereas the free protein appears to undergo fewer conformational changes, as seen for the structure of the dimer TBP not bound to DNA (5) and the observed DNA bending in other complexes (11). Despite these similarities in sequence homology and fold, the TBPs differ in distribution and numbers of positively charged amino acid residues (lysine and arginine), negatively charged residues (aspartate and glutamate), hydrophobic packing amino acids, and the number of β-sheets in the secondary structure (but exhibit an overall tertiary structural similarity for all TBPs). The halophilic hyperthermophilic PwTBP, with an equal number (25) of positively and negatively charged residues distributed over the entire protein, has an overall zero net charge. On the other hand, the mesophilic counterparts from Homo sapiens (Hs) and Saccharomyces cerevisiae (Sc) TBPs lack charged residues in the first 20 residues, and have a predominant number of positively charged residues, which results in an overall net charge of +16e and +12e in the HsTBP and ScTBP, respectively (Table 1).

FIGURE 1.

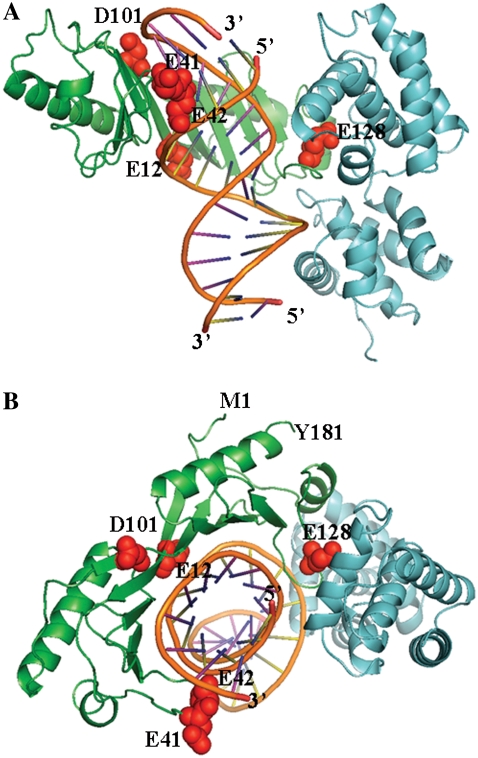
Schematic view of the archaeon Pyrococcus woesei TATA binding protein (green ribbon) in complex with DNA (orange), and transcription factor II (cyan ribbon) of the crystal structure (PDB entry 1AIS). Residues that are subject to mutations are indicated as red spheres and labeled by residue number and one-letter amino acid codes (E, Glu; D, Asp). The N-terminal (Met-1) and C-terminal (Tyr-181) ends of the PwTBP are labeled, and the 5′- and 3′-ends of the DNA are indicated. (A) View of the binding interface to DNA. (B) View along the z axis.

TABLE 1.

List of TBP-DNA complex crystallographic structures from human, yeast and archaeon Pyrococcus woesei

		Number of residues‡				Charged residues‖
PDB*	Species†	TBP	DNA	TF§	TATA¶	Negative	positive	total
1TGH	Hs	180	12	NA	TATATATA	13	29	+16
1CDW	Hs	179	16	NA	TATAAAAT	13	29	+16
1YTF	Sc	180	16	IIA	TATATAAA	15	27	+12
1YTB	Sc	180	15	NA	TATATAAA	15	27	+12
1D3U	Pw	181	23	IIB/BRE	TTTAAATA	25	25	0
1AIS	Pw	181	17	IIB	TTTTTAAA	25	25	0

^*PDB accession code for crystallographic structures of the TBPs used in this study.

^†The species used are Hs (Homo sapiens), Sc (Saccaromices cereviseae), and Pw (Pyrococcus woesei).

^‡Total number of protein residues and number of nucleotides in each DNA strand.

^§Transcription factor (if any) in a ternary complex with TBP-DNA. NA, not available.

^¶The TATA element or TATA box to which TBP binds in each crystal structure.

^‖Number of charged residues where Glu and Asp contribute to the negative charge count and Arg and Lys to the positive charge count. All other residues were assumed to be in their standard protonation state at pH 7.

By measuring the binding affinity, K_obs, of TBP to DNA at different salt concentrations, and estimating the coefficient, SK_obs, from a linear fit of log K_obs versus the logarithm of the instantaneous salt concentration of the solution, SK_obs = dlogK_obs/dlog[salt], two independent groups reported differences in DNA-binding behavior for the mesophilic and halophilic TBPs (12–14).

Brenowitz and co-workers performed a series of thermodynamic studies on the interaction of ScTBPs with DNA (12,13). They found that the K_obs of ScTBP to DNA decreases with increasing salt concentration, which is a classical signature of the polyelectrolyte nature of DNA. This is a commonly observed behavior of other mesophilic proteins that bind to DNA, and is rationalized as the release of solvent ions (i.e., Na⁺ and Cl⁻) upon protein-DNA binding. On the other hand, Ladbury and co-workers elaborated on the interactions of PwTBP with DNA at high temperatures and salt concentrations, and found instead that the K_obs of PwTBP to DNA increases with increased salt concentrations (14). They performed systematic site-directed mutagenesis and isothermal titration calorimetry (ITC) experiments and demonstrated that neutralizing or reversing the charge of certain combinations of acidic residues at the binding interface (e.g., E12, E42, E41, and E128), made the mutant PwTBP behave as classical mesophilic-like DNA binding proteins (15). Based on the widely known oligocation binding model, the authors inferred that the DNA binding of the wild-type PwTBP is due to an uptake of ions in the PwTBP-DNA complex (16).

If SK_obs > 0, then the binding of TBP to DNA is formed at some salt concentration and is strengthened with increasing salt concentration of the solvent. This appears to be the case for halophilic proteins/peptides that bind to nucleic acids (DNA or RNA). On the other hand, if SK_obs < 0, the TBP-DNA binding is weakened when the salinity is increased until—at some degree of salinity—the complex disintegrates and further binding is abolished. This is usually the case for mesophilic proteins/peptides binding to nucleic acids.

The interpretation of ion release (mesophilic DNA-binding proteins) and ion uptake (halophilic DNA-binding proteins) originates from the oligocationic binding model (17), which in turn is based on counterion condensation theory (18) and predicts that SK_obs = −Zψ in the absence of hydration and protonation effects. In this latter equation, Z represents the net charge of the oligocationic peptide (or number of cationic residues) or oligocationic protein patch (usually taken as the number of ion pairs, i.e., ionic charge contacts between cationic side chains and phosphate groups near the binding interface) and ψ denotes the fraction of counterions (e.g., Na⁺) that binds to and thus partially neutralizes the charged phosphate groups of the nucleic acid. This simple linear relationship provides a link between thermodynamics and structural information about the protein-nucleic acid complex and is successful when predicting the binding of small cationic molecules to nucleic acids. Usually, the ion pairs are counted within a predefined distance (4–6 Å) between the acceptor-donor atoms: the acceptor carboxylate oxygens on the Glu/Asp side chains or the phosphate oxygens on the nucleic acid to the donor amide nitrogen(s) on the Lys/Arg side chains (19). However, the model is less able to provide the correct prediction when acidic residues are involved in the nucleic binding interface. Record and co-workers suggested that the difference between the weak SK_obs and that predicted according to the oligocation model for the association of the integration host factor (IHF) to DNA could be explained by the DNA-coupled disruptions of dehydrated protein salt bridges that masked the presence of anionic residues close to the DNA-phosphate groups when the IHF-DNA complex is formed (20).

In our study, we used computational methods to investigate the salt-dependent binding behavior of DNA to TBPs in mesophilic and halophilic organisms. We combined molecular mechanics (MM) and Poisson-Boltzmann calculations on different TBPs in complex with DNA to understand the role of charged residues in modulating the electrostatic contribution in the binding affinity to DNA. Whenever possible, our results were compared with available data from experiments and we will refer to these experimental results throughout this article. In particular, we focused on the wild-type and mutant variants of the halophilic PwTBP and the mesophilic ScTBPs and HsTBP. All coordinates were optimized in explicit solvent with molecular mechanics, and the resulting coordinates were then subjected to the Poisson-Boltzmann equation (PBE) to obtain the electrostatic contribution to the binding free energy, ΔG_elec. We compute ΔG_elec over a range of monovalent salt concentrations, e.g., NaCl, and estimate the coefficient, SK_pred, from a linear fit of −ΔG_elec versus the logarithm of salt concentration, SK_pred = −dΔG_elec/dlog[salt]. Thus, the SK_pred may be viewed and qualitatively compared with the corresponding experimental SK_obs. We first analyzed SK_pred for the ScTBP-DNA interaction and compared it against similar thermodynamic data (12,13). We then computed SK_pred and compared it with the SK_obs from ITC thermodynamic experiments reported on the wild-type (wt) and mutant PwTBP-DNA association (15,21). We were able to reproduce the overall shape and experimental trends—but not absolute numbers—of the SK_obs, whereas the ΔSK_pred exhibits excellent agreement with ΔSK_obs (the ΔSK is expressed as SK_mut − SK_wt). Our analysis suggests that the different behavior of the binding of meso- and halophilic TBPs to DNA may be due to the screening of both favorable/unfavorable charge-charge interactions between any inter- and intramolecular DNA and protein residues in TBPs from different organisms.

METHODS AND THEORY

Molecular structures

Six TBP-DNA structures were selected and retrieved from the RCSB Protein Data Bank (PDB): the Pw archaeon (PDB codes 1AIS (9) and 1D3U (10)), the Hs human (PDB codes 1CDW (7), and 1TGH (8)), and the Sc yeast (PDB codes 1YTB (6) and 1YTF (22)) TATA binding proteins (Table 1). Any present cobinding protein or other molecules and crystallographic water oxygen atoms located further away than 6 Å from the TBP-DNA binary complex were removed.

The CHARMM program (23) and the all-atom CHARMM22/27 force field parameters and residue topologies (24,25) were used for all modeling and molecular mechanics/dynamics calculations. Hydrogen atoms were added with HBUILD (26). For 1AIS, the 5-iodo-uracil bases were replaced by thymine bases. We used the recommended default CHARMM-potential for handling the electrostatic and van der Waals interaction energies and forces. Keeping all nonhydrogen atoms fixed, the hydrogen atoms were minimized with 200 steps of steepest descent (SD) followed by adopted-basis Newton Raphson (ABNR) until the default convergence criteria of 0.0000 in the root mean-square (rms) gradient of the potential energy was achieved. The solute (i.e., protein, DNA, and crystallographic waters) were centered in a TIP3P (27) sphere of preequilibrated water molecules extending at least 13 Å from any atom away from the solute, resulting in a 47-Å-radius sphere of explicit water molecules surrounding the solute. A stochastic boundary potential (28) with a friction coefficient, β, of 50 ps⁻¹, was assigned to all water oxygen atoms. The solute was fixed and all solvent oxygen atoms were treated as Langevin particles while subjecting the solvent to 5000 steps of stochastic boundary molecular dynamics (SBMD) (29) at 298.15 K. The integrator time step was 0.002 ps, and SHAKE (30) was used to constrain any explicit hydrogen bonded to a nonhydrogen atom.

Thirty-six Na⁺ and four Cl⁻ ions were then added to the solute-solvent system to render overall charge neutrality for the PwTBP-DNA system (1AIS case). These ions were positioned randomly, but separated by at least 5.5 Å from each other and from any solute atom, resulting in a salt concentration of ∼156 mM. Additional 10,000 steps of SBMD were carried out at 298.15 K while still keeping the solute fixed and assigning the outermost 3-Å shell to the reservoir region, which means that atoms within 44 Å from the center of the sphere were treated according to Newton's laws and the remaining solvent atoms were treated as Langevin particles. The final structure of the PwTBP-DNA (from the 1AIS structure) served as the initial coordinates for modeling the mutant PwTBPs. All other TBP-DNA binary complexes were prepared with the same protocol but differ in the number of water molecules and added counter/coions. Typically, each solvated TBP-DNA complex contained ∼47,000 atoms, with the exception of the structure with PDB code 1D3U (a PwTBP in complex with 23 DNA basepairs), which required a larger sphere radius of water molecules.

Modeling PwTPB mutants

We selected only PwTBP mutants that have corresponding thermodynamic experimental data reported in the literature (15,21) listed in single-letters for amino acids: E12A, E42A, D101A, E128A, E12AE128A, E12AE42A, E12AE41KE128A and E12AE41KE42KE128A. Fig. 1 highlights the locations of the anionic glutamate (E) or Aspartate (D) residues that were mutated to either an alanine (A) or lysine (K).

All the PwTBP mutants were constructed by modifying the side-chain atoms (if any). For each mutation, the target-residue side chain was either truncated at the C_β-atom and had one hydrogen atom added—for substitution to an alanine—or missing atoms were built with available internal coordinates from the CHARMM topology (i.e., in an extended conformation for the lysine) in conjunction with existing Cartesian coordinates. If the PwTBP mutant(s) resulted in nonzero overall net charge, the corresponding number of ion(s)—sodium or chloride—in the solvent were transformed into a TIP3P water oxygen (and adding its two hydrogen atoms) to reset charge neutrality. Water molecules that overlapped the modified side chains were removed. The mutated side-chain was then minimized while keeping all other atoms fixed.

Energy minimization of the solvated TBP-DNA structures

The solvent was fixed and the solute was minimized for 5000 steps of SD followed by ABNR until the default convergence was reached. Then, a second round of minimization was carried out, where all atoms were allowed to move: the system was minimized with 5000 steps of SD, followed by ABNR, until the default convergence was reached. SHAKE was used to constrain all explicit bonds to hydrogen atoms throughout the minimizations. We did not observe any major dramatic changes in any of the minimized structures relative to the initial coordinates (not shown) and feel that our modeling is fairly realistic in mimicking the real world.

Modeling extended/truncated and mutant PwTBP-DNA complexes

To examine the effect of the presence of transcription factor IIB (TFIIB), DNA length, and differences in TATA element in the DNA-PwTBP complex, we performed other energy-minimization calculations as described below.

The entire PwTBP-DNA-TFIIB ternary complex (from the 1AIS crystal structure) was subjected to the same protocol for setup and minimization as described above. Then, the TFIIB protein was removed before Poisson-Boltzmann (PB) calculations. The DNA in the 1D3U initial coordinate set was truncated from 23 nucleotides in each strand to 16 nucleotides in each strand, keeping the TATA recognition site intact. The protocol before the minimization on this structure was the same as for the solvation of the other DNA-TBP structures. The DNA in the 1AIS structure (with 17 bases in each strand) was elongated to encompass 24 nucleotides in each strand. The modeling on the added bases was based on the internal coordinates of the DNA in the 1D3U structure (with 23 nucleotides in each strand). This was done on the final minimized 1AIS structure. Harmonic constraints with a force constant of 10 kcal mol⁻¹ Å⁻² were imposed on any of the nonhydrogen atoms that originated from the minimized 1AIS PwTBP-DNA coordinates, and the structure was subjected to a brief minimization in vacuum; 100 steps of SD followed by 200 steps of ABNR.

Poisson-Boltzmann calculations

All solvent atoms were removed and the minimized solute coordinates (protein and DNA) were transformed into protein charge radii (PQR) (31) format with an in-house program. For any atom, the charge and radii was adapted from the CHARMM 22/27 parameter and residue topology files. The PQR-formatted energy-minimized atomic coordinates were then used in all subsequent PB calculations.

We employed both linear and nonlinear PBE solvers to test the validity of the more approximate linear solution in reproducing the experimentally observed nonspecific salt dependence of the binding free energies. However, a parallel study in our lab clearly demonstrated that the nonlinear PBE (NLPB) stands alone in reproducing the experimental results (32), and we decided to continue with the NLPB whenever applicable. Thus, if not explicitly mentioned, we use the NLPB in this study.

All PB calculations were set at neutral pH (7.0) and room temperature (298 K). We varied the 1:1 salt (NaCl) concentration from 0.1 to 0.4 M. The solute (TBP and DNA) and solvent dielectric constants were 2 and 80, respectively. The solvent-excluded molecular surface (33), based on a water probe radius of 1.4 Å, defined the dielectric interface that separates the solute and solvent regions. No ion exclusion region was considered. We assumed that the protein residues Arg, Lys, Asp, and Glu were fully ionized and that His residues were neutral. The proper treatment of protonation effects, such as critical histidines (e.g., His-49) upon binding is very important, so we will address this issue elsewhere. The treatment of His does not change the conclusions drawn in this work (data not shown).

The total extent of the 3D grid was set to three times the largest dimension of the molecule to reduce outer boundary condition errors. Special outer-boundary and energy corrections are enforced to obtain very accurate salt-dependent electrostatic free energies (34). The dependence of the PB results on the finest grid resolution was examined and we choose a finest grid spacing of 0.3 Å for all PBE calculations for a compromise between accuracy and speed. All other default PBE code parameters were employed.

Salt dependence of the electrostatic binding free energy

In biomolecular processes, such as the binding of charged ligands to nucleic acids, the salt dependence of the total binding free energy can be obtained as the coefficient (SK_obs) from the linear fit of the logarithm of the binding constant (K_obs) versus the logarithm of salt concentration (17):

(1)

K_obs can be measured from thermodynamic experiments such as isothermal titration calorimetry (ITC) at various concentrations of salt, [M⁺], e.g., NaCl.

If we assume that the long-range electrostatic interaction energy predominates in the salt dependence of the binding process, we can use the relation ΔG = −RTlnK and approximate ΔG ≈ ΔG_elec. Then, log K_obs can be substituted for −ΔG_elec/ln 10 kT in Eq. 1. To avoid confusing the experimental SK_obs with the PB-predicted salt dependence of the binding free energy, we call the latter SK_pred:

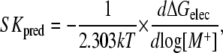(2)

where SK_pred is the salt derivative of the electrostatic binding free energy, ΔG_elec, which consists of four energy terms (35): Coulomb, reaction field, dielectric stress, and osmotic pressure is expressed in units of kT, where k is the Boltzmann constant, T is the absolute temperature (here taken as 298 K), and [M⁺] is the 1:1 salt concentration.

The righthand side of Eq. 2 is obtained by calculating the electrostatic binding free energy by solving the PB at different salt concentrations and plotting ΔG_elec versus the logarithmic of salt concentration. Our estimate of SK_pred is the coefficient obtained by a least-square fit of the calculated data, using an in-house program based on a Numerical Recipes algorithm (36).

ΔG_elec is computed as the difference between the electrostatic free energy of the complex and the electrostatic free energy of the individual binding partners in isolation at a fixed 1:1 salt concentration:

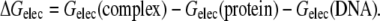(3)

Thus, by computing the electrostatic binding free energy of the various DNA-protein complexes over a specified range of salt concentration where the linearity between ΔG_elec and log[M⁺] holds, we can determine SK_pred and compare it with the corresponding experimental SK_obs whenever it is available. Given that the electrostatic contribution to the free energy of binding predominates in its salt-dependent behavior, Eqs. 2 and 3 then allow for a qualitative prediction of the overall salt-dependence trends of the binding process and thus may aid in suggesting new thermodynamic experiments.

The main concern of our PBE predictions involves the fact that free unbound molecules may undergo significant conformational changes upon binding that is not accounted for in most PBE computational studies. This is especially true for the DNA, whose central region of the DNA moiety is bent ∼180° in complex with TBP (see PDB entries in Table 1). We assumed the same conformations of the free DNA and protein as when they are in the minimized complex or bound state. Therefore, the difference between our computed SK_pred and the experimental SK_obs is in part due to the conformational adaptation of the binding partners upon their association.

Estimate of binding free energies

When the electrostatic free energy of binding is computed at one single salt concentration, 0.4 M, one can add the enthalpic contribution from the van der Waals energies (from the molecular mechanics force field) to the electrostatic free energy of binding:

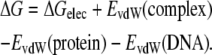(4)

From the above relation, we can estimate the double difference in binding free energy as

(5)

where ΔG_mut and ΔG_wt are the binding free energy of the mutant and wild-type TBP-DNA association process, respectively, as given by Eq. 4. When it comes to computing the ΔΔG, the conformational state of the free DNA may be set arbitrarily since the reference state cancels out, and in this case we are left with the conformational state of the free TBP (protein), which we do not account for in this work. However, our main conclusions are not limited by the assumption of static, unaltered conformations in the free and bound state, since our goal is not to make a direct comparison with the experimental thermodynamic binding data.

RESULTS AND DISCUSSION

Electrostatic signatures of mesophilic and halophilic TBPs: charge distribution and electrostatic potential

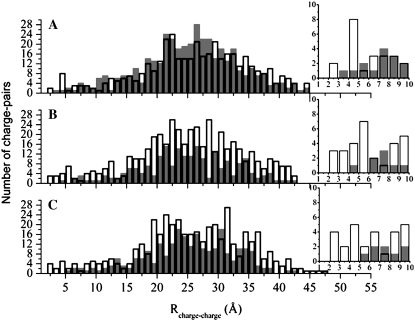
We defined a charge-charge pair based on the minimum distance from the nucleic acid phosphate oxygen atoms to the side-chain carboxylate oxygen of anionic (negatively charged) residues Asp or Glu or the side-chain amide nitrogen atoms of cationic (positively charged) residues Arg and Lys. The distribution of charge-charge pairs is shown in Fig. 2. The graph representing PwTBP shows a significant portion of anionic residues distributed close to the DNA phosphate backbone, with at least four anionic residues within 6 Å from the nearest phosphate group (Fig. 2 A and inset). On the other hand, for HsTBPs and ScTBPs, we see a predominance of cationic residues close to the DNA (Fig. 2, B and C, respectively), which is a trademark of most DNA binding proteins (11).

FIGURE 2.

Distribution of TBP-DNA charge-charge pairs defined by the minimum distance between OD1, OD2, OE1, OE2, HN1, HN2, and NZ protein atoms and OP1 and OP2 DNA atoms. The distribution of anionic charge-charge pairs is represented as gray filled bars, and that of cationic pairs as outlined empty columns. The number of pairs is depicted on the y axis of the graphs, whereas the x axis shows the distance R that separates them. (A) Distribution for halophilic PwTBP, where a large number of anionic residues are observed throughout the protein. (B and C) Distribution for mesophilic HsTBP (B) and ScTBP (C), where the trend seen in A is now reversed: mesophilic proteins show a large distribution of cationic residues. The insets in A–C show the distribution of charged residues within 10 Å of the nearest DNA phosphate group.

Since the overall charge in the mesophilic TBPs is positive (Table 1), the number of internal protein Coulombic charge-charge repulsions will be greater than the number of stabilizing Coulombic charge-charge attractions. The increased number of repulsions may explain the increase of stabilizing β-sheets present in the two mesophilic TBPs and not on PwTBP (less favorable charge-charge interactions are compensated by the formation of additional β-sheets). The favorable charge-charge attractions between the positively charged mesophilic TBP and the negatively charged DNA compensates for the Coulombic repulsion, thus making binding favorable. On the other hand, the halophilic TBP has a neutral net charge (Table 1) and overall negative charges are closer to the DNA (Fig. 2 A). We believe that the increased number of charge-charge repulsions between any equally charged residue in this case is being screened by salt in the high salt environment that PwTBP is subjected to.

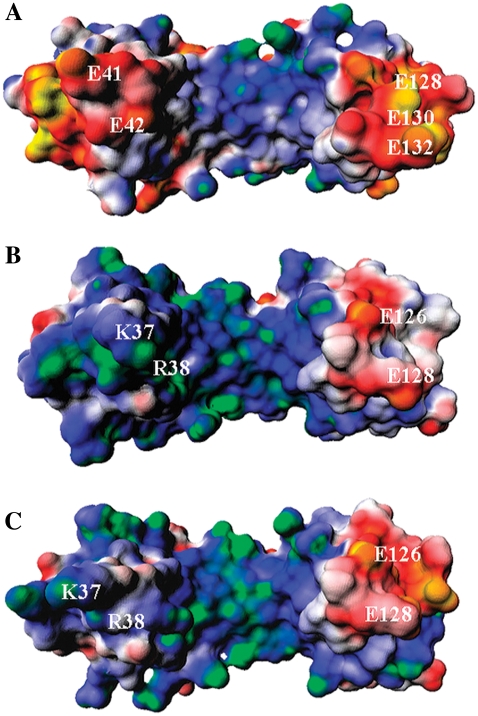
The electrostatic potential for the TBPs is shown in Fig. 3. On the regions flanking the DNA in the binding site, we notice two pronounced negative “stirrups” in this saddle-shaped halophilic protein (Fig. 3 A), when compared to its mesophilic counterparts (Fig. 3, B and C). One striking difference is observed on the stirrup in the left side of Fig. 3 A: PwTBP has a highly negative potential due to the presence of residues E41 and E42. This negative patch is, however, replaced by two positively charged residues (e.g., K45 and R46) in the mesophilic HsTBP and ScTBP, as seen in the sequence alignment of various TBPs (4). The stirrup seen on the right in Fig. 3, A–C, also shows different electrostatic characteristics among the TBPs. The larger negative electrostatic patch seen in PwTBP (Fig. 1) is probably due to three negatively charged residues (E128, E130, and E132), whereas its mesophilic counterparts only show two acidic residues (E126 and E128). In summary, the electrostatic potential maps largely depict the overall pattern previously identified in the charge-charge pair distributions (Fig. 2). Hs and ScTBPs display a higher similarity, reflected in the minimum distance distribution of cationic/anionic residues around DNA (Fig. 2) and the electrostatic potential maps (Fig. 3).

FIGURE 3.

Surface electrostatic potential maps for (A) PwTBP, (B) HsTBP, and (C) ScTBP. The electrostatic potential is colored from the most negative to the most positive and ranges from −2 kT/e to +2 kT/e: yellow-red, negative; white, neutral; and blue-green, positive. The orientations of the TBPs are the same as in Fig. 1 A and some key charged residues are highlighted.

Salt-mediated electrostatic effects in protein-nucleic acid association: halophilic versus mesophilic TBPs

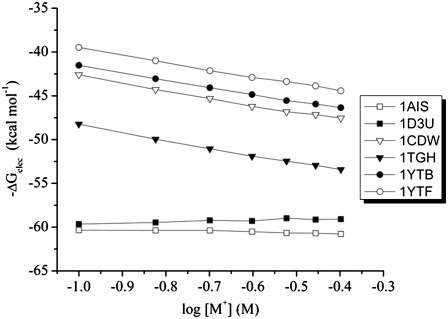
Our PB analysis shows that the absolute value of SK_pred is an order of magnitude greater for the mesophilic TBPs relative to the halophilic TBP (Table 2 and Fig. 4). This qualitative trend is also observed in the thermodynamic studies reported from two different laboratories (13–15,21).

TABLE 2.

Salt dependence of TBP-binding to DNA for mesophilic (Homo sapiens and Saccharomyces cerevisiae) and halophilic organisms (Pyrococcus woesei)

PDB code*	SKpred†	SKobs‡
Hs
1TGH	−6.26	NA
1CDW	−6.04	NA
Sc
1YTF	−5.94	−4.6
1YTB	−5.92	−4.6
Pw§
1D3U	0.73	2.1
1AIS	−0.56	2.1
1D3U-t	−0.04	2.1
1AIS-e	0.24	2.1
1AIS-c	0.16	2.1

^*PDB accession codes.

^†Computed salt-dependence in TBP-DNA-binding.

^‡Experimental salt-dependence (from (13,15)) in TBP-DNA-binding.

^§Pw: t, truncated DNA in the 1D3U structure; e, elongated DNA in the 1AIS structure; and c, energy minimization performed in the presence of transcription factor IIB, later removed for PB calculations.

FIGURE 4.

Salt dependence of the electrostatic contribution in the association of TBP to DNA: SK_pred = −dΔG_elec/dlog[salt] for the mesophilic Saccharomyces cerevisiae (PDB entries 1YTF and 1YTB), Homo sapiens (PDB entries 1CDW and 1TGH), and Pyrococcus woesei halophilic (PDB entries 1AIS and 1D3U).

There is a good agreement between our SK_pred for yeast TPB-DNA binding with the recent SK_obs obtained by Brenowitz and co-workers (13), considering the experimental error for yeast TBP. The authors report a SK_obs of −4.6 ± 0.5, whereas our result is −5.9 (Table 2). The difference in these values may reflect a contribution from structural differences and/or protonation effects upon binding; both of which are not accounted for in our PBE protocol. The comparison between our SK_pred and their SK_obs is further justified, since our PBE calculations reflect closely the experimental conditions from the Brenowitz lab (i.e., moderate salt concentrations and the same TATA element (see Table 1), with a total of 16 DNA basepairs). Besides, one of the crystallographic structures of yeast TBP (PDB entry 1YTB, Table 1) used in that study forms a binary complex with DNA, whereas the other (PDB entry 1YTF, Table 1) forms a ternary complex with DNA and the transcription factor IIA (TBP-DNA-TFIIA). However, the SK_preds of the two complexes are very similar. This implies that the conformations of the ternary (TBP-DNA-TFIIA) and binary (TBP-DNA) complexes of yeast TBPs are similar.

The SK_obs for the halophilic TPB-DNA association is 2.1 (15), whereas our SK_pred values are −0.56 and 0.73, for PwTBPs derived from the minimized PwTBP (PDB entries 1AIS and 1D3U, Table 2). Thus, for at least one of the halophilic TBP-DNA structures, we observe SK_pred >0, which is in good qualitative agreement with the experimental results. A direct comparison of our PB predictions with the experiments on PwTBP might not be appropriate, due to differences in experimental settings, such as DNA length, salt concentration, and temperature conditions. ITC experiments were carried out at high salt concentrations, in the range 0.4–1.9 M, and temperature ranges of 308–328 K (our calculations were done in a moderate salt range of 0.1–0.4 M and at room temperature). The experiments were conducted with 20 nucleotides in each DNA strand, whereas we performed our initial calculations on the 17-basepair DNA crystallographic structure (PDB entry 1AIS, Table 1).

We considered models that better mimic their experimental conditions and examined the impact of the SK_pred when the structure is modified; extending the number of basepairs in the 1AIS structure causes SK_pred to shift and become positive (1AIS-e, Table 2), which is closer to the experimental result (2.1) and correct in sign, whereas truncating the 23-basepair DNA (1D3U-t, Table 2) caused the SK_pred to shift toward a negative sign, as observed for the SK_pred in the 1AIS structure (Table 1). The experimental thermodynamic studies only considered the binary PwTBP-DNA complex. The experimental thermodynamic studies only considered the binary PwTBP-DNA complex. We subjected both binary and ternary complexes to two separate minimizations. For the ternary complex (1AIS-c, Table 2), the TFIIB was removed before PB calculations. This resulted in a positive sign of the SK_pred, probably due to the smaller spatial rearrangement of the complex in the minimization procedure (Table 2). We chose the 1AIS structure (Table 1) for modeling the mutant PwTBPs, since our primary goal is not to reproduce experimental data by exact numbers.

Salt dependence of the binding of mutant TBPs to DNA: SK_obs versus SK_pred

The SK_obs of wild-type PwTBP and its mutants to DNA reveals that all the binding curves converge at high salt concentrations (15), but diverge at moderate to low salt concentrations (i.e., below 1 M NaCl). The halophilic and triple/quadruple PwTPB mutants have an opposite binding behavior in the moderate to low salt end. We interpret only the results at this range of salt concentration since additional interactions can play a role at higher salt concentrations—hydration and specific ion effects such as the disruption of protein salt bridges might be responsible for an increase of the binding affinity with increasing salt concentrations.

The overall net charge of PwTBP is zero (Table 1). Given that positive ions originally bind to DNA phosphate backbone, it is not unreasonable to suggest that additional ions will be soaked into the PwTBP-TATA complex, since a number of anionic PwTBP residues are located quite close to the negatively charged sugar-phosphate backbone, despite the fact that the packing of DNA to TBP seems very tight in the crystal structures of the PwTBP. This does not exclude that ions are incorporated into the protein at residue sites not directly involved in nonspecific or specific DNA-binding. However, since we did not use any explicit ions in our PB calculations, we suggest that the nonspecific long-range electrostatic interactions are largely responsible for the salt dependence of the binding of PwTBP (wild-type and mutants) to DNA at moderate salt concentrations. We observed that the magnitude of SK_pred is increased when key anionic residues in the PwTBP-DNA binding interface are either neutralized (mutated to Ala), or reversed in charge (mutated to Lys) (see Table 3).

TABLE 3.

Salt dependence of the TBP-DNA binding for wild-type Pyrococcus woesei and its mutants

	SK
ID*	SKpred†	SKobs‡
WT	−0.56	2.1 ± 0.3
E12A	−1.51	1.3 ± 0.3
E42Af	−1.43	0.9 ± 0.8
D101A	−1.05	2.1 ± 1.1
E128A	−1.24	1.6 ± 0.3
E12AE128A	−2.13	0.3 ± 0.2
E12AE42Af	−2.36	0.8 ± 0.2
3	−3.98	−1.1 ± 0.1
4	−4.54	−1.7 ± 0.1

^*Wild-type and PwTBP mutants. Labels 3 and 4 represent multiple mutants E12AE41KE128A and E12AE41KE42KE128A, respectively.

^†SK_pred = −dΔG_elec/dlog[salt] is obtained as the coefficient from a least-square linear fit of the computed −ΔG_elec versus the log of [salt] in the range 0.1–0.4 M.

^‡The experimental SK_obs from previous works by Ladbury and co-workers (15,21).

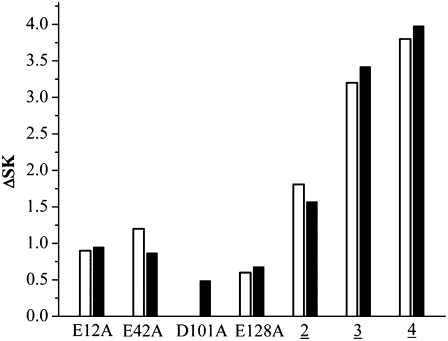
Our resulting ΔSK_pred for the mutant and wild-type PwTBPs agrees very well with the corresponding experimental ΔSK_obs, except for mutant D101A (in the experimental results, ΔSK_obs = 0 for the D101A (Table 3 and Fig. 5)). However, the large experimental error bar in binding energy reported for D101A is an order of magnitude larger than for the other PwTBP mutants (Table 3).

FIGURE 5.

Experimental ΔSK_obs (open bars) and calculated ΔSK_pred (black filled bars) defined as SK_mut − SK_wt. Mutants E12AE128A, E12AE42KE128A, and E12AE41KE42KE128A are labeled 2, 3, and 4, respectively.

As we progress from the double and triple to quadruple PwTBP mutants, the change in SK_pred becomes even more distinct (Table 3), approaching the corresponding SK_pred for human and yeast TBPs (Table 2). This is also observed for the experimental SK_obs (Table 3 and Fig. 5), albeit we can only account qualitatively for our computed SK_pred.

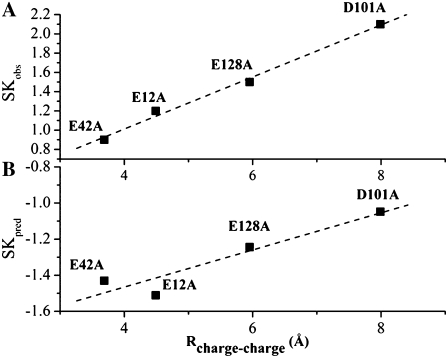
The ITC experimental SK_obs and our calculated SK_pred for single-point alanine mutations versus the charge-charge pair distance is shown in Fig. 6. There is a well defined linear correlation between SK_pred/SK_obs and distance, but it should be noted that the range of SK_obs versus distance differs. Therefore, our comparison can only be validated by relative means or shapes of the curves. Residue E42 is closer to DNA than residue E12, which should ideally result in a slope magnitude increase for the E42A mutant, as seen in the experimental data. In our case, E12A displays a greater increase in SK_pred than E42A (Fig. 6 B). However, the experimental error is larger for the E42A mutant (Table 3) (21), but another possible reason for this discrepancy may be that there is a failure of the MM protocol in completely capturing all conformational changes of the solute. If that proves to be the case, molecular dynamics simulations may be more appropriate to investigate this issue.

FIGURE 6.

SK_pred and SK_obs versus the charge-charge pair distances, R (Å), defined as the minimum distance between the carboxylate oxygens in the protein side-chain atoms and the nearest phosphate oxygen DNA atom as computed from the minimized wild-type coordinates. SK is shown for single-point alanine PwTBP mutants. The linear correlation between SK and R is shown as a dashed line and computed from (A) experiment (SK_obs) correlation coefficient, 0.996 ± 0.05, and (B) the modeled and minimized structure (SK_pred) correlation coefficient, 0.943 ± 0.08. Notice the different scales on the y axis.

Free energy calculations on PwTBP mutants versus thermodynamic data

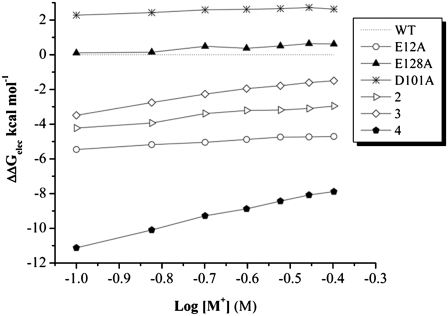
The empirical nonbonded van der Waals energies (vdW) from the Lennard-Jones interaction potential or Coulomb energies, both present in the force field, will be the same in all PB computations at different salt concentrations, since they are carried out on the same structure. Therefore, the magnitude of the slope will be the same (Fig. 7) and trends of the overall SK_pred behavior may actually obscure possible artifacts in our computations. We therefore computed an approximate ΔΔG at a fixed salt concentration (0.4 M) and included the force field vdW energy.

FIGURE 7.

ΔΔG_elec (kcal mol⁻¹) versus the logarithm of salt concentration (1:1 salt, in M). The calculations are based on the nonlinear solution to the Poisson-Boltzmann equation. The wild-type PwTBP is set as the reference energy. Mutants E12AE128A, E12AE42KE138A, and E12AD41KE42KE128A are labeled 2, 3, and 4, respectively.

As shown in Table 4, there is a significant contribution to ΔΔG from the vdW energy term, especially for the E128A mutant, which exhibits a stabilizing vdW contribution. This means that the contacts between the TBP and DNA are favored in this mutant. It appears that relative differences in binding free energies for our computed ΔΔG agrees well with the ITC experimental results, and further improvement is achieved when the vdW energy is included (Table 4). In particular, this is the case for single-point alanine mutations of anionic residues that are close to the DNA and in the binding interface. Thus, our calculations correctly rank the energies, with the exception of the D101A mutant: the opposite sign to the reported values may be due to protocol failure in capturing the conformational adaptability. A preliminary analysis of a molecular dynamics simulation done on the D101A mutant reveals changes in the hydrogen-bond pattern for this mutant (not shown). Given such subtleties (a single hydrogen bond can contribute 1–5 kcal mol⁻¹ to the total binding energy), it would be naïve to assume that the minimization protocol would faithfully take care of issues related to postmodifications done on a crystal wild-type structure. We have demonstrated that the computed SK_pred is indeed sensitive to conformational changes (37). However, SK_pred is less sensitive to the choice of PB parameters (e.g., atomic charge and radii, interior dielectric constant). Conversely, the E12AE41KE42KE128A mutant exhibits a large stabilizing effect that deviates 10 kcal mol⁻¹ from experiments due to stabilizing effects in both the vdW and electrostatic energies. When multiple mutated sites or mutations to bulkier/opposite-charged residue are present, a different picture might emerge due to conformational changes resulting from changes in the overall potential. Such changes may not be captured in the energy minimization calculations, because the energy surface explored may require kinetic energy to traverse energetic barriers that cannot be crossed in the minimization. We are currently exploring these effects by carrying out molecular dynamics simulations on some of the PwTBP mutants reported in this study (Bredenberg and Fenley, unpublished).

TABLE 4.

Comparison between computed and experimental double differences in binding free energies between mutant and wild-type PwTBP at 0.4 M salt concentration

PwTBP	ΔΔG (kcal mol−1)
ID*	ΔΔGelec†	ΔΔHvdW‡	Calculated§	Experimental¶
WT	0.0	0.0	0.0	0.0
E12A	−4.7	3.7	−1.0	−1.0
E42A	−5.7	4.3	−1.4	−0.3
D101A	2.6	0.2	2.8	−0.4
E128A	0.6	−3.2	−2.8	−0.5
E12AE128A	−2.9	1.5	−1.4	−1.3
E12AE42A	−9.7	9.4	−0.3	−1.1
3	−7.9	5.8	−2.1	−1.8
4	−8.2	−4.0	−12.2	−1.9

^*Wild-type and mutant PwTBPs. Labels 3 and 4 represent mutants E12AE41KE128A and E12AE41KE42KE128A, respectively.

^†The electrostatic energy difference between the mutant and the wild-type PwTBP, ΔΔG_elec, is computed from the nonlinear solution to the Poisson-Boltzmann equation.

^‡The vdW energy, ΔΔH_vdW, is the intermolecular DNA-TBP energy difference as computed from the empirical CHARMM 22/27 all-atom force field.

^§ΔΔG is approximated as ΔΔG_elec + ΔΔH_vdW for the mutant minus the wild-type.

^¶Experimental ΔΔG from previous works by Ladbury and co-workers (15,21).

Enthalpy changes and electrostatic potential for the quadruple PwTBP mutant versus the wild-type PwTBP

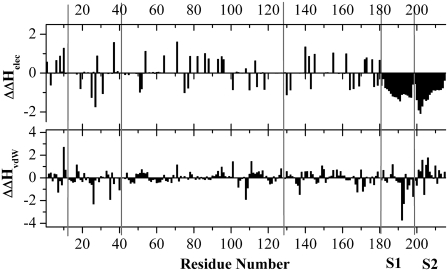
When a charged residue is mutated, the overall protein charge is shifted one unit for a mutation to a neutral residue, (e.g., Glu to Ala) and two units for a complete charge-reversal (e.g., Glu to Lys). Therefore, the PwTBP quadruple mutant (E12AE41KE42KE128A) will experience an overall charge shift by six units, changing its overall net charge to +6e. This poses a significant change when starting from the wild-type structure, which has an overall net charge of zero. Such changes will result in a new potential affecting the remaining unaltered protein residues and DNA. We computed the Coulomb and the empirical force-field van der Waal's energy acting on each residue from the solute (protein and DNA). For this calculation, all atom pairs were included (the conventional cutoff was set to “infinity”) as is the case in the PB calculations. For clarity, the Coulombic energies were scaled by 80 (i.e., roughly the dielectric of pure water). To achieve “real” Coulomb energies, each bar in Fig. 8 should be multiplied by 80 (or 40 to depict the setting in the PB calculations). Thus, it should be borne in mind that the “real” Coulombic energies are 80 times larger, and thus overwhelm the vdW energies. The calculations were done for the quadruple mutant and the wild-type PwTBP. We then subtracted the potential energy that residue “i” feels from any other residue in the protein and DNA for the quadruple mutant from the potential of the equivalent residue “i” in the wild-type PwTBP (Fig. 8).

FIGURE 8.

Residue-based double differences in Coulombic and nonbonded Lennard-Jones energies (i.e., approximated van der Waal's energy computed from the CHARMM empirical force-field function and parameters) between the E12AE41KE42KE128A mutant and wt PwTBP for the minimized structure. The units are in kcal mol⁻¹ and the dielectric constant was set to 80. All interactions between atom pairs were included in the calculations, i.e., no cutoff was used in the calculation of the Coulomb/vdW energy. The bars depict the difference in potential energy acting on each residue from its environment (protein and DNA): ΔE_mut − ΔE_wt = ΔΔH. The positions of residues E12, E41, E42, E128, and the C-terminal end of the PwTBP are indicated with gray lines. The first and second DNA strands (S1 and S2, each 17 nucleotides) are also indicated and begin at position 182. The actual recognition TATA element (see also Table 1) is found at positions 190–198 and 208–216 for S1 and S2, respectively.

A negative value for the double difference in enthalpic contribution from the molecular mechanics Coulomb and vdW energies (ΔΔH_elec and ΔΔH_vdW) for a certain residue at position “i” (where “i” denotes the residue number) indicates that the wild-type residue interacts less favorably with its environment than does the equivalent residue in the quadruple mutant. Only the differences between unmodified residues are viable, so the interaction energies for residues E12, E41, E42, and E128 were all set to zero in both the wild-type and quadruple-mutant PwTBP. We see that the Coulomb energy in the quadruple mutant is more favorable for any of the DNA residues and that the vdW energy is favored in the first strand and disfavored in the second strand relative to the wild-type protein (Fig. 8). Combined, the data indicate that the enthalpic contribution for the DNA is stabilized in complex with the PwTBP quadruple-mutant relative to the wild-type PwTBP. For the protein, all gas-phase Coulomb and vdW energies having a number greater than zero means that residue “i” in the wild-type is favored in the interaction with any other solute atom, whereas a number less than zero means that residue “i” in the mutant protein is favored. All distinct positive peaks in Fig. 8 upper represents positively charged residues Lys or Arg, whereas all distinct negative peaks represent Asp or Glu, suggesting that any of the acidic residues interact more favorably with the solute for the mutant protein. This makes sense since the overall net charge of the quadrupule mutant protein is +6e and thus the number of positively charged residues are in excess.

It is known that higher salt concentrations destabilize salt bridges, and this biophysical relationship has been reviewed recently by Karshikoff and Ladenstein (38). Thus, the less or more favorable relative differences in the Coulomb energies in Fig. 8 upper can be explained by the disruption of internal protein salt bridges and creation of charged residues lacking a binding partner (the overall charge of the PwTBP quadruple mutant is +6e). Although all acidic residues exhibit more favorable interactions in the wild-type, this hints at the actual salt dependence in binding: higher salt concentration weakens the salt bridges formed in the protein and at some level of concentration makes binding to DNA more favorable than being unbound or being a homodimer in solvent.

The experiments report that the melting temperature of the wild-type PwTBP increases at higher salt concentrations (5), but this might actually be the melting temperature of an increased intermolecular dimerization, because the high salinity in the solvent perturbs the intramolecular salt bridges in the monomer PwTBP, and instead promotes intermolecular hydrogen bonds (salt bridges) between the two monomers. Although the same study reports decreased melting temperatures in reducing conditions, this might imply the reduction of carboxylate groups forming intermolecular salt bridges in the PwTBP dimer, as well as the reduction of carboxylate groups forming intramolecular salt bridges in the PwTBP monomer. Very possibly, the reducing environment might also disrupt the internal PwTBP disulfide bridge (C33–C48), making the protein monomer less thermostable. On the other hand, the PwTBP is inert in binding to DNA at lower salt concentrations, because it is stabilized by the intramolecular protein salt bridges. At higher concentrations, these salt bridges are weakened and the protein loses some of its stability, making it more reactive and prone to DNA-binding.

When the stability of the protein is decreased—by experimentally designed site-directed mutagenesis—or when the salt concentration of the solvent is increased and all interactions are screened out, stabilizing salt bridges are weakened, but repulsive forces between equally charged molecules are also diminished. At some point during such solvent screening, unfavorable inter- and intramolecular interactions will be surpassed by the corresponding favorable inter- and intramolecular interactions, and a peptide/protein nucleic acid complex will either be formed or disintegrated. Therefore, an alternative interpretation of the SK_obs in binding of PwTBP to DNA (and other halophilic proteins) is facilitated at increased salinity because of charge-screening from the solvent and not an ion uptake. This screening effect from the solvent makes it tempting to speculate that the dispatch of mesophilic TBPs from DNA at higher salinity is because under such circumstances the TBPs gain in stability as a monomer (or perhaps dimer) rather than bound to DNA; an overall net charge of +16e is a significant portion of charge for the HsTBP, and at concentrations of ∼1–2 M, the protein is not active by means of DNA-binding, at least not in vivo.

The question is whether the PwTBP already is destabilized before DNA binding, or the binding is facilitated in the encounter with DNA such that the salt bridges are disrupted. The latter case has been proposed by Record and co-workers; DNA-binding is combined with disruption of salt bridges when the DNA wraps around the protein (20). However, it is not realistic to deduce such a scenario from a static structure, since alternating rotamers will change the conformation of both the free protein and the protein-DNA complex. Also, different mechanisms may be the case for different types of DNA (or RNA) binding to proteins, depending on how the nucleic acid chain associates (i.e., “wrapping”, induced fit, etc.), and might be revealed from MD simulations. An alternative pathway—at least for the PwTBP—would involve a disruption of the internal protein-protein salt bridges due to increased salt concentration before DNA binding. In such a scenario, the uptake of coions or counterions before DNA binding would be quite plausible. We plan to report a study on this topic in the near future (Bredenberg and Fenley, unpublished).

We observed that the E41K and E42K substitutions generate a positive potential in the TATA-binding site of the protein, which is not surprising, since all other TBPs have positively charged residues at these positions (4). Besides the charge reversal, the charge neutralizations E12A and E128A from quadruple-mutant E12AE41KE42KE128A result in a new electrostatic potential map (Fig. 9), resembling the human and yeast TBP electrostatic maps shown in Fig. 3, B and C. Thus, the change in net charge and the charge distribution of the PwTBP, like our quadruple mutant, causes a shift in its electrostatic signature toward the signature of mesophilic TBPs.

FIGURE 9.

Electrostatic potential map for the PwTBP quadruple mutant protein. The electrostatic potential ranges from −2 kT/e to +2 kT/e: yellow-red, negative; white, neutral; and blue-green, positive. The orientation of the quadruple-mutant PwTBP is the same as in Fig. 1 A.

CONCLUSIONS

The structural and MM-PB analysis reported in this work, and the overall good agreement between theory and experiment, allows us to reach the following proposals:

1. The difference in SK_pred between mesophilic and halophilic TBPs binding to DNA is largely due to the very unique charge and potential distribution of both TBPs, which consequently alters the number of repulsive and attractive electrostatic interactions and how the different salt-dependent energy contributions are affected by increasing salt concentration.

2. The overall net charge at the binding interface as the driving force of protein-nucleic acid association does not depict the whole picture of the salt dependence of the binding process. There is a significant contribution to SK_obs from the number of positive and/or negative charges present in the peptide/protein binding interface, yet it is the overall distribution of charges and the complex ionic network of the entire protein, which interacts with the strong electrostatic field of the DNA, that probably modulates the complex behavior reflected by SK_obs.

3. Our results from this extended view of charge pairs enhance the general rule of ion pairs and salt dependence of the binding of charged ligands to DNA that initially was proposed by Tom Record and co-workers (17). However, we cannot unambiguously state that there is a scenario of specific binding of solvent ions in the TBP-DNA complex, since we did not investigate that point in this study, whereas the Ladbury group suggests that ions are sequestered in the binding interface for the halophilic PwTBPs (14). This quite plausible mechanism should be investigated in future computational studies.