Initial Reaction Dynamics of Proteorhodopsin Observed by Femtosecond Infrared and Visible Spectroscopy

Abstract

We present a comparative study using femtosecond pump/probe spectroscopy in the visible and infrared of the early photodynamics of solubilized proteorhodopsin (green absorbing variant) in D₂O with deprotonated (pD 9.2) and protonated (pD 6.4) primary proton acceptor Asp-97. The vis-pump/vis-probe experiments show a kinetic isotope effect that is more pronounced for alkaline conditions, thus decreasing the previously reported pH-dependence of the primary reaction of proteorhodopsin in H₂O. This points to a pH dependent H-bonding network in the binding pocket of proteorhodopsin, that directly influences the primary photo-induced dynamics. The vis-pump/IR-probe experiments were carried out in two different spectral regions and allowed to monitor the retinal C=C (1500 cm⁻¹–1580 cm⁻¹) and C=N stretching vibration as well as the amide I mode of the protein (1590 cm⁻¹–1680 cm⁻¹). Like the FTIR spectra of the K intermediate (PR_K–PR difference spectra) in this spectral range, the kinetic parameters and also the quantum efficiency of photo-intermediate formation are found to be virtually independent of the pD value.

INTRODUCTION

Proteorhodopsins are new members of microbial rhodopsins found originally in uncultivated marine proteobacteria. Genes for almost 800 proteorhodopsin variants have been identified to date (1), whereas most of the publications deal with a green absorbing variant of proteorhodopsin (PR), which is believed to act as a light driven proton pump (2). Ion pumping retinal proteins are also present in archaea (bacteriorhodopsin (BR) and halorhodopsin (HR) (3–5)) and eucarya (channelrhodopsin I and II) (6,7). All of these seven-helix transmembrane proteins have the retinal chromophore covalently bound to a lysine residue via a Schiff base. On light excitation the chromophore isomerizes (from all-trans to 13-cis for BR, HR, and PR) leading to the first ground state intermediate K (PR_K) followed by a series of thermally driven reaction steps. During this so called photocycle an ion is transported across the membrane. In this process the primary proton acceptor (Asp-85 in BR, Asp-97 in PR) and donor (Asp-96 in BR, Glu-108 in PR) play a crucial role. The mechanism of translocation is well investigated for BR and HR (8–12).

A sequence comparison of PR and BR suggests that most amino acids involved in the proton transport are conserved. Friedrich et al. observed that the pumping direction of PR is pH dependent (13,14). At pH values above the pK_a of the primary proton acceptor Asp-97 of ∼7.0–8.2 (13–15) they monitored BR-like outward proton transport whereas at acidic pH inward directed pumping has been observed. This variable vectoriality is still under discussion because the inversion of the pumping direction could not be confirmed by photocurrent measurements of oriented membranes (16). Studies on the primary dynamics of PR pointed out that the first step of the photocycle is highly affected by pH (17,18). Lenz et al. (18) proposed a branched reaction model illustrating the different dynamics for pH 9 and pH 6. Abramzcyk (19) concluded that after photoexcitation into the Franck Condon region a stretching motion of the conjugated carbon chain on the order of 150 fs is followed by a torsion around the C₁₃–C₁₄ bond leading to a conical intersection (CI) with the ground state. Some molecules will not reach the CI directly, but end up in a minimum of the S₁ potential energy surface, which is separated from the CI by an energetic barrier. From here the CI can be accessed within some picoseconds. The pH dependent differences were visualized as a tilting of the S₁ surface leading to a different fraction of molecules in the faster or slower decay channel. Also the later events in the photo cycles depend strongly on the pH value. Under alkaline conditions the long time dynamics of PR is similar to BR, with the exception that no L-like intermediate is detectable (14), but kinetic measurements of the reaction cycle at acidic pH show only red-shifted spectral states (13,14,20–22). Also the M state, which is believed to be the key state for translocation, is spectroscopically silent, i.e., it was not detected in kinetic studies.

In this study, we investigated the primary dynamics of green absorbing PR in the first 2 ns combining fs time resolved spectroscopy in the IR and visible spectral range to gain a more detailed picture of the reaction dynamics. The spectral range between 1500 cm⁻¹ and 1580 cm⁻¹ contains the ethylenic (C=C) stretching vibration of the chromophore, which is sensitive to the degree of π-electron delocalization along the chain of conjugated double bonds. Therefore it should serve as marker band: the all-trans to 13-cis isomerization of the retinal changes the interaction between the polar protein environment and the protonated Schiff base hence it should influence the π-electron density. The primary dynamics was also investigated in the spectral range between 1590 cm⁻¹ and 1680 cm⁻¹, where the C=N stretching vibration of the retinal is found. Because this mode strongly couples to the N–H bending vibration of the Schiff base (23) it might serve as an indicator for pH dependent differences in the H bonding pattern of the Schiff base during the formation of the first intermediate state.

As the IR measurements were carried out in D₂O, also transient absorption experiments in the visible range were carried out, giving further information on the retinal dynamics under D₂O conditions. This also allows a direct comparison of the experiments in the IR and in the vis spectral range, accounting for changes in the reaction rates by a factor of ∼2 due to isotope effects as has been reported by Szakacs et al. (24)

MATERIALS AND METHODS

Sample preparation

Expression and purification after transformation of PR plasmids in Escherichia coli strain C43 (DE3) at 37°C was carried out similarly as described in Hohenfeld et al. (25). Cells were grown in LB broth supplemented with 50 μg/mL kanamycin, until an optical density at 578 nm (OD₅₇₈) of 0.6–0.7 was reached. PR expression was then induced with addition of 1 mM IPTG and 10 μM all-trans retinal (Sigma-Aldrich). After expression for 3 h, cells were harvested, washed, and resuspended in TRIS–HCl buffer (50 mM TRIS–HCl and 5 mM MgCl₂, pH 8) before submitting them to a cell disrupter (Basic Z Model Cell Disrupter, Constant Systems LTD, Königwinter, Germany). Membranes were pelleted at 220,000 g for 1 h at 4°C, homogenized and solubilized in buffer S (1.5% w/v dodecylmaltoside, 300 mM NaCl, and 5 mM imidazol, pH 6) for 16 h at 4°C. Sedimentation of the membranes at 150,000 g for 30 min left the solubilized PR in the dark red supernatant, which was then incubated with Ni-nitrilotriacetic-acid (Ni-NTA) agarose for 1 h at 4°C under slow shaking. The Ni-NTA resin was filled into a chromatography column and washed extensively with buffer W (0.15% w/v dodecylmaltoside, 300 mM NaCl, 50 mM morpholinoethanesulfonicacid (MES) and 50 mM imidazol, pH 6) until an OD₂₈₀ <0.05 was reached to remove unspecifically bound proteins. Finally, the hexa-His tagged PR was eluted in buffer E (0.5% w/v dodecylmatoside, 300 mM NaCl, 50 mM MES, and 200 mM imidazol, pH 7.5).

The measurements were carried out in D₂O buffer solution (500 mM NaCl and 0.1% n-dodecyl-β-D-maltoside, 20 mM TRIS at pD 6.4 and pD 9.2, respectively). The exchange of the buffer solution and the concentration of the solubilized PR was carried out in a Centriprep centrifugal filter (10 kD MW cut off, Millipore, Schwalback, Germany).

Vis-pump/IR-probe spectroscopy

The source for ultrashort laser pulses is a CLARK CPA 2001 (Clark-MXR, Dexter, MI). It provides laser pulses with a central wavelength of 775 nm, a pulse duration of 170 fs, and a pulse energy of 800 μJ at a repetition rate of 1 kHz. A noncollinear optical parametric amplifier (NOPA) provides the pump pulses with a pulse width of ∼100 fs that are focused into in the sample cell (∼250 μm focal diameter). The NOPA was tuned to a central wavelength of 525 nm. The generation of the IR probe light is based on the setup described in Hamm et al. (26). In a first step a two stage collinear optical parametric amplifier (OPA) converts ∼200 μJ of the laser fundamental to signal and idler photons in the near infrared (20 μJ in sum). In a second step the difference frequency of signal and idler is generated in an AgGaS₂ crystal. The resulting IR pulses are tunable in the range from 3 μm to 10 μm with a bandwidth >100 cm⁻¹. The pulse durations are typically <200 fs with a pulse energy of ∼1 μJ. A long pass filter with a band edge of 3.6 μm suppresses remaining signal and idler photons. The front- and backside reflections of a wedged CaF₂ window with pulse energies of some 10 nJ are used as probe and reference beam, and both were focused into the sample (∼200 μm diameter). The probe focus was adjusted for optimal spatial overlap with the pump spot, whereas the reference beam was displaced ∼2 mm. Both pump and probe beam were linearly polarized with parallel orientation. After transmission through the sample, both infrared beams are dispersed in a 250 mm spectrometer, (Sure Spectrum 250is, Chromex, Albuquerque, NM) and detected by a liquid nitrogen cooled detector with a double array (2 × 32) of MCT elements. The used grating had a groove density of 150 l/mm that results in a dispersion of 11.3 nm/channel, corresponding to ∼3 cm⁻¹ in the spectral region investigated here. The detector signals were sampled on a single shot basis using a multichannel integrator and analog to digital converter system. (IR-6416 Multi-Channel Laser Pulse Spectroscopy System, Infrared Systems Development, Winter Park, FL).

A chopper in the pump beam, running at half the repetition rate, blocked every second pump pulse. Statistical analysis and filtering of the data enabled us to discriminate the effects of sample inhomogeneities (e.g., air bubbles) before averaging and thus to improve the signal to noise ratio. In brief: first only those data are taken into account, where all intensity values are within given absolute limits, especially within the dynamic range of the analog to digital converter. Second, for a selected channel, i.e., one that detects high IR intensities, a intensity histogram of all data is calculated and within this histogram the main peak is fitted with a Gaussian function. The data that are not in a given range around the center of this peak (here: 11/2 times SD) are discarded. Data of successive laser shots (with and without pump pulse) are handled as a pair: the statistical analysis is carried out in both data arrays and shots that fail the limits are always deleted in both arrays. The resulting absorbance difference at each delay time depends on the mean value of the detected intensity of the probe and reference pulses, which passed the data filtering procedure, as:

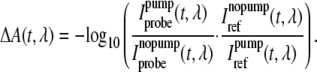(1)

The cuvette is built of two CaF₂ windows with 25-mm diameter and 2-mm thickness and a 50-μm thick PTFE spacer. This corresponds to a sample volume of <20 μL. The resulting absorbance of the sample was in the range of 0.2–0.3 at 525 nm. Rotation and translation of the sample cell guarantee that the probed sample volume is exchanged in between two successive laser shots and thus no photoproducts are excited.

The instrumental response function of the setup was determined in two complementary ways. The instantaneous photo-induced absorbance increase of a 500-μm thick ZnSe substrate was integrated over all channels. The cross correlation time and the time zero was estimated by fitting a Gaussian function to the first derivative. Modeling the cross phase modulation signal (27,28) of pure buffer solution using the procedure described by Kovalenko et al. (29) provides another alternative to determine these parameters. Both methods showed a cross correlation time of ∼0.25 ps. In addition it was found that the amplitude of the coherent signal is negligible for delay times t > 0.3 ps and that the time zero was virtually wavelength independent, i.e., smaller than the step size of 0.1 ps used in the PR measurements.

Vis-pump/vis-probe spectroscopy

The excitation pulses with a central wavelength of 525 nm and a pulse energy of 100 nJ are generated with a NOPA and focused into the sample cell with a focal diameter of 100 μm. Single filament white light pulses (supercontinuum, polarization parallel to excitation) are generated in a sapphire plate and split into two beams, probe and reference. Data detection is implemented in a referenced scheme using two 42-segment diode arrays providing a resolution of 10⁻⁴ absorbance units (30). An instrumental response function of ∼150 fs was achieved and a spectral range from 430 nm to 750 nm was covered.

The fused silica cuvette with 100 μm optical pathlength is moved laterally to ensure the exchange of the probed sample volume. The sample concentration was adjusted to an absorbance of ∼0.5 at the excitation wavelength of 525 nm.

UV/vis absorption spectra were taken before and after the time resolved experiments in the visible and IR to ensure that no long lived photoproducts or photodegradated proteins were accumulated.

Data analysis

For the quantitative data analysis we used a kinetic model that describes the data as sum of exponential decays. A Marquart downhill algorithm optimizes n global time constants τ_i for all wavelengths simultaneously with wavelength dependent amplitudes A_i(λ) for each component. Our model function assumes Gaussian pump and probe pulses with a (1/e) cross correlation width t_cc:

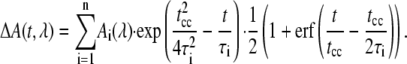(2)

The n wavelength dependent fit amplitudes 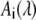represent the decay associated spectra (DAS) for each decay. In this definition an infinite time constant is equal to a time independent offset in the transient absorbance changes and therefore it mainly corresponds to the signal that remains at the maximum delay time in our experiments (∼2 ns).

The UV/vis data were corrected for coherent effects around time zero and for group velocity dispersion using a procedure described by Kovalenko et al. (29), which uses the temporal evolution of the coherent signal of the pure buffer solution.

For the pre-adjustment of the spatial and temporal overlap in the infrared setup a ZnSe substrate was used. For the final optimization the PR sample was used, and the delay time zero was directly estimated by the signal. In an independent experiment we compared the time zero with values derived from measurements of the ZnSe substrate and of the coherent signals of the pure buffer solution. The resulting deviation was smaller than 0.1 ps. It should be noted that both PR samples were measured under identical conditions, i.e., the delay time zero is the same for both the pD 6.4 and the pD 9.2 measurements.

For the transient IR spectra no correction for coherent effects was carried out: because the transient difference spectra show contributions of perturbed free induction decay (31,32) at negative delay times and cross phase modulation (27–29) around time zero, we restricted the data analysis to delay times t > 0.3 ps.

Recent investigations on wt-PR using FTIR (33) and NMR spectroscopy (34) have shown, that the dark adapted state of PR only contains all-trans retinal, so no isomer dependent heterogeneity was taken into account in this study.

RESULTS

UV-vis absorption spectroscopy

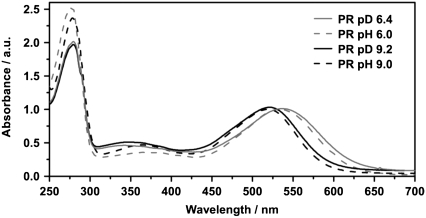
The UV-vis spectrum of PR (Fig. 1) shows a well documented pH dependent shift of the absorption maximum of the main retinal chromophore band (pD 9.2: 521 nm; pD 6.4: 531 nm). This shift is attributed to the protonation state of the primary proton acceptor Asp-97, which shows a surprisingly high pk_a value between 7 and 8.2. In PR solubilized in D₂O the retinal absorption maximum shows the same pH dependence as in PR in H₂O (17,18). Apparently H/D exchange in the protein has no significant influence on the absorption properties in the visible spectral range.

FIGURE 1.

Comparison of absorption spectra of solubilized PR at acidic and alkaline pH/pD values in H₂O and D₂O, respectively. The spectra are normalized with respect to the absorption maximum of the retinal at ∼530 nm. The different signal heights at the protein peak (280 nm) reflect the different purities of the preparation.

Vis-pump/IR-probe experiments

Transient IR absorption experiments were carried out for pD 9.2 and pD 6.4 in the range of 1490 cm⁻¹–1580 cm⁻¹ (region of the C=C stretching vibration of the chromophore, 100 nJ excitation energy) and in the range of 1590 cm⁻¹–1680 cm⁻¹ (region of the C=N stretching vibration of the protonated Schiff base, 400 nJ excitation energy). Both samples were measured without any changes in the optical path or further alignment, leading to directly comparable results. Recent FTIR experiments led to a consistent assignment of the investigated bands (14,23,35).

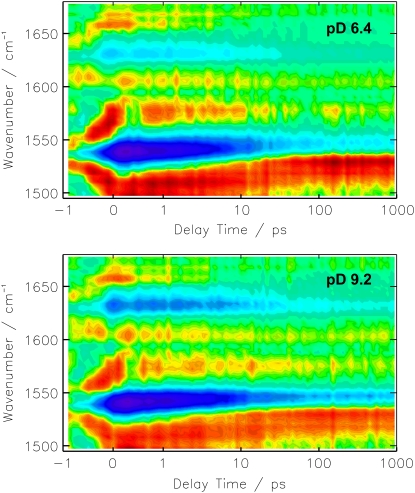
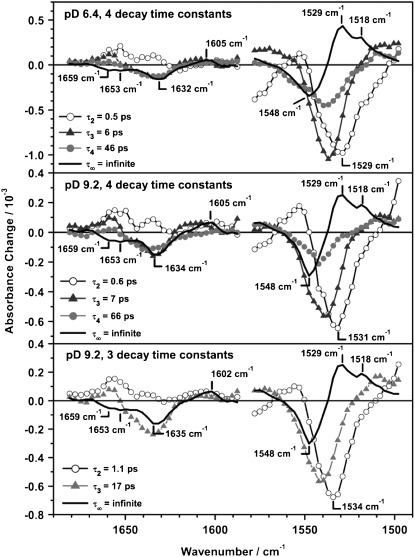
The color-coded 2D plots in Fig. 2 give an overview on the observed transient absorbance changes. The photo-induced absorbance changes appear at positive delay times, whereas effects at negative delay times result from the perturbed free induction decay (31). The signal at delay time zero, during the cross correlation time, is composed of these two effects and might show additional contributions of solvent signals like the cross phase modulation of pump and probe pulse. Negative (blue) features are due to the bleached ground state vibrations and positive (red) contributions represent newly formed (photo-induced) bands. It is evident from the 2D plot in Fig. 2, that the spectral positions of the difference bands are almost equal for pD 9.2 and pD 6.4, which is further substantiated by the transient spectra (Fig. 3). The differences of the amplitudes in the C=C stretching region (1490 cm⁻¹–1580 cm⁻¹) at different pD values are mainly caused by the sample concentration and shifts of the absorption maxima. Interestingly, even the temporal evolution of the difference bands does not show a significant difference between the pD 6.4 and pD 9.2 sample. The comparison of the resulting decay time constants and χ² values, which represent the quality of the fit (Table 1) shows significant improvement on expansion of the fit function from 3 to 4 decay time constants. In contrast, a fit with 5 decay time constants only affects the infinite component, which splits in two parts, i.e., one infinite and one in the range of some ns, which is still much longer than the maximum delay time in our experiment. We thus conclude that the global fit analysis using 4 decay time constants is best suited to describe the data and will be discussed in the following. Nevertheless, the DAS of the fit with 3 time constants already resemble the spectral components of the photoproduct formation, decay of the initial bleach signal and the PR_K–PR difference spectrum at long delay times (Fig. 4, bottom).

FIGURE 2.

Transient absorbance changes of solubilized PR in D₂O at pD 6.4 and pD 9.2 after photoexcitation at 525 nm. The amplitudes are color coded: red, positive; green, zero; blue, negative absorbance change. The time axis is linear in the range from −1 ps to +1 ps and logarithmic for longer delay times.

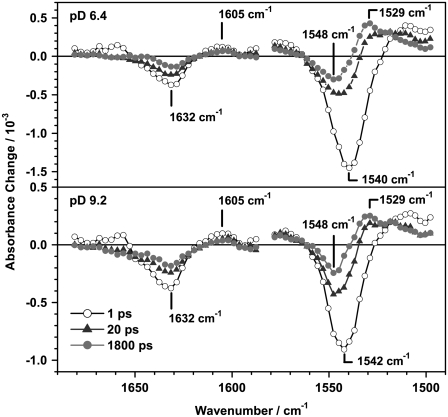
FIGURE 3.

Transient IR difference spectra of PR at pD 6.4 and pD 9.2 in the regions 1590 cm⁻¹–1680 cm⁻¹ (C=N stretching) and 1500 cm⁻¹–1580 cm⁻¹ (C=C stretching) at selected delay times. Differences in the amplitudes at the different pD values originate mainly from differences in the protein concentration.

TABLE 1.

Global fit analyses for the vis-pump/IR-probe data of solubilized PR in D₂O using a different number of decay time constants

Sample/fit parameter	τ2/ps	τ3/ps	τ4/ps	τ5/ps	τ∞	χ2/10−6
PR pD 6.4/3 decay times	1.2	17			Infinite	5.91
PR pD 6.4/4 decay times	0.5	6	46		Infinite	5.01
PR pD 6.4/5 decay times	0.4	6	40	3200	Infinite	4.91
PR pD 9.2/3 decay times	1.1	17			Infinite	3.20
PR pD 9.2/4 decay times	0.6	7	66		Infinite	2.84
PR pD 9.2/5 decay times	0,6	7	54	4800	Infinite	2.76

Due to the experimental response function τ₁(vis) can not be resolved. The numeration of time constants therefore starts at τ₂.

FIGURE 4.

DAS of the global fit analysis of PR at pD 6.4 and pD 9.2 using four decay time constants and pD 9.2 using 3 decay time constants. Four decay time constants are necessary for an optimized description of the data set, whereas an additional time constant does not improve the fit. Nevertheless, it is noticeable that all spectral features are also apparent in the DAS of the fit using 3 decay time constants. The labeling starts with τ₂ to allow a direct comparison to the results obtained in the visible.

The decay constants cannot unambiguously be assigned to distinct kinetic processes, like e.g., the S₁→S₀ transition for the following reasons. It can be assumed that internal vibrational redistribution leads to hot molecules in the excited state. After the transition to the ground state, hot molecules are also formed in the ground state of cis and trans configuration. The decrease of the related intramolecular temperature corresponds to time dependent shifts and inhomogeneous broadening of the vibrational bands. For the protonated Schiff base of all-trans retinal it was shown that the intramolecular temperature is 550 K directly after the S₁→S₀ transition and that vibrational cooling occurs within 50 ps (36). This leads to nonexponential temporal behavior, which can only be described insufficiently with the kinetic model used as has been shown e.g., for the vibrational cooling of azobenzene (37). Nevertheless, in the following we present a description of the global fit analysis as it was applied to other retinal proteins (38–40).

For a direct comparison with the results in the visible (Table 2), the labeling of the time constants starts with τ₂. The resulting decay times for the pD 6.4 measurement (τ₂ = 0.5 ps, τ₃ = 6 ps_, τ₄ = 46 ps_, τ_∞ = infinite) are only slightly different from values derived from the pD 9.2 measurement (τ₂ = 0.6 ps, τ₃ = 7 ps_, τ₄ = 66 ps_, τ_∞ = infinite). Because the DAS of both sample preparations are very similar (Fig. 4), the photo-induced transient spectra will be discussed independently of the pD value.

TABLE 2.

Global fit analyses for different vis-pump/vis-probe measurements of solubilized and reconstituted PR

Sample	τ1/ps	τ2/ps	τ3/ps	τ∞
PR solubilized, D2O pD 6.4	<0.15	1.6	25	Infinite
PR solubilized, H2O pH 6.4	0.15	1.0	16.2	Infinite
PR reconstituted, H2O pH 6.0	<0.2	0.7	15	Infinite
PR solubilized, D2O, pD 9.2	<0.15	0.7	21	Infinite
PR solubilized, H2O, pH 9.0	0.14	0.28	9.5	Infinite
PR reconstituted, H2O, pH 9.0	<0.2	0.4	8	Infinite

The values for H₂O solutions are taken from Huber et al. (17) and Lenz et al. (18).

1500 cm⁻¹–1580 cm⁻¹ (C=C stretching region)

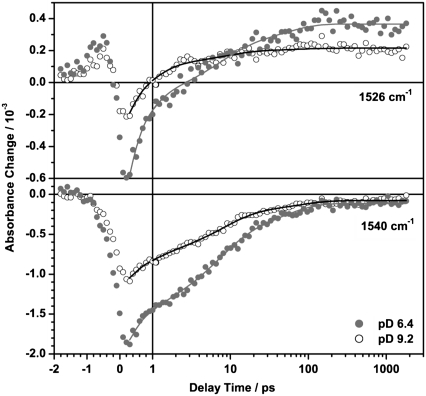
Immediately after excitation two dominant bands appear at 1540 cm⁻¹ (−) and 1510 cm⁻¹ (+). The negative band at 1540 cm⁻¹, which nicely shows the signature of the perturbed free induction decay at negative delay times, is assigned to the depopulation of the C=C stretching vibration of ground state PR. The peak position of this instantaneous bleach signal depends slightly on the pD value and is shifted by one channel (∼3 cm⁻¹). This is in good agreement with the empirical finding for several retinal proteins (41,42), where also a linear dependence of the chromophore absorption maximum in the visible and the position of the C=C stretching vibration (∼−4 nm/cm⁻¹) was shown. The positive band in the region of 1500 cm⁻¹–1530 cm⁻¹ can be attributed to the C=C stretching vibrations of vibrationally excited molecules in the S₁ and in the S₀ state. The signal at long delay times represents the spectral signature of the K intermediate.

The DAS of the infinite time constant τ_∞ (Fig. 4) represents the difference spectrum of the K intermediate and the ground state PR (PR_K–PR). It shows two bands at 1548 cm⁻¹ (−), 1529 cm⁻¹ (+), and a shoulder at 1518 cm⁻¹ (+) that resembles the spectral shape of the PR_K–PR difference spectrum taken in D₂O at cryogenic temperatures (35). The reported band positions in FTIR PR_K–PR difference spectra depend on the sample preparation and pH value and are in the range of 1546–1538 cm⁻¹ (−) / 1523–1514 cm⁻¹ (+) (14,35,43,44). To our knowledge, no photo-induced difference spectrum of PR in D₂O at room temperature is published, which has a sufficiently high time resolution for a direct comparison with the early K intermediate observed in this study. Taking into account the different sample conditions, the DAS of the infinite time constant resembles the published PR_K–PR difference spectra quite well.

The DAS of τ₃ (6 ps for pD 6.4 and 7 ps for pD 9.2) and τ₄ (46 ps for pD 6.4 and 66 ps for pD 9.2) show a dominant negative band whose position and shape correspond to the instantaneous negative signals around 1540 cm⁻¹ (−). Therefore we assign these time constants to a biphasic recovery of the initial bleach signal. The time evolution at the maximum of the ground state PR C=C band (1540 cm⁻¹) is shown in Fig. 5.

FIGURE 5.

Transient absorbance changes of PR at pD 6.4 (•) and pD 9.2 (○) at selected wavenumbers in the region of the C=C stretching vibration. Solid lines represent results of the global fit analysis of the data set. Main contributions arise from the product band (1526 cm⁻¹) and the bleaching signal due to the depopulation of the ground state vibration (1540 cm⁻¹).

The DAS of the shortest time constant τ₂ (0.5 ps for pD 6.4 and 0.6 ps for pD 9.2) significantly differs from the DAS of τ₃ and τ₄, thus the related process is not connected with the recovery of the PR ground state. The minimum (1529 cm⁻¹ for pD 6.4 and 1531 cm⁻¹ for pD 9.2) coincides with the maximum of the PR_K–PR difference spectrum (1529 cm⁻¹). Furthermore the shoulder at 1518 cm⁻¹ in the PR_K–PR spectrum correlates with the negative amplitude in the DAS of τ₂ whereas τ₃ and τ₄ do not contribute to the formation of this positive product band. This can be verified at 1526 cm⁻¹ (Fig. 5), where the transition of the initially negative contribution into the positive photoproduct signal is dominated by the shortest time constant. This holds also true for the temporal evolution of the positive product bands at wavenumbers above 1570 cm⁻¹ (pD 6.4) and 1564 cm⁻¹ (pD 9.2), respectively. An analogous, direct evidence for the formation of the negative PR_K–PR difference band (1548 cm⁻¹) cannot be given, because it is obscured by the instantaneous bleach and is thus not observable in any single transient.

Although the τ₂ process is associated with the formation of the PR_K–PR difference spectrum, its DAS is not an exact mirror image of the photoproduct spectrum, indicating that this decay channel does not populate the K intermediate state exclusively. Moreover it cannot be excluded that spectral features of PR_K appear within our time resolution and thus are not found in the global fit analysis.

1590 cm⁻¹–1650 cm⁻¹ (C=N stretching region)

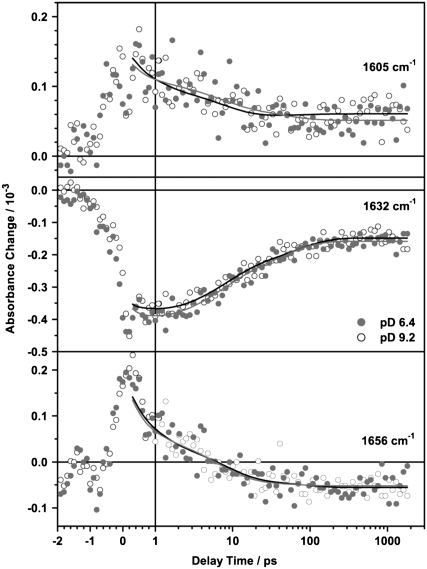
In the range from 1590 cm⁻¹ to 1680 cm⁻¹ PR shows a much higher overall protein absorption and smaller absorbance differences, resulting in a poorer signal to noise ratio. The higher excitation energy (400 nJ instead of 100 nJ) does not allow a direct comparison of the relative amplitudes in the C=C and the C=N spectral region.

The most prominent signals are a strong negative band at 1632 cm⁻¹ and a smaller positive band at around 1605 cm⁻¹, which partially decay on a 10 ps timescale. Around 1660 cm⁻¹ an initially positive band decays and turns negative within 20 ps. This is shown in the transient spectra (Fig. 3) and even more clearly in the corresponding transient absorbance changes at 1656 cm⁻¹ (Fig. 6, bottom). The C=N vibration of the Schiff base is coupled to the N–H or N–D bending mode, respectively and therefore shows a strong solvent dependence on H/D exchange (23,35,43). In D₂O the C=N stretching band is downshifted by ∼22 cm⁻¹ in comparison to H₂O. As we were measuring in D₂O buffer, the band is expected to appear at around 1635 cm⁻¹ for both pD values (23). Consequently, the band at 1632 cm⁻¹ can be assigned to the bleaching signal of the ground state C=N vibration and the small positive band observed around 1600 cm⁻¹ at long delay times corresponds to the C=N vibration of the K intermediate. The results of the global fit analysis in the region of 1590 cm⁻¹ to 1650 cm⁻¹ (Fig. 4) are interpreted as follows: the DAS of the infinite time constant represents the spectrum of the previously reported difference spectrum PR_K–PR (23,35,43). The DAS of τ₃ and τ₄ resemble the spectra of the bleached ground state vibration and therefore describe a biphasic recovery of the PR ground state. Unlike for the C=C region, the DAS of the fastest component τ₂ cannot be assigned to the formation of positive photoproduct bands, because a negative amplitude in the corresponding DAS in the C=N region is missing. However, due to the small absorbance changes and the low signal/noise ratio in this region, the accuracy of the fit is decreased and thus especially the DAS of the shortest time constant is not well defined.

FIGURE 6.

Transient absorbance changes of PR at pD 6.4 (•) and pD 9.2 (○) at selected wavenumbers in the region of the C=N stretching vibration. Solid lines represent results of the global fit analysis of the data set. Main contributions arise from the product band (1605 cm⁻¹), the bleaching signal due to the depopulation of the ground state vibration (1632 cm⁻¹), and a protein contribution in the amide I region (1656 cm⁻¹).

1650 cm⁻¹–1680 cm⁻¹ (protein contribution)

The negative band in the amide I region around 1660 cm⁻¹, appearing at long delay times, is ascribed to protein vibrations. Similar bands have been reported for FTIR PR_K–PR difference spectra (23,35,43), as for fs vis-pump/IR-probe experiments on BR in H₂O (39). The characteristics in this spectral region significantly differs from that in the region of the C=C stretching vibration and the C=N stretching vibration of the retinal. The negative signal, which evolves at long delay times, is clearly resolved in the DAS of the infinite time constant (Fig. 4) and in the corresponding transient absorbance changes (Fig. 6, bottom). In contrast to the C=C and the C=N stretching region, no vibrational bands of the retinal are expected in this spectral region and there is no evidence for an instantaneous bleach of a ground state vibration on electronic excitation, which would show the signature of the perturbed free induction decay. This is further confirmed by the global fit analysis: both τ₂ and τ₃ unambiguously contribute to the formation of this negative signal. The DAS of τ₄ shows a small positive amplitude, indicating that the related process is also contributing to the photoproduct in this region. The signal therefore reflects structural changes of the protein environment due to the conformational changes of the retinal.

Vis-pump/vis-probe experiments

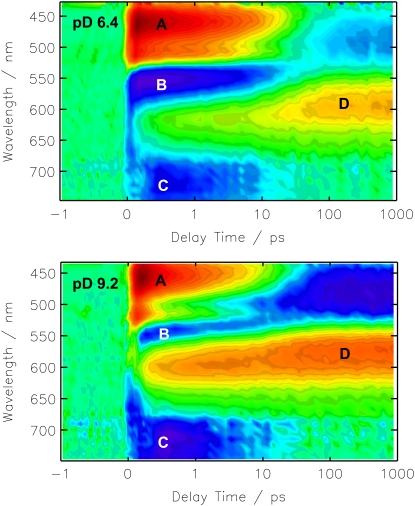
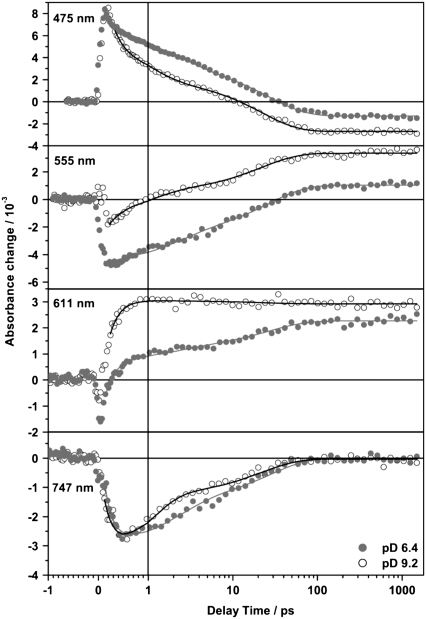
Fig. 7 shows the spectral evolution of PR in D₂O at pD 9.2 and pD 6.4 after photoexcitation. The color code is identical to Fig. 2. The general spectral features are similar to the data obtained for PR in H₂O (17,18) and the interpretation and assignment is essentially the same. Both photo-induced difference spectra show well resolved features in four spectral regions. Around 450 nm a positive absorbance change is observed, which is attributed to the excited state absorption. This signal arises within the time resolution and decays dependent on the pD value on a 10 ps timescale. At the red most end of the investigated spectral range, for wavelengths above 700 nm, both PR samples show negative contributions indicative for stimulated emission. These appear directly after photoexcitation and decay on the same timescale as the excited state absorption as can be seen in the DAS (Fig. 9). For the pD 9.2 sample around 550 nm a weak negative signal is observed at short delay times, which is due to the depopulation of the ground state and strongly overlapping the excited state absorption. After the decay of the excited state the residual ground state bleaching signal occurs blue shifted. This shift results from the overlap of the ground state bleach with a positive absorption band emerging around 580 nm, the main absorption band of the first ground state intermediate K. Slightly different features can be observed in the photo-induced difference spectra of the PR sample at pD 6.4. Here, for short delay times around 560 nm, the negative ground state bleaching signal is more prominent (Fig. 8). This is explained by the shifted ground state absorption maximum of the sample at pD 6.4. At long delay times the amplitudes of the induced absorption around 600 nm as well as of the negative absorption around 490 nm are half as high at pD 6.4 than at pD 9.2.

FIGURE 7.

Transient absorbance changes of solubilized PR in D₂O at pD 6.4 and pD 9.2 after photoexcitation at 525 nm. Main contributions arise from the excited state absorption (A), ground state bleaching (B), stimulated emission (C), and the formation of the red shifted intermediate (D). Color coding and scaling is according to Fig. 2.

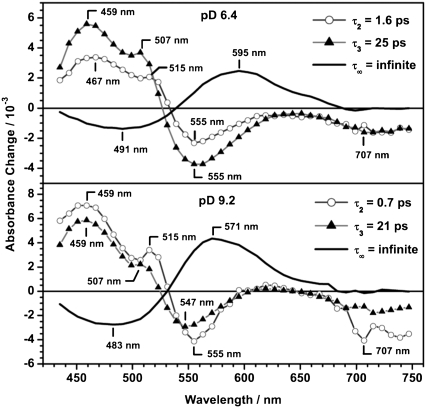
FIGURE 9.

DAS of PR at pD 6.4 and PR at pD 9.2 of the global fit analysis using four decay time constants. The DAS for the shortest decay time constant τ₁ is not shown (see text).

FIGURE 8.

Transient absorbance changes of PR at pD 6.4 (•) and pD 9.2 (○) at different wavelengths. Solid lines represent results of the global fit analysis of the data set. They show the decay of the excited state (475 nm), the recovery of the ground state (555 nm), the rise of the photoproduct band (611 nm), and the decay of the stimulated emission (747 nm).

Four time constants were used for an optimized fit of the data (Table 2). The smallest decay time constant τ₁ is in the range of the time resolution of this measurement and hence is obscured by coherent effects due to the temporal overlap of the pump and the probe pulse. Coherent effects like wavepacket motion and the dynamic Stokes shift also will influence the DAS of this short time constant. Because these processes can not be assigned to mono-exponential decay functions, the resulting DAS is not directly correlated to a discrete process. Thus, only the DAS of the slower kinetic components are shown (Fig. 9). Nevertheless, this time constant τ₁ is necessary to describe the data appropriately. The time constants derived in this work are about a factor of 2 higher (Table 2) than the results obtained for PR in H₂O buffer (17,18). This can be attributed to the kinetic isotope effect by H/D exchange and is in agreement with kinetic studies of the ion pumps BR, HR, and PR by Szakács et al. (24). They found that transitions that do not require large H-bond rearrangements and/or proton motions show a moderate isotope effect of a factor of 1.5–2. In the DAS of τ₂ and τ₃ strong contributions of excited state absorption and stimulated emission as well as ground state bleach are observed at both pD values. The process that is connected to these time constants is ascribed to a bi-exponential decay of the excited state. At pD 6.4 this process is dominated by the slower kinetic component τ₃. In contrast, at pD 9.2 the faster component has a higher amplitude, indicating that the faster reaction channel is preferred if Asp-97 is deprotonated. At both pD values the DAS of the infinite time constant (τ_∞) reflect the formation of the early K intermediate. Comparing the DAS of τ_∞ for pD 6.4 and 9.2 the overall spectral shape is conserved, whereas the amplitude is considerably higher for pD 9.2. This might either be due to pD dependent differences in the quantum yield or to different spectral overlaps of the positive PR_K absorption and the corresponding, negative ground state PR bleaching bands. This was analyzed more quantitatively with the following assumptions: The PR_K–PR difference spectrum is composed of two spectral components. The negative contribution is caused by the depopulation of the all-trans PR ground state and thus is directly correlated to the cw absorption spectrum of PR. The positive contribution is due to the absorption of the K state. Both absorption bands were treated as Gaussian functions. The spectral position and the half width of the bleach signal were directly extracted from the particular cw absorption spectrum of each pD value. For modeling of the positive PR_K band the half width of the respective ground state was assumed. The difference spectra were generated varying the spectral position of the positive PR_K band. For a spectral position of ∼550 nm the resulting difference spectrum matches the experimentally observed PR_K–PR difference spectrum for both pD values. Using the same, but normalized Gaussian functions the resulting difference spectra resemble both spectral shape and amplitude of the experimental spectra. In conclusion, the pD dependent differences in the DAS of τ_∞ mainly originate from the pD dependence of the cw absorption spectrum, and the isomerization quantum yield is not strongly affected by the pD value.

DISCUSSION

In this study we present a combined vibrational/electronic spectroscopic study of the primary dynamics of the transmembrane retinal protein PR. The measurements were carried out under identical sample conditions (protein preparation, buffer), so a direct comparison of the initial processes occurring within the first two nanoseconds after photoexcitation is possible.

pD dependence of the PR_k formation

As shown in the previous sections, different information concerning the spectral and temporal behavior were obtained in the visible and IR. On the one hand, pD dependent spectral differences are observed in the visible transient absorption data, which are due to the pD dependent shift of the main absorption band of the chromophore (13,14). On the other hand, the pD dependent shifts of the vibrational bands of the ground state PR are very small, which can be verified by the position of the initial bleach signal in the fs vis-pump/IR-probe experiments (Figs. 2 and 3). FTIR difference spectra (PR_K–PR) at low temperature show that the protonation of Asp-97 has only a minor influence on the position of difference bands of the C=C and the C=N stretching vibrations (35,43). The PR_K–PR difference spectrum in this spectral region is thus found to be nearly unaffected by an altered H-bonding pattern or changed electrostatic interactions at different pH values. This is in good agreement with our finding that the spectral properties of the DAS of τ_∞ in the IR experiment are virtually independent of the pD value. Consequently, the pD dependence of the quantum yield of PR_K formation can readily be derived from the infrared data, whereas the different superposition of pD dependent bands in the visible makes this evaluation difficult. As the initial bleach signal at delay time zero is proportional to the number of excited molecules, it can be used to normalize the data sets and to directly compare the DAS of the infinite time constants. The comparison shows that the quantum yield of photoproduct formation is virtually pD independent. This leads to the conclusion that predominantly shifted ground state absorption bands cause the differences in the PR_K–PR difference spectrum for changed pD values. The quantum efficiency of the primary reaction, i.e., the formation of the K intermediate, is therefore not affected by the protonation state of the primary proton acceptor Asp-97.

Kinetic analysis

The global analysis of the vis-pump/vis-probe data yields 4 decay time constants, which show a less pronounced pD dependence than the values for PR in H₂O (Table 2) (17,18). The shortest time constant τ₁ is attributed to a wavepacket motion out of the Franck Condon region. The subsequent transition to the electronic ground state is believed to occur via two decay channels (τ₂ and τ₃) leading both to the initial all-trans and the 13-cis photoproduct state. The DAS of the infinite time constant (τ_∞) represents the PR_K–PR difference spectrum.

Due to the instrumental response function of the IR setup time constants <200 fs cannot be resolved. The global analysis of the vis-pump/IR-probe data set was carried out with varying parameters, i.e., using 3, 4, and 5 decay time constants (Table 1). Although the values for a fit using 3 decay time constants are in the range of those derived for the visible spectral range, the comparison of the global fit analyses strongly suggests that 4 time constants yield an optimized description. Consequently, one additional time constant is required for the adequate description of the subsequent reaction dynamics in the IR. Because the identical sample was used for both experiments, these differences cannot originate from different sample conditions. We attribute it to the fact that the transient IR spectra are sensitive to local structural changes, internal vibrational redistribution, and vibrational cooling in the surrounding protein. These processes might even dominate the transient IR spectra and affect the shape and position of the difference bands. This results in nonexponential decays (see above), where the kinetic model (Eq. 2) yields only a severely limited description (36,37). Nevertheless, the kinetic analysis in the C=C region indicates that the formation of the photoproduct bands is associated with the shortest time constant τ₂. A similar statement cannot be given for the spectral range of 1590 cm⁻¹–1680 cm⁻¹ due to the reduced signal to noise ratio, although the DAS indicate that the photoproduct in the C=N region as well as the amide I contribution around 1650 cm⁻¹ already appear on a subpicosecond timescale. This is in agreement with a recent vis-pump/IR-probe study of reconstituted PR (green absorbing variant) in H₂O at pH 9.5 (45). It was shown that both the chromophore isomerization and the response of the protein backbone in the amide II region appear with a time constant of 0.5 ps to 0.7 ps.

The DAS of the subsequent time constants τ₃ and τ₄ resemble the spectral shape of the initial bleach signal in the C=C and C=N stretching region and are thus assigned to a biphasic recovery of the PR ground state vibrations. Moreover both time constants contribute to the formation of the negative amide I band at 1650 cm⁻¹.

However, the DAS and decay time constants for both pD 6.4 and pD 9.2 are practically identical. Thus, it must be concluded that the processes observed in the IR are not affected by the pD value, which can be explained as follows: On the one hand cooling processes might dominate the dynamics observed in the IR and obscure pD dependent differences in the data. On the other hand, vibrational bands observed in this study might not be directly correlated to the isomerization coordinate, e.g., the C=C stretching frequency of the retinal is supposed to reflect the π-electron delocalization, which is not correlated directly to the torsional motion. Atkinson et al. (46) compared the J intermediate formation in the photocycle of native BR and modified BR (BR_5.12), containing an artificial retinal with a five-membered ring spanning the C₁₂−C₁₃=C₁₄ bonds thereby blocking C₁₃=C₁₄ isomerization. Similar changes in the C=C stretching frequency were reported for both cases, indicating that the isomerization is not directly monitored in this spectral region. Amsden et al. (45) found for reconstituted PR in H₂O at pH 9.5 that the formation of the PR_K intermediate appears at the same timescale both in the C=C and the C–C (∼1200 cm⁻¹) stretching region. Further experiments in this spectral region will show whether this holds also true for PR under acidic conditions.

Kinetic isotope effect

The transient absorbance changes in the visible show a less pronounced pD-dependence for PR in D₂O than for PR in H₂O (17,18) (Table 2). For acidic pH both time constants τ₂ and τ₃ are increased by a factor of 1.6 in D₂O, whereas for alkaline pH they are increased by a factor of ∼2.3. This indicates that the isotope effect is more pronounced under alkaline conditions. As a high resolution structure of PR is not available yet, the structural origin is not clear, but modifications in the assembly of H₂O- or D₂O-clusters or changes in the hydrogen bonding strength of the Schiff base with these clusters are probable. Vibrational studies (23,35) reported pH dependent hydrogen bonding networks in the binding pocket of PR, which is in agreement with our assumption that the influence of the H/D exchange on the hydrogen bonding network is pH dependent.

Because the residues Asp-97 and Asp-227 are assumed to stabilize the proposed water cluster, the investigation of the D97N and the D227N mutant will yield more detailed information on the structure of the retinal binding pocket and its influence on the primary reaction dynamics.

CONCLUSION

Unlike the situation in archaeal rhodopsins like BR, where a single point mutation can suffice to change the functionality (e.g., from an outward directed H⁺ pump to an inward directed Cl⁻ pump (47,48)), the situation in the bacterial PR is more complex. Nevertheless, ultrafast photodynamics can be understood within the framework of an established reaction mechanism for archaeal retinal proteins in the IR (38–40,45,49–51) and visible spectral range (52–55). The transient absorption measurements of retinal proteins show that after excitation the wavepacket moves out of the Franck-Condon region. For BR this movement is discussed to be an in-plane stretching vibration of the conjugated carbon chain of the retinal initiating the isomerization reaction. For PR no indication could be found that the initial stretching mode is influenced by the protonation state of Asp-97 (18), which coincides with our vis-pump/vis-probe measurements in D₂O. The initial stretching is then followed by a torsional motion leading back to the ground state (19). For PR, time-resolved spectroscopy shows that the decay of the excited state is biphasic. Both the initial all-trans and the 13-cis photoproduct state are assumed to be populated via the two channels. The slower decay channel is favored for pD 6.4, whereas for pD 9.2 the faster channel is preferred.

On probing in the infrared spectral range, no indication for a pD dependent reaction was found. The spectral features of the PR_K–PR photoproduct evolve with a time constant of ∼0.5 ps. Also protein contributions develop on this timescale. This is in agreement with the result of Diller et al. (38) and Amsden et al. (45) that for retinal proteins collective conformational changes appear already on the picosecond timescale.