Magnetic Stimulation of One-Dimensional Neuronal Cultures

Abstract

Transcranial magnetic stimulation is a remarkable tool for neuroscience research, with a multitude of diagnostic and therapeutic applications. Surprisingly, application of the same magnetic stimulation directly to neurons that are dissected from the brain and grown in vitro was not reported to activate them to date. Here we report that central nervous system neurons patterned on large enough one-dimensional rings can be magnetically stimulated in vitro. In contrast, two-dimensional cultures with comparable size do not respond to excitation. This happens because the one-dimensional pattern enforces an ordering of the axons along the ring, which is designed to follow the lines of the magnetically induced electric field. A small group of sensitive (i.e., initiating) neurons respond even when the network is disconnected, and are presumed to excite the entire network when it is connected. This implies that morphological and electrophysiological properties of single neurons are crucial for magnetic stimulation. We conjecture that the existence of a select group of neurons with higher sensitivity may occur in the brain in vivo as well, with consequences for transcranial magnetic stimulation.

INTRODUCTION

Transcranial magnetic stimulation (TMS) is an exciting tool that allows probing the internal function of the brain in a noninvasive manner and promises treatment of a number of difficult mental illnesses such as depression (1–3). One surprising aspect of the technique is that the same magnetic stimulator that can excite neurons in the cortex when applied through the skull, was never reported to elicit any spiking activity in the same cortical neurons when they are grown in a dish. This is despite the fact that the magnetic coil can be brought closer to the neuronal culture than to the cortex, leading to a significantly larger induced electric field. This fact has remained a puzzle over the past two decades, with surprisingly little mention in the TMS literature. It has generally been ascribed among practitioners to the high sensitivity of finding the precise direction in which the magnetic coil should be placed over the brain, and perhaps to an enhanced sensitivity to magnetic stimulation of certain areas over others.

Solving this seeming paradox involves understanding the mechanisms of TMS from both a physical and an electrophysiological perspective. First, one must solve the electric field that is induced by the magnetic pulse. This is obtained using Maxwell's equations and is affected by the size, shape, and orientation of the coil (4) and by the shape of the magnetic pulse (5,6). A second physical question is the effect of finite boundaries, which accumulate charge that can weaken and distort the induced electric field (7,8). Boundary effects are in turn determined by the size, shape, and inhomogeneous electrical properties of the neuronal tissue (9–11).

Given an electric field, we must understand its effect on the electrophysiological behavior of the nerve. The accepted approach to this problem is modeling the nerve as a passive cable (12,13). Experiments on peripheral nerves proved this model successful (14), and both modeling and experimental evidence demonstrate the role of nerve orientation and geometry in determining its magnetic excitability (15–17). Additional findings demonstrated the importance of background neural activity for excitability in TMS (18–20).

Significant advances in our understanding of the physics behind mechanisms of TMS in vivo have been attained previously (21–29). Modeling of single (30) or multiple (31) central nervous system (CNS) neurons was attempted and single neurons in the brain were recorded during TMS (32) but it is already clear that without an in vitro model for TMS, advances will be limited (33). Indirect evidence of an effect in vitro was obtained from c-Fos expression in rat brain slices (34,35) and from cellular effects on rat hippocampal neurons in culture (36). An in vitro setup could bridge the gap, setting up geometries in which electromagnetic induction can be analytically solved and providing both control and information on tens of thousands of CNS neurons per coverslip.

An in vitro system will also give access to a multitude of protocols that cannot be applied in vivo, whether in animals or humans. Exhaustive searches can then be conducted in vitro, looking for optimal strategies of applying pharmacological agents (37,38) or repetitive TMS (39–41), which will ultimately be verified with relatively few experiments in vivo. We expect numerous additional rewards to arise as the use of such in vitro systems for TMS proliferates.

THEORETICAL BACKGROUND

Electromagnetic induction

As stated in the Introduction, an in vitro setup should simplify the problem of electromagnetic induction and charge accumulation in the sample. According to Faraday's law of electromagnetic induction, the induced electric field along a closed ring depends on the rate of change of the magnetic flux through that ring, and is directed along the tangent of the ring when the magnetic field is perpendicular to the plane of the ring. By patterning the cultures to grow on rings and placing them in a round dish containing a conducting solution concentrically below a circular magnetic coil (Fig. 1, A and B), charge accumulation is diminished (since all boundaries are parallel to the induced electric field). The problem of electromagnetic induction is then analytically solved (refer to the Appendix for the derivation) as

(1)

Here E_max is the maximal amplitude of the induced electric field that is directed along the tangent of the rings with magnitudes that remain constant for a constant radius r. B is the amplitude of the magnetic pulse and k₁ is a dimensional proportionality constant that takes into account the dynamics of the magnetic pulse and the geometry of the coil. As stated in the Appendix, since the pulse given by our magnetic stimulator (MS) is a sinusoidal pulse with a fixed cycle time, the rate of change of the magnetic flux is determined by the amplitude of the pulse, which in turn is set by the MS voltage load. We used a pickup coil in the experiment to obtain a value of k₁ = 13,800 ± 400 (SE) [1/s]. This equation is exact only for radii r smaller than the inner radius of the magnetic coil and for concentric positioning of the ring culture with respect to the coil. When the ring culture is larger than the coil, the electric field along the ring will start decreasing inversely proportional to r. If the ring culture is placed nonconcentrically under the circumference of the coil, charge will accumulate on the dish boundaries and decrease the total electric field.

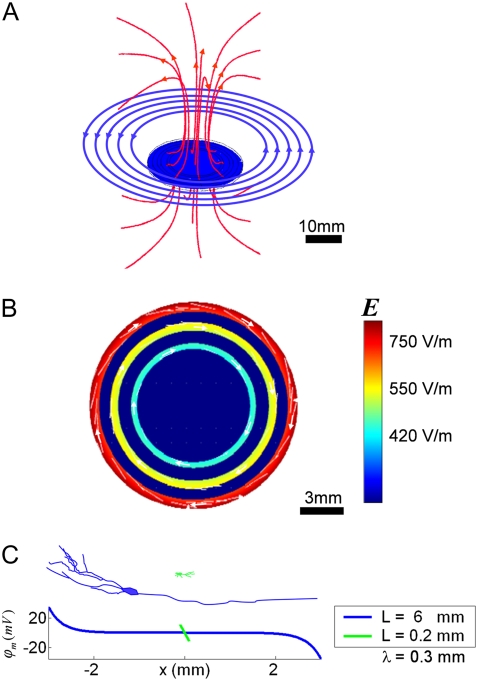
FIGURE 1.

A model of TvMS of one-dimensional neuronal cultures. (A) A circular coil (blue circles) is positioned 5 mm above one-dimensional neuronal ring cultures (blue disk). The rings are parallel to and concentric with the coil, which discharges a maximum voltage load of 5000 V from the MS capacitor. This creates a pulse of magnetic field which is oriented along the red lines (the mild deformation of magnetic field lines near the blue disk is due to the presence of a metal coating on the disk as is the case with our coverslips; see Methods). By Faraday's law, the induced electric field lies on planes that are parallel to the plane of the coil along rings concentric with the coil, and depends on the change of magnetic flux through these rings. (B) A closeup of the horizontal cross-section along the plane of the ring cultures in panel A. The relative value of the electric field is color-coded, and its direction depicted by white arrows. Larger rings enclose a larger area of flux and therefore the electric field induced at those rings is stronger. (C) The membrane potential of a neurite that is 0.2-mm long (green) compared to that of a neurite 6-mm long (blue). Both neurites have a length constant of λ = 0.3 mm. The induced electric field (300 V/m) is parallel to the neurite and the membrane potential peaks at the neurite ends. The membrane potential of neurites that are shorter than their length constant is simply linear with their length L, while the membrane potential of neurites that are longer than λ is governed by λ. The passive time constant is τ < 1 μs (see Theoretical Background).

Neuronal response

To describe the excitability of a neuron we focus on subthreshold dynamics that determine the potential of the neuronal membrane. This simplification is appropriate for our experiments since we measure the magnetic field threshold (B_T), which is correlated with the weakest induced electric field that elicits activity in the neuron. Superthreshold (active membrane) dynamics are negligible because an action potential will be generated at any point along the axon once the membrane potential there (determined by the subthreshold dynamics) exceeds the threshold potential of the axon. The magnetic field threshold is a good and consistent measure for the excitability of a neuron in response to magnetic stimulation (42).

As shown in the literature (12,13), subthreshold dynamics of the neuronal membrane voltage are readily expressed by the passive cable equation:

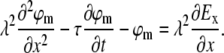(2)

Here ϕ_m is the deviation of the membrane potential from its resting value, λ is the passive length constant of the neurite, τ is the passive time constant of the neurite, and x is directed along the neurite, regardless of its true absolute orientation. E_x is the projection of the effective external electric field on the direction of the neurite at any point along it. In the case of magnetic stimulation, the external electric field E is the result of magnetic induction. The geometrical and electrophysiological parameters of neurons in our culture are given in Table 1.

TABLE 1.

Comparison between model parameters of axons and dendrites

Parameters	Dendrite	Axon	Reference
Diameter	5 μm	1 μm	Unpublished measurements.
Length constant λ	λ = 865 μm	λ = 384 μm	Axons (13), dendrites (56).
Physical length L	L ≤ 200 μm	L ≥ 1000 μm	Dendrites (44), unpub. measurements for axons.
Time constant τ	τ ≈ 5 ms	τ ≈ 300 μs	Axons (6,53), dendrites (57).
Dependence of ET on λ, L, and τ	ET ∝ L	ET ∝ √τ/λ	See Appendix.
Calculated threshold ET	ET ≥ 458 V/m	ET ≈ 280 V/m	See Appendix.

To find out whether the excitation of the neuron is dominated by the axon or by the dendrite, we evaluated the passive cable equation for the different physical parameters. We solve the equation for a finite neurite of length L with sealed ends at both sides, in the presence of an induced electric field that is oriented parallel to the neurite and completes a single cosine oscillation: E_x(x,t) = E_ocosωt with ωt∈[0,2π]. Assuming a voltage threshold ϕ_T above which the cell fires an action potential, the electric field threshold E_T is defined as the minimal amplitude of the induced electric field E_x that is needed to activate the nerve cell. We calculate E_T for the two biologically relevant set of parameters λ,τ, and L corresponding to an axon and to a dendrite (See Appendix and Table 1).

In the case of axons, where the length constant λ of the neurite is smaller than its physical length L and the time constant τ is shorter than the duration of the stimulus, we find that (see Appendix and Fig. 7):

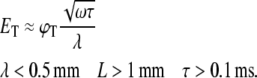(3)

In the case of dendrites, where their physical length L is smaller than their length constant λ and their time constant τ is much longer than the duration of the stimulus we find that (see Appendix and Fig. 7):

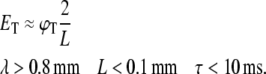(4)

Assuming a typical voltage threshold on the order of ϕ_T ≈ 30 mV, we calculate the predicted value of E_T for axons and dendrites and show that for biologically relevant values the threshold of axons for magnetic stimulation in our culture is always lower than that of dendrites (Table 1).

FIGURE 7.

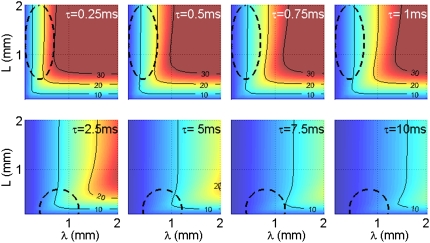
Modeling the membrane potential of a finite neurite undergoing magnetic stimulation. Color-coded maps of the maximal membrane potential that is reached in response to a 100 V/m induced electric field, portrayed as a function of λ and L. Each map was calculated for a different τ, with the top row corresponding to axons and the bottom row corresponding to dendrites. Dashed contours represent the biologically relevant ranges of L and λ in axons (ellipsoid, top row) and dendrites (half-circle, bottom row). The maximal membrane potential that can be attained in dendrites is approximately half what can be attained by axons. The membrane potential in each of the maps was calculated as described in the Appendix. Potential contour values are in mV.

The threshold potential ϕ_T is an electrophysiological property that can vary in a given neuronal population. If we make the realistic assumptions of a Gaussian distribution for ϕ_T (43) and of a fixed length constant λ that is much smaller than the length of the neurites, then we expect the electric field threshold E_T to be distributed in a Gaussian distribution as well.

The magnetic field threshold (B_T) is our experimentally measured variable that relates to the induced electric field threshold via Eq. 1 (B_T = E_T/13,800r). The expected distribution of B_T measurements in our experiment is derived from the Gaussian distribution of the electric field threshold and Eq. 1:

(5)

P(B_T,r) is the probability to measure a magnetic field threshold B_T at a radius r where μ and σ are the mean and standard deviation of the electric field threshold distribution and A is a normalization constant. As expected, this probability depends on the electric field only, with regions of equal probability correlating to regions of equal electric field (i.e., since: E_T ∼ B_T × r = const, then: B_T ∼1/r. See also Fig. 5 A). The maximal magnetic amplitude (max{B} = 3.9 Tesla) and the maximal ring size (max{r} = 14 mm) limit our experiment to an accessible phase space that in turn determines the maximum electric field threshold that can be attained:

(6)

FIGURE 5.

(A) Measurements of magnetic field thresholds in the experiment. The y-value of each point is the magnetic field threshold measured for a specific ring culture while the x-value of each point is the radius of that specific culture. The color coding denotes both the electric field threshold and the probability to measure an excitation. Regions of equal colors confine similar values of electric field threshold. Warmer colors (according to the color-bar in the figure) denote a higher probability to measure these thresholds (as described in Methods). The white frame outlines the experimentally accessible phase space. (B) The cumulative sum of the actual density of data points in each color region in panel A. For each value of electric field threshold (corresponding to similar color regions in A), the probability to measure a threshold as high as this value is plotted. Red line depicts the normal cumulative distribution that fits the data, with the parameters presented in the figure. (Inset) For each value of electric field threshold, the probability to measure a threshold at a bin around this value is plotted. Red line depicts the normal distribution that fits the data, with the same parameters presented in the main figure.

The predictions of the physical equations

The physical equations introduced in Theoretical Background emphasize two physical parameters that are important for magnetic excitation: the ring radius and the orientation of nerves. The electric field along ring cultures was shown in Eq. 1 to depend linearly on the ring radius; therefore, larger rings are predicted to be easier to stimulate magnetically. The membrane potential of nerves was shown in Eq. 2 to be affected only by the projection of the electric field along the nerve; therefore, patterned cultures that are oriented along the direction of the electric field are predicted to be easier to stimulate. Finally, by solving the passive cable equation we show that magnetic stimulation excites the axons and not the dendrites.

METHODS

Primary cultures

Primary cultures were prepared from rat hippocampi of 19-day-old embryos taken from Wistar rats. All procedures were approved by the Weizmann Ethics Committee (Institutional Animal Care and Use Committee). Pregnant rats were anesthetized with veterinary pentothal at a dose of 0.5 ml/kg to efficiently anesthetize the animal while minimizing the risk of affecting the embryo brains by the barbiturate. This was followed by cervical dislocation and swift extraction, which prevents damage to the brain tissue. The dissection was performed following Feinerman et al. (44) with two differences: the plating density was adjusted for the size of the coverslips used (2 × 10⁶ cells for each 24-mm coverslip, and 3 × 10⁶ cells for each 30-mm coverslip), and one-third of the medium volume was replaced twice a week starting from day 9 in culture. Two of the coverslips that responded to magnetic stimulation were plated with rat cortex using the same density and following a protocol for myelinated cultures (45).

Preparation of patterned coverslips

Following Feinerman and Moses (46), 24 mm #1 glass coverslips (Paul Marienfeld GmbH & Co. KG, Lauda-Königshofen, Germany) and 30 mm #0 glass coverslips (Menzel-Glaser, Braunschweig, Germany) were patterned to make only specific locations available for cell adhesion. After cleaning the coverslips in 20% ammonium hydroxide and 20% hydrogen peroxide in deionized distilled water (30 min 50°C), the coverslips were evaporated with 6 Å of chrome followed by 35 Å of gold and then immersed in a solution of 0.1% octadecanthiol (Sigma-Aldrich, St. Louis, MO) in ethanol (soluble via sonication for 15 min) for 2 h. Coverslips were then washed in ethanol, dried with nitrogen, immersed in a solution of 3.5% Pluronics F108 Prill (BASF, Ludwigshafen am Rhein, Germany) in Dulbecco's phosphate buffered saline (soluble via stirring) for 1 h and dried again. Then, using an HP 7475A plotter (Hewlett-Packard, Boston, MA) in which the pen was replaced by a sharp metal tip, patterns were scratched through this coating according to a computer-generated design. The entire coverslip was radiated by u.v. light for 10 min and then immersed overnight in 37°C in a solution of 3.5% Pluronics F108 Prill (BASF), 0.0028% laminin and 0.0028% fibronectin (both from Sigma-Aldrich) before being washed twice in Dulbecco's phosphate buffered saline and once in plating medium.

An alternative protocol was developed to control for the presence of metal in the coverslips. In this protocol, the stages of metal evaporation and octadecanthiol coating were replaced with the immersion of the coverslips in a solution of 0.1% octa-decyl-trichloro-silane (Sigma-Aldrich) in nine-parts chloroform and one part iso-octane for 3 min. Then the coverslips were washed three times in 9:1 chloroform: iso-octane, dried with nitrogen, washed two times in deionized distilled water, dried again in nitrogen and cured overnight in a vacuum oven at 250°C. The next day, coverslips were immersed in Pluronics solution and we continued with the original protocol as above.

As demonstrated in Fig. 2 A, each dish included a number of distinct disconnected concentric rings on which neurons grew, with ring radii ranging between 6 and 14 mm. All cultures in a single dish share the same growing conditions, but they can differ in their geometry and therefore in their interaction with the magnetic field. In one-dimensional ring cultures, two independent aspects of size are apparent: the radius of the ring and the size of the culture, i.e., its linear length. Most cultures were patterned into complete rings but to separate between the culture's radius and its linear length, some of the cultures were patterned into arcs of 180°, 120°, and 60°. Other control cultures were patterned on straight radial lines that were perpendicular to the induced electric field (Fig. 2 A).

FIGURE 2.

Experimental setup. (A) A bright field image of a patterned 24-mm coverslip. The white areas are neuronal cultures. The photographed pattern consists of ring cultures in arcs of different length. Radial lines serve as a control (see Methods). Each ring's width is ∼200 μm. (B and C) An inverted microscope images fluorescent dyes sensitive to calcium transients of neurons reacting to magnetic pulses. The magnetic coil (blue circles) is located 5 mm concentrically above the neuronal ring culture, which is placed in a petri dish (blue outline). A pickup coil (red circle) positioned on the circumference of the petri dish measures the voltage induced by the magnetic pulse. (D) The measured dynamics of the magnetic stimulator coil (MS capacitor voltage load = 5000 kV) as integrated from the pickup coil. Induced electric field (calculated for a ring radius of 14 mm) is depicted in green while the magnetic field is depicted in blue.

Preparation of two-dimensional cultures

As a control for the effect of patterned cultures, the experiment included nonpatterned two-dimensional cultures. Cultures were plated following Feinerman et al. (44) on 30-mm coverslips with an adjusted plating density of 5 × 10⁶ cells per coverslip. Starting from day 9 in culture, one-third of the medium volume was replaced twice a week.

Calcium imaging

Calcium imaging proved to be the most relevant measure for our experiment for several reasons. First, strong electromagnetic interferences that are induced in the vicinity of the coil by magnetic pulses introduce strong noise in all electrophysiological measurements. Imaging bypasses this problem since optical measurements are unaffected by the magnetic pulses. Second, imaging provides simultaneous monitoring of a large population of cells. This proved most efficient in the search for single neurons that respond to the magnetic stimulation. Third, calcium imaging has large signal/noise ratios compared to voltage-sensitive dyes. The major shortcoming of calcium imaging is the long time that it takes the fluorescence to recover, and this is irrelevant for us because of the large delay between network bursts. What interests us is the response of the network to stimulation, and for that, the rise time of the calcium-sensitive fluorescence is the relevant parameter. Finally, throughout the decades of research, transcranial magnetic stimulation was always regarded as a super threshold phenomenon. Magnetic stimulations were always measured by clear and obvious neural responses. It is our belief that this point of view should be kept in vitro and we therefore prefer to measure superthreshold neuronal responses, for which calcium imaging is most appropriate.

To image calcium transient in our experiment, cultures aged between 13 and 31 days in vitro were incubated for 60 min in the recording solution (128 mM NaCl, 4 mM KCl, 1 mM CaCl₂, 1 mM MgCl₂, 45 mM sucrose, 10 mM glucose, and 10 mM HEPES; pH is titrated to 7.4) in the presence of 2 μg/ml cell-permeant Fluo4-AM (Invitrogen, Carlsbad, CA), a calcium-sensitive dye. Cultures were then placed in fresh recording solution and imaged on an Axiovert (Zeiss, Oberkochen, Germany) 135TV inverted microscope (Fig. 2 B), photographed through a 5× or 10× lens by a model No. C2400-87 charge-coupled device camera (Hamamatsu, Hamamatsu City, Japan) fitted with a 0.5× adaptor to enlarge the field of view. The images were captured at 25 Hz, stored on videotape, and digitized with a PCI-1141 frame grabber (National Instruments, Austin, TX) and IMAQ software (LabVIEW, National Instruments). Deinterlacing was preformed to raise the time resolution to 50 Hz before subsequent off-line analysis.

Electrical stimulation

Some of the cultures were stimulated electrically to control for viability. Stimulation was achieved using bath electrodes made of two parallel platinum wires (0.005″ thick; AM Systems, Rancho Cucamonga, CA) 2-cm-long and 3-cm apart that were immersed in the recording dish. For stimulation, a bipolar square pulse was used, lasting between 0.1 and 10 ms with amplitudes of 1–10 V.

Trans-vessel magnetic stimulation (TvMS)

Before the magnetic stimulation, each coverslip was placed in a dish 35 mm in diameter and 5 mm high filled with 2 ml recording solution (see previous paragraphs). TvMS was achieved by a homemade magnetic stimulator (MS). A circular copper coil with 30-mm inner diameter, 46-mm outer diameter, and 13 turns with an inductance of L = 90 μH was positioned 5–7 mm above the culture, parallel to the coverslip and concentric with the ring patterns (Fig. 2 C). The magnetic pulse was sinusoidal with a rise time of 60 μs and a cycle of 240 μs. The rise time and cycle time remained constant throughout the experiments, while the intensity of the pulse varied in proportion to the voltage load on the MS capacitor (C = 110 μF, V = 0–5 kV).

The induced electric field was monitored via a pickup coil, which encircled the perimeter of the plastic dish that holds the coverslip with the neural culture under the MS coil (Fig. 2 C). The electric field induced by the magnetic pulse had the same cycle time as the magnetic pulse and its strength depended only on the intensity of the magnetic pulse and the radius at which it was measured. When the culture was placed 5 mm below the coil and the MS capacitor was loaded with a maximal voltage of 5 kV, the electric field reached a maximal value of 756 V/m (for the maximum available culture radius of 14 mm. See Fig. 2 D). The peak intensity of the magnetic pulse calculated from the measurements of the pickup coil was 3.9 Tesla.

Eleven of the cultures that responded to the homemade magnetic stimulation were also sensitive enough to be stimulated using a Magstim Rapid stimulator (Magstim, Whitland, Carmarthenshire, Wales) with 70 mm or 25 mm “figure-eight” coils. In these cases, one of the two circular parts that constitute the figure-eight was positioned concentrically above the ring cultures. The peak intensity of the magnetic pulse calculated from the pickup coil in these cases was 0.8 Tesla and 1.45 Tesla (for 70 mm and 25 mm figure-eight coils, respectively), thus the maximal fields that our homemade device outputs are up to five times stronger than those of standard commercial devices.

Experimental procedures—observing magnetic excitation of neurons

Neural cultures exhibit spontaneous and evoked activity, both taking the form of population bursts that are observed by calcium imaging as intensity peaks that rise rapidly well above the background noise (signal/noise ratio was 5–20 standard deviations). Discrimination between spontaneous and magnetically evoked activity was based on their timing: the evoked activity is synchronized with the magnetic pulses with a delay of 0.02–1 s, and the mean rate of TvMS is once every 25 s. Spontaneous activity rates range from 1 to 10 bursts every minute.

There is some probability for a spontaneous burst to coincide with the TvMS excitation. Considering the worst case from a statistical point of view in which the spontaneous rate is four times that of the stimulator rate, the chances for observing a spontaneous burst at precisely every 25 ± 0.5 s is not more than 6% for a single observation (assuming the Erlang distribution with mean rate of 6.25 s and a waiting time of 6.25 ± 0.5 s between two consecutive events) and 0.2% for two consecutive observations (assuming that 25 ± 0.5 s have elapsed between the first and the fifth spontaneous events) and decreases exponentially with the number of consecutive observations. We therefore define a successful TvMS as two consecutive bursts that both occur no more than 1 s after the magnetic pulses (this give a probability of p = 0.002 for a false-positive detection). The delay between the magnetic pulse and the response that sometimes occurs is due to a combination of burst initiation time (44,47) and signal conduction time (44). Since these delays are reproducible and consistent, the actual variability of the response is much smaller than 1 s and the chances for false detections are therefore even smaller.

Experimental procedures—measuring the magnetic field threshold of TvMS

The magnetic field threshold (B_T) is defined as the amplitude of the weakest magnetic pulse that evokes neural activity. The magnetic field threshold of each ring culture is determined by sweeping the MS capacitor voltage up and then down, to identify the point at which the culture ceases to respond. The magnetic field was calculated from the measurements of the pickup coil assuming a uniform magnetic field just below the inner circumference of the coil (this assumption was verified by analyzing measurements from pickup coils of different sizes).

Experimental procedures—disconnecting the network

Since rat hippocampal neurons are chemically coupled at the synapses it is interesting to test whether magnetic stimulation changes in the absence of chemical coupling. Synaptic connections between neurons in our culture are both excitatory and inhibitory in nature and are dominated by AMPA, NMDA, and GABA_A receptors (44). To block synaptic transmission we apply 10 μM of the NMDA receptor antagonist 2-amino-5 phosphonovaleric acid (Sigma-Aldrich), 50 μM GABA_A receptors antagonist bicuculline-methochloride (Sigma-Aldrich) and saturating concentrations (between 2 and 40 μM, as explained below) of the AMPA/kainate receptor antagonist 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX, Sigma-Aldrich).

CNQX along with 2-amino-5 phosphonovaleric acid is used to disrupt connectivity, and at saturating concentrations completely breaks down the network structure of the culture (43,44,48). CNQX was applied at gradually increasing concentrations until the network activity demonstrated no apparent connectivity (disconnected networks lose all occurrences of either spontaneous or stimulated synchronized bursts while maintaining a local response to external stimulations that increases with the strength of stimulation). Final concentrations that yielded this behavior varied between 2 and 40 μM depending on sample conditions such as the presence of neuronal aggregation in the culture.

Experimental procedures—blocking inhibition

To test for the effect of inhibition we measured the electric field threshold of cultures before and after applying saturating amounts of the GABA_A receptor antagonist bicuculline-methochloride. Bicuculline was administered at a final concentration of 50 μM, which completely blocks GABA_A receptors in the culture (44).

RESULTS

Observing magnetic excitation of neurons

Fig. 3 illustrates the activity of one of the ring cultures as measured by calcium imaging. The culture has both spontaneous activity, which is not synchronized with the TvMS, and evoked activity, which is well timed with the magnetic stimulations. The delay between the magnetic pulse and the evoked activity ranged between a minimum of 20 ms (our video resolution) and 1 s. Long delays were consistent and reproducible, and occurred when the activity was initiated at a distance from the observed site and had to propagate until it reached our field of view, or in cases where a buildup time was needed until the activity reached its full amplitude (44,47).

FIGURE 3.

Fluorescent measurements of calcium transients. (A, Top) Image taken with a low-magnification stereoscope of a 30-mm coverslip containing four concentric ring cultures (14, 13, 12, and 11 mm in radius) that were imaged during magnetic stimulation. The field of view of the high-magnification imaging microscope is marked with a green circle. (A, Bottom) A single fluorescence image from the field of view of the imaging microscope. Numbered boxes denote the regions of interest for which the average intensity is displayed in panel B. (B) The ΔF/F (i.e., the ratio between transient and background fluorescence) intensities of each green region in panel A is plotted versus time (blue traces, each trace was normalized according to its maximum amplitude, which was 5–10% ΔF/F in all regions). The exact timing of each of the TvMS pulses is marked with a dashed vertical black line and the amplitude of the magnetic pulse in Tesla is denoted above each line. Both spontaneous activity and evoked activity is observed. (C) The responses of each region to TvMS, clustered according to the strength of the stimulation. Each trace is taken from panel B during the 4 s that follow each stimulation. As illustrated in Fig. 5 A, ring cultures with larger radius (regions #1 and #2) respond to weaker stimulations and vice versa. The measured magnetic field threshold in this case is 1.3 T for regions #1 and #2, 1.7 T for region #3, and 2.7 T for region #4.

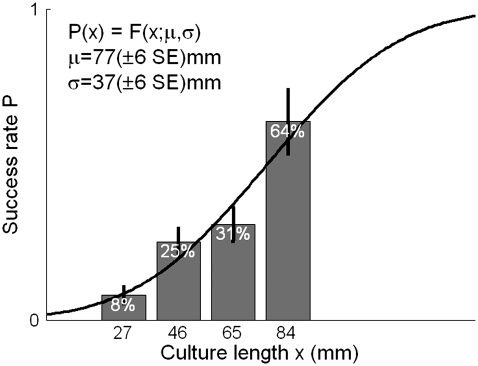
Out of 76 dishes containing a total of N = 308 cultures, TvMS induced neural activity in N = 65 cultures, or 22%. This rate strongly depended on the culture's linear length, which was varied independently of the radius by patterning the culture into arcs of similar radii and different lengths (see Methods and Fig. 2 A). The success rate of magnetic excitation increased to 64% when considering only the subset of longer cultures (75–88 mm, see Fig. 4). We calculated a critical culture length for which the TvMS success rate was 50%: μ = 77 ± 37 (SD) mm (Fig. 4). There was no observed difference between similar cultures with the same length and radius that responded to TvMS and those that did not: they had the same appearance when examined visually, had the same response to electrical stimulation using bath electrodes (see Methods) and had the same rate of spontaneous activity. Two of the successfully stimulated dishes were plated with rat cortex (see Methods) and one of the successfully stimulated dishes was prepared using the control protocol of Silane coating instead of metal evaporation (see Methods). Eleven of the cultures were also stimulated using the Magstim Rapid commercial stimulator and with a 70 mm or a 25 mm figure-eight coil (see Methods).

FIGURE 4.

The success rate of TvMS for different lengths of cultures. Black line depicts the normal cumulative distribution that fits the data, with the parameters presented in the figure.

Dependence on nerve orientation

To verify the effect of directionality, N = 29 control cultures were patterned on straight radial lines that were perpendicular to the induced electric field (see Fig. 2 A) and N = 11 control two-dimensional cultures were grown on unpatterned coverslips (controls were not included in the N = 308 regular cultures). Neither the perpendicular cultures nor the two-dimensional ones responded to TvMS. As in the previous section, there was no observed difference between the two-dimensional control cultures and the one-dimensional cultures that responded to TvMS: they had the same appearance when examined visually (the final cell density of two-dimensional cultures was half of that of the one-dimensional cultures), had the same response to electrical stimulation using bath electrodes (see Methods) and had the same rate of spontaneous activity. In one control experiment, the cultures were patterned into several straight lines, and the whole sample was rotated with respect to the field direction. The straight line cultures did not respond to TvMS when oriented perpendicular to the electric field, but did react when oriented parallel or at 45° inclination with respect to the induced electric field. This case was unique since only a culture that is patterned on a short straight line can be rotated with respect to the electric field. Unfortunately, we found no additional cultures that were similarly short and responded to magnetic stimulation. Indeed, this culture is one of the shortest cultures that responded to magnetic stimulation (the length of the culture was 8 mm, see Fig. 4).

The magnetic field threshold of TvMS—dependence on sample size

Fig. 5 A illustrates the expected distribution of magnetic field thresholds as regions with similar color coding (the distribution was derived in Theoretical Background) along with the measured magnetic field thresholds of all ring cultures that were activated in the experiment, demonstrating the dependence of TvMS on the ring radii. The voltage of the TvMS needed for neuronal excitation depends inversely on the radius of the ring cultures independently of their lengths. From this figure we can also deduce that 13.5 mm is the radius of the smallest ring that can be stimulated using conventional TMS devices, which produce magnetic fields of ∼1 Tesla at the plane of the culture.

Electric field threshold

Fig. 5 A demonstrates that the density of measured thresholds is higher within color regions that denote a higher theoretical probability to contain threshold measurements. These color regions also correspond to regions of similar electric field, as mentioned in Theoretical Background. It is therefore instructive to present the density of measured thresholds as a function of their electric field value (i.e., “how probable is it to measure a specific electric field threshold?”). The inset of Fig. 5 B describes how probable it is to measure each value of electric field threshold, while the rest of Fig. 5 B plots the cumulative probability of all electric field thresholds measured in our experiments. As predicted in Theoretical Background, the distribution of electric field thresholds of all cultures in our experiment fits a Gaussian. The mean and standard deviation of the distribution was 301 ± 128 (SD) V/m and there was no difference in the measurements of electric field thresholds between stimulations that were performed with the homemade stimulator and stimulations that were performed using the commercial Magstim Rapid.

Table 2 demonstrates that the average electric field threshold we measure is compatible with a variety of experiments in which thresholds for neural activation were measured. The fact that the average threshold for electric stimulation of cultures in vitro is lower than the average electric field threshold measured in our magnetic stimulation experiment is not surprising considering that the electrical stimulations last 10 ms—more than 100 times longer than the magnetic pulse. According to the strength-duration curve, it is expected that extremely short stimulations would have to be stronger to elicit the same response. We find that while some cultures can be excited by a short electrical pulse of ∼100 μs, most need longer durations, and almost all fire after 10 ms.

TABLE 2.

Comparison between electric thresholds of different nerves

Mean electric threshold	Description	Reference
ET = 301 ± 128 V/m	TvMS of one-dimensional neuronal culture.	This article.
ET ≈ 170 ± 20 V/m	Average threshold for electric stimulation of two-dimensional neuronal cultures in vitro (10 ms duration).	Breskin et al. (43).
ET ≈ 145 ± 90 V/m	Electric field threshold for magnetic stimulation of human motor cortex (from average motor threshold of index finger).	N. Levit-Binnun, personal communication, Physics of Complex Systems, Weizmann Institute of Science, 2006.
ET ≈ 130 ± 10 V/m	Average threshold for magnetic stimulation of a frog's sciatic nerve.	Rotem and Moses (42).

The fact that the average motor threshold measured with TMS on human subjects is lower than the average electric field threshold measured in our experiment can be attributed to differences in the resting potential of neurons, in the size of the system, in the length constant of neurons and in their myelin content (see Discussion).

As explained in Theoretical Background, we can predict the electric field threshold for dendrites and axons by substituting the approximated values of λ, L, and τ into the numerical solution of our model (Table 1). The predicted electric field threshold of axons is similar to the measured electric field threshold, and since the predicted electric field threshold of dendrites is almost twice as high, we see that stimulation must take place in the axons. Furthermore, from Eq. 3, we see that for long enough axons (longer than their length constant), the threshold value increases for longer time constants of the axon and decreases for longer length constants of the axon.

Disconnecting the network

In N = 5 of the cultures (each in a different dish), CNQX was applied at gradually increasing concentrations (see Methods). This resulted in a gradual breakdown of the network activity into subgroups of the culture. These subgroups were apparent at concentrations of 1 μM CNQX or higher and could be identified by spontaneous activity that was synchronized in each group but not between them. While we could not follow activity in the entire ring due to the microscope's limited field of view, we were able to ascertain that not all these subgroups were excited magnetically, and to find in each experiment one subgroup that did react. We also found that at higher, saturating concentrations only a small number of neurons in that subgroup responded to TvMS (Fig. 6). Those isolated neurons, termed “initiating neurons,” consistently responded to TvMS each with its own electric field threshold, which was always higher than that of the connected culture, with an average ratio of 1.89 ± 0.25 (SE).

FIGURE 6.

Single neuron response. (A) Fluorescent analysis of video taken from a 10× field of view. The image is the average intensity of the fluorescent signal across four events of 450 frames each. Green contour encloses areas that were spontaneously active during the first event (at 4.5 μM of CNQX, the highest concentration at which spontaneous bursting activity persisted across the whole culture). Red points represent locations that responded to TvMS during the last three events (at CNQX concentration of 9 μM, for which no bursting activity was observed). (B) Traces of the fluorescence signal (in units of the relative change of intensity as a fraction of the background intensity) during the four events: green traces (top row), average intensity of all coordinates enclosed in the green contour; and red traces (bottom row), average intensity of all red coordinates. TvMS pulses are marked with a dashed vertical line, with the intensity of the induced electric field indicated in V/m.

Blocking inhibition

To test for the effect of inhibition we applied saturating amounts of bicuculline (see Methods). Out of the N = 65 cultures that responded to TvMS, N = 40 cultures responded before application of bicuculline and continued to respond after that, while N = 25 responded only upon application of bicuculline. On average, there was no observable difference in the electric field threshold between cultures that responded before application of bicuculline and those that did not.

In N = 15 of the cultures that responded before the application of bicuculline, electric field thresholds were measured both before and after the addition of bicuculline. A wide range of responses was observed, with electric field thresholds both increasing and decreasing. An interesting observation was that in general, cultures younger than 16 days in vitro shifted with bicuculline to higher thresholds (by an average of 20%), while cultures that were older than 16 days in vitro shifted to lower thresholds (by an average of 20%).

Hysteresis

As mentioned in Methods, magnetic field thresholds were measured by sweeping the magnetic field strength up and then down. In N = 18 cultures, the magnetic field thresholds were measured initially by increasing the MS voltage load from 0 to the minimal value that evoked the first ever stimulated activity in those rings, and then decreasing it to the last value that still stimulated the rings. In all of these cultures, the final value was equal to or lower than the initial value, with an average ratio of final/initial = 0.84 ± 0.05 (SE). This hysteretic effect was observed both in the presence of bicuculline (N = 5) and without it (N = 13) with no significant differences in the ratio. The hysteresis did not recur upon repetition of the sweep in magnetic field strength: The first time that the culture was activated, its threshold was highest. After that, it always responded at the lowest threshold that the hysteretic loop reached.

DISCUSSION

The importance of being one-dimensional

The importance of size and orientation for increasing the sensitivity to stimulation are well documented both in vitro (14,21,49) and in vivo (22,24–28,41). While their role in our setup is perhaps not very surprising, a number of important remarks can be made. First, neither orientation nor size alone can bring about excitation, and our experimental capability had to be stretched to the maximum in both these parameters to obtain a response in the cultures. Thus, rings with small radii that were correctly directed along the field lines did not respond, and neither did two-dimensional cultures that were as large as we can make.

Neurons grown in one-dimensional cultures were previously shown to have the same intrinsic excitability and the same response to pharmacology as neurons grown in two-dimensional cultures (44). In the current experiment we verified that both the spontaneous activity of the one-dimensional cultures and their response to electric stimulation were the same as those of two-dimensional cultures. The difference in density between the two types of cultures is not expected to be the important parameter for magnetic excitation. The parameter that we have identified as relevant is the length of the one-dimensional culture, which we relate to the absolute number of neurons in the culture (cultures with more neurons are expected to be more responsive to magnetic stimulations, as discussed in Initiating Neurons, below). While this number is definitely affected by density, the two-dimensional cultures, which usually do have a slightly lower density, are spread over a much larger area, and therefore include many more neurons. Two-dimensional cultures include as much as 600,000 neurons, >20 times the maximal population in one-dimensional cultures, and still they do not respond to magnetic stimulation. The only parameter that remains substantially different between the two types of cultures is the neuronal morphology.

Axons may extend for a long distance in two-dimensional cultures, but since they zigzag rather than stretch along straight lines, charge accumulates at bends of the axon rather than at its ends. This leads only to subthreshold depolarization at multiple locations, which cannot initiate an action potential. Therefore, it is not the total projected length that counts in magnetic stimulation but rather the length of the longest contiguous stretch along the direction of the electric field. Obviously, obtaining alignment on a ring that is concentric with the coil in a two-dimensional culture is very hard, and we conjecture that it will take considerable resourcefulness to attain excitation in two dimensions. The importance of using one-dimensional lines is therefore in creating a massively high probability for axons of all neurons to have long contiguous projections along the direction of a predefined line (44). Aligning the line on a ring that is large and concentric with the magnetic coil gives the additional contribution that is crucial for excitation to succeed.

An interesting conjecture can be made regarding the comparison to electric stimulation (Table 2), and the long pulses that are required for electric excitation. First, we must remember that the rise time of the membrane potential is much shorter than the length of the long electric pulses. For a simple exponential membrane depolarization, the passive time constant of τ = 300 μs means that reaching the electric field threshold with a 100-μs square pulse needs only a 3.5 times higher field than that when using a 10-ms square pulse. The need for a long electric excitation must therefore arise from some other cause. The long durations needed hint that a new timescale is being introduced, and the best candidate is the dendritic time constant (see Table 1). We speculate that at longer pulses it is the dendritic tree that causes the neuron to fire. At these long timescales, the numerical solution to the equations (Fig. 7) indicates that dendrites can be excited. In that case, the imposed one-dimensional directionality is no longer needed, since every neuron sends dendrites in practically all directions. It is therefore predicted that neurons are excited electrically via their dendritic tree, and magnetically via their axonal tree.

An important intermediate between the in vitro culture and the in vivo whole brain is the ex vivo brain slice. If the massive connected lines of long axonal pathways that already exist in the brain can be retained, then excitation should be feasible. For rat slices, the issue of size is crucial, and the risk is high of creating boundary effects, of severing connections, or of creating too small an induction loop. We conjecture that this will eventually be successful, providing that large enough structures are preserved during the dissection.

In one-dimensional ring cultures, two different aspects of size are apparent. The radius of the ring is directly linked to the magnetic field threshold; larger radii lead to smaller thresholds. On the other hand, the size of the culture, i.e., its linear length, contributes to the success rate; longer lines lead to a higher probability to respond. These two aspects were shown to be independent parameters.

Initiating neurons

The existence of initiating neurons indicates that magnetic stimulation is a single neuron phenomenon. As in electric excitation, network activity is not essential for magnetic stimulation of neurons, and the effect of this stimulation is determined specifically for each neuron by its morphology and electrophysiology. Measurements of electric thresholds using bath electrodes have shown that the threshold of connected cultures is equal to the threshold of the most sensitive individual neurons when the culture is disconnected (43). This leads us to the assumption that although the thresholds of individual neurons in our experiments were, on average, higher than the threshold of the connected culture, there exist initiating neurons with thresholds as low as the threshold of the connected network. Since the cultures had large populations and sizes, it is highly probable that such neurons exist without being spotted during our experiment.

As explained above, one would, a priori, expect that the magnetic field threshold at which the network fires should coincide with the lowest field at which single neurons are excited. We conjecture that cultures do not respond at all if they do not have enough initiating neurons. This can explain why the cultures that do respond all fall beautifully on the theoretical curve that relates radius to magnetic threshold, while other cultures do not respond even to magnetic fields that are twice as strong. This implies that initiating neurons are at least twice as sensitive to the magnetic excitation as other neurons, but they are not abundant. Since the thresholds of “common” neurons are at least twice as high, they cannot be stimulated with the available setup, and the culture will not respond. The fact that blocking inhibition in the network improved the success rate can be explained by a decrease in the number of initiating neurons that are required for initiating the network activity.

Highly populated culture will have better chances to include enough initiating neurons. With constant neuronal density, the population of the culture is proportional to its length. A critical population limit for which the TvMS success rate is 50% can be calculated using the critical culture length μ = 77 mm (Fig. 4) and the linear density of our cultures (Γ = 0.3 cells/μm (44)) giving N_c = Γμ ≈ 23,000 cells.

Single neuron properties

The scarcity of initiating neurons may explain the low success rates but also raises new questions regarding the properties that make them unique. The analysis of Eqs. 3 and 4 shows that stimulation must take place in axons and that the excitability of long axons (longer than their length constant) is enhanced by larger length constants and/or shorter time constants. The length constant of an axon depends on the square root of its diameter (50) so thick axons may be one of these unique properties. The passive time constant depends on the distribution of different channel types in the soma and axon hillock. As discussed in Theoretical Background, the axonal morphology can increase the sensitivity to magnetic stimulations by 100% in the case of a 180° turn in the path of the axon (42) or even more in the case of an extensive branching point.

Some consequences for in vivo application to TMS

While obviously great care must be taken before making extensive conclusions about the brain, we conjecture that a number of consequences will hold up when applied to the whole brain.

Our finding that only a limited number of initiating neurons respond to the stimulation may be applicable to the brain. Unless the growth condition in the brain favor a higher sensitivity, then it is reasonable to expect that only a small number of neurons in the brain are similarly susceptible to excitation. Presumably, the same properties that made them sensitive in the dish will make them sensitive in the brain. During TMS activation in the brain a volume of 1 cm³ with >100,000,000 cells is affected (51), so that the observed success rates of ∼100% are reasonable when compared to the minimal number of 23,000 cells that we showed is needed for excitation.

In vivo, the main differences in length and time constants relate to myelin content. According to Eq. 3, myelinated axons are seven times more sensitive to magnetic stimulation than nonmyelinated ones (since they have a five-times longer length constant (13,52) and half the time constant (53)). One support for this conjecture is the observation that measurements of magnetic excitability in Multiple Sclerosis relapsing-intermitting patients are correlated with the different phases of the disease (29).

SUMMARY

CNS mammalian neurons in vitro can be magnetically stimulated with a commercial coil regardless of their connectivity and providing that they are oriented along rings of at least 13.5 mm in diameter. This finding singles out two geometrical properties that are sufficient for magnetic stimulation of CNS neurons in vitro: correct orientation and a large culturing substrate. We have also shown that very few neurons in the culture respond directly to the magnetic excitation and that their threshold is at least twice as low as that of most of the neuronal population. This implies the existence of single-neuron properties that account for variability of >100% in their magnetic threshold.

CNS cultures provide extensive control over orientation, morphology, and electrophysiology of neurons and, since safety limitations are minimized, they enable a wide-ranged investigation of pharmacology and of stimulation frequencies. Further developments may enable us to approach deep brain stimulation, long-term potentiation, long-term depression, mood therapy, and safety issues in TMS under controlled conditions in vitro. As more pieces of the puzzle will be filled in, better prediction and understanding of the interaction between TMS and living brains can be gained, and will hopefully improve the therapeutic abilities of TMS.

APPENDIX

Electric field induced at rings concentric with and below a magnetic coil

The geometry of interest includes a single coil of radius R in the x,y plane at height z = 0 and of neurons grown on a ring L in a plane parallel to that of the coil, displaced by a small height h ≪ R. According to Faraday's law of induction, the induced electric field E along the closed loop L (with radius r) is equal to the change in magnetic flux φ through the surface S enclosed by L:

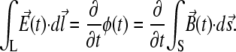(7)

Numerical analysis (see Fig. 1) shows that the magnetic field near and inside the coil perimeter can be assumed to be uniform and perpendicular to the coil plane, so that the magnetic flux φ through L is simply

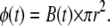(8)

A key role in determining the electric field is played by surface charges. If all boundaries of the vessel as well as the neurites are concentric with the coil, then there is no accumulation of surface charge, and the amplitude of the electric field is fixed for any given radius and is azimuthally directed. In this case, Faraday's law of induction simplifies to

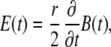(9)

where the direction of E lies on a circle of radius r around the center (Fig. 1). In our experiment, the cycle time of the magnetic pulses remained constant throughout the experiment, while their amplitudes were repeatedly varied (by varying the voltage load of the MS capacitor) to determine threshold stimulation values. The derivative therefore depends only on the amplitude of the magnetic field. Introducing the proportionality constant k₁ to account for the dynamics and for the geometry of the coil, we can obtain the maximal attained field by

(10)

B_max is the amplitude of the magnetic pulse (abbreviated in the text by B) and k₁ is calculated from measurements of the pickup coil in the experiment, giving k₁ = 13,800 ± 400 [1/s]. This provides us with the basic relation between the MS voltage load, which is our control parameter, and the amplitude of the induced electric field at any radius r on the coverslip:

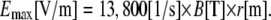(11)

The subthreshold response to magnetic stimulation

Subthreshold dynamics of the axonal membrane voltage are expressed by the passive cable equation (12,13):

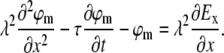(12)

Here φ_m is the deviation of the membrane potential from its resting value, λ is the passive length constant of the neurite, τ is the passive time constant of the neurite, and x is directed along the neurite, regardless of its true absolute orientation. The value E_x is the projection of the effective external electric field on the direction of the neurite at any point along it.

In our experiment, the electric field is induced by the magnetic pulse and is directed parallel to the concentric rings upon which the axons grow. The temporal pattern of this field consists of one sinusoidal cycle, with a cycle time that is kept constant at 240 μs throughout the experiment, changing only the amplitude of the pulse. The induced electric field can therefore be expressed as

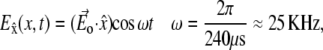(13)

where E_o is the maximum amplitude of the induced electric field, which depends on the strength of the magnetic pulse and on the geometrical features as detailed in the first part of the Appendix.

To study the dependence of magnetic stimulation on the biological properties of single neurons, we solve Eq. 12 for the case of a neurite of finite length L that lies parallel to the electrical field. The boundary conditions correspond to a neurite with sealed ends,

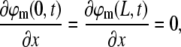(14)

and the membrane potential is assumed at rest before the stimulation,

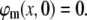(15)

The presence of a spatially uniform external field induces membrane currents at the two ends (0, L) of the neurite of the following form:

(16)

We solve Eq. 12 numerically with boundary conditions (Eq. 14), initial value (Eq. 15), and an external force (Eq. 16), using the PDE toolbox in MATLAB (The MathWorks, Natick, MA). We substitute the biologically relevant values for λ, L, and τ, and assume that a cell is activated when the resulting membrane potential reaches a threshold level, here chosen as ϕ_T = 30 mV. We then calculate the corresponding electric field threshold E_T as the minimal electric field amplitude E_o that fulfills this requirement:

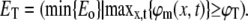(17)

Table 1 presents E_T for a typical dendrite and a typical axon using this numerical solution. We see that the electric field threshold of a typical dendrite is almost twice as high as the electric field threshold of a typical axon in our experiment.

To map the general effects of changing λ, L, and τ on the stimulation we combine our numerical simulation with an analytic solution for ϕ_m(x,t). Following Tuckwell (54), we use the separated variables Green's function approach for the particular case of a finite nerve with sealed ends. We define the Green's function:

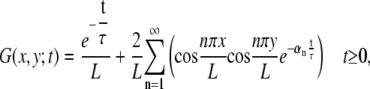(18)

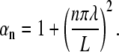(19)

The solution for the external field F (Eq. 16) is derived by convolving G with ϕ_m and F (54):

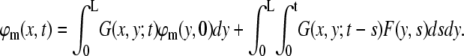(20)

Plugging in the initial value, which is zero, and the external field F, we have

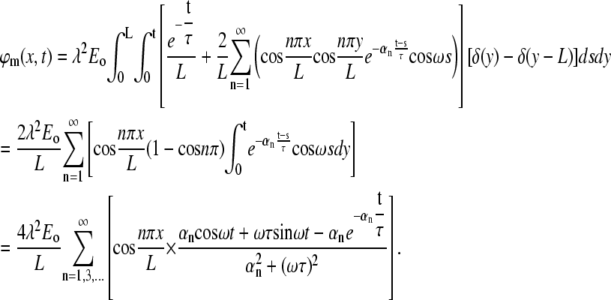(21)

So the solution can be presented as the following infinite sum:

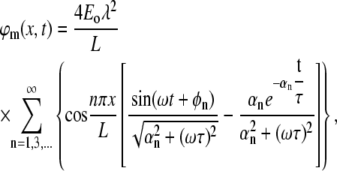(22)

(23)

From the numerical solution, we know that the maximal absolute value of φ_m(x,t) is obtained at the boundaries (0, L). We demonstrate the case of x = 0, where the solution becomes:

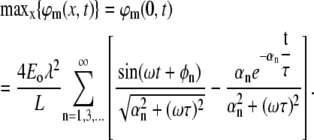(24)

The sum depends on the two dimensionless factors: λ/L and ωτ (note also that for any biologically relevant time constant τ, the factor ωτ is >1). A simple approximation can be obtained in the case of a typical dendrite, where λ/L ≫ ωτ ≫ 1:

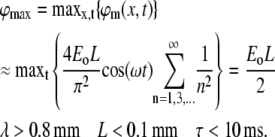(25)

This approximation is identical to the steady-state solution for neurites that are short compared to their length constant (55). When L is increased or λ decreased, then the solution gradually transforms into the case below, which corresponds to axons. The case that corresponds to axons is λ/L < ωτ, where the extreme limit λ/L ≪ ωτ is not attained. The maximum value of ϕ_m is then a sum with no simple approximation. However, by analyzing the sum numerically and verifying with the numerical solution of the full PDE for parameters within the working range of a typical axon, we have found the relation

(26)

The maximum value of ϕ_m cannot be increased by reducing τ, since decreasing it to <0.1 ms causes ϕ_m to saturate at a maximal value of ϕ_max = E_oλ. Note that, at this limit, we revert to the steady-state solution for neurites that are long compared to their length constant (55).

In summary, neither increasing L, λ, nor decreasing τ can increase ϕ_max indefinitely. For any optimal time constant τ, ϕ_max is limited by the minimum of the length constant λ and half the physical length of the neurite L/2:

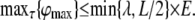(27)

Fig. 7 presents color-coded maps of the maximal membrane potential that is reached in response to a 100 V/m induced electric field, portrayed as a function of λ and L. Each map was calculated for a different τ, with the top row corresponding to axons and the bottom row corresponding to dendrites. The maximal membrane potential that can be attained in axons is found to be twice that of the dendrites.