Abstract
Fluorescence correlation spectroscopy (FCS) is a sensitive analytical tool that allows dynamics and hydrodynamics of biomolecules to be studied under a broad range of experimental conditions. One application of FCS of current interest is the determination of the size of protein molecules in the various states they sample along their folding reaction coordinate, which can be accessed through the measurement of diffusion coefficients. It has been pointed out that the analysis of FCS curves is prone to artifacts that may lead to erroneous size determination. To set the stage for FCS studies of unfolded proteins, we first show that the diffusion coefficients of small molecules as well as proteins can be determined accurately even in the presence of high concentrations of co-solutes that change the solution refractive index significantly. Indeed, it is found that the Stokes-Einstein relation between the measured diffusion coefficient and solution viscosity holds even in highly concentrated glycerol or guanidinium hydrochloride (GuHCl) solutions. These measurements form the basis for an investigation of the structure of the denatured state of two proteins, the small protein L and the larger, three-domain protein adenylate kinase (AK). FCS is found useful for probing expansion in the denatured state beyond the unfolding transition. It is shown that the denatured state of protein L expands as the denaturant concentration increases, in a process akin to the transition from a globule to a coil in polymers. This process continues at least up to 5 M GuHCl. On the other hand, the denatured state of AK does not seem to expand much beyond 2 M GuHCl, a result that is in qualitative accord with single-molecule fluorescence histograms. Because both the unfolding transition and the coil-globule transition of AK occur at a much lower denaturant concentration than those of protein L, a possible correlation between the two phenomena is suggested.
INTRODUCTION
It is now recognized that understanding the denatured states of proteins is a prerequisite for obtaining a full understanding of the protein folding reaction (1). For many years denatured proteins have been discussed as featureless random coils. However, even from the point of view of polymer physics, denatured proteins should change their structure in response to changes in temperature and solution conditions. Indeed, when a polymer molecule is transferred from a good solvent to a bad one, it undergoes a collapse from an expanded conformation to a contracted, globular conformation (2). This so-called coil-globule (CG) transition has been studied extensively in homopolymers (3). It is driven by a competition between the entropy of the chain (i.e., the excluded-volume interaction) and the attraction between monomers. In recent years it has been observed, using mainly single-molecule fluorescence techniques, that proteins may also undergo a similar transition, sometimes called hydrophobic collapse, in their denatured state (4–13). The theory of the CG transition was applied to quantitatively interpret such observations (8). Fluorescence correlation spectroscopy (FCS) is an attractive method to study changes in protein dimensions under denaturing conditions (14). In this study, we assess the use of FCS as a tool to probe the CG transition of denatured proteins.
FCS measures the fluctuations of fluorescence emitted from molecules diffusing through a laser beam focused by a high numerical aperture microscope objective. Statistical analysis of these fluctuations is used to interpret various dynamic molecular events, such as diffusion or conformational fluctuations of biomolecules (15–17). The final result of an FCS experiment is a correlation function, which is constructed from a large number of detected photons. The correlation function is then fitted to a model, which introduces any prior knowledge about the possible dynamic mechanisms that may contribute to fluorescence fluctuations, and from the fit one extracts various dynamic parameters, from reaction times to diffusion coefficients. In the context of this study we are particularly interested in the latter, because they are related to the hydrodynamic radii of the diffusing molecules, thus providing a sensitive method for size determination. FCS models typically represent the observation volume (that is a convolution of the excitation and detection volumes) as having a three-dimensional (3D) Gaussian shape, with one parameter describing the width of the Gaussian in the x-y plane and one parameter for the z direction (18). Indeed, it has been shown that a 3D Gaussian shape is a good approximation for the real observation volume under standard conditions (19), and that accurate determination of protein radii can be obtained using this approximation (20). However, it is not clear a priori that this approximation still holds in complex solutions containing various additives, which may lead to refractive index mismatches between the microscope objective and the sample. Changes in the index of refraction can alter the focal beam dimensions and thus may lead to poor or erroneous fits, and extracted parameters that cannot be interpreted readily (21). It is the goal of this study to show that it is possible to use FCS to extract meaningful parameters and obtain information about changes incurred by biomacromolecules in complex solutions. In particular, we will show how analysis of the diffusion coefficient of proteins measured with FCS under a broad range of conditions can lead to important new information on conformational changes they undergo as they denature.
We are particularly interested here in the effect of small solutes such as osmolytes (e.g., glycerol) or denaturants (e.g., guanidinium hydrochloride (GuHCl)), which are usually weak protein binders. These solutes are therefore added at high concentration to protein solutions, and may modulate their optical properties, particularly by changing their refractive indices. This can lead, in principle, to changes in the way light travels and focuses in these solutions. Because the determination of macromolecular sizes by FCS relies on knowledge of the shape and size of a focused laser beam, it is imperative to be able to control for solute effects and learn how to accurately analyze them. We show that it is possible to obtain accurate and consistent measurements of protein diffusion coefficients in solutions containing high concentrations of additives. Using rhodamine 6G (R6G) to measure and calibrate the observation volume dimensions, we show that the error on repeated measurements of a protein's diffusion coefficient can be as small as 4%, and that the Stokes-Einstein relation between diffusion and viscosity is well -reproduced. We then focus on the size of denatured proteins, and use FCS to search for expansion of their denatured state with increasing concentrations of a chemical denaturant, similar to the well-studied CG transition of synthetic polymers.
MATERIALS AND METHODS
Chemicals
Ultra-pure glycerol was purchased from ICN Biomedicals (Irvine, CA), and ultra-pure 8 M GuHCl was purchased from Pierce (Rockford, IL).
Viscosity and refractive index measurements
Macroscopic solution viscosity was measured using a Cannon-Fenske Routine Viscometer 150/I750 (Cannon, State College, PA) at 25°C in a water bath. Further viscosity measurements, for solutions with high viscosity, were done with a rotational viscometer (Haake RotoVisco 1, Thermo Electron, Karlsruhe, Germany). Measured values of viscosity for glycerol were in good agreement with published data (22). The viscosity of glycerol solutions was also assessed from their refractive indices, measured using a Fisher Tabletop Refractometer (Fisher Scientific, Rockford, IL). The viscosity of GuHCl solutions was also determined through measuring their refractive indices, using the same instrument, and applying the published relation between refractive index and viscosity (23).
Protein samples and labeling
BLIP
The mutant A1C of β-lactamase inhibitor protein (BLIP), with cysteine replacing the alanine residue at position 1, was expressed and purified according to methods developed previously (24). The mutant was found to be fully active by assaying its binding activity to the partner protein β-lactamase (using analytical gel filtration). A1C-BLIP was labeled with a maleimide derivative of the fluorescent probe Alexa Fluor 488 C5 maleimide (Alexa488, Molecular Probes, Eugene, OR) using standard procedures. Labeled BLIP was stored and measured in 10 mM Hepes, pH 7.2.
Protein L
A cysteine was introduced at position 1 (M1C) into histidine-tagged protein L (PL) by site-directed mutagenesis. PL molecules were labeled at this unique cysteine residue with Alexa488. Further details on PL overexpression, purification, and labeling procedures can be found in Sherman and Haran (8). The denaturation curve of PL in GuHCl solutions was measured by monitoring the fluorescence of Trp47 of the protein.
Adenylate kinase
The mutant C77A of Escherichia coli adenylate kinase (AK) was further modified by site-directed mutagenesis; Gln 28 was replaced by a cysteine (C77A,Q28C-AK) in the mutant used for FCS, whereas Ala 73 and Ala 203 were replaced by cysteines (C77A,A73C,A203C-AK) in the mutant used for single-molecule fluorescence. Protein expression and purification were done as described in Ratner et al. (26), except that the purification after labeling was done by ion exchange chromatography using a Mono-Q column (Pharmacia, Ramsey, MN). C77A,Q28C-AK was labeled with the fluorescent probe Atto 520 maleimide (Atto520, ATTO-TEC, Siegen, Germany). The labeling of C77A,A73C, A203C-AK with Alexa488 and Texas Red was described in Rhoades et al. (27). The labeled proteins showed reduced enzymatic activity (∼60% of the AK activity) and the thermal stability was mildly reduced (∼6 Kcal/mol) (26). The denaturation curve of the C77A,Q28C-AK mutant in GuHCl solutions was measured using circular dichroism (CD) spectroscopy.
Fluorescence correlation spectroscopy
FCS experiments were carried out using a home-built confocal microscope. This system was based on an Axiovert 135 TV inverted microscope (Zeiss, Jena, Germany) equipped with a water immersion UplanApo 60× NA 1.2 (Olympus, Melville, NY) objective. The collar setting of the objective was set to 0.17 throughout all measurements. The sample (typically at concentrations of 10–20 nM) was illuminated by a 488 nM Ar+ ion laser (35 LAP 431, Melles Griot, Carlsbad, CA), focused through the objective, at a power level of 15–30 μW Fluorescence was collected through the objective, and was then filtered by a dichroic mirror (500 DCLP, Chroma, Rockingham, VT) and a long-pass interference filter (HQ 500 LP, Chroma). The fluorescence was then focused by the microscope tube lens onto a 50-μm pinhole to filter out-of-focus light. It was split by a nonpolarizing beam splitter and focused on two identical single-photon counting avalanche photodiodes (Perkin Elmer, Fremont, CA; model SPCM-AQR-15). Data collection and generation of FCS curves were carried out using a hardware correlator (Correlator.com, Bridgewater, NJ, model Flex02-12D/C). Some measurements of labeled BLIP were carried out with a single detector and a counting card (National Instruments, Austin, TX), and correlation functions were calculated using the software correlation method of Wahl et al. (28).
Experimental correlation functions were fit to the equation appropriate for a 3D Gaussian beam shape:
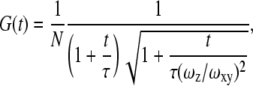 |
(1) |
where N is the total average number of molecules in the observation volume, τ is the mean diffusion time of a molecule through the observation volume, and 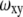 and
and 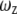 are the dimensions of the Gaussian beam waist perpendicular and parallel to the direction of light propagation, respectively (the observation volume is given by
are the dimensions of the Gaussian beam waist perpendicular and parallel to the direction of light propagation, respectively (the observation volume is given by 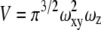 ). The diffusion coefficient is related to the above parameters through the relation
). The diffusion coefficient is related to the above parameters through the relation 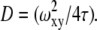
Single-molecule fluorescence measurements
Single-molecule fluorescence resonance energy transfer (smFRET) measurements on freely-diffusing AK molecules were carried out and analyzed using the same methodology described in Sherman and Haran (8).
RESULTS AND DISCUSSION
R6G as a diffusion standard
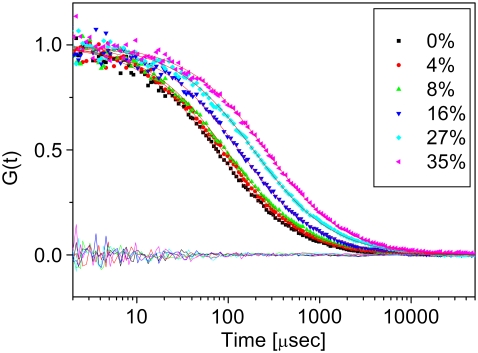
To obtain a well-behaved standard for the assessment of the effect of refractive index changes on apparent diffusion coefficients, we carried out a systematic study of the diffusion of R6G molecules in water solutions containing a broad range of concentrations of glycerol and GuHCl. Fig. 1 shows correlation curves from a series of measurements of R6G in glycerol solutions, with fits to Eq. 1 and residuals. Similar curves were obtained in GuHCl solutions. In a simple liquid, D is inversely proportional to the viscosity of the medium as described by the Stokes-Einstein (SE) relation: 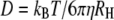 where kB is Boltzmann's constant, T is the absolute temperature, η is the viscosity of the solvent and RH is the hydrodynamic radius of the molecules. The SE relation implies that the diffusion time relative to that in water,
where kB is Boltzmann's constant, T is the absolute temperature, η is the viscosity of the solvent and RH is the hydrodynamic radius of the molecules. The SE relation implies that the diffusion time relative to that in water, 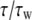 should be proportional to the viscosity relative to water viscosity,
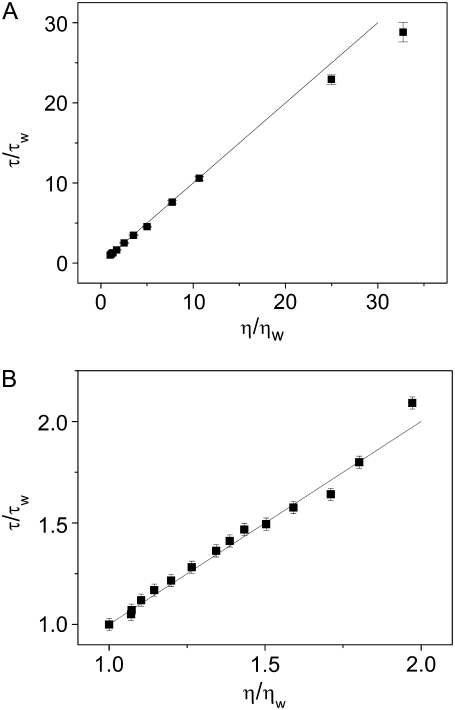
should be proportional to the viscosity relative to water viscosity, 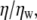 with a proportionality constant of 1. Fig. 2, A and B, show the calculated relative diffusion times of R6G in glycerol and GuHCl, respectively. The full line in both panels is not a fit, but rather represents the SE prediction with a slope of 1. Clearly the SE relation holds for R6G molecules in glycerol solutions up to a relative viscosity of ∼25, which corresponds to a concentration of ∼80% w/w. Also, the SE relation holds in all GuHCl solutions up to a concentration of 7.2 M.
with a proportionality constant of 1. Fig. 2, A and B, show the calculated relative diffusion times of R6G in glycerol and GuHCl, respectively. The full line in both panels is not a fit, but rather represents the SE prediction with a slope of 1. Clearly the SE relation holds for R6G molecules in glycerol solutions up to a relative viscosity of ∼25, which corresponds to a concentration of ∼80% w/w. Also, the SE relation holds in all GuHCl solutions up to a concentration of 7.2 M.
FIGURE 1.
Fluorescence correlation curves of R6G in glycerol solutions of the concentrations indicated in the legend. All curves were fitted to Eq. 1, and the fits are also shown, with matching residuals at the bottom of the figure. Curves shift to longer diffusion time due to the increase in viscosity with glycerol concentration.
FIGURE 2.
Relative diffusion time of R6G as a function of relative viscosity in glycerol solutions with concentrations of 0–80% w/w (A) and in GuHCl solutions with concentrations of 0–7.2M (B). The full line with a slope of 1 is not a fit, but rather represents the SE prediction.
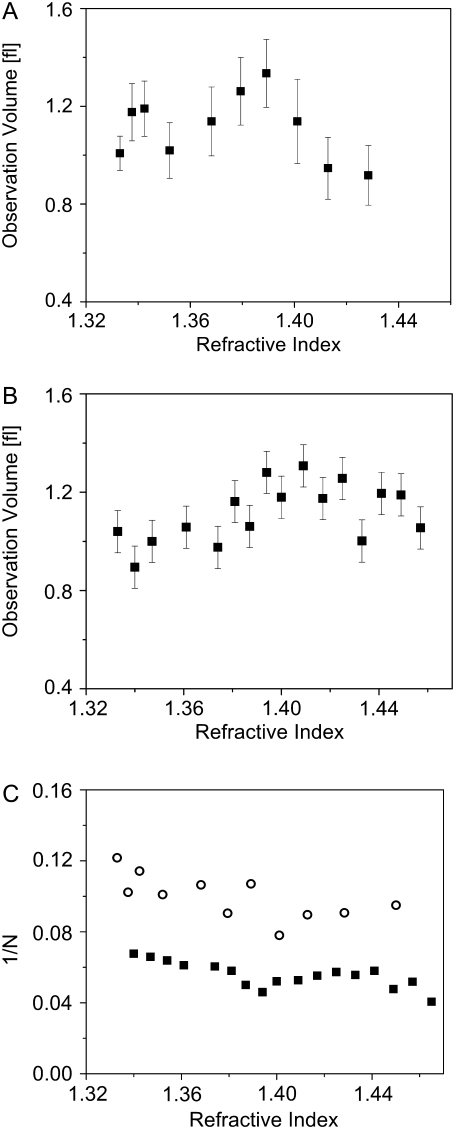
In Fig. 3 we analyze the same data in a different manner. We assume that the diffusion coefficients of R6G in the various solutions used can be calculated from the known coefficient in water (see Table 1 and related discussion below) together with the SE relation, and use these values to calculate the observation volume from the fit parameters. The values of the observation volume are then plotted as a function of refractive index, both for glycerol solutions (Fig. 3 A) and for GuHCl solutions (Fig. 3 B). The figure shows a fairly constant observation volume in solutions with refractive indices ranging from 1.33 to 1.46. The observation volume values obtained here span a range of ∼±10% around the mean. Note, however, that the diffusion coefficients are determined by 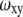 alone, which leads to even smaller errors (up to ±5%). For completion, we also plot the amplitude of the correlation functions, 1/N, which shows only little change throughout the range of glycerol and GuHCl concentrations used (Fig. 3 C).
alone, which leads to even smaller errors (up to ±5%). For completion, we also plot the amplitude of the correlation functions, 1/N, which shows only little change throughout the range of glycerol and GuHCl concentrations used (Fig. 3 C).
FIGURE 3.
The observation volume, calculated from FCS measurements of R6G in glycerol (A) and GuHCl (B), as a function of solution refractive index. The observation volume does not change by >10% throughout the range of additive concentrations used. (C) The reciprocal of the particle number of R6G molecules in the observation volume, 1/N, in glycerol (open circles) and GuHCl (solid squares).
TABLE 1.
Diffusion coefficient values for R6G found in the literature
| D × 106 (cm2/s) | Method used | Temperature (°C) | Reference |
|---|---|---|---|
| 2.5 ± 1.7 | Photon burst analysis | RT* | (43) |
| 2.8 ± 0.35 | FCS measurements with a known beam radius | 20 | (30) |
| 2.9 ± 0.7 | NMR (bipolar gradient stimulated echo technique) | (44) | |
| 3 | Two photon FCS of Rhodamine B | RT* | (45) |
| 4.14 ± 0.1† | Imaging of diffusion through a microfabricated fluidic device (static imaging) | 25 | (29) |
| 4.59 ± 0.06‡ | Imaging of diffusion through a microfabricated fluidic device with a varying electrical potential (E-field method) | 25 | (29) |
| 5.5 ± 0.8 | FCS and beam profiling | (46) |
Room temperature.
Value at 20°C is calculated to be 3.7 × 10−6 cm2/s.
Value at 20°C is calculated to be 4.1 × 10−6 cm2/s.
Chattopadhyay et al. (14) reported an elaborate calibration method involving the correction collar of the objective, which was required to get meaningful FCS results in GuHCl solutions. The results above show that our FCS spectrometer provides accurate numbers without the need for such calibration. The difference might lie in the use of a one-photon excitation scheme with a pinhole in our system, as opposed to the two-photon excitation scheme without a pinhole in the work of Chattopadhyay et al. (14). R6G can thus serve as a well-behaved standard for measurement of molecular diffusion. This is all that is necessary to get relative diffusion times of a protein in a series of solutions (shown below). It is important to know the diffusion coefficient of R6G as accurately as possible if one would like to obtain absolute measurements of the diffusion coefficient or the RH of a protein. Regrettably, scientific literature contains a rather broad range of values for the diffusion coefficient of R6G, which we compile in Table 1. Culbertson et al. (29) seem to provide diffusion coefficient values with the smallest error of all reported numbers, but their values are significantly larger than all previous measurements. Thus it will still be beneficial to carry out accurate measurements of the diffusion coefficient of R6G. We leave this to future work and will stick to 2.8 × 10−6 cm2/s, the value used most commonly (30).
Reproducibility of hydrodynamic radius measurements
We tested the usefulness of R6G as a standard for the measurement of protein diffusion times and hydrodynamic radii. We were particularly interested to learn whether this standard is able to reduce errors due to long-time drifts in the spectroscopic system, which might stem from either changes in alignment or to changes in temperature. Such drifts may lead to variations in extracted parameters of the observation volume. Over a period of several months, we carried out a series of FCS measurements of the protein BLIP, labeled with the dye Alexa488, at a concentration of 10 nM in buffer. Each measurement was preceded by a control measurement of an R6G sample. Using the known diffusion coefficient of R6G, we extracted from each control measurement both the aspect ratio (ωz/ωxy) of the observation volume and the diffusion time of R6G. We fitted the correlation curves measured with the protein solutions to obtain the diffusion times of BLIP, which were used to calculate the hydrodynamic radius of the protein as 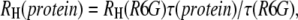 where
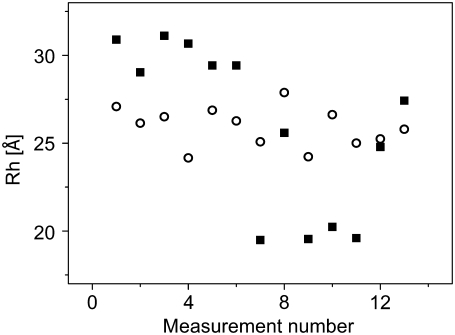
where 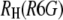 was calculated from the known diffusion coefficient of R6G (see above). The results are shown in Fig. 4. The points indicated by black squares in the figure were calculated using an average
was calculated from the known diffusion coefficient of R6G (see above). The results are shown in Fig. 4. The points indicated by black squares in the figure were calculated using an average 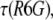 to mimic the situation where calibration with R6G is carried out only infrequently. The values show a pretty large scatter with a SD of 18% around a mean value of 25 Å. The points in red, on the other hand, were each calculated using the value of
to mimic the situation where calibration with R6G is carried out only infrequently. The values show a pretty large scatter with a SD of 18% around a mean value of 25 Å. The points in red, on the other hand, were each calculated using the value of 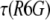 measured on the same day with the protein. Here, the scatter of the points is far narrower, with a SD of only 4.3% around its mean value of 25.9 Å. Thus, a measurement of the FCS curve of R6G coupled to every protein measurement allows accurate determination of the hydrodynamic radius with a much reduced error.
measured on the same day with the protein. Here, the scatter of the points is far narrower, with a SD of only 4.3% around its mean value of 25.9 Å. Thus, a measurement of the FCS curve of R6G coupled to every protein measurement allows accurate determination of the hydrodynamic radius with a much reduced error.
FIGURE 4.
RH values of BLIP in water solutions obtained from a series of measurements taken on different days. Solid squares show values calculated using an average value for the diffusion time of R6G. Open circles show values calculated using R6G diffusion times measured on the same day with the protein, which show a reduced spread.
Protein diffusion in glycerol solutions
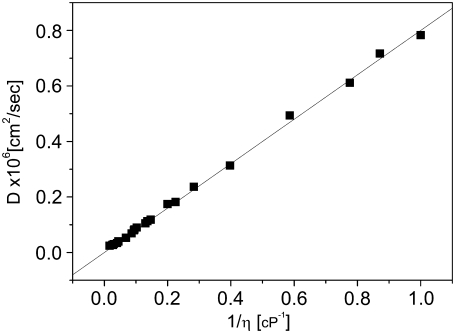
We have shown that the measured diffusion times of R6G in viscous water/glycerol solutions obey the SE relation. This indicates that no artifacts are introduced into the measurements due to refractive index mismatches. We tested whether the same result can be obtained with protein molecules as well. The diffusion of proteins in viscous solutions is of relevance to studies of crowding, i.e., the effect of various solution additives on biological reactions (31). There is no reason to believe that in solutions of small viscogens there will be any deviation from SE behavior. We thus measured BLIP diffusion in glycerol solutions, correcting the results at each concentration using R6G diffusion times, as discussed above. The diffusion coefficients obtained in glycerol solutions are plotted as a function of the inverse of the viscosity in Fig. 5 (black squares). That the points of this graph lie on a straight line is an indication of the validity of the SE relation. This relation holds up to a relative viscosity of ∼25 (close to the origin of Fig. 5). Above this relative viscosity we noticed increasing deviations from the SE behavior, with relative diffusion times smaller than expected. Because refractive index mismatch is expected to lead to apparently larger diffusion times, the deviations we see are unlikely to be optics-related. Rather, it is possible that in these viscous solutions additional effects lead to a change in the protein diffusion mechanism. Alternatively, it is possible that longer dwell times in the beam in viscous solutions increase photobleaching of the dyes, thus decreasing apparent diffusion times (32). This point requires further exploration. Fitting the data to the SE relation, we obtain a value for RH in glycerol solutions of is 26.5 ± 0.17 Å. The likeness of this value to the value obtained from repeated measurements of BLIP in buffer is another indication that the FCS measurement of diffusion of BLIP in solutions of varying refractive index provides valid values for measured parameters.
FIGURE 5.
Diffusion coefficient of BLIP as a function of inverse viscosity in glycerol solutions. The full line is a linear fit of the data, forced to cross the zero point. The slope of the line is proportional to 1/RH according to the SE relation.
Hydrodynamic radii of denatured proteins
A prerequisite for the accurate determination of the dimensions of denatured proteins, as well as of structural transitions they may undergo, is the ability to precisely and reproducibly determine size parameters, such as RH. Our observations show that it is possible to accurately determine RH by FCS, especially in solutions of small additives such as GuHCl, and opens the way to study the effect of denaturation on protein size. In this section, we use the technique to study the hydrodynamic radii of a small protein, PL, and a larger one, AK, in solutions of increasing GuHCl concentration, particularly looking for the CG transition in the denatured state.
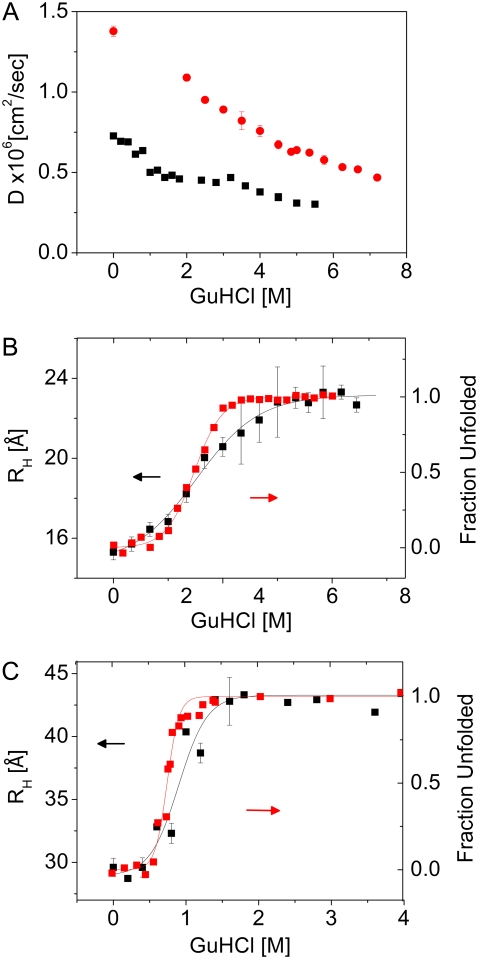
We obtained FCS curves of PL labeled at position 1 with Alexa488 and AK labeled at position 28 with Atto520. The diffusion coefficients of the two proteins in solution of increasing GuHCl concentrations are shown in Fig. 6 A. The diffusion coefficients of both proteins decrease with GuHCl concentration due to the increase in solvent viscosity (by a factor of ∼2), as well as the expansion of the protein chains on denaturation. The diffusion coefficients of PL are larger by a factor of ∼2 than those of AK, due to their significant difference in size and shape. To separate viscosity and size effects on diffusion we calculated the hydrodynamic radii of the two proteins. The radii obtained under native and highly denaturing conditions are given in Table 2. Interestingly, the value obtained for native AK is ∼50% of the longest dimension of this nonspherical structure. This stems from the fact that the hydrodynamic radius of a nonspherical body deviates from that of a spherical structure with the same volume only when the ratio of long-to-short dimensions becomes very large (33). In Fig. 6, B and C, we plot the hydrodynamic radii of protein L and AK, respectively, normalized to their native-state radii, as a function of GuHCl concentration. Each of the figures also contains the respective denaturation curve. Clearly, each of the proteins undergoes a significant expansion from its native state to its fully denatured state. Before discussing the course of this expansion and its implications in detail, we will first analyze the measured sizes of the native and fully denatured proteins and compare them to calculated values and values measured by other techniques.
FIGURE 6.
FCS measurements of PL and AK in GuHCl solutions. (A) Diffusion coefficients of PL (red dots) and AK (black squares). (B) Hydrodynamic radii of protein L (black squares), plotted together with the denaturation curve of the protein (red squares), obtained using Trp fluorescence. (C) Hydrodynamic radii of AK (black squares), plotted together with the denaturation curve of the protein, (red squares) obtained from the CD signals at 222 nM. For a summary of hydrodynamic radii of the native and fully unfolded proteins see Table 2. Red lines in B and C are fits to a two-state denaturation model. Black lines, following the FCS results, aim to emphasize the differences between the denaturation and the FCS curves. Note the different abscissa scales in B and C.
TABLE 2.
Hydrodynamic radii of native and fully-denatured PL and AK obtained by FCS
| RH | PL | AK |
|---|---|---|
| Native | 15.3 ± 0.4 Å | 29.6 ± 0.7 Å |
| Fully denatured GuHCl concentration | 23.1 ± 0.25 Å (5–6.3 M) | 42.7 ± 0.7 Å (1.8–3.6 M) |
It is possible to calculate the RH of native proteins from their crystal structures using the algorithm developed by Garcia de la Torre et al. (34) and implemented in the program HYDROPRO. The program represents the protein as an ensemble of spheres and calculates numerically the hydrodynamic properties of this ensemble. Using this program, we computed an RH of 16.3 Å for the native state of PL and 25.6 Å for the native state of AK. These are not far from our measured values of 15.3 ± 0.4 Å for PL and 29.6 ± 0.7 Å for AK. The hydrodynamic radii of proteins can also be estimated from their radii of gyration, Rg. This property can be found for native and denatured proteins using various scattering methods, such as small-angle x-ray scattering (SAXS) (35). For globular folded proteins, the expected relation between the radius of gyration and hydrodynamic radius of a sphere, 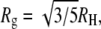 may be applied. SAXS measurements yielded an Rg value of 16.2 Å for native PL (36) and 20.0 Å for native AK (37). The Rg value of PL measured by SAXS is significantly larger than the Rg calculated directly from the crystal structure of the protein (13.2 Å), and indeed leads to a larger value for RH (20.9 Å) than the one measured by us. A somewhat better agreement is obtained in the case of AK, where the measured Rg is quite similar to that calculated from the crystal structure (20.2 Å). The hydrodynamic radius calculated from this value (25.8 Å) is close to the value we measure by FCS.
may be applied. SAXS measurements yielded an Rg value of 16.2 Å for native PL (36) and 20.0 Å for native AK (37). The Rg value of PL measured by SAXS is significantly larger than the Rg calculated directly from the crystal structure of the protein (13.2 Å), and indeed leads to a larger value for RH (20.9 Å) than the one measured by us. A somewhat better agreement is obtained in the case of AK, where the measured Rg is quite similar to that calculated from the crystal structure (20.2 Å). The hydrodynamic radius calculated from this value (25.8 Å) is close to the value we measure by FCS.
We next turn to the denatured state of the two proteins. Wilkins et al. (38) have proposed an empirical scaling law for the hydrodynamic radii of highly-denatured proteins, based on NMR diffusion measurements of a range of proteins: 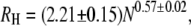 where N is the number of amino acid residues in a protein. Using this relation, we find values of 25.1 ± 1.7 Å for the 71 residue long PL (including its histidine tag) and 45.6 ± 3.2 Å for AK. These values are in good agreement with the values we measured (PL= 23.1 ± 0.25 Å; AK = 42.7 ± 0.7 Å), and agree also with time-resolved FRET experiments of AK (39). This agreement suggests that the two proteins achieve maximal chain expansion at the studied conditions (∼6 M and ∼2 M GuHCl, respectively).
where N is the number of amino acid residues in a protein. Using this relation, we find values of 25.1 ± 1.7 Å for the 71 residue long PL (including its histidine tag) and 45.6 ± 3.2 Å for AK. These values are in good agreement with the values we measured (PL= 23.1 ± 0.25 Å; AK = 42.7 ± 0.7 Å), and agree also with time-resolved FRET experiments of AK (39). This agreement suggests that the two proteins achieve maximal chain expansion at the studied conditions (∼6 M and ∼2 M GuHCl, respectively).
CG transition in protein L and AK
As noted in the previous section, Fig. 6, B and C, shows a significant expansion of the two proteins from native to fully unfolded. Is this expansion just a manifestation of the gradual population of the denatured state, or is there an additional expansion of the denatured state itself, i.e., the inverse of the hydrophobic collapse? To obtain an answer to this question we compare the GuHCl-dependent change in the hydrodynamic radius of each protein with its denaturation curve. In the case of PL (Fig. 6 B) the expansion of the chain continues much beyond the denaturation transition (that occurs at 2.05 M GuHCl). Indeed, the protein's RH grows from 17 ± 0.4 Å at 2 M GuHCl to 23.1 ± 0.25 Å at 5 M GuHCl. This significant expansion is clearly a manifestation of the CG transition (or more accurately its inverse) in the denatured state of the protein, which we (8), as well as Merchant et al. (11), have also seen using smFRET experiments. Interestingly, smFRET histograms, which measure the N- to C-terminus distance of the protein indicated an increase in protein size even up to 7 M GuHCl. The difference between the measurements might result from RH not growing as much as Rg (or the end-to-end distance) because as the denatured protein expands further and further, the hydrodynamic interactions between chain segments weaken.
How universal is this phenomenon of chain expansion in denatured proteins? Some recent reports suggest that a hydrophobic collapse may not precede folding in all proteins (36,40). This finding is surprising because it implies that the hydrophobic interactions, which tend to contract the chain in a bad solvent, are countered by some other interactions, perhaps suggesting that they do not play an important role in the folding of some proteins. Examining the hydrodynamic radius measurements of AK (Fig. 6 C), we find that beyond the unfolding transition there is only a small, if any, further change in the size of the denatured state, and it reaches its final size below 2 M GuHCl. Before concluding that this protein also belongs to the group of proteins not showing a hydrophobic collapse, it is necessary to test the possibility that most of the expansion of the denatured state of this protein occurs at denaturant concentrations below or around the denaturation transition mid-point. This region is difficult to explore with FCS, as contributions from both the native and the unfolded state are registered. Recent time-resolved FRET experiments show that under midtransition and pretransition concentrations of GuHCl the ensemble of AK molecules includes at least two subpopulations, one expanded and the other native-like (E. Haas, unpublished). These experiments further show that some specific interactions are formed in the collapsed state of the protein that are probably essential steps in the folding transition (39).
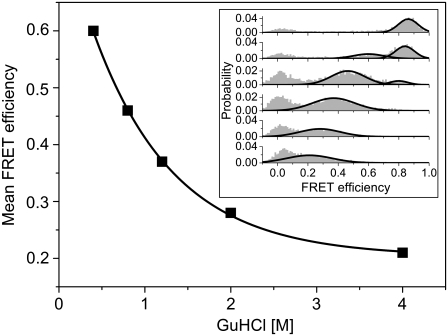
Single-molecule fluorescence experiments can, in principle, separate the contributions of the native and denatured states even under equilibrium conditions. Fig. 7 shows results from smFRET experiments conducted on AK molecules. These molecules were labeled with Alexa488 at position 203 and Texas Red at position 73 (27), and were measured as they diffused freely through the focus of a laser beam within a confocal microscope (8). The FRET histograms shown in the Fig. 7 inset clearly resolve the peaks due to the folded state (at high FRET efficiency) and the denatured state (at a lower FRET efficiency). The latter peak shifts to lower values as the GuHCl concentration increases. The mean FRET efficiency of the denatured state peak is plotted in the main figure as a function of denaturant concentration. The figure suggests strongly that denatured molecules of AK expand in the concentration range 0.5–3 M. Much of the change is already achieved at 2 M GuHCl, although the histograms do indicate some continued expansion beyond that seen in the RH curve, just as in the case of PL. This explains why it is difficult to observe expansion with FCS in this case.
FIGURE 7.
smFRET experiments on double-labeled AK molecules. The mean FRET efficiency of the denatured state species, extracted from the FRET histograms (inset), is plotted as a function of denaturant concentration. The full line is a guide to the eye. (Inset) FRET histograms constructed from fluorescence bursts of molecules freely-diffusing in solution through a focused laser beam, at increasing GuHCl concentrations (0, 0.4, 0.8, 1.2, 2, and 4 M GuHCl; from top to bottom). Three peaks are seen in the histograms, and are attributed to the folded species (at a high FRET efficiency), the denatured species (at a lower FRET efficiency) and a zero peak due to donor-only containing molecules.
CONCLUSION
In this study, we used FCS measurements to shed light on the CG transition in the denatured state of two proteins, protein L and AK. We showed that FCS can provide accurate and reproducible measurements of the hydrodynamic properties of protein molecules in solutions containing large concentrations of various additives relevant to biological studies. In the face of warnings about possible artifacts of the technique, we believe our results offer some reassurance regarding the usefulness of FCS in biochemistry and biophysics. With table-top instrumentation, rather simple experimental procedures, and very low sample concentrations, FCS can compete nicely with more established methods of size determination, and provides important information related to the diffusion of macromolecules in complex biological environments. FCS is simpler than smFRET spectroscopy, both technically and from the point-of-view of sample preparation—it requires labeling with only one fluorescent probe. Improvements in FCS technology (41) promise to make this method even more accurate, allowing determination of even smaller changes in protein size than detected here.
An interesting finding of this study is that denatured-state expansion spans a very different range of GuHCl concentration in the two proteins studied. Although the expansion of protein L continues even above 5 M GuHCl, AK attains its maximally-expanded state at ∼3 M GuHCl. The cause of this difference might be specific to the particular structure of the two proteins. However, this finding might also correlate with a more universal feature of proteins, namely the position of their denaturation transition midpoint. Indeed, the midpoint of AK is much lower than the midpoint of protein L. Thirumalai et al. (42) have already hinted, based on simulations, that there might be a relation between the collapse and folding transitions in efficiently-folding proteins. It will be interesting to see whether this correlation holds true in other proteins as well.
Acknowledgments
This research was made possible in part by the generosity of the Harold Perlman Family, as well as by partial financial support of the US-Israel Binational Science Foundation (grant 2002371 to G.H. and grant 2005270 to E.H.), the National Institutes of Health (grant 1R01GM080515-01 to GH), and the European Union (grant MTKD-CT-2005-029936 to E.H.).
Yosef Yehuda Kuttner's present address is Laboratory of Chemical Physics, National Institute of Diabetes and Digestive and Kidney Diseases, National Institutes of Health, Bethesda, MD 20892-0520.
Elizabeth Rhoades' present address is Dept. of Molecular Biophysics and Biochemistry, Yale University, New Haven, CT 06520-8114.
Editor: Elliot L. Elson.
References
- 1.Millet, I. S., S. Doniach, and K. W. Plaxco. 2002. Toward a taxonomy of the denatured state: small angle scattering studies of unfolded proteins. Adv. Protein Chem. 62:241–262. [DOI] [PubMed] [Google Scholar]
- 2.Grosberg A. Y., A. R. Kokhlov. 1994. Statistical Physics of Macromolecules. AIP Press, College Park, MD.
- 3.Baysal, B. M., and F. E. Karasz. 2003. Coil-globule collapse in flexible macromolecules. Macromol. Theory Simul. 12:627–646. [Google Scholar]
- 4.Lakshmikanth, G. S., K. Sridevi, G. Krishnamoorthy, and J. B. Udgaonkar. 2001. Structure is lost incrementally during the unfolding of barstar. Nat. Struct. Biol. 8:799–804. [DOI] [PubMed] [Google Scholar]
- 5.Schuler, B., E. A. Lipman, and W. A. Eaton. 2002. Probing the free energy surface for protein folding with single molecule fluorescence spectroscopy. Nature. 419:743–747. [DOI] [PubMed] [Google Scholar]
- 6.Laurence, T. A., X. Kong, M. Jäger, and S. Weiss. 2005. Probing structural heterogeneities and fluctuations of nucleic acids and denatured proteins. Proc. Natl. Acad. Sci. USA. 102:17348–17353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kuzmenkina, E. V., C. D. Heyes, and G. U. Nienhaus. 2006. Single-molecule FRET study of denaturant induced unfolding of RNase H. J. Mol. Biol. 357:313–324. [DOI] [PubMed] [Google Scholar]
- 8.Sherman, E., and G. Haran. 2006. Coil-globule transition in the denatured state of a small protein. Proc. Natl. Acad. Sci. USA. 103:11539–11543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Tezuka-Kawakami, T., C. Gell, D. J. Brockwell, S. E. Radford, and D. A. Smith. 2006. Urea-induced unfolding of the immunity protein Im9 monitored by spFRET. Biophys. J. 91:L42–L44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Mukhopadhyay, S., R. Krishnan, E. A. Lemke, S. Lindquist, and A. A. Deniz. 2007. A natively unfolded yeast prion monomer adopts an ensemble of collapsed and rapidly fluctuating structures. Proc. Natl. Acad. Sci. USA. 104:2649–2654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Merchant, K. A., R. B. Best, J. M. Louis, I. V. Gopich, and W. A. Eaton. 2007. Characterizing the unfolded states of proteins using single-molecule FRET spectroscopy and molecular simulations. Proc. Natl. Acad. Sci. USA. 104:1528–1533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hoffmann, A., A. Kane, D. Nettels, D. E. Hertzog, P. Baumgartel, J. Lengefeld, G. Reichardt, D. A. Horsley, R. Seckler, O. Bakajin, et al. 2007. Mapping protein collapse with single-molecule fluorescence and kinetic synchrotron radiation circular dichroism spectroscopy. Proc. Natl. Acad. Sci. USA. 104:105–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Huang, F., S. Sato, T. D. Sharpe, L. Ying, and A. R. Fersht. 2007. Distinguishing between cooperative and unimodal downhill protein folding. Proc. Natl. Acad. Sci. USA. 104:123–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chattopadhyay, K., S. Saffarian, E. L. Elson, and C. Frieden. 2005. Measuring unfolding of proteins in the presence of denaturant using fluorescence correlation spectroscopy. Biophys. J. 88:1413–1422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Magde, D., W. W. Webb, and E. Elson. 1972. Thermodynamic fluctuations in a reacting system - measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 29:705–708. [Google Scholar]
- 16.Widengren, J., and U. Mets. 2002. Conceptual basis of fluorescence correlation spectroscopy and related techniques as tools in bioscience. In Single Molecule Detection in Solution, 1st ed. C. Zander, J. Enderlein, and R. A. Keller, editors. Wiley-VCH Verlag Berlin GmbH, Berlin. 69–120.
- 17.Krichevsky, O., and G. Bonnet. 2002. Fluorescence correlation spectroscopy: the technique and its applications. Rep. Prog. Phys. 65:251–297. [Google Scholar]
- 18.Aragon, S. R., and R. Pecora. 1976. Fluorescence correlation spectroscopy as a probe of molecular-dynamics. J. Chem. Phys. 64:1791–1803. [Google Scholar]
- 19.Hess, S., and W. W. Webb. 2002. Focal volume optics and experimental artifacts in confocal fluorescence correlation spectroscopy. Biophys. J. 83:2300–2317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Krouglova, T., J. Vercammen, and Y. Engelborghs. 2004. Correct diffusion coefficients of proteins in fluorescence correlation spectroscopy. Application to tubulin oligomers induced by Mg2+ and paclitaxel. Biophys. J. 87:2635–2646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Enderlein, J., I. Gregor, D. Patra, and J. Fitter. 2004. Art and artifacts of fluorescence correlation spectroscopy. Curr. Pharm. Biotechnol. 5:155–161. [DOI] [PubMed] [Google Scholar]
- 22.Suhling, K., D. M. Davis, and D. Phillips. 2002. The influence of solvent viscosity on the fluorescence decay and time-resolved anisotropy of green fluorescent protein. J. Fluoresc. 12:91–95. [Google Scholar]
- 23.Nozaki, Y. 1972. The preparation of guanidine hydrochloride. Methods Enzymol. 26:43–50. [DOI] [PubMed] [Google Scholar]
- 24.Albeck, S., and G. Schreiber. 1999. Biophysical characterization of the interaction of the β−lactamase TEM-1 with its protein inhibitor BLIP. Biochemistry. 38:11–21. [DOI] [PubMed] [Google Scholar]
- 25.Reference deleted in proof.
- 26.Ratner, V., D. Amir, E. Kahana, and E. Haas. 2005. Fast collapse but slow formation of secondary structure elements in the refolding transition of E. coli adenylate kinase. J. Mol. Biol. 352:683–699. [DOI] [PubMed] [Google Scholar]
- 27.Rhoades, E., E. Gussakovsky, and G. Haran. 2003. Watching proteins fold one molecule at a time. Proc. Natl. Acad. Sci. USA. 100:3197–3202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wahl, M., I. Gregor, M. Patting, and J. Enderlein. 2003. Fast calculation of fluorescence correlation data with asynchronous time-correlated single-photon counting. Opt. Express. 11:3583–3591. [DOI] [PubMed] [Google Scholar]
- 29.Culbertson, C. T., S. C. Jacobson, and J. M. Ramsey. 2000. Microchip devices for high-efficiency separations. Anal. Chem. 72:5814–5819. [DOI] [PubMed] [Google Scholar]
- 30.Magde D., E. L. Elson, and W. W. Webb. 1974. Fluorescence correlation spectroscopy II. An experimental realization. Biopolymers. 13:29–61. [DOI] [PubMed] [Google Scholar]
- 31.Ellis, R. 2001. Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr. Opin. Struct. Biol. 11:114–119. [DOI] [PubMed] [Google Scholar]
- 32.Eggeling, C., J. Widengren, R. Rigler, and C. A. M. Seidel. 1998. Photobleaching of fluorescent dyes under conditions used for single-molecule detection: evidence of two-step photolysis. Anal. Chem. 70:2651–2659. [DOI] [PubMed] [Google Scholar]
- 33.Ortega, A., and J. Garcia de la Torre. 2003. Hydrodynamic properties of rodlike and disklike particles in dilute solution. J. Chem. Phys. 119:9914–9919. [Google Scholar]
- 34.Garcia de la Torre, J. G., M. L. Huertas, and B. Carrasco. 2000. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 78:719–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Doniach, S. 2001. Changes in biomolecular conformation seen by small angle x-ray scattering. Chem. Rev. 101:1763–1778. [DOI] [PubMed] [Google Scholar]
- 36.Plaxco, K. W., I. S. Millett, D. J. Segel, S. Doniach, and D. Baker. 1999. Chain collapse can occur concomitantly with the rate-limiting step in protein folding. Nat. Struct. Biol. 6:554–556. [DOI] [PubMed] [Google Scholar]
- 37.Zhang, H. J., X. M. Pan, J. M. Zhou, and H. Kihara. 1998. Activation and conformational changes of adenylate kinase in urea solution. Sci. China C Life Sci. 41:245–250. [DOI] [PubMed] [Google Scholar]
- 38.Wilkins, D. K., S. B. Grimshaw, V. Receveur, C. M. Dobson, J. A. Jones, and L. J. Smith. 1999. Hydrodynamic radii of native and denatured proteins measured by pulse field gradient NMR techniques. Biochemistry. 38:16424–16431. [DOI] [PubMed] [Google Scholar]
- 39.Haas, E. 2005. The study of protein folding and dynamics by determination of intramolecular distance distributions and their fluctuations using ensemble and single-molecule FRET measurements. ChemPhysChem. 6:858–870. [DOI] [PubMed] [Google Scholar]
- 40.Jacob, J., B. Krantz, R. S. Dothager, P. Thiyagarajan, and T. R. Sosnick. 2004. Early collapse is not an obligate step in protein folding. J. Mol. Biol. 338:369–382. [DOI] [PubMed] [Google Scholar]
- 41.Dertinger, T., V. Pacheco, I. von der Hocht, R. Hartmann, I. Gregor, and J. Enderlein. 2007. Two-focus fluorescence correlation spectroscopy: a new tool for accurate and absolute diffusion measurements. ChemPhysChem. 8:433–443. [DOI] [PubMed] [Google Scholar]
- 42.Klimov, D. K., and D. Thirumalai. 1998. Cooperativity in protein folding: from lattice models with sidechains to real proteins. Fold. Des. 3:127–139. [DOI] [PubMed] [Google Scholar]
- 43.Schuster, J., F. Cichos, J. Wrachtrup, and C. von Borczyskowski. 2001. Diffusion of single molecules close to interfaces. Single Molecules. 1:299–305. [Google Scholar]
- 44.Gell, C., D. J. Brockwell, G. S. Beddard, S. E. Radford, A. P. Kalverda, and D. A. Smith. 2001. Accurate use of single molecule fluorescence correlation spectroscopy to determine molecular diffusion times. Single Molecules. 2:177–181. [Google Scholar]
- 45.Mertz, J., C. Xu, and W. W. Webb. 1995. Single-molecule detection by two-photon-excited fluorescence. Opt. Lett. 20:2532–2534. [DOI] [PubMed] [Google Scholar]
- 46.Sorscher, S. M., and M. P. Klein. 1980. Profile of a focused collimated laser-beam near the focal minimum characterized by fluorescence correlation spectroscopy. Rev. Sci. Instrum. 51:98–102. [Google Scholar]