Three-Dimensional Resolution Doubling in Wide-Field Fluorescence Microscopy by Structured Illumination

Abstract

Structured illumination microscopy is a method that can increase the spatial resolution of wide-field fluorescence microscopy beyond its classical limit by using spatially structured illumination light. Here we describe how this method can be applied in three dimensions to double the axial as well as the lateral resolution, with true optical sectioning. A grating is used to generate three mutually coherent light beams, which interfere in the specimen to form an illumination pattern that varies both laterally and axially. The spatially structured excitation intensity causes normally unreachable high-resolution information to become encoded into the observed images through spatial frequency mixing. This new information is computationally extracted and used to generate a three-dimensional reconstruction with twice as high resolution, in all three dimensions, as is possible in a conventional wide-field microscope. The method has been demonstrated on both test objects and biological specimens, and has produced the first light microscopy images of the synaptonemal complex in which the lateral elements are clearly resolved.

INTRODUCTION

Light microscopy, and particularly fluorescence microscopy, is very widely used in the biological sciences, because of strengths such as its ability to study the three-dimensional interior of cells and organisms, and to visualize particular biomolecules with great specificity through fluorescent labeling. Its major weakness is its moderate spatial resolution, which is fundamentally limited by the wavelength of light.

The classical wide-field light microscope has another weakness in that it does not gather sufficiently complete information about the sample to allow true three-dimensional imaging—the missing-cone problem (1). The manifestation of the missing cone problem in the raw data (which are acquired as a sequence of two-dimensional images, referred to as sections, with different focus) is that each section of the data contains not only in-focus information from the corresponding section of the sample, but also out-of-focus blur from all other sections. Three-dimensional reconstructions from conventional microscope data presently have to rely on a priori constraints, such as the nonnegativity of the density of fluorescent dye, to attempt to compensate for the missing information (1).

Confocal microscopy (2,3) in principle alleviates both problems: by physically blocking the out-of-focus light using a pinhole, it provides true three-dimensional imaging and at the same time extends resolution somewhat beyond the conventional limit, both axially and laterally (2,3). The improvement of lateral resolution, however, only takes place if such a small pinhole is used that much in-focus light is discarded together with the unwanted out-of-focus light (4). In practice, it is rarely advantageous to use such a small pinhole: given the weak fluorescence of typical biological samples and the low sensitivity of detectors normally used in confocal microscopes, the detrimental loss of in-focus signal usually outweighs any resolution benefits. Confocal microscopes are therefore often operated with wider pinholes, producing a lateral resolution that is comparable to that of the conventional microscope.

It has been demonstrated that it is possible to double the lateral resolution of the fluorescence microscope without any loss of light, using spatially structured illumination light to frequency-mix high resolution information into the passband of the microscope (5–8). The method, structured illumination microscopy (SIM), also reaches higher effective lateral resolution than confocal microscopy (5). This strong resolution enhancement has so far only been experimentally demonstrated in two dimensions on thin samples (5–8). A slightly different form of laterally structured illumination has been used specifically to provide axial sectioning, but without strong effect on lateral resolution (9,10), and purely axial intensity structures have been used to encode high-resolution axial information (11). Three-dimensional resolution enhancement by SIM has been outlined theoretically (8,12,13), but to our knowledge no experimental demonstrations have been published.

In this article we demonstrate a modified form of structured illumination microscopy that provides true three-dimensional imaging without missing-cone problem, with twice the spatial resolution of the conventional microscope in both the axial and lateral dimensions.

THEORY

The resolution properties of a linear, translation-invariant optical system are described by its point spread function (PSF) H(r), the real-space blurred image formed by the system when the object is a point source. The observed data D(r) is a convolution of the emitting object (the distribution of fluorescent emission) E(r) with the PSF:

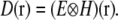(1)

By the convolution theorem, the Fourier transform of this convolution is a pointwise product: 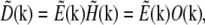where tildes (∼) indicate the Fourier transform of the corresponding real-space quantities, and 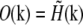is the optical transfer function. The complex value O(k) describes how strongly, and with what phase shift, the spatial frequency k of the object is transferred into the measured data. The classical resolution limit manifests itself in the fact that the OTF has a finite support, outside of which it is zero. The OTF support—the observable region of reciprocal space—thus defines which spatial frequencies the microscope can detect. The OTF support of the conventional microscope is a toruslike region (Fig. 1, a and b); the “hole” of the torus is the “missing cone” of information near the k_z axis. (The k_z direction of reciprocal space corresponds to the axial (z) direction in real space.) Extending the resolution, in a true sense, is equivalent to finding a way to detect information from outside of this observable region. That apparently self-contradictory task is possible because the structure of interest to the microscopist is not actually the emission E(r) but rather the object structure: the density distribution of fluorescent dye S(r). If an object is excited by an illumination intensity I(r), the resulting emission rate distribution is

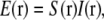(2)

where all proportionality constants, such as absorption cross section and quantum yield, have been suppressed for clarity. (Eq. 2 describes normal linear fluorescence; discussion of nonlinear fluorescent responses and their use for resolution purposes will be deferred to Discussion). The Fourier transform of the pointwise product in Eq. 2 is a convolution: 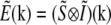. If 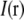is spatially varying, then 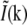is nontrivial (i.e., not a delta function), and the convolution operation becomes nonlocal; in particular the convolution can make the observed data within the observable region of 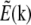depend on normally unobservable components of 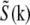from other parts of reciprocal space. That information is then observable in principle, but must be extracted.

FIGURE 1.

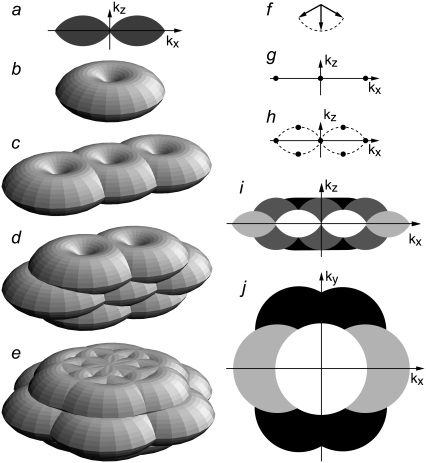
Enlargement of the observable region of reciprocal space through structured illumination. (a–e) Observable regions for (a and b) the conventional microscope, and for structured illumination microscopy using two illumination beams (c), and three illumination beams in one (d) or three (e) sequential orientations. (f) The three amplitude wave vectors corresponding to the three illumination beam directions. All three wave vectors have the same magnitude 1/λ. (g–h) The resulting spatial frequency components of the illumination intensity for the two-beam (g) and three-beam (h) case. The dotted outline in panel h indicates the set of spatial frequencies that are possible to generate by illumination through the objective lens; compare with the observable region in panel a. An intensity component occurs at each pairwise difference frequency between two of the amplitude wave vectors. (i, j): xz (i) and xy (j) sections through the OTF supports in panel b (shown in white), panel c (light shaded), panel d (dark shaded), and panel e (solid). The darker regions fully contain the lighter ones.

Extracting that information is nontrivial for general illumination patterns, but becomes simple if a few conditions are satisfied. First, the illumination pattern should be a sum of a finite number of components, each of which is separable into an axial and a lateral function,

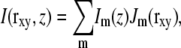(3)

where r_xy denotes the lateral coordinates (x,y). Second, each of those lateral functions J_m should be a simple harmonic wave (i.e., contain only a single spatial frequency). Thirdly, one of two conditions should be met: either the axial functions I_m are also purely harmonic, or, when the three-dimensional data are acquired as a sequence of two-dimensional images with different focus, the illumination pattern is maintained fixed in relation to the focal plane of the microscope, not in relation to the object. The latter condition is what we will discuss in this article, because it allows a broader choice of the axial function I_m.

The significance of the last condition can be understood by first considering the alternative arrangement where the illumination pattern is kept fixed in relation to the object during acquisition. In that case, Eqs. 1–3 apply directly and lead to the following convolution integral for the measured data:

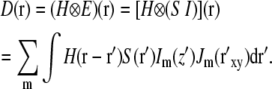(4)

In the above integral, primed coordinates r′ refer to the specimen reference frame, unprimed coordinates r refer to the data set reference frame (in particular, the axial coordinate z refers to the physical displacement of the specimen slide relative to the objective lens), and the difference coordinates, r– r′, refer to the reference frame of the objective lens. It is seen that the point spread function H depends on the difference coordinates r– r′. If we now consider holding the light pattern fixed relative to the objective lens's focal plane during focusing, that means that I_m will depend not on the specimen-frame's primed coordinate z′ but rather on the objective-lens-frame's difference coordinate z– z′, the same coordinate as the point spread function H depends on. Therefore the axial part of each illumination component multiplies the point spread function, not the object S, in the convolution integral:

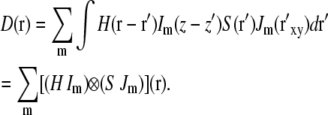(5)

As a result, if we let 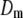denote the m^th term of the above sum, its Fourier transform will take the form

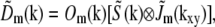(6)

where 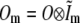is the Fourier transform of H I_m.

It was assumed above that J_m is a simple harmonic,

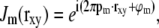(7)

which implies that 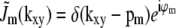. Substituted into Eq. 6, this implies that the observed data can be written as

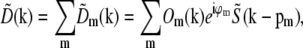(8)

a sum of a finite number of copies of the object information 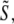each moved laterally in reciprocal space by a distance p_m, filtered (and band-limited) by a transfer function O_m, and phase-shifted by a phase ϕ_m. In summary, each lateral frequency component m of the illumination structure corresponds to a separate optical transfer function O_m, which is given by a convolution of the conventional detection OTF with the axial illumination structure of the m^th pattern component, and applies to a component of object information that has been translated in reciprocal space by the lateral wave vector p_m of that pattern component.

As seen in Eq. 8, a single raw data image is a sum of several different information components, one for each index m. To restore the data, these information components must be separated. This can be done by acquiring additional data sets with different known values of the phases ϕ_m. Changing the phase values by phase shifts δϕ_m alters the coefficients 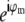in Eq. 8 from to 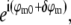leading to a linearly independent combination of the unknown information components. Each phase-shifted image thus supplies one independent linear equation in N unknowns (where N is the number of frequency components in Eq. 8). If data are acquired with at least N different phases, the number of equations is at least equal to the number of unknowns, allowing the N information components to be separated by applying a simple N×N matrix. (Of course, a badly chosen set of phases {ϕ_m} could lead to an ill-conditioned or even singular matrix, but the natural choice of equally spaced phases on the 0–2π interval produces a well-conditioned separation matrix, which in fact performs a discrete Fourier transform of the data with respect to the phase-shift variable.)

In practice, the situation is usually simplified further in several ways. A physical light intensity is a real-valued function; the exponentials in Eq. 7 must therefore occur in pairs with opposite p_m, corresponding to information from symmetrically located regions of reciprocal space. Because the Fourier transform 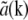of any real-valued function a(r) (such as the object structure) has the symmetry property that 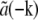is the complex conjugate of 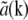, only one information component from each such pair has to be calculated; the values within the other component follow by symmetry. Secondly, if the set of different lateral spatial frequencies p_m of the illumination pattern is, in fact, the fundamental frequency and harmonics of a periodic pattern, then all the spatial frequencies are multiples of the fundamental: p_m = mp. If, furthermore, the phase-shifting of the illumination takes place by spatially translating a rigid pattern, then the phase-shifts δϕ_m are also multiples of a fundamental phase-shift: δϕ_m = mδϕ. For patterns with reflection symmetry, the same applies to the starting phases, ϕ_m0 = mϕ₀, and thus for the total phase: ϕ_m = mϕ. In this situation, which was the case in our experiments, we can rewrite Eq. 8 as

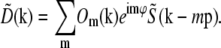(9)

It is seen from Eq. 9 that the measured data gains new (i.e., normally unobservable) information in two ways: the support of each transfer function O_m is extended axially, compared to the conventional OTF O, through the convolution with the axial function 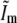; and the translation by mp moves new information laterally into the support of O_m.

Because the O_m and p_m are known, the separated information components can be computationally moved back (by a distance p_m) to their true positions in reciprocal space, recombined into a single extended-resolution data set, and retransformed to real space. This procedure will be discussed in more detail in Methods.

The total effective observable region with this method is given by the support of the convolution of the conventional OTF O with the total illumination structure 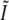. The maximal resolution increase in a given dimension is therefore equal to the maximum illumination spatial frequency in that dimension. Since the set of spatial frequencies that can be generated in the illumination is limited by diffraction in exactly the same way as the set of frequencies that can be observed (if the illumination and observation takes place through the same optical system), the maximum possible spatial frequency in the illumination equals the conventional resolution limit of the detection (except scaled by the ratio of emission and excitation wavelengths). The maximum resolution extension possible in this manner is therefore a factor of 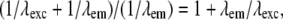slightly more than two, in each dimension. This is true axially as well as laterally. The next section describes a specific choice of illumination patterns that allows most of the information within this doubled resolution limit to be acquired in a modest number of exposures.

Three-beam illumination

In the two-dimensional structured-illumination microscope described previously (5), the sample was illuminated by two beams of light, which interfered to form a sinusoidal light intensity pattern 1 + cos(p · x), which has only three Fourier components (Fig. 1 g) (i.e., only three terms, m = {−1, 0, +1}, in Eqs. 3–9). If the same illumination pattern were applied in three-dimensional microscopy, the resulting observable region would consist of three shifted copies of the conventional three-dimensional OTF (Fig. 1 c). That region yields twice the normal lateral resolution, but suffers from the same missing cone problem as the conventional OTF, making three-dimensional reconstructions difficult. One way around this problem would be to use a coarser illumination pattern, i.e., a shorter pattern wave vector p, which would result in the three OTF components moving closer together and overlapping each other's missing cones (9,10). That approach, however, sacrifices lateral resolution. This tradeoff between filling in missing-cone information and maintaining resolution can be avoided by using a modified illumination structure. In the three-dimensional structured illumination microscope used in this article, the fluorescent sample is illuminated with three mutually coherent beams of excitation light (Fig. 1 f). In general, a coherent superposition of plane waves with wave vectors k_j produces a total light intensity

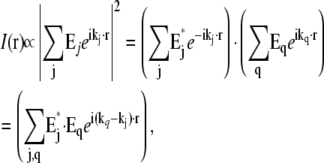(10)

which consists of one spatial component at each pairwise difference vector k_q–k_j between any two of the plane-wave propagation vectors. Interference between the three illumination beams thus produces a three-dimensional excitation intensity pattern that contains seven Fourier components, one at each difference vector between the three illumination wave vectors (Fig. 1 h). The observable region that becomes accessible with this illumination pattern is the convolution of the seven-dot illumination structure of Fig. 1 h with the conventional OTF support in Fig. 1, a and b, resulting in the region shown in Fig. 1 d. This region fills in the missing cone while maintaining the full factor of two of lateral resolution extension, and at the same time doubles the axial resolution. It extends lateral resolution only in one direction, but the procedure can of course be repeated with the illumination pattern rotated to other directions. Fig. 1 e shows the observable region using three pattern orientations. Whereas the observable region for a single pattern orientation has “dimples” at the missing cones of the side bands (Fig. 1 d), these dimples are effectively filled in once multiple pattern orientations are used (Fig. 1 e).

Only five lateral spatial frequencies (k_x values) occur in Fig. 1 h, two of them shared by pairs of intensity components. Thus only five transfer functions O_m(k), with m = {−2,−1,0,1,2}, contribute to the region in Fig. 1 d. Each O_m is formed by convolution of the conventional OTF with an axial function 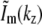that corresponds to an axial profile through Fig. 1 h at the corresponding k_x position. Three of these profiles, 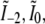and 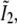each consists simply of a delta function at k_z = 0, but the two remaining profiles 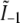and 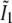each contain two delta functions (located at 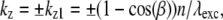where β is the angle between each side beam direction and the optic axis). Accordingly, each of the three transfer functions O₋₂, O₀, and O₂ is identical to the conventional OTF in Fig. 1 a; these are the three bands that are also seen in Fig. 1 c. The remaining transfer functions O₋₁ and O₁, on the other hand, each consist of two copies of the conventional OTF, offset by a distance ±k_z1 above and below the k_z = 0 plane (Fig. 1 d).

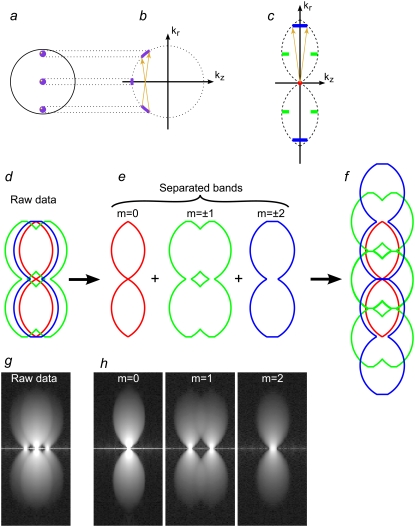
In the above discussion, and in Fig. 1, the illumination was assumed to be fully coherent. In practice, it can be attractive to introduce a slight spatial incoherence into the illumination light. One reason to do so is to help suppress stray interference fringes caused by scattering off dust particles, etc., which could otherwise cause artifacts; a separate reason is to confine the interference effects to a finite axial extent around the focal plane. For the experiments in this article, the three illumination beams were generated from a slightly spatially incoherent beam using a diffraction grating. The incoherence leads to a slight modification of the transfer functions in Fig. 1. The illumination light emanated from a circular source (actually the end face of a multimode optical fiber, see Methods); three uniformly spaced images of this source, corresponding to the –1, 0, and +1 diffraction orders of the grating, were projected onto the back focal plane (pupil) of the objective lens (Fig. 2 a). The source was spatially incoherent: each point of the source was effectively mutually incoherent with all other points of the source. Each point in any of the three source images in the pupil is therefore mutually coherent only with the corresponding point in the other two source images, and with no other point. In other words, the illumination consists of an incoherent superposition of coherent point triplets; one such point triplet is indicated in yellow in Fig. 2 a. The total light intensity pattern in the sample can therefore be calculated by considering each such point triplet separately, calculating the intensity interference pattern it produces, and integrating that intensity pattern over all such point triplets (i.e., over all points of the light source). Each point triplet corresponds to a beam triplet as in Fig. 1 f, and will produce an intensity interference pattern with seven components, corresponding to all pairwise difference vectors between the wave vectors of the three beams, as in Fig. 1 h. Corresponding difference vectors produced by separate source points will differ axially (Fig. 2 b, arrows), but will have identical lateral components, as long as the objective lens satisfies the Sine Condition (14), which requires that the radial position of a ray within the pupil plane be proportional to the lateral component of the amplitude spatial frequency of that ray. The effect of incoherence is therefore to cause the discrete side spots in Fig. 1, g and h, to take on a finite extent axially but not laterally (Fig. 2 c). The illumination structure thus remains of the form required by Eqs. 3 and 7 (i.e., it is a sum of a finite number (five) of components, each of which has a single lateral spatial frequency), so the theory outlined in previous paragraphs still applies. The incoherence simply causes a slight axial broadening of the transfer functions O_m of the side bands (Fig. 2, d–h) compared to the coherent case (Fig. 1, c–e).

FIGURE 2.

The optical transfer functions O_m and the effect of incoherence. (a) The location of the three illumination beams (purple dots) in the back focal plane of the objective lens. Each point within each beam is mutually coherent only with the corresponding point of each of the other beams (which originates from the same point of the light source); the yellow points illustrate one such coherent point triplet. (b) Spatial frequency components of the light amplitude. For an objective lens that satisfies the Sine Condition, the pupil plane maps directly onto the lateral spatial frequency (dotted lines from a to b). The difference vectors between mutually coherent amplitude components (amber arrows in b) will therefore have the same lateral extent, but will differ axially, for different source points. (c) Resulting spatial frequency components of the illumination intensity; the m = 0, ±1, and ±2 components are shown in red, green, and blue, respectively. The non-zero-m components, which get a contribution from each coherent point pair (amber arrows, corresponding to those in b), are axially broadened into line segments, but remain delta-function-like laterally. The raw data (d and g) is a sum of five information bands, corresponding to the five lateral illumination-intensity frequencies. Once five images are observed with different pattern phases, the bands can be separated (e and h; only the m = 0 (red), 1 (green), and 2 (blue) bands are shown), and computationally moved back to their correct lateral position (f). Each band has been broadened by convolution with the corresponding frequency component of the illumination intensity (corresponding colors); the order 1 component, for example, consists of two parts (e, green). The observed raw data (g) and separated bands (h) for a point-source object are in excellent agreement with the theoretical expectations.

METHODS

Apparatus

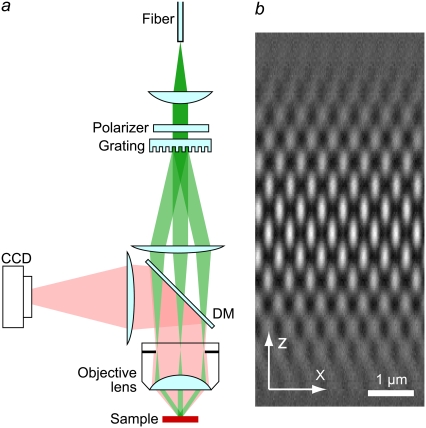
This method has been implemented in several prototype microscopes with similar illumination systems (Fig. 3 a). Laser light with a wavelength of 488 nm or 532 nm was spatially scrambled by a rotating holographic diffuser (Physical Optics, Torrance, CA) to remove spatial coherence, and coupled into a multimode optical fiber (core size 100 μm, NA 0.12), with the degree of scrambling chosen to approximately fill the mode space of the fiber. The input to the fiber is a rapidly time-varying superposition of modes, producing a rapidly time-varying speckle pattern at the output; over typical exposure times, the speckle pattern averages out to an approximately constant intensity, producing a simulated spatially incoherent (and unpolarized) light source at the fiber output. To increase the completeness of the scrambling (the space of independent speckle patterns being averaged), a section of the fiber was vibrated mechanically during exposure. The light exiting the fiber was collimated and directed to a fused silica linear transmission phase grating, which diffracted the beam into a large number of orders. A beam block in an intermediate pupil plane discarded all diffraction orders except orders 0 and ±1; these three orders together received ∼70% of the power incident on the grating. The grating was designed so that the intensity of order 0 was 70–80% of that of orders ±1; this unequal intensity ratio was picked to slightly strengthen the highest-lateral-frequency information components (m = ±2, blue in Fig. 2). The three beams were refocused so that each formed an image of the fiber end-face in the back focal plane of the objective lens. The beams produced as diffraction orders +1 and −1 were focused near opposing edges of the back focal plane aperture, and order 0 at its center (Fig. 2 a). The diameter of each fiber image was typically between 5% and 10% of the pupil diameter. The objective lens (100× PlanApo 1.4 NA) recollimated the beams and made them intersect each other in the objective lens's focal plane, where they interfered to form an illumination intensity pattern with both axial and lateral structure (Fig. 3 b). The illumination intensity pattern in the focal plane of the objective lens can equivalently be thought of as a demagnified image of the grating. Fluorescence light emitted by the sample was gathered by the same objective lens and deflected by a dichroic mirror to a cooled charge-coupled device camera; scattered excitation light was rejected by an emission filter (580–630 and 500–530 nm band pass for 532- and 488-nm excitation, respectively) in front of the camera. Three-dimensional datasets were acquired by translating the sample holder axially relative to the objective lens by using a piezoelectric translator under closed-loop control from a capacitive position sensor. The orientation and phase of the illumination pattern were controlled by rotating and laterally translating the grating. For this purpose, the grating was mounted on a piezoelectric translator, which in turn was mounted on a motorized rotation stage. The piezoelectric translator was controlled in closed loop using a custom-made capacitive distance sensor, which consisted of one convex electrode on one side of the grating holder, and one hollow cylindrical counter electrode that surrounded the grating holder, each flanked by a guard electrode. The counter electrode was rigidly attached to the optical table and served as a fixed reference, so that the position of the grating in the direction of its pattern wave vector could be controlled with nanometer precision and reproducibility without placing any unusual requirements on the precision or stability of the rotation stage bearings. The corresponding pattern-control precision in sample space is even tighter than this, by a factor of the magnification from sample plane to grating plane (typically ∼100).

FIGURE 3.

(a) Simplified diagram of the structured illumination apparatus. Scrambled laser light from a multimode fiber is collimated onto a linear phase grating. Diffraction orders –1, 0 and +1 are refocused into the back focal plane of an objective lens. The beams, recollimated by the objective lens, intersect at the focal plane in the sample, where they interfere and generate an intensity pattern with both lateral and axial structure (b). The finite axial extent of the pattern is related to the axial broadening of its spatial frequencies (Fig. 2 c). Emission light from the sample is observed by a charge-coupled device (CCD) camera via a dichroic mirror (DM).

To interfere with maximum contrast, the illumination beams in the sample must be s-polarized relative to each other, which corresponds to the beams diffracted by the grating being linearly polarized perpendicularly to the plane of diffraction. This polarization state was maintained at all orientations by a wire-grid linear polarizer (Moxtek, Orem, UT) that co-rotated with the grating. For pattern directions that are not parallel or perpendicular to the dichroic mirror, the often large retardance of a standard dichroic mirror could drastically alter the polarization state of the beams; we typically use custom multiband dichroic coatings operated in transmission (Chroma Technology, Rockingham, VT), which by design had small enough retardance at the laser wavelengths that the effect on pattern contrast was negligible. The coatings were deposited on 3.2-mm-thick optically flat substrates to preserve the wavefront quality in the reflected imaging beam. The flatness of these mirrors was checked interferometrically after mounting.

For ideal imaging, the grating face should be in an image plane, that is, perfectly conjugate to the camera. To optimize this parameter, the Fourier components of the illumination pattern were plotted as a function of z, by measuring, at each focus setting, the changes in overall emission of a single fluorescent bead as the pattern was phase-shifted. Guided by such measurements, the axial position of the grating stage was adjusted to make the plane of maximum pattern modulation (see Fig. 3 b) coincide with the focal plane (defined as the plane with peak intensity of the bead image). This parameter only needs to be aligned once (for a particular objective and wavelength), although it can be affected by spherical aberration if imaging deep into samples with ill-matched refractive index.

Optimal resolution is achieved when the illumination side beams traverse the objective pupil near its edges. To optimize for different objectives (with different pupil diameters) and wavelengths (with different diffraction angles at the grating) therefore requires changing either the grating, or the magnification between the grating plane and sample plane. We have implemented the latter approach, by mounting intermediate lenses (or combinations of lenses and mirrors) on interchangeable kinematic base plates, to allow quick switching between prealigned configurations for specific wavelengths and objectives. Prealignment includes the focusing step described in the previous paragraph. A configuration optimized for one wavelength typically allows operation at shorter wavelengths as well (albeit at slightly lower resolution compared to a system optimized for the shorter wavelength). An alternative solution would be to use zoom optics.

Sample preparation

Drops of fluorescent polystyrene microspheres (Invitrogen, Carlsbad, CA) diluted in water were allowed to dry on cover glasses, and mounted in Laser Liquid 5610 (R.P. Cargille Laboratories, Cedar Grove, NJ).

HL60 cells were grown and differentiated into a neutrophil-like state as described (15), briefly stimulated with their target chemoattractant formyl-methionyl-leucyl-phenylalanine, allowed to adhere to cover glasses, fixed with formaldehyde, labeled for actin with rhodamine phalloidin (Invitrogen), and mounted in 96% glycerol, 4% n-propyl gallate.

HeLa cells were grown on cover glasses, fixed with glutaraldehyde, quenched against autofluorescence with sodium borohydride, immunofluorescently labeled with anti-α-tubulin primary antibodies (DM1A, Sigma-Aldrich, St. Louis, MO) followed by Alexa-488-labeled secondary antibodies (Invitrogen), and mounted in glycerol (16).

Maize meiocytes, released from anthers fixed with 4% paraformaldehyde in buffer A (15 mM PIPES-NaOH (pH 6.8), 80 mM KCl, 20 mM NaCl, 2 mM EDTA, 0.5 mM EGTA, 0.2 mM spermine, 0.5 mM spermidine, 1 mM DTT, 0.32 M sorbitol), were treated briefly with cellulase and macerozyme, and permeabilized with 0.02% Triton X-100 in buffer A (17). The meiocytes were prepared for indirect immunofluorescence as described (18). Cells were stained with AFD1 antibody (19) and ASY1 antibody, kindly provided by C. Franklin (20), which were detected with Cy3- and Alexa-488-conjugated secondary antibodies, respectively. Slides were mounted in ProLong Gold antifade medium (Invitrogen).

For electron microscopy, flattened spreads of pachytene chromosomes were prepared from maize meiocytes according to published protocols (21), and stained with silver nitrate.

Acquisition

Three-dimensional data were acquired with five pattern phases (ϕ in Eq. 9) spaced by 2π/5, three pattern orientations spaced 60° apart, and a focus step of 122 or 125 nm. The axial range of the acquired data was typically made to extend somewhat (>0.5 μm) above and below the region of interest. The order of acquisition was to vary the phase most rapidly, then the focusing, and the pattern rotations most slowly, thus generating a full focus/phase stack for each orientation before proceeding to the next orientation. This order avoids placing any angular-reproducibility requirements on the rotation stage, and allows modest thermal drift to be measured and corrected (see Parameter Fitting below).

Point-spread function (PSF) data was acquired similarly, including the five phases but only one pattern orientation, on a sample consisting of a single fluorescent microsphere. The axial range of PSF data sets was similar to that of typical image data.

To allow fair comparisons without any questions about relative exposure times or photobleaching, conventional-microscopy data sets for comparison purposes were produced from the raw SIM data by summing the images acquired at different phases of the illumination pattern. Summing over the phase produces an image that corresponds to uniform illumination, because the imaging process is linear and the illumination patterns themselves (Eq. 7) add up to uniform illumination with the standard choice of pattern phases (regularly spaced on the 0–2π interval).

The time required for acquisition varies between the different prototypes, and of course with data set size and exposure time. One system that uses an electron-multiplying charge-coupled device camera read out at 10 MHz can acquire a data set comprising 80 sections of 512 × 512 pixels, each at five phases and three orientations, with 100-ms exposure times, in 140 s. The acquisition time is limited by the exposure time (a total of 120 s in that example), which can be decreased by increasing the illumination intensity. Because of the inherent parallelism of wide-field microscopy, as opposed to point scanning, the illumination intensity could be increased by many orders of magnitude without becoming limited by saturation.

The illumination intensity pattern (Fig. 3 b) was measured by recording the integrated emission intensity from a subresolution microsphere as a function of pattern phase and sample focus, and converting phase into lateral position using the known period of the pattern.

Transfer functions

A three-dimensional point spread function data set was three-dimensionally Fourier-transformed and separated into the terms 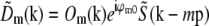of Eq. 9, using the phase-shift method described in Theory. Because the factor 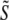is constant for a point source sample, and 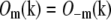by symmetry, 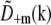and 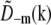are identical except for the phase factor 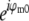. That phase factor, which is irrelevant as it depends on the arbitrary position of the bead, was estimated by comparing 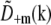with 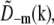and removed. Hence the measured 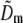is effectively a measurement of O_m. To decrease noise, each O_m was rotationally averaged around the k_z axis and set to zero outside of its known support.

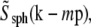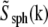The actual object, a fluorescent bead, was of course not a true point source but had a nonzero diameter (typically 115–120 nm); this fact was usually ignored, but can be compensated for by dividing the measured O_m, before rotational averaging, by where is the Fourier transform of a solid sphere with a diameter equal to the nominal diameter of the bead. (Explicitly, 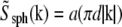where 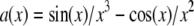and d is the bead diameter.) For such division to be well behaved, the first zero of 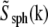must lie well outside the extended OTF support, which is the case for the beads used here (albeit barely).

Transfer functions need only be determined once for each combination of objective lens and wavelength, and can be applied to all subsequent data sets acquired on the same microscope under the same conditions.

Parameter fitting

All processing calculations were done in three dimensions where not otherwise noted. As a precaution against edge-related artifacts, the raw data were typically preprocessed by slightly intermixing opposing lateral edges (the outermost ∼10 pixels).

For each pattern orientation, the Fourier transform of the raw data is a sum in the form of Eq. 9. The terms 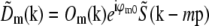of that sum (for the starting phase of the pattern) were separated as described in Theory. The central information component 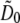is produced three times, once for each pattern orientation; this redundancy was exploited to detect thermal drift, by cross-correlating the three versions of D₀ in real space. The measured drift was removed by a compensating real-space shift of the data for orientations 1 and 2 relative to orientation 0, through multiplying by the corresponding phase gradients in frequency space. Drift within each orientation was not compensated for, but could be corrected sectionwise if known. The position offsets for each section could be estimated either by fitting a smooth curve to the three measured time-points of three-dimensional drift, or by using sectionwise two-dimensional (or sub-volume-wise three-dimensional) cross-correlations to get additional time points for a more precise curve fit.

The precise values of the pattern wave vector p, the starting phase ϕ_m0, and the modulation depths c_m were determined from the data by comparing the different information components in the regions of frequency space where they overlap. The modulation depths c_m are scale factors that are taken to multiply each O_m, to allow for the possibility that the contrast of each frequency component of the pattern may be subtly different in the image data than when the O_m were measured. A single starting phase ϕ_m0 was assumed to be valid for each pattern orientation m, that is, the pattern phase was assumed to be reproducible over the time required to acquire data for one pattern orientation. Specifically, for m = 1 and m = 2 separately, and using a predicted value of p, 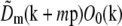was cross-correlated with 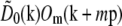. Because each 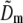contains a factor of O_m from the physical observation process, the two expressions being compared would be expected to contain the same values 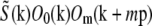at each point k within the overlap of their supports (for the correct shift vector p), except for noise and a constant factor 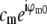. The cross correlation was done in three steps: first a standard fast-Fourier-transform-based cross-correlation in frequency space (yielding values only at discrete frequency-space pixels), then parabolic interpolation to locate the peak of that cross-correlation to subpixel accuracy, and finally refinement through an optimization in which subpixel frequency-space shifts were applied in the form of real-space phase gradients. The location of the cross-correlation peak yields the shift vector p; the parameters c_m and ϕ_m0 are found by complex linear regression of 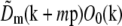against 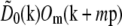for that value of p. Explicitly, the values of the two data sets at each pixel k_i within the overlap constitute a pair (a_i,b_i) of complex numbers, which in the absence of noise and errors would be proportional to each other: b_i = s a_i. The proportionality constant s (which here equals 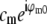) is estimated by complex linear regression as 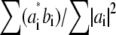. (Linear regression is not strictly the optimal estimator: it would be optimal if only b_i contained noise, but in our situation both a_i and b_i are noisy.) In the following, the factors 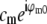are considered absorbed into the O_m, for simplicity of notation.

Reconstruction

Once the parameters were determined, the different information components 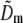were combined through a generalized Wiener filter,

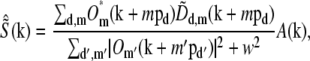(11)

where 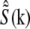is the estimate of the true sample information 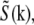the sums are taken over the three pattern orientations d and the five component orders m at each orientation, p_d is the pattern wave vector (i.e., direction and inverse period) of pattern orientation d, w² is the Wiener parameter (which was taken to be a constant and adjusted empirically), and A(k) is an apodization function (typically a three-dimensional triangle function, which decreases linearly from unity at the origin to zero at the surface of an oblate spheroid that approximates the extended OTF support).

Eq. 11 was implemented in the following (somewhat nonintuitive) way: each unshifted information component 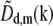was separately multiplied by a filter function 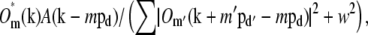and the filtered results were then padded with zeros (to provide space for shifting information by the vectors p_d, or equivalently to decrease the real-space pixel size to accommodate the increased resolution), transformed to real space, multiplied by the complex phase gradient 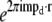(which represents the frequency-space shift by mp_d), and added together, to produce the final reconstruction. In this calculation, the transfer function values were calculated from the rotationally averaged measured O_m by interpolation. The pixel-size reduction is usually done laterally by a factor of two; larger factors, and axial as well as lateral reduction, can be used to produce smoother reconstructions.

This order of operations produces noticeably better results than the straightforward approach of first multiplying 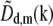by 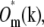shifting the product by mp_d, combining according to Eq. 11, and retransforming to real space. The reason has to do with edge artifacts. Because the shift vectors mp_d do not in general fall on integral pixels of the discrete frequency space, the shifts are implemented as multiplications by the corresponding phase gradients 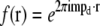in real space. Multiplying by f(r) corresponds in frequency space to a convolution by its discrete Fourier transform f(k), which is a discrete delta function δ(k − mp_d) if mp_d falls on a frequency-space pixel, but a nontrivial sinc-like function otherwise. Convolution by that function effectively “smears” the information in the k_x, k_y, and k_z directions. This smearing is not necessarily a problem in itself, but can become deleterious if the smeared information is amplified during subsequent processing. In the straightforward approach sketched above, the product 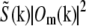is divided by the Wiener filter denominator 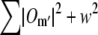after it is shifted by the vector mp_d. The three-dimensional transfer functions O_m′ are strongly peaked at the origin (in fact singular in the continuum limit, in the case of O₀), and their squares of course even more so. Dividing by the Wiener denominator thus boosts spatial frequencies that lie far from the origin, and from the pattern frequencies mp_d, relative to spatial frequencies that are close to those points. Boosting those frequencies greatly amplifies any information that was smeared into such regions by the shift operation, and this amplified smear can lead to artifacts in the reconstruction. In the processing order used here, on the other hand, the sample information is divided by the Wiener denominator before the shift is executed, so that there is no amplification of smeared information.

Only the information components with nonnegative m were calculated explicitly; the negative-m components, which are related to the positive-m counterparts by complex-conjugate symmetry, were supplied simply by discarding the imaginary part of the final reconstruction in real space.

Reconstruction (including data transfer and parameter fitting) of a data set comprising 72 axial sections of 400 × 400 pixels (each at five phases and three pattern orientations), which produces an 800 × 800 × 72 voxel reconstruction, required 138 s on a computer with two dual-core 2.2 GHz Opteron processors. On a well-characterized and reproducible system it may be possible to decrease processing time significantly by eliminating much of the parameter fitting.

RESULTS

An example of a measured three-dimensional OTF data set is shown in Fig. 2, g and h. Panel g shows a k_x-k_z view of a rotationally averaged three-dimensional Fourier transform of raw three-dimensional data acquired on a point source sample with a fixed, arbitrary phase of the illumination pattern. The data represent a sum of contributions from all the different information components, as described by Eq. 8 and illustrated schematically in Fig. 2 d. Similar data for five different phases of the illumination pattern allowed separation of five information components (Fig. 2 h). With sufficient reproducibility of the phase shifts, focus steps and illumination intensity, separation can be near-perfect, with negligible contamination of each information components by others. As seen by comparison of Fig. 2, e and h, the qualitative shape of each information component is in complete accordance with theoretical predictions, including the broadening due to spatial incoherence.

To demonstrate resolution performance, a planar cluster of red-fluorescent microspheres of nominal diameter 121 nm was imaged with the three-dimensional structured illumination method, and compared to three-dimensional conventional wide-field data (Fig. 4). As seen in the axial (xz) view (Fig. 4 d), the structured illumination method is indeed able to suppress the out-of-focus blur, above and below the focal plane, which is a dominant element in the conventional microscope data (Fig. 4 c). At the same time, the in-focus xy views (Fig. 4, a and b) illustrate the striking improvement in lateral resolution. (In comparing these panels, it should be kept in mind that the conventional data have not benefited from the linear filtering that is inherent in the SIM processing. Linear filtering is unsuitable for three-dimensional conventional microscopy data due to the missing-cone problem. A comparison of two-dimensional SIM to raw and linearly filtered conventional data has been published elsewhere (22).) Two microspheres are resolved as a pair at a separation of 125 nm, to be compared to the absolute resolution limit of the conventional microscope, which is ∼207 nm at this red observation wavelength (λ_em = 605 ± 25 nm).

FIGURE 4.

A cluster of red-fluorescent microspheres of nominal diameter 0.12 μm, imaged with (a and c) conventional microscopy, and (b and d) structured illumination microscopy. (a and b) Single in-focus x,y sections illustrating the improvement of lateral resolution. (c and d) Single x,z sections, at the y position indicated by horizontal lines in panel a, illustrating removal of out-of-focus blur above and below the plane of focus. (e) Histograms of the apparent lateral and axial full width at half-maximum (FWHM) of individual green-fluorescent beads observed by three-dimensional SIM.

To quantify the resolution, the apparent full width at half-maximum (FWHM) of isolated green-fluorescent microspheres of nominal diameter 115 nm was measured in a separate data set acquired with λ_em = 520 ± 17.5 nm and λ_exc = 488 nm, using a 100× 1.4 NA PlanApo objective lens, and with the side beams centered at 92% of the pupil radius. To allow accurate measurements, the lateral and axial pixel dimensions of this data set were decreased during processing by an extra factor of two compared to normal operation. Measurements on 100 microspheres, histogrammed in Fig. 4 e, yielded a mean FWHM of 103.9 nm laterally and 279.5 nm axially, with standard deviations of 1.5 nm and 2.9 nm, respectively. For comparison, the theoretical frequency-space resolution limits for three-dimensional SIM with these parameters are ∼(92 nm)⁻¹ and (265 nm)⁻¹ in the lateral and axial directions, respectively, and the true FWHM of a 115-nm solid sphere is nm = 99.6 nm.

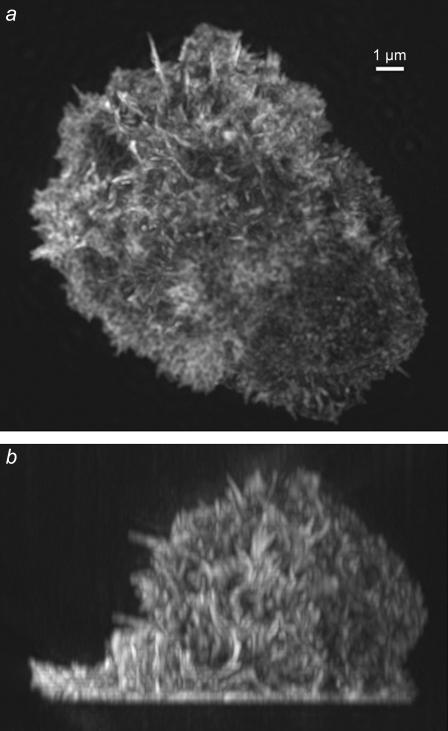
Fig. 5 and Supplementary Material, Data S1, Movie S1 show a structured illumination reconstruction of a biological sample with complex three-dimensional structure, the actin cytoskeleton in an HL60 cell which had been induced to differentiate into a neutrophil-like state. The cell was exposed to a low concentration of a bacterial peptide, formyl-methionyl-leucyl-phenylalanine, which is a chemotactic target for neutrophils; this stimulated the cell to ruffle into a complex three-dimensional shape. The images in Fig. 5 are maximum-intensity projections through the entire volume of the cell. As seen, the method yields a true three-dimensional reconstruction, largely devoid of out-of-focus blur.

FIGURE 5.

Maximum intensity projections through a three-dimensional structured illumination reconstruction of the actin cytoskeleton in an HL-60 cell, shown in top view (a) and side view (b). A video of this reconstruction is available on the journal web site (Movie S1).

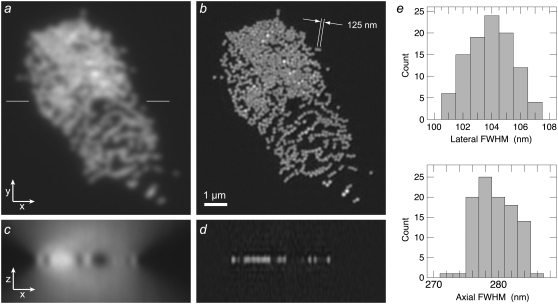
As a biological resolution test, we imaged the microtubule cytoskeleton in HeLa cells (Fig. 6, Movie S2). Individual microtubules can be followed throughout the cell volume. Two parallel microtubules are well resolved as separate at a distance of 125 nm (Fig. 6 b, inset) while entirely unresolved in the conventional microscopy image generated from the same data (Fig. 6 a, inset). To estimate the resolving power on biological specimens, 20 microtubules were chosen at random and their axial and lateral FWHM were measured; the average FWHM was 120 nm laterally and 309 nm axially.

FIGURE 6.

The microtubule cytoskeleton in HeLa cells. Axial maximum-intensity projections, using conventional microscopy (a) and structured-illumination microscopy (b), through a 244-nm-thick subset of the data (two sections). (Insets) two parallel microtubules spaced by 125 nm (arrows) are well resolved in the structured illumination reconstruction, but unresolved by conventional microscopy. The image contrast of the inset in a has been adjusted, for easier comparison. (c) Cross-eyed stereo view of projections through the structured-illumination reconstruction. The data value of each voxel controlled both the brightness and the opacity of that voxel in the rendering. A video of this reconstruction is available on the journal web site (Movie S2).

Fig. 7 shows an example of a biologically significant structure that cannot be resolved by conventional means: the synaptonemal complex (SC), which mediates pairing and recombination of homologous chromosomes during meiosis I (23). Maize meiocytes were immunofluorescently labeled in red and green against the proteins AFD1 and ASY1, respectively. Both proteins are associated with the axial/lateral element of the SC, which forms an axis along each chromosome (set of sister chromatids) before pairing, and aligns as two parallel strands (the lateral elements), on either side of a central element, after pairing and synapsis is complete (Fig. 7 b). The center-to-center distance between the lateral elements has been measured by electron microscopy to be ∼140 nm in maize (24). With our preparation protocol, the epitope for the ASY1 antibody becomes inaccessible for antibody binding after synapsis, hence the lateral elements of synapsed parts of the SC are labeled in red only, whereas unsynapsed parts of the SC are labeled in both red and green. Separate three-dimensional structured illumination data sets were acquired in red and green, reconstructed, and merged (Fig. 7 a). The nucleus shown was in the late zygotene stage of meiosis, when synapsis is nearly complete. In synapsed regions, the two lateral elements can be clearly resolved as separate and traced through the nucleus (Fig. 7 a, c, and e), which is not possible with conventional microscopy (Fig. 7 d and (19)). The apparent center-center distance between the lateral elements in our reconstructions is ∼170–180 nm, in reasonable agreement with the published values based on electron micrographs. (Perfect agreement is not necessarily expected, given our gentler preparation protocol and labeling of a particular protein component within the lateral element.) The axial elements in unsynapsed regions provide an internal control: the fact that they are clearly reconstructed as single strands, also in the red channel, establishes with certainty that the doublet appearance in the synapsed regions represents true structure (Fig. 7, a and c). A video illustrating the three-dimensional nature of this reconstruction (Movie S3), and separate renderings of the AFD1 and ASY1 channels (Fig. S1), are available at the journal website.

FIGURE 7.

The synaptonemal complex (SC) in a maize meiocyte nucleus during the late zygotene stage of meiosis. Fixed meiocytes were immunofluorescently labeled for the axial/lateral element components AFD1 (red fluorescence, here displayed as magenta) and ASY1 (green) of the synaptonemal complex. Under the fixation conditions used, the ASY1 epitope is inaccessible to the antibodies when synapsis is complete; the synapsed regions therefore fluoresce only in red, whereas the unsynapsed regions fluoresce in both green and red. In fully synapsed chromosomes, the lateral elements align as two parallel strands separated by ∼170 nm. (a) Maximum-intensity projection through a three-dimensional structured-illumination reconstruction of an entire nucleus (data set thickness, 8 μm). Separate renderings of the AFD1 and ASY1 channels of this image are available on the journal website (Fig. S1). (b) Transmission electron micrograph of a silver-stained chromosome-spread preparation of a maize pachytene meiocyte, showing the three elements of the SC surrounded by the paired chromosomes. (LE, lateral elements; CE, central element; Ch, chromatin.) (c) Magnification of the cyan-boxed region, maximum-intensity-projected through 1.5 μm of the sample thickness, showing a transition from unpaired to paired SC (arrows). (d and e) Magnifications of the white-boxed region of the specimen, imaged with conventional microscopy (d) or structured illumination microscopy (e). Panels d and e show maximum-intensity projections of only three axial sections, representing 375 nm of sample thickness, to avoid unnecessary blur in the conventional image. The lateral elements in synapsed regions, which are unresolvable by conventional microscopy (d), are well resolved by structured illumination microscopy (a, c, and e), and the twisting of the two strands around each other can be clearly followed (e, compare with b). A video of this reconstruction is available on the journal web site (Movie S3).

DISCUSSION

The form of structured illumination microscopy implemented here uses an illumination pattern that is structured in only one of the two lateral directions; to provide three-dimensional resolution extension the pattern is applied sequentially in a series of separate orientations. An alternative approach is to use an illumination pattern that contains structure in both lateral dimensions, for example by using a two-dimensional diffraction grating, thereby eliminating the need for rotation of the pattern. There would be a corresponding increase, however, in the number of information components that need to be separated, and therefore in the number of raw data images required for separation: a two-dimensional illumination pattern would typically be phase-shifted through a two-dimensional array of x and y phases. The total number of images required is comparable between the two approaches. We have chosen the sequential approach because it allows the polarization to be chosen for maximal pattern contrast, since for a single orientation there is a well-defined s-polarization direction. Two-dimensional patterns correspond to a nonplanar arrangement of illumination beams, which cannot all be s-polarized relative to each other, and therefore cannot produce maximal interference contrast. A detailed comparison of advantages and disadvantages of one-dimensional and two-dimensional illumination patterns will be published separately.

The application area of three-dimensional structured illumination microscopy overlaps with that of confocal microscopy, but the two techniques have different and complementary strengths. Structured illumination microscopy offers higher effective lateral resolution, because it concentrates much of the excitation light at the very highest illumination angles, which are most effective for encoding high-resolution information into the observed data, whereas confocal microscopy spreads out its illumination light more-or-less uniformly over all available angles to form a focused beam. For very thick and compactly fluorescent samples, however, confocal microscopy has an advantage in that its pinhole removes out-of focus light physically. Structured illumination microscopy is quite effective at removing out-of-focus light computationally, because it is not subject to the missing-cone problem, but computational removal leaves behind the associated shot noise. Therefore confocal microscopy may be preferable on very thick and dense samples, for which the in-focus information in a conventional microscope image would be overwhelmed by out-of-focus light, whereas structured illumination microscopy may be superior in a regime of thinner or sparser samples. At what thickness the crossover point falls will depend on the properties of each specimen. The data in Figs. 5 and 6 demonstrate that the 10–15-μm thickness range, which includes most single-cell specimens, lies well within the range where structured-illumination microscopy excels.

The reconstruction algorithm described here is completely linear (once the parameters are determined), and makes no use of a priori knowledge of the sample. The linearity implies that there is an effective PSF for the final reconstruction; the way a given feature is rendered is therefore independent of its surroundings (see Fig. 4 d, in which all beads in the reconstruction have the same shape, whether they are located in a cluster or isolated). Iterative deconvolution algorithms (1), which apply a priori constraints such as nonnegativity of the fluorophore density, are a routinely used tool in three-dimensional microscopy, and can under good circumstances provide effective resolution beyond the conventional limits (25). Such methods could also be applied to SIM data, and could be expected to provide similar benefits, at the expense of making the reconstruction of a given structure depend on its surroundings. In this article we have avoided all use of constraints, to eliminate any possibility of confusion between actual measurement of new high-resolution information by SIM, and extrapolation beyond the measured information based on constrained deconvolution.

As described above, structured illumination can be thought of as generated by interference of two or more mutually coherent beams. There are two main approaches to generating such beams: through diffractive beam splitting with a mask, grating, or other patterned device (5,6,8–10), which was used in this article, or by reflective beam splitting (7,26,28). Each method has advantages and disadvantages. Reflective beam splitting has an advantage for multicolor applications in that the positions of the illumination beams in the pupil plane can be made independent of their wavelength, whereas with diffractive beam splitting the distance of a beam from the pupil center is typically proportional to its wavelength and can therefore be strictly optimized only for one wavelength at a time. (Multiwavelength data sets can still be taken, by optimizing for the longest wavelength, with only minor performance penalties at the shorter wavelength channels (see Fig. 7).) On the other hand, reflective beam splitting has a severe disadvantage in that it typically causes the beams to be separated spatially and handled by separate optical components (mirrors, etc.); any nanometer-scale drift of any such component translates directly into a phase error in the data. With diffractive beam splitting, by contrast, all beams typically traverse the same optical components in an essentially common-path geometry, which decreases the sensitivity to component drift by several orders of magnitude. In addition, reflective beam splitting typically requires separate mirror sets for each pattern orientation, which becomes increasingly bulky as the number of pattern orientations increases; for this reason the approach has so far only been implemented for one (26,28) or two (7) pattern orientations, which is insufficient for isotropic resolution, and can force a tradeoff between resolution and anisotropy (7).

Since live microscopy is an area of much current excitement, it is important to consider to what extent three-dimensional SIM can be applied to live samples. The principles are fully compatible with living samples, assuming that a water-immersion objective lens is used to avoid unnecessary aberrations. Apart from the usual limits to total exposure set by photobleaching and phototoxicity, the only additional limitation relates to motion. The current algorithm treats the sample as an unchanging three-dimensional structure, and could therefore produce artifacts if substantial motion were to occur within the sample during data acquisition. As implemented here, three-dimensional SIM uses 15 raw images per axial section, and spaces the axial sections by typically 125 nm to provide Nyquist sampling relative to its axial resolution of <300 nm. This corresponds to 120 exposures per μm of data volume thickness; a data set of a thick three-dimensional sample can thus entail >1000 raw images. Even with a high-speed camera and rapid pattern generation hardware, such data sets could take seconds or minutes to acquire, a timescale during which many biological systems will undergo internal movements many times larger than the resolution scale of SIM. Sensitivity to motion can be decreased somewhat by using an acquisition order in which all images of a certain focal plane (for all pattern orientations as well as phases) are acquired before refocusing; in that mode, the time frame during which motion must be avoided may be decreased from that of the full data set to the time required to record a sample thickness corresponding to the axial extent of pattern modulation (see Fig. 3 b). Both limitations—motion and photobleaching/phototoxicity—become proportionately less stringent for thinner samples. Live imaging at SIM resolution should be quite feasible on a class of thin samples. At the thin limit, some structures could be treated as two-dimensional, including any sample viewed in total internal reflection mode and some structures such as lamellipodia that are naturally thinner than the conventional depth of field. SIM is fully compatible with the total internal reflection mode, as has recently been demonstrated in one dimension (26). With appropriate hardware, it should be possible to acquire time-sequence data of such samples by two-dimensional SIM at frame rates in the Hz range.

The algorithm described assumes that the three-dimensional data include the entire emitting object. If the data contain strong light that originates from beyond the edges of the imaged volume, artifacts could be expected to arise. We have reconstructed such data sets without major problems, using the processing order and other precautions outlined in Methods, but whenever possible we include the whole object of interest in the data set, and ideally a few out-of-focus sections above and below, to avoid this issue.

The method described in this article assumes a normal, linear relationship between the illumination intensity and the fluorescent emission rate, and achieves approximately a factor of two of resolution extension. It is known that two-dimensional wide-field resolution can be extended much further if the sample can be made to respond nonlinearly to illumination light (22,27,28). That concept, nonlinear structured illumination microscopy, can in principle be applied to the three-dimensional method described here in much the same way as it is used in two dimensions, and could enhance axial as well as lateral resolution. The main limitation is that the requirement for photostability of the fluorophores, already significant in two dimensions, would increase in proportion to the number of sections. The same concern, of dividing the available phototolerance over the sections when going from two-dimensional to three-dimensional imaging, may also affect other recent methods that have demonstrated very high resolution in two dimensions, such as PALM/FPALM/STORM (29–31). Highly nonlinear point-scanning methods such as STED (32) may be less subject to this effect, especially if using multiphoton excitation, to the extent that photodegradation can be confined to a small axial range near the focal plane.

The axial resolution of the conventional microscope is worse than the lateral resolution by a factor of approximately three (for high-NA objective lenses). The same anisotropy also applies to three-dimensional SIM as described here, which extends resolution by the same factor in all dimensions. However, the structured illumination concept is compatible with the opposing-objective-lens geometry of I⁵M, which allows access a much greater axial resolution (33). A straightforward combination of three-dimensional SIM and I⁵M, called I⁵S, can yield nearly isotropic three-dimensional imaging resolution in the 100-nm range (34).

In conclusion, three-dimensional structured-illumination microscopy can produce multicolor three-dimensional imaging reconstructions of fluorescently-labeled specimens with a lateral resolution, approaching 100 nm, which is unavailable in practice with conventional methods of three-dimensional light microscopy. At the same time it can provide axial resolution <300 nm, and remove out-of-focus blur deterministically. We believe that it has an important role to play in cell biology.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.