Correcting reaction rates measured by saturation-transfer magnetic resonance spectroscopy

Abstract

Off-resonance or spillover irradiation and incomplete saturation can introduce significant errors in the estimates of chemical rate constants measured by saturation-transfer magnetic resonance spectroscopy (MRS). Existing methods of correction are effective only over a limited parameter range. Here, a general approach of numerically solving the Bloch–McConnell equations to calculate exchange rates, relaxation times and concentrations for the saturation-transfer experiment is investigated, but found to require more measurements and higher signal-to-noise ratios than in vivo studies can practically afford. As an alternative, correction formulae for the reaction rate are provided which account for the expected parameter ranges and limited measurements available in vivo. The correction term is a quadratic function of experimental measurements. In computer simulations, the new formulae showed negligible bias and reduced the maximum error in the rate constants by about 3-fold compared to traditional formulae, and the error scatter by about 4-fold, over a wide range of parameters for conventional saturation transfer employing progressive saturation, and for the four-angle saturation-transfer method applied to the creatine kinase (CK) reaction in the human heart at 1.5 T. In normal in vivo spectra affected by spillover, the correction increases the mean calculated forward CK reaction rate by 6–16% over traditional and prior correction formulae.

1. Introduction

Flux through energy-producing metabolic reactions is critical for cellular viability and fueling key cellular functions. Adenosine triphosphate (ATP) is the chemical energy currency for most cells in the body and the dynamic turnover of ATP can be probed non-invasively with phosphorus (³¹P) magnetization-transfer magnetic resonance spectroscopy (MRS) techniques. The creatine kinase (CK) reaction:

$$\begin{array}{cc}\hfill & \text{Phosphocreatine}\left(\mathrm{Pcr}\right)+\text{Adenosine diphosphate}\left(\mathrm{ADP}\right)\hfill \\ \hfill & +{\mathrm{H}}^{+}\leftrightarrow \mathrm{ATP}+\text{creatine}\left(\mathrm{Cr}\right),\hfill \end{array}$$

is the prime short-term ATP reserve that serves to maintain constant ATP and ADP concentrations in the heart and may play a key role as an intracellular shuttle of high-energy phosphates between the mitochondria and sites of energy use in brain, skeletal muscle and heart [1]. In the failing heart, for example, abnormalities in CK flux in cardiomyopathies suggest an underlying energy supply defect [2-4]. Saturation-transfer MRS is an established method for measuring the CK reaction rate and flux in vivo, by selectively saturating one of the exchanging moieties, γ-ATP, and measuring the response in the reactant moiety, PCr.

In the standard two-site saturation-transfer experiment applied to two moieties A and B undergoing chemical exchange, the fractional reduction in the signal of A due to complete saturation of B, is equal to the pseudo-first order forward rate constant k in units of the apparent spin–lattice relaxation time of A, $T_{1\mathrm{A}}^{\mathrm{sat}}$ [5],

$${\mathit{kT}}_{1\mathrm{A}}^{\mathrm{sat}}=1-{\mathrm{A}}_{\mathrm{s}}∕{\mathrm{A}}_{\mathrm{n}}$$ (1)

where A_s and A_n are the steady-state fully-relaxed magnetization of A in the presence (subscript s), and absence (subscript n), of a saturating irradiation applied to B, and

$$1∕T_{1\mathrm{A}}^{\mathrm{sat}}=1∕T_{1\mathrm{A}}+k$$ (2)

where T_1A is the “intrinsic T₁” of A. The simplified notation used here is summarized in Table 1. The determination of k then requires measurements of A_s, A_n and $T_{1\mathrm{A}}^{\mathrm{sat}}$. The relaxation rate constant $T_{1\mathrm{A}}^{\mathrm{sat}}$ is commonly measured using standard progressive saturation [6], or, in humans using the more efficient four-angle saturation-transfer (FAST) method which uses a pulse repetition period, TR, much shorter than the spin–lattice relaxation times, T₁ [7].

Table 1.

Notation used in the saturation-transfer experiment for measuring the reaction rate constant between two moieties A and B

Symbol	Meaning
M0A, M0B	Equilibrium magnetization of A and B in absence of irradiation and chemical exchange
An, Bn	Equilibrium magnetization of A and B in presence of chemical exchange
As, Bs	Equilibrium magnetization of A and B in the presence of chemical exchange and selective irradiation of B
Ac, Bc	Equilibrium magnetization of A and B in the presence of chemical exchange and selective irradiation of the control site
Q	Irradiation spillover quality index: Q =Ac/An
T1A, T1B	The longitudinal relaxation time of A and B in the absence of irradiation and chemical exchange
$T_{1\mathrm{A}}^{\mathrm{sat}}$	The apparent longitudinal relaxation time of A in the presence of chemical exchange and selective irradiation of B

The derivation of Eq. (1) assumes both perfect saturation of B and an absence of off-resonance, or spillover irradiation effects on A while saturating B [5]. The conventional way to account for any spillover effect is to perform a control saturation experiment where the saturation is applied to the other side of A from B at a frequency, ω_RF, of 2ω_A − ω_B where ω_A and ω_B are the resonant frequencies of A and B, respectively. The magnetization of A during this control experiment, A_c, is then substituted for A_n in Eq. (1), to yield a conventional k,

$$k_{\mathrm{conv}}{T}_{1\mathrm{A}}^{\mathrm{sat}}=1-{\mathrm{A}}_{\mathrm{s}}∕{\mathrm{A}}_{\mathrm{c}}.$$ (3)

By this means, the saturating field is supposed to have the same spillover effect on A during both the B saturation and the control experiments, thereby canceling the error via the ratio A_s/A_c. However, this procedure ignores the effects of chemical exchange and of spillover irradiation on B during the control experiment [8,9].

Errors in the reaction rate and relaxation times arising from off-resonance and incomplete saturation effects have been reported [6,10-12]. Strategies for correcting these errors have been suggested, which typically require additional acquisitions with the saturating irradiation completely turned-off [8,9,13-15]. This includes a study by Kingsley and Monahan [13] in which existing and novel formulae for correcting k were compared in two models of proton (¹H) and phosphorus (³¹P) chemical exchange. They found that no single formula could provide an accurate correction over all levels of saturating field strengths, but the more accurate candidates to replace Eq. (3) were the Horska–Spencer (HS) formula [9]:

$$k_{\mathrm{HS}}{T}_{1\mathrm{A}}=\frac{({\mathrm{A}}_{\mathrm{c}}-{\mathrm{A}}_{\mathrm{s}})∕{\mathrm{A}}_{\mathrm{n}}}{({\mathrm{B}}_{\mathrm{c}}-{\mathrm{B}}_{\mathrm{s}})∕{\mathrm{B}}_{\mathrm{n}}-({\mathrm{A}}_{\mathrm{c}}-{\mathrm{A}}_{\mathrm{s}})∕{\mathrm{A}}_{\mathrm{n}}};$$ (4)

and the Kingsley–Monahan (KM) formula (their Eq. (27))

$$k_{\mathrm{KM}}{T}_{1\mathrm{A}}^{\mathrm{sat}}=\frac{({\mathrm{A}}_{\mathrm{c}}-{\mathrm{A}}_{\mathrm{s}})∕{\mathrm{A}}_{\mathrm{n}}}{({\mathrm{B}}_{\mathrm{c}}-{\mathrm{B}}_{\mathrm{s}})∕{\mathrm{B}}_{\mathrm{n}}}.$$ (5)

The latter performed best in their study [13] when limited to a single specified set of parameters representing the expected value for the resonant frequencies, concentrations, relaxation times and reaction rate constants for the two models. However, variations in these parameters still resulted in large errors in the calculated k [7].

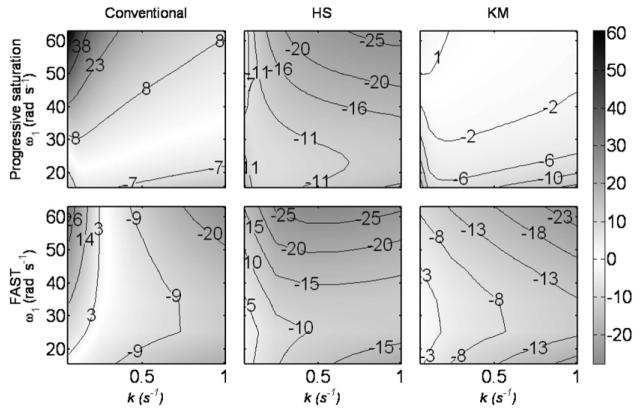
Consider for example, the ³¹P MRS saturation-transfer experiment for measuring the kinetics of the CK reaction above. Chemical exchange between the PCr (site A), and the γ-ATP moiety (site B), is measured in a simulated standard saturation-transfer experiment using both progressive saturation and FAST methods as described below in Section 3. The relative errors in k obtained when using Eqs. (3)-(5) computed with a numerical evaluation of the Bloch–McConnell (BM) equations [16] for the CK reaction are plotted in Fig. 1 with typical parameters within the ranges listed in Table 2. The error contours reflect relative errors in k of over 30%, which vary considerably over the range of k and the applied saturating field strength, ω₁.

Fig. 1.

Percent error in the estimated value of the reaction rate constant k for simulated ³¹P MRS saturation-transfer experiments of the CK reaction using the standard progressive saturation method (top) and the FAST method (below) as a function of ω₁ and k. The value of k is calculated using the conventional equation (3), the Horska–Spencer (HS) equation (4) and the Kingsley–Monahan (KM) equation (5) for T_1A = 6 s and M_0A/M_0B = 1.5. Errors are depicted both as contours and by the gray scale (right).

Table 2.

Parameters of the two sites of the CK reaction used in simulations

Parameter	Min	Max
M0A (PCr)	0.5	2
M0B (γ-ATP)	1	1
T1A (s)	4.4	6.5
T1B (s)	2	2
T2A (s)	0.1	0.1
T2B (s)	0.05	0.05
ωA (rad s−1)	0	0
ωB (rad s−1)	440	440
ω1 (rad s−1)	15.7	62.8

These potentially large errors motivated us to investigate new strategies for correcting the pseudo-first order forward CK reaction rate-constant measured with saturation transfer. While direct numerical solution of the BM equations for two-site chemical exchange might be considered a “gold standard” for accuracy, it nevertheless requires precise knowledge of a number of experimental measurements, which, due to the limited scan time of about an hour for localized in vivo human ³¹P MRS at current signal-to-noise ratios (SNR), is often unavailable. Therefore, we introduce two new solutions which add correction terms to k derived from the KM formula, to cancel out the systematic errors evident in Fig. 1, using practical measurable quantities. We validate these corrections using computer simulations, and compare the effect of different correction formulae on real data from in vivo FAST localized ³¹P MRS studies of the human heart.

2. Theory

2.1. The Bloch–McConnell (BM) equations

The BM equations [16] introduce a modification of the Bloch equations to describe the evolution of the magnetization M of chemically exchanging sites, A and B in a two-site system. During the application of a constant saturating RF field of strength ω₁ aligned with the x-axis of a frame of reference rotating at frequency ω_RF, the BM equations in matrix form are [7,8,16]

$$\frac{\mathrm{d}}{\mathrm{d}t}\mathbf{M}=\mathbf{SM}+\mathbf{C}$$ (6)

with M = (M_Ax M_Ay M_Az M_Bx M_By M_Bz)^T, C = (0 0 M_0A/T_1A 0 0 M_0B/T_1B)^T,

$$\mathbf{S}=\left(\begin{array}{cccccc}-\frac{1}{T_{2\mathrm{A}}}-k\hfill & \Delta {\omega }_{\mathrm{A}}\hfill & 0\hfill & k_{\mathrm{r}}\hfill & 0\hfill & 0\hfill \\ -\Delta {\omega }_{\mathrm{A}}\hfill & -\frac{1}{T_{2\mathrm{A}}}-k\hfill & {\omega }_1\hfill & 0\hfill & k_{\mathrm{r}}\hfill & 0\hfill \\ 0\hfill & -{\omega }_1\hfill & -\frac{1}{T_{1\mathrm{A}}}-k\hfill & 0\hfill & 0\hfill & k_{\mathrm{r}}\hfill \\ k\hfill & 0\hfill & 0\hfill & -\frac{1}{T_{2\mathrm{B}}}-k_{\mathrm{r}}\hfill & \Delta {\omega }_{\mathrm{B}}\hfill & 0\hfill \\ 0\hfill & k\hfill & 0\hfill & -\Delta {\omega }_{\mathrm{B}}\hfill & -\frac{1}{T_{2\mathrm{B}}}-k_{\mathrm{r}}\hfill & {\omega }_1\hfill \\ 0\hfill & 0\hfill & k\hfill & 0\hfill & -{\omega }_1\hfill & -\frac{1}{T_{1\mathrm{B}}}-k_{\mathrm{r}}\hfill \end{array}\right)$$

and where the superscript T denotes transposition; M_0A and M_0B are the fully relaxed equilibrium magnetization of A and B, respectively; Δω_A = ω_A − ω_RF, Δω_B = ω_B − ω_RF,(x, y, z) are coordinate axes in the rotating frame; and k_r = kM_0A/M_0B is the reverse reaction rate constant at equilibrium. The general solution of this equation is given by [7,11]:

$$\mathbf{M}\left(t\right)={\mathbf{e}}^{\mathbf{S}t}(\mathbf{M}(t=0)+{\mathbf{S}}^{-1}\mathbf{C})-{\mathbf{S}}^{-1}\mathbf{C}$$ (7)

Free precession in periods when the saturation field is turned-off, is similarly described by replacing S by a new matrix F = S(ω₁ = 0). Upon iterating periods of saturation and acquisition, the magnetization reaches a steady-state, and partial saturation occurs when the sequence repetition period, TR ∼ T₁ of the exchanging species. The steady-state magnetization after the last acquisition pulse is given by:

$$\begin{array}{cc}\hfill \mathbf{M}=& \mathbf{R}{\left(\mathbf{I}-{\mathbf{e}}^{\mathbf{S}\cdot (\mathrm{TR}-\mathrm{TF})}{\mathbf{e}}^{\mathbf{F}\cdot \mathrm{TF}}\mathbf{R}\right)}^{-1}[\left({\mathbf{e}}^{\mathbf{S}\cdot (\mathrm{TR}-\mathrm{TF})}-\mathbf{I}\right){\mathbf{S}}^{-1}\phantom{]}\hfill \\ \hfill & \phantom{[}+{\mathbf{e}}^{\mathbf{S}\cdot (\mathrm{TR}-\mathrm{TF})}({\mathbf{e}}^{\mathbf{F}\cdot \mathrm{TF}}-\mathbf{I}){\mathbf{F}}^{-1}]\mathbf{C}.\hfill \end{array}$$ (8)

Here TF is the time of free precession, I is a 6 × 6 identity matrix and R is a rotation matrix corresponding to an RF pulse with a flip angle α:

$$\mathbf{R}=\left[\begin{array}{cccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \cos \alpha \hfill & \hfill -\sin \alpha \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \sin \alpha \hfill & \hfill \cos \alpha \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cos \alpha \hfill & \hfill -\sin \alpha \hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \sin \alpha \hfill & \hfill \cos \alpha \hfill \end{array}\right].$$

2.2. Numerical solution of the BM equations

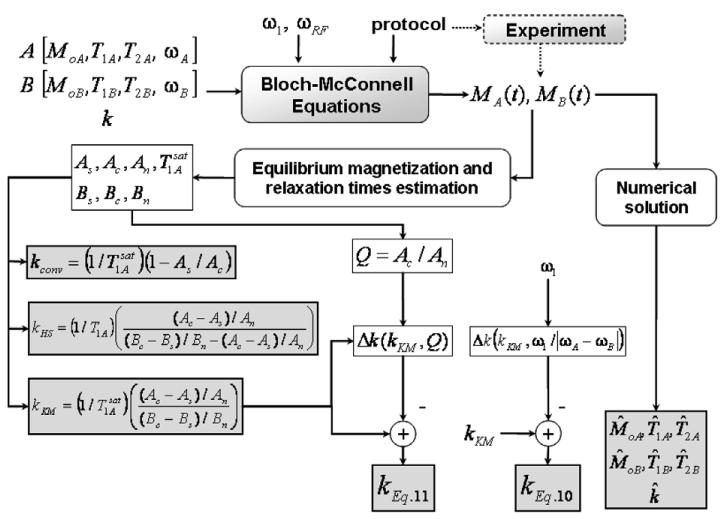
Using the BM equations above, the steady-state values of the magnetization of A and B resulting from the entire saturation-transfer experiment can be determined for the specified set of parameters. The standard saturation-transfer experiment involves a B-site saturation, a control-site saturation, and saturation-off sub-experiments [7]. The BM equations represent a nonlinear system whose analytical solution is unmanageable. However the problem is tractable with numerical approaches, as schematically shown in Fig. 2. By numerically inverting this system (iteratively obtaining the input parameters from the output magnetization), spillover and/or incomplete saturation effects can be correctly accounted for, provided that a sufficient number of accurate measurements are available. Inverting the system yields estimates of the concentrations and relaxation times of A and B, in addition to k. The remaining inputs to this system include ω₁, ω_RF, the frequency separation between A and B and experiment-specific parameters such as the type of the saturation transfer experiment (progressive saturation, inversion recovery, FAST, etc) and the experimental parameters TR, TF, α, etc., while the output of the system is the measured steady-state magnetization of A and B.

Fig. 2.

Correction strategies for k in steady-state saturation transfer experiments involving two-site chemical exchange. The parameters for each species are fed to the BM equations, from which the partially-saturated magnetizations are derived for a given experimental protocol. The fully-relaxed magnetizations and T₁'s are estimated and used to compute the ks by the various correction equations, in the presence of spillover irradiation. A direct numerical solution is also computed.

Thus, the solution is formulated as a multidimensional nonlinear optimization problem. The nonlinear least-squares method is used to minimize the norm of the deviation of the outputs of Eq. (8) from the measured magnetization values, over the specified parameter space. We found that the alternative global search technique of simulated annealing [17] offered little improvement in accuracy in return for its increased computational load compared to the least squares approach. Restricting the search space using prior knowledge about the exchanging sites, such as the expected range of T₁ and T₂, was employed to hasten calculations and enhance solution stability.

Although numerical inversion can accurately solve the problems of off-resonance and incomplete saturation under many conditions, at least seven independent measurements are required to solve for M_0A, T_1A, T_2A, M_0B, T_1B, T_2B, and k. For accuracy, even more measurements are necessary when SNR is low. Unfortunately, the number of measurements provided by in vivo experiments is limited by the tolerable scan time, for example, in patient studies. In such cases, the numerical solution of the BM equations is sensitive to noise. We will illustrate the potential of applying this method in simulations involving the limited set of measurements that are routinely acquired in a FAST experiment, in addition to a standard saturation transfer experiment employing the progressive saturation method. The latter provides more measurements but is presently too time-consuming to be practical for localized saturation-transfer experiments in humans.

2.3. Correcting systematic errors in conventional formulae

An alternative solution to the spillover irradiation/incomplete saturation problem is to correct for the systematic errors in k when calculated from one of the conventional formulae. Systematic errors in k are determined from an accurate simulation of the BM equations and the results either saved to a look-up table for post-correction, or fitted with a suitable basis function (e.g. a polynomial) to obtain a closed-form correction formula. The latter is feasible if the systematic error is smooth enough to be accurately modeled by the basis functions within acceptable residual errors, after correction. Hence, a conventional formula with a smooth error surface in k over a realistic parameter space is desired. This condition is satisfied by the KM formula, Eq. (5), and is presented in Section 4.

While all input parameters to the BM equations affect the calculated k, the most influential parameters are the actual value of k, the spillover degree as indexed by the ratio of the saturating field strength to the frequency separation between the two sites, ω₁/|ω_A − ω_B| [8], and TR. Since TR is usually fixed as a user-defined parameter for the FAST protocol, we will neglect its change. Subtracting a term Δk that depends on the relevant parameters, we obtain a corrected value of k, k_corr:

$$k_{\mathrm{corr}}=k_{\mathrm{KM}}-\Delta k(k_{\mathrm{KM}},{\omega }_1∕|{\omega }_{\mathrm{A}}-{\omega }_{\mathrm{B}}\left|\right)$$ (9)

Using polynomial basis functions, the correction is

$$k_{\mathrm{corr}}=k_{\mathrm{KM}}-P_k\left(k_{\mathrm{KM}}\right)P_{\omega }({\omega }_1∕|{\omega }_{\mathrm{A}}-{\omega }_{\mathrm{B}}\left|\right)$$ (10)

where P_k and P_ω are second-order polynomials in their arguments. A second-order polynomial was found to give acceptable error levels while only minor improvements were achieved with higher orders. The correction term Δk is fitted to the systematic errors in k_KM over the ranges of the parameters listed in Table 2 using the method of least squares. The polynomial factors that minimize the error in k are given in Table 3 where the factors a₁, a₂ and a₃ are the coefficients of the quadratic polynomial P(x) = a₁x² + a₂x + a₃.

Table 3.

Coefficients of the correction polynomials used in Eq. (10) for the progressive saturation and the FAST experiments

Protocol	Polynomial	a1	a2	a3
Progressive saturation	Pk	1.000	−0.403	0.046
	Pω	−48.067	10.035	−0.5951
FAST	Pk	1.000	0.225	−0.005
	Pω	−48.403	6.857	−0.363

A practical problem with this solution is that the saturating field strength experienced by the exchanging species, ω₁, must be known. However, in general, ω₁ differs from the specified transmitter power. For example, most ³¹P MRS is performed with surface coil excitation [2,4].In these cases ω₁ is spatially-dependent and not easily determinable. In practice, the saturating field strength is manually adjusted as a fraction of a maximum allowed power, until the saturation of B appears satisfactory. In this situation, the spillover irradiation factor, ω₁/|ω_A − ω_B| should be replaced by a suitable measure such as Q = A_c/A_n [7] which may vary spatially. The correction formula is then:

$$k_{\mathrm{corr}}=k_{\mathrm{KM}}-P_k\left(k_{\mathrm{KM}}\right)P_Q\left(Q\right)$$ (11)

where P_Q is a second-order polynomial in Q. The optimal polynomial factors in this case are given in Table 4, with a schematic of their derivation included in Fig. 2.

Table 4.

Coefficients of the correction polynomials used in Eq. (11) for the progressive saturation and FAST experiments with 0.05 ⩽ k ⩽ 1.0 and 0.1 ⩽ k ⩽ 0.5 (FAST*)

Protocol	Polynomial	a1	a2	a3
Progressive saturation	Pk	1.000	−0.120	−0.022
	PQ	−2.475	3.685	−1.426
FAST	Pk	1.000	0.135	−0.007
	PQ	−6.443	11.972	−5.712
FAST*	Pk	1.0000	−0.0534	−0.0534
	PQ	0.2025	0.0098	−0.2585

3. Methods

3.1. Simulations

The proposed correction methods are evaluated for a simulated CK reaction probed by two standard ³¹P saturation-transfer methods. The first is a conventional saturation-transfer experiment with progressive saturation to measure the apparent T_1A $T_{1\mathrm{A}}^{\mathrm{sat}}$. The progressive saturation portion includes acquisitions with TR = 0.6, 1, 2, 3, 4, 8, 12 and 16 s, with the B-site saturated. In addition, acquisitions with the control-site saturated, and with the saturation turned-off, are both recorded at TR = 16 s. The FAST experiment incorporates the dual-angle method for measuring $T_{1\mathrm{A}}^{\mathrm{sat}}$ [18]. In FAST, A is measured twice with B saturated, and twice with control irradiation (at 2ω_A − ω_B) using two different (adiabatic) flip-angles, 60° and 15° at each site and TR = 1 s [7]. An additional 60° saturation-off experiment is performed at the same TR. The values of ω₁, the concentration ratio M_0A/M_0B, and the relaxation constant T_1A are allowed to vary over the ranges listed in Table 2, which also lists the fixed model values. All these values are consistent with existing data from heart and brain [7,19-21].

The entire progressive saturation and FAST experiments are simulated using the steady-state equations above (Eq. (8)), with Matlab (The MathWorks, Natick, MA). The relative error in k, (k_calculated − k_true)/k_true where k_true is the input value of k in the range, is calculated for the conventional formula, Eq. (3), the HS formula, Eq. (4), the KM formula, Eq. (5), the numerical inversion method, and the new correction formulae provided here in Eqs. (10) and (11). For the numerical inversion method, 12 measurements are used in the progressive saturation method which are the partially-saturated magnetization values of A for the B-site saturation case at the eight different TR values in addition to the magnetization of A and B in the control and the saturation-off experiments. For FAST, only eight measurements are used to estimate the seven unknown variables. These are the partially-saturated magnetization values of A and B measured at the two different flip angles (60° and 15°) with B- and control-site saturation, which are all potentially available from a FAST experiment followed by an experiment in which no saturation is applied at a flip angle of 60° [7,19]. The simulations are done over two ranges of k: a broad range of 0.05 ⩽ k ⩽ 1.0 for general applications; and, to improve accuracy for in vivo cardiac FAST applications, a physiological range of 0.1 ⩽ k ⩽ 0.5 [4], denoted FAST*. Note that the magnetization of B in the B-saturation experiment, B_s, which corresponds to γ-ATP in the presence of saturation, cannot be reliably measured when SNR is low, as is typical of in vivo studies. It is therefore set to zero in all calculations. In this case Kingsley–Monahan's Eq. (27) reduces to their Eq. (34), and the HS equation reduces to Eq. (33) in the same Ref. [13]. As noted [13], these two equations tend to underestimate k.

To determine the effect of noise on k for each correction formula, a Monte Carlo analysis is performed for the FAST method with PCr SNR values of 20–50 as measured on the 15° acquisition recorded with γ-ATP saturated, and n = 100 trials. This analysis yields two measures of accuracy: (i) the difference between the mean corrected value and the true value, or bias; and (ii) the standard deviation (SD) of the corrected k value, or scatter.

3.2. Experiments

We applied the new correction to ³¹P MRS data available from prior studies of the human heart using the FAST method with one-dimensional chemical shift imaging (1D-CSI) localization, and a 1.5-T whole-body GE Signa scanner (Milwaukee, WI) system [4,7]. All experiments were performed using 4-ms BIRP adiabatic excitation pulses [7]. As in the simulations, the FAST method was applied at TR = 1 s, with four acquisitions employing flip angles of 15° and 60°, and with γ-ATP and control saturation applied at ±2.7 ppm relative to PCr. A fifth ³¹P MRS data set was acquired with a 60° pulse and no selective saturation to measure Q. The total duration of the complete image-guided localized MRS exam was about 60–75 min. Continuous RF applied at 2% of the maximum ³¹P MRS power level, provided the chemical-selective saturating field strength of 5–10 Hz over the sensitive volume of the detector coil. The saturating pulse was switched-off for TF = 180 ms during BIRP excitation and data acquisition. The pulse amplitude was set at the minimum level required to provide complete saturation of γ-ATP at visual inspection of surface coil ³¹P spectra acquired during set-up of each study. All ³¹P data acquisitions were preceded by a train of dummy excitations lasting 16–20 s, to establish steady-state equilibrium. All subjects provided informed consent, and these studies were approved by our institutional review board.

The effect of applying the conventional formula, the HS formula, the KM formula, and the correction formula in Eq. (11) on the reaction rate k was first calculated using the same 57 FAST data sets acquired from different cardiac slices in 18 healthy subjects. The numerical inversion method and Eq. (10) were excluded from the comparison because the experiments did not provide an accurate measure of ω₁. The analysis was performed three ways. First, because none of the correction formulae are strictly applicable to spectra with measured Q > 1, these data were excluded, resulting in a sample of 38 normal 1D-resolved cardiac spectra from 14 healthy subjects. Q > 1 is not meaningful, but arises when true Q ∼ 1 and SNR is low. Second, all data were included but we set Q = 1 when Q > 1 was measured. Third, all data were included with their actual measured Qs.

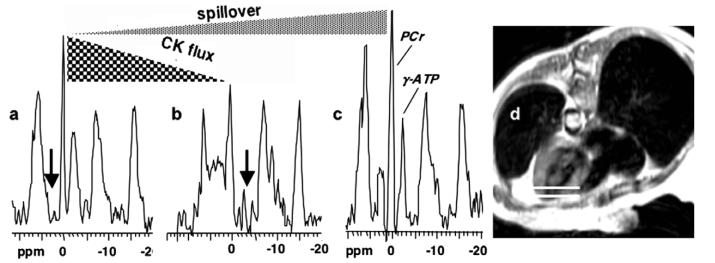
Next, the effect of varying both the experimental Q and k on the magnitude of the correction resulting from the application of the different correction formulae was investigated. In order to provide as wide a range of experimental Q and k values as possible, this analysis used the 38 cardiac spectra from the 14 healthy subjects above, along with 75 spectra from 34 patients with hypertrophic or dilated cardiomyopathies [4,7] that satisfied the Q ⩽ 1 criterion. Details of the patient selection criteria and the physiological interpretations of these data are provided elsewhere [4,7], and are beyond the scope of the present paper. Several typical localized cardiac ³¹P MRS spectra from a FAST study of a patient performed at 1.5 T, are shown in Fig. 3.

Fig. 3.

Typical ³¹P MRS spectra (a–c) of an exemplary 1-cm slice in the anterior myocardium (d; annotated with horizontal white lines) extracted from a FAST CK flux study of a 55-year-old woman with New York Heart Association Class I–II heart failure at 1.5 T [3,4]. (a,b) Two of the four FAST acquisitions excited with a 60° pulse and control saturation (a; vertical arrow), and with γ-ATP saturated (b). The reduction in PCr signal between (a) and (b) is due to CK flux in the heart. ³¹P Spectrum (c) is acquired with no saturation, to measure PCr concentration, and to measure the spillover effect. The reduction in PCr signal between (a) and (c) is due to spillover irradiation, and is quantified by Q.

4. Results

4.1. Simulations

The relative errors in the forward reaction rate constant calculated by different methods, as compared to the input k, are listed in Table 5. Of the pre-existing formulae Eqs. (3)-(5), the smallest range of errors in k for both progressive saturation and FAST, results from using the KM formula, justifying its choice here as a basis for correction in Eqs. (10) and (11). In applying the different correction methods to progressive saturation, the smallest errors are obtained by numerical inversion. The two proposed correcting formulae in Eqs. (10) and (11) perform similarly to the KM formula. Numerical inversion has the least bias and has 2–6 times less scatter (SD) in the error than the conventional, the HS, and the KM formulae, over the specified range of conditions. Our new Eqs. (10) and (11) exhibit negligible bias and up to four times lower SD than these formulae.

Table 5.

Means ± SD and range (min, max) of the percentage errors in the estimated k calculated by different correction methods

Correction method	Percent error in k, mean (bias) ± SD (min, max)
	Progressive saturation	FAST	FAST*
Conventional, Eq. (3)	7.4 ± 16.0 (−17.9, 70.0)	−5.8 ± 13.4 (−29.3, 39.7)	−1.5 ± 7.4 (−17.0, 27.3)
HS, Eq. (4)	−13.9 ± 15.2 (−35.6,−3.4)	−14.6 ± 16.2 (−33.7,−1.8)	−14.3 ± 15.7 (−33.5,−3.6)
KM, Eq. (5)	−3.0 ± 5.1 (−18.4,4.4)	−11.0 ± 12.7 (−27.3,0.8)	−8.4 ± 9.3 (−18.9,−0.7)
Numerical inversion	0.6 ± 2.6 (−12.6, 9.5)	0.2 ± 5.7 (−20.2, 29.1)	0.2 ± 4.6 (−12.8, 31.3)
Eq. (10)	1.8 ± 4.0 (−8.0, 12.3)	0.0 ± 2.2 (−10.4, 7.1)	0.1 ± 1.3 (−5.5, 3.5)
Eq. (11)	1.8 ± 5.5 (−25.5, 8.6)	−0.3 ± 3.2 (−12.8, 8.0)	0.1 ± 2.9 (−9.3, 4.7)

The errors are calculated for progressive saturation and FAST over the range of parameters listed in Table 2; for 0.05 ⩽ k ⩽ 1.0 and for FAST with 0.1 ⩽ k ⩽ 0.5 (FAST*).

For FAST, the smallest errors are obtained with the two new correcting formulae, Eqs. (10) and (11). Our new Eq. (10), shows no bias and has on average 6–7 times lower scatter than the conventional, the HS, and the KM formulae, while new Eq. (11) has a negligible bias with a 4- to 5-fold lower SD of the error. The numerical inversion method also shows negligible bias and has 2–3 times less scatter than the traditional formulae, but the errors are nevertheless, still about double those from Eqs. (10) and (11).

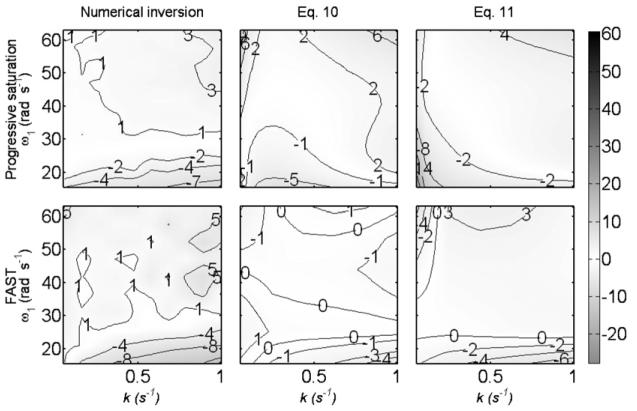
The errors in k for the conventional, the HS, and the KM formulae as a function of k and ω₁ at T_1A = 6 s and M_0A/M_0B = 1.5, are shown in Fig. 1. Of the pre-existing Eqs. (3)-(5), KM fares best for progressive saturation, but for FAST, the conventional Eq. (3) is better than Eqs. (4) and (5) over the parameter space. Plots of the errors after applying the numerical inversion method and the correction formulae in Eqs. (10) and (11) are shown in Fig. 4 for the same parameters. Compared to Fig. 1, Fig. 4 shows a major improvement in accuracy using any of the three proposed corrections.

Fig. 4.

Percent error in the estimated value of the reaction rate constant k for ³¹P-simulated saturation-transfer experiments of the CK reaction using the standard progressive-saturation method and the FAST method as a function of ω₁ and k. The value of k is calculated using the numerical inversion method, Eqs. (10) and (11) for T_1A = 6 s and M_0A/M_0B = 1.5. Errors are depicted both as contours and by the same gray scale used in Fig. 1.

Table 5 also shows that the errors over the physiological range 0.1 ⩽ k ⩽ 0.5 are smaller, although the reduction in error is not the same for all methods. The conventional formula provides significantly improved k estimation both in terms of bias and scatter, over the reduced range. This is mainly due to large errors at the very low and the very high values of k evident in Fig. 1. The KM formula, the numerical inversion method and Eqs. (10) and (11) show a moderate reduction in the scatter of error, while the HS formula shows the least improvement. Both Eqs. (10) and (11) retain their superior performance over the physiologic range of k in the human heart.

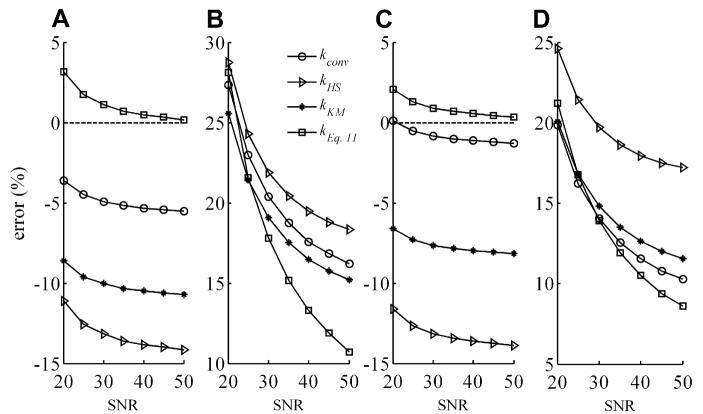
The results of the Monte Carlo analysis are plotted in Fig. 5. These show that the new Eq. (11) performs better than prior correction methods in the presence of noise, and that use of k_conv appears to be a better option than k_HS and k_KM, at least over the physiological range, 0.1 ⩽ k ⩽ 0.5.

Fig. 5.

Percent mean error or bias (A,C) and scatter in the error or SD (B,D) in the estimated value of the reaction rate constant k for simulated ³¹P FAST experiments of the CK reaction as a function of the SNR levels for the PCr signal in the 15° γ-ATP-saturation experiment, as determined by a 100-run Monte Carlo simulation. The value of k over both the wide range (0.05 ⩽ k ⩽ 1.0; (A,B); k_{Eq. (11)} using FAST coefficients from Table 4), and the more restrictive physiological range (0.1 ⩽ k ⩽ 0.5; (C,D); k_{Eq. (11)} using FAST* coefficients), was sampled by 6 points, as were T_1A, ω₁, and M_0A/M_0B over the ranges listed in Table 2. For each run, the mean error in k was calculated for the 6⁴ combinations of variables in the range, and the mean and SD error for the 100 runs reported.

4.2. Effect on experimental data

The forward reaction rate constants k, calculated from the different correction formulae as applied to healthy subjects, are listed in Table 6. These are the mean k from all subjects, after averaging the slices for each subject. With the Q > 1 data excluded, the correction provided by Eq. (11) results in a 6% higher estimate of k compared with the conventional formula (0.36 s⁻¹ vs. 0.34 s⁻¹). Both the HS and the KM formulae yield lower values than the conventional formula (0.31 and 0.32 s⁻¹ vs 0.34 s⁻¹), consistent with that seen previously in muscle [7] and in simulations [13]. These differences are all statistically significant (Table 6). The mean k values computed with Eq. (11) are not significantly affected by including data with Q > 1 either as is, or after setting measured Q values that are greater than one, equal to one.

Table 6.

Effect of different correction formulae on experimental subject-averaged forward cardiac CK reaction rates k (means ± SD) in normal subjects

Correction method	k for Q ⩽ 1 only (n = 14)	k with Q set to 1 when Q >1 (n = 18)	k using actual Q (n = 18)
Conventional, Eq. (3)	0.34 ± 0.09	0.36 ± 0.07	0.36 ± 0.07
Horska–Spencer, Eq. (4)	0.31 ± 0.09a	0.33 ± 0.08b	0.34 ± 0.08
Kingsley–Monahan, Eq. (5)	0.32 ± 0.08a	0.34 ± 0.07b	0.34 ± 0.07b
Eq. (11) with FAST* coefficients	0.36 ± 0.10a	0.37 ± 0.08a	0.36 ± 0.08

^aP ⩽ 0.01 vs conventional data in same column (2-tailed paired t-test).

^bP ⩽ 0.05 vs conventional data in same column (2-tailed paired t-test).

The percentage adjustment to k_conv by the different correction formulae are plotted in Fig. 6 as a function of k_conv and Q, with the second-order best-fit lines overlaid. The corrections to k_conv by both the HS and the KM formulae depend significantly on the spillover factor, Q, while Eq. (11) depends less on Q, than on k_conv. This is consistent with Fig. 1 which shows that errors in k_conv depend more on k than on ω₁, for which Q is a proxy, as compared with k_HS and k_KM which are more sensitive to ω₁ (Fig. 1). Note that while use of Eq. (11) alters the mean values as noted above, the significant differences between heart disease patients and healthy subjects reported earlier [3,4], are preserved.

Fig. 6.

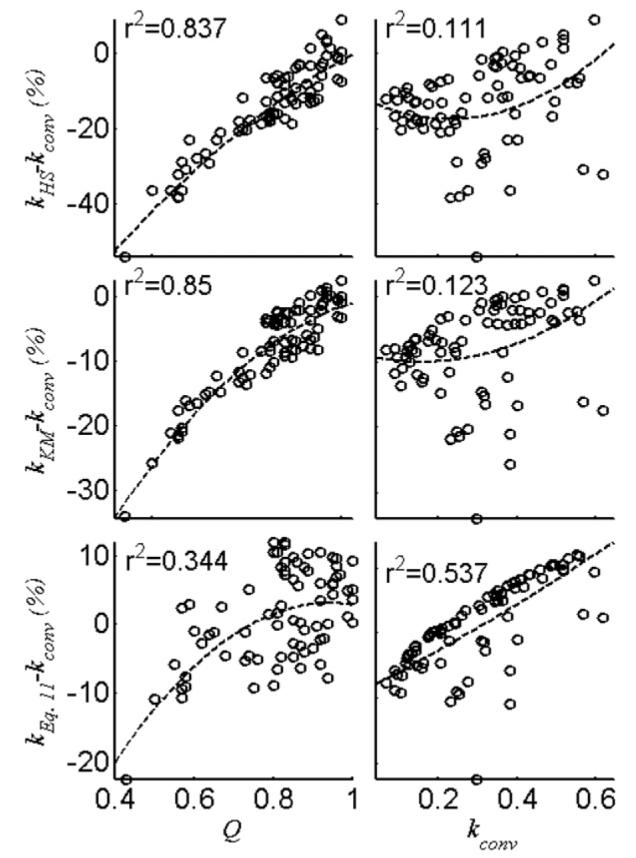
Percent adjustment made to k_conv by k_HS, k_KM and k_{Eq. (11)} (using FAST* coefficients from Table 4) as a function of Q and k_conv for the 113 individual slice FAST data from the 14 normal controls (38 spectra) and 34 patients (75 spectra) with Q ⩽ 1. Best-fit second-order curves are shown (dashed line) with the coefficient of determination, r².

5. Discussion

We have introduced three methods to correct the reaction rate constant for spillover irradiation effects. The simulations show that for the progressive saturation method, numerical solution of the BM equations performs best while for FAST, the formula in Eq. (10) performs best over the specified parameter space (Table 2). For the traditional formulae, k_conv, k_HS and k_KM, a large bias is evident (Table 5) and the worst errors are as large as 70%, 36% and 18% for the progressive saturation method, and as large as 40%, 34% and 27% for FAST, respectively. The new formulae show negligible bias and reduce the maximum errors by about 3-fold and the SD of the error by about 4-fold for both a progressive saturation/saturation transfer and a FAST experiment, over a wide range of parameters that are realistic for ³¹P MRS of the CK reaction in the heart, or even the brain, in vivo [20,21].

In FAST studies of CK flux in human hearts, the proposed correction in Eq. (11) produces mean k values that are 6% higher than those of the conventional formula, and 13–16% higher than the KM and the HS formulae, which have been applied in the past (Table 6). Indeed, Table 6 shows that for these cardiac studies, using the conventional formula may be more accurate than using either the HS or the KM formulae. Both the HS and KM formulae are more sensitive than the conventional formula to the spillover extent (ω₁) for FAST (Fig. 1). The KM formula outperforms the conventional formula for a conventional saturation-transfer/progressive-saturation experiment for which it is intended. The correction provided in Eq. (11), while relatively small (Table 6), is nevertheless significant for the assessment of CK ATP energy supply in absolute terms, which, in turn, is important for comparisons among various disease states from different studies as well as comparisons of this metabolic rate with other metabolic rates [3,4].

The first correction method investigated here, the numerical solution of the BM equations, has the potential to estimate all of the variables in a chemically exchanging system and to provide better estimates for k than existing approaches (Table 5). However, for FAST, the numerical inversion method performs worse than the corrections provided by Eqs. (10) and (11). This is because the numerical inversion jointly estimates all of the relaxation and concentrations of the two exchanging sites in addition to the reaction rate constant. The joint estimation is numerically more sensitive, especially when the number of measurements is as small as in FAST (eight measurements). This problem could be ameliorated by collecting more measurements and/or by measuring rather than estimating some of the parameters. However, both of these solutions are not really practical due to the limited scan time of patient studies, and the low SNR endemic to localized ³¹P MRS. In addition, both the numerical inversion method and Eq. (10), require measurements of ω₁, which, as noted, is not easily determined if the saturating field is non-uniform, such as with surface coils. This prompted our introduction of Q as a practical, measurable proxy.

The proposed correction in Eq. (11) accounts for variations in k and Q, which are the largest contributors to the error in k computed from the conventional formula. However, it is straightforward to extend the correction function to include other variables. For example, changes in TR which were not considered here because TR is fixed or known, can easily be added to Eq. (11). Note also that while Eq. (11) successfully reduces the error in k, the P_Q term in the correction factor does not vanish and the formula does not reduce to the conventional formula (Eq. (1)) when spillover vanishes (Q = 1), even though the difference is relatively small. This is because there will always be some degree of incomplete saturation if spillover is minimized for the ³¹P CK experiment at 1.5 T. In this case, the conventional formula is still an approximation that neglects the systematic error resulting from ignoring chemical exchange during the control experiment (quantified by the P_k term). It must also be remembered that optimization of the correction polynomials is performed for specific ranges of saturating field strength (15 ⩽ ω₁ ⩽ 63 rad s⁻¹) and frequency separation (440 rad s⁻¹ between PCr and γ-ATP at 1.5 T). In this regime, optimization of the saturation pulse is a difficult balance between incomplete saturation and excessive spillover, the effect of which is manifest in the range of empirical values seen in Q in Fig. 6.

The ³¹P MRS simulations and experiments in this work focus on the CK reaction, which is of interest to in vivo studies as a source of cellular energy and as a buffer to maintain ATP and ADP relatively constant [1-4]. While we provide an analysis of a conventional saturation-transfer experiment, in practice we have found that, to date, only the FAST protocol is efficient enough for performing spatially localized human cardiac studies within tolerable scan times at 1.5 T [4,7]. Even so, both scan-time and SNR are at a premium in such studies, and the accuracy of the calculation of k would certainly improve if more measurements and/or data with better SNR could be practically acquired. Indeed, there are alternative methods of measuring reaction rates such as 1D or 2D exchange spectroscopy (EXSY) [10,22-24] that do not use chemical-selective irradiation and hence do not suffer from spillover effects. However, combining 1D spatially localized in vivo ³¹P MRS with 1D or 2D EXSY, leads to impractical patient scan times, especially where fully-relaxed acquisitions are required [10], these being avoided by FAST. For saturation-transfer methods, the correction approaches described herein can be extended to proton spectra, other field strengths, and other protocols, requiring only re-calculation of the polynomial fitting coefficients for the new range of fitting parameters and available measurements.

In conclusion, we have introduced new solutions to the problems of irradiation spillover during the saturation-transfer experiment. These solutions provide corrections that significantly reduce errors in the calculated forward reaction rate constants in the practical implementation of ³¹P MRS to measure CK reaction kinetics, and can be developed for other reaction systems as well.