Modelling of the regulation of the hilA promoter of type three secretion system of Salmonella enterica serovar Typhimurium

Abstract

One of the most common modes of secretion of toxins in gram-negative bacteria is via the type three secretion system (TTSS), which enables the toxins to be specifically exported into the host cell. The hilA gene product is a key regulator of the expression of the TTSS located on the pathogenicity island (SPI-1) of Salmonella enterica serovar Typhimurium. It has been proposed earlier that the regulation of HilA expression is via a complex feedforward loop involving the transactivators HilD, HilC and RtsA. In this paper, we have constructed a mathematical model of regulation of hilA-promoter by all the three activators using two feedforward loops. We have modified the model to include additional complexities in regulation such as the proposed positive feedback and cross regulations of the three transactivators. Results of the various models indicate that the basic model involving two Type I coherent feedforward loops with an OR gate is sufficient to explain the published experimental observations. We also discuss two scenarios where the regulation can occur via monomers or heterodimers of the transactivators and propose experiments that can be performed to distinguish the two modes of regulator function.

Electronic supplementary material

The online version of this article (doi:10.1007/s11693-007-9009-5) contains supplementary material, which is available to authorized users.

Introduction

The virulence of several pathogens is determined by the secretion of toxins, which help in the establishment and propagation of disease in the host (Hueck 1998; Cornelis 2000). One of the most common modes of secretion of toxins in gram-negative bacteria is via the type three secretion system (TTSS), which enables the toxins to be specifically exported into the host cell (Mota et al. 2005).

The TTSS consists of a set of tightly regulated proteins including structural, regulatory and enzymatic proteins that are found to be critical for the invasion process. The TTSS is generally present in Pathogenicity Islands, which are compositionally distinct regions in the genome (Rajan et al. 2007). The genes encoding the structural elements of the TTSS are relatively well conserved among several species of pathogenic bacteria although they are regulated in unique ways to suit the needs of different bacteria (Hueck 1998; Winstanley and Hart 2001). Thus, a study of the regulatory mechanisms governing the TTSS of each pathogen may aid in understanding the dynamics of TTSS in the context of the environmental niche in which that particular organism is found.

Salmonella enterica serovar Typhimurium causes gastroenteritis in humans and a typhoid like disease in mice. It has been studied extensively as a model organism due to the ease of genetic manipulation (Hansen-Wester and Hensel 2001). The organism shows two distinct stages in infection process, the first being entry into the host via the intestinal epithelium followed by dissemination into host organs via entry and survival in the macrophages. The pathogen is known to possess two TTSS located on two distinct pathogenicity islands (SPI-1 and SPI-2), which are regulated hierarchically such that each system is turned on at a specific time. Both the secretion systems are essential for the virulence of the pathogen in the natural environment, although, each is required at different stages of the infection process. The first one, located on SPI-1 is required for the process of invasion via the intestinal epithelium and the second is required for survival in the macrophages (Lucas and Lee 2000; Marcus et al. 2000).

The SPI-1 consists of 39 genes encoding TTSS structural proteins, effector proteins and regulatory proteins (Hansen-Wester and Hensel 2001). The TTSS encoded by SPI-1 is regulated in a particularly complex fashion, and responds to several environmental and physiological signals, which are integrated to control the secretion of the effector proteins (Altier 2005; Jones 2005; Ellermeier and Slauch 2007).

The remarkable feature of regulation of the TTSS located on SPI-1 is that most of the varied signals that regulate the system impinge on a central regulator, HilA. Deletion studies have shown that the deletion of hilA is phenotypically equivalent to the deletion of the entire TTSS on SPI-1 (Ellermeier et al. 2005). It is thought that the expression of HilA is primarily regulated at the level of transcription (Rodriguez et al. 2002). Transcription from the hilA promoter is in turn mainly regulated by three transcription factors; HilD, HilC and RtsA, which in a complex arrangement of feedback and feedforward loops bring about maximal induction of HilA (Altier 2005; Jones 2005; Ellermeier and Slauch 2007). Of these regulators, HilD can be considered as the most important single regulator of the hilA promoter (P_hilA) since the hilD knockout strain shows nearly basal levels of HilA under inducing conditions (Lucas and Lee 2001; Boddicker et al. 2003; Ellermeier et al. 2005). The HilD protein is considered to be regulated mainly at the post-transcriptional level, with several factors controlling the stability of its mRNA (Lawhon et al. 2003; Fortune et al. 2006) and little control at the level of transcription. HilD controls the other regulators HilC and RtsA transcriptionally to some extent since the hilD knockout shows reduced expression levels of these proteins (Ellermeier et al. 2005).

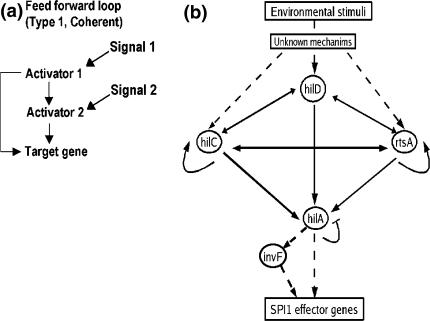
Recently, a model for the regulation of P_hilA expression has been proposed, which takes into consideration several of these complexities in the regulation of P_hilA. This model is based on the feedforward loop architecture proposed by Mangan et al. (2003) with several additional feedbacks and cross regulations (Ellermeier et al. 2005; Ellermeier and Slauch 2007). According to Mangan and Alon (2003), the feedforward loop is a three gene motif, composed of two transcription factors, one of which regulates the other, and both of which jointly regulate the target gene, which itself can be a transcription factor. A cartoon representation of one type of feedforward loop is shown in Fig. 1(a). Feedforward loops where all the regulatory interactions are activations, as in the case of the one considered here are classified as Type I Coherent. Such coherent feedforward loops show slow switching on and rapid switching off response to the presence and absence of input signal (Mangan et al. 2003).

Fig. 1.

(a) Cartoon representation of a Type 1 coherent feedforward loop where all the regulatory interactions are activations and (b) The network of regulatory interactions controlling the hilA promoter (P_hilA). The different transcription factors involved in the regulation are shown in circles, arrows represent activations, while the blunt ended line represents repression. Solid lines show the interactions, which have been considered in the models in this paper, while the other interactions are shown by dotted lines

We have used this to construct a simple mathematical model of P_hilA regulation and have compared our theoretical results to the existing experimental evidence. To the best of our knowledge, this is the first attempt to construct a mathematical model of the regulation of the Salmonella SPI-1 genes.

Methods

Setting up of the model

We started with a basic model of the regulation of the hilA promoter and progressively added more details to this model to represent the complex regulations of the hilA promoter. The various interactions considered in this paper are shown in Fig. 1(b). The basic model has the following features:

• The feedforward loop architecture described above (Fig. 1a) was modified to allow for three inputs (HilD, HilC and RtsA) to act on the hilA promoter rather than two.

• HilD was considered as the primary activator of the feedforward loop based on experimental evidence. HilD is considered to activate HilC, RtsA and HilA directly (Ellermeier et al. 2005; Ellermeier and Slauch 2007).

• HilC and RtsA were also considered to activate HilA directly (Ellermeier et al. 2005).

• HilA was considered to negatively regulate itself (De Keersmaecker et al. 2005).

• For the sake of simplicity, we did not consider any regulation on HilD. We assumed that the signal for induction of the SPI-1 is transmitted exclusively via HilD such that the presence or absence of the signal correlates with the presence or absence of HilD.

In the alternate models, the following differences were considered (Fig. 2):

• Activation of P_hilA can be achieved by AND or OR gate logic. In an AND gate, the output (i.e., transcription from the P_hilA) is a multiplicative function of the different inputs (i.e. the different activators, namely, HilD, HilC and RtsA). This means that transcription would occur only if all the activators simultaneously bind to and activate the promoter. In an OR gate, the output is an additive function of the inputs. This implies that each activator can activate the promoter to a different extent and maximal promoter activity would occur when all activators bind to and activate the promoter.

• The transcription factors, HilD, HilC and RtsA can function as monomers or homodimers or heterodimers (in combination) to bring about activation of P_hilA. This possibility was suggested since the binding sites for the different activators on the P_hilA promoter overlap (Olekhnovich and Kadner 2002). In the case of heterodimer binding, we have assumed that the three transactivators can bind in all possible combinations of dimers i.e. as HilD-HilC, HilD-RtsA and HilC-RtsA.

• Auto-activation of RtsA and HilC as well as the activation of RtsA by HilC and vice versa was considered in some models.

Fig. 2.

The different models constructed

The different models constructed

If [HilD], [HilC], [HilA] and [RtsA] represent the protein levels of the corresponding transactivators, then the three equations for the basic model are as follows:

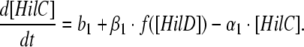In other words, the rate of change of HilC concentration depends on its basal synthesis (b₁; which is a constant) as well as on its activation by HilD and its own degradation rate (α₁).

Similarly, the rate of change of RtsA concentration depends on its basal synthesis (b₂; which is a constant) as well as on activation by HilD and its own degradation rate (α₂) and can be represented as:

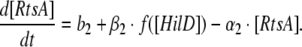Finally, the rate of change of HilA concentration is dependent on its basal synthesis (b₃; which is a constant), activation by the three transactivators (HilD, HilC and RtsA), autorepression as well as its own degradation rate (α₃). This is represented by the following equation:

In all the above equations, [HilD] can be either 1 or 0, depending on the presence or absence of the signal for induction, b₁, b₂ and b₃ are the basal rates of synthesis of HilC, RtsA and HilA respectively, β₁, β₂ and β₃ are amplification factors which can be thought of as analogous to translation, α₁, α₂ and α₃ and are the rates of degradation of HilC, RtsA and HilA respectively.

Using this basic model, five versions were constructed to study the regulation of P_hilAas shown in Fig. 2.

Model 1: Two feedforward loops with AND gate logic for regulation of P_hilA by HilD, HilC and RtsA

In this case, the input function for HilA expression is a multiplicative function of the three regulations as follows:

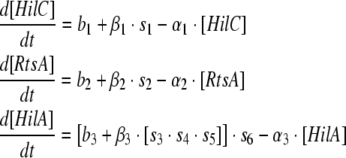Model 1

Thus, the rate of change of HilA concentration is a multiplicative function of the three inputs i.e. transactivators, HilD, HilC and RtsA via the functions s₃, s₄, and s₅, respectively.

In the above equations, s₁ to s₅ represent activation functions of the form

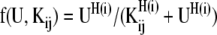where K_ij is the threshold of activation of the gene j by the transcription factor i and H(i) is the Hill co-efficient of the interaction of the transcription factor with the promoter and U is any of HilD, HilC, RtsA or HilA.

s₆ is the function for negative feedback of HilA on the P_hilAand is of the form

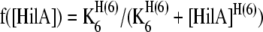where H(6) is the Hill co-efficient of the repression and K₆ is the threshold of the repression function.

Model 2: Two feedforward loops with OR gate logic for regulation of P_hilA by HilD, HilC and RtsA (monomer activation)

In this case, the rate of change of HilA concentration is a additive function of the three input transactivators via the functions s₃, s₄ and s₅ corresponding to HilD, HilC and RtsA respectively and is represented as:

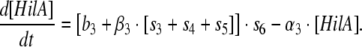Model 2

If Hill coefficients of all the activators are set to 2, the model generated represents the activation of P_hilA by homodimers.

Model 3: Two feedforward loops with OR gate model for regulation of P_hilA by monomers of HilD, HilC and RtsA and addition of positive feedback on RtsA and HilC as well as cross activations of RtsA on HilC and vice versa

The equations for this model are as follows:

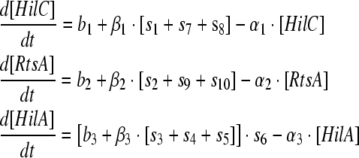Model 3

where functions s₇ and s₉ represent the auto-activation of HilC and RtsA respectively and functions s₈ and s₁₀ represent the cross activation of HilC by RtsA and vice versa respectively. These functions are also of the same form as the functions s₁ to s₅ described above.

Model 4: Two feedforward loops with OR gate model of regulation of P_hilA by heterodimers of HilC-HilD, HilC-RtsA and HilD-RtsA

In this case functions s₃, s₄ and s₅ are modified as follows:

This corresponds to activation via the heterodimeric complex of HilC and HilD with co-operativity H3 and threshold of activation K₃.

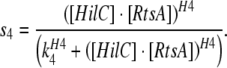This corresponds to activation via the heterodimeric complex of HilC and RtsA with cooperativity H4 and threshold of activation K₄.

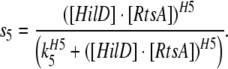Model 4

This corresponds to activation via the heterodimeric complex of HilD and RtsA with cooperativity H5 and threshold of activation K_5.

For the activation by the heterodimers, we have assumed that the rate of formation of the dimer complex is instantaneous and that the reverse reaction of the dissociation of the complex into the monomers is negligible so that concentration of the dimer is proportional to the concentration of the monomers.

Model 5: Two feedforward loops with OR gate model of regulation of P_hilA by heterodimers of HilC-HilD, HilC-RtsA and HilD-RtsA and additional positive feedback on RtsA and HilC as well as cross activations of RtsA on HilC and vice versa

This is of the same form as Model 3, except that the functions s₃, s₄ and s₅ are of the type considered in Model 4.

Parameter estimation

Following Mangan et al. (2003), the values of different parameters were set as follows:

The binding affinities of all the transcription factors (K_i) were assumed to be 0.5, while all the interactions were assumed to be non co-operative so that all the H(i) values were 1. The basal level production of the different proteins b_i was set to 0, while the amplification factor, β_i and the rate of degradation of the different proteins α_i were set to 1.

In the case of HilD, following changes were made to the parameters to reflect the fact that HilD has the maximum effect on the regulation of P_hilA.

K₃ = Binding affinity of HilD for P_hilA = 0.1

H3 = Hill co-efficient for the co-operativity of the interaction of HilD with P_hilA = 2

In the case of the heterodimer models (Model 4 and 5), the parameters K₃ and H3 represent the binding affinity and Hill-coefficient of the HilD-HilC heterodimer respectively.

In all the models, b₃ = Basal rate of production of HilA = 0.5 and the initial concentration of HilD was 1, which was set to 0 at a defined time point during the course of the simulation.

Simulation

All the simulations were carried out with XPP-AUT, freely available software for the simulation of systems of differential equations (http://www.math.pitt.edu/~bard/xpp/xpp.html). The equations were integrated using the Runge-Kutta fourth order algorithm available in this package, with a step size of 0.001. The data was subsequently re-plotted using Excel to generate the graphs shown in this paper.

Results and discussion

Basal behaviour of the different models

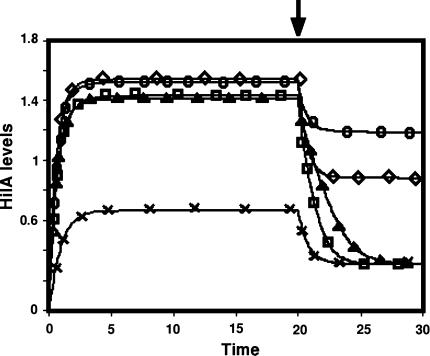
In order to assess the different models, we started with their behaviour under basal parameter values to represent the dynamics of HilA in the wild type (WT) Salmonella. As seen from Fig. 3, all the models showed a somewhat slow increase to steady state levels of HilA in the presence of the induction signal, HilD. When the signal (HilD) was turned off, the models showed a rapid decline to the new steady state level. This behaviour is as expected from a Type I coherent feedforward loop (Mangan et al. 2003).

Fig. 3.

The kinetics of HilA protein The basal behaviour of the five models. At the time point indicated by the arrow, the HilD level was set to 0. (×, Model 1; Δ, Model 2; ○, Model 3; □, Model 4; and ◊, Model 5). The X-axis shows the time in arbitrary units while the Y-axis shows the level of HilA in arbitrary units

Comparison of P_hilA regulation by AND and OR architectures involving three activators (HilD, HilC and RtsA)

We began our investigation of the regulation of P_hilA by comparing two basic architectures that could be present in the feedforward loop, namely the AND and the OR gates using Model 1 and Model 2. In both models, the regulation was considered to be via the action of monomeric activators (HilD, HilC and RtsA). The effect of different mutations on the dynamics of HilA expression was compared using numerical and experimental results. In the Model simulations, we set different parameters to 0 (given in Supplementary Table 1) to mimic the effect of knockouts of the corresponding genes and compared these to the experimentally determined effect of the knockouts.

To describe the simulation results, we used two parameters (See Supplementary Fig. 1). The first (Relative Expression, R.E.) is the ratio of the HilA expression in the mutant to that in the WT (obtained numerically). This is compared to the ratio of β-galactosidase produced from a hilA-lacZ fusion in the corresponding mutant strain to that in the WT. The second is a qualitative parameter, (Response to HilD, R.H.) describing whether a given mutant shows any response to the HilD signal. We have compared this parameter to the experimentally determined virulence of the corresponding strain. The virulence of the different mutants was determined experimentally by competition assays against the ΔhilC ΔhilD ΔrtsA triple mutant, which can be considered to be avirulent since its virulence is similar to that of the ΔhilA strain (Ellermeier et al. 2005).

As can be seen from Table 1, Model 1 (AND gate) failed to capture the effect of the different mutants on HilA expression levels since it predicted decrease to basal activity irrespective of which regulator was mutated. This is as per the logic of the AND gate, where activation can occur only when all activators are simultaneously present. On the other hand, the results of the OR gate model (Model 2) showed a better fit to the experimental data. Here, as in the case of the experiments, deletion of hilC or rtsA singly led to a decrease in the HilA levels, whereas deletion of hilD singly or in combination with the other activators caused HilA levels to decline to basal. In case of the ΔhilC ΔrtsA mutant, the model predicted a high level of HilA as well as a continued response to HilD, while experimental results indicated earlier that this mutant expresses low levels of HilA (i.e., β-galactosidase from the lacZ-hilA fusion) and is avirulent. Hence, this model probably did not represent the regulation of P_hilA. However, at this stage this model cannot be ruled out since it is possible that the level of HilA falls below the threshold required for activation of its downstream targets.

Table 1.

Comparison of the results from the different models studied

Condition		Model 1		Model 2		Model 3		Model 4		Model 5		Experimental
		RE	RH	RE	RH	RE	RH	RE	RH	RE	RH	RE	Virulence
1.	WT	1	Y	1	Y	1	Y	1	Y	1	Y	1	Y
2.	ΔhilD	0.52	N	0.22	N	0.79	N	0.21	N	0.58	N	0.3	N
3.	ΔhilC	0.52	N	0.83	Y	0.8	Y	0.54	Y	0.54	Y	0.4	Y
4.	ΔrtsA	0.52	N	0.83	Y	0.8	Y	0.62	Y	0.59	Y	0.7	Y
5.	ΔhilD ΔhilC	0.52	N	0.24	Nd	0.51	N	0.21	N	0.2	N	0.2	NA
6.	ΔhilD ΔrtsA	0.52	N	0.24	Nd	0.51	N	0.21	N	0.2	N	0.25	NA
7.	ΔhilC ΔrtsA	0.52	N	0.63	Y	0.59	Y	0.21	N	0.2	N	0.35	N
8.	ΔhilC ΔhilD ΔrtsA	0.52	N	0.22	N	0.2	N	0.21	N	0.2	N	0.2	N

RE = Relative Expression levels

In the case of the numerical simulations, the ratio of the steady state (in the presence of signal) in the mutant to that in the Wild Type is taken

In the case of experimental results, the ratio of β-galactosidase produced from a hilA-lacZ fusion in the mutant strain to that in the WT is taken

RH = Response to HilD

If the particular mutant shows an amplification of HilA in response to the presence of the signal, then it is taken as Y otherwise as N

N^d, A small pulse of HilA is seen in response to the signal (see Supplementary Fig. 2 for different types of dynamics exhibited by the models)

NA, Data not available on the virulence of these strains. However, since hilD is also knocked out in these strains, they may be considered avirulent

Virulence - In the experimental results, if the particular mutant showed significantly better virulence as compared to the triple mutant in oral competition experiments, then it is taken as Y, otherwise as N. (The triple mutant was compared to the ΔhilA mutant and shown to be phenotypically similar to it, Ellermeier et al. 2005)

Different modifications of the OR gate model were therefore created to explain the experimental data more convincingly.

Studies on regulation of P_hilAby different types of OR-gate architectures involving three activators (HilD, HilC and RtsA)

It has been suggested earlier that P_hilA may be activated by heterodimers of the three activators instead of by monomers (Ellermeier et al. 2005). Model 4 was constructed to take into account this possibility. HilC and RtsA are thought to activate themselves (positive feedback) as well each other (cross activation) in addition to their effect on HilD. The significance of these interactions, however, is not yet proven (Ellermeier et al. 2005; Ellermeier and Slauch 2003). To check if these interactions could influence the dynamics of the model, we included these interactions in Models 2 and 4 to get Models 3 and 5 respectively.

Regulation of P_hilA by monomeric activators model with additional regulations (Model 3)

Comparison of the results of Models 2 and 3 (shown in Table 1), indicated that the response to HilD did not change qualitatively due to the additional feedback loops and cross activations. However, Model 3 showed a higher level of HilA even in the absence of HilD induction than the simpler model. This is probably due to the additional regulations considered in this model, whereby HilC and RtsA were amplified even in the absence of HilD. The complete deletion of all the three activators led to identical behaviour as compared to Model 2.

Regulation of P_hilAby heterodimers of activators (Models 4 and 5)

In these models (Models 4 and 5), the co-operativity of the HilC-HilD heterodimer alone was considered to be 2, since HilC and HilD are thought to affect HilA expression more than RtsA. As seen from Table 1, the additional regulations did not qualitatively affect the response to HilD, although the basal expression level in the absence of HilD was greater.

Comparison of models of P_hilAregulation by monomers or heterodimers of activators

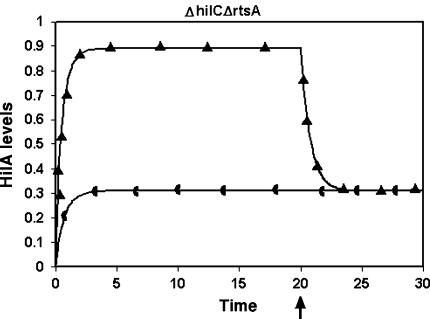
It is not yet known whether the regulation of P_hilA occurs via the formation of heterodimers or monomers/homodimers of the activators. Therefore, Models 2 and 4 were compared with respect to effect of different mutations on the dynamics of HilA. As can be seen from Table 1, the two models differed only in the effect of the ΔhilC ΔrtsA double mutant. The heterodimer model (Model 4) showed no response to HilD in this mutant and the levels of HilA were basal, whereas there was a response to HilD in the monomer model (Model 2), although it was not at wild type levels. From the experimental results, we can see that this double mutant is not virulent. However, this does not indicate which of the two models is right since it is likely that the HilA expression falls below the threshold required for the activation of the SPI-1 genes in both cases, thus leading to the avirulent phenotype seen in the mutant. This can be resolved experimentally by determining the dynamics of HilA expression in the double mutant and comparing it to the triple mutant since the predicted dynamics of the double mutant was dramatically different in the two models (Fig. 4). In the heterodimer model, the ΔhilC ΔrtsA mutant as well as the triple mutant showed similar dynamics whereas in the monomer model, the ΔhilC ΔrtsA mutant and the triple mutant showed very different dynamics.

Fig. 4.

The dynamics of the ΔhilC ΔrtsA double mutant as predicted by Model 2 (▲) and Model 4 (◖). The arrow indicates the time point at which HilD is removed. The X-axis shows the time in arbitrary units while the Y-axis shows the level of HilA in arbitrary units

Conclusion

In the work presented here, we have constructed a simple model of the regulation of type three secretion system present on SPI-1 pathogenicity island of Salmonella enterica serovar Typhiumurium, beginning with a generic model of a coherent feedforward loop and have tried out alternative models to explain the experimental data. Through comparison of numerical results with experimentally observed data, we arrived at two models that are simple and yet sufficient to explain the experimental results obtained so far. We have also suggested an experiment that could help in resolving the question of whether the regulation of P_hilA occurs via the formation of monomers/homodimers as opposed to formation of heterodimers.

We have also tried to determine if the postulated positive feedback of RtsA and HilC as well as their cross activations affect the dynamics of our models. Our results indicate that these additional complexities do not affect the behaviour of the models qualitatively. However, at this stage, we cannot rule out the possible significance of these interactions in controlling the dynamics of HilA since it is possible that both HilC and RtsA are regulated in more complex ways than considered here. In the ΔhilD strain neither HilC nor RtsA expression is reduced to basal levels (Ellermeier et al. 2005). Hence, it is possible that HilC and RtsA could be activated independently of HilD, by other, as yet unknown regulators (for e.g, oxygen regulation as suggested in Ellermeier et al. 2005). This activation may then be amplified by the cross regulations and positive feedback, leading to expression of P_hilA. These additional regulations would have to be taken into account in future models to get a clearer picture regarding the significance of the cross activations and positive feedback.

In our models, we have also included the reported negative autoregulation of HilA although it does not affect the dynamics of the models qualitatively. In this network, it appears that several interactions (such as the positive feedback, the cross activations or the negative feedback) do not directly affect the qualitative dynamics of the target. However, they may still play significant roles in the transient dynamics of the network i.e., the dynamics immediately upon receiving the signal. For example, negative autoregulation is known to decrease the time taken to reach a steady state (Rosenfeld et al. 2002). Similarly, positive feedback can act in the opposite manner and delay the time to reach a steady state (Maeda and Sano 2006). These modes of control can also affect the population dynamics, which could lead to differences between the individuals in the population (Becskei and Serrano 2000; Becskei et al. 2002). There have been few studies on the population distribution of the SPI-1 regulators and how this distribution changes over the course of invasion (Boddicker and Jones 2004). Such studies would also help to address questions pertaining to the effect of noise or stochasticity, which have been studied theoretically for this type of architecture (Ghosh et al. 2005).

Future work can also take into account the differential binding affinities of HilD and HilC on the hilA promoter as shown by Olekhnovich and Kadner (2002) and include the regulation of HilC and HilD by CsrA/B as demonstrated by Lawhon et al. (2003) and Fortune et al. (2006) to get a better picture of the complex interactions involved in the regulation of P_hilA. Our model provides a basis for understanding the complex regulation of P_hilA and can form the nucleus for further efforts in this direction.

Summary

The HilA protein is a crucial regulator of the SPI-1 pathogenicity island of Salmonella enterica serovar Typhimurium, which is controlled by a complex network of regulators. We have created a mathematical model of the regulation of this promoter, which is able to explain the reported experimental results and suggested experiments to distinguish different modes of regulation of this promoter.

Abbreviations

SPI-1

Salmonella pathogenicity island-1

TTSS

Type three secretion system

WT

Wild type