Using Perturbation Theory to Compute the Morphological Similarity of Diffusion Tensors

Abstract

Computing the morphological similarity of Diffusion Tensors (DTs) at neighboring voxels within a DT image, or at corresponding locations across different DT images, is a fundamental and ubiquitous operation in the post-processing of DT images. The morphological similarity of DTs typically has been computed using either the Principal Directions (PDs) of DTs (i.e., the direction along which water molecules diffuse preferentially) or their tensor elements. Although comparing PDs allows the similarity of one morphological feature of DTs to be visualized directly in eigenspace, this method takes into account only a single eigenvector, and it is therefore sensitive to the presence of noise in the images that can introduce error into the estimation of that vector. Although comparing tensor elements, rather than PDs, is comparatively more robust to the effects of noise, the individual elements of a given tensor do not directly reflect the diffusion properties of water molecules. We propose a measure for computing the morphological similarity of DTs that uses both their eigenvalues and eigenvectors, and that also accounts for the noise levels present in DT images. Our measure presupposes that DTs in a homogeneous region within or across DT images are random perturbations of one another in the presence of noise. The similarity values that are computed using our method are smooth (in the sense that small changes in eigenvalues and eigenvectors cause only small changes in similarity), and they are symmetric when differences in eigenvalues and eigenvectors are also symmetric. In addition, our method does not presuppose that the corresponding eigenvectors across two DTs have been identified accurately, an assumption that is problematic in the presence of noise. Because we compute the similarity between DTs using their eigenspace components, our similarity measure relates directly to both the magnitude and the direction of the diffusion of water molecules. The favorable performance characteristics of our measure offer the prospect of substantially improving additional post-processing operations that are commonly performed on DTI datasets, such as image segmentation, fiber tracking, noise filtering, and spatial normalization.

1 Introduction

Diffusion Tensor (DT) Magnetic Resonance Imaging (MRI) quantitatively measures the diffusivity of free water molecules in different directions within the human brain [1]. Whereas free water diffuses equally in all directions, the presence of cell membranes or cellular organelles within axons, or myelin sheaths surrounding them, will restrict the diffusion of water molecules in directions perpendicular to the long axis of a nerve fiber, particularly in myelinated axons within white matter of the brain. Thus by tracking the principal direction of the diffusion of water molecules, we can track the direction of fiber bundles along the length of axons in white matter. Diffusion is quantitatively estimated from a series of Diffusion-Weighted Images (DWIs) that are acquired using diffusion-sensitizing MRI gradients applied in multiple directions (ranging 6 to 51) [2]. Once estimated, diffusion is represented by a symmetric 3 × 3 Diffusion Tensor (DT), H, which encodes both the magnitude and direction of diffusion [1, 3]. A DT image defines a tensor at each voxel within the image. Therefore, analytic operations (including, for example, reconstruction of fiber tracts, removal of noise from images, and comparison of fiber tracts across groups of subjects) require computation of the degree of similarity between the various diffusion properties of DTs at neighboring voxels within the image and across corresponding voxels of images from differing individuals. Computing the similarity of tensors is thus one of the most fundamental and important procedures in the postprocessing of DT images [4].

A number of methods have been proposed for computing the similarity between two DTs, including the tensor scalar product [5], the sum of squared scalar products between each pair of semi-major axes [1], the Euclidean distance metric [6], and the similarity of the Principal Directions (PDs) of diffusion [7]. The first three of these use individual tensor elements to compute the similarity between two tensors. Tensor elements, however, are only nonlinearly related to the features of greatest interest–eigenvalues and eigenvectors–that measure respectively the magnitude and direction, respectively, of the diffusion of water molecules. Changes in the diffusion properties of water molecules therefore will not be reflected by changes in the value of a similarity measure that is computed using tensor elements. In contrast, measures that compare tensors based on their principal eigenvectors do produce similarity values that vary with changes in the direction of diffusion. Because these measures exclude much of the information that defines tensors, however, including all of the eigenvalues and two of the eigenvectors of the tensors, they are highly susceptible to any error that noise introduces in the DT images when estimating the PDs. The PD of a DT therefore will not be defined clearly, for example, when noise in a DT perturbs its two largest eigenvalues whose values are similar. Thus a PD-based measure cannot compare tensors reliably, because noise will too often cause incorrect identification of their PDs.

The valid comparison of tensors using a similarity measure requires that changes in the measure are symmetric and smooth when changes in the corresponding diffusion properties of a water molecule are also symmetric and smooth. By symmetric we mean that the similarity measure between two tensors decreases for either an increase or a decrease in diffusion along a specified direction in one tensor, as well as for either a clockwise or counterclockwise rotation of the tensor. By smooth we mean that changes in the similarity measure will be small for small changes, or large for large changes, in the magnitude or direction of diffusion, and those changes in the similarity measure will be a differential function of change. The magnitude of similarity is unimportant, because similarity is computed within the context of a single image. Extant methods used to compute the similarity between two DTs thus far fail to satisfy either one or both of these symmetry and smoothness preconditions for the validity of the measures.

We propose a method for computing the similarity between two tensors at neighboring voxels that is based on perturbation theory [8, 9]. We model variations in tensors in a homogeneous region as perturbations of their neighbors. The similarity between two tensors can thus be computed from the conditional probabilities of the eigenvalues and eigenvectors of an unperturbed tensor, given the perturbations in the elements of the other tensor. Our method accounts for the effects of noise in DT images. Moreover, these measures vary symmetrically and smoothly with symmetric and smooth changes in the tensors. Because our method uses all the eigenspace components of two tensors to compute similarity, the similarity measure relates directly to the diffusional properties of water molecules within those tensors. Our method also obviates the need to establish an accurate correspondence between the eigenvectors of the two tensors when computing conditional probabilities for those eigenvectors.

2 Method

Our method computes the similarity between tensors within the context of DT images by accounting for noise in the tensor elements. DTs are most commonly reconstructed from noisy, gray-scale values in diffusion weighted images using the Stejskal and Tanner equation [10] together with least-squares estimation. Estimated tensor elements are therefore random variables. Assuming that noise in the tensor elements is Gaussian-distributed, the least-squares estimates are also the maximum likelihood estimates. We therefore estimate variance in the tensor elements from the least-squares procedure and then use the estimated variance to compute the probability of perturbations in the eigenvalues. Because variance in the tensor elements depends upon the amount of noise present in the image, our measure accounts for the presence of noise in DT images and its effects on tensor maps.

We compute the conditional probabilities of the eigenvectors of an unperturbed tensor, given the perturbed tensor, using the wavefunction renormalization constant from perturbation theory. Our formulation for computing these probabilities can be divided broadly into two categories those for either nondegenerate or degenerate tensors, depending on the eigenvalues of the unperturbed tensor. Nondegenerate analysis is used when each eigenvalue is unique; otherwise, degenerate analysis is used. To compute the probability of one tensor given the other, we assume that the eigenvalues and two eigenvectors of a tensor are independently distributed. (Although the eigenvalues of tensors are independently distributed, their eigenvectors are not independent, because specification of one eigenvector will restrict the remaining two to the 2D vector space that is orthogonal to the first. Nevertheless, one of the eigenvectors in the orthogonal space still has a large degree of freedom and can be oriented in any direction within the orthogonal space). Finally, we combine the conditional probabilities for the three eigenvalues and the two eigenvectors to compute the similarity of the two tensors.

2.1 Noise in Tensor Elements

2.1.1 The Stejskal and Tanner Equation

The Stejskal and Tanner equation [10] relates diffusion-weighted measurements S_b to non-diffusion-weighted measurements S₀ as:

$$S_b=S_{0}exp(-\sum _{i,j=1}^3{b}_{\mathit{ij}}{H}_{\mathit{ij}})+\eta ,$$ (1)

where η is noise in the measurements S_b, H_ij are the elements of a diffusion tensor H; and b_ij are the elements of a weighting matrix b given by $b_{\mathit{ij}}={\gamma }^2{G}_i{G}_j{\delta }^2(\mathrm{\Delta }-\frac{\delta }{3})$, where G_i is the amplitude of the gradient pulse in the i^th direction, δ is the pulse duration, Δ is the time interval between rising edges of the two pulses, and γ is the gyromagnetic ratio [2]. If a unit vector r = (r₁, r₂, r₃)^T denotes the direction in which a gradient is applied and $G_0={(G_1^2+G_2^2+G_3^2)}^{1/2}$ denotes the magnitude of the applied gradient, then G_i = r_iG₀, and $b_{\mathit{ij}}=r_i{r}_j{\gamma }^2{G}_0^2{\delta }^2(\mathrm{\Delta }-\frac{\delta }{3})$. Hence, trace tr(b) of the matrix b is given as $\mathit{tr}(b)={\gamma }^2{G}_0^2{\delta }^2(\mathrm{\Delta }-\frac{\delta }{3})$ [10]. Thus, with b_ij = r_ir_j tr(b), Eqn. (1) can be rewritten as:

$$S_b=S_{0}exp(-\mathit{tr}(b)r^T\mathit{Hr})+\eta .$$ (2)

2.1.2 Correction for the Rician Distribution

The voxel intensities within the brain, and therefore their noise η, are approximately Gaussian distributed, i.e., η ~ N (0, σ_η). If A_b is the voxel intensity in the absence of noise, then the probability distribution p(S_b) of the voxel intensity S_b follows a Rician distribution [11, 12, 13, 14, 15, 16], i.e.:

$$p(S_b)=\frac{S_b}{{\sigma }_{\eta }^2}exp[-\frac{S_b^2+A_b^2}{2{\sigma }_n^2}]I_0\left(\frac{A_b\cdot S_b}{{\sigma }_n^2}\right),$$ (3)

where I₀ (·) is the modified Bessel function of zeroth order. This distribution however, in the regions where the Signal-to-Noise Ratio (SNR) is greater than or equal to 3 [15], can be approximated with a Gaussian distribution of mean $\sqrt{A_b^2+{\sigma }_{\eta }^2}$ and variance ${\sigma }_{\eta }^2$, i.e.,

$$p(S_b)\approx \frac{1}{\sqrt{2\pi {\sigma }_{\eta }^2}}exp\left[-\frac{{\left(S_b-\sqrt{A_b^2+{\sigma }_{\eta }^2}\right)}^2}{2{\sigma }_{\eta }^2}\right]\cdot$$ (4)

In DW images from most MRI scanners, SNR is well above 3, and in the in vivo images used in the present study, SNR within the brain ranged from 5 to 10. Therefore, we used the Gaussian distribution (Eqn. 4) to approximate the noise η in the DW images.

We estimated ${\sigma }_{\eta }^2$ from the variance σ² of the intensities in the background of the image. Because the signal A_b is zero in the background, i.e. A_b = 0, the intensities S_b are Rayleigh distributed [17, 15]:

$$p(S_b)=\frac{S_b}{{\sigma }_{\eta }^2}exp\left[-\frac{S_b^2}{2{\sigma }_{\eta }^2}\right],$$ (5)

with mean $\mu ={\sigma }_{\eta }\sqrt{\pi /2}$ and variance ${\sigma }^2=(2-\pi /2){\sigma }_{\eta }^2$ [17]. We therefore estimated σ_η by computing the square of the mean (μ) of the background intensities [15], i.e.,

$${\sigma }_{\eta }^2=\frac{2}{\pi }{\mu }^2\cdot$$

2.2 Least-Squares Estimates

Taking the natural logarithm and using Taylor’s expansion, Eqn. (2) can be rewritten as:

$$ln(S_b)=ln(S_0)-\mathit{tr}(b)r^T\mathit{Hr}+\mathit{ϵ}$$ (6)

Where ϵ represents Gaussian-distributed noise with zero mean and variance ${\sigma }_{\mathit{ϵ}}^2=\frac{{\sigma }_{\eta }^2}{{\langle S_b\rangle }^2}$, i.e. ϵ ~ N (0, σ_ϵ), which depends upon the weighting matrix b [9]. However, in the procedure for the least-squares estimates of the tensor elements, the noise terms ϵ are assumed to be independently and identically distributed (i.i.d.) with equal variance (i.e., they are assumed to exhibit homoskedasticity) [18, 19]. We therefore compute the noise variance by averaging the variances for different weighting matrices. Furthermore, averaging also reduces the variability in the computed variance. For diffusion-weighted measurements S_b in a direction specified by the matrix b, Eqn. (6) can be written as

$$ln(S_b)=(1-b_{11}-b_{22}-b_{33}-2b_{12}-2b_{13}-2b_{23})\beta +\mathit{ϵ},$$ (7)

where β = (ln (S₀), H₁₁, H₁₂, H₁₃, H₂₂, H₂₃, H₃₃)^T is a vector of elements of the diffusion tensor H and S₀.

Let y denote the vector of the logarithm of diffusion-weighted measurements and B denote a matrix with rows of elements for each gradient direction. Eqn. (7) can then be written in matrix notation as y = Bβ + ϵ. The least-squares estimates β̂ of β are computed as β̂ = (B′B)⁻¹B′y, and the covariance matrix V ar(β ^) of β̂ is [18]:

$$\mathit{Var}(\widehat{\beta })={\sigma }_{\mathit{ϵ}}^2{(B\prime B)}^{-1}.$$ (8)

In the following analysis, we use the covariance matrix to V ar(β̂) to compute the conditional probability of the eigenvalues.

2.2.1 Heteroskedasticity Conditions

The noise values ϵ do not have equal variance for differing weighting matrices b, i.e., ϵ are heteroskedastic. Under heteroskedasticity, if variances for each weighting matrix can be estimated reliably at each voxel of the image, then the covariance matrix V ar(β̂) of the least-squares estimates β̂ can be computed as [18]:

$$\mathit{Var}(\widehat{\beta })={(B\prime B)}^{-1}B\prime {\mathrm{\Sigma }}_{\mathit{ϵ}}B{(B\prime B)}^{-1},$$ (9)

where Σ_ϵ is a diagonal matrix with entries ${\sigma }_{\mathit{ϵ}(b)}^2$.

2.3 Computing Similarities Using Perturbation Theory

We use the following notation [8]: n⁽⁰⁾ denotes the nth unperturbed eigenvector of a tensor H₀; n′⁽⁰⁾ denotes the transpose of the vector n⁽⁰⁾; n denotes the nth perturbed eigenvector of a perturbed tensor H; n^(j) denotes the jth-order perturbation of the eigenvector n; and ${\mathrm{\Delta }}_n^{(j)}$ denotes the jth-order perturbation of the difference, Δ_n, in the eigenvalues and $E_n^{(0)}$ and E_n associated with the eigenvectors n⁽⁰⁾ and n, respectively.

We use perturbation theory to compute the wavefunction renormalization constant that is used as the conditional probability of the unperturbed eigenvector for a given perturbed eigenvector. The renormalization constant is computed differently for differing cases depending on the eigenvalues of the unperturbed tensor. We use a nondegenerate analysis when each eigenvalue is unique and a degenerate analysis when 2 or 3 eigenvalues of a tensor equal one another. Additionally, we estimate the first-order change in the eigenvalue and its variance to compute the conditional probability of the unperturbed eigenvalue for a given perturbed eigenvalue. We then combine the two conditional probabilities to compute the similarity between the two tensors.

2.3.1 Nondegenerate Analysis

Let H₀ denote the unperturbed tensor whose eigenvectors (n⁽⁰⁾) and eigenvalues $(E_n^{(0)})$ are known exactly, i.e., $H_0{n}^{(0)}=E_n^{(0)}{n}^{(0)}$, where $E_i^{(0)}\ne E_j^{(0)},\forall i\ne j$; and the set of eigenvectors {n⁽⁰⁾}_(n=1,2,3) is complete, that is, $1={\mathrm{\Sigma }}_n{n}^{(0)}{n\prime }^{(0)}$, where 1 is the identity matrix. Let H denote the perturbed tensor obtained by perturbing H₀ by matrix V, i.e., H = H₀ + V. For small perturbations V, eigenvalues E_n and eigenvectors n of the perturbed tensor H can be estimated as perturbations of $E_n^{(0)}$ and n⁽⁰⁾, respectively.

In the presence of perturbations, the eigenvalue-eigenvector problem to be solved is (H₀ + V) n = E_n n. Instead, we used the customary procedure of estimating the eigenvalues and eigenvectors of (H₀ + λV) n = E_n n, where λ is a continuous real parameter which varies from 0 to 1. If Δ_n denotes the energy shift in the nth eigenvalues, i.e., ${\mathrm{\Delta }}_n=E_n-E_n^{(0)}$, then the above equation can be written as:

$$(E_n^{(0)}-H_0)n=(\mathrm{\lambda }V-{\mathrm{\Delta }}_n)n.$$ (10)

In Eqn. (10), n and Δ_n are estimated by first expanding them in the powers of λ, i.e.,

$$n=n^{(0)}+\mathrm{\lambda }{n}^{(1)}+{\mathrm{\lambda }}^2{n}^{(2)}+\dots ,{\mathrm{\Delta }}_n=\mathrm{\lambda }{\mathrm{\Delta }}_n^{(1)}+{\mathrm{\lambda }}^2{\mathrm{\Delta }}_n^{(2)}+\dots ;$$

and then by matching the coefficients of the powers of λ. Thus, the difference Δ_n in the eigenvalues is

$${\mathrm{\Delta }}_n=E_n-E_n^{(0)}=\mathrm{\lambda }{V}_{\mathit{nn}}+{\mathrm{\lambda }}^2\sum _{k\ne n}\frac{{|V_{\mathit{nk}}|}^2}{E_n^{(0)}-E_k^{(0)}}+\dots ;$$ (11)

and the perturbed eigenvector (n) is

$$n=n^{(0)}+\mathrm{\lambda }\sum _{k\ne n}{k}^{(0)}\frac{V_{\mathit{kn}}}{E_n^{(0)}-E_k^{(0)}}+{\mathrm{\lambda }}^2\left(\sum _{k\ne n}\sum _{l\ne n}{k}^{(0)}\frac{V_{\mathit{kl}}{V}_{\mathit{ln}}}{(E_n^{(0)}-E_k^{(0)})(E_n^{(0)}-E_l^{(0)})}-\sum _{k\ne n}{k}^{(0)}\frac{V_{\mathit{nn}}{V}_{\mathit{kn}}}{{(E_n^{(0)}-E_k^{(0)})}^2}\right)+O({\mathrm{\lambda }}^3),$$ (12)

where V_nk = n′⁽⁰⁾V k⁽⁰⁾.

Wavefunction Renormalization

The perturbed eigenvector n is normalized to a unit length vector $n_N=Z_n^{1/2}$ n using a normalization constant Z_n, determined such that n′_Nn_N = Z_nn′n = 1. Therefore, the normalization constant Z_n is estimated as:

$$\begin{array}{ll}{Z}_n^{-1}& =n\prime n=({n\prime }^{(0)}+\mathrm{\lambda }{n\prime }^{(1)}+{\mathrm{\lambda }}^2{n\prime }^{(2)}+\dots )(n^{(0)}+\mathrm{\lambda }{n}^{(1)}+{\mathrm{\lambda }}^2{n}^{(2)}+\dots )\\ & =1+{\mathrm{\lambda }}^2\sum _{k\ne n}\frac{{|V_{\mathit{kn}}|}^2}{{(E_n^{(0)}-E_k^{(0)})}^2}+O({\mathrm{\lambda }}^3).\\ Z_n& \approx 1-{\mathrm{\lambda }}^2\sum _{k\ne n}\frac{{|V_{\mathit{kn}}|}^2}{{(E_n^{(0)}-E_k^{(0)})}^2}.\end{array}$$

According to this mathematical formulation, the normalization constant Z_n is equal to 1 when the perturbed eigenvector is identical to an unperturbed eigenvector, and equal to 0 for large perturbations. In between, Z_n smoothly varies to zero for increasing amounts of perturbations. Thus, Z_n has been used as the probability that a perturbed eigenvector will be identical to an unperturbed eigenvector (see [8]). We therefore define the conditional probability Pr(n⁽⁰⁾ ∣ n) of the nth unperturbed eigenvector n⁽⁰⁾, given the perturbed eigenvector n as:

$$\mathit{Pr}(n^{(0)}|n)=Z_n=1-{\mathrm{\lambda }}^2\sum _{k\ne n}\frac{{|V_{\mathit{kn}}|}^2}{{(E_n^{(0)}-E_k^{(0)})}^2}.$$ (13)

However, Z_n can be negative for large perturbations. For large perturbations (for example, perturbations at the interface of gray matter and white matter will be large because of the rapid change in diffusion properties of water molecules across the interface) when Z_n is negative, we set the conditional probability Pr(n⁽⁰⁾ ∣ n) equal to 0. Furthermore, note that because our conditional probability is computed completely in terms of the eigenvectors and eigenvalues of the unperturbed tensor H₀, and that the perturbed tensor H is incorporated only through the perturbation matrix V, our method eliminates the need to establish correspondence between eigenvectors of the two DTs.

Noise Estimates in ${\mathrm{\Delta }}_n^{(1)}$

We use the first-order change ${\mathrm{\Delta }}_n^{(1)}$ (Eqn. 11) in the eigenvalues $E_n^{(0)}$ and E_n to calculate the conditional probability $\mathit{Pr}(E_n^{(0)}|E_n)$ of $E_n^{(0)}$ given E_n. Assuming that ${\mathrm{\Delta }}_n^{(1)}$ is Gaussian distributed with zero mean, an estimate of the variance ${\sigma }_{{\mathrm{\Delta }}_n^{(1)}}^2$ is used to compute the probability $\mathit{Pr}(E_n^{(0)}|E_n)$ of $E_n^{(0)}$. Because the first-order perturbations ${\mathrm{\Delta }}_n^{(1)}=V_{\mathit{nn}}={n\prime }^{(0)}V{n}^{(0)}={\sum }_{\mathit{ij}}{n}_{\mathit{ij}}{V}_{\mathit{ij}}$, where n_ij are the i, jth element of the matrix n⁽⁰⁾n′⁽⁰⁾, the variance ${\sigma }_{{\mathrm{\Delta }}_n^{(1)}}^2$ is computed as:

$${\sigma }_{{\mathrm{\Delta }}_n^{(1)}}^2=\sum _{\mathit{ij}}\sum _{\mathit{kl}}{n}_{\mathit{ij}}{n}_{\mathit{kl}}\mathrm{E}(V_{\mathit{ij}}{V}_{\mathit{kl}}).$$ (14)

Thus, we compute the probability $\mathit{Pr}(E_n^{(0)}|E_n)$ of $E_n^{(0)}$ given E_n as:

$$\mathit{Pr}(E_n^{(0)}|E_n)=\frac{1}{{\sigma }_{{\mathrm{\Delta }}_n^{(1)}}\sqrt{2\pi }}exp[-\frac{1}{2}{\left(\frac{{\mathrm{\Delta }}_n^{(1)}}{{\sigma }_{{\mathrm{\Delta }}_n^{(1)}}}\right)}^2].$$ (15)

To compute the expected values E(V_ijV_kl), we use the covariance matrix V ar(β̂) (Eqn. 8). For two tensors H₁ and H₂, the perturbation matrix V = H₂ − H₁; therefore, the variance and covariance of the elements V_ij of the perturbation matrix V can be calculated as

$${\sigma }_{V_{\mathit{ij}}}^2=2{\sigma }_{H_{\mathit{ij}}}^2,\mathrm{E}(V_{\mathit{ij}})=0,\mathrm{and}\mathrm{E}(V_{\mathit{ij}}{V}_{\mathit{kl}})=2\left[\mathrm{E}(H_{\mathit{ij}}{H}_{\mathit{kl}})-\mathrm{E}(H_{\mathit{ij}})\mathrm{E}(H_{\mathit{kl}})\right].$$

where we have used the fact that noise independently and identically perturbs the neighboring tensors H₁ and H₂. Values from the covariance matrix V ar(β̂) are then used to compute the variance ${\sigma }_{{\mathrm{\Delta }}_n^{(1)}}$, which is in turn used to calculate the conditional probability $\mathit{Pr}(E_n^{(0)}|E_n)$.

2.3.2 Degenerate Analysis

In the degenerate case, we use the following notations for dummy variables: (1) m will denote eigenvectors that span the entire degenerate subspace; (2) l will also denote the eigenvectors that not only span the degenerate subspace but also diagonalize the perturbation matrix V; (3) j will denote eigenvectors in the degenerate subspace that differ from l but diagonalize the matrix V; and (4) k will denote the eigenvectors that span the nondegenerate subspace.

In the degenerate case, two or more eigenvalues (called degenerate) of an unperturbed tensor are equal. The subspace spanned by the eigenvectors which correspond to the degenerate eigenvalues is called the degenerate subspace D. Because the degenerate space is spherical, any set of orthonormal vectors in D can be chosen as the basis set. We use this fact to select a set of eigenvectors in D that diagonalizes the perturbation matrix V in this subspace. Diagonalization of the perturbation matrix avoids the problem of vanishing denominators (the denominator is equal to 0 when two or more eigenvalues are equal in Eqn. 12) when computing the first-order perturbation in eigenvectors.

In the case of a g-fold degeneracy, eigenvalues of g eigenvectors in the set {m⁽⁰⁾} are equal to the unperturbed eigenvalues $E_D^{(0)}$. Perturbation removes degeneracy – i.e., the eigenvalues of all g perturbed eigenvectors will differ. Let {l⁽⁰⁾} be the set of eigenvectors in the degenerate subspace D that diagonalizes the perturbation matrix V. Note that eigenvalues of the eigenvectors in the set {l⁽⁰⁾} will still be equal to $E_D^{(0)}$. Perturbations transform this set of eigenvectors into the set {l} such that {l} → {l⁽⁰⁾} as λ goes to zero. Because a DT has 3 eigenvalues, degenerate cases occur in two types, with either 2 or 3 eigenvalues of the unperturbed tensor being equal.

Case I: Two Equal Eigenvalues

If P₀ and P₁ are two projection operators that project an eigenvector onto degenerate and nondegenerate sub-spaces, respectively, then the first-order perturbation l⁽¹⁾ of the eigenvector l is calculated as (see Appendix A for details):

$$\begin{array}{ll}{l}^{(1)}& =P_0{l}^{(1)}+P_1{l}^{(1)}\\ & =\sum _{k\notin D}\left(\frac{V_{\mathit{kl}}}{E_D^{(0)}-E_k^{(0)}}\right)k^{(0)}+\sum _{j\ne l,jϵD}\sum _{k\notin D}\left(\frac{V_{\mathit{jk}}{V}_{\mathit{kl}}}{({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)})(E_D^{(0)}-E_k^{(0)})}\right)j^{(0)}\\ & =\sum _{k\notin D}C(k,l)k^{(0)}+\sum _{j\ne l,jϵD}\sum _{k\notin D}C(j,k,l)j^{(0)};\end{array}$$ (16)

where C(k, l) are C(j, k, l) are defined as

$$C(k,l)=\left(\frac{V_{\mathit{kl}}}{E_D^{(0)}-E_k^{(0)}}\right),C(j,k,l)=\left(\frac{V_{\mathit{jk}}{V}_{\mathit{kl}}}{({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)})(E_D^{(0)}-E_k^{(0)})}\right).$$

The eigenvectors in the nondegenerate subspace are calculated using Eqn. (12) of the nondegenerate case. Also, the first-order change in the eigenvalues is calculated as in the nondegenerate case.

Wavefunction Renormalization

We normalize the eigenvector l such that the normalized eigenvector $l_N=Z_l^{1/2}l$ is of unit length, i.e., l′_Nl_N = Z_ll′l = 1. Therefore, Z_l is calculated as:

$$\begin{array}{ll}{Z}_l^{-1}& =1+{\mathrm{\lambda }}^2{l\prime }^{(1)}{l}^{(1)}+O({\mathrm{\lambda }}^3)\\ & =1+{\mathrm{\lambda }}^2\left[\sum _{k\notin D}C{(k,l)}^2+\sum _{j\ne l,jϵD}\sum _{k,q\notin D}C(j,k,l)C(j,q,l)\right]+O({\mathrm{\lambda }}^3),\\ Z_l& \approx 1-{\mathrm{\lambda }}^2\left[{\sum _{k\notin D}C(k,l)}^2+\sum _{j\ne l,jϵD}\sum _{k,q\notin D}C(j,k,l)C(j,q,l)\right].\end{array}$$

As in the nondegenerate case, Z_l lies between 0 and 1 for small perturbations; therefore, we define Z_l as the conditional probability of the unperturbed degenerate eigenvector given the perturbed eigenvector. Hence, for the eigenvectors in the degenerate subspace, we compute the probability Pr(l⁽⁰⁾ ∣ l) as:

$$\mathit{Pr}(l^{(0)}|l)=Z_l=1-{\mathrm{\lambda }}^2[\sum _{k\notin D}C{(k,l)}^2+\sum _{j\ne l,jϵD}\sum _{k,q\notin D}C(j,k,l)C(j,q,l)].$$ (17)

For large perturbations when Z_l is negative, we set the conditional probability equal to 0. The conditional probabilities of the eigenvectors in the nondegenerate eigenspace are calculated using Eqn. (13), and the conditional probabilities of the eigenvalues are calculated using Eqn. (15).

Case II: Three Equal Eigenvalues

In this case, the unperturbed tensor is spherical, and each eigenvector evolves up to the first order independently of the other eigenvectors in the presence of perturbations; i.e., perturbations of an eigenvector are orthogonal to other eigenvectors (see Appendix B for details). Thus, the conditional probability of an unperturbed eigenvector, given the perturbed eigenvector, always equals 1.0. We therefore compute the similarity between tensors for this case using only their eigenvalues (Eqn. (15)).

2.4 Computing the Similarity of Two Tensors

A symmetric, positive-semidefinite tensor H⁽⁰⁾ can be expressed using its eigenvectors n⁽⁰⁾ and eigenvalues $E_n^{(0)}$ as [20]:

$$H^{(0)}=\sum _{n=1}^3{E}_n^{(0)}{n}^{(0)}{n\prime }^{(0)}.$$

Because eigenvectors are orthonormal, one eigenvector is completely defined (up to a sign) by the other two eigenvectors; hence, a tensor is completely defined by its two eigenvectors and three eigenvalues. We therefore compute the probability Pr(H⁽⁰⁾ ∣ H) of H₀ (unperturbed) given H (perturbed) as:

$$\begin{array}{ll}\mathit{Pr}(H^{(0)}|H)& =\mathit{Pr}(1^{(0)},2^{(0)},E_1^{(0)},E_2^{(0)},E_3^{(0)}|1,2,E_1,E_2,E_3)\\ & =\mathit{Pr}(1^{(0)}|1)\cdot \mathit{Pr}(2^{(0)}|2)\cdot \mathit{Pr}(E_1^{(0)},E_2^{(0)},E_3^{(0)}|E_1,E_2,E_3);\end{array}$$ (18)

where we have assumed that the eigenvalues and eigenvectors are statistically independent. Whereas specification of one eigenvector constrains the possible realizations of the second eigenvector because eigenvectors are be orthogonal, the second eigenvector can lie anywhere in the plane orthogonal to the first eigenvector, and therefore it still retains a large number of possible realizations. Thus, the independence assumption is reasonable (and it also performed well in our experiments, as shown below). The probability Pr(n⁽⁰⁾ ∣ n)is calculated using either Eqn. (13) for the nondegenerate case or Eqn. (17) for the degenerate case.

We model the first-order perturbation ${\mathrm{\Delta }}_n^{(1)}$ in the difference between eigenvalues as a Gaussian distributed random variable with zero mean and variance ${\sigma }_{{\mathrm{\Delta }}_n^{(1)}}$ computed in Eqn. (14). Therefore, using the results in Eqn. (15), we compute the conditional probability of the unperturbed eigenvalues given the perturbed as:

$$\begin{array}{ll}\mathit{Pr}(E_1^{(0)},E_2^{(0)},E_3^{(0)}|E_1,E_2,E_3)& =\mathit{Pr}(E_1^{(0)}|E_1)\cdot \mathit{Pr}(E_2^{(0)}|E_2)\cdot \mathit{Pr}(E_3^{(0)}|E_3)\\ & =\prod _{n=1}^3\frac{1}{{\sigma }_{{\mathrm{\Delta }}_n^{(1)}}\sqrt{2\pi }}exp\left[-\frac{1}{2}{\left(\frac{{\mathrm{\Delta }}_n^{(1)}}{{\sigma }_{{\mathrm{\Delta }}_n^{(1)}}}\right)}^2\right],\end{array}$$ (19)

where we have assumed that eigenvalues are statistically independent.

2.5 Testing Our Formulation

Comparing the performance of methods for computing the similarity between two tensors is a challenging task. A true similarity between tensors is not defined and therefore tensors with a priori known amounts of dissimilarity cannot be generated. Thus, to compare the performance of the methods such that our comparisons are not biased in favor of a particular method, we used synthetic and real-world datasets that were generated independently of the methods that we studied. The 6 methods that we used to compute similarity between the perturbed and the unperturbed tensors are:

1. the tensor probability Pr(H₀ ∣ H₁), calculated using our method (with ${\sigma }_{\mathit{ϵ}}^2=2.0$);

2. the deviatoric tensor product $H_0\cdot H_1={\sum }_{i,j=1}^3{H}_{\mathit{ij}}^0\cdot H_{\mathit{ij}}^1-\frac{1}{3}\mathrm{Trace}(H_0)\cdot \mathrm{Trace}(H_1)$;

3. the deviatoric sum of the squared scalar products between each pair of eigenvectors $H_0:H_1={{\sum }_{i,j=1}^3{\mathrm{\lambda }}_i^0{\mathrm{\lambda }}_j^1(e_i^0\cdot e_j^1)}^2-\frac{1}{3}\mathrm{Trace}(H_0)\cdot \mathrm{Trace}(H_1)$;

4. the tensor Euclidean distance $d(H_0,H_1)=\sqrt{\mathrm{Trace}\left[{(H_0-H_1)}^2\right]}$ [6];

5. the log-Euclidean distance $\mathit{LogEuclid}(H_0,H_1)=\sqrt{\mathrm{Trace}\left[{(\log (H_0)-\log (H_1))}^2\right]}$, where logarithm of a tensor is calculated by first computing the logarithm of its eigenvalues and then recomputing the tensor using the logarithmic eigenvalues [21, 22]; and

6. the Riemannian distance $\mathit{Riemann}(H_0,H_1)=\parallel \log (H_0^{-1}{H}_1)\parallel =\sqrt{{\sum }_{i=1}^3{ln}^2{\mathrm{\lambda }}_i}$, where λ_i are the eigenvalues of the matrix $H_0^{-1}{H}_1$ [23, 24, 25, 26].

For comparison with the tensor probabilities, we scaled values of H₀ ·H₁, H₀ : H₁, d(H₀, H₁), LogEuclid(H₀, H₁), and Riemann(H₀, H₁) to lie between 0 and 1. Also, the negatives of the distance values (d(H₀, H₁), LogEuclid(H₀, H₁), and Riemann(H₀, H₁)) are used as the measure of similarity of two tensors. Note that because the diffusion tensor space is not an Euclidean space in R⁶ [26], the Euclidean metric is not the right metric to compute similarity between two tensors in general. However, we are interested in computing similarity between two tensors within a small neighborhood where the tensors can be viewed as perturbations of other tensors in the neighborhood. In these small neighborhoods, we expect Euclidean distances to be close to the geodesic distances between any two tensors. Furthermore, the Euclidean metric has been extensively used throughout the image processing literature for postprocessing DT images. We therefore compare the performance of these six methods for computing similarity between tensors.

2.5.1 Synthetic Data

We generated five sets of tensors by perturbing an anisotropic tensor with eigenvalues of 20, 10, and 5, and eigenvectors aligned along the X-, Y-, and Z-axes. To study the effect a of single eigenvalue on various similarity measures, we generated the first set of tensors by varying the largest eigenvalue (20 in this case) between 10 and 30. The second set of tensors was generated by rotating the unperturbed tensor around the Z-axis (i.e., by varing the angle γ) from −50° to +50°. The third set of tensors was generated by varying two eigenvalues (20 and 10 of the unperturbed tensor) between 10 and 30, and keeping the third eigenvalue equal to 5. In the fourth set, the perturbed tensors were generated by rotating the unperturbed tensors around two axes, the Z-axis (angle γ denotes the rotations about the Z-axis) and the Y-axis (angle β denotes rotations about the Y-axis), from −50° to +50°. Finally, to simulate a more realistic situation, we generated the fifth set of tensors to include perturbed tensors by varying the eigenvalue between 10 and 30, and rotating the tensor around Z-axis from −50° to +50°.

Our measure of the similarity of tensors depends on the noise in the DT image, which we quantify through the value of its variance ${\sigma }_{\mathit{ϵ}}^2$ in Eqns. (15) and (19). Therefore, to assess the effect of ${\sigma }_{\mathit{ϵ}}^2$ on the computed probability, we compared perturbed tensors in the first two sets to the unperturbed tensor by varying ${\sigma }_{\mathit{ϵ}}^2$ from 2.0 to 12.0. We then plotted the graph of the similarity between tensors for varying amounts of ${\sigma }_{\mathit{ϵ}}^2$.

2.5.2 Real-World Data Sets

We quantitatively and visually evaluated the performance of the methods for computing similarity using DT images from two individuals. The raw Diffusion-Weighted (DW) images were acquired using a diffusion-sensitizing gradient of strength b = 1000s/mm² applied along 6 directions: (1, 0, 1), (-1, 0, 1), (0, 1, 1), (0, 1,-1), (1, 1, 0), and (-1, 1, 0). The DW images data consisted of 58 slices acquired in the axial orientation, with a scan matrix of size 128 × 128 in each slice. The image voxels were isotropic with resolution 2 × 2 × 2 mm.

To ensure that the reconstructed tensors were positive-definite, we masked out the background in the images and reconstructed tensors in the brain only. Rarely, a reconstructed tensor within the brain was not positive-definite. For these tensors, we imposed the positivity constraint by reversing the sign of the negative eigenvalue and then recomputing the tensor. Such an approach reduced computation time without compromising the imaging data or findings. More advanced methods, including constrained nonlinear least-squares estimation [27, 28, 19], could be used to ensure that the reconstructed tensors are positive-definite; however, these approaches are computationally expensive.

2.5.2.1 A DT Image from a Single Individual

We generated synthetic DT images from this single DT image (the template image) by translating it along the X-axis (the in-plane, or ear-to-ear axis) or by rotating it around the Z-axis (the vertical, or superior-to-inferior, axis) by varying amounts. To avoid uncertainties in interpolating tensors on neighboring voxels, we generated the translated or rotated versions of the template image by first translating or rotating each DW image by specified amounts and then reconstructing the synthetic DT image. Furthermore, rotating DW images by rotation matrix R will rotate the locations of tensors in the image, without rotating the tensors themselves. Thus, in the sythetic images obtained by rotating the template image, tensor at location X will be equal to the tensor at location R⁻¹X, except for interpolation errors, in the original image. We then computed the similarity between DTs in synthetic DT images and the template image at corresponding voxels. We expected that increasing amounts of translation and rotation would the reduce similarity between tensors in the synthetic and the template images. Similarity values were gray-scale encoded and displayed at each voxel in the template imaging space.

To evaluate quantitatively the performance of these methods, for all voxels in the brain, we plotted a histogram of the Euclidean distances between the voxel locations of the most similar tensors in the template image and the synthetic image. The tensor in the synthetic image most similar to a tensor in the template image was found by searching in a 3D neighborhood of size 11 × 11 × 11 voxels for translations, and 15 × 15 × 15 voxels for rotations, in the synthetic image. Within this neighborhood, if two tensors were equally similar to the unperturbed tensor, the Euclidean distance of the tensor closest to the unperturbed tensor was used to plot the histogram of distances. We therefore expected the histogram to be skewed towards smaller distance. For translated versions of the template image, we also plotted the histograms by restricting our search for the most similar tensor to a neighborhood of 11 voxels along the X-axis alone. Because the synthetic images were translated by known amounts along the X-axis, we expected that histograms for each method would show increasing distances between similar tensors. In contrast, when the synthetic images were generated by rotating the template image, even for a small amount of rotation (e.g., γ = 5°), tensors far from the axis of rotation would be translated by large distances from their locations within the template image. However, for an object of interest (the brain in our images), the number of voxels decrease for increasing distance from the axis of rotation. We therefore expected that the histograms would show a peak at the center for rotations across images.

2.5.2.2 DT Images from Two Individuals

We studied the performance of the three methods by computing the similarity between DTs in images from two individuals, both before and after they were spatially normalized (i.e., rigidly coregistered, nonlinearly warped, and reoriented) into a common template space. The DT image from each individual was acquired along 6 directions (8 averaged measurements per slice for each direction) on a Siemens 1.5 Tesla MRI scanner, with Repetition Time (TR) = 4000ms, Echo Time (TE) = 96 ms, an image matrix of size 128 × 128, and a Field of View (FOV) of 240 millimeters. Nineteen slices, each 4 mm thick with no spacing between slices, were acquired in the sagittal orientation, such that the 10th slice was positioned as the interhemispheric slice. In the template space, the image volumes were resliced to a 1 mm thickness.

To spatially register the DT images (using rigid registration and nonlinear warping), we first chose an anatomical MR image of one individual as the template image that defined the common coordinate space. We then registered and reoriented the two DT images into this space in two steps [29, 30]. First, we warped the Fractional Anisotropy (FA) image of an individual to its corresponding anatomical MR image such that the mutual information across the images was maximized [31]. Second, we warped the anatomical image from the individual to the template image using a method of fluid dynamics such that intensity differences between the images were minimized [32]. Thus, two deformation fields for each individual were estimated in these two steps. A composite of these two deformation fields was then used to warp the two DT images into the template space. To reorient the tensors correctly in the template space, we used Procrustean estimation, which uses local statistical information for optimal reorientation [33]. We visually verified that the outlines of the two FA images matched well in the template space. To assess quantitatively the performance of the three methods for computing the similarity of tensors, we plotted the histograms of similarity values between tensors at the same locations in the template space, both before and after normalization of the two images. We expected that the similarity of tensors across the two brains would increase after the DT images had been normalized. Because the method used to normalize the DT images was independent of any method used to compute similarity (i.e., normalization of DT images was not based on increasing any similarity value of the tensors in the two brains), improvement in the computed similarity of tensors through spatial normalization when comparing our metric with other standard measures of similarity would validate our proposed method. Ideally, in the normalized images, similarity should equal 1.0 for our method and 0.0 for both the Euclidean and Riemannian distances between tensors at all voxels. The similarity computed using our measure depends upon the covariance matrix V ar(β̂), which differs across images from different individuals. We therefore computed the variance ${\sigma }_{{\delta }_n^{(1)}}^2$, and therefore the similarity between two tensors, using three methods and compared their performance. First, we assumed that the larger amounts of noise in one image can perturb tensors in that image more than the perturbation in the other image and therefore tensors in one DT image normalized to the other DT image can be viewed as tensors perturbed by this larger amount of noise. At each voxel we therefore used the larger variance to compute the similarity between tensors at that voxel. Second, under heteroskedasticity, we used the larger of the two covariance matrices ∑_ϵ (i.e., the matrix whose sum of the diagonal entries was larger than the sum for the other matrix) to compute similarity between tensors. Third, because the tensors elements are independent and multivariate Gaussian distributed, we computed the sum of the covariance matrices V ar(β̂), and used this summed matrix to compute similarity between tensors. Finally, to study the effects of ${\sigma }_{\mathit{ϵ}}^2$ on our similarity measure, we varied the values of ${\sigma }_{\mathit{ϵ}}^2$ from 100.0 to 20000.0. We expected the similarity of corresponding DTs to increase for increasing values of ${\sigma }_{\mathit{ϵ}}^2$.

3 Results

3.1 Synthetic Data

Although both H₀ · H₁ and H₀ : H₁ varied reasonably for varying amounts of rotation, their monotonic increases failed to capture variations in eigenvalues, such as elongations or contractions of the perturbed tensors (Fig. 1). Therefore, when both the angle γ (i.e., rotations around the Z-axis) and eigenvalue were varied to generate the perturbed tensors, the similarity computed using these methods was maximal for a perturbed tensor that significantly differed from the unperturbed tensor (Fig. 2). Thus, these two measures are not suitable to compute the similarity of two tensors.

Figure 1.

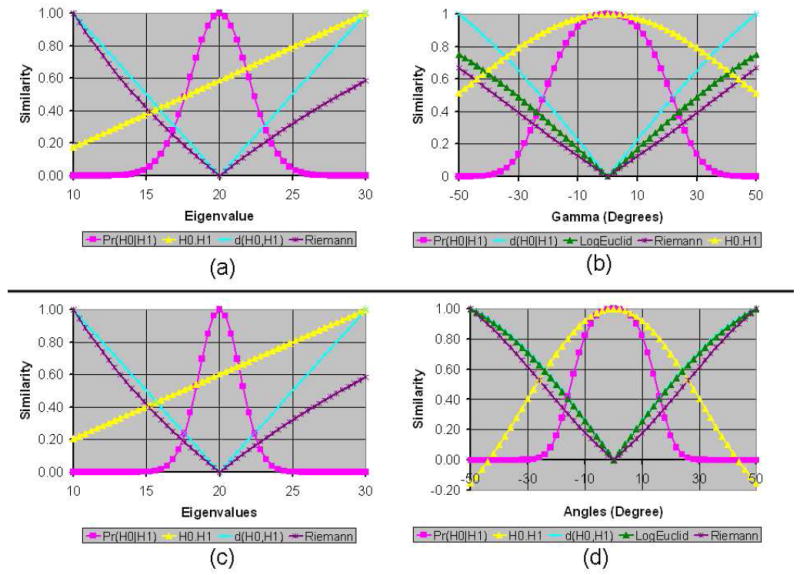
Graphs of Various Similarity Measures for between the unperturbed tensor and the perturbed tensor. The perturbed tensor was obtained from the unperturbed tensor by (a) only varying the largest eigenvalue from 10 to 30, (b) only varying the angle γ (i.e., rotations around the Z-axis) from −50° to 50°, (c) only varying the largest two eigenvalues by the same amount from 10 to 30, and (d) only varying the angles β (i.e., rotations around the Y-axis) and γ by the same amount from −50° to 50°. The eigenvectors of the unperturbed tensor were aligned along the X-, Y-, and Z-axes, with eigenvalues 20, 10, and 5, respectively. The similarity between tensors was computed using six methods: Pr(H₀∣H₁), H₀ · H₁, H₀ : H₁, d(H₀, H₁), LogEuclid(H₀, H₁), and Riemann(H₀, H₁). For comparison, we scaled the similarity values to lie between 0 and 1 for all of measures. Because the values that were computed using H₀ : H₁ were close to the values of H₀ · H₁, for clarity we plotted only the values of H₀ · H₁. Also, for varying eigenvalues, LogEuclide(H₀, H₁) values were close to those of Riemann(H₀, H₁); we therefore plotted only the values of Riemann(H₀, H₁) for varying eigenvalues. The negatives of distance measures are used as the similarity values between tensors. The graph of similarity values computed using our measure is bell-shaped and symmetric around the point where the perturbed tensor equals the unperturbed tensor.

Figure 2. Graphs of Similarity Values for Varying Eigenvalues and Rotations.

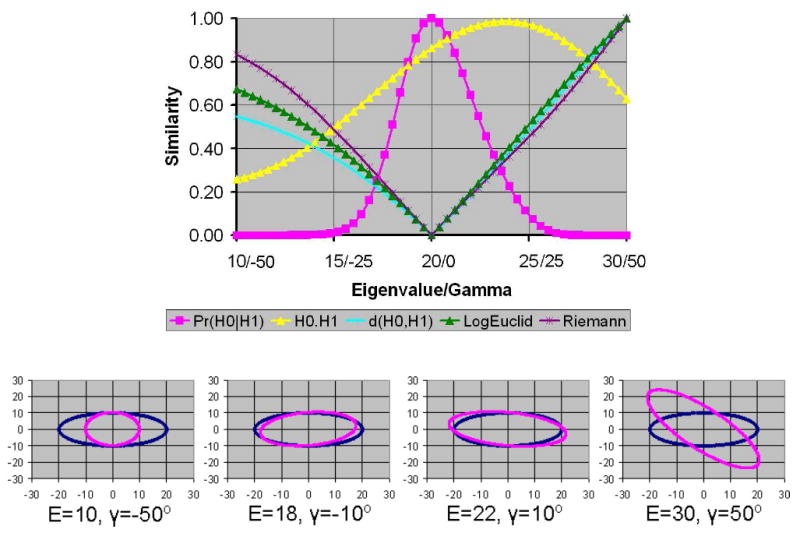
Here we compared the similarity of the unperturbed tensor with perturbed tensors generated by varying both the largest eigenvalue (20 in the unperturbed tensor) and the angle γ (i.e., rotations around the Z-axis). All similarity measures are skewed to the right. Both H₀ · H₁ and H₀ : H₁ computed the largest similarity for a perturbed tensor that was unequal to the unperturbed tensor. The bottom row of the figure shows the profile of the perturbed tensor (purple) and the unperturbed tensor (blue) for varying eigenvalues (E) and angles γ.

The LogEuclid(H₀, H₁) and Riemann(H₀, H₁) methods performed well when the perturbed tensors were generated by rotating the unperturbed tensor about either the Z-axis only or about both the Z-and Y-axes (Fig. 1 b & d). For rotations, their computed similarity values were symmetrical for symmetrical rotations of the perturbed tensors and the unrotated tensor was determined to be most similar to the unperturbed tensor. Also, both LogEuclid(H₀, H₁) and Riemann(H₀, H₁) varied smoothly for variations in either one or two eigen-values (Fig. 1 a & c). Their computed similarity values, however, were skewed toward tensors with smaller eigenvalues – i.e., contracted tensors were computed to be more similar to the unperturbed tensor than were elongated tensors. Using these measures, for example, a tensor with an eigenvalue of 10 had nearly twice the computed similarity to the unperturbed tensor than did the tensor with an eigenvalue of 30, even though the magnitudes of the differences in eigenvalues of the perturbed tensors from the unperturbed one were identical. However, when the perturbed tensors were generated by varying both the angle and eigenvalue of the perturbed tensor, the similarity values were skewed to the right – i.e., elongated tensors were computed to be more similar to the unperturbed tensor than were contracted tensors (Fig. 2). These differing skews in computed similarity under differing noise conditions could lead to erratic and erroneous conclusions concerning the similarity of tensor morphologies when processing real-world datasets.

Both our measure of similarity, Pr(H₀∣H₁), and the tensor Euclidean distance, d(H₀, H₁), performed well, although d(H₀∣H₁) did not vary with and therefore did not account for noise levels in the DT image. Pr(H₀∣H₁), in contrast, computed similarities within the context of noise in the DT image, and indeed the similarity of different tensors based on this measure increased with increasing noise levels in the image, indicating that the difficulty in discriminating differences in the morphologies of tensors is proportional to the noise levels in the image (Fig. 3). Additionally, our similarity measure varied smoothly with variations in eigenvalue or rotation, and it was symmetric for symmetrical variations of the tensor. The probabilities of similarity between tensors declined when a tensor was elongated or contracted (Fig. 1 a & c), or when a perturbed tensor was rotated away from the unperturbed tensor (Fig. 1 b & d).

Figure 3. The Morphological Similarity of Tensors in the Presence of Varying Noise Levels.

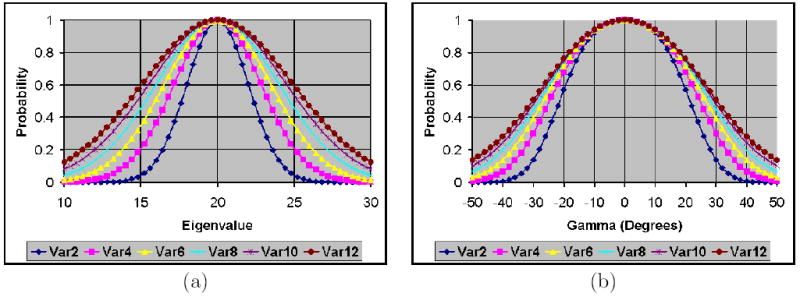
Similarities were computed using our measure for (a) varying eigenvalues and (b) varying angles of rotation. The eigenvectors of the unperturbed tensor were aligned along the coordinate axes with eigenvalues 5, 10, and 20. The width of the bell-shaped distribution of similarity values increased with increasing noise levels. The graphs labeled var2, var4, var6, var8, var10, and var12 are similarity values for noise variance equal to 2, 4, 6, 8, 10, and 12, respectively.

When the perturbed tensors were generated by varying both the eigenvalue and γ, elongated tensors were determined to be more similar to the unperturbed tensor using all measures of similarity. Although our measure still determined that identical tensors were most similar, its values were slightly right-skewed (Fig. 2). This slight skew was expected using our measure, and can be understood in an example: the profile of a tensor with eigenvalues 22, 10, and 5 that has been rotated around the Z-axis by 10° matches better the unperturbed tensor than does a a tensor with eigenvalues 18, 10, and 5 that has been rotated around the Z-axis by −10° (Fig. 2, middle two panels of bottom row). Thus, our measure consistently reflected better the actual degree of similarity in tensor morphology than did the other measures within these synthetic data.

Finally, as expected, our similarity measure increased with increasing noise levels (Fig. 3). High noise levels cause large perturbations in tensors within a homogeneous region. Therefore, the increasing degree of similarity computed using our measure reduces the effect of perturbations from noise in the DTI dataset.

3.2 Real-World Datasets

In our synthetic data, the similarity of tensors computed using LogEuclid(H₀, H₁) followed closely the similarity computed using Riemann(H₀, H₁). Both H₀ · H₁ and H₀ : H₁, however, performed poorly as measure of similarity. For our real-world datasets, we therefore compared the performance of only three methods: Pr(H₀∣H₁), d(H₀, H₁), and Riemann(H₀, H₁).

3.2.1 DT Image from a Single Individual

For all three measures, the similarity between tensors in the template and its translated versions decreased for increasing amounts of translation (Figs. 4, 5, & 6). The histograms show that the Euclidean distance between the voxel locations of the most similar tensors along the X-axis increased for increasing amounts of translation (Fig. 5). For the synthetic image translated by a half-voxel along the X-axis, the histogram had two peaks for all three methods: one at 0 and the other at 1 voxel in distance. Because tensors in the synthetic image that were translated by a half-voxel were computed by interpolating the voxel’s values by equal amounts on neighboring voxels, we expected these two peaks ideally to be of equal magnitude, which was nearly true for our measure but considerably less so for the other two measures (Fig. 5). Furthermore, the histogram for Riemann(H₀,H₁) has small, but clearly discernible, peaks at distances greater than 1 voxel. Thus, our measure is more sensitive than are the others in differentiating tensors with small perturbations. For translations of 1, 2, or 3 voxels, we expected to see only one peak at distances 1, 2, or 3 voxels, respectively, in the histogram. The histograms for all three methods have only one peak at the expected distances (Fig. 5).

Figure 4. Effects of Translation on Similarity Measures.

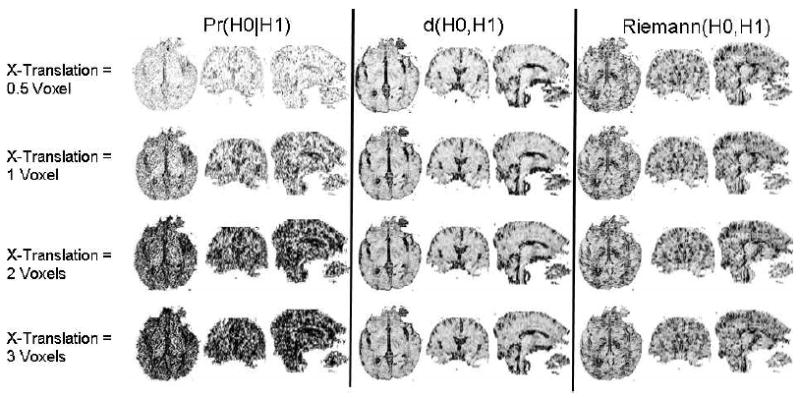
Three orthogonal views (axial, coronal, and sagittal) of similarity values between tensors at corresponding locations in a DT image of a real subject (template) and its translated copies along the X-axis (ear-to-ear axis in the axial view). Three methods were used to compute similarity: Pr(H₀∣H₁), d(H₀, H₁), and Riemann(H₀, H₁). (The performance of LogEuclid(H₀, H₁) was similar to that of Riemann(H₀, H₁).) Large values of Pr(H₀∣H₁) and small values of d(H₀, H₁) and Riemann(H₀, H₁) usually indicate that the tensors matched well, but for ease of comparisons with our measure, we inverted the intensities in the images for d(H₀, H₁) and Riemann(H₀, H₁). The similarity of tensors across the template and translated datasets declined for increasing degrees of translation. Clearly, our measure was the most sensitive indicator of both similarities and dissimilarities in tensor morphology.

Figure 5. Histogram of Distances Between the Most Similar Tensors Along the X-Axis.

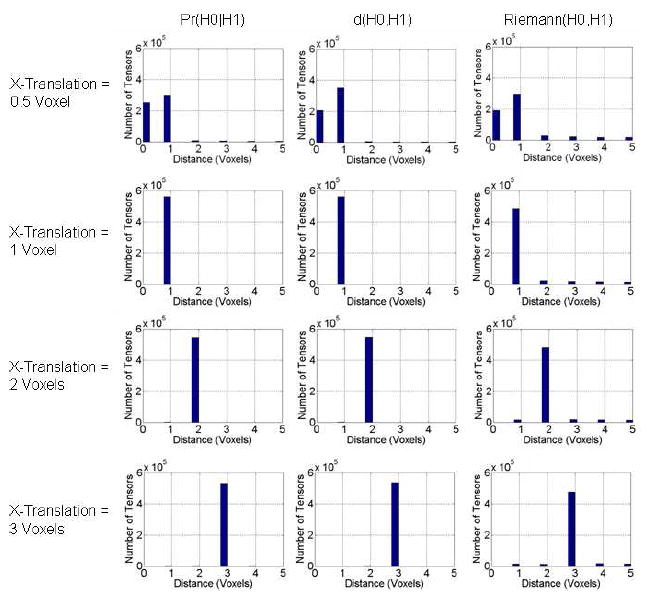
From a single template image, we generated simulated images that were shifted along the X-axis by varying amounts (Fig. 4). We then used one of the three similarity measures, Pr(H₀∣H₁), d(H₀, H₁), and Riemann(H₀, H₁), to find a tensor along the X-axis in the shifted image that was most similar to the unperturbed tensor. We computed the Euclidean distance between the most similar tensors and plotted the histograms. For increasing amounts of translation, the distance between tensors increased, especially when the most similar tensor was searched using our method. Our measure therefore was most sensitive to perturbations in tensors and distinguished better tensors with differing morphologies in neighboring voxels.

Figure 6. Histogram of Distances Between Similar Tensors Across Images.

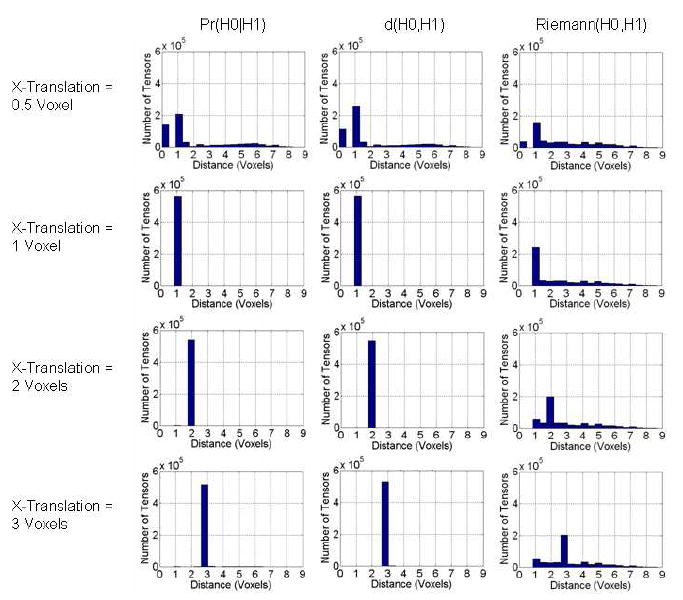
Here we plotted the histogram of distances between the most similar tensors acrossthe template image and its translated versions. We searched for the most similar tensor in a 3D neighborhood 11 × 11 × 11 voxels in size, and we used the Euclidean distance between them to plot the histograms. If two tensors in the synthetic image were equally similar to the unperturbed tensor in the template image, we used the Euclidean distance of the tensor closest to the unperturbed tensor to plot the histogram. For increasing amounts of translation, the spread of distances in the histogram shifted to larger distances between similar tensors, especially for our method.

In real-world data, however, the true translations are unknown. We therefore also plotted histograms of distances between the unperturbed tensor in the template image and a most similar tensor in a 3D neighborhood of 11 × 11 × 11 voxels in size in the synthetic image (Fig. 6). These histograms show that the Riemann(H₀,H₁) measure was least able to distinguish neighboring tensors among the three methods. The histogram for our measure shows two distinct peaks when the DT image was shifted by only a half-voxel, and shows that distances increased for increasing amounts of translation. The performance of the d(H₀,H₁) measure was similar to ours.

All 3 similarity measures decreased for increasing degrees of rotation along the Z-axis (vertical axis in the sagittal view of the images in Fig. 7). Tensors in the regions near the axis of rotation had larger values for our Pr(H₀∣H₁) measure and smaller values for d(H₀, H₁) and Riemann(H₀, H₁) (Fig. 7). Tensors farther from the axis of rotation were less similar. In addition, the size of the region around the axis where DTs matched well decreased for increasing degrees of rotation between images. The histogram of distances between the most similar tensors in the template image and the rotated image as expected shows a large spread of distances and a single peak in the middle for both our measure and d(H₀, H₁) (Fig. 8). These two methods therefore correctly determined similar tensors across the template and the rotated images. The method based on the Riemann(H₀,H₁) distance, however, failed to determine the appropriate similar tensors across the two images. Thus, both our method and d(H₀,H₁) performed well when computing the similarity between tensors across real-world images, although our method was able to distinguish better among differing tensors.

Figure 7. Effects of Rotation on Similarity Measures.

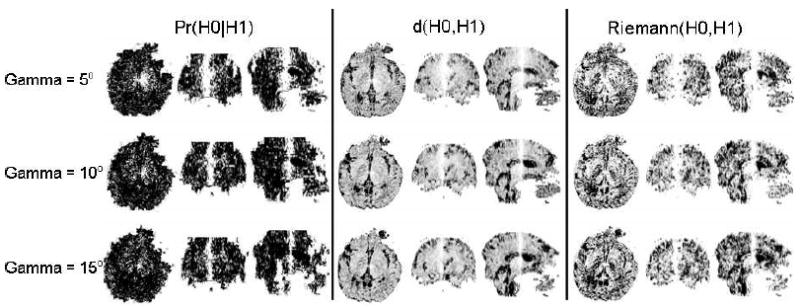
Plots of similarity between tensors across a template image and synthetic images obtained by rotating the template image around the Z-axis (the superior-to-inferior axis in the sagittal view). Similarity was computed using three methods: Pr(H₀∣H₁), d(H₀, H₁), and Riemann(H₀, H₁). (The performance of LogEuclid(H₀, H₁) was similar to that of Riemann(H₀, H₁).) Three orthogonal views (axial, coronal, and sagittal) of the similarity maps are displayed. Tensors in the neighborhood of the axis of rotation (i.e., the Z-axis) are most similar to tensors at corresponding locations in the template image. For ease of comparison across method, we inverted the intensities of the similarity maps for d(H₀, H₁) and Riemann(H₀, H₁). The similarity between tensors reduces rapidly for increasing rotation between images, as is evident when the rotation is increased from 5° (top row) to 15° (bottom row). Our similarity measure is the most sensitive indicator of differences in tensor morphology in the template and rotated images.

Figure 8.

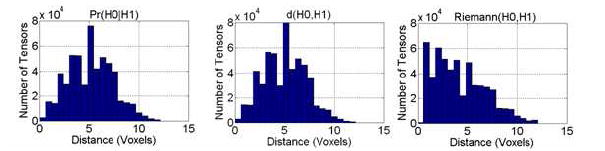
Histogram of Euclidean Distances Between the Most Similar Tensors across the template image and the synthetic image rotated by 5° around the Z-axis. Even for a small amount of rotation, tensors far from the axis of rotation are translated by large amounts. To plot the histogram, we searched for the most similar tensor in a 3D neighborhood 15 × 15 × 15 voxels in size. We computed these histograms for three similarity measures: Pr(H₀∣H₁), d(H₀, H₁), and Riemann(H₀, H₁). As expected, histograms for both Pr(H₀∣H₁) and d(H₀, H₁) show a large spread and a peak in the middle of distances between the tensors that are most similar across the images.

3.2.2 DT Images from Two Individuals

Similarity increased across tensors in the two DT images after they were normalized into the template space (Fig. 9). The histograms of similarity values for our measure and for the measure d(H₀,H₁) showed that spatial normalization produced marked improvements in the similarity of tensors across corresponding voxels of the two images (Fig. 10). The number of tensors with similarity greater than 0.5 computed using our method increased by 480 % after normalization. However, the Riemann(H₀,H₁) measure detected only minimal improvements in similarity (Fig. 10). Similarity computed between tensors in images from two individuals under heteroskedasticity shows that after normalization the number of tensors with similarity greater than 0.5 increased by 930 % and 422 % when using the sum of the two covariance matrices (Fig. 11, (a)) and the larger two matrices (Fig. 11, (b)), respectively. Because the method that spatially normalized the images was independent of the methods used to compute similarity between tensors, and because the similarity of the tensors was expected to be greater in the normalized images, these findings show that our measure is more sensitive to perturbations in tensors, and therefore more correctly detected differences in the similarity of tensor morphologies, than do the other commonly used measures.

Figure 9. The Similarity of Tensors in DT Images from Two Differing Individuals.

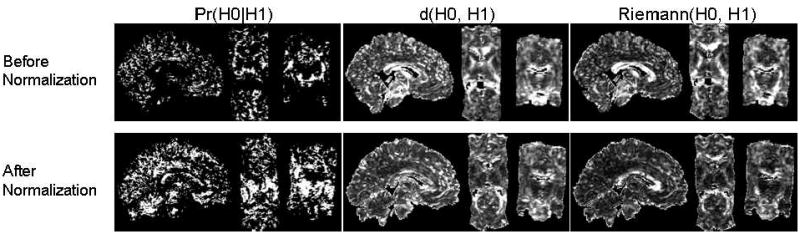
Shown is the comparison of tensors at corresponding locations across DT images of two individuals before (top row) and after (bottom row) they were spatially normalized (i.e. nonlinearly warped and reoriented) into a common template space [29, 30]. Three orthogonal views (sagittal, axial, and coronal) through the 3D dataset show three similarity measures: Pr(H₀∣H₁), d(H₀, H₁), and Riemann(H₀, H₁). The similarity between tensors across normalized images improved significantly (bottom row).

Figure 10.

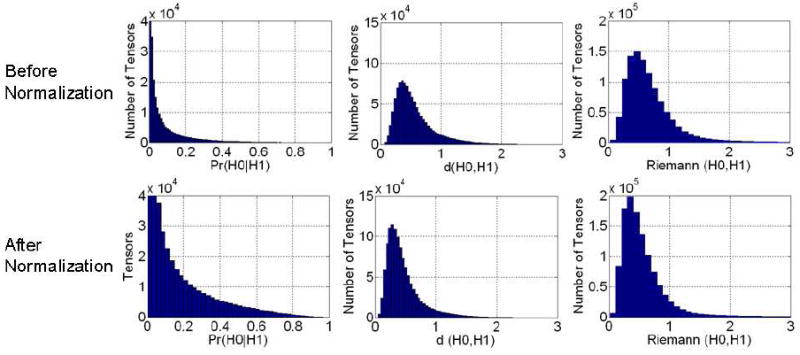
Histogram of Similarity Values at Corresponding Locations across two individual images (Fig. 9) both before and after normalization. We expected the similarity between tensors at corresponding locations to increase significantly following normalization. Histograms in the left column show that after normalization, more tensors were similar across images when similarity was assessed using our measure. In our method, the number of tensors with similarity greater than 0.5 in the normalized images increased by 480 % as compared to those in images before normalization.

Figure 11.

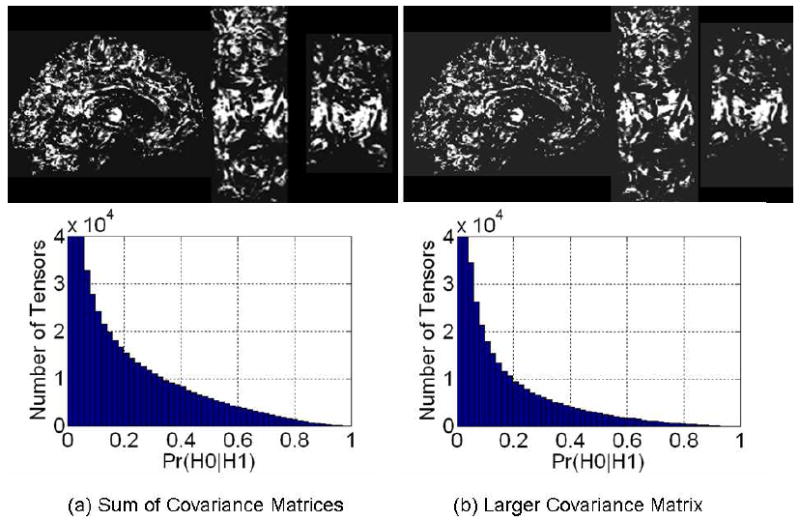
Similarity Computed Across Images After Normalization with covariance matrix V ar(β̂) of the noise calculated using Eqn. (9), i.e. under heteroskedasticity of the noise in the tensor elements. To compute similarity between tensors across the two images normalized into the common space, we consider the tensors in the normalized image as perturbations of the tensors in the other image. The noise in the tensor elements is multivariate Gaussian that is assumed to be independently distributed across images from two individuals. Assuming heteroskedasticity, we computed noise variance in tensor elements using two methods: (a) because the noise in the two images is independently Gaussian distributed, we computed the covariance matrix of the noise as the sum of the two covariance matrices V ar(β̂) of the noise in the two images, and (b) using the larger matrix of the two covariance matrices in the two images. We then used the estimated covariance matrix to compute similarity between tensors at corresponding locations across the two images. The number of tensors with similarity greater than 0.5 in the normalized images increased by (a) 930 %, and (b) 422 % as compared to those in images before normalization (Fig. 9, top row).

Our metric of similarity increased proportionally with synthetically manipulated noise levels in the DT images (Fig. 12). Because two tensors therefore cannot be differentiated using our metric in the presence of large amounts of noise, the asymptotic similarity of any two tensors is 1.0. Our metric is robust to the presence of noise because it explicitly uses noise levels in its computation.

Figure 12. The Effects of Varying Noise Levels on Our Similarity Measure.

Similarity was computed between tensors using our measure at corresponding locations in normalized DT images from two differing individuals. The similarity of tensors increased with increasing noise levels.

4 Discussion

Computing the morphological similarity of tensors at neighboring voxels within a DT image, or at corresponding voxels across DT images from differing individuals, is a fundamental and ubiquitous operation in the postprocessing of DT images. Various methods have been proposed to compute similarity measures, and we compared quantitatively the performance of our measure with that of five other similarity measures frequently employed in the post-processing of DT images. Of these six measures, the Euclidean distance d(H₀,H₁) and ours performed better than the other methods in both synthetic and real-world datasets. Our method, however, was more sensitive to morphological differences and better able to distinguish tensors that differed by only small perturbations than were the d(H₀,H₁) and Riemann(H₀,H₁) measures. Additionally, our method exhibited a clear advantage in computing a similarity value that related directly to the diffusion properties of water molecules (i.e., to their eigenspace components). Finally, our metric was explicitly developed to be sensitive to noise levels in the DT images, and our demonstration of its dependence on synthetically generated noise levels also demonstrated that the behavior of our metric in the presence of noise was smoother and less erratic than were the behaviors of the other measures.

Computing the similarity of two tensors is a local operation in most post-processing procedures for DT images, including fiber tracking, noise filtering, local nonlinear warping, and image segmentation. Our experiments using synthetic tensors showed that both d(H₀,H₁) and Riemann(H₀,H₁) performed equally well in small neighborhoods of the tensor space (Figs. 1 & 2). Within imaging space, however, tensors may differ significantly in a small neighborhood because of differing tissue type and because of differing orientation of fibers passing through a region of the brain. In these regions of the brain, tensors on neighboring voxels may differ significantly, and d(H₀,H₁) is therefore not an appropriate measure to compute similarity between tensors within these regions. On the other hand, although Riemann(H₀,H₁) will compute similarity that is mathematically meaningful, we believe that the similarity of tensors across differing brain regions is not well-defined – i.e., a numerical value representing the similarity of two ellipsoids that have vastly differing morphologies provides no more information to an investigator than simply stating that the two tensors differ in shape. Tensors will be oriented differently across various tissues and brain regions, and therefore comparing eigenvectors of the tensors across differing regions is undesirable. (In that instance, if the investigator is interested in studying differences only in the eigenvalues of the two tensors, then the similarity of tensors can be computed using only the eigenvalue terms in our formulation; other methods to compute similarity do not provide such flexibility.) Our measure therefore will not differentiate tensors well that differ greatly in morphology (as would be encountered, for example, when spatially normalizing one DT image to match another), because it will not distinguish differing degrees of similarity when the tensors are not similar at all. Nevertheless, our measure will be considerably more robust in the presence of noise and more sensitive in discriminating differences in tensor morphologies, than are the other measures in post-processing procedures, including the registration of images that are already in close approximation, because it better distinguishes tensors that differ by only small morphological perturbations, and because most post-processing steps are localized operations.

A similarity measure for diffusion tensors must generate similarity values that change smoothly and symmetrically for corresponding smooth and symmetrical changes in the diffusion properties of water molecules. Otherwise, small changes in diffusion could produce large changes in the similarity measure, which in turn could produce errors in the post-processing operations that use it and that depend crucially on the validity and accuracy of the measure, such as the tracking of fiber pathways, that depend crucially on the validity and accuracy of the similarity measure. Our synthetic examples showed that both H₀ ·H₁ and H₀ : H₁ performed increasingly poorly with increasing morphological differences between tensors. The tensor Euclidean distances d(H₀,H₁) was symmetric and continuous but not smooth. Finally, although the LogEuclid(H₀,H₁), and Riemann(H₀,H₁) measures were continuous, they were not symmetric. Our similarity measure, in contrast, increased smoothly, continuously, and symmetrically for smooth, continuous, and symmetrical differences across tensors.

Measures that assess the morphological similarity of tensors should account for the noise level in the image, because the noise present in all DT images will produce unknown variations in a tensor’s eigenvalues and eigenvectors. Using synthetic examples and real-world DT datasets, as well as manipulation of noise levels in the images, we showed that our similarity measure accounts for noise in the images by appropriately increasing in proportion to increasing noise levels, unlike more commonly used measures. In other words, the sensitivity of our measure (the change in similarity value for small changes in diffusion properties) for detecting differences in eigenspace components decreases with increasing noise in the image. Because two tensors are perturbed more in the presence of increasing noise, our method accounts for these perturbations by increasing the similarity value of the two tensors. In the limiting case in which noise increases to a very large value, our measure will approach a value of 1 for all tensors, because no information can reliably differentiate the DTs in the presence of this much noise (note also that our similarity measure equals 1 when comparing two identical tensors).

Improving the sensitivity of similarity measures to detect variations in tensor morphology will improve the discrimination of those morphologies and therefore will improve the validity and accuracy of other post-processing operations that are commonly performed on DT images, such as image segmentation [34, 35, 36], fiber tracking [37, 38, 39, 40, 41, 42], noise filtering [43], and spatial normalization [33, 31, 44, 45, 46, 47, 48, 49, 50]. Despite the importance of their validity and accuracy, few studies have ever actually compared directly the performances of differing similarity measures. We therefore compared quantitatively the performance of our similarity measure with those of five others. We showed that ours was most sensitive to perturbations in tensor morphology and that its performance was most robust in the presence of noise in the DT images. Furthermore, our method can be employed easily in additional post-processing procedures. Guided by this improved understanding of the performance characteristics of the various measures, we are developing methods for reducing noise in DTI datasets that exploit this improved ability to compute the similarity of neighboring tensors.

Because diffusion tensors are randomly distributed in the presence of noise, a similarity measure will itself be a random variable. When processing DTI datasets from many individuals, the analytical distribution and statistical properties of the similarity measure can be useful in the further post-processing of DTI datasets [51, 36, 52, 26]. Our measure computes the probability of similarity, which is a product of various conditional probabilities (Eqn. 18). It therefore can be regarded as a test statistic between tensors, because it is simply a transformation of random tensors. Computing the analytical probability distribution of our similarity is challenging, however. The computed conditional probability of eigenvectors in this measure is a sum of the ratio of squared random variables (Eqns. 13 & 17). If the numerators and denominators are assumed to be Gaussian-distributed, then these ratios, and therefore the conditional probability of the eigenvectors, will be F-distributed. Furthermore, if the conditional probabilities of the eigenvalues (Eqn. 15) are assumed to be Gaussian-distributed, then computing the analytical distribution of our similarity measure will require derivation of the distribution of the sums of products of random variables that are Gaussian-and F-distributed – a most challenging task. Nevertheless, various statistical properties of our similarity measure can be computed accurately using nonparametric methods, including bootstrapping and permutation statistics [53, 54, 16], thereby providing at least one option for performing rigorous statistical comparisons of the measure without the need first to compute its analytical probability distribution.

The valid mathematical formulation of our measure rests on two assumptions: (i) the wavefunction renormalization constants Z_n and Z_l (Eqns. 13 & 16, respectively), define the conditional probability of an unperturbed eigenvector for a specified perturbed eigenvector, and (ii) eigenvectors and eigenvalues of a DT are distributed independently. The renormalization constant is not a true conditional probability because it can be negative for large perturbations. Our experiments show, however, that the renormalization constant is nonnegative for a sufficiently large range of perturbations (±35° rotations) that are realistically plausible for tensors within structurally homogeneous regions of the brain. For larger perturbations, we set the renormalization constant, and hence the corresponding conditional probability, equal to 0, thereby forcing the conditional probability to lie between 0 and 1. Note that even though the conditional probability is set to 0 for large perturbations, our computed similarity measure is smooth because it smoothly reduces to zero for increasing perturbations (Figs. 1 & 2). Once the computed similarity reduces to zero, our ad hoc procedures set the probability equal to zero for larger amounts of perturbation. This procedure allows us to interpret the renormalization constant as a conditional probability, an assumption whose validity was supported by our experiments with simulated and real data. As discussed earlier, although the eigenvectors of a tensor are not independently distributed, the assumption of independence allowed us to formulate the conditional tensor probability in mathematically simple terms.

Future studies should investigate the computation of the conditional probability using the component of the second eigenvector that evolves in the 2D vector space orthogonal to the tensor’s principal eigenvector. This will obviate the need to assume that the eigenvectors of a DT are independent, which will in turn improve the accuracy of the computed similarity measure. Nevertheless, our similarity metric as currently computed performed well in all of our experiments, thereby supporting its computational utility while assuming the independence of the tensor’s eigenvectors.

A Degenerate Theory

Although derivations for the nondegenerate case are available in any standard text on quantum mechanics (for example see [8]) these books do not provide the intermediate steps for derivations in the degenerate case. Therefore, for the sake of completeness, we herein derive and present all the steps needed to compute the wavefunction normalization constant in the degenerate case.

Eqn. (12) cannot compute perturbations in eigenvectors when two or more unperturbed eigenvalues are equal, because the denominators will equal zero (vanishing denominators). Vanishing denominators can be avoided by using a set of eigenvectors that diagonalizes the perturbation matrix V in the degenerate space.

For a g-fold degeneracy, eigenvalues of g unperturbed eigenvectors equal $E_D^{(0)}$. Let the set of degenerate eigenvectors be denoted by {m⁽⁰⁾}. Perturbations remove degeneracy, and therefore eigenvalues of the corresponding g-perturbed eigenvectors will differ. Because the set of eigenvectors {m⁽⁰⁾}) is degenerate, we select another set of eigenvectors {l⁽⁰⁾} in the degenerate subspace D (subspace spanned by {m⁽⁰⁾}) that diagonalizes the matrix V (i.e., V_nk = 0, ∀n ≠ k). This set of eigenvectors is perturbed to a set of eigenvectors {l} such that {l} → {l⁽⁰⁾} as λ goes to zero. (Eigenvectors in the set {l⁽⁰⁾} are also eigenvectors of the unperturbed matrix H₀, each with eigenvalue $E_D^{(0)}$.

Let P₀ be the projection operator that projects l onto the degenerate subspace spanned by {l⁽⁰⁾}, i.e., $P_0={\sum }_l{l}^{(0)}{l\prime }^{(0)}$. Then the projection operator P₁ that projects eigenvectors onto a subspace orthogonal to D is defined as P₁ = 1 − P₀. Thus, the perturbed eigenvector l can be written as the sum of its projections on these two subspaces: l = P₀l + P₁l. We will use the following result in our derivations:

$$\begin{array}{ll}{H}_0{P}_0& =H_0\sum _l{l}^{(0)}{l\prime }^{(0)}=\sum _l{H}_0{l}^{(0)}{l\prime }^{(0)}\\ & =\sum _l{E}_D^{(0)}{l}^{(0)}{l\prime }^{(0)}=E_D^{(0)}\sum _l{l}^{(0)}{l\prime }^{(0)}=E_D^{(0)}{P}_0.\end{array}$$ (20)

where Eqn. (20) follows from the unperturbed eigenvalue-eigenvector problem.

In the degenerate case, the exact perturbation problem to be solved is (H₀ + λV)l = El, which can be rewritten as

$$\begin{array}{ll}0& =(E-H_0-\mathrm{\lambda }V)l=(E-H_0-\mathrm{\lambda }V)(P_{0}l+P_{1}l)\\ & =(E-H_0-\mathrm{\lambda }V)P_{0}l+(E-H_0-\mathrm{\lambda }V)P_{1}l=(E-E_D^{(0)}-\mathrm{\lambda }V)P_{0}l+(E-H_0-\mathrm{\lambda }V)P_{1}l.\end{array}$$ (21)

To calculate the total perturbation in the eigenvector l, we divide the problem into two subproblems: first, we compute the first-order perturbations of l in the nondegenerate subspace; second, we compute the first-order perturbations of l in the degenerate subspace. We then add the two first-order perturbations to calculate total perturbation in the eigenvector l.

A.1 Projecting on the Nondegenerate Subspace using Operator P₁

Taking projection from the left using P₁ in Eqn. (21), we obtain

$$\begin{array}{ll}0& =P_1(E-E_D^{(0)}-\mathrm{\lambda }V)P_{0}l+P_1(E-H_0-\mathrm{\lambda }V)P_{1}l\\ & =-\mathrm{\lambda }{P}_{1}V{P}_{0}l+(E_D^{(0)}+{\mathrm{\Delta }}_l-H_0-\mathrm{\lambda }{P}_{1}V)P_{1}l\\ (E_D^{(0)}-H_0)P_{1}l& =\mathrm{\lambda }{P}_{1}V{P}_{0}l-({\mathrm{\Delta }}_l-\mathrm{\lambda }{P}_{1}V)P_{1}l\end{array}$$ (22)

because P₁P₁l = P₁l and P₁P₀l = 0. We can solve this problem in the P₁ subspace because the operator P₁(E − H₀ − λP₁V P₁) is nonsingular and the eigenvalues of P₁H₀P₁ are all unique and differ from $E_D^{(0)}$.

Substituting approximations l = l⁽⁰⁾ + λl⁽¹⁾ + … and $E-E_D^{(0)}={\mathrm{\Delta }}_l=\mathrm{\lambda }{l\prime }^{(0)}Vl=\mathrm{\lambda }{\mathrm{\Delta }}_l^{(1)}+{\mathrm{\lambda }}^2{\mathrm{\Delta }}_l^{(2)}+\dots$ in Eqn. (22), we have

$$(E_D^{(0)}-H_0)P_1(l^{(0)}+\mathrm{\lambda }{l}^{(1)}+\dots )=\mathrm{\lambda }{P}_{1}V{P}_0(l^{(0)}+\mathrm{\lambda }{l}^{(1)}+\dots )-[(\mathrm{\lambda }{\mathrm{\Delta }}_l^{(1)}+{\mathrm{\lambda }}^2{\mathrm{\Delta }}_l^{(2)}+\dots )-\mathrm{\lambda }{P}_{1}V]P_1(l^{(0)}+\mathrm{\lambda }{l}^{(1)}+\dots ).$$

Keeping the terms up to the second power in λ, we have,

$$(E_D^{(0)}-H_0)P_1(\mathrm{\lambda }{l}^{(1)}+{\mathrm{\lambda }}^2{l}^{(2)})=\mathrm{\lambda }{P}_{1}V{P}_0(l^{(0)}+\mathrm{\lambda }{l}^{(1)})-{\mathrm{\lambda }}^2({\mathrm{\Delta }}_l^{(1)}-P_{1}V)P_1{l}^{(1)}.$$

Equating terms that are first-order in λ, we obtain

$$\begin{array}{ll}(E_D^{(0)}-H_0)P_1{l}^{(1)}& =P_{1}V{P}_0{l}^{(0)}\\ P_1{l}^{(1)}& =\frac{1}{E_D^{(0)}-H_0}{P}_{1}V{P}_0{l}^{(0)}=\frac{1}{E_D^{(0)}-H_0}{P}_{1}V{l}^{(0)}\\ & =\sum _{k\notin D}\frac{1}{E_D^{(0)}-E_k^{(0)}}{k}^{(0)}{k\prime }^{(0)}V{l}^{(0)}=\sum _{k\notin D}\frac{1}{E_D^{(0)}-E_k^{(0)}}{k}^{(0)}{V}_{\mathit{kl}},\end{array}$$

where we have used the facts that P₀l⁽⁰⁾ = l⁽⁰⁾, and that the inverse operator $\frac{1}{E_D^{(0)}-H_0}$ acting on P_l can besimplified as

$$\frac{1}{E_D^{(0)}-H_0}{P}_1=\sum _{k\notin D}\frac{1}{E_D^{(0)}-E_k^{(0)}}{k}^{(0)}{k\prime }^{(0)}.$$

because $P_1=(1-P_0)=\sum _{k\notin D}{k}^{(0)}k\prime (0).$

Therefore, the first-order perturbation of the eigenvector l in the nondegenerate subspace is computed as:

$$P_1{l}^{(1)}=\sum _{k\notin D}{k}^{(0)}\frac{V_{\mathit{kl}}}{E_D^{(0)}-E_k^{(0)}}.$$ (23)

A.2 Projecting on the Degenerate Subspace using OperatorP₀

Next, we compute the perturbations of the eigenvector l in the degenerate subspace D by taking the projection from the left in Eqn. (21):

$$\begin{array}{ll}0& =P_0(E-E_D^{(0)}-\mathrm{\lambda }V)P_{0}l+P_0(E-H_0-\mathrm{\lambda }V)P_{1}l\\ & =({\mathrm{\Delta }}_l-\mathrm{\lambda }{P}_{0}V)P_{0}l-\mathrm{\lambda }{P}_{0}V{P}_{1}l,\end{array}$$

because P₀P₀l = P₀l, and P₀P₁l = 0.

Substituting approximations for Δ_l and l is this equation, we obtain

$$\left[(\mathrm{\lambda }{\mathrm{\Delta }}_l^{(1)}+{\mathrm{\lambda }}^2{\mathrm{\Delta }}_l^{(2)}+\dots )-\mathrm{\lambda }{P}_{0}V\right]P_0(l^{(0)}+\mathrm{\lambda }{l}^{(1)}+{\mathrm{\lambda }}^2{l}^{(2)}+\dots )=\mathrm{\lambda }{P}_{0}V{P}_1(\mathrm{\lambda }{l}^{(1)}+{\mathrm{\lambda }}^2{l}^{(2)}+\dots )$$

because P₁l⁽⁰⁾ = 0. Because λ is non-zero, we divide by λ and keep the terms up to second order in λ,

$$\left[{\mathrm{\Delta }}_l^{(1)}+\mathrm{\lambda }{\mathrm{\Delta }}_l^{(2)}+{\mathrm{\lambda }}^2{\mathrm{\Delta }}_l^{(3)}-P_{0}V\right]P_0(l^{(0)}+\mathrm{\lambda }{l}^{(1)}+{\mathrm{\lambda }}^{(2)}{l}^{(2)})=P_{0}V{P}_1(\mathrm{\lambda }{l}^{(1)}+{\mathrm{\lambda }}^2{l}^{(2)}).$$ (24)

By equating the zero-order terms in Eqn. (24), we obtain

$$({\mathrm{\Delta }}_l^{(1)}-P_{0}V)P_0{l}^{(0)}=0\mathrm{or}{\mathrm{\Delta }}_l^{(1)}{l}^{(0)}=P_{0}V{P}_0{l}^{(0)}.$$

Thus, l⁽⁰⁾ and ${\mathrm{\Delta }}_l^{(1)}$ are eigenvectors and eigenvalues, respectively, of the perturbation matrix V when projected into the degenerate subspace D (i.e., eigenvalues and eigenvectors of the matrix P₀V P₀).

By equating the first-order terms in the powers of λ in Eqn. (24), we obtain

$${\mathrm{\Delta }}_l^{(2)}{P}_0{l}^{(0)}+({\mathrm{\Delta }}_l^{(1)}-P_{0}V)P_0{l}^{(1)}=P_{0}V{P}_1{l}^{(1)}$$

$$({\mathrm{\Delta }}_l^{(1)}-P_{0}V)P_0{l}^{(1)}=P_{0}V{P}_1{l}^{(1)}-{\mathrm{\Delta }}_l^{(2)}{P}_0{l}^{(0)}$$

$$({\mathrm{\Delta }}_l^{(1)}{P}_0-P_{0}V{P}_0)P_0{l}^{(1)}=P_{0}V{P}_1{l}^{(1)}-{\mathrm{\Delta }}_l^{(2)}{P}_0{l}^{(0)}$$ (25)

(This equation can be used to show that l⁽⁰⁾ and l⁽¹⁾ are orthogonal.) Premultiplying Eqn. (25) with j′⁽⁰⁾ where j ϵ D but j ≠ l, and noting that

$${j\prime }^{(0)}{\mathrm{\Delta }}_l^{(2)}{P}_0{l}^{(0)}={j\prime }^{(0)}{\mathrm{\Delta }}_l^{(2)}{l}^{(0)}={\mathrm{\Delta }}_l^{(2)}{j\prime }^{(0)}{l}^{(0)}=0,$$

we obtain

$${j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}{P}_0-P_{0}V{P}_0)P_0{l}^{(1)}={j\prime }^{(0)}{P}_{0}V{P}_1{l}^{(1)}.$$

The left-hand side term in this equation can be rewritten as

$$\begin{array}{ll}{j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}{P}_0-P_{0}V{P}_0)& ={\mathrm{\Delta }}_l^{(1)}{j\prime }^{(0)}-{j\prime }^{(0)}{P}_{0}V{P}_0={\mathrm{\Delta }}_l^{(1)}{j\prime }^{(0)}-{\mathrm{\Delta }}_j^{(1)}{j\prime }^{(0)}\\ & ={j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)}).\end{array}$$

Therefore, we have

$${j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)})P_0{l}^{(1)}={j\prime }^{(0)}{P}_{0}V{P}_1{l}^{(1)}.$$

Pre-multiplying this equation by j⁽⁰⁾, we obtain

$$j^{(0)}{j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)})P_0{l}^{(1)}=j^{(0)}{j\prime }^{(0)}{P}_{0}V{P}_1{l}^{(1)},$$

$$j^{(0)}{j\prime }^{(0)}{P}_0{l}^{(1)}=\frac{j^{(0)}}{{\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)}}{j\prime }^{(0)}{P}_{0}V{P}_1{l}^{(1)}.$$

Thus, the last equation evaluates the projection of P₀l⁽¹⁾ on the subspace defined by the eigenvector j⁽⁰⁾. Because P₀l⁽¹⁾ is orthogonal to both the eigenvector l⁽⁰⁾ and the subspace defined by P₁, we obtain P₀l⁽¹⁾, by summing its projections on all eigenvectors j⁽⁰⁾ where j ≠ l and j ϵ D.

Thus, the projection of the first-order perturbations P₀l⁽¹⁾ in the degenerate subspace is

$$P_0{l}^{(1)}=\sum _{j\ne l,jϵD}{j}^{(0)}{j\prime }^{(0)}{P}_0{l}^{(1)}=\sum _{j\ne l,jϵD}\frac{j^{(0)}}{{\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)}}{j\prime }^{(0)}{P}_{0}V{P}_1{l}^{(1)}.$$ (26)

Using Eqn. (23), we can rewrite Eqn. (26) as

$$\begin{array}{ll}{P}_0{l}^{(1)}& =\sum _{j\ne l,jϵD}\frac{j^{(0)}}{{\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)}}{j\prime }^{(0)}{P}_{0}V\sum _{k\notin D}\left(\frac{V_{\mathit{kl}}}{E_D^{(0)}-E_k^{(0)}}\right)k^{(0)}\\ & =\sum _{j\ne l,jϵD}\sum _{k\notin D}\left(\frac{V_{\mathit{jk}}{V}_{\mathit{kl}}}{({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)})(E_D^{(0)}-E_k^{(0)})}\right)j^{(0)}.\end{array}$$ (27)

Therefore, the total first-order perturbation l⁽¹⁾ in the eigenvector l⁽⁰⁾ is obtained by summing Eqns. (23) and (27):

$$\begin{array}{ll}{l}^{(1)}& =P_0{l}^{(1)}+P_1{l}^{(1)}\\ & =\sum _{k\notin D}\left(\frac{V_{\mathit{kl}}}{E_D^{(0)}-E_k^{(0)}}\right)k^{(0)}+\sum _{j\ne l,jϵD}\sum _{k\notin D}\left(\frac{V_{\mathit{jk}}{V}_{\mathit{kl}}}{({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)})(E_D^{(0)}-E_k^{(0)})}\right)j^{(0)}\\ & =\sum _{k\notin D}C(k,l)k^{(0)}+\sum _{j\ne l,jϵD}\sum _{k\notin D}C(j,k,l)j^{(0)},\end{array}$$

and the eigenvector l is approximated as: l = l⁽⁰⁾ + λl⁽¹⁾ + Ο(λ²).

As in the nongenerate case, we use the normalization l′⁽⁰⁾l = 1, which allows us to compute the change in the eigenvalues ${\mathrm{\Delta }}_l=E-E_D^{(0)}=\mathrm{\lambda }{l\prime }^{(0)}Vl$ that is approximated as ${\mathrm{\Delta }}_l=\mathrm{\lambda }{\mathrm{\Delta }}_l^{(1)}+{\mathrm{\lambda }}^2{\mathrm{\Delta }}_l^{(2)}+\dots .$

The first-order term ${\mathrm{\Delta }}_l^{(1)}$ is eigenvalue of the operator P₀V P₀, and the second-order correction term ${\mathrm{\Delta }}_l^{(2)}$ can be shown to be:

$${\mathrm{\Delta }}_l^{(2)}=\sum _{k\notin D}\frac{{|V_{\mathit{kl}}|}^2}{E_D^{(0)}-E_k^{(0)}}$$

The eigenvectors not in the degenerate subspace evolve according to nondegenerate theory (see Eqn. (12)).

A.3 Wavefunction Renormalization

From the eigenvector l we calculate normalized eigenvector $l_N=Z_l^{1/2}l$ such that _Nl′l_N = Z_ll′l = 1. Therefore, the normalization constant Z_l is computed as follows:

$$\begin{array}{ll}{Z}_l^{-1}& =1+{\mathrm{\lambda }}^2{l\prime }^{(1)}{l}^{(1)}+O({\mathrm{\lambda }}^3)\\ & =1+{\mathrm{\lambda }}^2\left[\sum _{a\notin D}C(a,l){a\prime }^{(0)}+\sum _{b\ne l,bϵD}\sum _{q\notin D}C(b,q,l){b\prime }^{(0)}\right]\left[\sum _{k\notin D}C(k,l)k^{(0)}+\sum _{j\ne l,jϵD}\sum _{k\notin D}C(j,k,l)j^{(0)}\right]+O({\mathrm{\lambda }}^3)\\ & =1+{\mathrm{\lambda }}^2\left[\sum _{k\notin D}C{(k,l)}^2+\sum _{j\ne l,jϵD}\sum _{k,q\notin D}C(j,k,l)C(j,q,l)\right]+O({\mathrm{\lambda }}^3).\\ Z_l& \approx 1-{\mathrm{\lambda }}^2\left[\sum _{k\notin D}C{(k,l)}^2+\sum _{j\ne l,jϵD}\sum _{k,q\notin D}C(j,k,l)C(j,q,l)\right].\end{array}$$

B When All Eigenvalues are Equal

When all eigenvalues are equal, each perturbed eigenvector evolves independently (orthogonal) of the other perturbed eigenvectors. And because the DT is spherical, its perturbed eigenvectors are the same as the unperturbed ones. The exact eigenvalue-eigenvector problem to solve in this case is:

$$0=(E-E_D^{(0)}-\mathrm{\lambda }{P}_{0}V)P_{0}l=({\mathrm{\Delta }}_l-\mathrm{\lambda }{P}_{0}V)P_{0}l,$$

where P₀ is the projection operator projecting eigenvectors onto the degenerate subspace, which is the complete space for this case. Substituting approximations for Δ_l and l, we obtain

$$0=\left[(\mathrm{\lambda }{\mathrm{\Delta }}_l^{(1)}+{\mathrm{\lambda }}^2{\mathrm{\Delta }}_l^{(2)}+\dots )-\mathrm{\lambda }{P}_{0}V\right]P_0(l^{(0)}+\mathrm{\lambda }{l}^{(1)}+{\mathrm{\lambda }}^2{l}^{(2)}+\dots ).$$

As λ is non zero, dividing by λ and keeping only the terms up to the second-order in λ, we obtain

$$0=\left[({\mathrm{\Delta }}_l^{(1)}+\mathrm{\lambda }{\mathrm{\Delta }}_l^{(2)}+{\mathrm{\lambda }}^2{\mathrm{\Delta }}_l^{(3})-\mathrm{\lambda }{P}_{0}V\right]P_0(l^{(0)}+\mathrm{\lambda }{l}^{(1)}+{\mathrm{\lambda }}^2{l}^{(2)}).$$

Equating the zero-order terms in λ, we obtain ${\mathrm{\Delta }}_l^{(1)}{P}_0{l}^{(0)}=P_{0}V{P}_0{l}^{(0)}$, which is the eigenvalue-eigenvector problem to solve in this case. Equating the first-order terms in λ, we have

$$({\mathrm{\Delta }}_l^{(1)}-P_{0}V)P_0{l}^{(1)}+{\mathrm{\Delta }}_l^{(2)}{P}_0{l}^{(0)}=0$$

$$({\mathrm{\Delta }}_l^{(1)}-P_{0}V)P_0{l}^{(1)}+{\mathrm{\Delta }}_l^{(2)}{l}^{(0)}=0.$$

Pre-multiplying this equation by j′⁽⁰⁾, with j ≠ l, and noting that ${j\prime }^{(0)}{\mathrm{\Delta }}_l^{(2)}{l}^{(0)}={\mathrm{\Delta }}_l^{(2)}{j\prime }^{(0)}{l}^{(0)}=0$ (because eigenvectors are orthogonal), we obtain: ${j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}{P}_0-P_{0}V{P}_0)P_0{l}^{(1)}=0$. Using the identity ${j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}{P}_0-P_{0}V{P}_0)={j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)})$, we can write the above equation as

$$\begin{array}{ll}{j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}{P}_0-P_{0}V{P}_0)P_0{l}^{(1)}& ={j\prime }^{(0)}({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)})P_0{l}^{(1)}\\ & =({\mathrm{\Delta }}_l^{(1)}-{\mathrm{\Delta }}_j^{(1)}){j\prime }^{(0)}{l}^{(1)}=0.\end{array}$$

Because perturbations remove degeneracy, i.e. ${\mathrm{\Delta }}_l^{(1)}\ne {\mathrm{\Delta }}_j^{(1)}$, the previous equation yields: j′⁽⁰⁾l⁽¹⁾ = 0; that is, perturbations in one eigenvector are orthogonal to the other eigenvectors. Therefore, the conditional probability of the unperturbed eigenvector given the perturbed eigenvector will be 1.0.