EFFECTS OF MECHANICAL COMPRESSION ON METABOLISM AND DISTRIBUTION OF OXYGEN AND LACTATE IN INTERVERTEBRAL DISC

Abstract

The objective of this study was to examine the effects of mechanical compression on metabolism and distributions of oxygen and lactate in the intervertebral disc (IVD) using a new formulation of the triphasic theory. In this study, the cellular metabolic rates of oxygen and lactate were incorporated into the newly developed formulation of the mechano-electrochemical mixture model [Huang and Gu, J. Biomech. Eng., 129:423–429, 2007]. The model was used to numerically analyze metabolism and transport of oxygen and lactate in the IVD under static or dynamic compression. The theoretical analyses demonstrated that compressive loading could affect transport and metabolism of nutrients. Dynamic compression increased oxygen concentration, reduced lactate accumulation, and promoted oxygen consumption and lactate production (i.e., energy conversion) within the IVD. Such effects of dynamic loading were dependent on strain level and loading frequency, and more pronounced in the IVD with less permeable endplate. In contrast, static compression exhibited inverse effects on transport and metabolism of oxygen and lactate. The theoretical predictions in this study are in good agreement with those in the literature. This study established a new theoretical model for analyzing cellular metabolism of nutrients in hydrated, fibrous soft tissues under mechanical compression.

INTRODUCTION

Intervertebral disc (IVD) is the largest avascular structure in the human body with the nucleus pulposus (NP) being centered and surrounded on its periphery by the annulus fibrosus (AF), and superiorly and inferiorly by cartilaginous endplates (CEP) (Figure 1). The NP is composed from randomly oriented collagen fibrils enmeshed in a proteoglycan gel while the AF is formed from a series of concentric lamellae consisting of collagen fibers (Hickey and Hukins, 1980; Marchand and Ahmed, 1990; Urban and Maroudas, 1980; Lundon and Bolton, 2001). Water is the major component of the IVD (65–90% wet weight). The other major components in IVD are collagen (15–65% dry weight), proteoglycan (10–60% dry weight), and other matrix proteins (15–45% dry weight) (Eyre et al., 1989; Johnstone et al., 1992; Gu et al., 1999a; Iatridis et al., 2007; Kraemer et al., 1985; Panagiotacopulos et al., 1987; Pearce, 1993). The IVD is primarily subjected to compressive load in vivo and has a strong propensity for swelling (Urban and Maroudas, 1981; Urban and McMullin, 1988; Yao et al., 2002). The osmotic pressure of the IVD is mainly due to the high density of charged carboxyl and sulfate groups on the glycosaminoglycans of the proteoglycans within the tissue (Urban and Maroudas, 1980; Urban et al., 1979). When an IVD is deformed under loading, interstitial fluid flow occurs, even though the hydraulic permeability of the tissue is very low (Best et al., 1994; Gu et al., 1999a; Gu and Yao, 2003; Houben et al., 1997; Iatridis et al., 1998; Perie et al., 2005). The electrical response of the IVD also changes when a disc is compressed (Yao and Gu, 2007b), due to the effects of diffusion potential and streaming potential (Lai et al., 2000; Gu et al., 1999b).

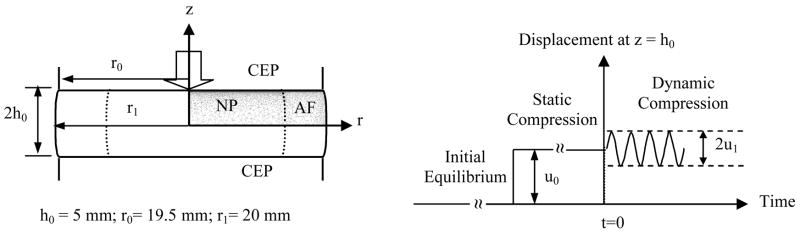
Figure 1.

Schematic of loading configuration for the finite element analysis of oxygen and lactate distributions. A constant displacement (10% of disc height) was applied during the static compression test. For dynamic compression test, a sinusoidal displacement (u₁ =2.5% or 5% of disc height and frequency = 0.1 or 0.01 Hz) was imposed.

Vital nutrients are supplied to the IVD from the blood vessels located at the margins of the disc (Brodin, 1955; Brown and Tsaltas, 1976; Holm et al., 1981; Maroudas et al., 1975; Ogata and Whiteside, 1981; Urban et al., 1982). The transport of nutrients through the dense complex extracellular matrix to IVD cells relies mainly on diffusion. Therefore, poor nutrient supply has been suggested as a potential mechanism for disc degeneration (Bibby et al., 2002; Bibby and Urban, 2004; Horner and Urban, 2001).

There are two possible pathways for nutrient transport into (and waste transport out of) the IVD: the cartilage endplate route or the perianular route (Nachemson et al., 1970; Horner and Urban, 2001; Maroudas et al., 1975; Urban et al., 1977; Urban et al., 1978; Ogata and Whiteside, 1981; Holm et al., 1981; Crock and Goldwasser, 1984; Moore et al., 1992; Roberts et al., 1996). Since determining the in vivo distribution of nutrients in human IVD is often invasive and difficult (Bartels et al., 1998), the knowledge on nutrient transport in human IVD is limited. It is still unclear as to how the nutrition level in IVD is regulated by mechanical and biological factors, such as applied stress or strain, tissue degeneration, and endplate calcification. Recently, numerical analyses have been used to investigate the transport of nutrients and metabolites (e.g., oxygen, glucose, and lactate) within the human IVD (Selard et al., 2003; Soukane et al., 2005). In these previous theoretical studies, the complex geometry and nonhomogeneous properties of the human IVD were considered and the distribution of oxygen, glucose, and lactate within the IVD were shown to depend on solute diffusivity, cellular metabolic rates, the coupling effects between solute concentrations and consumptions/productions, and boundary conditions (Selard et al., 2003; Soukane et al., 2005). Most recently, Soukane et al. suggested that fluid loss and change in disc geometry which were assumed to be caused by static compression could affect the transport of nutrients and metabolites (Soukane et al., 2007). However, only diffusion of solutes was considered in these theoretical studies.

It is well-known that dynamic compression augments the transport of large solutes in cartilaginous tissues (Bonassar et al., 2000; Evans and Quinn, 2006a; Evans and Quinn, 2006b; Huang and Gu, 2007; Mauck et al., 2003; O’Hara et al., 1990; Urban et al., 1982; Yao and Gu, 2004; Yao and Gu, 2007a). Recently, our theoretical study suggested that dynamic compression could promote transport of neutral solute in the anisotropic cartilaginous tissue by enhancing both diffusive and convective solute fluxes (Huang and Gu, 2007). However, the effect of mechanical compression on the distribution and metabolism of nutrients in the human IVD has not been studied. Therefore, the objective of this study was to examine the effects of static and dynamic compressions on distribution and metabolism of oxygen and lactate in the IVD under using a new model based on the mechano-electrochemical mixture theory (Lai et al., 1991), due to the fact that IVD is a charged hydrated soft tissue.

THEORETICAL MODEL

In this study, a new theoretical formulation was extended from our previous theoretical framework (Yao and Gu, 2004; Huang and Gu, 2007) by incorporating the cellular metabolic rates into the equation of balance of mass for solutes (Bedford and Drumheller, 1983):

$$\partial ({\phi }^w{c}^{\alpha })/\partial t+\nabla \cdot ({\mathbf{J}}^{\alpha }+{\phi }^w{c}^{\alpha }{\mathbf{v}}^{\mathbf{s}})=Q^{\alpha },$$ (1)

where J^α is the molar flux of solute α relative to the solid phase, φ^w is the tissue porosity (volume fraction of water), c^α is the concentration of solute α (per unit interstitial water volume), v^s is the velocity of solid matrix, and Q^α is the cellular metabolic rate of solute α per unit tissue volume.

Two neutral solutes (oxygen (O₂) and lactate), sodium ion (+), and chloride ion (−) were considered in this study. The inclusion of charged ions is necessary to balance the fixed, negative charges on the solid matrix since it can affect the swelling pressure and swelling strain even at equilibrium under static loading. The consumption rates of oxygen were pH dependent (Bibby et al., 2005) and given as (Huang et al., 2007):

$$Q^{O_2}=-\frac{V_{max}^{\prime }(pH-4.95)c^{O_2}}{K_m^{\prime }(pH-4.59)+c^{O_2}}{\rho }^{\mathit{cell}},$$ (2)

where the unit of c^O₂ is μM, $V_{max}^{\prime }=5.27$ nmol/million cells-hr for NP cells and 3.64 nmol/million cells-hr for AF cells, and $K_m^{\prime }=3.4$ μM for NP cells and 12.3 μM for AF cells. Since there is no information about the lactate production rate of AF cells in the literature, the most recent finding of NP lactate production rate (Bibby et al., 2005) was used for both NP and AF cells in the simulation:

$$Q^{\mathit{Lactage}}=exp(-2.47+0.93\times pH+0.16\times c^{o_2}-0.0058\times {c^{o_2}}^2){\rho }^{\mathit{cell}},$$ (3)

where the unit of c^O₂ is kPa. The metabolic rates of sodium and chloride ions were assumed to be zero (i.e., Q⁺=Q⁻=0). Based on the experimental data reported in the literature (Soukane et al., 2005; Bibby et al., 2005), an approximate linear relationship between pH and lactate was used to calculate pH within the IVD in this study and given as:

$$pH=A{c}^{\mathit{lactate}}+B(0<c^{\mathit{lactate}}<30\text{mM})$$ (4)

where A = −0.1 mM⁻¹ and B = 7.5.

The theoretical model also takes into consideration the tension-compression nonlinearity of the solid matrix (i.e., the Conewise Linear Elasticity (CLE) model) (Curnier et al., 1995; Soltz and Ateshian, 2000; Huang et al., 2001) and the strain-dependent properties (i.e., intrinsic permeability, solute diffusivity, fixed charged density, and tissue porosity) (Lai et al., 1991; Gu et al., 2003a; Gu et al., 2004; Yao and Gu, 2004). This model is an extension of the framework of mechano-electrochemical mixture theories (Lai et al., 1991; Gu et al., 1998; Yao and Gu, 2007a). More details of the theoretical formulation can be found in our previous studies (Huang and Gu, 2007; Yao and Gu, 2004; Yao and Gu, 2006; Yao and Gu, 2007a).

FINITE ELEMENT ANALYSIS

The lumbar IVD was assumed to be an axisymmetric object which consisted of two distinct anatomical regions (NP and AF) with dimensions similar to those reported in the literature (Selard et al., 2003; Soukane et al., 2005) (Figure 1). The transport and metabolism of oxygen and lactate in the IVD under three loading configurations (no compressive deformation, static compression, and dynamic compression) were analyzed. Initially, the IVD was equilibrated with prescribed boundary conditions without compression. During static compression, the disc was compressed between two endplates with a constant displacement (−u₀) until the tissue reached equilibrium. For the dynamic loading test, the equilibrium state of static compression was used as the initial condition and the disc was subjected to a sinusoidal displacement with amplitude of u₁ and frequency of f (Figure 1). The solute exchange area was either 50% (partially permeable) or 0% (impermeable) for the endplate region adjacent to the NP while the endplate adjacent to the AF was calcified (no solute exchange). The boundary conditions for oxygen and lactate were adopted from a previous study (Soukane et al., 2005). The specific boundary conditions for the problems under consideration are given in Table 1. The unit conversion of oxygen concentration between kPa and μM can be performed using the solubility of oxygen in water (i.e., 1.0268×10⁻⁶mol/kPa-100mL (Soukane et al., 2005)). The parameters of the theoretical model were the same as those used in our previous study (Huang and Gu, 2007), except the properties listed in Table 2.

Table 1.

Specific boundary conditions of the finite element analysis^a

	At the AF edge	At the endplate(i.e., z=h0)
Oxygen/Lactate	c+ = c− =0.15 M, co2= =5.8 kPa, clactate= 0.9 mM.	$\{\begin{array}{ll}{J}_z^{+}=J_z^{-}=J_z^{O_2}=J_z^{\mathit{lactate}}=0\text{ (molar solute flux)}\hfill & \text{if impermeable}\hfill \\ c^{+}=c^{-}=0.15\text{M},c^{O_2}=5.1\text{kPa},c^{\mathit{lactate}}=0.8\text{mM}\hfill & \text{if permeable}\hfill \end{array}$
Solid Matrix	σr = σrz = 0	$\begin{array}{l}{u}_z^b=\{\begin{array}{ll}0\hfill & \text{when without compression}\hfill \\ -u_0\hfill & \text{when with static compression}\hfill \\ -u_0-u_{1}sin(2\pi ft)\hfill & \text{when with dynamic compression}\hfill \end{array}\\ u_r=0\end{array}$

^aThe rest of boundary conditions for stress and strain of solid matrix, fluid pressure, and fluxes of water and solute for the 2-D axisymmetric case of unconfined compression were described in our previous study (Huang and Gu, 2007).

^bu₀ =10% of disc height (i.e., 0.1h₀), f=0.1 or 0.01Hz, and u₁ =2.5% or 5% of disc height (i.e., 0.025h₀ or 0.05h₀).

Table 2.

Tissue properties in the theoretical analysis

Region	Water volume fraction φWa	CLE parameters(MPa)	Cell density ρcell (cells/mm3)	Parameters for the constitutive equation of diffusivityc	Parameters for the constitutive equation of hydraulic permeabilityf
AF	${\phi }_0^w=0.75$	H+A =2.52; H−A = 0.19; λ2 =0.14; μ = 0.025	9000b	A=1.29 d B=0.375d	a= 0.00339 nm2 g n=3.24 g
NP	${\phi }_0^w=0.85$	H+A = H−A =0.14; λ2 = 0.1; μ =0.02	4000 b	A=1.25 e B=0.681e	a= 0.00044 nm2 g n=7.1929 g

^aThe tissue porosity (φ^w) is related to the tissue dilatation (e) and the porosity $({\phi }_0^w)$ at the reference configuration: ${\phi }^w=\frac{{\phi }_0^w+e}{1+e}$

^b(Maroudas et al., 1975)

^cTissue diffusivity was estimated using the constitutive equation: $\frac{D^{\alpha }}{D_0^{\alpha }}=exp\left(-A{\left(\frac{r_s^{\alpha }}{\sqrt{k\eta }}\right)}^B\right)$ (Gu et al., 2004) where $D_0^{\alpha }$ is the solute diffusivity in aqueous solution $(D_0^{O_2}=3\times {10}^{-9}{\text{m}}^2/2;D_0^{\mathit{lactate}}=1.28\times {10}^{-9}{\text{m}}^2/\text{s})$, r_s is the hydrodynamic radius of solute $\alpha (r_s^{{\text{O}}_2}=0.1\text{nm};r_s^{\mathit{lactate}}=0.255\text{nm})$, k is the hydraulic permeability, η is the viscosity of water, and A and B are the material constants.

^dDetermined from porcine AF tissues (Gu et al., 2004).

^eDetermined from agarose gels (Gu et al., 2004).

^fHydraulic permeability (k) of the tissue was estimated using the constitutive equation: $k=\frac{a}{\eta }{\left(\frac{{\phi }^w}{1-{\phi }^w}\right)}^n$ (Gu et al., 2003b) where a and n are material constants.

^gGu et al., 2003.

Non-dimensionalization and Numerical method

The variables were non-dimensionalized for numerical calculation. The definitions of the non-dimensional quantities are similar to those described in our previous study (Huang and Gu, 2007) and the key quantities used in data presentation are listed as follows:

$$\begin{array}{l}\widehat{r}=\frac{r}{h_0},\widehat{z}=\frac{z}{h_0},\widehat{t}=\frac{t}{h_0^2/H_A^{\ast }{k}_0},{\widehat{c}}^{{\text{O}}_2}=\frac{c^{{\text{O}}_2}}{c^{O_2\ast }},{\widehat{c}}^{\text{lactate}}=\frac{c^{\text{lactate}}}{c^{\mathit{lactate}\ast }},\\ {\widehat{Q}}^{{\text{O}}_2}=\frac{Q^{{\text{O}}_2}}{H_A^{\ast }{k}_0{c}^{O_2\ast }/h_0^2},{\widehat{Q}}^{\mathit{latacte}}=\frac{Q^{\mathit{latacte}}}{H_A^{\ast }{k}_0{c}^{\mathit{lactate}\ast }/h_0^2}\end{array}$$ (5)

where k₀ is the reference permeability which was chosen as 5×10⁻¹⁶m⁴/Ns, H*_A is the reference equilibrium modulus which was chosen as H_−A of NP and c^O₂* and c^lactate* are the reference concentrations of oxygen and lactate, respectively, which were chosen as boundary conditions on the endplate.

The details of the finite element method and numerical implementation were described in our previous studies (Sun et al., 1999; Yao and Gu, 2004; Huang and Gu, 2007). A mesh of ~3400 second-order triangle Lagrange elemen ts was used to analyze the two-dimensional upper quadrant portion of the disc. For the 50% permeable endplate boundary (above the NP), an alternated boundary condition was assigned at every other element (see Table 1).

The averaged concentration of oxygen or lactate in the tissue was determined as

$${\overline{c}}^{\alpha }=\int \int c^{\alpha }2\pi \widehat{r}d\widehat{r}d\widehat{z}/\int \int 2\pi \widehat{r}d\widehat{r}d\widehat{z}(\alpha ={\text{O}}_2\text{ or lactate})$$ (6)

The averaged oxygen consumption or lactate production in the tissue was calculated as

$${\overline{Q}}^{\alpha }=\int \int {\widehat{Q}}^{\alpha }2\pi \widehat{r}d\widehat{r}d\widehat{z}/\int \int 2\pi \widehat{r}d\widehat{r}d\widehat{z}(\alpha ={\text{O}}_2\text{ or lactate})$$ (7)

The amount of oxygen consumption or lactate production in the tissue from t̂ = t̂₁ to t̂ = t̂₂ was evaluated as

$${\widehat{M}}^{\alpha }={\int }_{{\widehat{t}}_1}^{{\widehat{t}}_2}\left[\int \int {\widehat{Q}}^{\alpha }2\pi \widehat{r}d\widehat{r}d\widehat{z}\right]d\widehat{t}.(\alpha ={\text{O}}_2\text{ or lactate})$$ (8)

The effect of dynamic loading on cellular metabolism was evaluated by calculating the relative increase in the amount of oxygen consumption or lactate production with dynamic compression compared to static compression:

$${\mathrm{\Delta }}^{\alpha }=\frac{{\widehat{M}}_{\text{Dynamic}}^{\alpha }-{\widehat{M}}_{\text{Static}}^{\alpha }}{{\widehat{M}}_{\text{Static}}^{\alpha }}(\alpha ={\text{O}}_2\text{ or lactate})$$ (9)

Dynamic loading would enhance solute metabolism if Δ^α is positive.

RESULTS

Effect of Static Compression

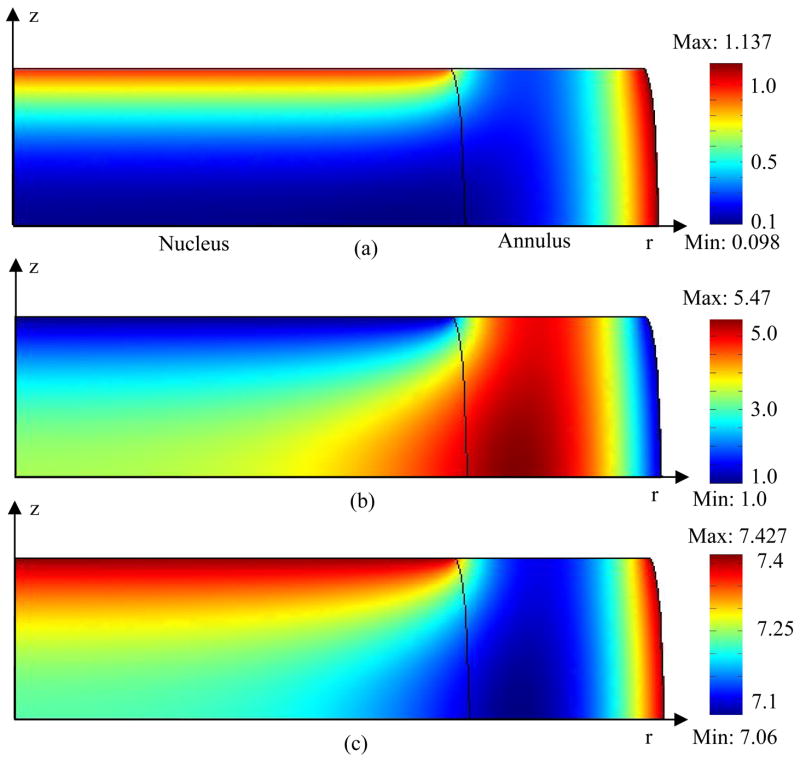
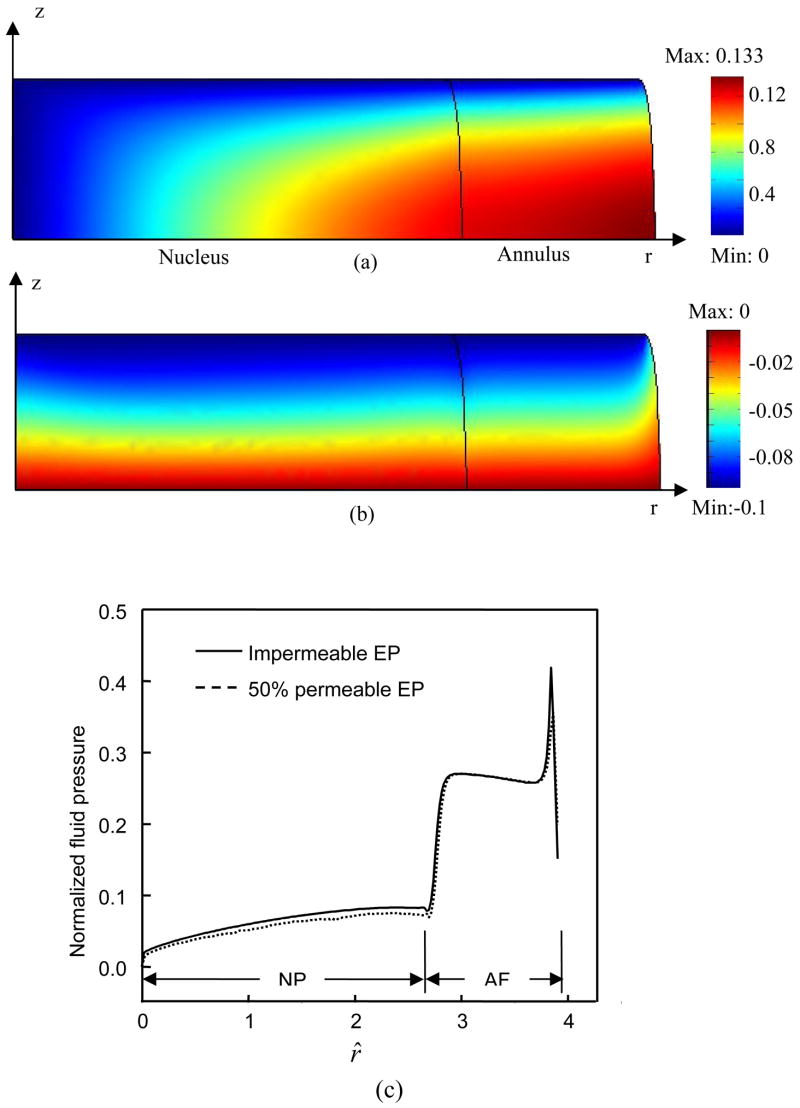
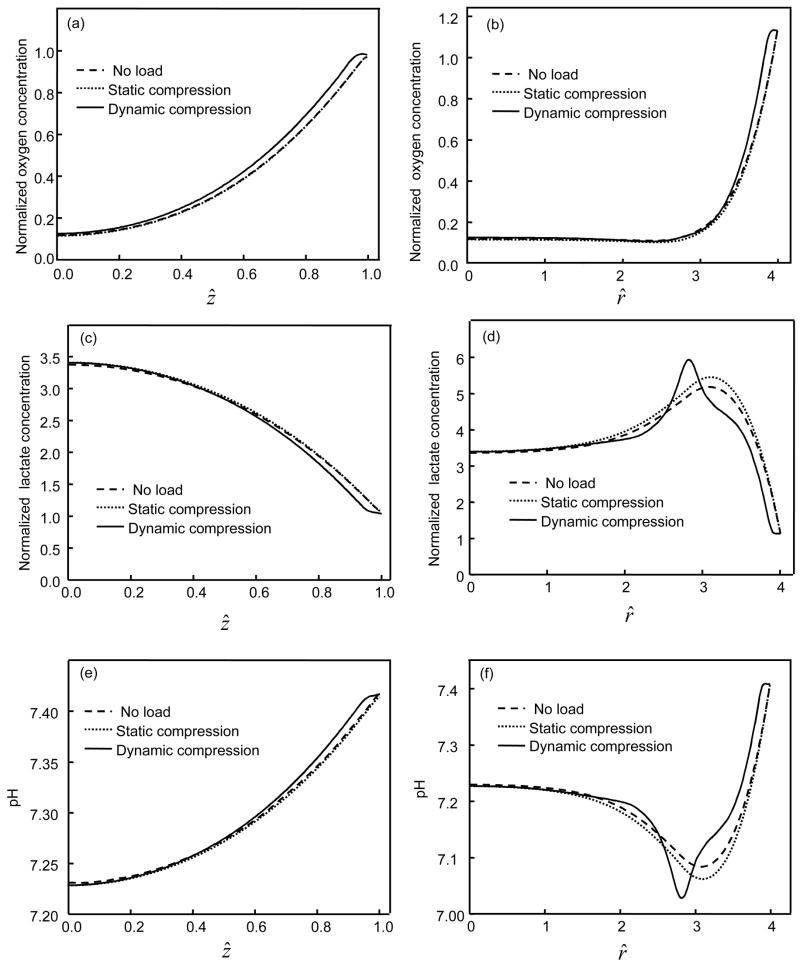
In general, oxygen concentration decreased and lactate concentration increased with distance from the blood supply at the endplate and at the periphery of the IVD (Figures 2 and 3). For the cases where endplate was 50% permeable or completely impermeable, the minimum oxygen concentration was located in the NP region (Figures 2 and 3). The maximum lactate concentration located in the AF region for the 50% permeable case (Figure 2) and in the NP region for the impermeable case (Figure 3). The displacements within the IVD under static compression were shown in Figures 4a and 4b. The endplate boundary conditions (50% permeable vs. impermeable) had little effects on the mechanical responses (e.g., stress, strain, and fluid pressure) of the IVD under dynamic loading. For example, only a minor difference was seen on fluid pressure at the endplate above the NP regions (Figure 4c). Static compression caused a small decrease in oxygen concentration (Figures 5b and 6a) but greater changes in both lactate concentration and pH within the IVD (Figures 5d&f and 6b&c), especially at the interface between NP and AF. For the case where endplate was 50% permeable, the averaged oxygen concentration at equilibrium decreased 1.6% in the NP region and 3% in the AF region while the averaged lactate concentration increased 2.4% in the NP region and 5.1% in the AF region. For the case where endplate was impermeable, the averaged oxygen concentration at equilibrium decreased 14.3% in the NP region and 2.5% in the AF region while the averaged lactate concentration increased 5.4% in the NP region and 6.4% in the AF region.

Figure 2.

Distribution of (a) oxygen, (b) lactate, and (c) pH within the IVD under static compression with 50% permeable endplate boundary above the nucleus. Concentrations of oxygen and lactate were normalized by their boundary concentrations at the endplate region above the nucleus. A constant displacement (10% of disc height) was applied to the IVD.

Figure 3.

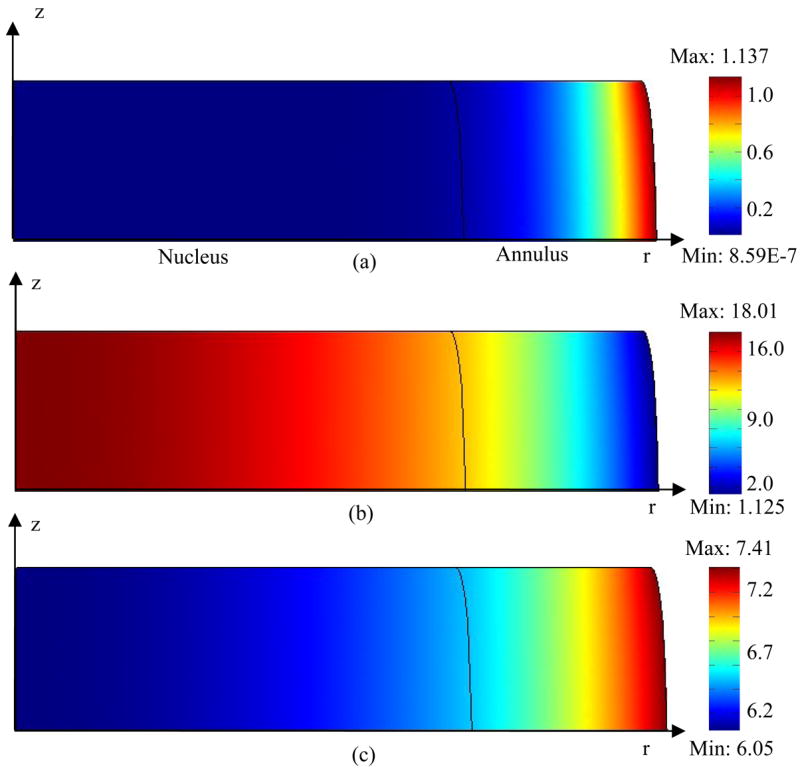
Distribution of (a) oxygen, (b) lactate, and (c) pH within the IVD under static compression with impermeable endplate boundary above the nucleus. Concentrations of oxygen and lactate were normalized by their boundary concentrations at the endplate region above the nucleus. A constant displacement (10% of disc height) was applied to the IVD.

Figure 4.

Displacements in (a) radial and (b) axial directions within the IVD under static compression with 50% permeable endplate boundary above the nucleus. Displacements were normalized by the half height of the disk (h₀). (c) Radial distributions of normalized fluid pressure (at z^ =1) in the IVDs with different endplate boundary conditions at the first peak of the first cycle of sinusoidal loading (f=0.1 Hz, u₁=5% of disc height). The fluid pressure (p) is normalized by p/(RTc*), where R is universal gas constant, T is absolute temperature, and c* is the concentration of saline (i.e., c*=0.15 M) (Huang and Gu, 2007).

Figure 5.

Comparison of (a,b) oxygen, (c,d) lactate, and (e,f) pH distributions along the radius at ẑ =0 (a,c,e) and the center line at r^ =0 (b,d,f) among the IVDs with 50% permeable endplate boundary above the nucleus. For the static compression test, a constant displacement (10% of disc height) was applied on the IVD. For the dynamic compression test, the IVD was subjected to a sinusoidal displacement (f=0.1 Hz, u₁=5% of disc height) for 200 cycles. Concentrations of oxygen and lactate were normalized by their boundary concentrations at the endplate region above the nucleus.

Figure 6.

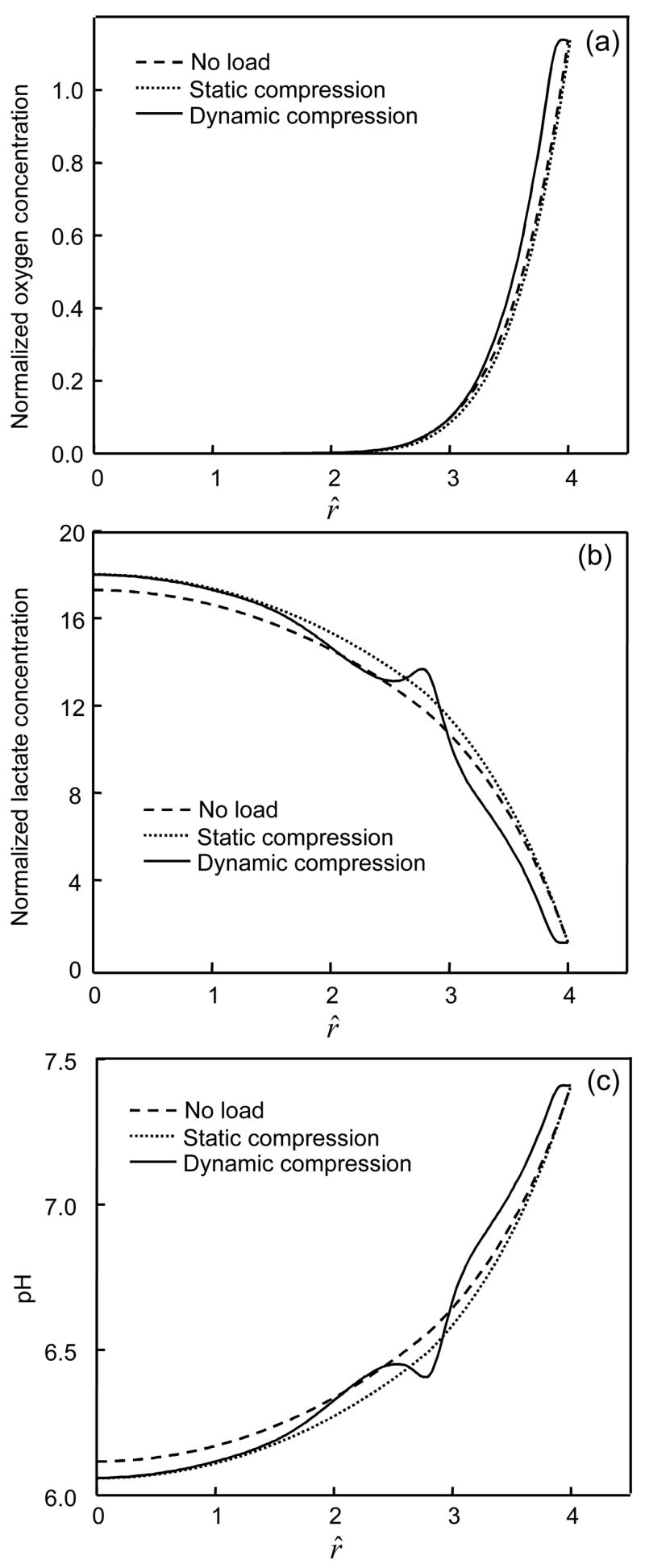
Comparison of (a) oxygen, (b) lactate, and (c) pH distributions along the center line at r^ =0 among the IVDs with impermeable endplate boundary above the nucleus. For the static compression test, a constant displacement (10% of disc height) was applied on the IVD. For the dynamic compression test, the IVD was subjected to a sinusoidal displacement (f=0.1 Hz, u₁=5% of disc height) for 200 cycles. Concentrations of oxygen and lactate were normalized by their boundary concentrations at the endplate region above the nucleus.

Effect of Dynamic Compression

When tissue was subjected to dynamic loading, the oxygen concentration and pH increased while lactate concentration decreased within the IVD except for the region near the NP-AF interface (Figures 6 and 7). For the case where endplate was 50% permeable, after 200 cycles of loading (f=0.1 Hz, u₁=0.1h₀), the averaged oxygen concentration increased 8.2% in the NP region and 16.8% in the AF region while the averaged lactate concentration decreased 3.3% in the NP region and 8.3% in the AF region. For the case where endplate was impermeable, after 200 cycles of loading (f=0.1 Hz, u₁=0.1h₀), the averaged oxygen concentration increased 33.3% in the NP region and 22.2% in the AF region while the averaged lactate concentration decreased 1.6% in the NP region and 10.9% in the AF region. The effects of dynamic loading on transport of oxygen and lactate were more pronounced in the region close to the endplate or the edge of AF (Figures 5 and 6).

Figure 7.

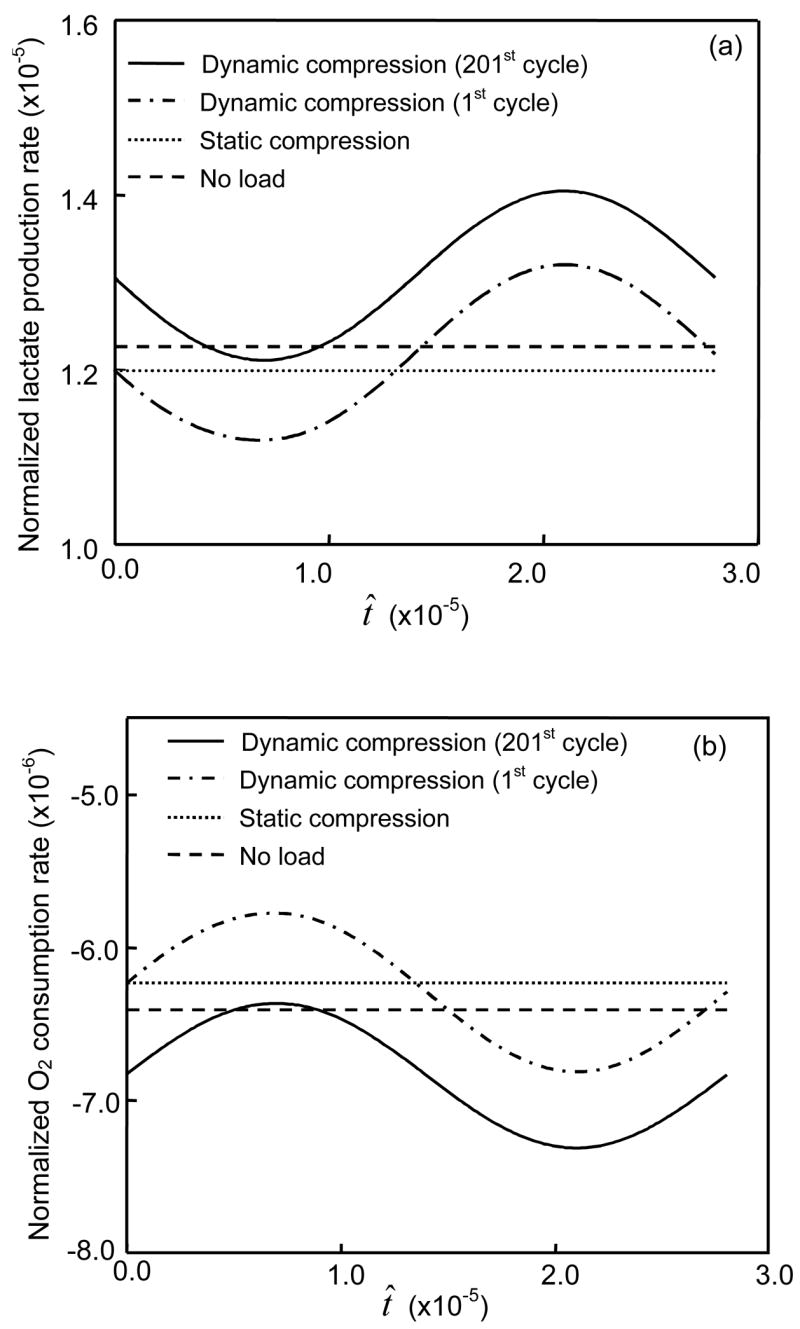
Effects of compressive loading on averaged rates of (a) oxygen consumption and (b) lactate production in the annulus region of the IVD with 50% permeable endplate boundary above the nucleus. For the static compression test, a constant displacement (10% of disc height) in was applied on the IVD. For the dynamic compression test, the IVD was subjected to a sinusoidal displacement (f=0.1 Hz, u₁=5% of disc height) for one or 200 cycles.

Dynamic loading enhanced the oxygen consumption and lactate production. The rates of oxygen consumption and lactate production increased with increasing period of dynamic loading (Figure 7). These effects of dynamic loading on oxygen consumption and lactate production increased with increasing strain amplitude (see Figures 8a and 8b) and loading frequency (Figure 9). For the IVD with impermeable endplate, oxygen consumption and lactate production were profoundly promoted by dynamic loading (Figure 8c).

Figure 8.

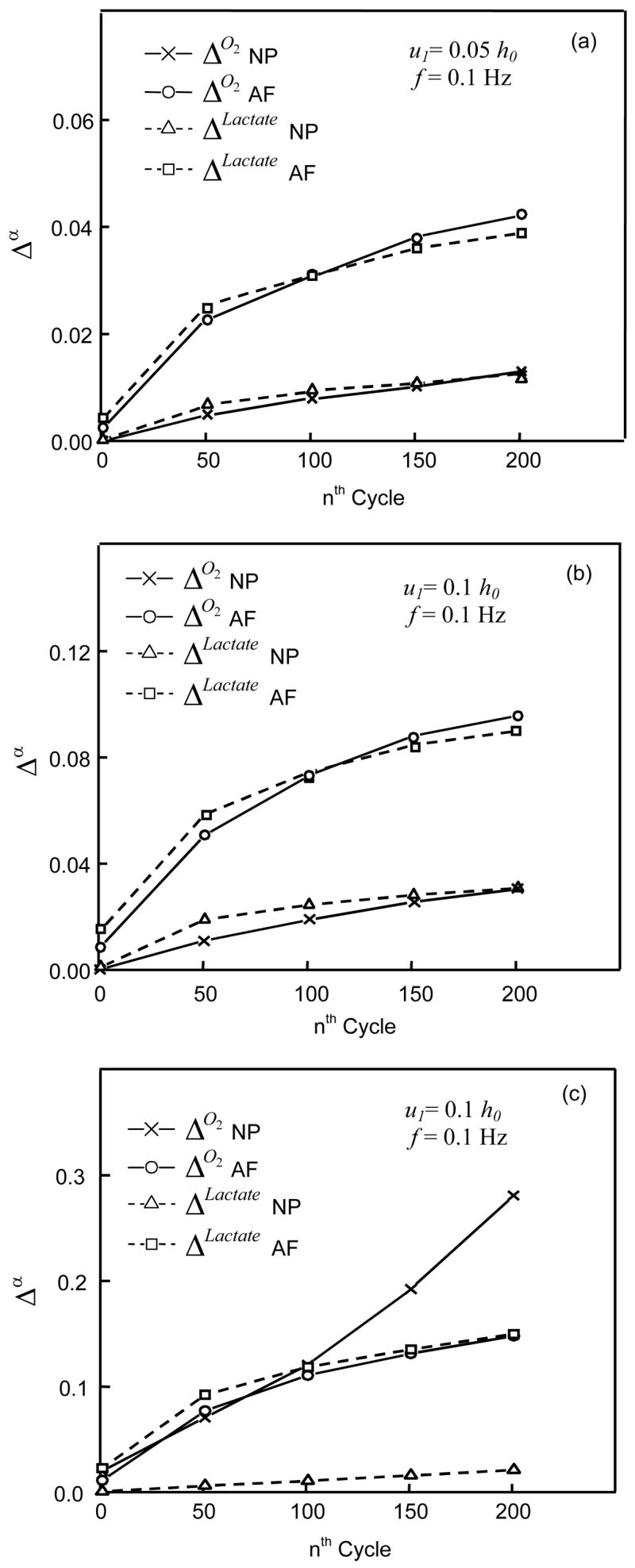
Δ^o₂ and Δ^Lactate for two different anatomical regions (NP and AF) of IVDs under dynamic loading with the conditions of (a and b) 50% permeable and (c) impermeable endplates. For the dynamic compression test, the loading frequency was 0.1Hz and amplitude was either (a) 2.5% or (b and c) 5% of disc In (b), the Δ^o₂ height increased from 0.03% during the 1^st cycle to 3% during the 201^st cycle for NP and from 0.9% to 9.6% for AF while the Δ^Lactate increased from 0.1% during the 1^st cycle to 3.1% during the 201^st cycle for NP and from 1.5% to 9% for AF. In (c), the Δ^o₂ increased from 2% during the 1^st cycle to 28.1% during the 201^st cycle for NP and from 1.1% to 15.8% for AF, while the Δ^Lactate increased from 0.08% during the 1^st cycle to 2.1% during the 201^st cycle for NP and from 2.2% to 15% for AF

Figure 9.

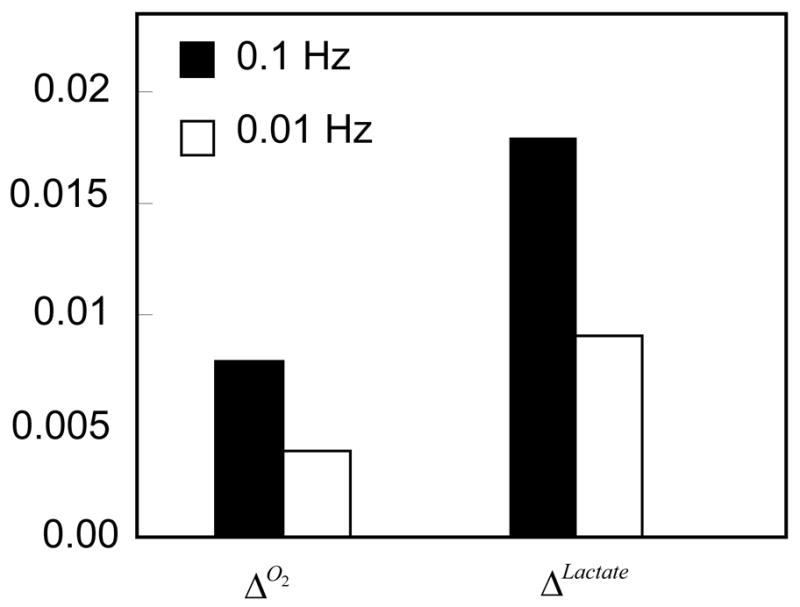
Effects of loading frequency on Δ^o₂ and Δ^Lactate of IVDs with 50% permeable endplates. The loading amplitude was 5% of disc height, the loading duration was 100 sec, and the frequency was either 0.1Hz or 0.01Hz.

DISCUSSION AND CONCLUSION

During body motion, IVDs transmit large loads between bony vertebral bodies. Many studies have demonstrated that mechanical loading affects the transport of solutes within cartilaginous tissues by changing solute diffusivity in tissue (Quinn et al., 2000; Quinn et al., 2001; Nimer et al., 2003) and/or enhancing solute convection (Evans and Quinn, 2006b; Evans and Quinn, 2006a; Huang and Gu, 2007; O’Hara et al., 1990; Yao and Gu, 2004; Yao and Gu, 2007b). Since the nutrient metabolism of IVD cells (i.e., oxygen and glucose) was regulated by nutrient concentrations (Huang et al., 2007; Bibby et al., 2005; Holm et al., 1981; Ishihara and Urban, 1999), mechanical loading may influence the cellular metabolism of nutrients by altering nutrient transport within the IVD. Due to the difficulty in examining the transport and cellular metabolism of nutrients within the IVD in vivo (especially for the discs under mechanical loads), in this study, a new theoretical formulation was developed by incorporating the metabolic rates of solutes into the mechano-electrochemical mixture model (Huang and Gu, 2007; Yao and Gu, 2004; Yao and Gu, 2007b; Lai et al., 1991; Gu et al., 1998) to numerically investigate the transport and metabolism of nutrients within the IVD under mechanical loading. To our knowledge, this study was the first to theoretically demonstrate the effects of dynamic and static compressions on transport and metabolism of oxygen and lactate in the IVD.

At the equilibrium state, the balance between the metabolism and transport of solute determines local solute concentration. Cellular metabolism of solutes alters local solute concentration to the level that can be maintained through diffusion and convection. Static compression reduces tissue porosity, leading to a decrease in solute diffusion in or out the IVD. Such a reduction changes the local solute concentration and, in turn, alters the metabolic rate of solute until the solute concentration reaches a new level of balance. Therefore, static compression reduces oxygen concentration and enhances lactate accumulation within the IVD.

On the other hand, dynamic loading can cause an increase in oxygen concentration and a decrease in lactate accumulation within the IVD (Figures 5 and 6). This is mainly due to the metabolic rate of cells that depends nonlinearly on solute concentration (Eqs. 2 and 3). Changes in the concentrations of oxygen and lactate due to dynamic loading would affect their metabolic rate, which would influence the concentration distributions of solutes through mass balance equation (1).

The metabolic rates of oxygen and lactate of IVD cells increase with increasing oxygen concentration or pH (i.e., Eqs. (2) and (3)) (Huang and Gu, 2007; Bibby et al., 2005) and pH is inversely dependent on lactate concentration, e.g., Eq. (4) (Soukane et al., 2005; Bibby et al., 2005). Therefore, an increase in oxygen concentration and/or a decrease in lactate concentration within the IVD by dynamic loading would augment oxygen consumption and lactate production of cells (Figure 7). Lactate is converted from glucose through glycolysis, a main process that supplies energy for IVD cells (Bibby et al., 2005; Holm et al., 1981). Therefore, the findings suggest that dynamic loading could also increase glucose consumption of IVD cells and promotes energy production. However, static compressive loading exhibited inverse effects on cellular metabolism of oxygen and lactate (Figure 7).

The concentration profiles of oxygen and lactate (Figures 2, 3, 5, and 6) are consistent with the previous studies in the literature (Selard et al., 2003; Soukane et al., 2005; Holm et al., 1981; Ejeskar and Holm, 1979). For the IVD under static compression with 50% permeable endplate above NP region, the minimum oxygen concentration, maximum lactate concentration, and minimum pH were calculated as 0.49 kPa, 4.37 nmol/mm³, and 7.1, respectively. These data are in agreement with the previous studies that reported the range of 0.3–1.06 kPa for oxygen concentration in canine NP (Holm et al., 1981; Ejeskar and Holm, 1979), the range of 2–6 nmol/mm³ for lactate concentration in human discs (Bartels et al., 1998), and the averaged pH of 7.14 in human discs (Kitano et al., 1993). Therefore, the new theoretical model developed in this study is suitable for investigating the transport and metabolism of nutrients in the IVD.

The lactate production rates were assumed to be the same for NP and AF cells (i.e., Eq. (3)) in this study. Since the cell density is higher in the AF than in the NP, the lactate production per unit volume is greater for the AF than for the NP at the same oxygen concentration and pH. This difference may explain why the maximum lactate concentration was located in the AF region near the NP-AF interface of the IVD with 50% impermeable endplate (Figure 5d). The effects of this difference on lactate distribution were more pronounced in the IVDs under dynamic loading (Figures 5d and 6b). However, due to the differences in oxygen consumption rate between the NP and AF cells, the oxygen consumption per unit volume between the AF and NP became similar after taking into account cell density. Therefore, no peak occurred in oxygen tension near the NP-AF interface (Figure 5). Conversely, if the oxygen consumption rates of NP and AF cells are assumed to be the same, the distribution profile of oxygen would be different with a minimum value of oxygen concentration located in the AF region (Soukane et al., 2005). Because the difference in metabolic rates between the AF and NP has an influence on the distributions of nutrients and metabolites, it may be necessary to investigate the difference in lactate production between the AF and NP cells.

Although the permeability of endplate did not appear to influence the mechanical responses of the IVD tissue significantly (e.g., Figure 4c), it is an important factor that strongly affects the distribution of nutrients and metabolites. When the endplate is impermeable, the minimum oxygen concentration reduces to almost zero (Figure 6a), maximum lactate concentration increases to 14.4 nmol/mm³ (Figure 6b with a normalization factor of 0.8 mM, see Table 1), and minimum pH falls around 6.1 (Figure 6c). A similar high level of lactate has been found in the discs of patients with scoliosis (16 nmol/mm³) and back pain (12 nmol/mm³) (Bartels et al., 1998). The value of pH below 6.5 has been measured in human discs (Nachemson, 1969). However, no previous data in literature were found to support such extreme case of oxygen tension. Since the measurement of in vivo oxygen tension in the IVD is usually performed using invasive techniques, it may be difficult to obtain an accurate measurement of such low level of oxygen as extra oxygen may be introduced into the disc by invasive procedures. It is also possible that the condition of impermeable endplate does not occur since the IVD cells may not survive long at low oxygen level (Bibby et al., 2005; Horner and Urban, 2001). Nevertheless, in this study the case of impermeable endplate was used to demonstrate the dramatic effect of dynamic loading on cellular metabolism when the porosity of endplate decreases. Dynamic loading can cause almost 30% increase in oxygen consumption of NP cells (during the 201^st cycle, Figure 8c) compared to the static compression case. Such an increment can be higher as the duration of dynamic loading increases. Therefore, dynamic loading may be beneficial for aged and diseased discs whose endplates tend to be calcified (Bernick and Cailliet, 1982; Nachemson et al., 1970). However, it should be noted that some of the parameters (i.e., the rates of oxygen consumption and lactate production and tissue diffusivity) used in the theoretical analysis were obtained from different animal IVD cells or tissues (i.e., porcine and bovine). In order to precisely predict the distribution of nutrients in human IVD under dynamic loading, all parameters of human IVD need to be determined in the future studies.

The theoretical model in this study has taken into account the realistic complex material properties of extracellular matrix such as tissue tension-compression nonlinearity and strain-dependent properties. It can provide a realistic prediction of solute transport in the IVD. However, since many studies have shown that mechanical loading would regulate cellular responses of IVD such biosynthesis of extracellular matrix (Ohshima et al., 1995; Walsh and Lotz, 2004; Chen et al., 2004; MacLean et al., 2005), it is reasonable to expect that mechanical loading may also have an intrinsic influence on cellular metabolic rates of nutrients and metabolites (i.e., the parameters in Eqs. (2) and (3) were affected by mechanical loading). Therefore, the strain-dependent cellular metabolic rates may be needed to accurately predict the distribution of nutrients and metabolites within the disc.

In summary, dynamic compression increases oxygen concentration, reduces lactate accumulation, and promotes oxygen consumption and lactate production (i.e., energy conversion). Such effects of dynamic loading are dependent on strain level and loading frequency and more pronounced in the IVD with reduced permeability of endplate. However, static compression exhibits inverse effects on distributions and metabolism of oxygen and lactate. This study has established a new theoretical model for analyzing cellular metabolism of nutrients in hydrated, fibrous soft tissues under mechanical loading.