Systematic derivation of partition functions for ligand binding to two-dimensional lattices

Abstract

The Ising problem consists in finding the analytical solution of the partition function of a lattice once the interaction geometry among its elements is specified. No general analytical solution is available for this problem, except for the one-dimensional case. Using site-specific thermodynamics, it is shown that the partition function for ligand binding to a two-dimensional lattice can be obtained from those of one-dimensional lattices with known solution. The complexity of the lattice is reduced recursively by application of a contact transformation that involves a relatively small number of steps. The transformation implemented in a computer code solves the partition function of the lattice by operating on the connectivity matrix of the graph associated with it. This provides a powerful new approach to the Ising problem, and enables a systematic analysis of two-dimensional lattices that model many biologically relevant phenomena. Application of this approach to finite two-dimensional lattices with positive cooperativity indicates that the binding capacity per site diverges as N^a (N = number of sites in the lattice) and experiences a phase-transition-like discontinuity in the thermodynamic limit N → ∞. The zeroes of the partition function tend to distribute on a slightly distorted unit circle in complex plane and approach the positive real axis already for a 5×5 square lattice. When the lattice has negative cooperativity, its properties mimic those of a system composed of two classes of independent sites with the apparent population of low-affinity binding sites increasing with the size of the lattice, thereby accounting for a phenomenon encountered in many ligand-receptor interactions.

Ising lattices with nearest-neighbor interactions have long been used to model cooperative transitions. Originally developed to understand the properties of ferromagnets (1), these lattices have also found myriad applications in polymer statistics (2), ligand binding and condensation (3), helix–coil transitions (4, 5), protein folding (6), molecular recognition (7), and gel-fluid transitions of lipid membranes (8). A fascinating aspect of Ising lattices, which has enticed outstanding theoretical chemists and physicists over the past 70 years, stems from the contrast between the simplicity of the underlying assumptions and the extraordinary complexity of the combinatorics involved. The Ising problem consists in finding the analytical solution of the partition function of a lattice once the interaction geometry among its elements is specified. Presently, this problem remains one of the toughest unsolved puzzles of statistical thermodynamics (9). Any significant contribution made toward solution of the Ising problem would broaden our basic understanding of cooperative transitions in physics, chemistry, and biology.

Exact analytical solutions of the Ising problem are available for the one-dimensional case and for certain two-dimensional cases with symmetry properties in the thermodynamic limit of an infinite number of elements. The solution in the one-dimensional case poses no mathematical difficulties and is obtained using the celebrated method of the transfer matrix (10). In the two-dimensional case with symmetry related elements two such matrices must be defined, one for each dimension, and the solution emerges from a monumental sequence of mathematical transformations (11, 12). No solution is available for the three-dimensional Ising problem and, even in the two-dimensional case, the method based on the transfer matrix cannot be exploited in general (9). Hence, there is much need for alternative methods of approach to the Ising problem, especially in those cases where the lattice is finite, lacks symmetry, and has an arbitrary interaction geometry. These lattices are most relevant in biology because they can model molecular recognition and protein folding (6, 7), ligand binding to nucleic acids or to receptors on the cell membrane (13), protein–lipid interactions on a membrane (8), as well as related site-specific effects (14).

Ideally, one would like to have a systematic method that derives the partition function of the lattice from the connectivity matrix of the graph associated with it. A brute force approach that exhausts all possible configurations of the lattice has been used (7, 15), but is severely limited by computing power. For a lattice composed of N elements, existing in two possible states, this approach must calculate each of the 2^N terms in the partition function. The task becomes rapidly unrealistic for N > 20 (7). In this study we introduce a method based on site-specific thermodynamics (14) that simplifies considerably the combinatorics of the Ising problem.

The Contact Transformation

We will deal specifically with the problem of ligand binding to a finite two-dimensional lattice composed of N sites. This problem is formally equivalent to the spin transitions of a ferromagnet under the influence of an external field (16) and cannot be handled in terms of the Onsager–Kaufman solution (11, 12), which applies to infinite lattices in the absence of external field. Each site of the lattice can be free or bound to the ligand, whose concentration in solution is x. The equilibrium binding constant K for the free → bound transition of the site is assumed to be the same for all sites and, therefore, the partition function of the lattice can be cast in terms of a scaled concentration, or activity variable ω = Kx (14). When nearest-neighbor sites in the lattice are in contact, they are coupled according to the lattice–gas interaction rule (3, 14). This rule states that the two neighbor sites in contact experience an interaction when they are both bound. The strength of the interaction is quantified by the dimensionless parameter σ, which is bound from 0 to ∞. The value of σ signals the presence of positive cooperativity (σ > 1), negative cooperativity (σ < 1), or absence of cooperativity (σ = 1). Physically, σ is the equilibrium constant for the dismutation reaction involving two pairs of neighboring sites, each pair being in contact

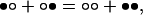1

where ○ denotes a site free and • denotes a site bound. The partition function for a simple lattice composed of two sites in contact is therefore

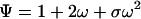2

The first term is contributed by the fully unligated form of the lattice, which is used as reference; the second term refers to the two equivalent configurations with one site bound; and the third term refers to the doubly ligated configuration, where the sites interact according to the lattice–gas rule.

A consequence of the lattice–gas rule is that keeping a site free is equivalent to eliminating that site from the lattice. This elimination principle expresses the fact that a given site in the lattice can influence other sites only when it is bound. When a site is free, all sites in contact with it behave as though the site were not present. Though somewhat obvious, the elimination principle has unexpectedly profound consequences, one of which is given below.

It follows from site-specific thermodynamics (14) that the partition function Ψ of an Ising lattice can be written as

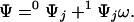3

⁰Ψ_j denotes the first-order contracted partition function containing all possible ligated configurations of the other sites when site j is free and ¹Ψ_j is the analogous term containing all configurations with site j bound. For a lattice composed of N sites, Ψ is a polynomial of degree N in ω and contains 2^N terms, half of which define ⁰Ψ_j, whereas the other half define ¹Ψ_j. The term contracted reflects the reduction in the degree of the polynomial defining the partition function due to fixing a particular site, or set of sites, in a given ligated state. Eq. 3 holds for any site j. Each first-order contracted partition function can itself be expressed in terms of second-order contracted partition functions by considering the ligation states of a second site i as follows:

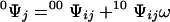4a

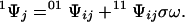4b

⁰⁰Ψ_ij denotes the second-order contracted partition function containing all configurations of the other sites when sites i and j are free, ⁰¹Ψ_ij is the analogous term containing all configurations with sites i free and j bound, and so forth for the other terms. Eq. 4 holds for any two sites i ≠ j. The factor σ in Eq. 4b must appear if the two sites i and j are in contact. Hence, the partition function of the lattice can be written in terms of contracted forms over two sites in contact by substituting Eq. 4 into Eq. 3, so that

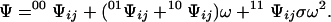5

Consider now another lattice that differs from the original one only in that the contact between sites i and j has been removed. The partition function for this lattice is evidently

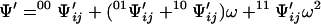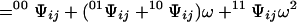6

and differs from Eq. 5 only because σ does not appear in the factor of the last term of the second-order expansion. Fixing the ligation state of sites i and j produces contracted partition functions that do not depend on the contact between these sites. Simple transformations involving Eqs. 4–6 yield

7

The partition function of the original lattice, Ψ, can be expressed in terms of those of simpler lattices obtained by deleting the contact between two sites, Ψ′, and either or both sites, ⁰Ψ_i, ⁰Ψ_j, and ⁰⁰Ψ_ij. The elimination principle and recursive application of the contact transformation embodied by Eq. 7 reduce Ψ to elementary partition functions with known analytical solution. This result, which applies to any Ising lattice, provides a powerful new tool for tackling the Ising problem both analytically and computationally.

As a simple application of the contact transformation we derive the partition function of a one-dimensional ring from that of linear lattices. If Ψ is the partition function of the ring of N sites, then Ψ′ is the partition function of a perturbed ring where the contact between two neighbor sites, i and j, has been removed. This perturbed ring is de facto a linear lattice of N sites where sites i and j are the end sites. ⁰⁰Ψ_ij is the contracted partition function of the ring with the sites in contact i and j free. By virtue of the elimination principle, this is equivalent to the partition function of a linear lattice of N − 2 sites. Similar arguments prove that ⁰Ψ_i and ⁰Ψ_j are the partition functions of a linear lattice of N − 1 sites. Let N = 3 for the sake of simplicity. Then,

8a

8b

8c

Hence,

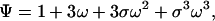9

which is, in fact, the partition function of the ring of three sites.

The Algorithm

The result embodied by Eq. 7 can be implemented in a computer code. Fig. 1 illustrates how this is done in practice for the case of a 3×3 square lattice. The algorithm operates a series of transformations on the connectivity matrix of the lattice (17)

10

The element c_ij of this symmetric matrix specifies the number of contacts between sites i and j, whereas the sum of all elements over the ith row or column gives the total number of sites in contact with site i. The algorithm starts from the first site in the sequence that has the largest number of contacts (site 5). Among its neighbors (sites 2, 4, 6, 8), the first one in the sequence that itself has the largest number of contacts is then identified (site 2). At this point, Eq. 7 is applied to eliminate the contact between these sites (sites 5 and 2). Four lattices are generated in the first step, labeled from “1” through “4,” one for each term of Eq 7. Specifically, “1” denotes removal of the contact between the sites, “2” denotes deletion of the two sites, “3” and “4” denote deletion of the first and second site in the sequence. In the next step, the algorithm is applied to each one of these lattices and the resulting lattices are labeled in the same way. Hence, lattices “11,” “12,” “13,” and “14” are generated from lattice “1.” The algorithm produces a new generation of lattices at each step and iterates until all connectivity matrices contain sites that contact at most two neighbors. In this case, the associated lattice is one-dimensional and its partition function is known analytically. The terminal lattices are boxed in Fig. 1. The partition function of the original 3×3 square lattice is the sum over those of all boxed lattices, each multiplied by a proper factor defined by the label. It follows from Eq 7 that “1” contributes a term σ, “2” contributes (σ − 1), “3” and “4” contribute (1 − σ). For example, the term contributed by the one-dimensional lattice “1314” to the partition function of the 3×3 square lattice is σ²(1 − σ)²L₁L₃², where L_n denotes the partition function of a linear lattice of n sites (14). The final expression containing the contribution of all terminal one-dimensional lattices is then converted by the symbolic algebraic language Mathematica into a polynomial expansion in the independent variable ω.

Figure 1.

Illustration of the algorithm based on Eq. 7 for the case of a 3×3 square lattice. Sites are numbered as shown in the lattice at the top. Lattices generated at each step are labeled from “1” to “4” based on the terms at the right-hand site of Eq. 7. The proper factors coupled to these terms are listed at the top of the manifold. Boxed latticescontribute one-dimensional terms to the partition function of the 3×3 square lattice.

The advantage of the recursive algorithm over the brute force approach is already perceived from Fig. 1. Solution of the problem for the 3×3 square lattice requires handling 76 matrices, 58 of which define the partition function, as opposed to 2⁹ = 512 configurations in the brute force approach. The algorithm based on the contact transformation scales as 2^N, like the brute force approach (see Fig. 2), but it does reduce the number of terms in the partition function by more than 10-fold. This reduction is quite significant from a computational standpoint. Furthermore, the algorithm scales as 1.2^N for σ = 0 providing a substantial advantage over the brute force approach in the study of ligand binding to a lattice with overlapping sites (13). In this case, the partition function for a 10×10 square lattice can be solved in a few hours (see Results), whereas no computer can handle in a reasonable time frame the 2¹⁰⁰ configurations required by the brute force approach. Finally, the most significant advantage of the method based on Eq. 7 is that it dissects the partition function in terms of elementary one-dimensional components. This brings important new insight into the Ising problem and may be conducive to an analytical solution in terms of the partition functions of elementary one-dimensional lattices rather than individual lattice configurations.

Figure 2.

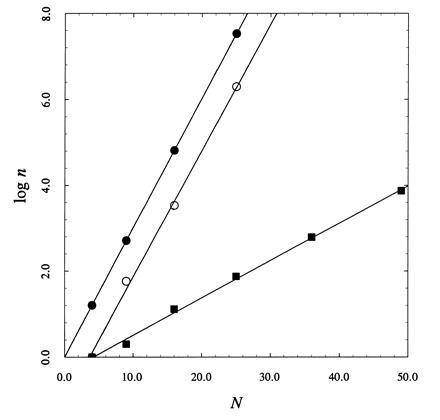
Dependence of the logarithm (base 10) of the number of terms, n, to define the partition function versus the number of sites, N, in the lattice for the brute force approach (•) and the approach based on Eq. 7 for finite σ (○) and for σ = 0 (▪). Continuous lines are the best-fits of logn according to the expression logn = a + bN, with: (•) a = 0, b = log2; (○) a = −1.1 ± 0.2, b = 0.29 ± 0.01; (▪) a = −0.36 ± 0.06, b = 0.087 ± 0.002. Note how the method based on Eq. 7 scales as 2^N for finite σ, but involves a number of terms about 13-fold smaller compared with the brute force approach. For σ = 0, the method based on Eq. 7 scales as 1.2^N, thereby involving 1.7^N fewer terms than the brute force approach.

Results

The availability of the partition function enables the systematic analysis of the cooperative properties of two-dimensional lattices. The binding capacity per site is the binding analogue of the heat capacity in thermal transitions and provides a direct measure of cooperativity (14). This quantity is shown in Fig. 3 for two-dimensional square lattices up to 5×5 sites in the case of positive cooperativity. The fundamental question is whether the binding capacity per site undergoes a phase-transition-like discontinuity in the two-dimensional case, as seen for the heat capacity per spin in the ferromagnet (9). Increasing the number of sites in the lattice, while keeping the interaction constant the same, brings about an increase in cooperativity signaled by a more peaked binding capacity. The maximum value of the binding capacity per site, b_max, scales with the number of sites according to the simple expression b_max ≈ N^a, as documented by the log–log plot in Fig. 4. This divergence predicts the existence of a phase-transition-like discontinuity in the thermodynamic limit N → ∞, which echoes the classical Onsager–Kaufman result for the heat capacity per spin (11, 12). As for the ferromagnet, this result is peculiar of the two-dimensional case because in the one-dimensional case b_max is independent of N in the thermodynamic limit.

Figure 3.

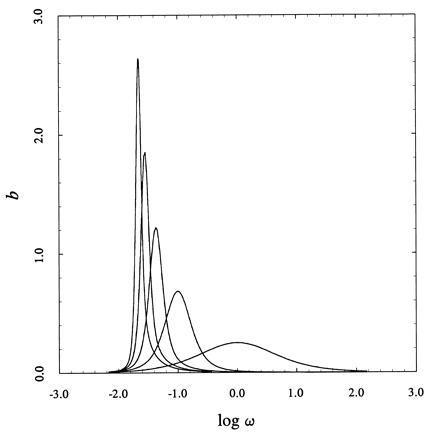
Binding capacity per site b = d² ln Ψ/d ln ω² for two-dimensional lattices (from left to right: 5×5, 4×4, 3×3, 2×2, 1×1) with σ = 10. The increase in b with N is conducive to a phase-transition-like discontinuity in the thermodynamic limit N → ∞.

Figure 4.

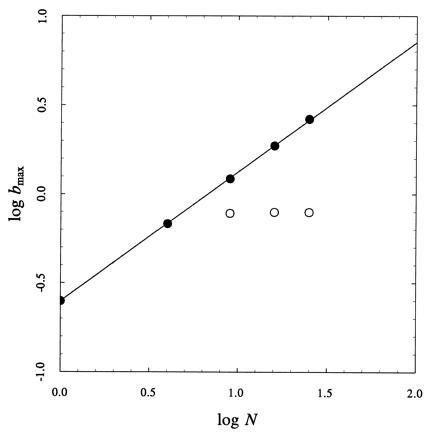
Effect of the number of sites N on the cooperativity of the lattice, expressed by the maximum value of the binding capacity per site shown in Fig. 3. In the two-dimensional case (•) (1×1, 2×2, 3×3, 4×4, 5×5) the log–log plot is linear and implies a divergence of b_max according to N^a (a = 0.727 ± 0.002). This is conducive to a phase-transition-like discontinuity in the function b in the thermodynamic limit N → ∞. No such behavior is observed in the one-dimensional case (○) (N = 1, 4, 9, 16, 25). The value of the interaction constant is σ = 10.

It is remarkable that a basic property of two-dimensional lattices, like the existence of a discontinuity for b in the thermodynamic limit, can be predicted from the behavior of finite lattices of relatively small size. The prediction is reinforced by the distribution of zeroes of the partition function shown in Fig. 5. The zeroes for the 5×5 square lattice already approach very closely the positive real axis on which the partition function can vanish only if it is no longer analytical (9). Upon a simple conformal mapping, the zeroes distribute on a slightly distorted unit circle. A systematic analysis of lattices of larger size will reveal if this distortion disappears in the thermodynamic limit, which is the result predicted by the Lee–Yang theorem in the case of temperature-driven phase transitions for the ferromagnet (16).

Figure 5.

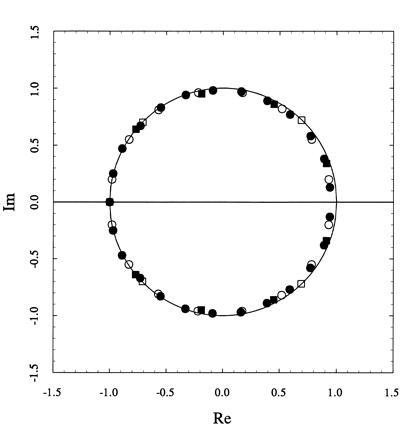
Distribution of zeroes of the partition function for σ = 100 for two-dimensional square lattices: (□) 2×2, (▪) 3×3, (○) 4×4, (•) 5×5. Upon a conformal mapping, the zeroes tend to distribute on a slightly distorted unit circle and rapidly approach the positive real axis already for the 5×5 square lattice.

When the lattice shows negative cooperativity, the algorithm based on Eq. 7 enables the study of larger systems. The binding capacity per site in the case σ = 0 is shown in Fig. 6 for square lattices up to 10×10 sites. This value of the interaction parameter models the biologically relevant phenomenon of ligand binding to overlapping sites, also known as the parking problem (3). Binding to a given site prevents binding to neighbor sites because of steric hindrance, as typically seen in the interaction of ligands with nucleic acids and receptors on the cell membrane (13, 18). In the range where this problem can be approached with the brute force method (4×4 sites), the lattice shows the expected negative cooperativity with a binding capacity profile that is indistinguishable from that of a system composed of multiple classes of independent sites. In particular, the profile for the 4×4 lattice suggests the existence of two dominant classes of sites, which are almost equally populated. The algorithm based on Eq. 7 allows for an analysis of this problem for larger lattices and reveals a different behavior as N increases. The binding capacity profile remains bimodal, but shows an important and unexpected property in that it brings about a higher population of low-affinity binding sites. This phenomenon is encountered in many ligand-receptor interactions (19) and is typically interpreted by invoking the existence of two classes of receptors: one specific, with high affinity and low population, the other nonspecific, with low affinity and higher population. The results shown in Fig. 6 offer an alternative interpretation. If the receptors on the cell membrane are modeled in terms of a two-dimensional Ising lattice with overlapping sites (σ = 0), then one class of sites suffices to explain the data in the limit of large N. The asymmetric bimodal profile of the binding capacity is an “artifact” of the parking problem in two dimensions when the number of sites becomes on the order of 100, which is certainly a realistic value for practical applications. Interestingly, the effect shown in Fig. 6 seems to saturate already for a lattice of 7×7 sites, indicating that the study of “small” lattices can be revealing of the properties of “large” systems as seen for the positively cooperative case (see Fig. 3).

Figure 6.

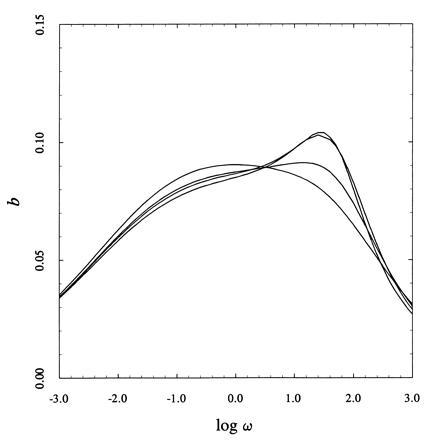
Binding capacity per site b = d² ln Ψ/d ln ω² for two-dimensional lattices (from left to right: 4×4, 6×6, 7×7, 10×10) with σ = 0. The bimodal profile of the binding capacity becomes increasingly asymmetric as N increases and mimics the behavior of a system composed of two classes of sites, with the low affinity sites being more populated. This behavior is typically seen in the interaction of ligands with receptors on the cell membrane (19).

Discussion

The contact transformation and the algorithm based on it provide a powerful new approach to the Ising problem. This method simplifies significantly the combinatorics of the problem and reveals how the complex behavior of two-dimensional lattices emerges from the contribution of one-dimensional lattices. Although the method still scales exponentially with the size of the system, it offers a significant reduction of the number of terms defining the partition function and has enabled a complete characterization of positively cooperative ligand binding to two-dimensional lattices up to 5×5 sites. As we have shown, these “small” lattices already encapsulate the salient features of two-dimensional lattices of larger size and provide unprecedented insight into ligand binding in two dimensions. Lattices of up to 10×10 sites can easily be studied with this method for σ = 0, whereas the brute force approach would hardly go beyond a 6×6 lattice even on a parallel supercomputer. Extension of our method to the study of three-dimensional lattices is also possible because the connectivity matrix can be defined in any dimension.

An important implication of this method is that it offers a systematic analysis of cooperativity at the global and site-specific levels. We have illustrated some key features of the global properties like the divergence of b_max in the thermodynamic limit and the distribution of zeroes of the partition function. The systematic method can be used to derive all contracted forms of the partition function and hence the behavior of the lattice at each separate site (14). This information, which is absolutely crucial to models of ligand binding and molecular recognition, can be obtained within a computer time frame where the brute force approach would only provide information on the partition function of the system and hence its global properties. For example, the charged, polar, and nonpolar contacts of an interface defining a protein–ligand interaction can be modeled as sites of a two-dimensional Ising lattice (7). This typically involves values of N from 10 to 30, well within the range of analysis of our method, but already at the limits of current computational capabilities when using the brute force approach. All of the transition modes (7, 14) of the lattice can be computed from knowledge of the partition function and its contracted forms leading to specific predictions on the binding free energy for protein–ligand interaction, as illustrated recently for the biologically relevant case of hirudin binding to thrombin (7).

The availability of a systematic method for solving the partition function of Ising lattices with arbitrary interaction geometry among the sites makes it possible to use these lattices as toy models for studying structure–function relations. In fact, the topology of the lattice reflected by the connectivity matrix associated with it encodes its cooperative properties. Structural perturbations of the lattice, like missing contacts or sites, can be analyzed to unravel the effects on site-specific and global binding properties. A detailed understanding of how cooperativity is encoded in the structure of the lattice will make it possible to predict the cooperative behavior of any lattice from the connectivity matrix. The basic knowledge arising from such a systematic analysis is likely to bring our understanding of the Ising problem and cooperativity to an entirely new level.