A model for estimating ultrasound attenuation along the propagation path to the fetus from backscattered waveforms

Abstract

Accurate estimates of the ultrasound pressure and/or intensity incident on the developing fetus on a patient-specific basis could improve the diagnostic potential of medical ultrasound by allowing the clinician to increase the transmit power while still avoiding the potential for harmful bioeffects. Neglecting nonlinear effects, the pressure/intensity can be estimated if an accurate estimate of the attenuation along the propagation path (i.e., total attenuation) can be obtained. Herein, a method for determining the total attenuation from the backscattered power spectrum from the developing fetus is proposed. The boundaries between amnion and either the fetus’ skull or soft tissue are each modeled as planar impedance boundaries at an unknown orientation with respect to the sound beam. A mathematical analysis demonstrates that the normalized returned voltage spectrum from this model is independent of the planes orientation. Hence, the total attenuation can be estimated by comparing the location of the spectral peak in the reflection from the fetus to the location of the spectral peak in a reflection obtained from a rigid plane in a water bath. The independence of the attenuation estimate and plane orientation is then demonstrated experimentally using a Plexiglas plate, a rat’s skull, and a tissue-mimicking phantom.

LIST OF SYMBOLS.

f = frequency

fpeak = frequency corresponding to the spectral peak at each inclination angle (i.e., $\mid V_{plane}(\omega )\mid /{max}_{\forall \omega }\mid V_{plane}(\omega )\mid \hspace{0.17em}\cong exp{[-(f-f_{peak})}^2/2{\sigma }_{\omega p}^2]$).

g(r⃗d, r⃗′) = effective Green’s function valid from the scattering region to the detector

Go = geometric gain value for velocity potential field at focus when Wsource is approximated by a Gaussian (m)

GT = dimensionless aperture gain function that accounts for the focusing of the ultrasound source

H = dimensionless filtering characteristics for the ultrasound source

k = effective wave number along the propagation path

k̃ = effective complex wave number along the propagation path (i.e., k̃ = k + iα)

KuV = conversion constant relating voltage to particle velocity for ultrasound source (m/s V−1)

Mimage = matrix used to generate image point

n⃗f = the outward normal for the plane at arbitrary angle to beam axis

pplane = pressure field from rigid plane placed near focal plane

r⃗f = locations on inclined plane

r⃗1 = points on aperture plane of image source

r⃗T , r⃗d = locations on aperture plane of transmitter/detector

Sf = surface of inclined plane near focal plane

SI = aperture area of image source

ST = aperture area of ultrasound transmitter

Vinc = voltage applied to the ultrasound source during transmit

Vplane = voltage from ultrasound source due to the backscatter from rigid plane near focus

wx, wy, wz = equivalent Gaussian dimensions on receive of pressure field in focal region

xI, yI, zI = coordinate location of image point

zf = distance of rigid plane to the focal plane

zp = distance along the beam axis from the focus to the intersection of the plane with the beam axis

zT, zd = distance of the aperture plane of the ultra-sound transmitter/detector to the focal plane

α = effective attenuation along the propagation path

αerror = error in attenuation associated with inclination angle of plane

αo = slope of attenuation assuming strict linear frequency dependence (i.e., α =αof)

Γplane = reflection coefficient of plane

θf , φf = angles describing orientation of plane with beam axis

ξx , ξy , ξz = coordinate system for the image source

ξ̂x , ξ̂y , ξ̂z = unit normal vectors defining coordinate system for the image source

ρ = density

σωp = Gaussian bandwidth for reflected voltage from inclined plane (i.e., $\mid V_{plane}(\omega )\mid /{max}_{\forall \omega }\mid V_{plane}(\omega )\mid \hspace{0.17em}\cong exp{[-((f-f_{peak})}^2/2{\sigma }_{\omega p}^2])$).

ω = radian frequency

ωmax = radian frequency corresponding to spectral peak

• = dot product

I. INTRODUCTION

Over the years, ultrasound as a medical diagnostic tool has become increasingly valuable. This can be attributed, in part, to its ability to display gray-scale images of anatomy and color-coded blood flow in real time. A specific benefit that is provided by diagnostic ultrasound is its ability to “safely” image embryos and fetuses in utero. This allows the medical professionals to accurately diagnose and monitor the different embryo/fetal developmental stages during pregnancy. Although high-quality images can be obtained for many patients, some patients are challenging to image due to increased attenuation along the propagation path, thus degrading the backscattered signals. A simple solution would be to increase the transmit power of the ultrasound source, but increased output power translates to increased tissue heating as well as the possibility of other mechanical bioeffects (AIUM, 1988, 1993, 2000; NCRP, 2002). Of particular importance is the heating near the developing cranial bone because heating of the developing brain tissue has the potential to result in long-term neurological disorders (Barnett, 2000). Heating is of greater concern when the ultrasound beam impinges on the developing cranial bone due to the large absorption of the ossified bone tissue (Myers, 2004; Barnett, 2001; Fuji et al. 1999; Drewniak and Dunn, 1996; O’Neil et al., 1994; Haken et al., 1992; Wu and Du, 1990; Carstensen et al., 1990; Drewniak et al., 1989). Currently, these heating concerns are avoided by requiring that the output levels be kept artificially much less than those anticipated to produce biologically significant temperature increases.

The risk for tissue heating is currently assessed by assuming that the attenuation along the propagation path is 0.3 dB/cm-MHz, a conservative lower limit for the attenuation of biological tissue (AIUM/NEMA, 1998, Abbott, 1999). However, in a study of 23 nonpregnant female volunteers (Siddiqi et al., 1992), the measured attenuation coefficient for the abdominal wall varied from 0.40 to 4.0 dB/cm-MHz (mean of 1.39 dB/cm-MHz with a standard deviation of ±0.89 dB/cm-MHz). Hence, based only on attenuation of the abdominal wall, the potential exists for patient variability as high as 3.4 dB/cm-MHz, or as high as 1.8 dB/cm-MHz using the two standard deviation criterion. But, for transabdominal ultrasound scanning, the entire propagation path needs to be considered, including abdominal wall, bladder, myometrium, and vaginal wall. In another in vivo study (Siddiqi et al., 1999) that also combined the results from two other separate in vivo studies, the total attenuation along the propagation path from the abdominal wall through the vagina was from 0.8±0.4 dB/ cm-MHz for 57 subjects with empty bladders and 0.6±0.3 dB/cm-MHz for 64 subjects with full bladders. Based on total attenuation, the potential exists for patient variability as high as 0.8 dB/cm-MHz for empty bladders and 0.6 dB/cm-MHz for full bladders (two standard deviation criterion). These examples demonstrate a large patient-specific variability.

As the attenuation along the propagation path is increased, more of the transmitted ultrasound energy is absorbed before it can reach the developing skull, thus reducing the in vivo exposure pressure/intensity. Hence, the resulting temperature increase is reduced as the total attenuation along the propagation path is increased. As a result, the transmit power could be increased to improve the image quality on the challenging patients without endangering the fetus provided that the in vivo and in situ pressure and/or intensity could be estimated on a patient-specific basis. Neglecting nonlinear effects, the in vivo pressure and/or intensity can be obtained by measuring the pressure and/or intensity in a water bath using a calibrated hydrophone and then derating the measured waveform using the attenuation coefficient as measured for a specific patient.

In this study, one possibility of estimating the attenuation along the propagation path leading to the fetus on a patient-specific basis has been investigated. The hypothesis is that if an accurate model of the scattering structure can be developed, then the attenuation along the propagation path can be estimated by comparing the in vivo backscattered spectrum to a reference spectrum obtained in a water bath. The simplest scattering structure would be a planar boundary between two impedances where the sound beam is incident at some arbitrary angle with respect to the planar boundary. One possible example of a planar boundary in utero might be the tissue/skull boundary of the fetus. Hence, the theoretical voltage spectrum from an inclined planar boundary is first derived. When the backscattered radio frequency (rf) spectrum from the planar boundary is then compared to a reference spectrum, an estimate for the attenuation along the propagation path is obtained by measuring the frequency location of the main spectral peak. The theoretical analysis is then validated using both a Plexiglas plate and a rat’s skull in water baths at different inclination angles. Unfortunately, the simple plane model may not be valid for the skull in the early developmental stages due to the ossification process of the skull. Hence, the simple plane model is also evaluated for a soft-tissue/water boundary, similar to the aminiotic fluid/ soft tissue boundary in utero, using a soft-tissue-mimicking phantom in a water bath. Lastly, the applicability of the results to estimating the exposure conditions of the fetus is discussed.

II. THEORETICAL CALCULATIONS

In this section, the voltage received by the ultrasound source when operating in pulse echo mode when a planar boundary is placed in the focal region will be derived. It is assumed that the velocity potential field in the focal region follows a three-dimensional Gaussian distribution as was verified by Bigelow and O’Brien (2004a). The coordinate system for the problem is shown in Fig. 1. In this figure, n⃗_f is the outward normal for the plane that intersects the z axis (beam axis) at a distance of z_p from the focus (positive for z_p > 0) with n_fx , n_fy , n_fz given by

FIG. 1.

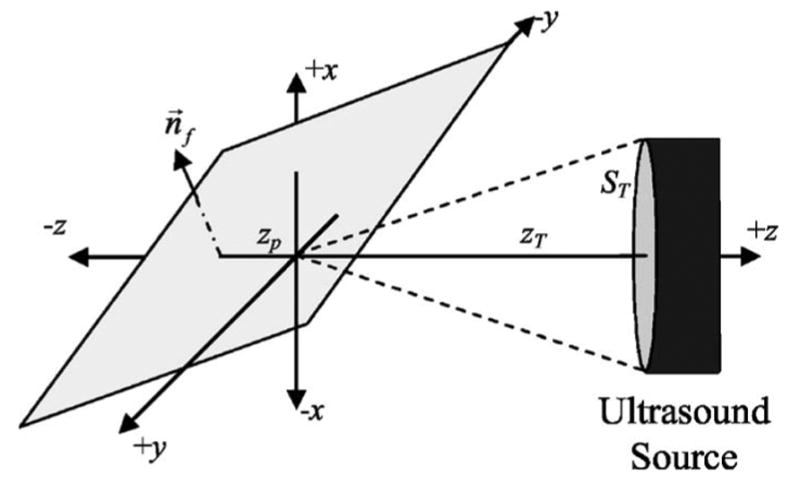
Coordinate system for reflection from plane placed in the focal region.

$$\begin{array}{l}{n}_{fx}\widehat{x}=sin({\theta }_f)cos({\phi }_f)\widehat{x},\\ n_{fy}\widehat{y}=sin({\theta }_f)sin({\phi }_f)\widehat{y},\\ n_{fz}\widehat{z}=cos({\theta }_f)(-\widehat{z}).\end{array}$$ (1)

Hence, the equation describing the plane is given by

$$xsin({\theta }_f)cos({\phi }_f)+ysin({\theta }_f)sin({\phi }_f)+(z_p-z)cos({\theta }_f)=0.$$ (2)

The goal is to solve for the reflected longitudinal waves in the region of the ultrasound source. Shear waves were not included in the initial developments in order to simplify the analysis. The impact of neglecting shear waves is beyond the scope of the current work, but, in general, the influence of shear waves on the reflected longitudinal waves is small when the incident angle of the wave with respect to the plane normal is small (Mayer, 1964). Hence, the derived equations will be limited to small incident angles for the ultrasound beam.

After applying the Kirchoff-Helmholtz integral theorem, the pressure field reflected by a planar specular reflector in the focal region is given by (Pierce, 1991)

$$\begin{array}{l}{p}_{plane}({\vec{r}}_d,\omega )=\frac{1}{4\pi }\int {\int }_{S_f}d{\vec{r}}_f{\vec{n}}_f\cdot (g({\vec{r}}_d,{\vec{r}}_f){\nabla }_f{p}_{plane}({\vec{r}}_f,\omega )\\ -p_{plane}({\vec{r}}_f,\omega ){\nabla }_{f}g({\vec{r}}_d,{\vec{r}}_f)),\end{array}$$ (3)

which, after applying the appropriate Green’s function g, becomes (Pierce, 1991)

$$p_{plane}({\vec{r}}_d,\omega )=\frac{1}{2\pi }{\int \int }_{S_f}d{\vec{r}}_f{\vec{n}}_f\cdot \left(\frac{e^{i\stackrel{\sim }{k}\mid {\vec{r}}_d-{\vec{r}}_f\mid }}{\mid {\vec{r}}_d-{\vec{r}}_f\mid }{\nabla }_f{p}_{plane}({\vec{r}}_f,\omega )\right).$$ (4)

Once the reflected pressure field at the planar surface [i.e., p_plane(r⃗_f, ω)]is known, the reflected pressure field everywhere [i.e., p_plane(r⃗_f, ω)] can be determined.

In order to find the pressure field immediately after reflection, an appropriate image source was generated corresponding to the original transmitting source similar to the work done by Pedersen and Orofino (1996). The field from the image source was then determined at the plane. Image sources are normally used to quickly satisfy the boundary conditions of either pressure release or rigid surfaces (i.e., magnitude of reflection coefficient equal to one). When the magnitude of the reflection coefficient is different from one, the use of image sources must be modified to include the angle of incidence of the fields decomposed into a set of plane waves (Morse and Ingard, 1968). However, if the incident angles are small, the angular dependence of the reflection coefficient can be ignored in a first-order calculation.

The location of the image source can be found by reflecting the original source across the plane. The reflection of an arbitrary point across the plane was performed by transforming the coordinate system until the plane was aligned with a new x−y plane with the origin at the intersection between the beam axis of the ultrasound source and the plane using a translation transformation and two rotation transformations. Then, the point was reflected to the other side of the plane along the z axis, and the coordinate system was returned to its original orientation with two additional rotation transformations and a translation transformation (Hearn and Baker, 1997). The transformations are illustrated in Eq. (5):

$$\begin{array}{l}\left[\begin{array}{c}{x}_I\\ y_I\\ z_I\\ 1\end{array}\right]=\stackrel{\text{Translation}}{\overbrace{\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& z_p\\ 0& 0& 0& 1\end{array}\right]}}\stackrel{\phi -\text{Rotation}}{\overbrace{\left[\begin{array}{cccc}-cos({\phi }_f)& sin({\phi }_f)& 0& 0\\ -sin({\phi }_f)& -cos({\phi }_f)& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]}}\stackrel{\theta -\text{Rotation}}{\overbrace{\left[\begin{array}{cccc}-cos({\theta }_f)& 0& -sin({\theta }_f)& 0\\ 0& 1& 0& 0\\ sin({\theta }_f)& 0& -cos({\theta }_f)& 0\\ 0& 0& 0& 1\end{array}\right]}}\\ \times \stackrel{\text{Reflection}}{\overbrace{\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& 1\end{array}\right]}}\stackrel{\theta -\text{Rotation}}{\overbrace{\left[\begin{array}{cccc}-cos({\theta }_f)& 0& sin({\theta }_f)& 0\\ 0& 1& 0& 0\\ -sin({\theta }_f)& 0& -cos({\theta }_f)& 0\\ 0& 0& 0& 1\end{array}\right]}}\stackrel{\phi -\text{Rotation}}{\overbrace{\left[\begin{array}{cccc}-cos({\phi }_f)& -sin({\phi }_f)& 0& 0\\ sin({\phi }_f)& -cos({\phi }_f)& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]}}\stackrel{\text{Translation}}{\overbrace{\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& -z_p\\ 0& 0& 0& 1\end{array}\right]}}\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\\ =\left[\begin{array}{cccc}{\mathbf{M}}_{image}^{\text{1},\text{1}}& {\mathbf{M}}_{image}^{\text{1},\text{2}}& {\mathbf{M}}_{image}^{\text{1},\text{3}}& {\mathbf{M}}_{image}^{\text{1},\text{4}}\\ {\mathbf{M}}_{image}^{\text{2},\text{1}}& {\mathbf{M}}_{image}^{\text{2},\text{2}}& {\mathbf{M}}_{image}^{\text{2},\text{3}}& {\mathbf{M}}_{image}^{\text{2},\text{4}}\\ {\mathbf{M}}_{image}^{\text{3},\text{1}}& {\mathbf{M}}_{image}^{\text{3},\text{2}}& {\mathbf{M}}_{image}^{\text{3},\text{3}}& {\mathbf{M}}_{image}^{\text{3},\text{4}}\\ \text{0}& \text{0}& \text{0}& \text{1}\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]={\mathbf{M}}_{image}\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right],\end{array}$$ (5)

where

$$\begin{array}{l}{\mathbf{M}}_{image}^{:,\text{1}}=\left[\begin{array}{c}1-2{sin}^2({\theta }_f){cos}^2({\phi }_f)\\ -2{sin}^2({\theta }_f)sin({\phi }_f)cos({\phi }_f)\\ 2sin({\theta }_f)cos({\phi }_f)cos({\theta }_f)\\ 0\end{array}\right],\\ {\mathbf{M}}_{image}^{:,\text{2}}=\left[\begin{array}{c}-2{sin}^2({\theta }_f)sin({\phi }_f)cos({\phi }_f)\\ 1-2{sin}^2({\theta }_f){sin}^2({\phi }_f)\\ 2sin({\theta }_f)sin({\phi }_f)cos({\theta }_f)\\ 0\end{array}\right],\\ {\mathbf{M}}_{image}^{:,\text{3}}=\left[\begin{array}{c}2sin({\theta }_f)cos({\phi }_f)cos({\theta }_f)\\ 2sin({\theta }_f)sin({\phi }_f)cos({\theta }_f)\\ 1-2{cos}^2({\theta }_f)\\ 0\end{array}\right],\\ {\mathbf{M}}_{image}^{:,\text{4}}=\left[\begin{array}{c}-2z_{p}sin({\theta }_f)cos({\phi }_f)cos({\theta }_f)\\ -2z_{p}sin({\theta }_f)sin({\phi }_f)cos({\theta }_f)\\ 2z_p{cos}^2({\theta }_f)\\ 1\end{array}\right],\end{array}$$ (6)

and (x_I , y_I , z_I) is the image of the original point. Therefore, the field from the image source would be given by

$$\begin{array}{l}{p}_{plane}({\vec{r}}_f,\omega )=\frac{-i\omega \rho {\mathrm{\Gamma }}_{plane}{K}_{uV}(\omega )V_{inc}(\omega )H(\omega )}{2\pi }\\ \times {\int \int }_{S_I}d{\vec{r}}_I{G}_T({\vec{r}}_I,\omega )\frac{e^{i\stackrel{\sim }{k}\mid {\vec{r}}_I-{\vec{r}}_f\mid }}{\mid {\vec{r}}_I-{\vec{r}}_f\mid },\end{array}$$ (7)

where Γ_plane accounts for the fact that the plane may not be a perfect reflector. Also, assuming that the planar surface is near the focus (i.e., |r⃗_f| is small compared to |r⃗_I|, Eq. (7) becomes

$$\begin{array}{l}{p}_{plane}({\vec{r}}_f,\omega )\cong \frac{-i\omega \rho {\mathrm{\Gamma }}_{plane}{K}_{uV}(\omega )V_{inc}(\omega )H(\omega )}{2\pi }\\ \times {\int \int }_{S_I}d{\vec{r}}_I{G}_T({\vec{r}}_I,\omega )\frac{e^{i\stackrel{\sim }{k}{r}_I}}{r_I},e^{i\stackrel{\sim }{k}}\left(\frac{{\vec{r}}_I}{r_I}\right){\vec{r}}_f,\end{array}$$ (8)

which can be written in closed form if the velocity potential field near the focus can be approximated as a three-dimensional Gaussian distribution, an assumption that was shown to be valid for scattering problems by Bigelow and O’Brien (2004a). Hence, Eq. (8) becomes

$$\begin{array}{l}{p}_{plane}({\vec{r}}_f,\omega )=\frac{-i\omega \rho {\mathrm{\Gamma }}_{plane}{K}_{uV}(\omega )V_{inc}(\omega )H(\omega )G_o}{2\pi }\\ \times \hspace{0.17em}{e}^{-({({\xi }_x({\vec{r}}_f)/w_x)}^2+{({\xi }_y({\vec{r}}_f)/w_y)}^2+{({\xi }_z({\vec{r}}_f)/w_z)}^2)}{e}^{i\stackrel{\sim }{k}(z_T-{\xi }_z)},\end{array}$$ (9)

where (ξ_x, ξ_y, ξ_z) refer to the coordinate system for the image source and z_T is the distance of the aperture plane of the image source from its focus (same as for the original source).

The locations of points (ξ_x, ξ_y, ξ_z) now need to be determined in the original coordinate system. Because the ξ_x, ξ_y, and ξ_z axes are the image of the x, y, and z axes, Eq. (5) yields

$$\begin{array}{l}{\widehat{\xi }}_x\cdot \widehat{x}={\mathbf{M}}_{image}^{1,1},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\xi }}_y\cdot \widehat{x}={\mathbf{M}}_{image}^{1,2},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\xi }}_z\cdot \widehat{x}={\mathbf{M}}_{image}^{1,3},\\ {\widehat{\xi }}_x\cdot \widehat{y}={\mathbf{M}}_{image}^{\text{2},\text{1}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\xi }}_y\cdot \widehat{y}={\mathbf{M}}_{image}^{\text{2},\text{2}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\xi }}_z\cdot \widehat{y}={\mathbf{M}}_{image}^{\text{2},\text{3}},\\ {\widehat{\xi }}_x\cdot \widehat{z}={\mathbf{M}}_{image}^{\text{3},\text{1}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\xi }}_y\cdot \widehat{z}={\mathbf{M}}_{image}^{\text{2},\text{3}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\xi }}_z\cdot \widehat{z}={\mathbf{M}}_{image}^{\text{3},\text{3}},\end{array}$$ (10)

and the origin of the (ξ_x, ξ_y, ξ_z) coordinate system is located at ( ${\mathbf{M}}_{image}^{\text{1},\text{4}},{\mathbf{M}}_{image}^{\text{2},\text{4}},\hspace{0.17em}{\mathbf{M}}_{image}^{\text{3},\text{4}}$). Therefore, (ξ_x, ξ_y, ξ_z) in (x,y,z) coordinates are given by

$$\begin{array}{l}{\xi }_x=x{\mathbf{M}}_{image}^{\text{1},\text{1}}+y{\mathbf{M}}_{image}^{\text{2},\text{1}}+z{\mathbf{M}}_{image}^{\text{3},\text{1}}+{\mathbf{M}}_{image}^{\text{1},\text{4}},\\ {\xi }_y=x{\mathbf{M}}_{image}^{\text{1},\text{2}}+y{\mathbf{M}}_{image}^{\text{2},\text{2}}+z{\mathbf{M}}_{image}^{\text{3},\text{2}}+{\mathbf{M}}_{image}^{\text{2},\text{4}},\\ {\xi }_z=x{\mathbf{M}}_{image}^{\text{1},\text{3}}+y{\mathbf{M}}_{image}^{\text{2},\text{3}}+z{\mathbf{M}}_{image}^{\text{3},\text{3}}+{\mathbf{M}}_{image}^{\text{3},\text{4}},\end{array}$$ (11)

thus providing an expression for (r⃗_f ,ω) in closed form.

Now n⃗_f ·∇_fp_plane (r⃗_f ,ω) can be calculated and substituted into Eq. (4). After simplify the results by assuming that θ_f is small, Eq. (4) becomes

$$\begin{array}{l}{p}_{plane}({\vec{r}}_d,\omega )=\frac{-\stackrel{\sim }{k}\omega \rho {\mathrm{\Gamma }}_{plane}{K}_{uV}(\omega )V_{inc}(\omega )H(\omega )G_{o}cos({\theta }_f)}{{(2\pi )}^2}\\ \cdot {\int \int }_{S_f}d{\vec{r}}_f\frac{e^{i\stackrel{\sim }{k}\mid {\vec{r}}_d-{\vec{r}}_f\mid }}{\mid {\vec{r}}_d-{\vec{r}}_f\mid }\\ \times \hspace{0.17em}{e}^{-({({\xi }_x({\vec{r}}_f)/w_x)}^2+{({\xi }_y({\vec{r}}_f)/w_y)}^2+{({\xi }_z({\vec{r}}_f/w_z))}^2}{e}^{i\stackrel{\sim }{k}(z_T-{\xi }_z)},\end{array}$$ (12)

where ξ_x, ξ_y, and ξ_z are given by Eq. (11).

After determining the reflected fields in the region containing the original ultrasound source, these fields need to be translated to a voltage output by the transducer. The voltage output by the source can be found from (Bigelow and O’Brien, 2004a)

$$V_{plane}(\omega )=\frac{H(\omega )}{i\omega \rho S_T{K}_{uV}(\omega )}{\int \int }_{S_T}d{\vec{r}}_d{G}_T({\vec{r}}_d,\omega )\frac{\partial p_{plane}}{\partial z_d},$$ (13)

where

$$\begin{array}{l}\frac{\partial }{\partial z_d}{p}_{plane}({\vec{r}}_d,\omega )\cong \frac{-i{\stackrel{\sim }{k}}^2\omega \rho {\mathrm{\Gamma }}_{plane}{K}_{uV}(\omega )V_{inc}(\omega )H(\omega )G_{o}cos({\theta }_f)}{{(2\pi )}^2}\cdot {\int \int }_{S_f}d{\vec{r}}_f(e^{-({({\xi }_x({\vec{r}}_f)/w_x)}^2+{({\xi }_y({\vec{r}}_f)/w_y)}^2+{({\xi }_z({\vec{r}}_f)/w_z)}^2)}{e}^{i\stackrel{\sim }{k}(z_T-{\xi }_z)})\\ \times \frac{e^{i\stackrel{\sim }{k}{r}_d-i\stackrel{\sim }{k}{\vec{r}}_f\cdot ({\vec{r}}_f/r_d)}}{r_d}.\end{array}$$ (14)

Hence, the reflected voltage from the inclined plane is given by

$$\begin{array}{l}{V}_{plane}(\omega )\cong \frac{-{\stackrel{\sim }{k}}^2{\mathrm{\Gamma }}_{plane}{V}_{inc}(\omega )H^2(\omega )G_{o}cos({\theta }_f)}{S_T{(2\pi )}^2}\cdot {\int \int }_{S_T}d{\vec{r}}_d{G}_T({\vec{r}}_d,\omega ){\int \int }_{S_f}d{\vec{r}}_f\\ \times \hspace{0.17em}(e^{-({({\xi }_x({\vec{r}}_f)/w_x)}^2+{({\xi }_y({\vec{r}}_f)/w_y)}^2+{({\xi }_z({\vec{r}}_f)/w_z)}^2)}{e}^{i\stackrel{\sim }{k}(z_T-{\xi }_z)})\frac{e^{i\stackrel{\sim }{k}{r}_d-i\stackrel{\sim }{k}{\vec{r}}_f\cdot ({\vec{r}}_d/r_d)}}{r_d}\\ =\frac{-{\stackrel{\sim }{k}}^2{\mathrm{\Gamma }}_{plane}{V}_{inc}(\omega )H^2(\omega )G_o^{2}cos({\theta }_f)}{S_T{(2\pi )}^2}{e}^{i2\stackrel{\sim }{k}{z}_T}{\int \int }_{S_f}d{\vec{r}}_f\left(e^{-}\left(\frac{{\xi }_x^2+x_f^2}{w_x^2}+\frac{{\xi }_y^2+y_f^2}{w_y^2}+\frac{{\xi }_z^2+z_f^2}{w_z^2}+i\stackrel{\sim }{k}({\xi }_x+z_f)\right)\right),\end{array}$$ (15)

where the velocity potential fields have been assumed to have a three-dimensional Gaussian distribution once again. The integral in Eq. (15) can be integrated by expressing all of the spatial coordinates in terms of x_f and y_f. Performing the integration while assuming that θ_f is small yields

$$\begin{array}{l}{V}_{plane}(\omega )\cong \frac{-\pi w_x{w}_y{\stackrel{\sim }{k}}^2{\mathrm{\Gamma }}_{plane}{V}_{inc}(\omega )H^2(\omega )G_o^{2}cos({\theta }_f)}{2S_T{(2\pi )}^2}exp\left(-\frac{2z_p^2}{w_z^2}-2i\stackrel{\sim }{k}{z}_p+2i\stackrel{\sim }{k}{z}_T\right)\\ \times \left(1-\frac{w_x^2{tan}^2({\theta }_f){cos}^2({\phi }_f)}{2w_z^2}-\frac{w_y^2{tan}^2({\theta }_f){sin}^2({\phi }_f)}{2w_z^2}\right)exp\left(\frac{w_y^2{tan}^2({\theta }_f){sin}^2({\phi }_f)}{2}\left(\frac{4z_p^2}{w_z^4}+i\stackrel{\sim }{k}\frac{4z_p}{w_z^2}-{\stackrel{\sim }{k}}^2\right)\right)\\ \times exp\left(\frac{w_x^2{tan}^2({\theta }_f){cos}^2({\phi }_f)}{2}\left(\frac{4z_p^2}{w_z^4}+i\stackrel{\sim }{k}\frac{4z_p}{w_z^2}-{\stackrel{\sim }{k}}^2\right)\right),\end{array}$$ (16)

where z_p is the distance along the beam axis from the focus to the intersection of the plane with the beam axis. Equation (16) can be further simplified by noting that typically $4z_p^2/w_z^4\ll Re\left\{{\stackrel{\sim }{k}}^2\right\}$ and w_x, w_y, ≪ w_z, thus yielding

$$\begin{array}{l}{V}_{plane}(\omega )\cong \frac{-w_x{w}_y{\stackrel{\sim }{k}}^2{\mathrm{\Gamma }}_{plane}{V}_{inc}(\omega )H^2(\omega )G_o^{2}cos({\theta }_f)}{8\pi S_T}\\ \times \hspace{0.17em}{e}^{i2\stackrel{\sim }{k}(z_T-z_p)}{e}^{-2z_p^2/w_z^2}exp(-{\stackrel{\sim }{k}}^2\frac{{tan}^2({\theta }_f)}{2}\\ \times \hspace{0.17em}(w_x^2{cos}^2({\phi }_f)+w_y^2{sin}^2({\phi }_f))).\end{array}$$ (17)

Now that an expression for the voltage returned from the inclined plane has been derived, the equation can be checked by considering a special case. First, if w_x = w_y, as would be the case for circularly symmetric source, then Eq. (17) becomes

$$\begin{array}{l}{V}_{plane}(\omega )\cong \frac{-w_x^2{\stackrel{\sim }{k}}^2{\mathrm{\Gamma }}_{plane}{V}_{inc}(\omega )H^2(\omega )G_o^{2}cos({\theta }_f)}{8\pi S_T}\\ \times \hspace{0.17em}{e}^{i2\stackrel{\sim }{k}(z_T-z_p)}exp\left(-\frac{2z_p^2}{w_z^2}-w_x^2{\stackrel{\sim }{k}}^2\frac{{tan}^2({\theta }_f)}{2}\right),\end{array}$$ (18)

which is no longer dependent on φ_f as would be expected. Second, if θ_f goes to zero, then Eq. (18) becomes

$$\begin{array}{l}{V}_{plane}(\omega )\cong \frac{-w_x{w}_y{\stackrel{\sim }{k}}^2{\mathrm{\Gamma }}_{plane}{V}_{inc}(\omega )H^2(\omega )G_o^2}{8\pi S_T}\\ \times \hspace{0.17em}{e}^{i2\stackrel{\sim }{k}(z_T-z_p)}{e}^{-2z_p^2/w_z^2},\end{array}$$ (19)

which is the same as was derived previously for a plane placed parallel to the focal plane (Bigelow and O’Brien, 2004a).

Equation (17) is a complete description of the backscattered voltage spectrum, but the equation contains more information than is required to determine the total attenuation along the propagation path. Hence, |V_plane(ω)| in Eq. (17) is normalized by its peak value at the specific angle for the plane yielding

$$\frac{\mid V_{plane}(\omega )\mid }{\underset{\forall \omega }{max}\mid V_{plane}(\omega )\mid }\cong \frac{V_{inc}(\omega )H^2(\omega )e^{-2{\alpha }_{o}f(z_T-z_p)}}{V_{inc}({\omega }_{max})H^2({\omega }_{max})e^{-2{\alpha }_o{f}_{max}(z_T-z_p)}},$$ (20)

where it is assumed that w_x and w_y are strictly proportional to wavelength (i.e., kw_x and kw_y are independent of frequency) and that the attenuation, assumed to be much smaller than the wave number, is strictly proportional to frequency (i.e., α =α_of). Equation (20) is independent of the inclination angle of the plane because all of the angle dependences in Eq. (17) are removed by the normalization. Although the inclination angle of the plane impacts the absolute magnitude of the reflected spectrum, the shape of the reflected spectrum is not affected by θ_f. Hence, if we compare the normalized spectrum from a plane positioned at an unknown orientation in an unknown lossy medium to the normalized reference spectrum from a plane placed at the focal plane in a water bath, then the only difference between the two spectra should be the attenuation along the propagation path, α_o(z_T − z_p), in the unknown lossy medium.

There are many ways to compare the reference and measured spectrum. The most robust method for the work reported herein was to fit the normalized voltage spectrum from Eq. (20) with a Gaussian function of the form $\mid V_{plane}(\omega )\mid /{max}_{\forall \omega }\mid V_{plane}(\omega )\mid \hspace{0.17em}\cong exp{((f-f_{peak})}^2/2{\sigma }_{\omega p}^2)$. Although this is a crude assumption, it is reasonably accurate over a limited range of frequencies near the spectral peak for backscattered waveforms. The attenuation along the propagation path leading to the planar boundary in the unknown medium would then be given by the downshift in the center frequency expressed as (Narayana and Ophir, 1983)

$${\alpha }_o(z_T-z_p)=\frac{f_{peak}{\mid }_{reference}-f_{peak}{\mid }_{unknown}}{2{\sigma }_{\omega p}^2}.$$ (21)

III. EXPERIMENTAL VERIFICATION

Before Eq. (21) can be used to estimate in vivo signal intensities, we need to verify that the normalized backscattered voltage spectrum is independent of the orientation of the plane [i.e., demonstrate the validity of Eq. (20)]. In this section, the backscattered voltage spectrum from a Plexiglas plate, a rat’s skull, and a tissue mimicking phantom (Model 539; ATS Laboratories, Inc., Bridgport, CT) are compared for various orientation angels in a water bath (i.e., α_o assumed lossless). Water was selected due to its ease of use, but the conclusions would be valid with any attenuating fluid because when estimating the attenuation from backscattered waveforms the accuracy and precision of the estimate are not dependent on the attenuation along the propagation path (Huisman and Thijssen, 1996; Bigelow and O’Brien, 2005). The experiments were performed using a spherically focused f /2 transducer (Valpey Fisher Instruments, Inc., Hopkinton, MA). The transducer had a diameter of 2.1 cm, a center frequency of 8.7 MHz, and a -3-dB bandwidth of 1.6 MHz as measured from a wire reflection (Raum and O’Brien, 1997). Also, the equivalent Gaussian dimensions for the transducer were measured as is discussed by Bigelow and O’Brien (2004b) and were found to be w_z =17.1λ +924×10⁻⁶ m and w_x =1.57λ +27.0×10⁻⁶ m. The transducer was placed in a water bath and shock excited using a Panametrics 5900 pulser/receiver (Waltham, MA) operating in pulse-echo mode, and the returned waveforms were recorded using a digital oscilloscope at a sampling frequency of 100 MHz (Lecroy 9354 TM; Chestnut Ridge, NY) and averaged at least 100 times to remove electronic noise. The impact of noise on the estimation technique was beyond the scope of the current investigation.

A. Plexiglas experiment

The initial experiments were performed using a piece of smooth Plexiglas to act as the plane placed near the focal plane of the transducer. The Plexiglas plate was placed in the focal plane by positioning the plate so that the pulse-echo peak-to-peak voltage was a maximum. The Plexiglas was then rotated so that θ_f swept out angles from −10° to 10°, while maintaining a z_p of approximately zero; the pulse-echo waveform was recorded in steps of 1° change of θ_f. The scan was repeated four times with the focus moved along the axis of rotation for the plate, perpendicular to the beam axis, in steps of 0.1 mm (i.e., 0, 0.1, 0.2, and 0.3 mm). The results at each angle for all four scans were then averaged together. Also, the value of z_p was then estimated from the location of the time-domain waveforms and the corresponding spectra were multiplied by exp(2(z_p / w_z)²). However, the correction term for z_p did not significantly affect the final results (max value for |z_p| of 395 μm).

Recall that the purpose of the derivation was to use the inclined plane to approximate the skull interface of the fetus. The backscattered signals from the skull could then be analyzed to assess properties such as attenuation of the intervening tissue layers. Hence, the experimental results were evaluated in terms of the errors of the attenuation estimate (i.e., deviations from known α_o of 0 dB/cm-MHz) that would have resulted from the backscattered signals at each inclination angle of the plane. Because the total attenuation was to be measured from the downshift in the location of the main spectral peak, errors in the attenuation estimate would result from the voltage spectrum not peaking at the same frequency for all incident angles. Hence, the error in the attenuation estimate in Np/MHz for different inclination angles would be given by

$${\alpha }_{error}=\frac{f_{peak}({\theta }_f=0)-f_{peak}({\theta }_f)}{2{\sigma }_{\omega p}^2},$$ (22)

where f_peak is the frequency corresponding to the spectral peak at each inclination angle.

Figure 2(a) shows the error in the attenuation calculated using Eq. (22) for θ_f swept out angles from −10° to 10°. The frequencies selected for the Gaussian fit given by $\mid V_{plane}(\omega )\mid /{max}_{\forall \omega }\mid V_{plane}(\omega )\mid \hspace{0.17em}\cong exp{(-(f-f_{peak})}^2/2{\sigma }_{\omega p}^2)$ were all the frequencies for which the backscattered voltage spectrum was greater than $\frac{1}{2}$ its maximum value for a θ_f of 0° (i.e., 7.29 to 9.79 MHz). The error introduced by θ_f is small (less than 0.1 dB/MHz) for angles from −6° to at least 10°. The asymmetry in the attenuation errors indicates that the Plexiglas plate was not perfectly aligned at the beginning of the scan (i.e., an inclination angle of 0° does not correspond to a θ_f of 0°). The magnitude of the voltage at the spectral peak (i.e., f_peak) for each value of θ_f relative to the value for a θ_f of 0° is also provided [Figure 2(b)]. The magnitude of the backscatter decreases quickly with increasing inclination angle of the Plexiglas plate. This decrease results from the tangent squared of θ_f in the exponent of Eq. (18).

FIG. 2.

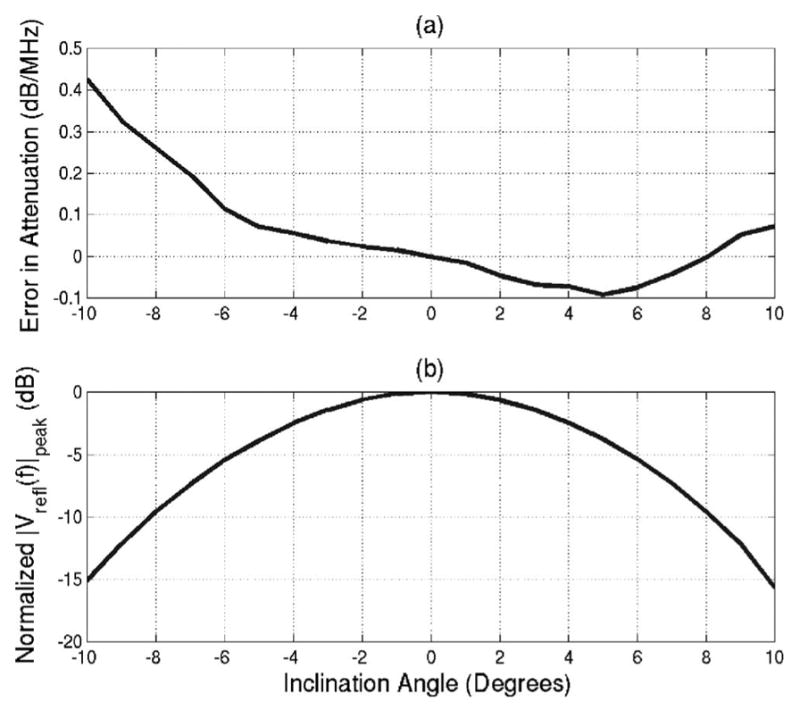
(a) Error in attenuation estimates resulting from inclination angle and (b) normalized magnitude of spectrum peak of backscattered signal for various inclination angles of the Plexiglas plate.

In order to further validate Eq. (20) using the Plexiglas plate, the amount of spectral distortion introduced at each inclination angle was also assessed for frequencies in the −6 dB bandwidth of the transducer (i.e., 7.29 to 9.79 MHz). The assessment was done by comparing the normalized spectrum given by Eq. (20) at each inclination angle to the normalized spectrum at normal incidence as described by Eq. (23).

$$\begin{array}{l}\text{Distortion\hspace{0.17em}(}\omega \text{)}=\text{20\hspace{0.17em}}{\text{log}}_{\text{10}}\left[{\left(\frac{\mid V_{plane}(\omega )\mid }{\underset{\forall \omega }{max}\mid V_{plane}(\omega )\mid }\right)\mid }_{{\theta }_f}\right]\\ -\text{20\hspace{0.17em}}\hspace{0.17em}{\text{log}}_{\text{10}}\left[{\left(\frac{\mid V_{plane}(\omega )\mid }{\underset{\forall \omega }{max}\mid V_{plane}(\omega )\mid }\right)\mid }_{{\theta }_f=\hspace{0.17em}{0}^{\circ }}\right].\end{array}$$ (23)

The results for θ_f of −10°, −8°, −5°, and −2° are shown in Fig. 3(a) while the results for θ_f of 10°, 8°, 5°, and 2° are shown in Fig. 3(b). The distortion is always less than 2 dB, indicating that the spectral shape is not affected by the inclination angle of the plane as was predicted by Eq. (20). Also, the distortion is slightly larger for the negative values of θ_f [Fig. 3(a) ]as compared to the positive values of θ_f [Figure 3(b)], indicating once again that the Plexiglas plate was not perfectly aligned at the beginning of the scan.

FIG. 3.

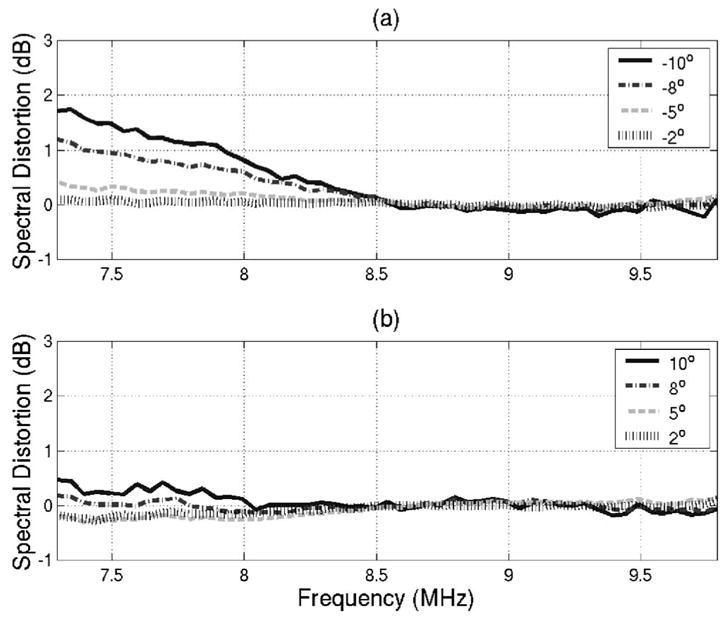
Amount of spectral distortion introduced for inclination angles of (a) −10°, −8°, −5°, −2° and (b) 10°, 8°, 5°, and 2° for frequencies in the −6 −dB bandwidth of the transducer.

B. Bone experiment

After performing the Plexiglas experiments, the procedure was repeated using a rat’s skull from an adult Sprague-Dawley rat (Harlan Sprague Dawley Laboratories, Indianapolis, IN). The experimental protocol was approved by the Laboratory Animal Care Advisory Committee at the University of Illinois at Urbana-Champaign and satisfied all campus and National Institutes of Health (NIH) rules for the human use of laboratory animals. The rat was housed in an Association for Assessment and Accreditation of Laboratory Animal Care (AAALAC)-approved animal facility. The rat was placed in a polycarbonate cage with β-chip bedding and a wire bar lid and provided with food and water ad lib. The rat was euthanized by cervical dislocation while under anesthesia in a humane fashion prior to extracting the skull. AAALAC (Rockville, MD) is a private nonprofit organization that promotes the humane treatment of animals in science through a voluntary accreditation program.

The skull was obtained by first trimming away the skin on the head. Then, the top portion of the skull was cut using scissors from the eyes to the ears. The cut skull was then pulled gently from the brain and the connective tissue was trimmed away from both sides of the removed skull plate. Finally, the skull was rinsed and placed in a sterile saline solution. The skull/saline solution was refrigerated for several days before the ultrasound experiment was performed.

The skull was positioned so that the focus would be on the outer surface of the skull with the beam at approximately normal incidence by adjusting the position of the skull and transducer to achieve the maximum peak-to-peak voltage of the backscattered time-domain waveform. The skull was rotated so that the inclination angle of the beam would change from −10° to +10° and the backscattered waveform from the skull was recorded in steps of 1°. However, the axis of rotation did not coincide with the focus so the value of z_p changed as the skull was rotated (max value for |z_p| of 1.15 mm). After acquiring the waveforms, the impact of z_p was removed by analyzing the time-domain signals. The error in the attenuation for each value of inclination angle was then found from

$${\alpha }_{error}=\frac{f_{peak}{\mid }_{reference}-f_{peak}({\theta }_f)}{2{\sigma }_{\omega p}^2{\mid }_{reference}},$$ (24)

where the reference spectrum was the reflected spectrum from the Plexiglas at normal incidence.

The error in the attenuation is shown in Fig. 4(a). In addition, the magnitude of the voltage at the spectral peak (i.e., f_peak) for the signal returned from the skull for each inclination angle relative to the magnitude of the voltage at the spectral peak for the signal returned from the Plexiglas for a θ_f of 0° is shown in Fig. 4(b). The magnitude signal from the skull [Fig. 4(b)] is much less than the magnitude of the signal from the Plexiglas plate. The voltage magnitude does not decay with increasing incident angle like the Plexiglas plate that dropped by 15 dB when θ_f was changed by 10°. The error in attenuation due to inclination angle [Fig. 4(a) ] for the skull was always smaller than 0.1 dB/MHz. The constant magnitude of the voltage returned from the skull and the low error values in the attenuation are probably due to the surface roughness reducing the impact of the incident angle. In Fig. 2(b), the received voltage decayed quickly with increasing incident angle. Hence, only portions of the skull oriented close to normal incidence are likely to influence the backscattered voltage spectrum. Therefore, the surface roughness of the skull reduces the importance of the inclination angle on the measurement of attenuation from the backscattered waveforms.

FIG. 4.

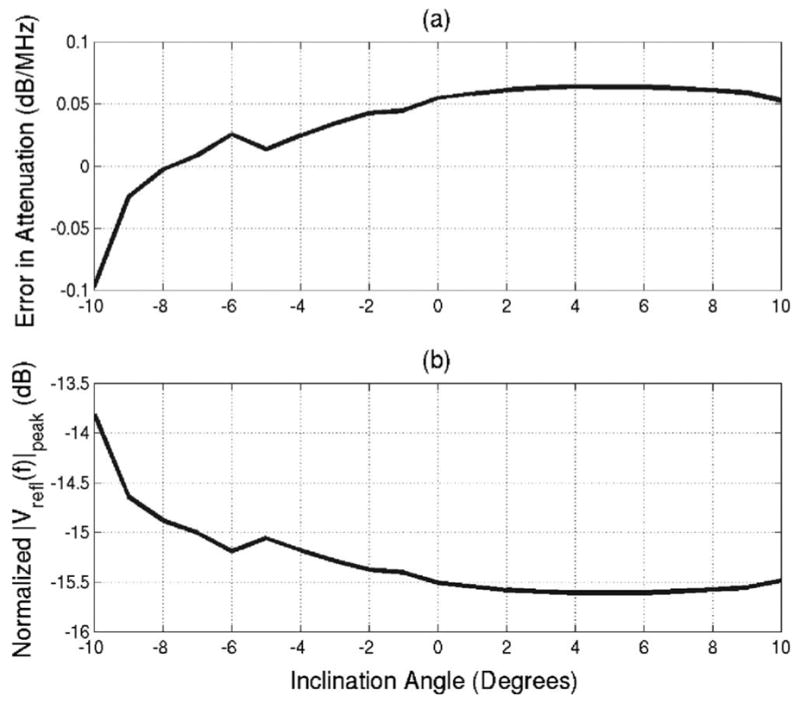
(a) Error in attenuation estimates resulting from inclination angle and (b) normalized magnitude of spectrum peak of backscattered signal for various inclination angles of the rat skull.

C. Tissue - mimicking phantom experiment

Although the rat’s skull and associated planar model may be similar in structure to the fetal skull near the end of the gestational period, the planar model would not be appropriate at the beginning of the ossification process. In the developing skull of humans, as well as many other animals, the parietal bones, frontal bone, a small part of the occipital bones, and much of the temporal bones are ossified by the direct formation of bone without a cartilage intermediate step (Carlson, 1994). Rather, the ossification begins near the center of the bone and proceeds along branching tubules until the bone plate has filled in (Nishimura et al., 1977). It is doubtful that the branching tubules could be adequately modeled by the simple planar boundary model developed in this paper. However, a clear impedance boundary exists between the amniotic fluid and soft tissue of the developing fetus. Hence, it may be possible to apply the planar model to the amniotic fluid/soft-tissue boundary.

In order to determine if the reflection of the ultrasound off soft tissue could also be used to estimate the attenuation along the propagation path, the experiment was repeated using a soft-tissue mimicking phantom (Model 539; ATS Laboratories, Inc., Bridgport, CT). The front surface of the phantom was placed in the focal plane of the ultrasound transducer by maximizing the pulse-echo peak-to-peak voltage. Then, the ultrasound transducer was rotated from −10° to +10° in steps of 1°. The transducer was rotated instead of the phantom due to the large size of the phantom. At each angle, the distance between the transducer and the phantom was adjusted until the location of the first pressure peak corresponded in time to the location of the first pressure peak at normal incidence (i.e., z_p approximately zero for all inclination angles) before the backscattered waveform was stored by the oscilloscope.

Before finding the spectrum for each backscattered waveform at each inclination angle, care was taken so that the speckle from within the phantom/soft-tissue did not affect the location of the spectral peak. The problem is avoided when reflecting the ultrasound signal from the skull because the magnitude of the speckle is much smaller than the magnitude of the reflection from the bone due to the larger impedance difference. However, when dealing with the soft tissue, the speckle is on the same order as the reflection from the water/phantom boundary, especially at the larger inclination angles. Therefore, in order to reduce the impact of the speckle, the time-domain waveform for each inclination angle was windowed using a Hamming window that spanned the reflections from the water/phantom boundary while minimizing the distortion introduced by the window. The starting location for the Hamming window was given by the first location in time for which absolute value of the backscattered voltage waveform was greater than 10% its maximum value. In order to find the optimal Hamming window, the length of the window was varied from 1 to 6 periods in steps of 0.05 periods corresponding to the period of the center frequency of the transducer (i.e., 0.1149 to 0.6897 μs in steps of 5.747 ns corresponding to a center frequency of 8.7 MHz). The reference signal (i.e., the Plexiglas at normal incidence) was also windowed with the same Hamming window. The reference pulse amplitude exceeded 10% of its maximum value for a duration of 0.66 μs. The reference spectrum and phantom spectra were then found by taking the Fourier transform of the windowed time domain signals. Then, the error in attenuation for each of the phantom spectra for each window was calculated using Eq. (24).

The mean value and standard deviation for the attenuation error over all of the inclination angles for each of the window lengths are shown in Figs. 5(a) and 5(b), respectively. In addition, the location of the spectral peak from the reference spectrum for each window length is shown in Fig. 5(c). The accuracy [Fig. 5(a)] and the precision [Fig. 5(b)] of the attenuation estimate degrade quickly when the Hamming window length exceeds 2 periods (window length of 0.23 μs). The frequency location of the reference spectral peak [Fig. 5(c)] asymptotically approaches ~8.7 MHz as the window length is increased and is within 10% of its final value for a window length of 2 periods. The downshift of the reference spectral peak for smaller Hamming windows is a measure of the amount of distortion introduced by the windowing. Hence, a Hamming window length of 2 periods appears to be the best choice for reducing the effect of the speckle while still minimizing the distortion introduced by the window.

FIG. 5.

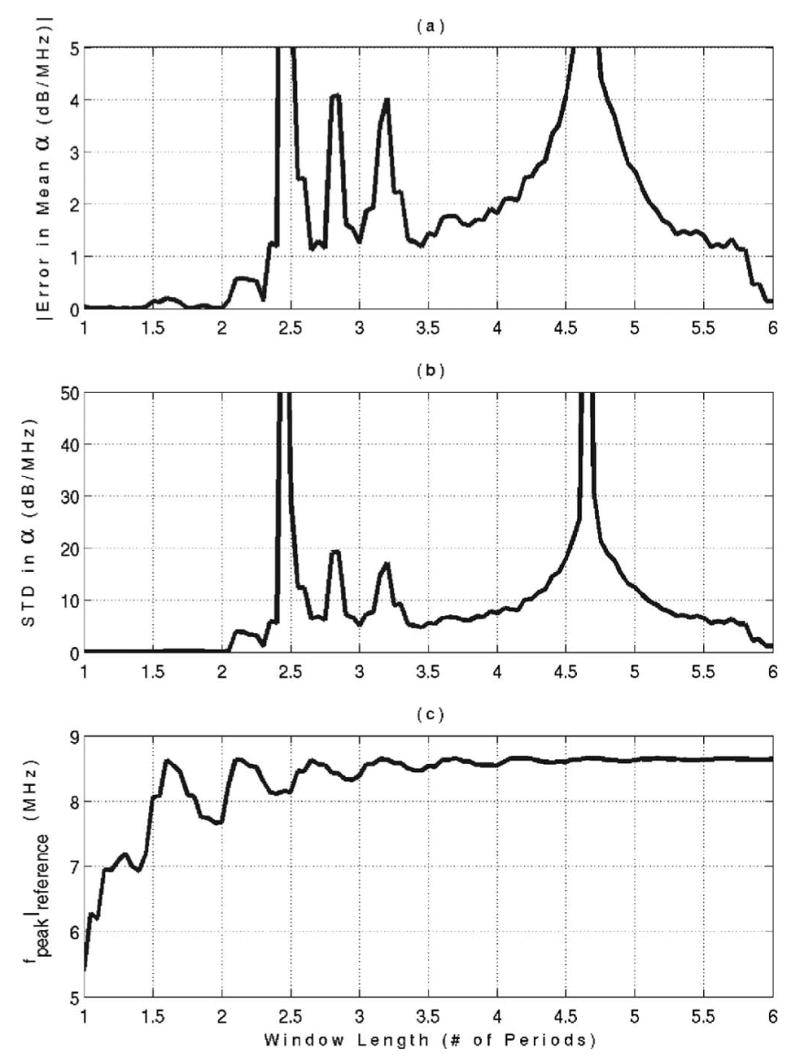
Mean value of attenuation error (a), standard deviation of attenuation error (b), and frequency location of spectral peak from the reference waveform (c) as a function of Hamming window length for the phantom experiment.

The error in the attenuation estimate for each inclination angle using a Hamming window with a length of 2 periods is shown in Fig. 6(a). The error in the attenuation estimate is always less than 0.25 dB/MHz. Therefore, it may be possible to estimate the attenuation along the propagation path from the backscatter returned by the soft fetal tissue. The error in the attenuation estimates shown in Fig. 6(a) was obtained for a single backscattered waveform. The accuracy of the estimate might be improved if the spectra or waveforms from several locations were averaged together. Combining the information from several waveforms is beyond the scope of the current investigation.

FIG. 6.

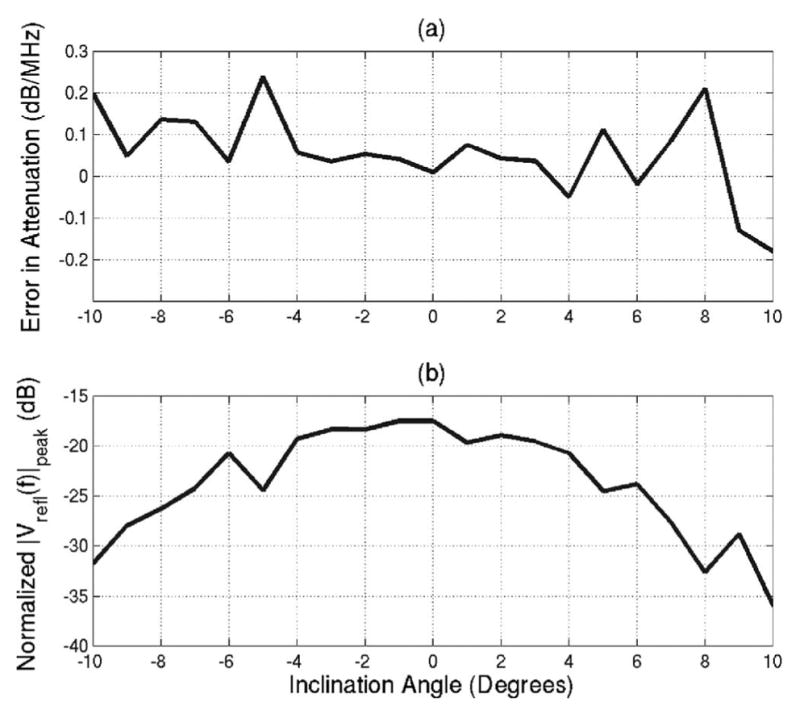
(a) Error in attenuation estimates resulting from inclination angle and (b) normalized magnitude of spectrum peak of backscattered signal for various inclination angles of the tissue mimicking phantom.

In addition to the attenuation estimate, the magnitude of the voltage at the spectral peak (i.e., f_peak) for the signal returned from phantom for each inclination angle relative to the magnitude of the voltage at the spectral peak for the signal returned from the Plexiglas for a θ_f of 0° is also shown in Fig. 6(b). The magnitude of the voltage peak returned from the phantom is always less than the magnitude of the voltage peak returned from the skull. Also, the magnitude decays quickly with increasing inclination angle just as was observed with the experiment with the Plexiglas plate. Hence, surface roughness does not play a dominate role in the reflection from the tissue-mimicking phantom. However, surface roughness may have a larger impact on the reflection from the fetus in utero.

IV. DISCUSSION AND CONCLUSIONS

A method for determining the attenuation along the propagation path leading to a developing fetus has been proposed. Initially, the fetal skull was modeled as a planar boundary at some unknown orientation with respect to the incident ultrasound beam. Theoretical calculations demonstrated that the shape of the backscattered spectrum would be independent of the inclination angle of the impinging sound beam. Hence, the spectrum from the skull could be compared to a reference spectrum obtained in a water bath to yield an estimate for the total attenuation along the propagation path. The theoretical calculations were validated using a Plexiglas plate and a rat’s skull positioned at various angles with respect to the sound beam. The error in the attenuation estimate due to the inclination angle of the rat’s skull was always less than 0.1 dB/MHz for all of the tested inclination angles. The surface roughness of the skull when compared to the smooth Plexiglas appeared to improve the attenuation estimate at the larger incidence angles. Based on the skull results, estimating the attenuation using reflections from the fetal skull appears to be very promising.

After performing the skull experiments, it was noted that the simple planar boundary model would probably not be valid for the skull in the early stages of fetal development. Ossification of most of the skull bones begins with branching tubules that cannot be approximated as a simple planar boundary. Hence, the estimation technique was extended to the amniotic fluid/soft fetal tissue boundary and tested using a water/tissue mimicking phantom boundary. The phantom waveforms were windowed with Hamming windows in order to limit the impact of the speckle from within the phantom on the attenuation estimate. The best window length was found to be 2 periods of the fundamental frequency of the ultrasound transducer. Using this window length, the error in the attenuation estimate was always less than 0.25 dB/MHz. This error might be reduced further if the information from more than one waveform were averaged together.

The phantom results show great promise for extending the estimation technique to any gestational age due to the prevalence of soft fetal tissue very early in development. However, the results should still be validated using fetal tissue from an appropriate animal model. In addition to working with an animal model, the attenuation estimate could probably be improved by using an autoregressive (AR) estimation scheme rather than windowing to reduce the impact of the speckle (Girault et al., 1998). AR estimation may also improve the computation time of the attenuation estimate.

Although the results are promising, estimating the exposure pressure and/or intensity using the attenuation along the propagation path using a simple derating procedure requires that nonlinear propagation be neglected. Neglecting nonlinear effects may not be reasonable especially when estimating the exposure intensity/pressure at higher transmit powers (Christopher and Carstensen, 1996). Hence, before being clinically implemented, the impact of nonlinear propagation needs to be addressed. It may still be possible to “quickly” estimate the in vivo exposure pressure and/or intensity to a reasonable level of accuracy on a patient specific basis from the attenuation along the propagation path by assuming that all of the attenuation occurs in an infinitesimally thin sheet at the surface of the transducer. Then, potentially, a look-up table could be designed to estimate the pressure/intensity at the focus.