Using nonequilibrium measurements to determine macromolecule free-energy differences

Since the advent of techniques that enable experimentalists to manipulate individual macromolecules, there has been a need for accurate estimates of free-energy changes between an initial equilibrium state and a second equilibrium state that is arrived at by a nonequilibrium manipulation. Atomic force microscopy and optical laser tweezers, often using macromolecules attached to μm-sized magnetic beads or polystyrene beads, are techniques that enable researchers to perform experiments on individual molecules, such as proteins and the polynucleic acids RNA and DNA. Traditional thermodynamic theory states that an estimate of the Helmholtz free-energy difference between two states, A and B, of a macromolecular system in contact with a thermal reservoir, ΔF = F_B – F_A, can be achieved by perturbing the system so that a transition between the two states takes place. For repeated trials, the averaged work done satisfies the inequality 〈W〉 ≥ ΔF. Only for infinitely slow, quasi-static processes can equality be achieved. Thus, in practice it once seemed that obtaining free-energy differences by macromolecular manipulations was virtually impossible. However, in 1997, Chris Jarzynski (1) derived the identity

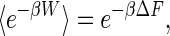[1]

in which β is the reciprocal of the product of the absolute temperature and Boltzmann's constant. In effect, the exponential weighting of the work performed emphasizes rare values of work in the work distribution function tail that are less than the free-energy change. Although this weighting may be expected to improve the estimate, the surprise here is the strict equality. The path integral proof of this identity found in Jarzynski's Physical Review E paper (2) is accessible and clear, and a broader setting and more general proof were subsequently published by Crooks (3). A number of numerical simulations and molecular dynamics calculations were done that confirmed the identity. Thinking about atomic force microscopy and laser tweezers techniques, Hummer and Szabo (4) analyzed how an experiment could be done so that rigorous free-energy profiles are obtained. If the experiment is done at constant temperature and pressure, then the free energy obtained from the generalized Jarzynski equality is the Gibbs free energy rather than the Helmholtz free energy in the original identity (4). In fact, this result is what was subsequently obtained in a real experiment involving the unfolding of a single RNA molecule (5). From a practical point of view, how many trials need to be run to get accurate results? Should one run many fast trials or relatively few slow ones for a fixed total amount of available time? What is the minimum number of trials required to get decent results? These are the sorts of issues addressed in the article by Gore et al. (6) in this issue of PNAS.

Application of the Jarzynski equality is not straightforward because the behavior of estimates based on finite numbers of trials is still not well understood. The free energy obtained from a finite number of trials is called the Jarzynski estimator and is given below. How well an estimator works had not been systematically studied previously. To begin to remedy this situation, the authors study bias, the variance, and the mean square error (MSE) for the Jarzynski estimator as a function of the number of trials, N. In numerical simulations, it is easy to run 10⁵ to 10⁶ trials. In real experiments (5), N is usually <10². This result creates a problem because application of the Jarzynski estimator requires sampling the rare trajectories in the low energy tail of the work distribution. Insufficient sampling may miss these rare events altogether. To explore this problem in depth, Gore et al. focus on a near-equilibrium regime in which the perturbation caused by manipulation is sufficiently slow that the work distribution is Gaussian. This explicit distribution function permits closed form calculations of several characteristic quantities that can be used for comparisons. For finite N, it is generally appreciated that the Jarzynski estimator is biased, but by how much was unknown. For the Gaussian case, some answers can be gleaned. In addition, the Gaussian case permits comparison with two other estimators, the mean work estimator ΔF̂_MW and the fluctuation–dissipation (FD) theorem estimator ΔF̂_FD. These estimators are to be compared with the Jarzynski estimator for a finite number of trials given by

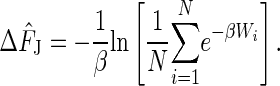[2]

The bias, the variance, and the MSE are three important properties associated with any estimator and are given, respectively, by

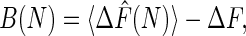[3]

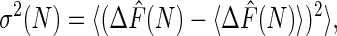[4]

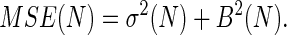[5]

The bias represents systematic error created by finite sampling. The variance measures statistical error, and the MSE measures the quality of the estimator. The Jarzynski estimator is biased for all finite N. However, it decreases monotonically with increasing N and vanishes for infinite N (7). For large N, a simple linear relationship exists between the bias and the variance for the Jarzynski estimator. This result has the effect that, for large N, the Jarzynski MSE is dominated by the variance.

By analyzing the detailed behavior of these quantities for the near-equilibrium Gaussian work distribution, several conclusions were drawn. The common question in computational studies, whether it is better to perform a few slow runs or many fast runs for a given amount of computer time, is answered for the Jarzynski estimator as follows. In the linear response regime near equilibrium, the Jarzynski MSE is always lower if fewer slow runs are used. The Jarzynski MSE is always better or equivalent to the mean work MSE in this same regime. The Jarzynski estimator is better than the FD estimator for small N but not as good for large N, at least in the near-equilibrium regime. For larger perturbations, the Jarzynski estimator is expected to be superior to the FD estimator for all N. A bias-corrected Jarzynski estimator is proposed by the authors. It uses the dissipated work, the difference between the trial work and the free-energy change being estimated. For large enough dissipated work and large enough N, there is a real improvement. However, for smaller values of the dissipated work that are closer to the typical experimental regime, the correction actually makes the results worse, and more sophisticated techniques need to be developed. Generally, Gore et al. (6) believe that future research on improving the Jarzynski estimator will focus on smaller sample sizes.

Recently, single molecule studies were reported on unzipping double-stranded λ-phage DNA at constant force (8). This system seems to be ideal for the determination of Gibbs free-energy changes by using the Jarzynski estimator, much like what was done for RNA stretching earlier (5). The experimental setup used involves attaching one end of the DNA to an antibody-coated round glass capillary and the other end to a magnetic bead. Dozens of antibody sites exist on the capillary and permit dozens of DNA-unzipping experiments to be run in parallel. This technique represents one way that individual macromolecule manipulations can be designed so that the trial numbers can be larger. If looked at from the Jarzynski viewpoint, will the free-energy changes determined be consistent with our independent biochemical knowledge of what they should be? Will such free-energy values be of utility in understanding the unzipping process in vitro? It would be very nice to have a benchmark case that shows that accurate free-energy changes can be determined from the Jarzynski estimator and that such information actually helps us to understand a basic biochemical mechanism. Perhaps λ-phage DNA can serve this purpose.

The promise of the Jarzynski identity for the determination of free-energy changes from nonequilibrium measurements in individual macromolecule manipulations has not been realized yet. Gore et al. have made major progress toward a better understanding of the consequences of finite sampling on the utility of the Jarzynski estimator. Hopefully, a compelling case will be made in the near future.