Coloration strategies in peacock feathers

Abstract

We report the mechanism of color production in peacock feathers. We find that the cortex in differently colored barbules, which contains a 2D photonic-crystal structure, is responsible for coloration. Simulations reveal that the photonic-crystal structure possesses a partial photonic bandgap along the direction normal to the cortex surface, for frequencies within which light is strongly reflected. Coloration strategies in peacock feathers are very ingenious and simple: controlling the lattice constant and the number of periods in the photonic-crystal structure. Varying the lattice constant produces diversified colors. The reduction of the number of periods brings additional colors, causing mixed coloration.

Color production in nature takes advantage of either structural coloration (1, 2) or pigmentation. Structural colors result from the interaction of light waves with a featured structure having the same order of size as the light wavelength. Structural colors in avian feathers have been usually qualitatively understood by thin-film interference (3–5) or the scattering from a spongy matrix structure incoherently (6, 7) or coherently (8, 9). Although the structural colors of avian feathers have been studied for a long time (10–14), many questions remain to be answered. In particular, the precise physical mechanism that produces the diversified colors in peacock tail feathers has not been established.

Materials and Methods

The male peacock tail contains spectacular beauty because of the brilliant, iridescent, diversified colors and the intricate, colorful eye patterns. Peacock feathers serve as an excellent canonical example for investigating structural colors in avian feathers. The structures of the blue, green, yellow, and brown barbules in the eye pattern of a male green peacock (Pavo muticus) feather were characterized by using an optical microscope and a scanning electron microscope. The peacock tail feather has a central stem with an array of barbs on each side. On each side of a barb there is an array of flat barbules. Each barbule has round indentations of typically ≈20–30 μm, which disperse the incident light, causing coloration. The round indentation has a smoothly curved crescent-like profile in transverse cross section (14).

To understand the detailed mechanisms of color production in peacock feathers, a plane-wave expansion method (15) was used to calculate the photonic band structure of the periodic photonic structures. A transfer matrix method (16) was adopted to compute the reflectance spectra to compare with experimental results.

Results and Discussion

Fig. 1 shows the submicron structures of barbules. The transverse cross sections reveal that a barbule consists of a medullar core of ≈3 μm enclosed by a cortex layer. Interestingly, the cortex of all differently colored barbules contains a 2D photonic-crystal structure (14, 17–19) made up of melanin rods connected by keratin. The longitudinal cross section shows that the melanin rod length is ≈0.7 μm. Melanin is created by melanocyte cells, deposited in developing feathers, and becomes fixed in the keratinized feather structure (6). Photonic-crystal structures in all differently colored barbules are quite similar. In the blue, green, and yellow barbules, the lattice structure is nearly square, whereas in the brown barbule it is a rectangular lattice. The only differences are the lattice constant (rod spacing) and the number of periods (melanin rod layers) along the direction normal to the cortex surface. We will show later that these differences are the cause of the diversified colors.

Fig. 1.

Scanning electron microscope images of barbule structures. (A) Transverse cross section of the green barbule. The outer cortex layer contains a periodic structure. The central part is the medullar layer. Transverse cross section of the cortex under higher magnification is shown for the green (B) and brown (C) barbules. The surface of the cortex is a thin keratin layer. Beneath the surface keratin layer, there is a 2D photonic crystal-like structure. This 2D photonic crystal is made up of an array of melanin rods connected by keratin. The remaining hollows are air holes (dark gray). Melanin rods are parallel to the cortex surface. The melanin rods embedded in the surface keratin layer can be clearly seen. (D) Longitudinal cross section of the green barbule with the surface keratin layer removed.

Note that one or two layers of melanin rods are buried in the surface keratin layer. The lattice constants for the blue, green, and yellow barbules are ≈140, 150, and 165 nm, respectively. In the brown barbule the lattice structure is less regular, with the lattice constants of ≈150 and 185 nm along the directions parallel and perpendicular to the cortex surface, respectively. The number of periods is ≈9–12 for the blue and green barbules, ≈6 for the yellow barbule, and ≈4 for the brown barbule.

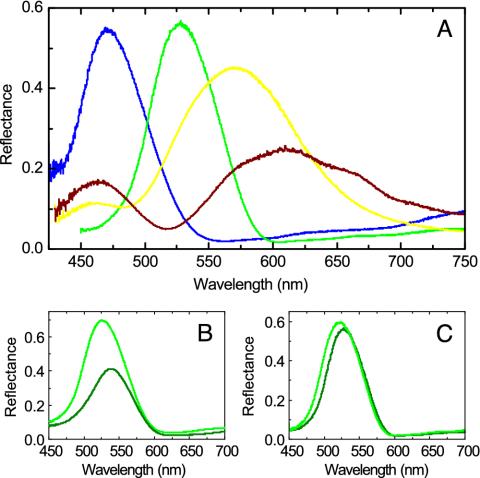
In Fig. 2A we show the measured reflectance by using a microspectrophotometer for differently colored barbules at normal incidence with the electric vector parallel to the melanin rods (E polarization). The reflectance spectra for the blue and green barbules show a number of features distinct from those of the yellow and brown barbules. The blue and green barbules have a narrower width of the main peaks with the peak positions located into the blue and green wavelengths, respectively. For the yellow barbule, the main peak ranges from the green to the orange wavelength and from the green to the red wavelength for the brown barbule, indicating that the yellow and brown colors are mixed colors. In addition, a side peak appears at the blue wavelength in the yellow and brown barbules.

Fig. 2.

Measured reflectance at normal incidence. (A) Measured reflectance of differently colored barbules for E polarization. Blue, green, yellow, and brown lines indicate the results of the blue, green, yellow, and brown barbules, respectively. (B) Measured reflectance of the green barbule with (dark green) and without (green) glycerine infiltrated for E polarization. (C) Measured reflectance of the green barbule for E (green) and H (dark green) polarizations.

To confirm that coloration in peacock feathers is produced structurally, barbules were immersed into glycerin (refractive index, 1.47) to fill the air holes. The infiltration of glycerin reduces the refractive index contrast and increases the average refractive index of the system. All peak positions in the reflectance spectra for the glycerin-infiltrated barbules shift to the longer wavelengths (Fig. 2B). This fact, together with the iridescent phenomenon, indicates that coloration in peacock feathers is caused by structural colors, instead of pigmentation.

For a 2D photonic crystal, reflectance spectra for E and H (with the electric vector perpendicular to the melanin rods) polarizations should be different. The measured reflectance spectra for two polarizations show that there is only a small difference in the peak position (Fig. 2C). Other colored barbules exhibit the same feature, indicating that coloration in peacock feathers is not altered by polarization.

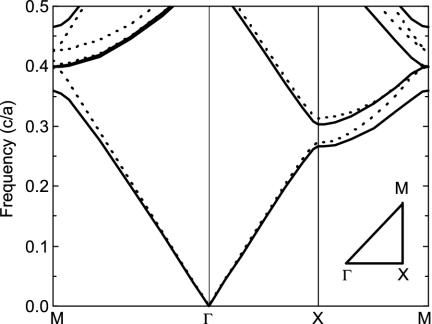
To explore the origin of coloration in peacock feathers, we calculated the photonic band structure of an infinite 2D photonic crystal by a plane-wave expansion method (15), shown in Fig. 3. The structural parameters for this photonic crystal are taken from the measurements, i.e., r_rod/a = 0.4 and r_air/a = 0.25, where r_rod and r_air are the radii of the melanin rods and air holes, respectively, and a is the lattice constant. The refractive indices of keratin and melanin are taken to be 1.54 (20) and 2.0 (5), respectively. This 2D photonic crystal does not exhibit a complete photonic bandgap. However, a partial photonic bandgap for both E and H polarizations exists along the Γ–X direction. The difference between the midgap frequencies of two polarizations is rather small, confirming the experimental observation (Fig. 2C). It is known that a strong reflection is expected for frequencies within the partial photonic bandgap along the Γ–X direction (19). The partial photonic bandgap is hence the cause of color production. It should be mentioned that the partial photonic bandgap shifts to a higher frequency range with the increasing angle of incidence, leading to iridescent colors.

Fig. 3.

Calculated photonic band structure of an infinite 2D photonic crystal for E (solid lines) and H (dashed lines) polarizations. Frequency is in units of c/a, where c is the speed of light in vacuum and a is the lattice constant. (Inset) The irreducible Brillouin zone is shown. Γ, X, and M are the center, edge center, and corner of the first Brillouin zone, respectively. Note that the Γ–X direction is along the direction normal to the cortex surface.

Note that the midgap frequency scales inversely with the lattice constant. Thus the color strategy in peacock feathers is very simple: the variation of the lattice constant results in different colors. In fact, using the lattice constants for differently colored barbules, the resultant midgap wavelengths match well with the main peak positions observed in the experiment.

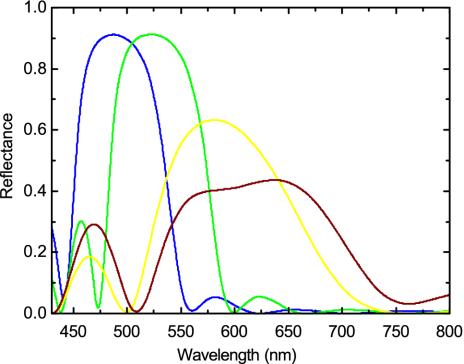
To confirm the predictions from the photonic band structure, we calculated the reflectance spectra of generic 2D photonic crystals with a finite number of periods by a transfer matrix method (16), shown in Fig. 4. The lattice constant and the number of periods in differently colored barbules are taken from the measurements. For melanin an imaginary refractive index of 0.01 is introduced to take into account light absorption. The calculated reflectance spectra correctly reproduce the main features of the experiment. Importantly, the predicted peak positions are in good agreement with the experimental observations, although there are some differences in shapes. Note that within the partial photonic bandgap the reflectance decreases and the peak width increases with the decreasing number of periods.

Fig. 4.

Calculated reflectance of generic 2D photonic-crystal structures with a finite number of periods for E polarization. Structure parameters are taken from the measurements. Results for the blue, green, yellow, and brown barbules are indicated by the correspondingly colored lines, and their periods are 10, 10, 6, and 4, respectively.

On both sides of the main peaks, the reflectance spectra show some oscillations, due to the Fabry-Perot interference because there are two interfaces in the finite photonic crystal. It is more distinct on the lower wavelength side than on the higher wavelength side. For a photonic crystal consisting of dielectric rods without touching each other, it is the opposite case. The calculated side peaks at the blue wavelength in the yellow and brown barbules agree well with the experimental observations. It should be mentioned that the side peak intensity is more enhanced with the decreasing number of periods. For photonic crystal with a large number of periods, the effect of the partial photonic bandgap is dominant. However, with the decreasing number of periods side peaks also play a role in coloration, giving rise to an additional color.

The glycerin immersion measurements reveal that the peak positions in the reflectance spectra shift to longer wavelengths, as shown in Fig. 2B. We also calculated the reflectance spectra of glycerin-immersed barbules. The calculated wavelength shifts are in good agreement with the measured ones. For example, for the green barbule, the measured wavelength shift is ≈12 nm, whereas the theoretical one is ≈10 nm.

Conclusion

Our experiment and simulations reveal that the coloration in peacock feathers takes advantage of the partial photonic bandgap of the 2D photonic-crystal structure in the cortex. The strategies for color production in peacock feathers are very ingenious and rather simple, i.e., by means of the variation of the lattice constant or the number of periods. Varying the lattice constant shifts the midgap frequency of the partial photonic bandgap. The number of periods controls the production of additional colors, eventually leading to the additive, mixed coloration. Diversified colors can be produced by means of these strategies. The revealed physical mechanisms and coloration strategies in peacock feathers could be of great help in understanding structural colors in avian feathers and color steering in nature.