Olivo-cerebellar cluster-based universal control system

Abstract

The olivo-cerebellar network plays a key role in the organization of vertebrate motor control. The oscillatory properties of inferior olive (IO) neurons have been shown to provide timing signals for motor coordination in which spatio-temporal coherent oscillatory neuronal clusters control movement dynamics. Based on the neuronal connectivity and electrophysiology of the olivo-cerebellar network we have developed a general-purpose control approach, which we refer to as a universal control system (UCS), capable of dealing with a large number of actuator parameters in real time. In this UCS, the imposed goal and the resultant feedback from the actuators specify system properties. The goal is realized through implementing an architecture that can regulate a large number of parameters simultaneously by providing stimuli-modulated spatio-temporal cluster dynamics.

The olivo-cerebellar system, one of the key neuronal circuits in the brain, has been shown to provide highly coordinated signals concerned with the temporal organization of movement execution (1–3). This neuronal network involves inferior olive (IO) neurons whose axons, the climbing fibers, terminate as excitatory inputs onto Purkinje cells in the cerebellar cortex and as en-passant collaterals onto the cerebellar nuclear neurons. The Purkinje cells, in turn, exert a powerful synaptic inhibition onto these cerebellar nuclear neurons (4). Much of the intrinsic activity in this network is supported by autonomous subthreshold membrane potential oscillations in IO neurons that display a close-to 10-Hz frequency (5–7). Action potentials in IO neurons occur at the depolarization apex of these oscillations (5).

To implement motor coordination via the olivo-cerebellar system, the IO nucleus is organized such that the dendrites of the IO neurons are electrotonically coupled (8, 9) via dendritic gap junctions (10) and receive inhibitory feedback from the cerebellar nuclei (11–14). It was originally proposed that this inhibitory input produced a dynamic decoupling of the IO neurons (9). This finding was later demonstrated to be correct by using multiple electrode recordings at the cerebellar cortex (15). Thus, the coupling serves to synchronize the oscillatory phase of IO neurons whereas the return nuclear inhibition, by transiently shunting dendritic coupling, controls cluster size and contour. The interplay between these two processes provides the pattern formation responsible for motor control via “cluster dynamics” in the IO (16). Such functional clusters have been demonstrated in vitro by using voltage-dependent dye imaging of the IO (16) and in vivo at the Purkinje cell layer by using multiple electrode recordings (17, 18). The temporal dynamics of the cluster activity have been shown to be directly correlated with premotor temporal patterns of Purkinje cell activity during motor execution (19).

The control complexity that the CNS must implement to execute movements as simple as merely grasping an object requires the simultaneous activation of 50 key muscles with over 10¹⁵ possible combinations (2). A digital control system attempting optimal combination of such a large set of variables at a real time of 1 KHz would require a 10⁶ GHz clock rate; thus, even with present day computers, a simple movement will result in computational overload.

By contrast, the olivo-cerebellar system works with a radically different strategy. To avoid a huge computational overload, IO cells fire in a noncontinuous burst with a frequency not exceeding 10 Hz and control groups, rather than individual neurons. Their activity is reflected in physiological tremor and underlies the noncontinuous nature of motor execution (1). At the same time, to smooth the movement discontinuities, the lower timing rate demands recurrent upgrade compensation every 100 ms. This timing is implemented through the dynamic activation of nucleo-cerebellar inhibitory feedback onto IO cells by modulating electrotonic coupling during their oscillatory phase. Thus, movement control implements synchronized time-step activation of different muscles, or synergistic muscle groups.

Accordingly, the system can be viewed as a set of phase-coherent oscillatory clusters where their spatial configuration corresponds to a particular movement (set of muscular activation) and where ongoing cluster dynamics “choose” the optimal configuration for the next time step. Note that such internal representation of the parameter space provides a high degree of resilience in the system. Indeed, the controller can rapidly rearrange the cluster distribution and execute the required action in the presence of unit damage. From this perspective, the olivo-cerebellar controller does not compute; rather, it deals with analog signals and represents the parameters under control (muscles) as space-time patterns (motor patterns).

Methods and Results

We have developed a general-purpose control model, which we refer to as a universal control system (UCS). Using cluster control principles, the UCS reproduces the key features of the motor control dynamics of the olivo-cerebellar system in an electronic circuit. The circuit has four component: (i) parameter processing units (chips) that emulate IO neuron electrophysiology, (ii) a coupling controller, that emulate the inhibitory cerebellar nuclear function, (iii) a motor intention pattern input representing the motor strategy to be implemented, and (iv) an actuator system that implements motor command tactics. The UCS also includes internal and external feedback loops.

Parameter-Processing Units. The electrical properties of IO neurons have been mathematically modeled previously by using a Van der Pole oscillator (20). Here, we present a second model of the IO neurons that is functionally equivalent to the previous model but provides a better fit with the experimental data, as well as a faster response to a stimulus. This model generates oscillations by appropriate parameter choice. The robust subthreshold oscillations of each unit emerge from Andronov–Hopf bifurcation, in the first subthreshold state. The oscillatory signal goes to the second (suprathreshold) state, which hovers up and down relative to action potential threshold. When reaching threshold at the peak of a subthreshold oscillation, the unit generates a spike. The timing of the spiking is thus determined by the subthreshold oscillations. Depending on the values of the control parameters, the model qualitatively reproduces the spontaneous and stimuli-induced oscillations observed in IO neurons (5). These properties can be described by a mathematical model comprising a set of four nonlinear differential equations:

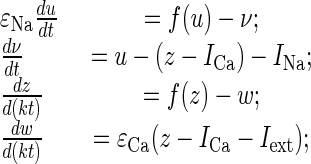1

where the variables z and w are responsible for the subthreshold oscillations and low-threshold (Ca²⁺-dependent) spiking, and the variables u and v describe the higher-threshold (Na⁺-dependent) spiking. The parameters ε_Ca and ε_Na control the oscillation time scales; I_Ca and I_Na drive the depolarization level of the two blocks; f is a cubic shape nonlinearity, f(x) = x (x - a)(1 - x); and the parameter k sets a relative time scale between the two blocks. For a particular choice of parameters (ε_Na = 0.001; ε_Ca = 0.02; k = 10; I_Ca = 0.01; I_Na = -0.59; a = 0.01), the model displays oscillations with the maximum spiking frequency (one spike per period) (20). I_ext has non-zero value only when the intention template is activated.

A Hardwired UCS. Based on the above mathematical model, a set of hybrid electronic IO chips was designed and manufactured. Each chip (Fig. 1A) serves as a parameter-processing unit. Specifically, each chip comprises five emitter follower circuits and two field-effect transistor-driven multivibrators and is capable of generating subthreshold oscillations and two distinct firing levels corresponding to the low-threshold and highthreshold spikes (5). On reaching a specified potential (at the peak of an oscillation), the system generates spikes (Fig. 1B).

Fig. 1.

(A) Hybrid microchip hardware model of IO neuron. (B) Oscillations generated by the hardware model at the maximum spike frequency.

These chips were then assembled into a network based on the general connectivity of the olivo-cerebellar system. A set of chips, wired together in a rectangular grid, form the processing unit component of the UCS.

The UCS reproduces the key features of the olivo-cerebellar system as follows: (i) The UCS comprises parameter-processing units that are robust oscillators generating spikes with precise timing, τ. (ii) Coupling among processing units provides phase synchronization among units. Such coupling is influenced by inhibitory feedback resulting in variable clustering of units. (iii) The UCS has an effective phase-resetting mechanism that drives different cluster configurations at a rapid time scale (≈τ). The system reconfigures clusters on feedback signals from the execution system.

We expected that the “computing” power of the UCS could be substantially higher than that of a digital computer. Using a computer model of the UCS, we found that, given N parameters to be controlled, the UCS must have at least N chips such that a given chip will be associated with, and monitor, a given control parameter. The model also indicated that a chip could hold the specific phase that controls the state of a given parameter by mapping phase values onto possible values of the parameter.

In this context, if M represents the number of levels of phase that could be resolved by the system, then, at the timing interval, τ, the UCS would “resolve” M^N possible combinations of different parameter states. In terms of digital processing the upper limit of the UCS computing power would be:

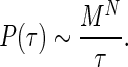2

In the olivo-cerebellar system, the precision of spike synchrony at the Purkinje cells innervated by an IO cluster is on the order of 1 ms (21). By “clusters,” we mean groups of neighboring neurons that demonstrate phase-coherent oscillation. Thus, the number of possible states for a 100-ms period can be estimated as M = 100 if we implement the biological parameters.

Note, however, that, in the UCS, the timing window can be substantially decreased to the energetic limits of the constituent materials. Eq. 2 gives only the upper limit for the UCS. Within any particular template of activity, the number of possible states will be smaller and will depend on the particular task the template is required to accomplish. (Compared with a digital system, this template resembles the limits that a particular operating system or algorithm imposes on the speed of calculations.)

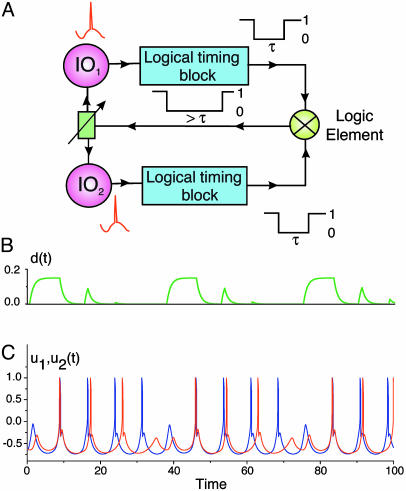
Interunit Synchronization and Time Binding. As with IO neurons, where electrotonic coupling leads to phase synchronization, resistive coupling between IO chips demonstrates similar properties. This finding is demonstrated by using a circuit comprising two chips as shown in Fig. 2. In this circuit, when a subthreshold oscillation in the processing units (IO₁ and IO₂) reaches threshold, a spike is generated (red spike). The logical timing blocks generate a pulse of duration τ in response to each spike. These pulses then enter the logic element (coupling controller), which performs an AND function, and the durations of the pulses are summed. This new pulse is then used to control coupling between the processing units. Here, the logical timing blocks generated LOW (0) pulses so the output of the logic element leads to decoupling. When the processing units fire asynchronously, as in this example, the decoupling period is >τ. An arbitrary value simulation of this circuit is shown in Fig. 2 B and C. Coupling [d(t)] between two units [u₁(t) and u₂(t)] is shown in Fig. 2B, and unit output is shown in Fig. 2C. Note that, in the absence of action potentials, coupling increases and the two units fire synchronously. Because synchrony is not perfect, through the feedback circuit, this firing tends to reduce coupling. The units are not strongly coupled again until the processing units return to the subthreshold state.

Fig. 2.

Spike-controlled coupling circuit and simulation. In this example, processing units (IO₁ and IO₂) are resistively coupled. Their output controls the resistive coupling via feedback through a logical timing block and a logic element. Each time a unit generates a spike (red spike), the timing block generates a pulse with duration τ. The logic element performs an AND function, summing the duration of the pulses from the timing block set. When the units fire asynchronously, the summed pulse is >τ, as indicated in A. A simulation of this circuit shows coupling [d(t)] between the two units (B) and unit output [u₁(t), u₂(t)] (C). Note that, in the absence of spikes, coupling increases, and the two units fire synchronously. Feedback from the spikes, when their synchrony is not perfect, tends to uncouple the units. The units are not strongly coupled again until the units return to the subthreshold state.

Cluster Control Architecture. At the next step, the activity of the N parameter-processing unit activity is integrated into the dynamics of the UCS by using the principles of cluster control architecture. Because the units (chips) are locally coupled, an individual unit can influence its neighboring units directly. The coupling inhibitory feedback signal generated as a function of spiking activity in one unit will thus directly influence the unit itself, and its neighbors (Fig. 2). Local groups of units that are directly coupled and have the same oscillatory phase form clusters. Using such clusters, the system is capable of maintaining local oscillatory coherence and can tune neighboring unit phase. This parallel processing feature is significant when groups of chips control certain parameters or closely linked groups of parameters. The global coherence of many clusters determines a particular execution (output) pattern. Such coherence is determined by signals returning via the internal feedback loop (chip activity to the coupling controller) and by feedback from the actuator system.

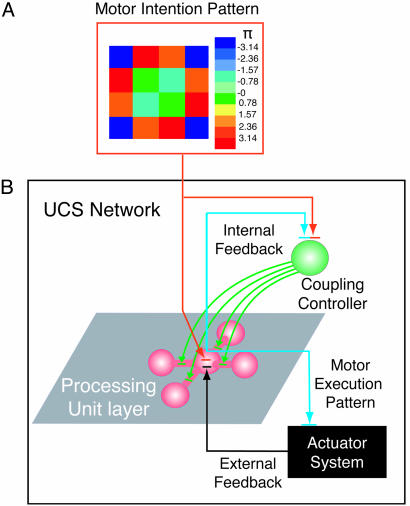
This template is illustrated in Fig. 3, which includes a motor intention pattern (Fig. 3A) and a schematic representation of an UCS (Fig. 3B). The UCS comprises a coupling controller and a layer of N processing units (chips) that can be organized into clusters. For clarity, only one example cluster is shown. This cluster comprises a central unit linked to four units by spike-controlled, variable coupling connections.

Fig. 3.

Schematic representation of UCS architecture. A motor intention pattern (A) and the components of the UCS (N processing units, coupling controller and actuator system; B) are shown with their connections. The color of each pixel in the intention pattern encodes for the corresponding processing unit an inner product of the required oscillatory phase (-π to +π) (to the coupling controlled) and the magnitude of an oscillatory reset signal (directly to the processing unit layer) (A). The processing units may be organized into clusters. An example cluster comprising a central unit linked to four units by spike-controlled, variable coupling connections is shown. In addition to the intention pattern, the coupling controller receives feedback from the processing unit layer (internal feedback loop). This is the same signal that leaves the UCS to stimulate the actuator system. Note that, in addition to input from the intention pattern and coupling controller, the processing units receive feedback from the actuator system (external feedback loop).

The intention pattern projects to the processing units both directly and indirectly (through the coupling controller). The direct projection acts to reset oscillatory phase in individual units. Signals through the coupling controller act to inhibit the interunit coupling according to the intention pattern. The color of each pixel (Fig. 3A) in the intention pattern encodes an action potential for the indirect pathway and the phase magnitude (from -π to +π) of an oscillatory reset signal for the direct pathway. The latter is specified in units of depolarizing current (I_ext) in the system of equations in Eqs. 1.

Neighboring units can be highly synchronized. Such synchronization would provide coherence during a controlled state when the goal is to trigger actuator activity, for example. Functional flexibility is provided when the units are decoupled. In this state, they can either operate autonomously, to compensate for the control discontinuity, or their phase may be reset according to incoming stimuli. External feedback signals from the actuator system directly “reports” the current state of the executing system to the UCS via the IO chips. This input resets the phase differences among clusters. In this case, they could reconfigure themselves to be tuned for another motor intention pattern

Because synchronization of the processing units is tuned through an internal feedback loop, the intention pattern sets only a general control strategy as the system needs to use only the key features of the input pattern. For example, in the motor intention pattern shown in Fig. 3A, the system requires only pattern contours separating units or groups of units with different phases. Effective UCS function does not require that the intention pattern be perfectly implemented initially. Rather, specification of the contours (borders) of the clusters is the critical parameter. Thus, if some elements of a particular cluster in the pattern were to fall out of synchronization with the rest of the pattern, the performance of the system would not be affected.

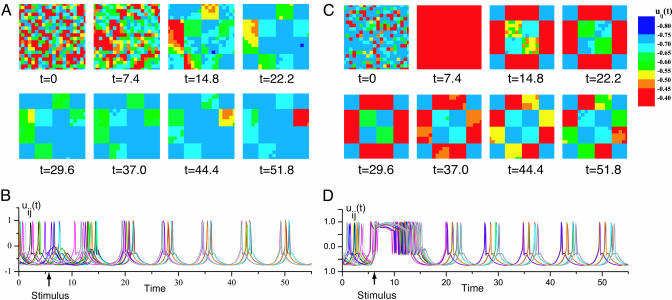
The UCS processes both input from the intention template and the executing system rapidly, updating the clusters on a time scale of τ. The UCS generates an optimal motor execution pattern (Fig. 3B) for a given input signal and current state of the executing system. Such a sequence of motor execution patterns and unit output was obtained by an arbitrary value simulation (Fig. 4). At t = 7.4, the UCS was stimulated with the motor intention pattern shown in Fig. 3A. Before, and at the moment of delivery of the motor intention pattern (stimulus, t = 7.4), there is little coherence among the 400 processing units. After delivery of the stimulus, the network organized itself into square configurations of clusters corresponding to the stimulus (Fig. 3A). Note the increased synchronization of firing of individual units after the stimulus was delivered (Fig. 4B).

Fig. 4.

Motor execution patterns and output of individual oscillator units. (A) Sequence of snapshots of the motor execution pattern before (t = 0) and after delivery of the motor intention pattern. Note that at t = 0 and 7.4 there is little coherence among the processing units. After delivery of the stimulus (Stimulus in B), the network organized itself into square configurations of clusters corresponding to the stimulus (intention pattern in Fig. 3A). Note the increased synchronization of firing of individual units after the stimulus was delivered (B). Delivery of a higher intensity stimulus synchronized unit phase (t = 7.4, C) and firing (D). The motor execution pattern resembled the motor intention pattern after only one iteration (t = 14.8). More iterations were required to achieve such coherence with the lower intensity stimulus (A). (Data were obtained by computer simulation of a UCS with 400 units.)

As mentioned above, the UCS uses input from the actuator system to reset the phase differences among clusters. This actuator feedback returns directly to chip units. As shown in the unit model (Eq. 2), a stimulus resets the unit's oscillatory phase to a value corresponding to the duration and magnitude of the input signal. Thus, UCS network activation with an increased magnitude intention pattern (Fig. 4 C and D) is associated with increased level of intensity of the motor pattern, resulting in the required synchronization between clusters. As shown in Fig. 4C, delivery of the stimulus synchronizes all of the units (t = 7.4), and the motor pattern is attained after the first cycle through the processing units (t = 14.8). This result is also seen in the near-synchronous firing of the individual units immediately after delivery of the stimulus (Fig. 4D).

These results may be compared with pattern formation in the gradient neural networks (e.g., Hopfield, ref. 22) where it is necessary to define all possible N² interunit connections for a given pattern (Hebbian learning rule). By contrast, the UCS needs to have only a few percent of this value modified, thus avoiding possible overloads. In the chessboard pattern example, a UCS composed of N = 400 units uses only ≈10² couplings from 1.6 × 10⁴ possibilities, i.e., only a few percent.

Note also that the phase difference between the clusters is not fixed, but depends on the initial (or previous) state of the system. Thus, for a given stimulus, the UCS yields a pool of possible cluster configurations. Because the system does not require a fixed phase difference between clusters, the number of possible patterns that are satisfactory for an imposed intention template provides a pool of possible solutions. This result not only makes the system robust with respect to the malfunctioning of one or more individual oscillators, but also ensures a given level of tolerance to external obstacles that are introduced to the system as perturbations to the pattern of activity. In response to perturbations, the UCS switches to another pattern from the pool that avoids “accommodating” the obstacles by avoiding them.

Discussion

The olivo-cerebellar system represents a high level controller for movement execution. It can simultaneously address an enormous number of tasks coordinating all muscles to work in the synchrony required for smooth movements. The system is agile and robust and capable of reorganizing itself according to current conditions. For a given task, it presents a pool of possible solutions to the executing system. The system is, de facto, tolerant of external perturbations, local internal controller damage, and damage to the input–output pathways, or to the executing mechanism. In modeling the structure and functions of the olivo-cerebellar controller, we have found a solution that approaches a universal control system, in the sense that it is applicable to a large set of control requirements. The UCS does not demand specification of parameters under control and has no restriction on the number of the parameters to be tuned. Such universality opens a wide area for its application. For instance, as a model of a motor control system, the UCS could hold in tune robot actuators, solving the problems of stability and adaptability simultaneously. Indeed, given any device to be controlled, the UCS must be supplied with the input–output connectivity providing the interface between the parameter under control and the phase of UCS's oscillators. In contrast to existing controllers (mostly based on digital computing systems), the UCS does not operate numerically. It works by internal analogous emulation of a set of possible solutions for a given task.