Optical tweezers for single cells

Abstract

Optical tweezers (OT) have emerged as an essential tool for manipulating single biological cells and performing sophisticated biophysical/biomechanical characterizations. Distinct advantages of using tweezers for these characterizations include non-contact force for cell manipulation, force resolution as accurate as 100 aN and amiability to liquid medium environments. Their wide range of applications, such as transporting foreign materials into single cells, delivering cells to specific locations and sorting cells in microfluidic systems, are reviewed in this article. Recent developments of OT for nanomechanical characterization of various biological cells are discussed in terms of both their theoretical and experimental advancements. The future trends of employing OT in single cells, especially in stem cell delivery, tissue engineering and regenerative medicine, are prospected. More importantly, current limitations and future challenges of OT for these new paradigms are also highlighted in this review.

1. Introduction

Manipulating single cells is of paramount importance in areas of biomedical research such as in vitro fertilization, cell–cell interaction, cell adhesion, embryology, microbiology, stem cell, tissue engineering and regenerative medicine and single cell transfection. The examination of how individual cells operate, function and interact with each other can reveal invisible processes such as single cell gene expression and chemical communication inside a singe cell, and can elucidate connections between subcellular processes and population-level behaviour. Two major types of techniques have been developed for manipulation of single cells: one is scanning probes such as the atomic force microscope (AFM) and scanning tunnel microscope (STM) and the other is field gradient traps such as optical tweezers (OT), magnetic tweezers (MT) and dielectrophoretic (DEP) traps. The working principles, merits and demerits of those techniques are summarized in table 1.

Table 1.

Comparison of common micromanipulation tools for single cells^a. (AFM, atomic force microscopy; MT, magnetic tweezers; DEP, dielectrophoresis; OT, optical tweezers.)

tools		principle	type	length-scale probe (nm)	typical force range (pN)	stiffness (pN nm−1)	advantages	disadvantages
scanning probes	AFM	a sharp tip normal to the free end of a cantilever	point; contact	1–10 000	5–10 000	10–10 000	active force clamp	single cell needs to adhere tightly to a surface; random attachment
field gradient traps	MT	electromagnetic field gradients; magnetic beads that are attached to single cell surface	global/point; non-contact	10–10 000	0.05–20	10−6– 0.1	constant force; angular force for out-of-plane rotation of single cell	magnetic beads to covalent or specific non-covalent attached to cells
	DEP	high-gradient electric field; cell dielectric properties and the surrounding medium	global; non-contact	20–100 000	0.01–50	—	simple operation	heating; two-dimensional trap
	OT	A highly focused beam to produce optical gradient; cell refraction index	point; non-contact	0.1–1000	0.1–100	10−6– 0.1	non-contact force; active or passive force clamp; well-defined geometries	photodamage or thermal damage

^aSome data are cited from Greenleaf et al. (2007).

OT have been widely applied to single molecular and cellular studies. At a single molecular level, biological motors including kinesin (Asbury et al. 2003; Block et al. 2003), cytoplasmic dynein (Mallik et al. 2004), myosin (Knight et al. 2001; Swank et al. 2001), nucleic acid-based enzymes (Pease et al. 2005; Dumont et al. 2006) and flagellar motors (Ryu et al. 2000) have been extensively studied as well as RNA and DNA mechanics (Allemand et al. 2003; Bustamante et al. 2003), protein conformational changes in folding/unfolding pathway (Cecconi et al. 2005), protein–protein binding/unbinding process (Thoumine et al. 2000; Litvinov et al. 2005) and DNA–protein interaction (Williams et al. 2001; Huisstede et al. 2007). Comprehensive reviews have been made for the OT: physical theory of optical trapping (Ashkin 1997, 2007), microsurgery (Berns 1998) and biophysical analysis of single molecules (Hormeno & Arias-Gonzalez 2006). A summary concerning the theory, construction and applications of OT can be found in Sheetz (1998), Ashkin (2007) and Berns & Greulich (2007).

In this review, the focus is mainly on how to apply OT for manipulating single cells and their mechanical characterization. Various cell types, including mammalian cells, Escherichia coli, red blood cells (RBCs), nerve cells, gametes and stem cells, have been studied. Modelling of cell mechanics and cell deformation in optical trapping is also appraised. Finally, future trends of OT for single cells, especially stem cells for tissue engineering and regenerative medicines, are prospected.

2. Working principles

2.1 Trapping mechanisms

OT use a highly focused laser beam to trap and manipulate microscopic, neutral objects such as small dielectric spherical particles that experience two kinds of forces as explained in figure 1a, namely the scattering force produced by the photons striking the cell along their propagation direction and the gradient force produced by a gradient of field intensity. Scattering and gradient forces exerted on the particles depend on the wavelength of the laser beam (λ) and the particle size (r). Particles trapped by the OT can be divided into three regimes: Mie regime (r≫λ); Rayleigh regime (r≪λ); and regime in between them (r∼λ) (Ashkin & Dziedzic 1987; Ashkin 2007).

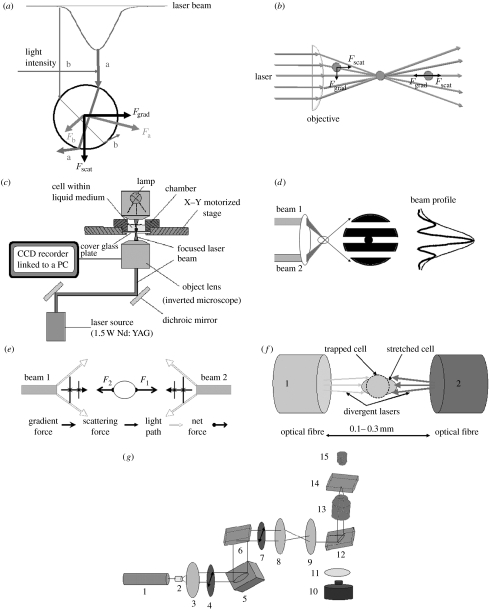
Figure 1.

Working principles of optical tweezers. (a) The scattering (F_scat) and gradient (F_grad) components of optical forces on a dielectric sphere due to a Gaussian laser beam (light intensity increases from b to a). (b) Schematic of optical tweezers. Light enters the objective lens of a microscope and is focused to a diffraction-limited beam waist, creating a three-dimensional light gradient; a particle that is out of trap is brought back to the centre of the trap. (c) Typical experimental set-up of optical tweezers, adapted from the technical note of Cell Robotic Inc., USA. (d) Two-beam interferometric optical tweezers, adapted from Chiou et al. (1997). (e) Schematic of gradient and scattering forces for two beams, adapted from Constable et al. (1993). (f) Schematic of optical stretcher, adapted from Guck et al. (2000). (g) Schematic of holographic optical tweezers generated from a spatial light modulator (SLM), adapted from Martin-Badosa et al. (2007). 1, laser beam; 2, LC lens; 3, LE lens; 4, polarizing element; 5, SLM; 6, dichroic mirror; 7, polarizing element; 8, telescope; 9, telescope; 10, CCD camera; 11, tube lens; 12, dichroic mirror; 13, microscopic objective; 14, sample; 15, illumination.

In the Mie regime, where the particle size is larger than the wavelength of the irradiation light, both the magnitude and the direction of the forces depend on the particle shape and trapping is generally restricted to spheres and ellipsoids. The conservation of momentum model or ray optics is applicable to this case (Ashkin 1997). Any change of momentum from individual rays of light when striking the particle results in an equal, opposite momentum change on the particle. A more intensive beam imparts a larger momentum change towards the centre of the trap than the less intensive beam. As shown in figure 1b, when the particle is out of trapping focus, the net momentum changes, or net force, can draw the particle back to the centre of the trap. When the particle is located in the centre of the trap, individual rays of light are refracting through the particle symmetrically, resulting in zero net lateral force and cancelling out the scattering force of the laser light (Ashkin & Dziedzic 1987; Svoboda & Block 1994).

If the particle size is substantially less than the wavelength, then the particle is in the Rayleigh regime. The direction of the force is independent of the particle shape and its magnitude varies with the particle orientation. The trapping particle can be considered as an induced dipole and the electromagnetic field of the light pulls the particle towards the brightest part of the beam, where the induced dipole may minimize its energy. In this case, the scattering force is proportional to the optical intensity and points towards the propagation of the laser light, while the gradient force is proportional to the gradient intensity and points in the direction of the intensity gradient. The gradient force attracts the particle into the region of the highest intensity, but the scattering force draws the particle into an equilibrium position that is slightly downstream of the maximum intensity. The competition between the two forces can result in stable trapping (Ashkin 1992).

When the particle sizes are comparable with the wavelength of the trapping laser, neither the ray optic nor the dipole approach is valid. More complete electromagnetic theories are needed for particles in this intermediate size range, although some recent theoretical calculations of forces on a sphere in this regime (0.1–10λ). Because the majority of objects are in this size range (0.1–10λ), such as bacteria, yeast, organelles of larger cells and dielectric microspheres used alone or as handles to manipulate other biological objects, a computational toolbox has been developed for a quantitative description of optical trapping (Nieminen et al. 2007).

2.2 Trapping force calibration

The trapping forces depend on the intensity of laser power, the shape of laser focus, the size and shape of the trapped particles and the index of refraction of the trapped particles relative to the surrounding medium. It is difficult to measure the trapping forces directly but there are several ways to calibrate them. The forces can be calibrated by a power spectrum of Brownian motion of a trapped particle and the trapping stiffness can be determined (Sheetz 1998; Berg-Sorensen & Flyvbjerg 2004). Another way of calibration is based on the fact that the external forces applied to a single particle within an optical trapping can push a single particle away from the focal region, and the force from the OT usually draws the particle back to the centre of the trap. In the equilibrium position, the external force equals the force from the OT. For a small displacement, the force from the OT, termed as restoring force, can be estimated by

$$F=-kX,$$ (2.1)

where k is the trap stiffness and X is the displacement of the particle away from the centre of the trap, when displacements are smaller than half the radius of the particle within the focal region.

Once the trap stiffness is determined or given, the external force applied on the particle can be determined by accurately monitoring the position of a particle in an optical trap. OT, therefore, have been widely used as a passive force measurement tool. Accurate position detection and measurement are essential for a quantitative optical trapping. Different position detection methods, such as video-based position detection, imaging position detection with a quadrant photodiode (QPD) and laser-based position detection with a QPD, have been reviewed in Neuman & Block (2004). A QPD can measure nanometres displacement at a rate of 10 kHz; therefore, small forces can be measured with a very high time resolution. However, it is difficult to implement a QPD for multiple particles simultaneously. Video cameras allow multi-particle tracking, with an accuracy order of 5 nm and a video acquisition rate of 25–120 Hz. Temporal resolution can be improved through the use of high-speed video cameras (Keen et al. 2007) but high-speed video tracking will be ultimately limited because spatial resolution decreases as the frame rate increases (Neuman & Block 2004).

Similar to the method described previously, the drag force method is to apply a known viscous drag force F and measure the displacement X away from the centre. In practice, drag force is usually produced by periodic movement of stage in an either triangular or sine waves of displacement while holding the particle in the trap.

The direct and widely used calibration approach is the escape force method. For a free particle of radius r in solution far away from the surface, knowing the critical velocity v when the particle escapes from the trap, the maximum trapping force F, which equals the opposing viscous drag force according to Svoboda & Block (1994) can be calculated as

$$F=6\pi \eta rv,$$ (2.2)

where η is the viscosity of the surrounding liquid.

2.3 Instrument

A simple set-up for OT in figure 1c is directing a laser beam through the interior of a microscope and filling the back aperture of a microscopic objective. The numerical aperture (NA) equals the index of refraction of the immersion fluid. Typically, the system is implemented using a high NA objective to ensure that true three-dimensional trapping is achieved. The irradiation source is a laser and the most popular power source is Nd:YAG (wavelength of 1064 nm) for single cell applications due to its biological amiability. The detailed discussion for each part of the set-up can be found in a review by Neuman & Block (2004) and a book by Sheetz (1998). Conventional OT use a microscopic objective lens and a standard Gaussian laser beam. Non-Gaussian laser beams, dual beams and multiple traps have been developed for OT so this emerging tool can be widely used in cell manipulation and characterization.

2.3.1 Non-Gaussian laser beams

In conventional OT, the laser intensity profile shows a Gaussian radial distribution; as a result, such a beam can be used to trap a single particle at one time. These conventional techniques have no capacity to tailor the optical potential in a three-dimensional space. A Bessel beam with a radial intensity profile presenting as a zero-order Bessel function has been explored to replace traditional Gaussian beams (Durnin 1987). In contrast to the single (bell-shaped) central maximum of a Gaussian beam, a Bessel beam consists of a bright centre spot surrounded by series of concentric rings of decreasing intensity. By continually reconstructing and supporting this central maximum, the concentric rings of a Bessel beam allow it to maintain its shape and resist spreading, even when an object such as an optically trapped particle lies in its path. Through the use of such a beam as OT, it is possible to trap and manipulate many different particles distributed over a distance of approximately 3 mm simultaneously (Garces-Chavez et al. 2002). However, Bessel beams only allow particles to be optically confined within perpendicular two-dimensional planes, and the particles are free to move in the direction of the beam.

A Laguerre–Gaussian mode has been created to obtain a rotating asymmetric intensity profile. This light beam possesses helical wavefronts that carry an orbital angular momentum (Allen et al. 1992; He et al. 1995). This beam is characterized by an intensity maxima spiral around a dark centre core, that is, a zero on-axis intensity. With their zero on-axis intensity, the axial trapping efficiency of OT has also been improved. The Laguerre–Gaussian beams within OT, termed as ‘optical vortices’, are able to offer stable three-dimensional confinement of hollow glass spheres from 2 to 50 μm (Gahagan & Swartzlander 1998). Particles that have a lower refractive index than their surrounding media are repelled from the beam axis using a conventional Gaussian beam. This problem can be overcome by the Laguerre–Gaussian beams. The optical vortices can also hold high-index particles to the normal position of just below the beam focus (Gahagan & Swartzlander 1999). The optical vortex tweezers can also apply controlled torques on trapped objects. The technique is flexible in changing the rotational symmetry of the interference pattern by adjusting the indices of the Laguerre–Gaussian mode, thereby potentially optimizing the shape of the intensity pattern to the shape of the object to be rotated.

2.3.2 Dual beams

Two optical beams, usually produced from a beam splitter, have been widely used to create dual optical traps (Fallman & Axner 1997). This requires that two light paths are controlled by different x–y deflector systems, so it is complicated to control two light beams and hard to achieve position stability. The two beams can be placed either to be parallel or to be counter propagating. Two parallel beams are used to create an interference pattern, as shown in figure 1d, the intensity profile within which gives rise to a gradient force confining both spherical and ‘rod-like’ particles. This OT is also termed as ‘interferometric OT’ (Chiou et al. 1997). Adjusting the path difference between the two beams results in a translation of the interference pattern and trapping particle. By ensuring the two beams are slightly displaced, the interference patterns can be confined to a centre portion of the field of view with ‘non-fringed’, high-intensity regions on either side, which could provide complete confinement of manipulated particles. This technique has been applied for trapping simultaneously both low- and high-index particles. MacDonald et al. (2003) used a simple-etched hologram to produce a five-beam interference pattern that creates an optical lattice. This three-dimensional optical lattice provides the ability to sort particles through a three-dimensional flow. Ladavac et al. (2004) created a complicated sorting sieve based on tailing the relative phases and intensities of the interfering beams. Schonbrun et al. (2005) further developed this technique to afford three-dimensional traps by an optical lattice formed by interference of multiple plane waves, which were generated through a single phase-only spatial light modulator (SLM).

Two divergent counter-propagating beams were first used by Ashkin (1970) to demonstrate the first actual trap. Constable et al. (1993) tried to place two beams in an exactly counter-propagating way and they provided an equation to calculate the scattering force for these two beams. The gradient and scattering forces are shown in figure 1e. For two identical beams from the opposite side, although the net force (F₁−F₂) or the scattering force exerted on the trapped particle is zero, the surface force stretches the particle with (F₁+F₂)/2 and the stretch force can be up to several hundred pN (Guck et al. 2000). This technique is attractive for stretching single cells or single polymer molecules and is known as optical stretching (OS) and can be used to measure the elasticity of biological cells (Guck et al. 2000, 2001, 2002), as shown in figure 1f. The advantages include that optical deformation does not require any kind of mechanical contact and covers a stress range previously inaccessible to cell elasticity measurements. Another advantage of using two divergent beams is to reduce photodamage or any two-photon-induced damage caused by a tightly focused light beam, which will be discussed in §2.4 (Jess et al. 2006).

2.3.3 Multiple traps

OT have been configured to create multiple traps so that multiple particles can be trapped simultaneously. These traps can be implemented by splitting the beam early in the optical circuit to produce two separate light paths that are combined before entering the microscope, rapid scanning of a single beam between two or more trapping positions and using computer-generated holograms to produce multiple beams simultaneously.

Two and more beams have been discussed in §2.3.2. Techniques to generate controllable multiple beams have also been developed. The vertical cavity surface-emitting laser (VCSEL) arrays, in which each laser is focused and acts as an individual trap and manipulation source, are able to provide an inexpensive compact package (Flynn et al. 2002; Ozkan et al. 2003a,b). However, they have a relatively low power input. Eriksen et al. (2002) used an alternative technique, generalized phase contrast (GPC) and a prefabricated phase mask to generate a laser beam array. A phase-only SLM encodes the desired pattern in the phase component of a collimated and expanded laser beam. This phase-encoded information serves as the input for a GPC system, in which a phase-contrast filter generates a high-contrast intensity pattern that directly corresponds to the phase perturbation of the input wavefront. The intensity pattern is focused using a microscope objective lens for trapping microscopic particles. Another approach used by Rodrigo et al. (2003) was based on the Shack–Hartmann wavefront sensor. A beam passes through a phase modulation from a reflection- or transmission-type SLM. Spatial Fourier transformation of the SLM-coded patterns is performed by a lenslet array. Then, the hologram enters the objective lens to be focused to a diffraction-limited spot or a single OT. This straightforward process enables an adjustable number of traps and real-time control of the position, size, shape and intensity of each individual beam in arbitrary arrays by encoding the appropriate phase pattern on the SLM in two and three dimensions (Rodrigo et al. 2006).

Scanning techniques generally use acousto-optic deflectors (AODs) that can scan a beam from point to point at kilohertz rates (Visscher et al. 1993). The AODs appear to be excellent for two-dimensional optical landscapes. By time sharing the light between trapping sites, the beam must revisit each trapping object often enough that the object has not diffused a significant distance. As a result, a limited number of objects can be manipulated. Up to 20×20 optical traps and partly in three dimensions have been demonstrated by using rapid AODs (Vossen et al. 2004).

To achieve true three-dimensional multiple optical traps, one must turn to holographic optical tweezers (HOTs). Multiple optical traps are created by using diffractive optical elements to split and steer the light from a single beam between multiple traps, which can easily become dynamic by using liquid crystal devices, such as SLMs, to display phase-only holograms (Curtis et al. 2002). The working principles of HOTs generated from an SLM are illustrated in figure 1g (Martin-Badosa et al. 2007). A continuous-wave TEM₀₀ laser beam is first expanded and then collimated by two lenses. A pinhole spatially filters the light at the back focal plane of the expander lens to ensure clean Gaussian illumination on the SLM that is designed to modulate the phase of the laser front and it introduces a hologram (a complex diffraction pattern) to the laser light distribution. It may operate by either reflectance or transmittance and is sandwiched between polarizing elements with specific orientations. After passing through a telescope, the beam is reflected upwards by a dichroic mirror and is focused by the high NA microscope objective on the sample plane. HOTs offer complete flexibility in manipulating multiple particles independently through the creation of arbitrary optical landscapes and other modes of light such as optical vortices can be created (Curtis & Grier 2003). Advanced SLM technology and real-time hologram calculation algorithms have allowed the creation of an array of up to 400 optical traps (Curtis et al. 2002).

Multiple traps have been able to be created by the three methods described above; however, their characterization and calibration simultaneously remains challenging. Theoretical approaches have been developed for absolute and precise calibration for a single beam (Hansen et al. 2006; Viana et al. 2007) and those models will be extended for multiple traps. Experimental methods using a QDP to detect the nanometre resolution displacement of beads have been used to characterize and calibrate multiple traps (Guilford et al. 2004; Dharmadhikari et al. 2007). However, it is challenging to track many particles simultaneously using a QDP. A high-speed video camera was used for multiple traps and centre-of-mass tracking was adopted to avoid out-of-memory problems (Keen et al. 2007). This high-speed camera could be very useful to characterize and calibrate multiple traps.

2.3.4 OT in combination with other instruments

Other enabling techniques have been combined with OT to allow exploring further applications of OT. Sensitive position detection is an essential tool for quantitative optical trapping as nanoscale measurement of both force and displacement relies on a well-calibrated system for determining position. This position detection technique allows calibration of the trap to work out the trapping stiffness from equation (2.1). This is especially useful for multiple traps, like for scanning multiple traps or HOTs, as the drag force calibration method discussed in §2.2 is not feasible for multiple traps. After the trapping stiffness is given, the position displacement of a particle in an optical trap can be used to work out the forces applied on the particle. Therefore, position detection is an essential part for OT as a force measurement tool. A review of position detection techniques has been introduced by Neuman & Block (2004). The position-sensing capacities for optical traps have been pushed to angstrom precision, and one is able to observe a distance of approximately 3.4 Å (Abbondanzieri et al. 2005; Greenleaf et al. 2005). Rohrbach (2005) has measured a controlled 25 fN force on a 533 nm latex sphere. This suggests that OT can be applied to measure the smallest forces that cannot be achieved by traditional AFM and other tools.

Raman spectroscopy can provide information about chemical bonds in molecules by identifying spectral patterns excited by a near-infrared laser beam. Therefore, OT are often combined with Raman spectroscopy to provide essential intracellular information (Xie et al. 2002, 2005; Creely et al. 2005; Jess et al. 2006). Other techniques, such as total internal reflection microscopy (TIFT; Oheim & Schapper 2005), confocal microscopy (Hoffmann et al. 2000) and cellular microscopy (Emiliani et al. 2005), have been reported to combine with OT.

Microfluidics is another area where OT show great promise for its application. Microfluidic channels offer a fluid flow system with sample volume as small as the order of a few nanolitres where cells can be transported, manipulated, sorted and isolated with their surrounding media. OT as an important contact-free cell-friendly manipulation tool have been integrated with microfluidic devices (Enger et al. 2004; Paterson et al. 2005; Wang et al. 2005; Jess et al. 2006; Monat et al. 2008).

2.4 Intricate problems: heating and photodamage

Laser adsorption by the sample can lead to damage or ‘opticution’ as a highly focused spot with power intensities of megawatts per square centimetre is used for OT (Dholakia & Reece 2006). This may occur with both one- and two-photon processes. Wavelength is an important issue when biological cells are trapped. The photodamage throughout the near infrared region favoured for optical trapping (790–1064 nm) was investigated and the action spectrum for photodamage exhibited minima at 830 and 970 nm and maxima at 870 and 930 nm for both E. coli (Neuman et al. 1999) and Chinese hamster ovary cells (Liang et al. 1996). However, the damage was reduced to background levels under anaerobic conditions, implicating oxygen in the photodamage pathway (Neuman et al. 1999). Even at a wavelength of 1064 nm, the division and growth of E. coli cells were affected when cells were radiated to OT by using an on-chip cultivation system (Ayano et al. 2006).

Shorter wavelengths below 800 nm can also bring great damage to biological cells that were observed by Konig et al. (1996a,b) and Leitz et al. (2002). Leitz et al. (2002) systematically investigated effects of illumination from OT by using different laser powers, irradiation time and wavelength on cell damage. A transgenic strain of Caenorhabditis elegans, which had been used as a sensitive biomonitor responsive to various types of external stresses, carried a reporter gene (E. coli lacZ) that was under the transcriptional control of a specific heat shock promoter. By exposing the cells to illumination from the OT at wavelengths from 700 to 850 nm for 30–240 s, the highest frequency of induction of the gene expression activated by the gene promoter was found to be at 760 nm laser radiation mainly due to photochemical effects. At a wavelength above 800 nm, the cell damage was found to be mainly due to photothermal effects.

The thermal effects on cells from high photon intensities can be seen by direct temperature rise. When using 100 mW laser tweezers (1064 nm in wavelength), the trap-induced temperature increase is between 1 and 2°C. In trapped human sperm cells, hamster ovary cells and liposomes, the temperature increases were measured to be of the order of 10, 11.5 and 14.5°C W⁻¹, respectively (Liu et al. 1995, 1996). This is confirmed by Peterman et al. (2003). This effect has also been investigated by cell metabolic activities. Tethering a single E. coli cell to a glass cover-slip by a single flagellum so that the single cell rotates at a rate proportional to its membrane proton potential, then monitoring the rotational rates of the single cell subjected to laser illumination is a rapid and quantitative measure of its metabolic states.

To reduce photodamaging effects of OT to cells, near-infrared lasers such as Nd:YAG (1064 nm in wavelength), Nd:YLF and diode or Ti:sapphire lasers can be chosen as the laser source. Alternatively, the laser can strike on particles rather than cells to avoid direct contact between photons and cells by attaching one or more particles to cells. Apart from these methods, two divergent optical beams rather than a single highly focused beam are used for reducing the photodamage in optical trapping. To reduce the heating effect, heavy water (D₂O) rather than usual water can be used because it absorbs less than usual water over typical trapping wavelengths. At a wavelength of 780 nm, the absorption coefficients for D₂O are two orders of magnitude smaller than those for H₂O (Dholakia & Reece 2006).

3. Applications for single cells

3.1 Active nanomanipulation

OT have been widely employed as a tool for actively manipulating and positioning biological objects at the nano/microscale. One of the most popular applications is to apply tweezers to confine or constrain single cells, as well as to organize, assemble, locate, sort and modify them.

3.1.1 Positioning cells

OT have been used to hold cells in a static or fluid flow environment. The simple application was to measure volume changes of a single isolated kidney cell under osmotic shock and a phenomenological analysis of water transport. A single Madin-Darby canine kidney cell was grabbed and suspended in liquid without touching either the glass substrate or other cells with the aid of OT (Lucio et al. 2003). Water permeability, osmotic influx rate and regulatory volume were obtained by using videomicroscopy with digital image analysis.

When a single cell is trapped by OT, light hitting the cell surface changes the intensity and direction of the bouncing photons. The intensity of scattered light from A375 cells, lymphocytes and granulocytes was recorded over an angular range of 0.5–179.5° with 30 ms time resolution and exhibited a significant and complex time dependence (Watson et al. 2004). The specific diagram of light scattering for a single cell within an optical trap can be used to identify different internal structures of the cell, distinguish living cells from dead cells and separate cells based on the differences of cell size, shape, refractive index and morphology.

By capturing a single cell in an optical trap, Raman spectrometry has been used to provide essential intracellular information for a single cell. This technique has been used for single biological cells (Xie et al. 2002) and this group further applied this technique to identify and discriminate six different bacterial species at various growth conditions (Xie et al. 2005). The highly reproducible biomolecular fingerprint of each cell provided from the instrument has been successfully applied to distinguish normal human lymphocytes from transformed Jurkat and Raji lymphocyte cell lines (Chan et al. 2006) and cancer cells from normal cells (Zheng et al. 2007). This technique could be applied to study identification, differentiation and maturation of stem cells.

Singh et al. (2005) used this technique for a quantitative study of the fermentation process for a single yeast cell in real time, so that real-time monitoring of cell biochemistry can be achieved. However, the cell will generally rotate in a trap about the trapping axis (Grover et al. 2000); multiple beams around the periphery of the cell have been used to provide a stable trap. Creely et al. (2005) used HOTs to stably trap Jurkat cells in suspension, and scan back and forth across the focus of the stationary excitation beam. In this way, the space-resolved spectra of entire cells have been obtained. Jess et al. (2006) adopted a similar technique, but chose two divergent beams to confine a primary human keratinocyte cell and recorded separate spectra from the membrane, cytoplasm and the nucleus.

By combining micro-Raman spectroscopy with OT and a microfluidic system, the oxygenation cycle of a single RBC can be selectively trapped by OT and monitored in real time while different buffers were transported through a microfluidic channel using electro-osmotic flow (Ramser et al. 2005). This technique holds potential for in vitro monitoring of cellular drug response by feeding the pharmaceutical solution to the fixed cells and measuring physical and chemical changes in cellular components.

3.1.2 Cell transportation

OT are able to move single cells in a liquid medium without contact. This unique feature is highly desirable for cell manipulation in sterile conditions. OT have been applied to relocate neuron cells to form cell groups (Townes-Anderson et al. 1998). Some of the neuron cells were cultured on the adherent side of a culture dish and others on the less adhesive side. Unattached cells were trapped and relocated next to cells lying on an adhesive culture substrate to allow interactions among cells. For example, when a rod cell was relocated to a group containing a cone cell and a multipolar neuron, then it was found that prominent growth of the neuron was inhibited by the relocated rod cell. Optical trapping did not affect the ability of neurons to subsequently attach to the culture substrate, and organelles, nuclear and cytoplasmic structure of manipulated cells were completely normal. OT provide a benign tool for micromanipulating whole neurons.

Arrayed cells can also be moved by VCSEL arrays that were used as a miniaturized source of infrared light for remote manipulation (Ozkan et al. 2003a,b). 3T3 mouse fibroblasts and primary rat hepatocytes were transported into a specific location. This system allows capturing selected individual or multiple cells and performing conventional molecular characterization. The limitation is that only cells smaller than 10 μm in size can be moved using the current VCSEL-driven OT. Since large arrays (32×32) of VCSELs are now commercially available, this system has the potential to be extended to the parallel manipulation of many cells simultaneously.

Wakamoto et al. (2001) reported the building of two microchambers for analysis and cultivation, the two chambers being connected through a narrow channel through which a single E. coli cell was trapped and transported by OT. After an E. coli cell in the analysis chamber was divided into two daughter cells, one daughter cell was trapped and transported into the cultivation chamber for further differentiation. This technique allows comparing genetically identical cells under contamination-free environment, which will shed light on heterogeneous phenomena such as unequal cell division. Enger et al. (2004) designed a similar system so that E. coli cells were moved between reservoirs filled with different media on a time scale of a few seconds. It was found that there was no contamination when cells were dragged to a place with a different liquid medium and then transferred back again from different channels. This group (Eriksson et al. 2007) used this technique to investigate the cell response to a sharp glucose concentration gradient between the two channels in which 25 yeast cells were moved back and forth between the two media by holographic OT. This provides a new method to investigate real-time cell responses to various extracellular environment conditions without being removed from the field of view of the microscope.

3.1.3 Cell sorting

A traditional and widely used method to sort and fraction cells is fluorescence-activated cell sorting (FACS; Herzenberg et al. 2002). The cells are to be chosen from the decision based on the fluorescence signal from the detection region. This is termed as ‘active sorting’ (Dholakia et al. 2007) as some markers have to be attached to the cells. While hydrodynamic focusing is maintained for a macroscopic FACS machine, optical force is used for cell deflection of microfluidic FACS (figure 2). Buican et al. (1987) pioneered the use of a deflection beam to separate cells and a propulsion beam to maintain the travelling path of separated cells up to several millimetres. Ozkan et al. (2003b) designed a T-type microchannel junction for transporting cell solution and used VCSEL-driven OT to trap and deliver several target cells to a collection reservoir simultaneously. Similarly, Enger et al. (2004) used a Y-type junction coupled with OT for cell separation. In these reports, only a few cells were used and laser beams were manually operated to demonstrate the concept.

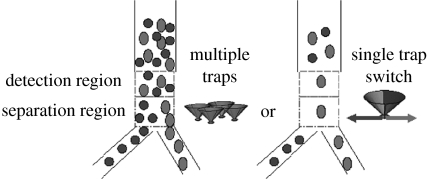
Figure 2.

Optical tweezers for cell sorting. Targeted cells are detected in the detection region and identification of those cells triggers switching on either multiple traps or single trap. Cells are driven by optical tweezers to be delivered to the collection output while all other cells flow to the waste output. Adapted from Wang et al. (2005).

A functional microfluidic FACS has been reported by Wang et al. (2005). Two laser sources have been used in this cell sorter: a near-infrared laser for the optical switch and a visible wavelength laser for the detection and fluorescence measurement. Cells flowing in from the sample input were aligned to a narrow stream by hydrodynamic focusing. First, cells in the focused flow passed into the analytical region and then through the optical switch region. When a cell was detected and determined to be a target cell, an acousto-optical modulator was triggered to switch the cell based on a gating of fluorescence signal. A focused laser spot deflected the cell to the target output channel. The cells without being subjected to a laser beam flew out to the waste channel. For example, the cells from a stable-transfected HeLa cell line constitutively expressing a fused histone-green fluorescent protein and non-expressing parental HeLa cells were mixed and separated by passing through the cell sorter. High purity in the collection channel was obtained in varied starting ratios of target cells and the recovery rate was above 85% except in the case of high throughput of 10⁶ cells s⁻¹.

Other active sorting techniques, such as simple cell identification by video microscopy and cell deflection by multiple-beam OT, have been developed (Ericsson et al. 2000; Grover et al. 2001; Oakey et al. 2002; Rodrigo et al. 2003; Applegate et al. 2006). For example, Grover et al. (2001) used an image-processing technique for single cell identification and a counter-propagating dual beam to separate blood cells; Applegate et al. (2004) generated a line trap, rather than a point trap, by focusing a diode bar, and bovine RBCs were captured by the line trap and directed with an angle to chosen flow streamlines through a seven-channel sorting device; they further wrote about an integrated optical waveguide within two channels for exciting fluorescent-dyed particles and generating microfluidic FACS (Applegate et al. 2006). Cran-McGreehin et al. (2006) integrated microfluidic channels with semiconductor laser materials, which allow detecting particles and distinguishing between different sizes by measuring the power or photocurrent reduction due to the presence of a particle in the beam path.

Passive sorting is a marker-free approach, which has advantages of keeping cells in their untouched state (Dholakia et al. 2007). There is no need to develop an appropriate marker for cells and to remove markers after separation. Without specific markers, selectivity is based on size, shape and refractive index difference. Within a microfluidic channel, cells are sorted via a size- and shape-dependent gradient force in competition with a size- and shape-dependent viscous drag force. MacDonald et al. (2003, 2004) demonstrated the separation of erythrocytes from lymphocytes based on shape difference by using an angled optical lattice that can be extended to any general two- or three-dimensional potential energy landscapes (Ladavac et al. 2004; Milne et al. 2007; Smith et al. 2007).

Cells can also be separated due to the interplay between the radiation pressure and fluid drag, termed as ‘optical chromatography’ as proposed by Imasaka et al. (1995). In this case, a weakly focused laser beam is installed in the counter-propagating fluid flow. When cells flow along the channel, the scattering force from the laser beam pushes cells into the focal region of the laser beam. The net force between the scattering and drag forces results in different equilibrium positions for different cells. This method can be used to separate a range of cells including blood cells (Kaneta et al. 1997), bacterial spores and cells (Hart et al. 2006, 2007) and pollen (Terray et al. 2005).

Passive optical sorting can also be achieved without fluid flow. The Bessel beam has been used for flow-free optical separation of lymphocytes from erythrocytes (Paterson et al. 2005) using its unique optical landscape, which has been discussed in §2.3.1. When higher power was used, the biconcave-shaped erythrocytes locked into outer rings of the Bessel beam (third, fourth and fifth), while spherically shaped lymphocytes rapidly moved directly to the beam centre and they were collected from the centre core. Zemanek et al. (2004) described using a three-beam interference light field to locate big particles in intensity minimum but small particles in intensity maximum. A size-selective optical-moving pattern is a more productive way to enhance separation, such as a vibrating fringe pattern (Ricardez-Vargas et al. 2006), a moving periodic light pattern (Cizmar et al. 2006) and time-dependent optical potential energy landscape (Libal et al. 2006; Smith et al. 2007).

3.1.4 Assembling and organizing cells

OT can be used to relocate, assemble and organize cells so that a group of cells can be formed into a new structure. An optical trap can be used to grab an object which in turn could be used to grab other objects. A microsphere of 5 μm in diameter was trapped first and then used as a handle to trap and manipulate several microspheres (approx. 2 μm in diameter). The assembly of microspheres remained stable as it moved inside a 100 μm channel (Ozkan et al. 2003b). This technique can be used to select and place multiple objectives for optically assisting self-assembly processes.

The assembly function of OT can also be realized through computer-controlled SLMs built on holographic OT because this technique allows manipulating particles both laterally and axially over several tens of micrometres so that particles can be rearranged into three-dimensional configurations. This assembly function has been demonstrated with 18 trapped silica spheres positioned to form a diamond lattice with a unit cell size of 15 μm and four glass beads trapped in the corners of an imaginary tetrahedron by Leach et al. (2004). This group has applied the technique to move individual E. coli cells in liquid gelatin at predefined positions. When the cells were fixed in place, the lasers were switched off. The three-dimensional configurations of cells within a gelatin sample at predefined positions remained intact for many days. The cells survived within the gelatin matrix for several days when appropriate nutrients were provided. This technique can be used to help in understanding the role of position, proximity and the number of neighbouring cells, not only in cell culture but also in cell differentiation. The ability to form such viable three-dimensional structures will open a wide range of future applications, including the arrangement of various cell types in complex architectures, as motifs for promoting tissue differentiation and growth within the field of cell engineering (Jordan et al. 2005).

Using arrays of time-multiplexed holographic OT with a combination of SLM and AOD, Akselrod et al. (2006) demonstrated the assembly of three-dimensional heterotypic microarrays consisting of a Swiss 3T3 mouse fibroblast surrounded by a ring of Pseudomonas aeruginosa bacteria. The mammalian cell was trapped with nine 2 mW beams, and 16 single 2 mW beams were dedicated to 16 bacteria and all cells were detected to remain viable. The cell-to-cell distance was able to be controlled to less than 400 nm. This technique allows investigating the bacterial infection process through control of colonization and the biochemical library in the microenvironment of a cell and it also has a huge impact on tissue engineering and synthetic biology.

3.1.5 Laser scissors/scalpels and opto-injection

OT can be combined with UV or Nd:YAG laser microbeams to function as scalpels or scissors, which allows precise cutting with submicrometre resolution (Colombelli et al. 2004). Novel surgery tools coupled with OT perform separation of individual cells from cell clusters (Leitz et al. 2003) as well as dissection of cellular organelles, cytoskeletal filaments (Kumar et al. 2006) or chromosomes (Berns et al. 1989; Berns 1998).

Transient permeabilization of cell membranes by short-time laser irradiation allows cell fusion and molecular injection (opto-injection). Steubing et al. (1991) pioneered bringing two cells into contact in an optical trap and then fusing them by cutting the common wall of the two cells with several pulses of UV laser microbeams. This method provides an effective way of generating hybrid cells without losing cell functions and has been used to selectively transport individual sperm to its eventual contact with oocytes (Schopper et al. 1999).

Opto-injection involves the locally restricted short-term opening of a cell membrane by focusing a single ultraviolet pulse on the phospholipid bilayer so that foreign species in the external solution can be injected or flowed into the cell in a passive manner. Florescent biomolecules have been injected into the cytosol and nucleus of Neuro-2A mouse neuroblastoma cells (Stuhrmann et al. 2006).

3.1.6 Optical guiding

OT have also been used for neuronal cell growth, where laser radiation focused on the leading edge of an actively advancing growth cone affects intracellular processes and induces growth towards the laser focus at wavelengths in the range of 800–900 nm. PC12 cells, a neuron precursor cell line, were reported to respond to light by growth towards a laser beam at a wavelength of 800 nm and a relatively low power (Ehrlicher et al. 2002). This optical-guiding process occurs as the light pools actin monomers and provides nucleation sites for actin polymerization, which is the driving force for neuronal growth (Ehrlicher et al. 2002; Dent & Gertler 2003). Other cell types reported for this optical-guiding process include N1E-115 cells from a neuroblastoma tumour (Mohanty et al. 2005b), NG108, a rat/mouse hybrid neuroblastoma cell line that produces active growth cones (Stevenson et al. 2006), as well as primary embryonic chicken retina cells (Stuhrmann et al. 2006).

3.2 Passive piconewton force measurement for single cells

Owing to their precisely controllable force-exerting characteristics, OT are often used for a variety of mechanical force measurements in the pN range for single cells. Although most cells are not conducive to direct optical tweezing due to their size, shape and adherent properties, a small number of cell types such as yeast cells, RBCs and spermatozoa are readily tweezed and provide model systems for force studies (Dholakia & Reece 2006). For those cells that cannot easily be tweezed, the use of microspheres as handles for force probes has allowed the measurement of cellular properties such as membrane tension.

3.2.1 Deformability measurement of unilamellar vesicles

Unilamellar vesicles, composed of a phospholipid bilayer that is the main constituent of biological membranes, have been widely accepted as a model for cell mechanical studies (Ichikawa & Yoshikawa 2001). The mechanical deformation of vesicles by OT was characterized (Foo et al. 2004) and the thermal effect on the deformation was investigated (Foo et al. 2003). This provides essential information on coupled thermal and hydrodynamics effects on the biomechanical properties of biological cell membrane in physiological flow. OT can also excite lipid bilayers and result in the dynamic instabilities and shape transformations of liposomes under laser trapping (Bar-Ziv et al. 1998).

3.2.2 Mechanical characterization of RBCs

The changes in the elastic and viscoelastic properties in RBCs are often correlated with the manner in which the cells respond to structural and molecular alterations induced by the onset and progression of a disease (Suresh et al. 2005). The elastic and viscoelastic properties of healthy and infected RBCs have been investigated using OT. By fixing one side of an RBC membrane and pulling the other side with aid of OT, the cell membrane is deformed. The cell deformation under certain force can be used to calculate the mechanical properties (shear modulus), as shown in figure 3. OT have also been used to calculate the relaxation time for RBCs, which is the duration from a distorted shape back to its original one. Using three optical traps to deform RBCs into a parachute shape and then removing all three optical traps, the shape recovery was recorded and the relaxation time was obtained for the cell. The experimental measurement of shear modulus and relaxation time from different groups are summarized in table 2. It can be seen from table 2 that by comparing the shear modulus of different cells, a single healthy RBC can be distinguished from a malaria-infected RBC. The shear modulus of infected RBCs at a late stage was found to be up to an order of magnitude higher than that of healthy RBCs.

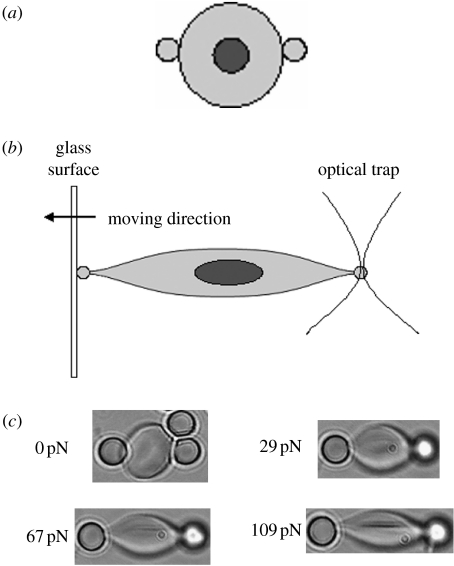
Figure 3.

Stretching RBCs by optical tweezers. (a) Two diametrically opposed silica beads of 4.1 μm are attached onto an RBC surface. (b) One bead is trapped by optical tweezers while the other is fixed onto a glass surface. Deformation is achieved by moving the glass surface to the opposite direction. (c) Large deformations of RBCs in phosphate buffer saline solution at room temperature are captured by optical micrographs under different trapping forces. Adapted from Lim et al. (2004a).

Table 2.

Experimental studies of human red blood cells (RBCs) by optical tweezers.

authors	experimental methods	major findings
Bronkhorst et al. (1995)	RBC was vertically oriented in three traps and then the middle trap moved at very low speed to change the cell shape. Finally, all traps were removed and the cell relaxed to its original shape	‘young’ cells have shorter (162 ms) and ‘old’ cells have longer (353 ms) relaxation times compared with the total population (271 ms). The relaxation time is markedly shorter (114 ms) when the plasma surrounding the cells is replaced by a phosphate-buffered saline solution
Henon et al. (1999)	force generated between 10 and 15 pN	shear modulus of 2.5±0.4 μN m−1 for both discotic and nearly spherical swollen cells
Sleep et al. (1999)	two independently movable single-beam traps on two beads attached to cells and bead positions detected by a photodiode quadrant detector	shear modulus of 200 μN m−1 for unmodified cell ghost and 200 μN m−1 for modified cells by chymotrypsin, PCMS and NEM. For chymotrypsin-treated cells, by imposing a series of stretches, cells relaxed to a condition of a near equilibrium tension after each stretch
Guck et al. (2000, 2001, 2002)	two counter-propagating divergent beams providing a stretching force up to 400 pN	shear modulus of 13.0±5.0 μN m−1 for spherical cells and a relative increase of radius up to 14% below a stress of 1.47 N m−2; nonlinear distortion above a stress of 2 N m−2, a relative increase in radius up to 82% at a stress of 2.55 N m−2
Lenormand et al. (2001)	three optical traps were used for a blood cell via three beads bound to its membrane	area expansion modulus of 4.8±2.7 μN m−1, and shear modulus of 2.4±0.7 μN m−1 for the spectrin skeleton in low hypotonic buffer (25 mOsm kg−1), and both values were higher in isotonic buffer
Dao et al. (2003) and Lim et al. (2004a,b)	laser light was directed on larger beads (4.12 μm) attached to the cell membrane and the procedure was as described in figure 3a–c. The maximum force was estimated to be approximately 193±20 pN	the shear modulus at larger strain was estimated to be 5.5 μN m−1 when the force was exerted up to 85 pN. The largest deformation of 50% was achieved
Suresh et al. (2005)	RBCs infected by Plasmodium falciparum at different erythrocytic developmental stages (ring, trophozoite and schizont stages) were subjected to optical forces up to 150 pN	elastic shear modulus for infected RBC at ring, trophozoite and schizont stages of 16, 21.3 and 53.3 μN m−1, respectively
Li et al. (2006)	force ranging from 0 to 16 pN	shear modulus of 4.6–5.2 μN m−1
Gu et al. (2007)	a single beam near-field optical trap to rotate, stretch and fold RBCs	rotational speed increased up to 1.6g and folding angle increased up to 60° as the power increased; ratio of deformation by stretching up to 23%

Apart from stretching bead-attached RBCs, the cells can also be stretched by two counter-propagating divergent beams, which has been carried out by Guck et al. (2000, 2001, 2002). The stretching force can be up to several hundreds of piconewtons and a deformation of up to 80% was observed by this method. They further applied this method to detect changes in the deformability of cells as a function of cancer progression (Guck et al. 2005).

Rotation and folding of RBCs have also been investigated by optical traps. Mohanty et al. (2004, 2005a) observed that in hypertonic buffer, a normal round RBC rotated when trapped by OT and the rotational speed increases linearly at lower trap beam powers and more rapidly at higher powers. By contrast, a malarial parasite-infected RBC did not rotate under the same experimental conditions. The rotational speeds of other RBCs from malaria-infected samples were found to be an order of magnitude less than that of normal RBCs and also increased much more slowly with an increase in trap beam power than that of normal RBCs. When a single live RBC is placed in an optical trap, the normal and infected bioconcave shape of RBCs has been observed to fold into a rod-like shape. If the laser beam is circularly polarized, the folded normal and infected RBCs rotate. However, normal RBCs did not respond to a linearly polarized light while infected RBCs were able to rotate. Rotation speed of the infected RBCs varied from 19g to 300g and appeared to depend on the stage of infection. Fast rotation was observed at the early trophozoite stage whereas slow rotation occurred at the mature schizonts stage (Dharmadhikari et al. 2004).

Recently, Gu et al. (2007) developed a single beam near-field laser trapping technique using focused evanescent wave illumination to stretch, rotate and fold RBCs. The ratio of deformation from its original size was as large as approximately 23%. Both rotation and folding of the RBCs were linearly increased as the laser power increased.

One should note that most of the experimental results in table 2 were obtained at room temperature and those results may not truly reflect the deformation of RBCs in the human body. It has been found that the mechanical properties of RBCs can be changed due to temperature change in the human body (Waugh & Evans 1979). Foo et al. (2006) investigated the effect of heating and cooling on mechanical properties of a single RBC trapped by OT. It was found that the extra deformation under hydrodynamic flow for an RBC at body temperature (37°C) was significantly higher than that at room temperature. When heating the liquid medium from 23 to 42°C and then cooling back to 23°C, the degree of RBC deformation was found to be irreversible and the RBC became much softer, which may be due to the irreversible transformation of the membrane molecular structures.

3.2.3 Mammalian cells with intracellular organelles

Unlike simple bilayers in model lipid vesicles and RBCs, other human cells are coupled with the cell cytoskeleton and extracellular environment via molecular interactions including lipid–protein bonds, transmembrane protein linkage to cytoskeleton and the extracellular matrix. Similar to human RBCs, OT have also been applied to study the mechanical properties of cell membranes. Tether extraction is the most accurate method to quantitatively characterize the plasma membrane. To form a membrane tether, micrometre-sized beads are typically used as handles to grab the cell membrane. The force to manipulate the bead can be quantitatively obtained from OT.

The tether formation force of a single OT-stretched chondrocyte cell was measured to be approximately 232 pN when cells were cultured after 1 hour while it was 591 pN after 6 hour. The culture time was found to have a significant effect on the chondrocyte cell adhesion process (Huang et al. 2003). A bigger tether formation force for outer hair cells from the lateral wall (499±152 pN) than that from the basal end (142±49 pN) was consistent with an extensive cytoskeletal framework associated with the lateral wall (Li et al. 2002).

The membrane mechanics of human mesenchymal stem cells (hMSCs) has been shown to critically affect MSC differentiation. The average tether lengths were found as 10.6±1.1 μm for hMSCs and 3.0±0.5 μm for fibroblasts measured by using OT stretching. During tether elongation, the extraction force on the bead fluctuated around a constant value and this demonstrated that there was a small bilayer reservoir on the membrane to buffer minor fluctuations in the membrane tension (Titushkin & Cho 2006).

Membrane mechanics directly affects cell adhesion and reorientation. Curtis & Spatz (2004) applied holographic OT techniques to study hyaluronan-mediated adhesion processes of chondrocyte cells. The early stage cells had reversible adhesion with negatively charged and fibronectin-coated microspheres even after they were held at the cell surface for 10 s. By contrast, late-stage cells stuck irreversibly to all types of beads: positive, negative, fibronectin and hyaluronan coated. Additionally, only the late-stage cells produced membrane tethers. These observations suggest that the late-stage chondrocytes have less surface associated with hyaluronan and have interesting implications for the role of hyaluronan in the early stages of cell adhesion. Other reports on using OT for cell adhesion include short-term binding of fibroblasts to fibronectin-coated glass (Thoumine et al. 2000), haematopoietic stem cells adherent to the host bone marrow microenvironment (Askenasy & Farkas 2002), macrophages adherent to different polymer templates for growing artificial artery grafts (Knoner et al. 2006) and human bone cells attached to implant surfaces (Andersson et al. 2007a).

OT can also offer a well-defined piconewton force on a single cell, which allows investigating cell response to defined load or stress. Walker et al. (1999) used a single optical trap to exert 7 pN force on bone- and cartilage-derived cells. Changes in intracellular calcium levels were observed using Fluo-3 labelling. Human-derived osteoblasts responded to optical trap force with an immediate increase in calcium concentration. Response to the same force by the different bone- and cartilage-derived cells varied from 2% (chondrocyte) to 50% (human osteoblast) increase in fluorescent intensity.

OT have also been used for manipulating and determining the force generation and swimming properties of sperm. Nascimento et al. (2006) described the effects of laser trap duration and laser trapping power on sperm motility between sperm swimming force, swimming speed and speed of progression score and concluded that sperm swimming forces measured by optical trapping provide new and valuable quantitative information to assess sperm motility. Shi et al. (2006) developed a real-time tracking system for single sperm under optical traps and Shao et al. (2007) used a three-dimensional ring-shaped optical trap to characterize sperm mobility.

3.2.4 Mechanical properties of microbiological cells

Microbiological cells have been widely used for optical manipulation (Ashkin & Dziedzic 1987; Leach et al. 2004; Singh et al. 2005; Hart et al. 2006, 2007). OT have also been a quantitative tool for the measurement of mechanical properties of micro-organisms as they can trap objects as small as 5 nm and exert forces exceeding 100 pN (Grier 2003). The optical method allows investigating the mechanical properties of some components of bacterial cells, such as tether formation, mechanical behaviour of individual P pili, twitching mobility of pilus and flagella rotation.

Tethers can be formed between a living E. coli cell and a bead by unspecifically attaching the bead to the outer membrane and pulling it away using OT. These tethers were measured to be tens of micrometres long, several times the bacterial length. Visco-elastic tether force–extension relationships were observed: a spring constant of 10–12 pN μm⁻¹ was reported for the first pulling of tethers while it decreased to 6–7 pN μm⁻¹ for subsequent pulling of tethers and typical relaxation time scales of hundreds of seconds were reported. This unspecific tethered attachment mechanism could be important in the initiation of bacterial adhesion (Jauffred et al. 2007).

The adhesion of micro-organisms to the surface of host tissue is often a precursor in pathogenesis. In this process, bacterial pili are responsible for mediating adhesion and maintaining bacteria–host contact during the early stage of an infection. Jass et al. (2004) investigated the mechanical behaviour of individual P pili of a uropathogenic E. coli. Three elongation regions of P pili were identified. In region I, P pili stretched elastically up to an averaged relative elongation of 16%. In region II, the pili unfolded their helix structure and the elongation was found to be under constant force. This unfolding elongated the pilus up to approximately seven times its unstretched length. In region III, pili elongated in a nonlinear manner as a result of stretching until the bond ruptured. These findings suggest that bacterial pili can withstand tension over a broad range of lengths. Andersson et al. (2007b) compared P pili and type I pili of uropathogenic E. coli in the urinary tract by in-site measurement: a similar unfolding force of 30 pN was found and an elongational speed of 6 nm s⁻¹ for type I pili and 400 nm s⁻¹ for P pili. The quantitative data can be used to understand the infection process and design novel drugs for bacterial infection.

Type IV pilus is also involved in bacterial cell adhesion to host mammalian cells as well as bacterial motility. OT have been used to measure the pilus retraction and elongation at a resolution of several nanometres. A single pilus from bacterial cells can generate a force in excess of 100 pN making pili the strongest linear motors (Maier et al. 2004; Maier 2005).

Interaction between bacterial cell and surface can also be characterized. Liang et al. (2000) quantified the adhesion forces from the interaction of uropathogenic E. coli to self-assembled monolayers (SAMs) by breaking a single interaction of approximately 1.7 pN between pilus and mannose groups linked to the SAM. Fallman et al. (2004) measured the binding forces of E. coli cells to galabiose-functionalized beads. Forces of 10–15 pN, when the starting position of the bacterial cell was close yet separated from the bead, and 50–100 pN, when the starting position of the bacterial cell was in direct contact with the bead, were obtained.

Torque generated by flagella rotation in E. coli is another interesting application of OT to micro-organisms. Bacterial cells containing locomotive-specific appendages such as flagella have been a model system for the measurement of force transduction and the motility of cells. A comprehensive review has been made by Berry & Berg (1997) and, recently, the bacterial rotor has been reported by Reid et al. (2006) and Darnton et al. (2007).

Apart from bacterial cells, OT have also been applied to a range of fungal cell studies. Wright et al. (2007) and Burnham et al. (2007) have demonstrated the use of single or holographic OT to generate mechanical stimuli for hyphal tips of single fungal cells. The OT have been used to move and rotate a single fungal cell. They can also trap and move organelles with high refractive index, such as a Woronin body within a hypha of Neurospora crass. However, organelles of lower refractive index than their surroundings were repelled by the trap. By making use of this function, the laser was located to the side of such an organelle, Spitzenkorper within the hyphal tip, and this resulted in the redirection of hyphal tip growth away from the trap. Using an optically trapped 4 μm polystyrene bead as an obstacle on the tip of a leading hypha, the hypha was able to push the bead out of the trap so that the growth force of the leading hypha can be estimated. Another mechanostimulus to growing hyphal tips was applied by a 10 μm bead moving back and forth against the hyphal tip at high speeds (up to 40 μm s⁻¹) and repeatedly hitting a growing tip of a leading hypha tip. By driving three porous beads soaked with chemicals, such as latrunculin-B, the chemicals can be delivered to localized regions of hyphae. These wide ranges of techniques using OT for fungal cells can also be applied to other cells.

4. Optical–mechanical interplay

Most biological cells are highly deformable compared with other colloidal particles. Hence, the holding force generated from photon scattering in optical trapping could impose a certain force on the cell membranes and consequently cause them to deform. Such a complex optical–mechanical effect has not been studied enough, although it could profoundly influence the cell behaviours. Recently, a few studies have attempted to investigate and model such intricate phenomena for RBCs. Guck et al. (2000) calculated the stress distribution generated from two divergent counter-propagating beams around a single cell but the cell deformation was obtained from experimental measurements. Dao et al. (2003), Lim et al. (2004a) and Liu et al. (2006) presented numerical simulations, based on mechanical models for two-bead attached RBCs, while Bareil et al. (2006) numerically simulated the deformation of RBCs by OS. A model using the concept of Euler buckling instability has been used to capture the essential physics of RBC folding in an optical trap (Ghosh et al. 2006).

However, the force exerted on cell membranes which is generated from laser trapping still needs to be further quantified. Recently, the models developed for the calculation of the trapping force have been refined and developed (Mazolli et al. 2003; Lock 2004; Mao et al. 2007; Bonessi et al. 2007) and a computational toolbox is also available (Nieminen et al. 2007).

5. Prospects

OT have been widely used for nanomechanical characterization as they have the advantages of non-contact force for cell manipulation, force resolution as accurate as 100 aN and amiability to liquid medium environments. This powerful emerging tool is envisaged in many applications for single cell studies in the coming decades. Three future trends in manipulating single cells which can be envisaged are reported here.

5.1 Enabling techniques for improving the capability of OT

Other techniques, such as rapid detection and position devices, Raman spectroscopy and confocal microscopy, and rapid imaging methods, will be combined with the OT. Position tracking of spherical particles has been available; however, precise position detection of irregularly shaped objects will be more challenging. This technique can be used to measure the deformation of cells exposed to optical laser beams. Various spectroscopy techniques, such as Raman spectrometry, have been used to detect subtle changes at the molecular level so that the response of cells to mechanical and chemical stimuli can be quantitatively characterized. Fluorescence resonance energy transfer (Huebsch & Mooney 2007), a useful technique to probe the response of biological cells to different biomaterials for tissue engineering, and other techniques could be combined with OT for applications in regenerative medicine. Advanced imaging techniques, such as digital holographic microscopy (Lee & Grier 2007) and multiphoton microscopy (Goksör et al. 2004), have been used for cell analysis and in combination with these imaging techniques, more applications of OT for single cells are envisioned for the future.

5.2 OT integrated with lab-on-chip devices

OT are easily integrated with microfluidic devices for single cell manipulation (Monat et al. 2008). Single cell cultivation in the microfluidic devices with the aid of optical manipulation will produce homogeneous daughter cells that have a significant impact on cell therapy. How cells respond to neighbouring cells, biomaterials or surfaces, and chemical/mechanical stimuli will be studied in the microfluidic platform integrated with optical traps. Cell sorting in the microfluidic platform has been intensively investigated. High throughput, automated, passive cell sorting will become popular for biologists. The cell sorting throughput efficiency will be improved by introducing multiple optical traps. Recently, both near-field optics using the evanescent waves and holographic techniques have been used for the manipulation of a large number of particles simultaneously. Optically bound arrays (Mellor & Bain 2006) and large-area manipulation using surface plasmon field enhancement (Garces-Chavez et al. 2006) have been reported for near-field optics. As holographic traps are already under computer control, it is relatively easy to combine HOTs with pattern recognition to automate particle capture and sorting (Chapin et al. 2006).

5.3 Creation of three-dimensional complex architecture by OT

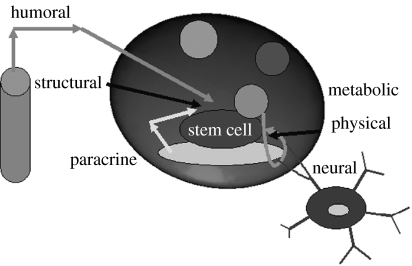
HOTs can create multiple traps with free and independent movement in three dimensions. One or more cell types can be organized into spatially well-defined three-dimensional arrays and functional tissues can be produced. Through advanced computer-controlled algorithms, HOTs can create complex patterns and geometries to match real biological tissues. One of the attractive three-dimensional architectural structures is a stem cell niche that is depicted in figure 4. Stem cells can only be functional to reproduce or self-renew when they reside in such an architectural space. The niche includes the stem cell, niche cell or hub cell, extracellular matrix and other extracellular components. These elements have to be placed to their anatomic and functional locations and the contact between these elements allows molecular interactions that are crucial for regulating stem cell function (Scadden 2006). HOTs are a potential tool to be employed to accurately place niche cell, stem cell and matrix into the correct sites to create a complex and functional niche. Stem cells cultured in this micromanipulated niche will be developed into functional and sustaining tissues.

Figure 4.

Stem cell niche. Elements are identified for regulating the system of a stem cell, including the constraints of the architectural space, physical engagement of the cell membrane, signalling interactions, neural input and metabolic products of tissue activity. Adapted from Scadden (2006).