Grid cell firing may arise from interference of theta frequency membrane potential oscillations in single neurons

Abstract

Intracellular recording and computational modelling suggest that interactions of subthreshold membrane potential oscillation frequency in different dendritic branches of entorhinal cortex stellate cells could underlie the functional coding of continuous dimensions of space and time. Among other things, these interactions could underlie properties of grid cell field spacing. The relationship between experimental data on membrane potential oscillation frequency (f) and grid cell field spacing (G) indicates a constant scaling factor H=fG. This constant scaling factor between temporal oscillation frequency and spatial periodicity provides a starting constraint that is used to derive the model of Burgess, Barry and O’Keefe (Hippocampus, in press). This model provides a consistent quantitative link between single cell physiological properties and properties of spiking units in awake behaving animals. Further properties and predictions of this model about single cell and network physiological properties are analyzed. In particular, the model makes quantitative predictions about the change in membrane potential, single cell oscillation frequency and network oscillation frequency associated with speed of movement, about the independence of single cell properties from network theta rhythm oscillations, and about the effect of variations in initial oscillatory phase on the pattern of grid cell firing fields. These same mechanisms of subthreshold oscillations may play a more general role in memory function, by providing a method for learning arbitrary time intervals in memory sequences.

Introduction

Considerable research has focused on modelling the function of the hippocampus and its role in encoding of episodic memory and spatial memory (McNaughton and Morris, 1987; Jensen and Lisman, 1996; Levy, 1996; Tsodyks et al., 1996; Wallenstein and Hasselmo, 1997; Hasselmo and Eichenbaum, 2005; Hasselmo, 2005; Howard et al., 2005). Many of these models focus on modification of excitatory synaptic connections for encoding associations between spatial locations, sensory information and behavioural context. However, experimental data (Giocomo et al., 2007) and computational modelling (Burgess et al., 2005; Burgess et al., 2007; Giocomo et al., 2007) indicate the importance of novel intrinsic single cell mechanisms for representing information about space and time. This mechanism involves the interaction of intrinsic subthreshold oscillations within a single neuron. Prominent subthreshold membrane potential oscillations (mpo) have been shown in stellate cells in layer II of entorhinal cortex (Alonso and Llinas, 1989; Alonso and Klink, 1993; Dickson et al., 2000). These small amplitude (< 5 mV) membrane potential oscillations occur when the cell is depolarized near firing threshold, and appear to arise from the interaction of voltage-sensitive membrane currents (White et al., 1995; Dickson et al., 2000; Fransen et al., 2004). This paper describes how these mechanisms could encode both space and time, and describes some additional predictions of the model relevant to future experimental work.

Recordings from individual neurons in the entorhinal cortex of rats actively exploring an open field environment show a strikingly regular pattern of response relative to the location of the rat in the environment (Hafting et al., 2005; Sargolini et al., 2006; Fyhn et al., 2007). Individual neurons fire at an array of locations distributed in a grid-like pattern of tessellated equilateral triangles (hexagons) that covers environments of different sizes with the same regular pattern (Hafting et al., 2005; Sargolini et al., 2006; Fyhn et al., 2007). The spatial periodicity of the grid pattern changes along the dorsal to ventral axis of the entorhinal cortex (Hafting et al., 2005; Sargolini et al., 2006), with smaller distances between small grid cell firing fields for neurons in the most dorsal portion of entorhinal cortex (near the border with postrhinal cortex) and larger distances between larger firing fields for cells in the more ventral regions of entorhinal cortex (at greater distances from the postrhinal border). A plot of the relationship between grid field spacing (G) and the dorsal-ventral anatomical position (z) shows an apparently linear relationship between the spacing distance G and dorsal to ventral position.

Recent experimental data from our laboratory indicate that the intrinsic subthreshold oscillation frequency (f) of entorhinal cortex neurons also differs systematically along the dorsal to ventral axis (z) of entorhinal cortex (Giocomo et al., 2007). The time period (reciprocal of frequency) of subthreshold oscillation cycles changes in a manner proportional to the change in grid cell field spacing. This paper presents analysis of the experimental relationship between intrinsic oscillations and grid field spacing, and uses this relationship to derive the model by Burgess and colleagues (O’Keefe and Burgess, 2005; Burgess et al., 2005; Burgess et al., 2007) which is related to models of theta phase precession (O’Keefe and Recce, 1993; Lengyel et al., 2003). Analysis of the model demonstrates how the phase of oscillatory interference integrates velocity and therefore maps directly to spatial coordinates as a mechanism for path integration (McNaughton et al., 1991; O’Keefe and Burgess, 2005; McNaughton et al., 2006; Burgess et al., 2007).

The implications of this model are discussed in relationship to entorhinal physiology, including 1.) the necessary scaling of stellate cell dendritic depolarization to running speed, and the relationship to data on changes in network theta rhythm frequency with running speed, 2.) the relationship of firing threshold in the model to the width and area of grid fields, 3.) the properties of grid cell response that would result from different angles of selectivity of head direction cells and different numbers of head direction cell inputs (and the effects of random angles), 4.) the ability of membrane potential oscillation frequency in the dendrites to influence field spacing despite the consistent network theta rhythm field potential frequency throughout entorhinal cortex, and 5.) the structure of phase shifts necessary to cause translation of grid cell firing fields, and the patterns of grid cell firing that would be associated with random shifts in different initial oscillation phases. The interference of membrane potential oscillations within a single cell is also relevant to functions beyond the properties of grid cells. Additional discussion addresses how the interference between subthreshold oscillations in the soma and different dendrites within a single neuron could provide mechanisms relevant to the encoding of continuous time for episodic memory function.

Experimental data shows scaling of oscillation frequency f and grid field spacing G

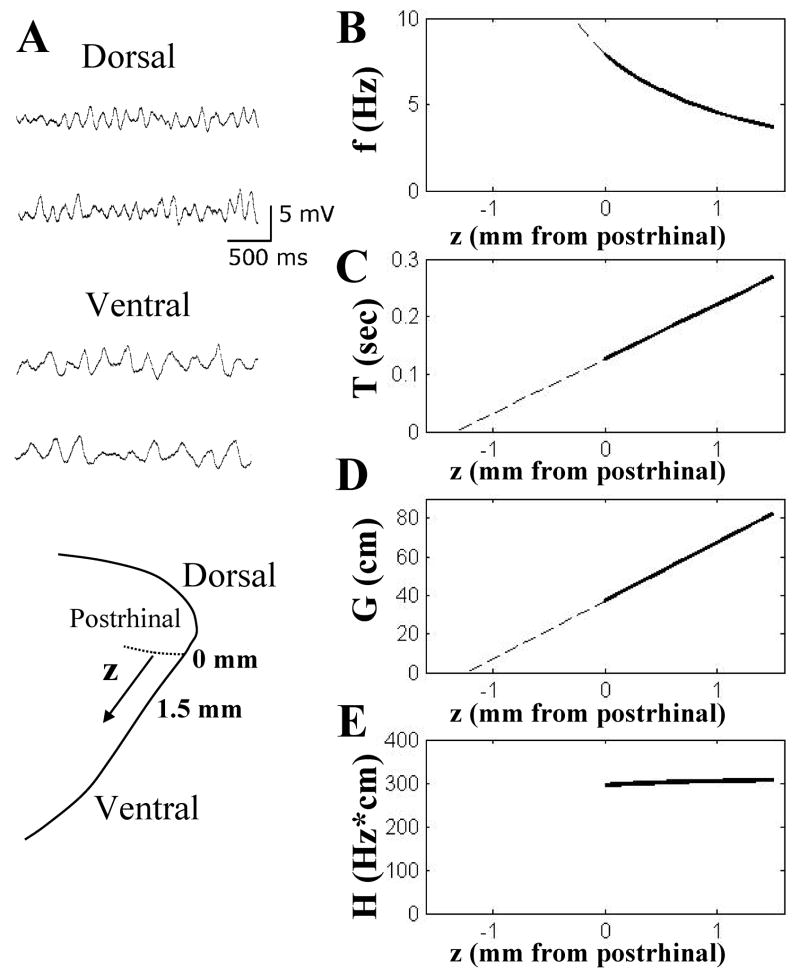
Experiments have demonstrated that subthreshold membrane potential oscillations in stellate cells show different mean frequencies in slices derived from different positions along the dorsal to ventral axis of the entorhinal cortex (Giocomo et al., 2007). As shown in Figures 1A & 1B, stellate neurons in slices of dorsal entorhinal cortex (near the postrhinal border) show higher frequencies of subthreshold oscillations, whereas stellate neurons in slices obtained from more ventral portions of entorhinal cortex (more distant from the postrhinal border) show lower frequencies of subthreshold oscillations. Figure 1C plots the linear fit obtained for data on the mean oscillation cycle period (T) of subthreshold oscillations relative to dorsal-ventral position (z). The linear fit to the data obtained from slices between 0 and 1.5 mm from the postrhinal border has the equation: T (z_d) = 0.094z_d − 0.25. Note that the subscript d indicates that z_d represents vertical distance in mm from the dorsal surface of the brain, which was the distance measured in the brain slice experiments (Giocomo et al., 2007). The dorsal border between entorhinal and postrhinal cortex is located at about 3.8–4 mm from the dorsal surface of the brain (Paxinos and Watson, 1998). The corresponding change in oscillation frequency f(z)=1/T(z) relative to dorsal-ventral position is shown in Fig. 1B.

Figure 1.

A. Neurons show higher frequency of subthreshold oscillations in slices of dorsal entorhinal cortex (top traces) and lower frequency in ventral slices (bottom traces). Schematic diagram at bottom shows distance from the dorsal border with postrhinal cortex. B. Plot of change in subthreshold oscillation frequency f (in Hz) with distance from postrhinal border (z, in mm) based on reciprocal of data shown in 1C. C. Plot of period (T, in sec) of subthreshold oscillations relative to distance from postrhinal border (z, in mm) directly based on the equation from linear fit of data (Giocomo et al., 2007). Dashed line shows extrapolation beyond border. D. Plot of grid cell field spacing (G, in cm) relative to distance from postrhinal border (z, in mm) based on equation from linear fit of previously published data (Sargolini et al., 2006). E. Plot of scaling value H (in Hz-cm) based on product of f and G. Note that this value stays near 300 Hz-cm.

Similar to the plot of oscillation cycle period, the plot of the grid cell field spacing G (cm) relative to dorsal-ventral position (z) shows a linear relationship, as shown in Fig. 1D. In the supplementary material of the paper from the Moser laboratory (Sargolini et al., 2006), this data was fit with the following equation provided by Hafting: G(z) = 30z + 37.09 (the coefficient was originally 0.03 for data in microns). Note that without a subscript, z indicates distance in mm from the border of postrhinal cortex, as measured for the recording sites of in vivo experiments (Sargolini et al., 2006). Because grid cell data in that study was obtained from 0 to 1.5 mm from the postrhinal border, the plot of stellate cell oscillation frequency presented here was restricted to this range.

We can analyze these equations in relation to each other by converting to use the same distance in mm from the postrhinal border, by using the relationship z+4=z_d. This gives the equation: T(z) = 0.094z + 0.13. This equation for T has an x intercept at z_T0=−1.38 mm, as shown by the dashed line in Fig. 1C. This is remarkably close to the x intercept for the equation fitting grid cell field spacing (G) which has a value of z_G0=−1.24, as shown by the dashed line in Fig 1D. The two x intercepts differ by only about 0.1 mm. In fact, if we consider the postrhinal border to be at 3.9 mm below the dorsal surface, the intercepts differ by only 0.04 mm.

The distance from postrhinal border is measured along the length of entorhinal cortex layer II, which is at an angle of about 30 degrees from vertical in stereotaxic coordinates. Accounting for this angle would use a conversion equation of z cos(30) + 4 = z_d. This yields a slightly different equation of T(z) = 0.081z + 0.13 and an intercept of 1.6.

This analysis is presented to indicate that the equations can be scaled relative to one another. Grid cell patterns do not appear on the other side of the border in postrhinal cortex (Fyhn et al., 2004), and the lack of grid patterns beyond the postrhinal border might reflect biophysical limitations on the maximal frequency of subthreshold oscillations, as the frequencies would have to grow as f(z) = 1/0.094(z − z_T0). Whole cell patch recordings across the border in postrhinal cortex show an absence of subthreshold oscillations and sag current (Giocomo, unpublished data). Note that the limit of grid cell field spacing and subthreshold oscillation frequency at the postrhinal border could be a factor affecting the resolution of rat spatial memory.

The grid cell spacing function G(z) and the subthreshold oscillation period function 1/f(z) can be scaled to one another by a scaling function H(z), such that H(z)/f(z) = G(z). Combining the equations for linear fits of the experimental data gives the equation: H(z) = 317.8 − 31.3/(z − z_T0). The plot of H(z) relative to dorsal to ventral position z is shown in Figure 1E. As can be seen in this plot, the function H(z) appears to be nearly constant within the entorhinal cortex across all positive values of z along the dorsal to ventral axis. For positive values of z, the change in H(z) is within the range of the variance in the experimental data used to obtain f(z) and G(z). The slope is steeper using the correction of cos(30) but is still within the range of variance. Therefore, for the rest of this paper, the experimentally determined function H(z) will be assumed to be a constant H, such that:

$$G(z)=H/f(z)$$ (1)

In the range of the experimental data, the value of this experimentally determined constant is approximately 300 Hz*cm. This constant can be used to estimate the spacing G for a given subthreshold oscillation frequency f. For example, when the frequency is 7.5 Hz (at z=0.077), equation 1 gives G=300/7.5=40 cm which is very close to the actual value of 39.4 cm from the linear fit to data on grid field spacing. Similarly, when the frequency is 3.75 Hz (at z=1.49), equation 1 gives G=300/3.75=80 cm which is again very close to the actual value of 81.8 cm for spacing at that anatomical location z. The scaling factor essentially relates the slopes of the two linear fits. The linear fit to the membrane potential oscillation period has a slope of about 0.1 Hz per mm of distance from postrhinal border. Multiplication by the scaling factor 300 gives a slope of 30 cm of grid spacing per mm of distance from the postrhinal border for the linear fit to the grid cell spacing G.

Derivation of Burgess model from experimental constant H

This section demonstrates how equation 1, determined entirely from experimental data, can be used to derive the model of grid cells presented by Burgess and colleagues (Burgess et al., 2005; Burgess et al., 2007). This derivation demonstrates that the model is not just an ad hoc account for grid cell properties, but is specifically indicated by the pattern of experimental results described above. Other models designed to show grid cell firing properties based on network dynamics (Fuhs and Touretzky, 2006) cannot be derived from the constraints of this data on intrinsic oscillation frequency, and do not account for it in their present form.

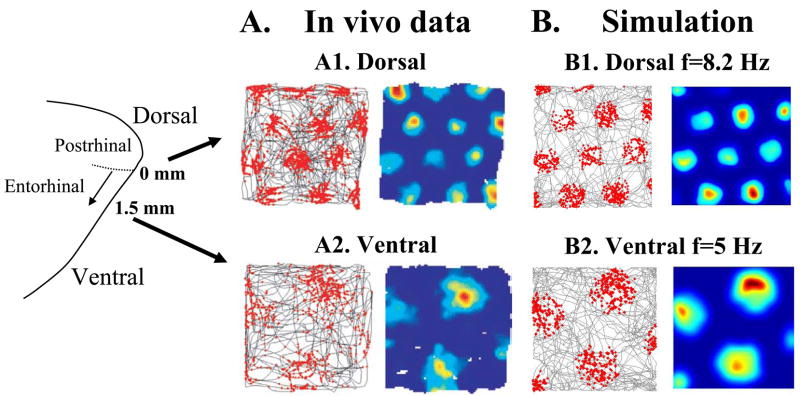
As shown in Figure 2, this model effectively links the frequency of membrane potential oscillations (Figure 1A) to the grid cell field spacing (Hafting et al., 2005), providing an excellent match with the in vivo recording data. As shown in Figure 3, the model simulates spiking activity during complex movements of a virtual rat through a virtual environment. In the model, interference between membrane potential oscillations with different frequencies causes spiking that falls within grid cell firing fields that remain consistent between the initial 40 seconds of running and longer periods of running. Details about simulation of the model are described in a separate section below.

Figure 2.

Simulation of the Burgess model with different oscillation frequencies replicates differences in dorsal to ventral grid cell spacing. A1. Previously published recording data (Hafting et al., 2005) from a single dorsal grid cell showing closely spaced grid fields. Plot on left shows the location of the rat at the time of each spike in red and the overall rat movement trajectory in gray. Right plot shows Gaussian smoothing of mean firing rate (red=high rate, blue=no firing). A2. Data from a single ventral cell showing larger spacing between grid fields in both spike location plots (left) and firing rate plots (right). B1. Simulation of grid fields using membrane potential oscillation frequency of 8.2 Hz, with rat starting position at x=−4, y=−8 cm, and head direction cells at 60 degree intervals starting at 36 degrees. Left plot shows location of simulated rat during each spike in red with trajectory in gray produced by random movement algorithm. Mean firing rate is shown in right plot. B2. Simulation of ventral grid fields with oscillation frequency of 5 Hz, starting position x=15, y=30 cm, and head direction cells at 60 degree intervals starting at -12 degrees. Plots show wider grid field spacing with the lower frequency.

Figure 3.

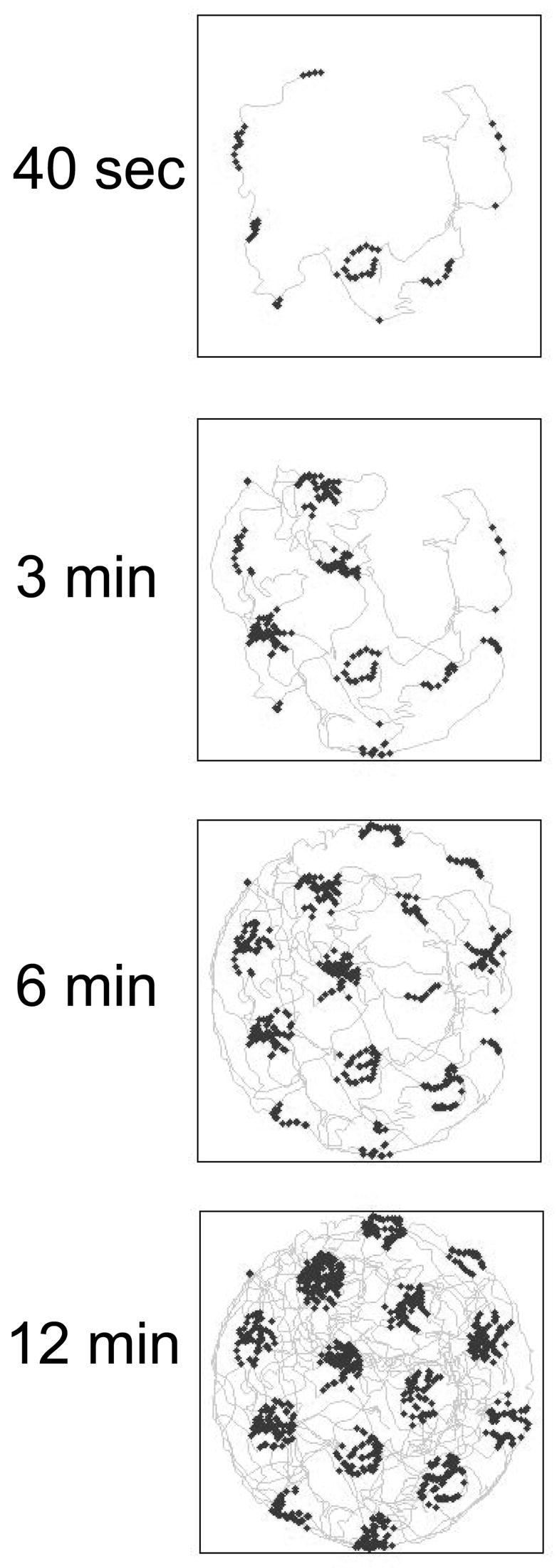
Plot of single simulated grid cell with subthreshold oscillation frequency of 6.42 Hz, summed over different time periods from the start of exploration (first 40 seconds, 3 min, 6 min, 12 min). Note that the firing of the neuron occurs in specific regularly spaced grid fields, even though the simulated rat follows an irregular trajectory with varying direction and speed based on experimental data (Hafting et al., 2005).

The pattern of grid cell spacing is highly reproducible regardless of the trajectory followed by a rat in the environment. Data by Hafting and Fyhn from the Moser lab (Hafting et al., 2005) shows clear grid pattern firing over extended periods during which the rat randomly forages in the environment, moving at a very wide range of speeds and directions. This provides an interesting problem for understanding how the temporal oscillations of neurons at one anatomical location could map in a consistent manner to spatial periodicity of neurons at that location. If the soma of a neuron is oscillating at one frequency f, then how can it underlie a spike in one grid field and a later spike in a different grid field when the trajectory that the rat follows between these two grid fields could be a straight line taking two seconds, or it could be a complex path with multiple stops taking ten or twenty seconds? The mechanism of grid cell firing somehow operates with invariance for speed and direction of movement.

Consider a neuron at one anatomical position z along the dorsal to ventral axis, and consider the experimentally derived value of the soma oscillation frequency f of this neuron. On its own, this membrane potential oscillation frequency should not cause regular spiking, because it would result in random spatial firing of the neuron because of the random speed and direction of the rat. However, this subthreshold oscillation frequency can interact with other subthreshold oscillations in the neuron, for example on different dendrites, and the relative phase of these subthreshold oscillations can determine whether the neuron spikes. Therefore, we can obtain spiking which occurs due to the effect on membrane voltage V(t) of the sum of soma oscillations at one frequency f and dendritic oscillations at another frequency f_d:

$$V(t)=cos(f2\pi t)+cos(f_{d}2\pi t)$$ (2)

As shown in Figure 4, the interaction of these two frequencies will result in an interference pattern with an envelope that varies in amplitude at a lower frequency. This is similar to the interference pattern between two musical notes that are close in frequency and result in a slow “beat” frequency. The beat frequency will have the frequency f_b=f_d−f. If the subthreshold oscillations are large, the sum of the two subthreshold oscillations can bring the cell over its firing threshold, resulting in spiking activity appearing at intervals of the beat frequency. The beat frequency f_b can be used to calculate the time period of an individual cycle, or T_b, which would correspond to the time period between suprathreshold spiking activity of the neuron. The period is the reciprocal of frequency: T_b=1/f_b. This time period can be quite large for frequencies that are close to each other.

Figure 4.

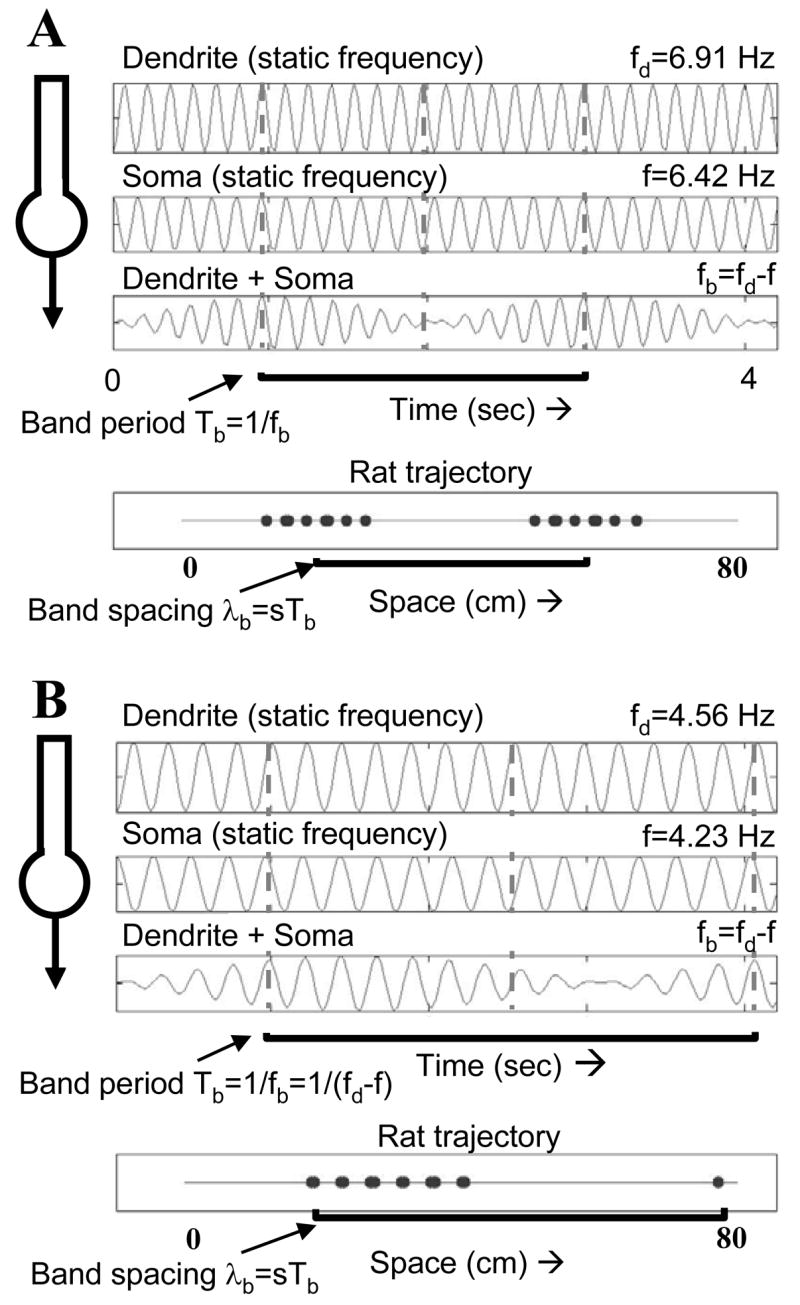
Simulations of interference between oscillations in dendrite and soma. A. Static frequencies of 6.91 Hz in the dendrite and 6.42 Hz in the soma (mean dorsal frequency in data) result in an oscillatory interference pattern with frequency f_b 0.49 Hz and period T_b of 2.04 sec. At a speed of 20 cm/sec this results in a distance between firing (spatial wavelength λ_b) of about 40 cm. B. Shifting the frequencies to lower levels representing ventral frequencies 4.56 Hz in dendrite and 4.23 Hz in soma results in interference with frequency of 0.33 Hz and period of 3.03 sec. At a constant speed of 20 cm/sec this results in a spatial wavelength of about 60 cm.

Consider a rat starting movement in the center of a grid field, where the dendrite and soma are firing at the same phase, and the summed depolarization is sufficient to cause spiking activity. As the rat moves at a constant speed, the difference in frequency between the dendrite and the soma progressively increases the phase difference between dendrite and soma, reducing constructive interference and increasing destructive interference, which results in less depolarization on each cycle of oscillation and a cessation of firing as the rat moves (corresponding to movement out of a grid field). As the rat continues moving and the oscillations continue, gradually the dendrite and soma oscillations will come back into phase with each other, causing constructive interference that can depolarize the cell enough to cause spiking activity again. This would be the entry into another grid field.

Figure 4A shows a plot of the soma oscillation with frequency f and the dendritic oscillation with frequency f_d, and shows the resulting interference pattern that causes suprathreshold spiking activity with frequency f_b, or period T_b. If we assume a constant speed s and constant direction of movement of the rat over the time period T_b, then we get spikes which appear at a fixed spatial wavelength λ_b =s*T_b, corresponding to distance covered between areas of firing. This distance λ_b is simply the period of the interference cycle T_b times the speed s. Figure 4B shows that if we assume different baseline frequencies in the soma that correspond to different frequencies in dorsal versus ventral entorhinal cortex, it will result in different distances (λ_b) between firing fields.

Of course, it is extremely rare for a real rat to run in one direction at a constant speed. Obviously, if the rat moves at different speeds and directions relative to the starting point, the firing will occur at the same time interval T, but this time interval will correspond to different distances d depending on the speed and direction of rat movement. Thus, temporal oscillations alone are not an effective model of grid cell firing, which shows constant spatial locations of grid fields over time and constant distances G between grid fields. How can we obtain this invariance of the spatial location of firing despite the variation in speed s and direction φ of the rat? That is, how can we maintain regular firing at a regular wavelength λ_b?

Consider the rat moving with a velocity vector v⃗ corresponding to a varying speed s at a varying angle φ. The rat is moving in two dimensions, but we can consider the amount of movement in one allocentric Cartesian dimension of movement in the environment, x. The amount of movement in the dimension x corresponds to the projection of the velocity vector v on that dimension x, which is the dot product of v and x: v⃗ • x⃗. Given the angle φ of movement relative to dimension x, then the amount of movement per unit time in that direction is Δx = s cos(φ). This requires representation of the speed and angle relative to a reference direction (Burgess et al., 2007). Physiologically, this is available in the form of the response of head direction cells, which are neurons in areas such as the dorsal presubiculum (also known as postsubiculum) and anterior thalamus that respond selectively on the basis of the heading direction of the rat (Taube et al., 1990a; Blair and Sharp, 1995; Taube et al., 1996; Goodridge and Taube, 1997; Blair et al., 1997; Taube, 1998; Blair et al., 1998; Sharp et al., 2001b; Taube and Bassett, 2003). The postsubiculum and anterior thalamus have strong interconnections, and the postsubiculum (dorsal presubiculum) sends projections to medial entorhinal cortex (Kohler, 1985; van Groen and Wyss, 1990; Caballero-Bleda and Witter, 1993). Neurons in deeper layers of entorhinal cortex show grid cell firing properties and head direction tuning as well as sensitivity to movement speed (Sargolini et al., 2006). The speed modulation of deep entorhinal head direction cells is relatively weak, but recordings in postsubiculum have also shown some modulation of head direction firing by translational movement speed (Taube et al., 1990a; Sharp, 1996). Thus, cells providing input to entorhinal cortex can respond in a manner dependent on speed and the direction of the rat relative to the preferred direction of the head direction cell φ_HD. In addition, neurons in other regions have been shown to respond systematically dependent on the speed of the rat (Burgess et al., 1997; Sharp and Turner-Williams, 2005; Sharp et al., 2006). Thus, consistent with physiological data, the model combines information about rat speed s and head direction φ to code the movement (velocity v⃗ or change in location Δx⃗) in the dimension x determined by the preferred head direction φ_HD of a given head direction cell:

$$\overrightarrow{v}=s\hspace{0.17em}cos(\phi -{\phi }_{HD}).$$ (3)

If we consider the distance between firing locations, our measure of wavelength turns the speed in an arbitrary direction into a distance in dimension x (spatial wavelength λ_b):

$${\lambda }_b=v{T}_b=scos(\phi -{\phi }_{HD})/f_b.$$ (4)

To maintain stable spatial firing, we want the spatial wavelength λ_b to remain constant regardless of random changes in speed s or heading angle φ. From the equation, it is clear that the wavelength will remain constant if we change the beat frequency f_b in a way that compensates for changes in speed and angle of movement. Thus, we can keep spatial wavelength constant by changing beat frequency according to: f_b = Bs cos(φ − φ_HD), where B is a constant. With this change, the wavelength in equation 4 will be λ_b = 1/B.

Because the beat frequency results from the difference in soma oscillation frequency f and dendrite oscillation frequency f_d, we rearrange the equation f_b = f_d − f and obtain:

$$f_d=f+\mathit{Bs}cos(\phi -{\phi }_{HD}).$$ (5)

This equation maintains constant spatial wavelength of interference in the dimension of one head direction cell. This is the additive model for dendritic frequency used in the Burgess model (Burgess et al., 2005; Burgess et al., 2007). Figures 5, 6 and 7 show how scaling the dendritic oscillation f_d relative to the speed and angle of movement of the rat ensures that the spatial wavelength λ_b of firing stays fixed. With these conditions, the neuron shows interference in spatial waves with wavelength λ_b in the direction φ_HD. Note that the figures use the multiplicative modulation of dendritic frequency described below. As shown in Figure 8, the largest amplitude of the summed oscillations occurs in bands of locations perpendicular to the preferred head direction. This interference will be referred to as band interference.

Figure 5.

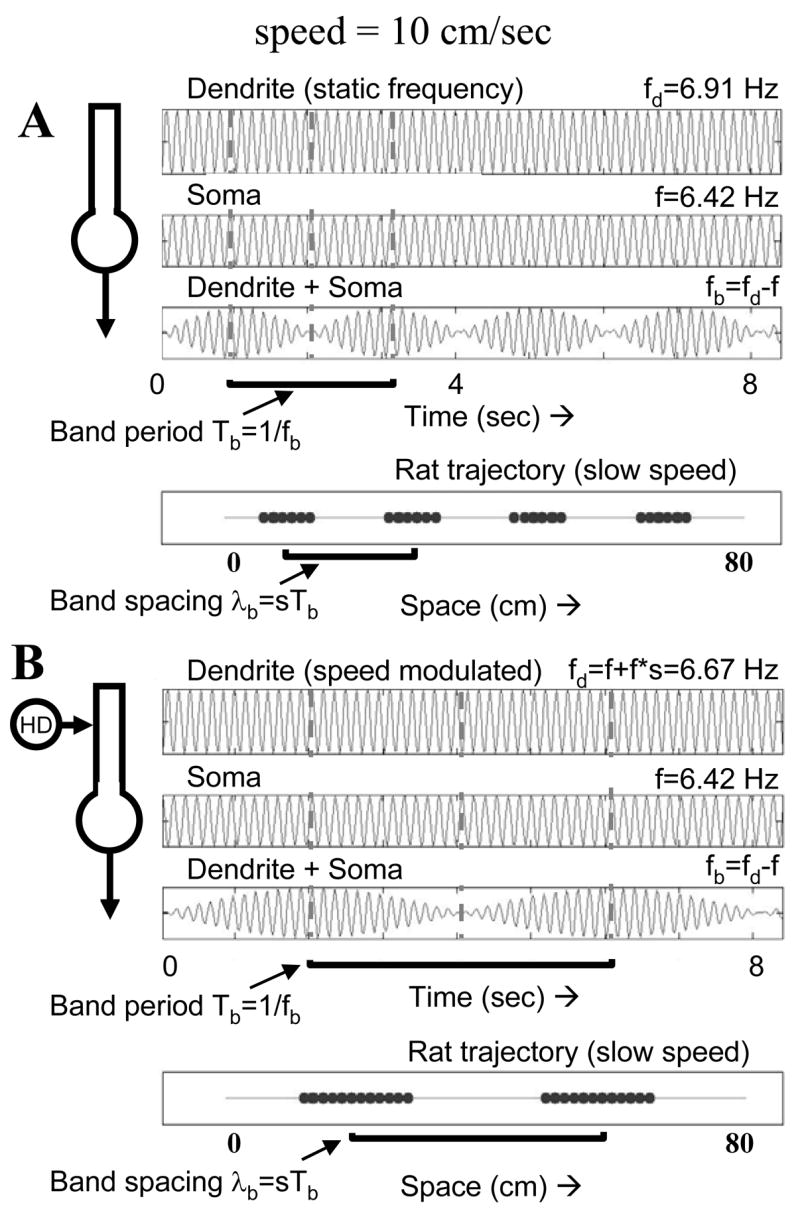
Differences in speed require scaling of dendrite frequency by speed. A. The same frequencies used in Figure 4A are used with a rat speed of 10 cm/sec. The time scale is doubled to show the same range of spatial movement of the rat. The period of interference is still 2.04 sec, but at a speed of 10 cm/sec the spacing between firing is about 20 cm. B. Modulation of dendrite frequency proportional to speed ensures that grid cell field spacing stays the same. For a speed of 10 cm/sec, the speed-scaled modulation results in the dendrite frequency being 6.67 Hz. This reduces the interference frequency to 0.25 Hz and increases the period to 4 sec. This results in a spatial wavelength of 40 cm. The same spatial wavelength was obtained in Figure 4A at a speed 20 cm/sec, where dendrite frequency was modulated to 6.91 Hz, causing a period of 2 seconds and wavelength of 40 cm.

Figure 6.

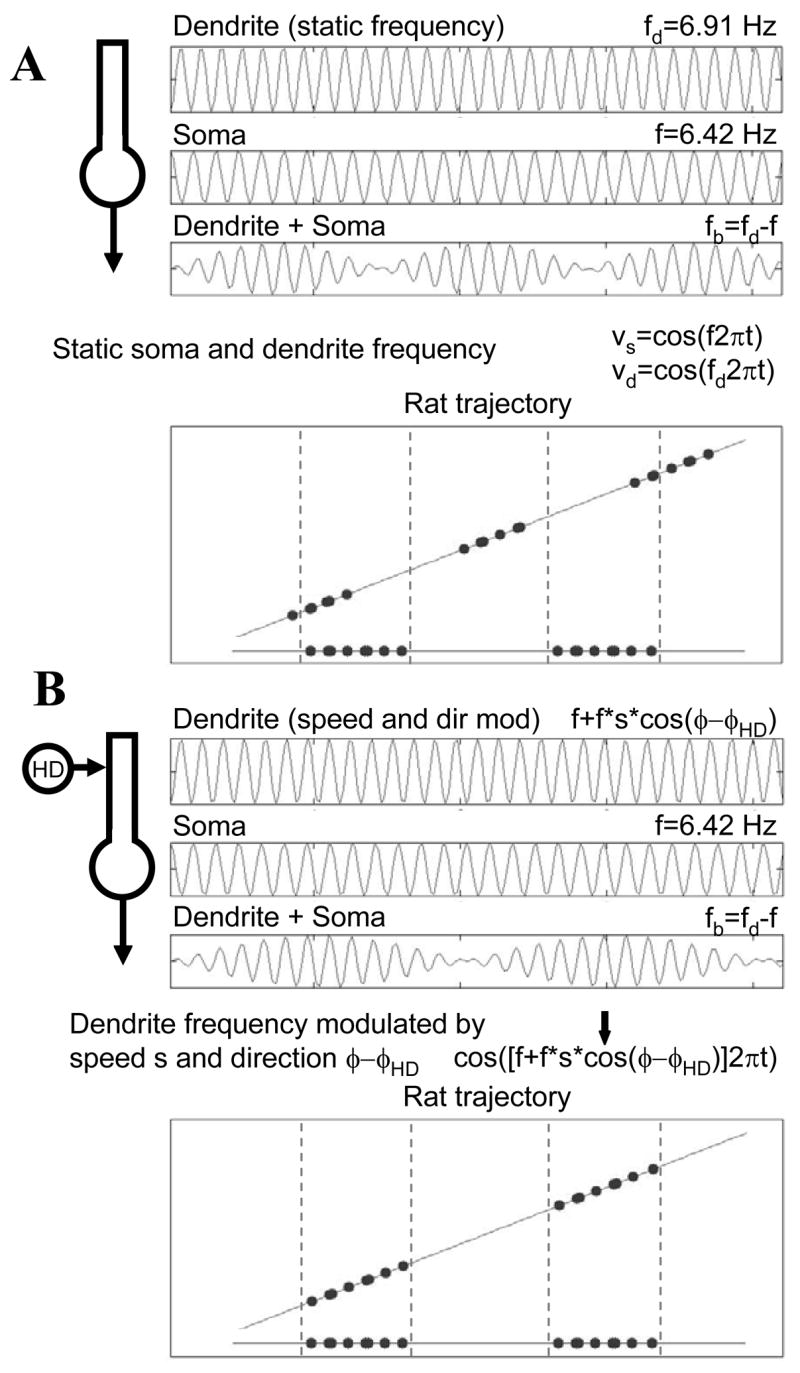
Changes in direction of movement also need compensation. A. Comparison of two directions of movement showing that with static frequency the spiking occurs at the same temporal interval but does not match the spatial wavelength. B. Modulation of dendritic frequency proportional to the cosine of head direction allows the spiking activity to line up with a consistent spatial wavelength λ_b in one dimension (as indicated by vertical lines). This modulation based on head direction can be provided by a head direction cell represented by the circle with HD.

Figure 7.

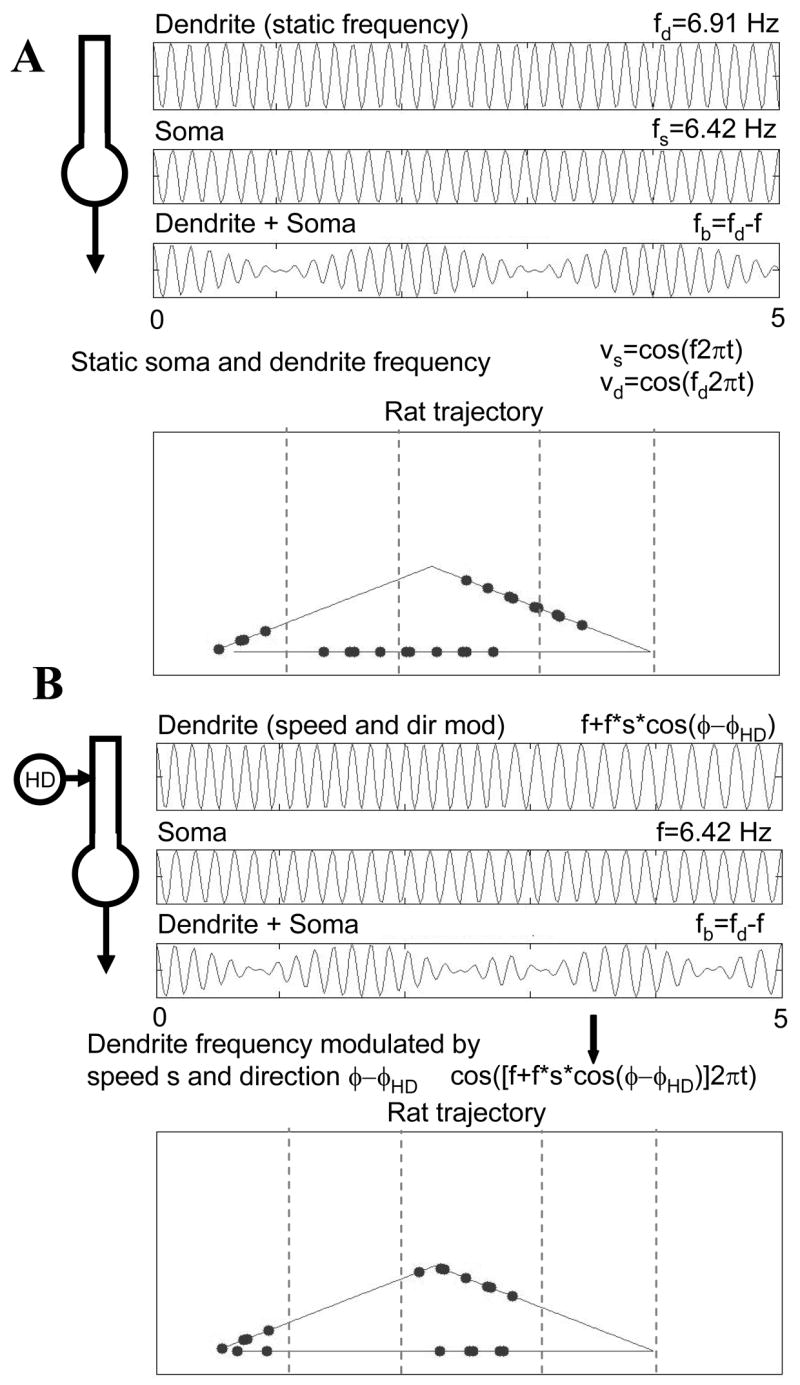
Spiking activity during movement along a triangular pathway through the environment. A. Static oscillation frequencies in dendrite and soma result in spiking at regular temporal intervals, but do not show consistency with spatial dimensions. B. In contrast, modulation of dendritic frequency by speed and head direction ensures that firing occurs consistently within vertical spatial bands (defined relative to horizontal position). The vertical dotted lines indicate the consistent intervals of spatial firing.

Figure 8.

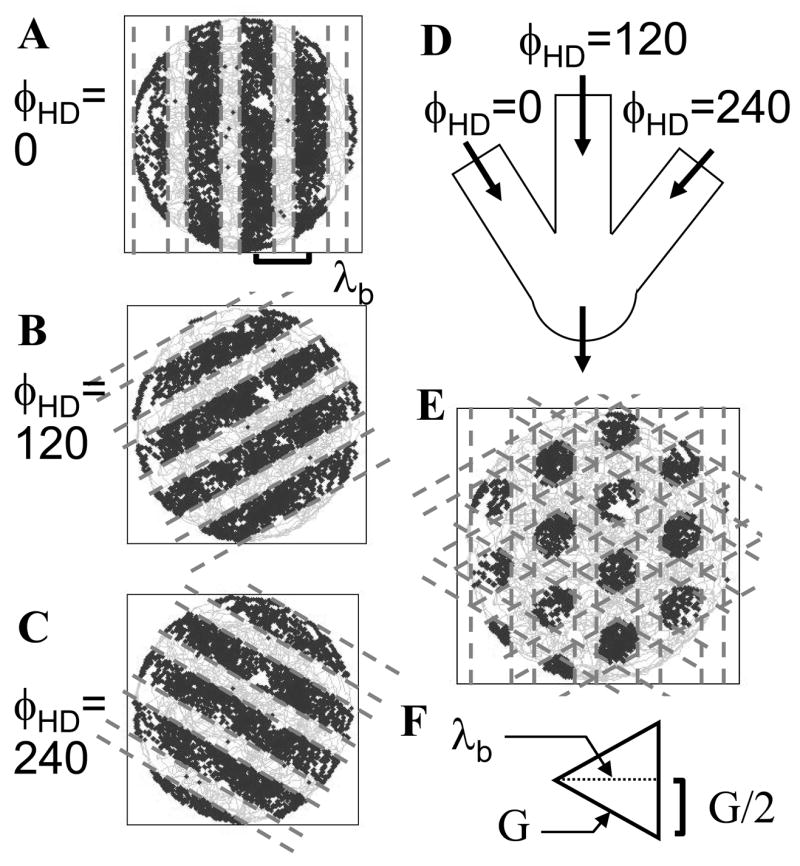
Combination of bands of interference from different dendrites results in the grid cell firing pattern. Each head direction cell causes interference with consistent spatial wavelength in bands running perpendicular to the selective direction preference of the individual head direction cell. A–C. Interference bands due to modulation of dendritic frequency by head direction cells with specific direction preferences angles at zero (A), 120 degrees (B) and 240 degrees (C). D. Schematic of the interaction of different dendrites with interference bands modulated by input from different head direction cells. E. The product of interference bands due to different dendritic oscillations cause the soma to cross firing threshold in a pattern matching grid cell firing fields. F. Equilateral triangle illustrating the relationship between the spatial wavelength λ_b of band interference (height of triangle) and the grid cell spacing G (length of one side).

This does not yet fully explain the firing pattern in grid cells that appears as tessellated equilateral triangles with firing fields at each vertex. Assuming the band interference is usually subthreshold, then grid cell firing fields can be obtained by combining multiple interference patterns in a single neuron (Burgess et al., 2007). This requires a new property of neuronal function, consisting of the computation of interference patterns between different dendrites that could interact at the soma to cause neuronal firing. It is notable that stellate cells of the entorhinal cortex obtained their name because of their specific anatomical structure, in which multiple primary dendrites extend directly off the soma (Alonso and Klink, 1993). This could be the ideal morphological structure to allow interaction of interference patterns between different independent dendritic branches and the soma. Thus, this functional model has the potential to generate predictions concerning the morphology of individual neurons and the structure of dendritic trees. This requires analysis of the dynamics of oscillatory interactions within compartmental biophysical simulations of entorhinal cortex stellate cells (Fransen et al., 2004).

As shown in Figure 8, grid cell firing fields can be obtained by combining oscillatory interference bands associated with different dendritic inputs from different head direction cells by multiplying the membrane potential oscillations. Figure 9 shows the effect of combining different numbers of head direction cells with different intervals in selectivity angle ranging from 30 to 120 degrees. The creation of a pattern of grid cell firing on the vertices of tessellated equilateral triangles (hexagons) in the model requires that head direction cells providing input to the grid cell have preferred directions that fall at multiples of 60 degrees. The model can tolerate small variation in the preferred direction, but the requirement of head direction input at multiples of 60 degrees is a strong prediction of the model about the relative preference of head direction cells providing input to individual neurons.

Figure 9.

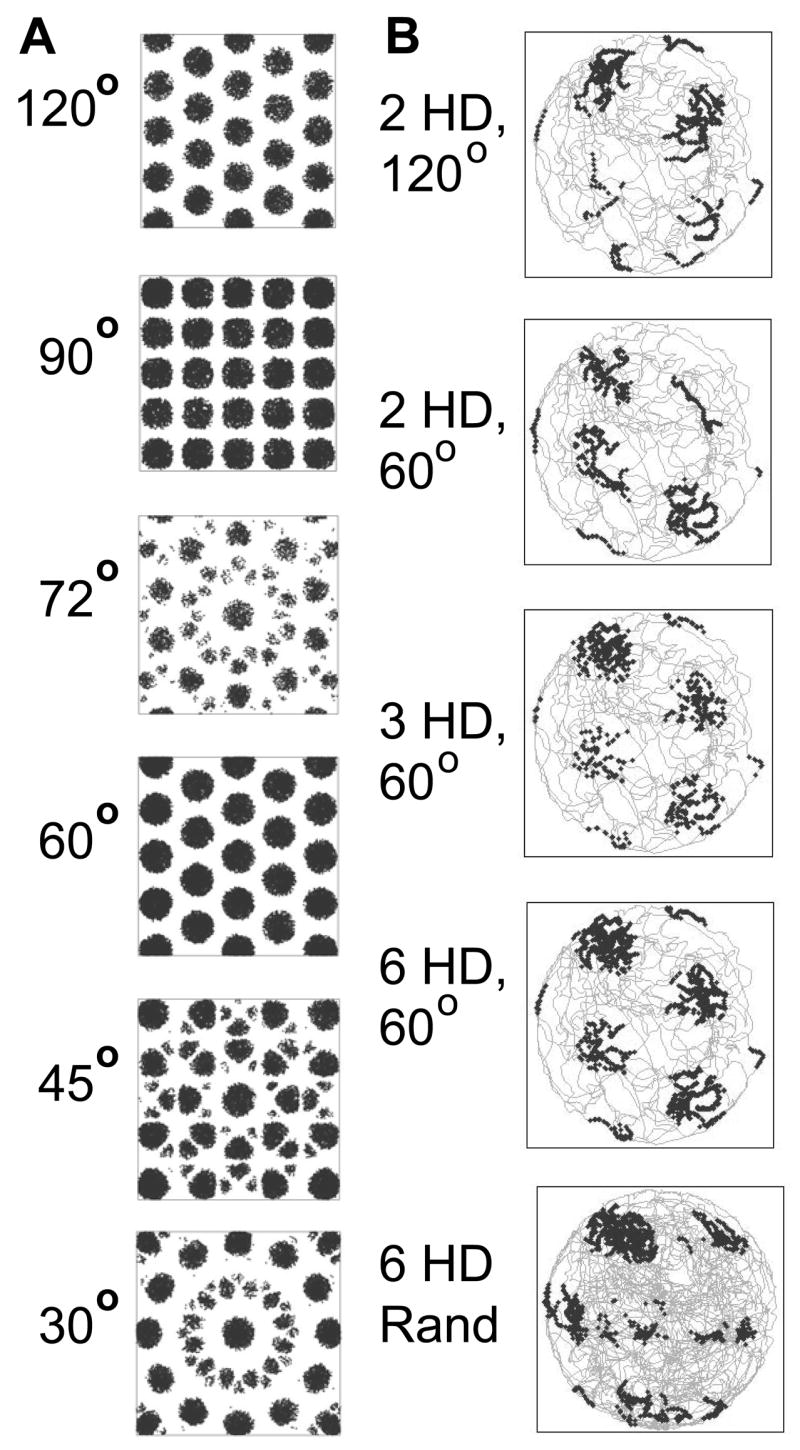
A. Effect of different head direction inputs with different intervals between direction preference angles on simulated grid cell firing fields for a neuron with intrinsic frequency of 7 Hz. A1. Input from three head direction cells (3 HD) at 120 degree intervals of selectivity (top) gives grid patterns of tessellated equilateral triangles (hexagons). A2. Four head direction cells with 90 degree selectivity intervals create a square grid. A3. 5 HD cells at 72 degree intervals create a complex pattern with radial symmetry but no translational equivalence. A4. Six HD cells at 60 degree intervals create a grid pattern similar to that for 120 degree intervals. A5 and A6. 8 HD cells at 45 degrees and 12 HD cells at 30 degree intervals create complex patterns with radial symmetry but no translational equivalence. B. Simulated grid cells with different numbers of head direction inputs show a less consistent grid pattern with two HD cells, but similar properties with 3 HD and 6 HD cell inputs. The simulated grid cell has an intrinsic frequency of 4 Hz in B.

As shown in Figure 8, the distance covered between periods of constructive interference for an individual dendrite is not quite the grid cell spacing, because in the model the equilateral triangle (hexagon) pattern of grid fields results from band interference in multiple dendrites. As shown in Figure 8F, the wavelength λ_b of band interference corresponds to the height of an equilateral triangle, whereas the grid cell field spacing G corresponds to the length of one side of the equilateral triangle. Thus, if we consider half of the equilateral triangle, we have a right triangle with one side λ_b, one side G/2, and the hypotenuse of length G. The trigonometric relationship G² = (G/2)² + λ_b² yields $G={\lambda }_b(2/\sqrt{3})$. Combining this result with λ_b=1/B, gives us the relationship: $G(z)=2/\sqrt{3}B$.

However, this framework does not accurately relate the spacing G to subthreshold oscillation frequency. G is dependent on the constant B but not on changes in f, so it does not yet satisfy our experimentally derived constraint in equation 1. The model derived so far is the Burgess model as it was originally presented in additive form (Burgess et al., 2005). However, the data guided derivation of a different version (Giocomo et al., 2007) that is presented as the multiplicative model in the paper by Burgess (Burgess et al., 2007). The experimental data provides the constraint in equation 1 that G(z) = H/f(z) for different dorsal-ventral positions z. This can be obtained in the model by simply setting B = B_H f(z), using the parameter $B_H=2/\sqrt{3}H$ defined using the experimental constant H, and thereby converting the equation for dendritic frequency (equation 5) into:

$$f_d=f+{fB}_{H}scos(\phi -{\phi }_{HD})$$ (6)

Incorporating this relationship into the full model gives the full model for generation of grid cells used in most of the remaining simulations in this paper. The different membrane potential oscillations V(t) are multiplied together to obtain the pattern of grid cell firing as follows:

$$g(t)=\mathrm{\Theta }[\prod _{HD}(cos(f2\pi t)+cos((f+{fB}_{H}scos(\phi -{\phi }_{HD}))2\pi t)+\varphi )]$$ (7)

Where g(t) represents the grid cell firing pattern over time, Θ is a step function with threshold set at 1.8 in the simulation, and Π represents the product across different dendrites receiving input from different head direction cells with selectivity angles φ_HD. The parameter ϕ represents the initial phase of each membrane potential in the neuron and is described further below. Note that most simulations used a rectified version of the cosine function as described below. Equation 7 is the multiplicative modification of the model described by Burgess (Burgess et al., 2007) with insertion of the experimentally determined constant B_H (Giocomo et al., 2007).

This modification of the model gives us the relationship:

$$G(z)=2/(\sqrt{3}{B}_{H}f(z)).$$ (8)

This is exactly equivalent to the experimental constraint in equation 1 if we set $H=2/\sqrt{3}{B}_H$. Thus, the steps described above show how equation 1, determined entirely from experimental data, can be used to derive the multiplicative version of the Burgess model. This also shows how the experimentally derived constant of H=300 can be used to set the value of B_H=0.00385 to obtain the appropriate grid cell field spacing G(z) at location z for a given temporal frequency f(z). Note that H has units of Hz*cm that combine the frequency of subthreshold oscillations (Hz=cycles(mpo)/sec) and the spacing of grid fields (cm/cycles(spatial)). These units can be rearranged to give B_H units appropriate for the model: (sec/cm)*(cycles(spatial)/cycles(mpo)). The units of this parameter have the dimensions of sec/cm, as it must compensate for the speed of the rat, and it also scales the number of temporal oscillations in cycles(mpo) to the number of spatial cycles. This completes the derivation of the model of grid cells presented by Burgess (Burgess et al., 2005; Burgess et al., 2007). On a cell by cell basis, at specific anatomical positions z, this model relates the baseline subthreshold oscillation frequency f(z) to the distance G(z) between grid fields exhibited by that cell. Note that this modulation of dendritic oscillation frequency by multiple head direction cells provides an effective functional framework that allows the single neuron to maintain an accurate representation of the spatial location of the rat in continuous two-dimensional space, dependent only on input from head direction cells whose continuous firing rate updates the phase and interaction of different dendritic oscillations. In effect, a single neuron receiving input from three head direction cells can perform path integration. Most other models of path integration propose larger scale population interactions (McNaughton et al., 1991; Touretzky and Redish, 1996; Redish and Touretzky, 1998; McNaughton et al., 2006; Fuhs and Touretzky, 2006). This illustrates the power of this new cellular mechanism for the coding of continuous variables.

ANALYSIS AND PREDICTIONS OF THE MODEL

Demonstration of transformation to spatial coordinates

The structure of the model is primarily described in terms of oscillations in time, whereas the properties of grid cells are primarily described in terms of dimensions of space. A useful further analysis of the model demonstrates the conversion of temporal oscillations into activity dependent on spatial location. This analysis can be understood in terms of the components of the simulation. In simulations the change in spatial location is represented by the velocity, which is the change in spatial coordinates for a given change in time (Δx/Δt, Δy/Δt). The heading angle of the rat is computed as φ = arctan((Δy/Δt)/(Δx/Δt)) and the speed is $s=\sqrt{{(\mathrm{\Delta }x/\mathrm{\Delta }t)}^2+{(\mathrm{\Delta }y/\mathrm{\Delta }t)}^2}$. When these equations for the heading angle and speed of the rat are plugged into the equation for the cosine function representing the head direction cell tuning, the result can be simplified analytically using the relationship: $cos(arctan((\mathrm{\Delta }y/\mathrm{\Delta }t)/(\mathrm{\Delta }x/\mathrm{\Delta }t)))=(\mathrm{\Delta }x/\mathrm{\Delta }t)/\sqrt{{(\mathrm{\Delta }x/\mathrm{\Delta }t)}^2+{(\mathrm{\Delta }y/\mathrm{\Delta }t)}^2}$. For movement relative to one head direction with preference angle φ_HD=0, these equations can be inserted into equation 6 to obtain: f_b = fB_H s cos(φ − φ_HD) = fB_H Δx/Δt.

Instead of considering the oscillation over time, it is simpler to focus on the change in phase ϕ_b of the beat oscillation with frequency f_b=f_d−f over time. Using the above relationship, the change in phase with time can be transformed into a change in phase with location:

$$\mathrm{\Delta }{\varphi }_b=f_b(2\pi \mathrm{\Delta }t)=({fB}_H\mathrm{\Delta }x/\mathrm{\Delta }t)(2\pi \mathrm{\Delta }t)={fB}_H\mathrm{\Delta }x$$ (9)

Summing this equation from the starting point shows that phase depends directly on position relative to the starting location x₀:

$${\varphi }_b-{\varphi }_0={fB}_H(x-x_0)$$ (10)

The beat frequency oscillation will depend directly on this phase signal determined relative to a specific head direction cell. Therefore, the overall equation 7 can be written as a function of spatial location x as follows:

$$g=\mathrm{\Theta }[\sum _{h}cos(2\pi {fB}_H(\overrightarrow{x}-{\overrightarrow{x}}_0)•\overrightarrow{h})]$$ (11)

Where x is a vector representing spatial location and h is a vector pointing in the preferred direction of a specific head direction cell. The result of this derivation is similar to a representation of grid cells used previously without derivation (Solstad et al., 2006). Note that in this representation the sum of the different components is used in order to avoid doubling the frequency by taking the product of the negative phase of the cosine function.

Scaling of dendritic depolarization to running speed

This model proposes an experimentally testable relationship between the quantitative properties of single neuron membrane potential oscillations, and the quantitative properties of grid cell firing fields observed in recordings from awake behaving rats, in contrast to a model of grid cells based on network attractor dynamics (Fuhs and Touretzky, 2006) that only uses temporal oscillations during development. A central requirement of this model is that the magnitude of change in dendritic frequency should be scaled to the running speed of the rat. This is consistent with proposals for speed modulated update of neural activity for path integration (McNaughton et al., 2006). The model gives an explicit scaling between running speed in a specific direction and membrane potential oscillation frequency as shown in equations 6 and 7.

As shown in Figures 4 and 5, for an example dorsal neuron, at a speed of 0, dendritic membrane potential oscillations will be at the baseline frequency of 6.42 Hz. At 10 cm/sec, dendritic frequency will increase to 6.67 Hz, and at 20 cm/sec the frequency will increase to 6.91 Hz. Thus, the model predicts an increase in subthreshold oscillation frequency per unit of speed (in cm/sec) that would be 0.025 Hz*sec/cm in dorsal neurons with a mean frequency of 6.42 Hz. In ventral neurons with a mean frequency of 4.23 Hz, the change in oscillation frequency per unit of speed would be 0.66*0.025=0.016 Hz*sec/cm. In addition to influencing the beat frequency, the subthreshold oscillation frequency also influences the rhythmicity of spiking within a given grid field. The resulting spiking across the population of grid cells in entorhinal cortex should influence the frequency of theta rhythm observed in stratum lacunosum-moleculare of hippocampal region CA1 (Brankack et al., 1993). Thus, this model can be tested by comparison with previous experimental data on the modulation of frequency of hippocampal theta rhythm by different running speeds (Whishaw and Vanderwolf, 1973; Rivas et al., 1996; Slawinska and Kasicki, 1998; Maurer et al., 2005; Geisler et al., 2007). This experimental test can support this model in contrast to a model of grid cell firing based on network attractor dynamics (Fuhs and Touretzky, 2006) that does not address oscillation frequency changes during behavior.

A recent measurement of the slope of the change in frequency with running speed in the hippocampus showed a mean slope of 0.0057 Hz*sec/cm for dorsal hippocampus and 0.0098 Hz*sec/cm for middle regions of hippocampus (Maurer et al., 2005). The value for middle hippocampus is about half of the value of 0.016 Hz*sec/cm that was predicted above for single ventral neurons providing input to hippocampus. However, the speed modulation of network theta oscillations should differ from speed modulation in single dendrites, and may combine the slope of modulation of dendritic theta with an absence of speed modulation at the soma, resulting in a lower slope. This is consistent with the fact that the higher frequency carrier wave during beat oscillations averages the two frequencies undergoing interference.

The mean oscillation frequency of dorsal neurons observed in the experimental data (Giocomo et al., 2007) goes from a frequency of 6.42 Hz at −50 mV to 7.18 Hz at −45 mV, so a 5 mV change in membrane voltage is sufficient to represent speeds up to (7.18–6.42)/6.42B_H=30.76 cm/sec. Mean running speed in most experiments is around 20–25 cm/sec. Thus, the change in voltages necessary to code the range of normal running speeds of the rat is consistent with the voltage influence of synaptic inputs on a dendritic branch. Based on the mean values at −50 mV and −45 mV, the data has a slope of 0.152 Hz per mV. Linear fits to the frequency of oscillations at a range of different voltages give similar slopes of 0.20 Hz per mV for both dorsal and ventral neurons. Combining this data with the model indicates that the change per unit speed of the membrane potential of a component of a stellate cell should be about 0.125 mV*sec/cm. If it proves feasible to record intracellularly from awake behaving rats (Lee et al., 2006), then this is an experimentally testable prediction that can support this model relative to models of network attractor dynamics.

Analysis of the model suggests that the modulation of dendritic frequency should not occur in a stationary rat, in order to avoid changes in phase of a grid cell when a rat stops in the environment. Note that this does not necessarily require that head direction cell firing go to zero. It is possible that the activity of head direction cells at zero speed corresponds to the resting baseline frequency of the dendrite f, and positive speeds increase from this value. Another possibility is that the lack of frequency modulation for zero speed could be implemented by a threshold for oscillation frequency in the dendrite, that might be consistent with the lack of subthreshold oscillations at lower levels of depolarization. However, this would require some mechanism for maintenance of phase information during the period without oscillations, as the oscillations would need to start again at the correct phase. One mechanism for maintenance of phase would be the maintenance of oscillations on distal dendrites that would only be gated to the cell body when depolarizing input is applied on more proximal portions of the dendrite. This would be consistent with the role of proximal input in hippocampal region CA1 gating input activity of distal dendrites (Jarsky et al., 2005). If distal dendrites hold phase information even when proximal dendrites are not oscillating, this could underlie the theta frequency oscillations observed among distal dendrites in stratum lacunosum-moleculare of region CA1 during current source density analysis (Brankack et al., 1993). These oscillations do not appear to correlate in a clear manner with spiking activity in entorhinal cortex (Stewart et al., 1992; Brankack et al., 1993), but could simply reflect local maintenance of relative phase information that holds information about current location and position in a sequence. Thus, spatial location might be maintained in the form of the phase of large amplitude membrane potential oscillations on specific dendritic branches, due to interactions of the voltage sensitive persistent sodium current and h current. The presence of strong oscillations in distal dendrites in region CA1 would be consistent with the evidence that the density of h current increases on more distal dendrites in region CA1 (Magee, 1998). These density differences could interact with increases in other voltage-sensitive currents on distal dendrites (Magee et al., 1998). These data further support the hypothesis that dendritic oscillations play a role in theta phase precession (O’Keefe and Recce, 1993; Magee, 2001; Lengyel et al., 2003; Burgess et al., 2007). These models of intrinsic mechanisms for theta phase precession are related to other models that focus on the interactions between populations of neurons in mediating grid cell firing (Blair et al., 2007) and theta phase precession (Bose et al., 2000).

One difficulty with this current model concerns the sensitivity to variability or noise in the head direction input. Any noise in the speed or head direction input will cause a gradual drift from the correct tracking of location, which will accumulate over time. In the initial presentation of the model, Burgess proposed that this difficulty could be overcome by periodically resetting the correct phase of the model with place cell input (Burgess et al., 2005). This is important, as individual head direction inputs would provide a spike train (as opposed to a smooth continuous input used in this model) and individual head direction cells show variability in their inter-spike intervals (Taube, 2004).

Width and area of grid fields

The mathematical framework of the Burgess model also addresses the differences in width and area of grid fields observed in previous experimental work (Hafting et al., 2005; Sargolini et al., 2006). The width of the fields can be approximated by analyzing where the summed activity in equation 11 crosses zero. This will occur between −π/2 < 2πfB_Hx < π/2, or −1/4 fB_H < x <1/4 fB_H. This gives formulas for field diameter of 1/2fB_H and area π/(4 fB_H)² that explicitly describe the dependence of these parameters on the differences in intrinsic oscillation frequency along the dorsal to ventral axis of entorhinal cortex. This can be compared with the actual physiological data and used to compute the requirements for threshold of firing of individual neurons. The data shows an area of 350 square cm at the dorsal border and 650 square cm at 1 mm from the postrhinal border (Hafting et al., 2005). At the postrhinal border, the linear fit to frequency data gives a frequency of 7.9 Hz. Using the equation for zero crossings gives a grid field diameter of 16.4 cm and area of 212 sq cm which is small relative to the measured data. At 1 mm, the linear fit to frequency data gives f=4.5. For this frequency, the zero crossing formula gives a diameter of 28.9 cm and an area of 654 sq cm which matches the data well. The difference between the model predictions and the data in more dorsal areas could be compensated by a change in threshold, with a higher threshold in more dorsal regions. However, note that this computation was done with the scaling factor derived from spacing measurements in the Sargolini data whereas the width measurements were obtained from the Hafting data (Hafting et al., 2005) that differs from the Sargolini data (Sargolini et al., 2006) in the linear fit.

Differences in relative head direction selectivity

The initial model presented here uses input from three head direction cells with selectivity for head direction angles that differ by about 120 degrees. To replicate the observed properties of grid cells, the model has a strong requirement that the difference in angles of head direction preference be near multiples of 60 degrees. Figure 9 shows examples of the effect of input from head direction cells with different angles between preferred firing directions. The results primarily depend on the interval between preference angles. Similar patterns appear with different numbers of head direction cells. With 120 degree preference angle differences the model fires at the vertices of a grid of equilateral triangles (hexagons). With head direction cell inputs at a 90 degree difference in angle of preference, the cell fires in locations making a square grid. With six head direction inputs at 60 degree angle differences, the network fires in a pattern similar to the results with 120 degrees (the firing fields become slightly oval if smaller numbers of inputs are used (for example, 3 head direction inputs at 0, 60 and 120 degrees). With preference angle differences of 72, 45 or 30 degrees, the pattern of firing becomes more complex, but retains radial symmetry about the starting point (phase zero).

Two dimensional tracking of position can function somewhat even with just two head direction cells. However, with only two head direction cells as input, the grid cell misses firing on many trajectories through the correct grid fields, as shown in Figure 9B. Thus, two head direction inputs are not as accurate as three head direction inputs for consistently coding spatial location. Three head direction cells provide more reliable firing on every trajectory through an individual grid field. Larger numbers of head direction cells cause more frequent firing on a given trajectory, and cause the grid field to be larger because the product of multiple inputs gets to higher values and crosses threshold in a larger area. However, if the threshold is scaled with the number of head direction cell inputs, the firing field has the same shape and same reliability of firing within the field for many head direction inputs as for three head direction inputs, as long as the head direction cells have preference angles that fall predominantly at multiples of 120 degrees. Head direction preference data from neurons in deep layers of entorhinal cortex (Sargolini et al., 2006) does not show an overall selectivity for specific angles, but visual inspection of the responses in each local region shown in supplementary figure S5 suggests that they might fall predominantly at multiples of 60 degrees (e.g. in figure S5 B,D,E,G,H and K). There may be some mechanism for self-organization to strengthen synaptic connections between specific head direction cells and specific grid cells. The shift in orientation of single grid cells between different environments (Fyhn et al., 2007) could arise from the different orientation of head direction cells in different environments.

The influence of head direction cells in postsubiculum (dorsal presubiculum) on grid cells in superficial medial entorhinal cortex may be gated by cells in deep layers of medial entorhinal cortex. Deep layers show both head direction sensitivity and grid cell properties, and the postsubiculum (dorsal presubiculum) has been proposed to project to deep layers of entorhinal cortex (van Groen and Wyss, 1990), though other research shows projections of presubiculum primarily to superficial layer III (Kohler, 1985; Caballero-Bleda and Witter, 1993), with projections from parasubiculum to layer II. The deep layers of entorhinal cortex also receive input from hippocampal region CA1 that would allow synaptic modification to form associations between location (coded by place cells) and head direction input during movement along a trajectory. This could allow retrieval of a trajectory by reactivation of previous head directions in a given location that would then update phase activity to the sequentially encoded location that would then evoke retrieval of the next associated head direction to guide retrieval to the next encoded location. This iterative process could allow retrieval of full trajectories previously traversed in an environment. The encoding of the trajectory might need to be separated from retrieval by separate dynamics within theta rhythm oscillations (Hasselmo et al., 2002) or during different states of cholinergic modulation (Hasselmo, 2006).

Effect of network theta frequency on grid cell firing properties

The model described above uses different cellular frequencies at different positions along the dorsal to ventral axis of entorhinal cortex. However, at the circuit level, the network theta rhythm oscillation appears to be consistent at different positions in the entorhinal cortex and along the septo-temporal length of the hippocampus (Bullock et al., 1990; Sabolek et al., 2007). As shown in this section, this is not a problem for the Burgess model, because the differences in dendritic frequency will cause grid cell firing patterns even if the soma frequency is held fixed and only the dendritic frequency is altered.

Demonstration of the lack of sensitivity to network theta frequency requires a simple modification of the model. The model is modified to have a separate baseline frequency for the dendrites (f_D) that replaces fB_Hs with f_DB_Hs in equation 7, as follows:

$$g(t)=\mathrm{\Theta }[\prod _{HD}(cos(f2\pi t)+cos((f+f_D{B}_{H}scos(\phi -{\phi }_{HD}))2\pi t)+\varphi )]$$ (12)

This baseline frequency of the dendrites is the only frequency modulated by speed and head direction, while both the soma and the dendrite are also influenced by a separate non-modulated network frequency (f). The difference in the effect of these frequencies depends on which frequency is modulated by speed and head direction.

The grid cell field spacing always depends upon the beat frequency, which corresponds to the difference in frequency of the two oscillations: f_b=(f+f_D)−f which is simply f_D. Therefore, the grid cell spacing depends upon f_D alone, and is completely independent of the soma frequency f. In this case, grid spacing depends only on the baseline dendritic frequency f_D, as follows: $G(z)=2/(\sqrt{3}{B}_H{f}_D(z))$. Thus, grid cell firing depends on the relative phase of different dendritic oscillations. Figure 10A shows that the spacing and width of fields varies dependent upon the value of f_D even when the soma frequency f representing a constant network theta rhythm frequency remains the same in the simulations. Figure 10B shows separate simulations demonstrating that the spacing and width of grid fields stays the same when f_D is the same and does not vary significantly even when the soma frequency f is varied between values ranging from 0 Hz to 256 Hz. Thus, the variation in the intrinsic properties of individual neurons can determine the properties of grid cells independent of an influence of network theta rhythm oscillations.

Figure 10.

A. The simulated grid cell field spacing depends on the baseline frequency in dendrites (Dend), even when the frequency at the soma remains static at 6 Hz (Soma). Examples are shown for dendritic baseline frequencies of Dend=2, 3, 4, 5, 6 and 7 Hz. B. In contrast, the simulated grid cell field spacing does not depend on different soma frequencies, even when these are varied in a range between Soma=0 and Soma=256 Hz. The grid field spacing depends only on the dendritic frequency (Dend=6) which is modulated by speed and head direction.

Note that the difference in the functional role described for soma and dendrite in this analysis is dependent on which oscillation frequency is being modulated by speed and direction, as that oscillation will then influence grid cell spacing. In contrast, the grid cell properties will be affected if there is an influence of network theta rhythm on the modulation of speed and head direction, or if there is a difference in the baseline frequency of soma and dendrite. For example, if the dendritic oscillation frequency takes the form: f_d = f_D + f_DsB cos(φ − φ_HD), this will superimpose additional interference patterns on the grid cell firing pattern.

Sources of variation in grid cell firing

The Burgess model very effectively accounts for many of the basic properties of grid cell firing fields as reported in the experimental data, including spacing, orientation and spatial phase. As shown in Figure 2, for any grid cell, these properties can be matched by manipulating the parameters f (frequency) to affect spacing, φ_HD (head direction preference) to affect orientation) and ϕ (temporal phase) to affect spatial phase. The model makes experimentally testable predictions about how manipulations that affect these parameters should affect grid cell properties. For example, stimulation that causes reset of the temporal phase ϕ of a cell should have a corresponding effect on the spatial phase of that cell (particularly if visual cues are not available). This prediction contrasts with the prediction of network attractor models that assume a fixed pattern of synaptic connectivity that will be less sensitive to manipulations of the physiological properties of single neurons.

The data have tended to focus on grid cell firing patterns that are highly regular (Hafting et al., 2005; Sargolini et al., 2006; Fyhn et al., 2007), whereas many neurons in the entorhinal cortex do not show regular grid cell firing patterns (Sargolini et al., 2006). The model specifically predicts that other, less regular patterns would appear due to variations in both the angle of selectivity of the head direction input, as well as variation in the initial temporal phase of oscillations in different regions of an entorhinal stellate cell. The term initial phase refers to the vector of phase shifts ϕ of the different dendritic segments in equation 12, which would correspond to the timing of the peak of oscillations in different dendritic segments.

The effect of variation in the initial phase of oscillations on different dendritic segments is shown in Figure 11A. The effect of random variation in the angle of selectivity of head direction cell input is shown in Figure 11B2. Both types of variation cause characteristic patterns that deviate from normal grid field patterns. In particular, random variation in initial phase causes the appearance of small firing fields between the larger grid fields (as shown in Fig. 11A3). The intra-field firing fields can be large enough that the pattern of equilateral triangles (hexagons) is replaced by overlapping open hexagons without central firing fields, as shown in Figure 11A4. In fact, uniform initial phase shift of all oscillations causes this same pattern of open hexagons, as shown in Figure 11A5. Thus, the model makes a strong prediction that random variation in initial phase should cause some cells to fire with a pattern of open hexagons. Simulations of multiple different random combinations of initial phase show that the effects of random shifts in initial phase all appear as different gradations between the normal grid pattern and the open hexagon pattern shown in Figure 11A4 and A5. This pattern of open hexagons does not appear in any of the published data from the Moser laboratory, suggesting that oscillations within a single neuron do not undergo unstructured initial phase shifts of the type shown in Figures 11A3, A4 and A5.

Figure 11.

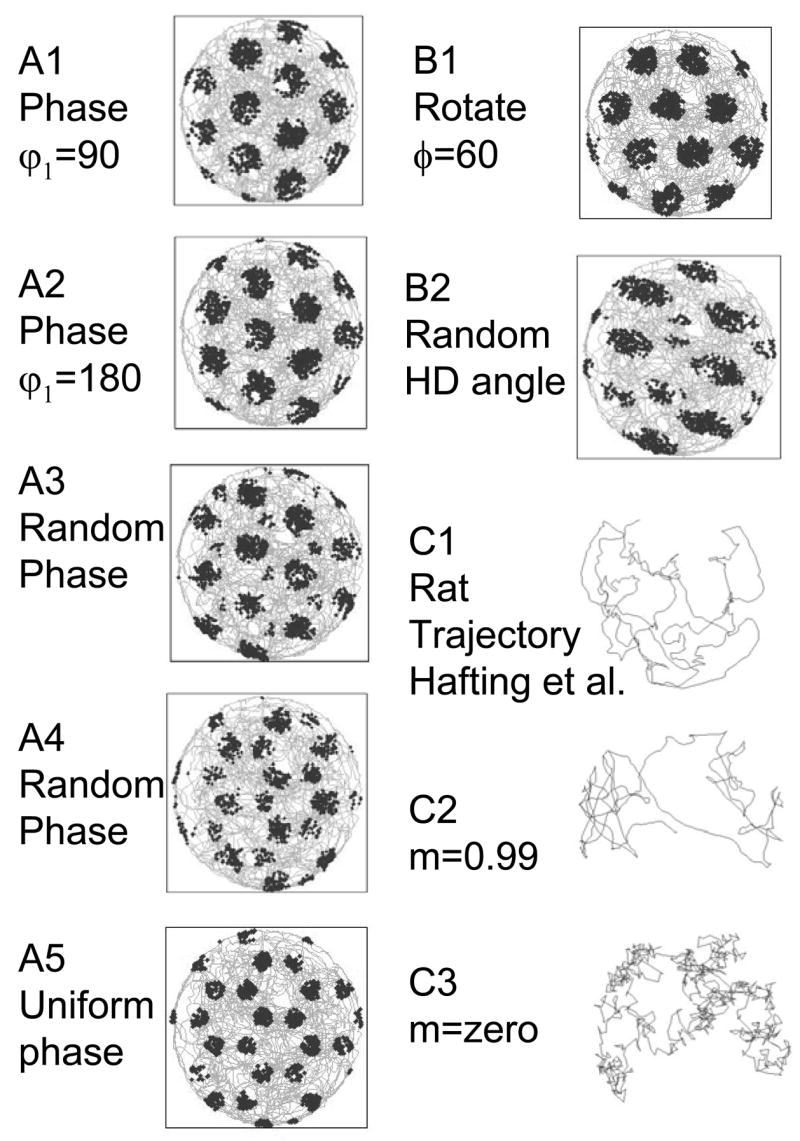
A. Examples of different grid cell firing patterns with manipulations of the phase of oscillations in different dendrites. A1. The grid field shows a 90 degree rightward translation with the following phase shift (in radians) for the dendrites ϕ_d = (π/2 −π/2 0). A2. Change in grid fields with phase shift of ϕ_d = (π −π 0) in radians. A3. Effect of random phase shifts ϕ_d = (2.8 0.1 5.2) in radians. A4. Effect of random phase shifts ϕ_d = (5.3 3.3 1.3) in radians that resembles the effect of a uniform phase shift. A5. Effect of uniform phase shift of ϕ_d = (π π π). B1. Rotation of grid fields with addition of 60 degrees (π/6 radians) to each HD cell angle. B2. Effect of input from HD cells with random selectivity angles of φ_HD = (4.4 3.9 5.0). C1. Plot of the trajectory of a real rat from the experimental data by Hafting et al. (2005). C2. Trajectory of the virtual rat with momentum set at m=0.99. C3. Trajectory of the virtual rat with no momentum (m=0), showing the abrupt direction shifts that do not resemble the real rat trajectory.

In contrast, the initial phase shift of oscillations in the different dendritic branches causes a simple translation of the grid if the initial phase shift in different dendritic segments maintains the same relationship as head direction cells: ϕ = (bcos(φ − 0) b cos(φ −120) b cos(φ − 240)) where b is the magnitude of the shift and φ is the direction angle. Examples of translations caused by these structured initial phase shifts are shown in Figures 11A1 and 11A2 and Figure 12. Figure 12 shows that spatial translation in the horizontal direction with magnitude b and vertical direction with magnitude a can be obtained with the initial phase shift vector: $\varphi =\left(b\mathrm{\hspace{0.17em} }\sqrt{3}a/2-b/2\mathrm{\hspace{0.17em} }-\sqrt{3}a/2-b/2\right)$. These types of initial phase shifts could underlie the translations that appear between cells or for a single cell in different environments in the data from the Moser laboratory. This suggests that the initial phases of individual dendrites within grid cells are somehow scaled to the head direction inputs received by those dendrites.

Figure 12.

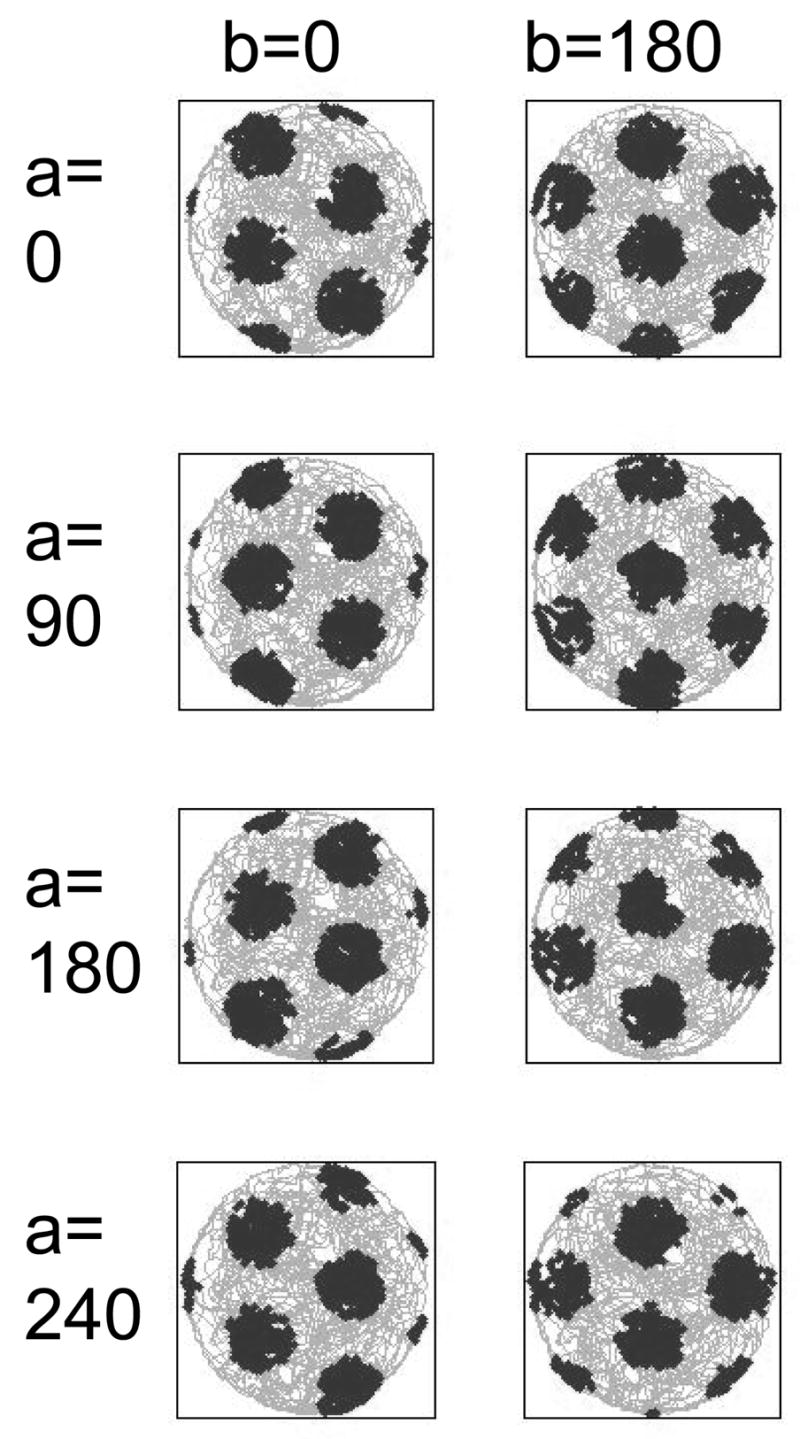
Effect of systematic initial phase shifts on grid cell firing patterns using different values of a and b in the formula for translation of grid fields in horizontal (b) and vertical (a) directions. The two columns show the effect of simultaneously setting b at 0 or 180 degrees (0 or π radians). The four rows show the effect of phase shifts using a=0, 90, 180 and 240 degrees (0, π/2, π, 3π/2 radians).

A uniform shift in the angle of selectivity of all head direction cells will cause a simple rotation of the grid field. For example, Figure 11B1 shows the effect of the following HD cell angles: φ_HD = (0 +π/6 π/3 +π/6 2π/3 +π/6). However, if the angle of selectivity of head direction cells appears at irregular intervals, this often causes a different type of pattern in the firing response, in which individual grid fields become elongated in one dimension and become intermixed with smaller grid fields in a less regular firing pattern. For example, Figure 11B2 shows the grid pattern for φ_HD = (4.4 3.9 5.0). These preference angles of head direction input cause grid cell firing fields to have an elongated, fusiform shape. This resembles the pattern of neural firing seen in some data from the Moser lab (Hafting et al., 2005), including cells t5c1 and t7c2 in Figure S7 and cell t1c2 in Figure S4. Thus, it appears that in the entorhinal cortex, head direction preference may show more variability than temporal phase of oscillations. More extensive analysis of less regular grid cell firing fields in the experimental data could further test these predictions of the model.

The model predicts that complete loss of head direction input due to a lesion of the postsubiculum ought to greatly impair grid cell activity (and place cell activity) in a novel environment, but would not prevent grid cell activity from being updated by place cell input in a familiar environment. In a familiar environment, the interaction of place cells and grid cells might be sufficient to perform path integration and maintain consistent place cell firing location, as observed in studies of place cells after postsubiculum lesions which show similar numbers of place cells with some increases in outfield firing in a familiar environment (Calton et al., 2003). As discussed in that article, the place cell firing could also result from head direction input from other regions. However, the loss of head direction input could prevent resetting of the orientation of grid cells (and place cells) when visual cues are rotated. This is consistent with the unpredictable rotation of place fields and greater loss of place field firing during rotation of visual cues after postsubiculum lesions (Calton et al., 2003). The effect of postsubiculum lesions on grid cell and place cell firing should be tested in novel environments.

DETAILS OF SIMULATION OF GRID CELLS

As shown in the figures, the grid cell model by Burgess et al. (Burgess et al., 2005; Burgess et al., 2007) was used to simulate the properties of grid cells dependent upon the frequency of intrinsic subthreshold membrane potential oscillations. The model was simulated using MATLAB. Figure 2 demonstrates how effectively this model addresses properties of experimental data on grid cells. This section describes in detail how the parameters of the model were set to match the experimental data.

Algorithm for random rat exploration

The script can be used to simulate the oscillatory activity within a single stellate cell as a virtual rat explores an environment. In simulations the change in spatial location is represented by the change Δx, Δy in spatial coordinates. In the simulations shown in some figures, the virtual rat followed the real trajectory of a rat from experimental data on a study of grid cells made available on line at www.cbm.ntnu.no by Hafting and Fyhn in the Moser lab (Hafting et al., 2005). The data had a time step of Δt=0.020 sec, and movements were computed by subtracting sequential locations: Δx=x(t)−x(t−1) and Δy=y(t)−y(t−1).

In other cases, the virtual rat explored the environment guided by an algorithm simulating random movement with a momentum term. This used the following equations for movement:

$$\mathrm{\Delta }x(t)=S(1-m)p+m\mathrm{\Delta }x(t-1)$$ (13)

$$\mathrm{\Delta }y(t)=S(1-m)p+m\mathrm{\Delta }y(t-1)$$ (14)

Where Δx and Δy are changes in location from time t−1 to time t (using a time step of Δt=0.020 sec), S is an average step size (set at 5), m is the momentum term (set at 0.99), and p is a random number selected separately for x and y on each step from a normal distribution with mean 0 and standard deviation 1. If the virtual rat generated a movement across a barrier in a dimension, then the movement in that dimension was replaced with a reversed form of the same step Δx_r (t) = −RΔx(t), where the reverse step size R was set at 0.5. This ensured that the virtual rat moved away from barriers without clinging to the barrier constantly. As shown in Figure 11C, use of the momentum term in these equations gave behaviour that showed smooth changes in direction and covered the environment effectively as in studies of open field behaviour that use random presentation of food reward in the environment to ensure extensive exploration throughout the environment (Muller et al., 1987; Hafting et al., 2005). During initial exploration of a novel environment, a real rat will follow walls, and simulation of this might require the reverse step size R to be smaller.

Computation of frequency change

For simulation of the effect of head direction input on dendritic oscillation frequency, the movement in Cartesian coordinates was represented in the polar coordinates of a speed-modulated head direction cell. Thus, the heading angle of the virtual rat was computed as φ = arctan((Δy/Δt)/(Δx/Δt)) and the speed of the virtual rat was computed as $s=\sqrt{{(\mathrm{\Delta }x/\mathrm{\Delta }t)}^2+{(\mathrm{\Delta }y/\mathrm{\Delta }t)}^2}$. The effect on dendritic oscillation frequency was then be computed as shown in equations 6 and 7.

An important feature to remember for the implementation of this model is that phase is varying continuously due to frequency changes. It is incorrect to try to simulate this using regular time intervals and simply plugging the change of frequency into equation 7, as this will compute the oscillation at time t as if that frequency were present since the start of the simulation, giving an incorrect phase. Instead, our implementation of the model uses the updated frequency on each time step to separately update the phase of each membrane potential oscillation, using the relationship: Δϕ_i = f_i (2πΔt). Because the frequency varies over time, the phase must be computed as $\varphi (T)={\displaystyle \sum _{i=1}^T}{f}_i(2\pi \mathrm{\Delta }t)$, where T represents current time and i represents individual time steps. For continuous time this corresponds to the integral over the frequency function f(t) (which depends on velocity).

Starting position or phase determines translation of grid

In the simulations, the position of the grid fields within the environment depends upon the initial starting position of the virtual rat. This occurs because the simulation starts with all dendritic and somatic oscillations in phase with each other, so that the simulated stellate cell is firing. The regular grid pattern then forms relative to this position. In the simulations shown in Figure 2, the starting position was chosen to match the translation of grid fields, with starting positions x=−4, y=−8 in Figure 2B1 and x=15, y=30 in Figure 2B2. This property of the model makes the prediction that in a novel environment, the starting position of the rat should determine the translation of the grid field relative to the environment. As noted above, the translation of the grid can also be altered by setting the initial phase of the different dendritic compartments receiving different head direction inputs. The phase shift can cause a simple translation of the grid pattern, but the phase shift must maintain a relationship such as that shown in Figure 12 or there will be a loss of internal consistency of grid cell firing as shown in Figure 11A. The effect of random shifts in phase is discussed above.

Orientation of head direction cells determines rotation of grid

In the simulations, the orientation of the grid field depends upon the absolute orientation of the head direction cells. In most simulations, the head direction cells were given angles of preference falling at 120 degree intervals. To match the rotation of grid fields in Figure 2, all three head direction cells are offset by an additional angle of pi/5 in 2B1 and by -pi/15 in 2B2. This property of the model predicts that in a novel environment, the set of head direction cells giving input to a particular set of grid cells should be flexibly selected to have different preferred directions in different environments, but to maintain differences in preferred angle at multiples of 60 degrees, because the cells in a specific region tend to show shared rotational preference of grid firing. This suggests that the orientation selectivity of head direction cells providing input to a specific region of entorhinal cortex are not fixed, but are selected by initial conditions in a new environment. Previous studies have shown that there is little or no change in the direction preference and firing rate of individual head direction cells in the postsubiculum during transitions into novel portions of an environment (Taube and Burton, 1995). Therefore, it is possible that this flexibility depends upon the head direction selectivity of cells in deeper layers of entorhinal cortex, that could shift their overall preference dependent upon initial conditions and feedback from the hippocampus. These cells could mediate between the more fixed head direction selectivity of neurons in the postsubiculum (Taube et al., 1990b; Sharp et al., 2001a; Taube and Bassett, 2003) and the more flexible capacity of grid cells to rotate between different environments. Alternately, it is possible that the head direction input for a given entorhinal region is fixed, and the difference between environments reflects a different orientation of the head direction system in that environment.

Use of cosine function versus rectified cosine function

The mathematical description of the model analyzed here primarily uses a representation of head direction with a cosine function of heading angle versus preferred HD cell angle. However, the simulation of the model was primarily performed with a rectified version of the cosine function. In this form, the head direction input does not go negative, which is consistent with the fact that most head direction cells show increases in firing rate from very low background activity (Taube et al., 1990a) and appear to be excitatory principal neurons. In the rectified cosine model, a single cosine function input to each dendritic branch is replaced with two rectified cosine functions to different sub-branches of a single branch coming off the soma. This requires six head direction cell inputs (e.g. at 0, 60, 120, 180, 240 and 300 degrees) and also requires pairing of dendritic inputs from head direction cells with opposite angles of selectivity (e.g. 0 and 180 degrees). In this version of the model, when the virtual rat is moving in direction 0 degrees, the head direction cell coding 0 degrees is fully active, and the head direction cells coding 60 or 300 degrees show half activity, whereas the cells coding 120, 180 and 240 degrees are inactive. The use of rectified cosines has the additional advantage of making simulated phase precession show the correct shift in phase relative to the movement of the rat through its firing field as described by Burgess (Burgess et al., 2007). However, the use of rectified cosines does not fully match head direction firing functions which are triangular and show a 90 degree range that is narrower than the 180 degree range of a cosine function (Taube et al., 1990a).

IMPLICATIONS FOR CODING OF CONTINUOUS TIME

Potential mechanisms for coding of continuous time

Interference between dendritic oscillations can also code for continuous time, or for the temporal duration of the presence of specific stimuli. This framework is actually simpler than coding for continuous space because it does not require a transformation from temporal to spatial dimensions. Instead, the interference pattern can function in the temporal domain alone. Interference could provide a general clock, but it is more likely to provide associative timing of intervals between different events in the environment. Previous publications have proposed a role for the hippocampus in forming associations between stimuli which are separated by intervals in both time and space (Rawlins, 1985; Wallenstein et al., 1998). The ability to represent and encode continuous temporal intervals could underlie the role of hippocampus in specific behavioural memory tasks, including both trace conditioning and episodic memory.

Lesions of the hippocampus have been shown to impair trace conditioning (Yoon and Otto, 2007), and the presence of theta rhythm oscillations in the hippocampus correlate with the ability to encode trace conditioning (Griffin et al., 2004) as well as delay conditioning (Berry and Seager, 2001). Lesions of the entorhinal cortex also impair trace conditioning (Mering and Butenko, 1982; Ryou et al., 2001), though an early study did not see such impairments (Yeo et al., 1984). In trace conditioning, hippocampal unit responses start out responding during the trace period and become timed to occur just before the conditioned response (Hoehler and Thompson, 1980; Solomon et al., 1986). These unit responses shift to fire at a new interval before behavioural responses shift to a new interval. Hippocampal lesions appear to shift the timing of the conditioned response (Port et al., 1986; James et al., 1987). Based on this research, extensive modelling addressed the possible role of the hippocampus in adaptive timing of responses to conditioned stimuli (Grossberg and Merrill, 1992; Rodriguez and Levy, 2001; Gorchetchnikov and Grossberg, 2007). Extensive models also focused on the role of the cerebellum in this process (Mauk et al., 2000). These previous models focused on network dynamics to provide the long delays necessary to learn intervals on the order of 500 msec. In contrast to these models of network dynamics, the interference of subthreshold oscillations can provide selective timing mechanisms at a single cell level that can implement learning of intervals at many times the order of magnitude of the subthreshold oscillations themselves. This could include the much longer intervals at which hippocampal lesions cause impairments for fear conditioning (Chowdhury et al., 2005).

This framework indicates why the hippocampus is particularly important for trace conditioning. The data suggest that the hippocampus is especially important when there is a stimulus-free delay between the termination of the conditioned stimulus and the onset of the unconditioned stimulus. The role in timing of trace conditioning could reflect an interaction of the subthreshold oscillatory characteristics with mechanisms for the persistent firing of individual neurons in entorhinal cortex (Klink and Alonso, 1997; Egorov et al., 2002; Fransén et al., 2006; Hasselmo and Stern, 2006). In delay conditioning, sensory input could drive the timing of an interval. In contrast, trace conditioning would require some neural mechanism for indicating that a conditioned stimulus had occurred, to initiate and maintain the timing until the conditioned response. In this framework, a CS would induce firing activity in entorhinal cortex pyramidal cells, which would maintain persistent firing even after termination of the CS. The input from these entorhinal pyramidal cells to entorhinal stellate cells would drive the subthreshold oscillations which would show interference with different time periods depending on the baseline frequency and voltage sensitivity of individual neurons. Stellate cells would fire at multiple different intervals after the onset of the pyramidal cell input. These stellate neurons would form stronger excitatory inputs to the hippocampus due to Hebbian modifications of connections between firing stellate neurons and the neurons in the hippocampus showing spiking response to the unconditioned stimulus (Berger and Thompson, 1978; Hoehler and Thompson, 1980; Berger et al., 1983). Subsequent presentation of the same CS will activate persistent firing in the same pyramidal cells. These cells would drive stellate cells to fire at varying intervals, and those with strengthened connections would drive the hippocampus units that predict in advance the timing of the conditioned response (Hoehler and Thompson, 1980; Solomon et al., 1986). These mechanisms provide a potential mechanism for coding of long temporal delays which could be complementary to the delayed timing of firing shown for some pyramidal and non-pyramidal cells in perirhinal cortex (Beggs et al., 2000; McGann et al., 2001).

Relationship to mechanisms of episodic memory function

The mechanisms for computing timing intervals described above is also relevant to the encoding and retrieval of episodic memories. Episodic memories consist of series of events that are spatially and temporally discontiguous. The events do not occur at regular intervals, and in fact features of the episode will start and stop at different overlapping times. For example, consider the memory of a conversation in which different people enter and leave the conversation at different times. At any one time, there are multiple different people involved in the conversation.

Previous work has already shown that sequences are not effectively encoded by simple chaining of the component events. Chaining of memories would involve sequential linking from event A to B to C to D. However, data indicates that one element (e.g. B) can be lost, or recalled out of order (e.g. switching of B and C) without losing memories for later items in the sequence (e.g. D) (Burgess and Hitch, 2005). Thus, there must be some redundant means of encoding the temporal relationships of the stimuli, for example A seems to be associated separately with individual time intervals for B, C and D. This could be provided by an external clock, but it is more likely that the memory for intervals is relative, that is, that an interval is timed relative to the onset of a previous stimulus.

The encoding of time intervals between each item in a sequence and other items in the sequence can be provided by the interaction of persistent firing in entorhinal pyramidal cells, and interference between subthreshold dendritic oscillations in stellate cells. Specifically, each event in an episode (e.g. appearance of item A) could initiate persistent firing in a set of pyramidal cells. This persistent firing drives a set of stellate cells with different intrinsic interference properties, causing these stellate cells to fire at varying intervals after onset of input. One set of stellate cells might fire at 3 seconds, when item B appears, and become associated with appearance of item B. Another set of stellate cells might fire at 7.5 seconds, and become associated with appearance of item C. And another set might fire around 8.2 seconds, and become associated with appearance of item D. This framework allows cueing of the sequence with item A, and retrieval of items B, C and D by different stellate cells firing at the correct relative intervals. Failure to retrieve item B does not affect retrieval of items C or D.

Dendritic oscillations and theta rhythm field potential oscillations

As noted above, the dendritic oscillations that form the basis for the model would also appear as theta rhythm oscillations in the field potential. The subthreshold oscillations involve oscillations in the magnitude of cross-membrane currents that would appear as oscillations in the field potential and oscillatory changes in current sources and sinks in current source density analysis. The subthreshold oscillations would have a range of different phases and frequencies, but across the population the oscillations could have sufficient coherence to contribute to theta rhythm oscillations in the entorhinal cortex (Mitchell and Ranck, 1980; Mitchell et al., 1982; Alonso and Garcia-Austt, 1987a; Alonso and Garcia-Austt, 1987b) and in subregions of the hippocampal formation (Buzsaki et al., 1983; Brankack et al., 1993; Hasselmo, 2005). In particular, the model shows that consistency of network oscillations does not interfere with the computation of individual neurons. Within a population of neurons, the oscillations at the soma can have a single fixed frequency f, while the dendrites can have different baseline frequencies f_D. For modelling of grid cells, the spacing of grid fields depends on the dendritic baseline frequency f_D independently of the soma frequency, and the computations for grid fields depends only on the difference between the dendritic frequencies. Thus, the network can manifest a field potential oscillation caused by synchrony among neurons that does not interfere with computation by individual neurons.

The field potential effects could be modelled by simulating the currents underlying the subthreshold oscillations. Models of the subthreshold oscillations utilize the persistent sodium current (NaP), an inward current, interacting with either a reduction in the hyperpolarization activated h-current (causing reduced inward current) (Dickson et al., 2000; Fransen et al., 2004) or an increase in a depolarization activated potassium current such as the M-current (causing increased outward current) (White et al., 1995). In either case, the subthreshold oscillations would correspond to an oscillation in net membrane current. Though recordings at the cell body show relatively small amplitude of oscillations, the oscillation amplitude could be considerably higher on distal dendrites, as the density of the h-current increases on more distal dendrites (Magee, 1998), and dendritic oscillations will not be interrupted by fast somatic oscillations. Membrane potential oscillations due to interactions of persistent sodium and H current could involve amplitudes of tens of millivolts. Summed across the dendrites of a full population of pyramidal cells, these currents could be substantial enough to cause the large current sources and sinks appearing in stratum lacunosum-moleculare of region CA1 and the outer molecular layer of the dentate gyrus (Buzsaki et al., 1983; Brankack et al., 1993; Hasselmo, 2005). This could explain the presence of large rhythmic current sinks in stratum lacunosum-moleculare that appear out of phase with most rhythmic firing of principal neurons in entorhinal cortex (Stewart et al., 1992; Brankack et al., 1993). These oscillations of membrane potential in the distal dendrites of pyramidal cells could play a role in maintenance of phase information even when there is no spiking activity at the soma.