Spatial organization and state-dependent mechanisms for respiratory rhythm and pattern generation

Abstract

The brainstem respiratory network can operate in multiple functional states engaging different state-dependent neural mechanisms. These mechanisms were studied in the in situ perfused rat brainstem–spinal cord preparation using sequential brainstem transections and administration of riluzole, a pharmacological blocker of persistent sodium current (I_NaP). Dramatic transformations in the rhythmogenic mechanisms and respiratory motor pattern were observed after removal of the pons and subsequent medullary transactions down to the rostral end of pre-Bötzinger complex (pre-BötC). A computational model of the brainstem respiratory network was developed to reproduce and explain these experimental findings. The model incorporates several interacting neuronal compartments, including the ventral respiratory group (VRG), pre-BötC, Bötzinger complex (BötC), and pons. Simulations mimicking the removal of circuit components following transections closely reproduce the respiratory motor output patterns recorded from the intact and sequentially reduced brainstem preparations. The model suggests that both the operating rhythmogenic mechanism (i.e., network-based or pacemaker-driven) and the respiratory pattern generated (e.g., three-phase, two-phase, or one-phase) depend on the state of the pre-BötC (expression of I_NaP-dependent intrinsic rhythmogenic mechanisms) and the BötC (providing expiratory inhibition in the network). At the same time, tonic drives from pons and multiple medullary chemoreceptive sites appear to control the state of these compartments and hence the operating rhythmogenic mechanism and motor pattern. Our results suggest that the brainstem respiratory network has a spatial (rostral-to-caudal) organization extending from the rostral pons to the VRG, in which each functional compartment is controlled by more rostral compartments. The model predicts a continuum of respiratory network states relying on different contributions of intrinsic cellular properties versus synaptic interactions for the generation and control of the respiratory rhythm and pattern.

Introduction

Breathing movements in mammals are produced by the respiratory central pattern generator (CPG). The network architecture and neural mechanisms for rhythmic pattern generation in most CPGs in the vertebrate brain are not well understood and are under intense investigation (Grillner et al., 2005). In the mammalian respiratory CPG, rhythm generation appears to involve multiple complex, nonlinear, cross-level interactions of cellular, network and systems-level mechanisms. Because of these nonlinear interactions, the respiratory CPG can operate in multiple functional states engaging and integrating different cellular and network mechanisms. Revealing these complex interactions and state-dependent reorganizations of neural circuits involved in rhythm generation would have a broad impact on our understanding of the key principles of brain/neural control of movements, and especially control of rhythmic movements and processes. Our goal was to investigate the spatial and functional organization of the mammalian respiratory CPG and the neuronal circuits and mechanisms underlying the state-dependency of the rhythm and pattern generation.

The respiratory cycle in mammals consists of two major phases: inspiration (I) and expiration (Cohen, 1979; Euler, 1986; Feldman, 1986). Expiration in turn comprises two phases, post-inspiration (post-I or E1) and active expiration (E2). Therefore, during eupnea (normal breathing), the respiratory motor activity appears to have a three-phase pattern, i.e., contain three phases: I, post-I, and E2 (Richter and Ballantyne, 1983; Richter, 1996), which can be recognized in the integrated activities of the phrenic (PN) and cranial (e.g., laryngeal) nerves. Respiratory neurons are usually classified based on their firing pattern (e.g., decrementing, augmenting) and the phase of activity relative to the breathing cycle, e.g., early-inspiratory (early-I) with decrementing inspiratory pattern; ramp-inspiratory (ramp-I) with augmenting inspiratory pattern; post-inspiratory (post-I) or decrementing expiratory (dec-E); augmenting or stage II expiratory (aug-E or E2); pre-inspiratory (pre-I), etc. (see Richter, 1996, for review).

The location of the respiratory CPG in the lower brainstem was established in vivo using a combination of anatomical and physiological approaches including lesions at different levels of the brainstem and spinal cord. It was shown that the generation of eupnea involves several respiratory regions in the medulla and pons (Lumsden, 1923; Cohen, 1979; Euler, 1986; Feldman, 1986, see Fig. 1A, B). The major concentration of bulbospinal respiratory neurons (projecting to the spinal motoneurons) are found in a region called “the ventral respiratory group” (VRG) located in the ventrolateral medulla. This region is subdivided into the rostral (rVRG) and caudal (cVRG) parts (Fig. 1A, B). The premotor (bulbospinal) inspiratory neurons are dominantly present in rVRG, whereas the bulbospinal expiratory neurons dominate in cVRG. Rostrally to rVRG, there is a region known as the pre-Bötzinger Complex (pre-BötC) that was shown to be a major source of endogenous (inspiratory) rhythmicity in vitro (Smith et al., 1991, 2000; Rekling and Feldman, 1998). More rostrally there is the Bötzinger Complex (BötC), a compact cluster of cells that is considered a principal source of expiratory inhibition within the network (Ezure, 1990; Jiang and Lipski, 1990; Tian et al., 1999). The pontine respiratory regions include the Kölliker–Fuse (KF) nucleus and parabrachial (PB) complex (lateral, LPB, and medial, MPB, nuclei) in the dorsolateral pons and several areas in the ventrolateral pons (see Fig. 1A). The specific role of pontine structures in the generation and control of the respiratory pattern has hitherto not been well defined. However, the pontine structures appear to have specific interactions with multiple medullary compartments, and the pons as a whole provides strong modulation of the medullary respiratory network via tonic and/or respiratory modulated drives (St.-John, 1998; Alheid et al., 2004). In addition, several medullary structures, specifically the retrotrapezoid nucleus (RTN, located rostrally to BötC below the facial nucleus) and the medullary raphe nucleus, both involved in the central chemoreception, also modulate the medullary respiratory network performance via various drives defining the metabolic state of the system (the level of oxygen and carbon dioxide, pH, etc.) (Mulkey et al., 2004; Guyenet et al., 2005).

Fig. 1.

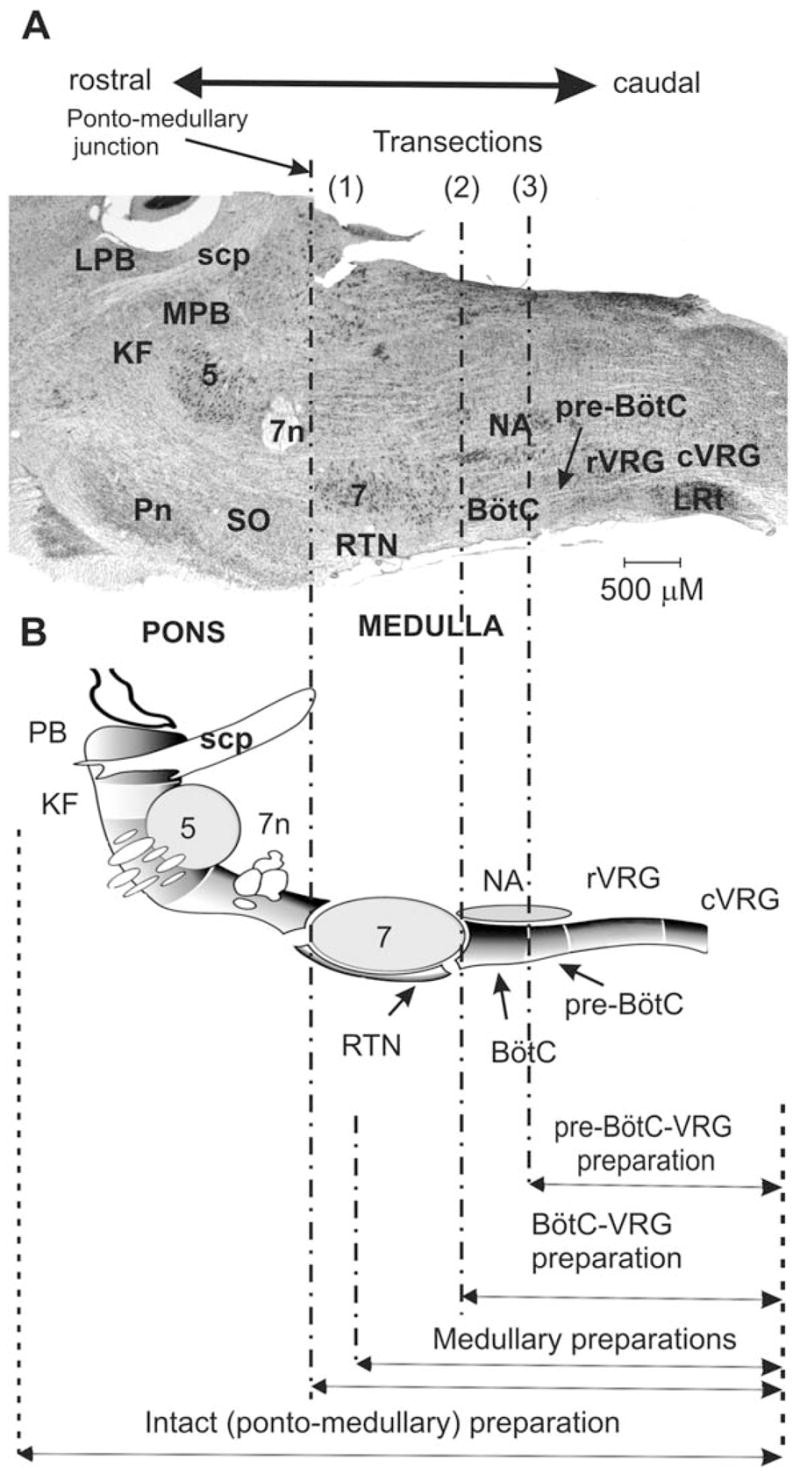
Parasagittal view of rodent brainstem (section through the level of the compact part of nucleus ambiguus) and spatially arrayed compartments of respiratory CPG network. (A) Respiratory-related ponto-medullary regions in the mature rat brainstem with several transection planes (dot-dashed lines) used in experimental studies. (B) Corresponding schematic diagram of respiratory-related brainstem compartments in parasagittal section of rat brain (created by George Alheid and used with permission) with transactions and resultant reduced preparations indicated at the bottom. Abbreviations: 5 – trigeminal nucleus; 7 — facial nucleus; 7n — facial nerve; BötC — Bötzinger Complex; cVRG — caudal ventral respiratory group; KF —Kölliker–Fuse nucleus; LPB — lateral parabrachial nucleus; LRt: lateral reticular nucleus; MPB — medial parabrachial nucleus; NA — nucleus ambiguus; PB — parabrachial nuclei; Pn —pontine nuclei; pre-BötC — pre-Bötzinger Complex; RTN —retrotrapezoid nucleus; rVRG — rostral ventral respiratory group; scp — superior cerebellar peduncle; SO — superior olive.

Despite a long history of studies there is still no commonly accepted view on the neural mechanisms for respiratory rhythm generation. Proposed mechanisms have been mostly based on particular sets of data obtained from different preparations (decerebrate and/or vagotomized in vivo, arterially perfused in situ brainstem–spinal cord, in vitro isolated brainstem–spinal cord and/or slices from neonatal rodents), which operate under different, often abnormal, metabolic conditions or have significantly reduced circuitry. We believe that the ongoing debate (e.g., Feldman and Smith, 1995; Richter, 1996; Smith et al., 2000; Feldman and Del Negro, 2006) about whether rhythm generation normally is a “pacemaker-driven” or an “emergent” network process has been posed as a mechanistic dichotomy that is largely artificial and requires reframing to take into account the multiple nonlinear state-dependent interactions and potentially different rhythmogenic mechanisms that may emerge and operate in different states. Indeed, we believe that the rhythmogenic mechanism is strongly dependent on the system’s state, external inputs, metabolic conditions, etc. Changing these interactions or full elimination of some interactions in reduced preparations by removing part of the network may alter the operating rhythmogenic mechanism and the respiratory pattern generated. For example, the pre-BötC isolated from slice preparations in vitro can intrinsically generate rhythmic inspiratory activity. The rhythm generation in this reduced network involves a persistent sodium current-dependent cellular mechanism operating in the context of an excitatory network (Butera et al., 1999a, b; Koshiya and Smith, 1999; Johnson et al., 2001). However, in the intact system, the pre-BötC is embedded within a wider respiratory network, and its state, operating conditions, and functioning may alter by, and depend on, the excitatory and inhibitory inputs from other parts of the network (Smith et al., 2000; Rybak et al., 2002, 2004a).

Although most respiratory regions are not homogenous and may contain multiple neuron types, a consideration of the neuronal types that predominate in each region leads to the suggestion that the respiratory CPG has a specific functional and spatial organization within the brainstem “respiratory column” that extends in the rostral-to-caudal direction from the pons to the VRG. To test this hypothesis we developed an approach allowing sequential reduction of the respiratory network using highly precise brainstem transactions to remove particular respiratory regions and investigation of the resultant reorganization of the rhythm-generating mechanism by studying alterations in the firing patterns of different neuronal population and motor outputs. Using this approach, we have revealed novel insights into the topographical organization and state-dependency of brainstem mechanisms for respiratory rhythm and pattern generation.

Experimental studies

The experimental studies were performed using the in situ perfused brainstem–spinal cord preparation of the juvenile rat (Paton, 1996). The cranial and spinal nerves in this preparation exhibit discharge patterns similar to those recorded in vivo during eupnea and under different experimental conditions (St.-John and Paton, 2000). A particular advantage of this preparation is that it allows precise control of the perfusion of the brainstem combined with independent control of oxygen and carbon dioxide concentrations in the artificial perfusate. This is crucial when the transections of the brainstem are applied which in vivo would cause hemorrhage leading to brain ischemia. Another advantage is that this preparation allows for administration of pharmacological agents through the perfusate that would be incompatible with viability of in vivo preparations. Juvenile Wistar rats (80–100 g, approximately 4–6 weeks of age) were used. Recordings were obtained from PN, central vagal (cVN), and hypoglossal (XII) motor nerves simultaneously. All procedures were described in detail previously (Paton, 1996; St.-John and Paton, 2000; St.-John et al., 2002; Paton et al., 2006).

The proposed spatial organization of the respiratory CPG defined the experimental approach we adopted. We sequentially reduced the brainstem respiratory network by a series of brainstem transections, starting from a transection at the ponto-medullary junction and continuing with parallel transections though the medulla with the cutting plane sequentially shifted to a caudal direction. The transections were performed by a special, custom-made, piezo cutting and x-y-z translation system, allowing precision microsectioning of the brainstem. The precise level of transactions was confirmed histologically post hoc. After each transection, the resultant alterations in the discharge patterns of the PN, cVN, and XII motor nerves were investigated. Riluzole (3–20 μM), a pharmacological blocker of persistent sodium current (I_NaP), was applied to the perfusate in the intact and each reduced preparation to determine a role of I_NaP for rhythm generation in each given preparation.

The first (most rostral) transection of the brainstem was usually made at the ponto-medullary junction [indicated in Fig. 1 by (1)], which removed the pons. This transection was followed by a series of parallel transections applied by sequential shifting the position of the cutting plane to a caudal direction. These medullary transections went through the facial nucleus (indicated by “7” in Fig. 1) and sequentially removed rostral parts of the medulla. We called the remaining caudal parts the “medullary” preparations (see Fig. 1). The transection at the rostral end of BötC [indicated in Fig. 1 by (2)] reduced the original, intact preparation to a “BötC–VRG” preparation. Finally, a transection was made at the rostral end of pre-BötC [indicated in Fig. 1 by (3)], which produced a “pre-BötC–VRG” preparation. Note that no rhythm could be evoked if a transection was made caudal to pre-BötC.

Figure 2A shows an example of PN, XII, and cVN nerve activities recorded from the intact preparation (containing a complete ponto-medullary circuitry). The discharge patterns of these nerves have the following characteristics, which are also typical for a three-phase eupneic respiratory rhythm recoded in vivo (Duffin, 2003; St.-John and Paton, 2003): (i) the PN bursts have an augmenting shape (the spike frequency increases during the burst); (ii) the onset of the XII bursts usually precedes (50–100 ms) the onset of PN bursts (i.e., XII bursts have a pre-I component); and (iii) the cVN bursts include a prominent decrementing post-I activity.

Fig. 2.

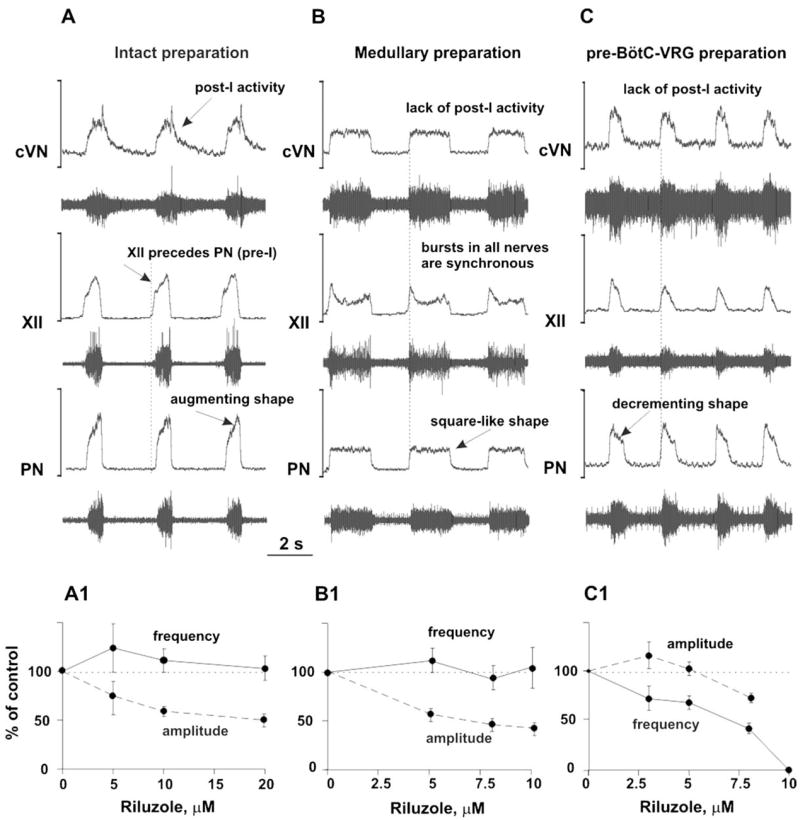
(A–C) Activity patterns of phrenic (PN), hypoglossal (XII), and central vagus (cVN) nerves from the intact (A), medullary (B), and pre-BötC–VGR (C) preparations. Each diagram shows the recorded (bottom trace) and integrated (upper trace) motor output activities. See text for details. (A1–C1) Dose-dependent effects of I_NaP current blocker riluzole on the frequency (solid lines) and amplitude (dashed lines) of PN bursts in the intact (A1), medullary (B1), and pre-BötC–VGR (C1) preparations. Riluzole in the concentrations shown in horizontal axes was added to the perfusate. Note that the frequency of PN bursts does not significantly change in the intact and medullary preparations (A1 and B1), but dramatically decreases with riluzole concentration in the pre-BötC–VGR preparation and, finally, the PN activity was abolished at riluzole concentration of 10 μM (C1).

Brainstem transections between the ponto-medullary junction [indicated in Fig. 1 by (1)] and the rostral border of BötC [indicated in Fig. 1 by (2)] removed the pons and other rostral compartments and hence reduced the intact ponto-medullary preparation to a “medullary” or, in the extreme case, a “BötC–VRG” preparation (see Fig. 1). These transections converted the three-phase rhythm described above into a “two-phase” rhythm (lacking the post-I phase) with the following characteristics: (i) the PN (and XII and cVN) bursts have a “square-like” shape; (ii) bursts in all three nerves are synchronized (i.e., XII burst onset does not precede PN burst); and (iii) the post-I component in cVN bursts disappears. A typical example of this two-phase rhythm is shown in Fig. 2B.

A transection between BötC and pre-BötC [indicated in Fig. 1 by (3)] resulted in further reduction of the preparation to the pre-BötC–VRG (see Fig. 1). This preparation typically generated a respiratory (inspiratory) motor pattern characterized by: (i) a decrementing shape of the burst in all three nerves; (ii) a synchronized activity in all three nerves; and (iii) a lack of post-I activity in vagal nerve (see an example in Fig. 2C). The pattern of this inspiratory activity is very similar to that recorded from pre-BötC and XII nerve in the slice in vitro (e.g., see Koshiya and Smith, 1999; Johnson et al., 2001) and is likely generated due to endogenous bursting mechanisms operating within the pre-BötC without involving inhibitory interactions with other “half-centers”. Therefore, we characterize this rhythmic activity as a “one-phase” inspiratory rhythm.

The role of the persistent sodium current for rhythm generation was assessed in each of the three above states (related to the three-, two- and one-phase rhythms, respectively). Figure 2A1–C1 shows the effect of riluzole on the frequency and amplitude of PN discharges. In the intact and the medullary (e.g., BötC–VRG) preparations, riluzole produced a dose-dependent effect on the amplitude of PN discharges but did not affect burst frequency (see Fig. 2A1, A2). In contrast in the pre-BötC–VRG preparation, riluzole had much less effect on the PN amplitude but caused a dose-dependent reduction of PN burst frequency and finally abolished the rhythm at a concentration of about 10 μM (see Fig. 2C1). These data suggest that an intrinsic persistent sodium current-dependent mechanism is essential for the rhythm generation in the pre-BötC–VRG preparation (i.e., for the one-phase rhythm), but its contribution to rhythmogenesis in the BötC–VRG and intact ponto-medullary network (two- and three-phase rhythms, respectively) appears to be less important.

Computational modeling of the brainstem respiratory network

The objectives of our modeling studies were to build a model of the spatially distributed brainstem respiratory network that could reproduce the above experimental findings and suggest an explanation for possible transformations of the rhythm-generating mechanism after sequential reduction of the network. The model has been developed based on a previous model (Rybak et al., 2004a) and represents an extension of the “hybrid pacemaker-network model” proposed by Smith et al. (2000). All neurons were modeled in the Hodgkin–Huxley style (one-compartment models) and incorporated known biophysical properties and channel kinetics characterized in respiratory neurons in vitro. Specifically, the fast sodium (I_Na) and the persistent (slowly inactivating, I_NaP) sodium currents were described using experimental data obtained from the studies of neurons acutely isolated from the rat’s ventrolateral medulla (Rybak et al., 2003a) at the level of the pre-BötC; the high-voltage activated calcium current (I_CaL) was described based on the data of Elsen and Ramirez (1998); the intracellular calcium dynamics was described to fit the data of Frermann et al. (1999); the description of potassium rectifier (I_K) and calcium-dependent potassium (I_K,Ca) currents and all other cellular parameters were the same as in the previous models (Rybak et al., 1997a–c, 2003b, 2004a, b). Each neuronal type was represented by a population of 50 neurons with some parameters and initial conditions randomized within the population. The full description of the model and model parameters can be found in Appendix.

The schematic of the full model is shown in Fig. 3A. Three major medullary regions are considered (in the rostral-to-caudal direction): Bötzinger Complex (BötC), pre-Bötzinger Complex (pre-BötC) and rostral VRG (rVRG). The BötC compartment includes inhibitory populations, aug-E(1) and post-I, each of which serves as a source of expiratory inhibition widely distributed within the medullary respiratory network (Ezure, 1990; Jiang and Lipski, 1990; Tian et al., 1999). In the model, these populations inhibit all populations in the pre-BötC and rVRG compartments and each other (see Fig. 3A). The BötC compartment also includes a second aug-E (aug-E(2)) inhibitory population, providing the additional control of the duration of expiration via inhibition of post-I activity, and an excitatory post-I (post-I(e)) population that provides the expiratory output (e.g., contributes to the cVN motor output). All neurons in the BötC compartment (in the post-I, post-I(e), aug-E(1) and aug-E(2) populations) have intrinsic adapting properties defined by I_CaL and I_K,Ca. Because of this, the post-I neurons exhibit decrementing discharge patterns during expiration. In contrast, the aug-E neurons (under normal conditions) start firing later in expiration and exhibit augmenting patterns because of the slow disinhibition from the adapting inhibitory post-I neurons.

Fig. 3.

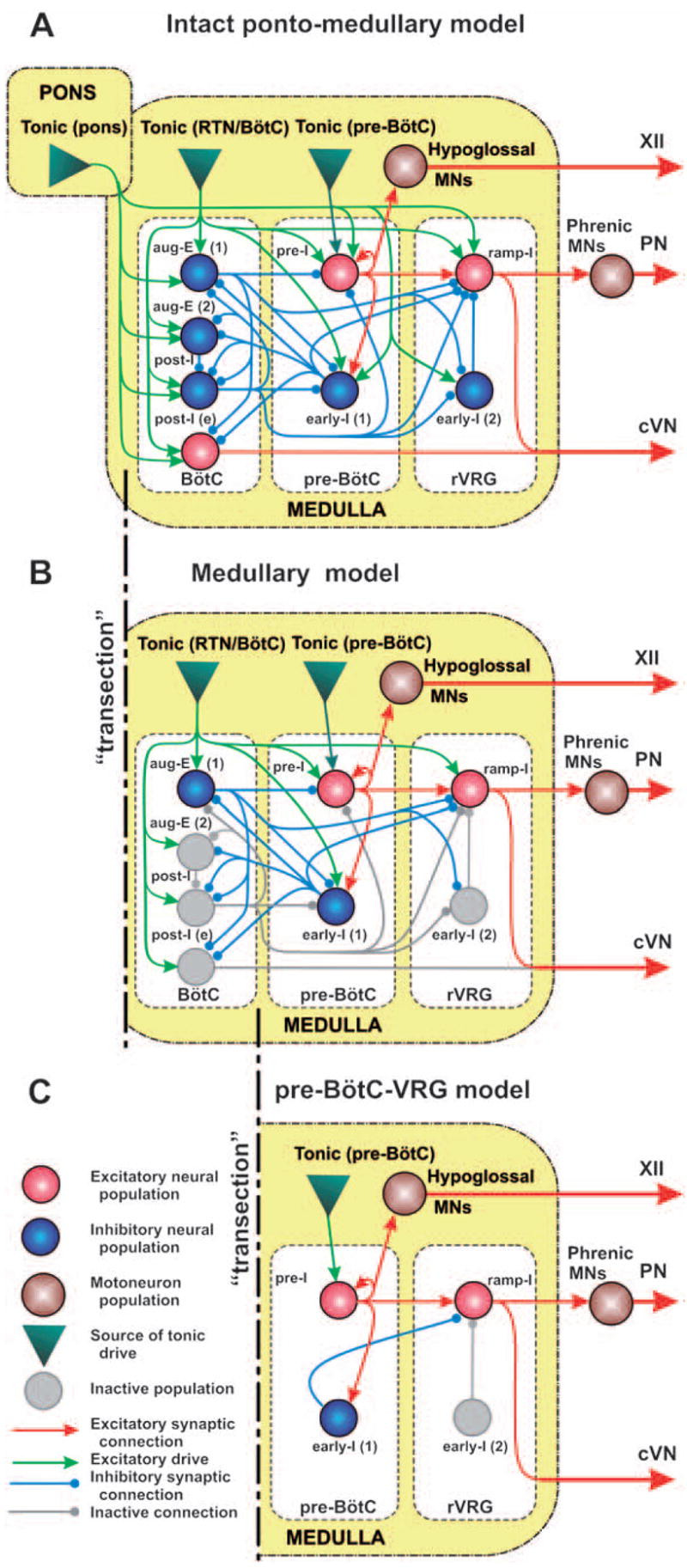
The schematic of the full (intact) model (A) and the reduced medullary (B) and pre-BötC–VGR (C) models. Neural populations are represented by spheres. Excitatory and inhibitory synaptic connections are shown by arrows and small circles, respectively. Sources of excitatory drives are shown by triangles. All conditional symbols are shown in the left bottom corner. See explanations in the text.

The pre-BötC compartment includes two neural populations: pre-I, and early-I(1) (see Fig. 3A). The pre-I population is the major source of inspiratory activity in the network. It projects to the pre-motor inspiratory ramp-I population of rVRG and also defines the XII motor output. The pre-I population in the model is comprised by excitatory neurons with I_NaP-dependent endogenous bursting properties and mutual excitatory synaptic interconnections within the population. Under certain conditions (depending on total tonic drive, phasic inhibition, etc), this population can operate in a bursting mode and intrinsically generate rhythmic inspiratory activity (Butera et al., 1999a, b; Smith et al., 2000; Rybak et al., 2003b, 2004b) similar to that recorded in vitro (Koshiya and Smith, 1999; Johnson et al., 2001). However, in the model under normal conditions, most neurons of this population operate in a tonic spiking mode due to high tonic excitatory input, and are inhibited by expiratory neurons (post-I, aug-E(1)) during expiration. The early-I(1) population of pre-BötC is a population of inhibitory neurons with adapting properties (defined by I_CaL and I_K,Ca). This population receives excitation from the pre-I population and serves as a major source of inspiratory inhibition. In the model, this population inhibits all expiratory neurons during inspiration (see Fig. 3A).

The rVRG compartment contains ramp-I, and early-I(2) populations (Fig. 3A). Ramp-I is a population of excitatory premotor inspiratory neurons that project to PN motor output, and contribute to cVN activity (see Fig. 3A). The major role of the inhibitory early-I(2) population (with adapting neurons containing I_CaL and I_K,Ca) is shaping the augmenting patterns of ramp-I neurons.

The maintenance of normal breathing at the appropriate homeostatic level depends on a variety of afferent inputs to different clusters of respiratory neurons within the brainstem. These inputs are viewed as “excitatory drives” that carry state-characterizing information provided by multiple sources distributed within the brainstem (pons, RTN, raphe, NTS, etc.), including those considered to be major chemoreceptor sites (sensing CO₂/pH), and activated by peripheral chemo-receptors (sensing CO₂/pH and low O₂) (Nattie, 1999; Guyenet et al., 2005). Although currently undefined, these drives appear to have a certain spatial organization with specific mapping on the spatial organization of the brainstem respiratory network. In our model, these drives are conditionally represented by three separate sources located in different compartments (pons, RTN/BötC, and pre-BötC) and providing drives to different respiratory populations (see Fig. 3A).

Figure 4A, B shows the performance of the intact model. The activity of each population is represented by the average spike frequency histogram of population activity. The post-I population of BötC shows decrementing activity during expiration. This population inhibits all other populations (except post-I(e)) during the first half of expiration (post-inspiratory phase). Because of the reduction of post-I inhibition with the adaptation in the post-I activity, the aug-E(1) and then the aug-E(2) population start activity later in expiration forming a late expiratory (E2) phase. At the very end of expiration, the pre-I population of pre-BötC is released from inhibition and activates the early-I(1) population, which inhibits all expiratory populations of BötC. As a result, the ramp-I (and early-I(2)) populations of rVRG release from inhibition (with some delay relative to pre-I) giving the start to the next inspiratory phase (onset of inspiration). During inspiration, the activity of early-I(2) population decreases providing the ramp increase of ramp-I population activity (and PN burst). The activity of early-I(1) population of pre-BötC decreases during inspiration providing a slow disinhibition of the post-I population of BötC. Finally, the post-I population fires and inhibits all inspiratory activity completing inspiratory off-switching. Then the process repeats. In summary, the respiratory rhythm (with a typical three-phase pattern) is generated in the intact model by the neuronal ring comprising the early-I(1), post-I, and aug-E(1) inhibitory populations with the pre-I population participating in the onset of inspiration.

Fig. 4.

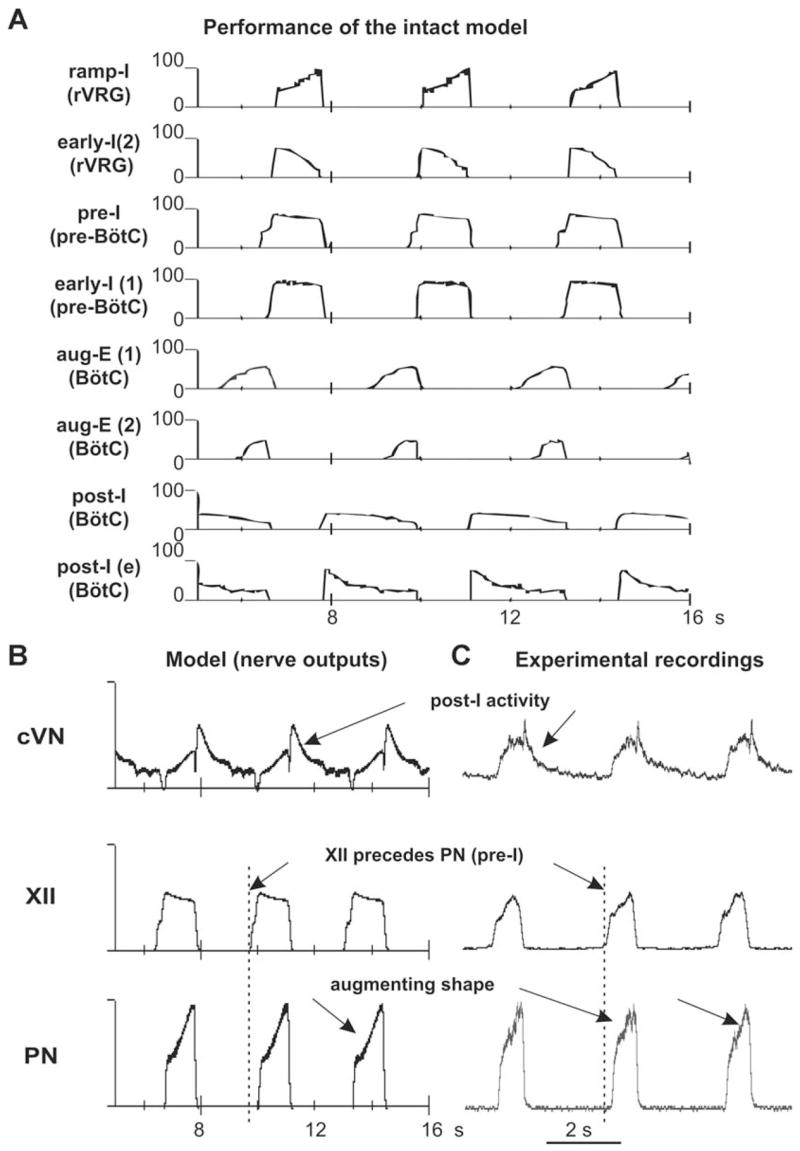
Performance of the intact model (network architecture shown in Fig. 3A). (A) Activity of each neural population (labeled on the left) is represented by the histogram of average neuronal spiking frequency (number of spikes per second per neuron, bin = 30 ms). See explanations in the text. (B) Integrated activity of motor (nerve) outputs (PN, XII, and cVN) in this model. (C) Integrated patterns of activity of phrenic (PN), hypoglossal (XII), and central vagus (cVN) nerves obtained from the intact preparation (from Fig. 2A) shown for comparison. See all explanations in the text.

The motor output patterns of the model (PN, XII, and cVN) are shown in Fig. 4B and may be compared with the integrated activities of the corresponding nerves obtained from our experimental studies (Fig. 4C). A comparison clearly demonstrates that the model reproduces all major characteristics of the respiratory pattern recorded under normal conditions from the intact preparation: (i) an augmenting shape of the PN bursts; (ii) a delay in the onset of the PN bursts relative to the XII bursts; and (iii) a decrementing post-I component in cVN bursts. However, the shape of XII busts in the model is slightly different which suggests that the neural organization of the pre-BötC and/or the hypoglossal motor output in the real system is more complicated (more heterogeneous) than that in our model.

Figure 3B shows a schematic of the reduced (“medullary”) model used for simulation of a reduced experimental preparation remaining after medullary transections removing the pons or the pons together with an adjacent part of the medulla (e.g., a part of Facial nucleus and RTN). The performance of this model is shown in Fig. 5A, B. Based on indirect evidence about a strong excitatory influence of the pons on the post-I neurons (Rybak et al., 2004a; Dutschmann and Herbert, 2006), we have suggested that with the removal of the pons and adjacent medullary regions, all post-I populations of BötC lose a significant portion of the excitatory drive (see Fig. 3B), whereas the drive to aug-E(2) is less dependent on these regions. As a result, a balance of mutual inhibitory interactions between aug-E(1) and post-I shifts to the domination of aug-E. The latter now demonstrates a “natural” decrementing pattern (see in Fig. 5A) and completely inhibits all post-inspiratory activity in the network (Figs. 3B and 5A). The respiratory oscillations in this state are generated by a half-center mechanism based on the mutual inhibitory interactions between the adapting early-I(1) and aug-E(1) populations (see Figs. 3B and 5A). The model now generates a typical two-phase rhythm (lacking the post-I phase). In addition, elimination of the drive from more rostral compartments reduces excitability and firing frequency of the pre-I and ramp-I populations, which reduces the amplitudes of all motor outputs of the model (PN, XII, and cVN, see Fig. 5B). Also, because of this drive reduction, the early-I(2) population becomes silent and does not influence the ramp-I population activity, which changes the shape of ramp-I (Fig. 5A) and PN (Fig. 5B) bursts from an augmenting to a square-like pattern. Finally, the patterns of motor outputs in the model (PN, XII, and cVN, Fig. 5B) are very similar to the integrated activities of the corresponding nerves obtained in our experimental studies (Fig. 5C). This reduced model reproduces all major characteristics of the respiratory pattern recorded in the corresponding reduced preparations: (i) an apneustic “square-like” shape of the PN bursts; (ii) a synchronized activities in all three nerves; and (iii) a lack of the post-I component in the cVN bursts.

Fig. 5.

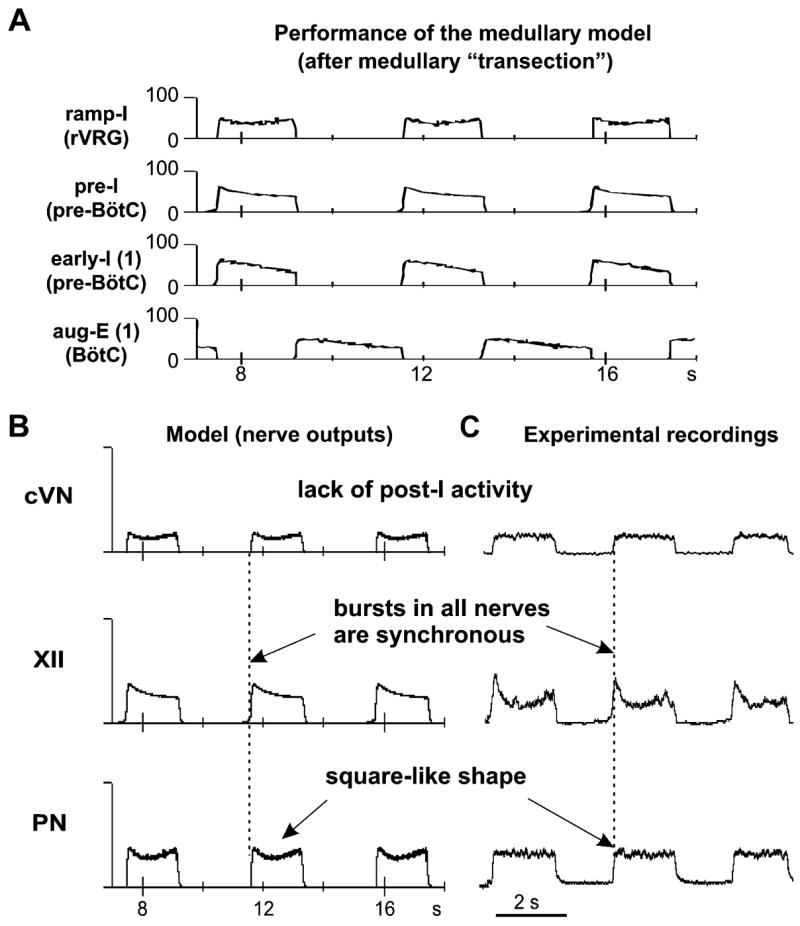
Neuronal population activities and motor output patterns of the medullary model (shown in Fig. 3B). (A) Activity (spike frequency histograms) of all neural populations (labeled on the left). See explanations in the text. (B) Integrated activity of motor (nerve) outputs (PN, XII, and cVN) in this model. (C) Integrated patterns of activity of phrenic (PN), hypoglossal (XII), and central vagus (cVN) nerves obtained from a medullary preparation (from Fig. 2B) shown for comparison. See explanations in the text.

Figure 3C represents a more reduced model used for simulation of behavior of the reduced pre-BötC–VRG preparation after a transection at the rostral end of pre-BötC. The performance of this model is shown in Fig. 6A, B. As shown in previous modeling studies (Butera et al., 1999a, b; Smith et al., 2000; Rybak et al., 2003b, 2004b) a population of neurons with I_NaP-dependent endogenous bursting properties and mutual excitatory connections (as the pre-I population of pre-BötC in the present model) can, under certain conditions, intrinsically generate a population bursting activity similar to that recorded in pre-BötC in vitro (Koshiya and Smith, 1999; Johnson et al., 2001). Specifically, increasing tonic excitatory drive switches the population from a quiescent state to rhythmic population bursting, and then to asynchronous tonic activity (Butera et al., 1999b; Rybak et al., 2003b, 2004b). A relatively strong excitatory drive to this population causes inactivation of NaP channels and maintenance of tonic activity. Alternatively, a reduction of the excitatory drive may hence switch this population to the regime of endogenous bursting activity. In the intact and medullary models above, the pre-I population of pre-BötC receives the total excitatory drive, which is large enough to keep this population in the state of tonic activity. This tonic activity is interrupted by the phasic expiratory inhibition from the post-I (intact model) or aug-E(medullary model) population. Removal of all compartments located caudal to pre-BötC results in further reduction of the drive to the pre-I population (Fig. 3C). In addition, phasic inhibition from expiratory populations of BötC is also eliminated. As described above, with the reduction of tonic excitatory drive and elimination of phasic inhibition, the behavior of pre-I population switches to the regime of endogenous bursting activity. This population now intrinsically generates oscillations with a decrementing burst shape (similar to those recorded in vitro) (see Fig. 6A). Moreover, the bursting activity of the pre-I population now drives the activity of the ramp-I population (Fig. 6A) and all motor outputs that now exhibit one-phase (inspiratory) oscillations with a decrementing burst shape (PN, XII, cVN, see Fig. 6B) similar to that recorded in the pre-BötC–VRG preparation (see Fig. 6C).

Fig. 6.

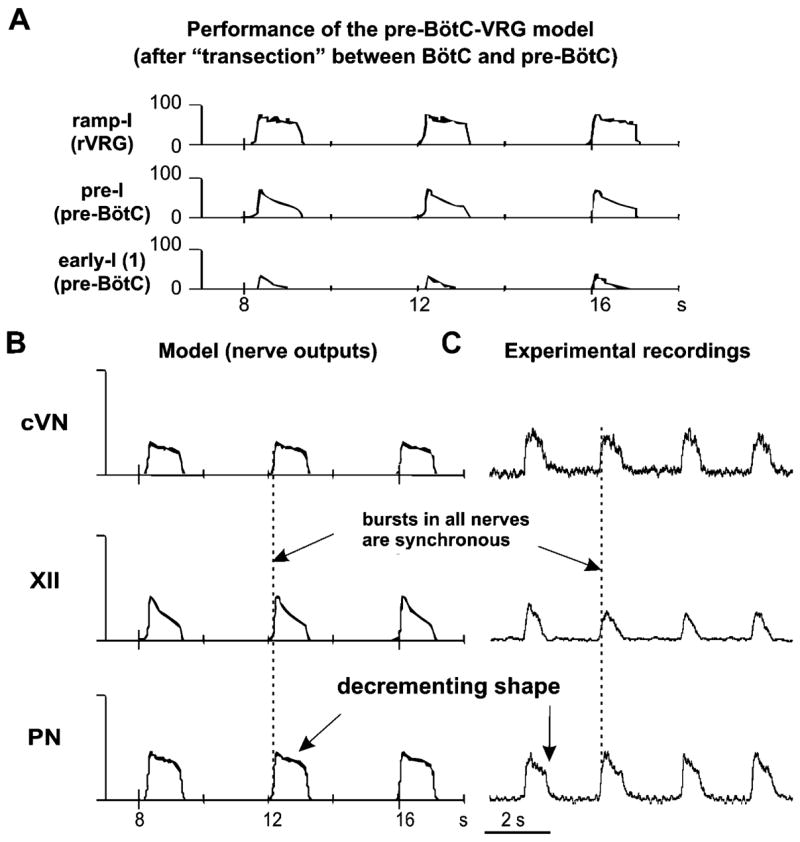
Performance of the pre-BötC–VGR model (shown in Fig. 3C). (A) Activity of all neural populations (labeled on the left). See explanations in the text. (B) Integrated activity of motor (nerve) outputs (PN, XII, and cVN) in this model. (C) Integrated patterns of activity of phrenic (PN), hypoglossal (XII), and central vagus (cVN) nerves obtained from a pre-BötC–VGR preparation (from Fig. 2C) shown for comparison. See all explanations in the text.

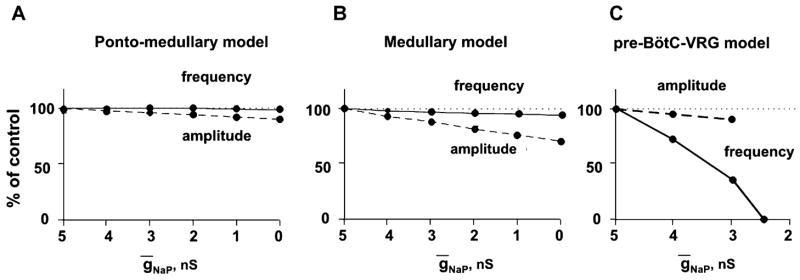
In order to investigate the role of the persistent sodium current (I_NaP) in the intact (Fig. 3A) and sequentially reduced models (Fig. 3B, C) and compare model behaviors to the corresponding experimental data on the dose-dependent effect of the I_NaP blocker riluzole (Fig. 2A1–C1), the maximal conductance of NaP channel (ḡ_NaP) was sequentially reduced in all neurons of the model. The results are shown in Fig. 7A–C. The progressive reduction of ḡ_NaP (up to zero) in the intact and medullary models does not affect the frequency of respiratory (PN) oscillations and causes only a small reduction of the amplitude of PN bursts (see Fig. 7A, B). This occurs because a relatively high total excitatory tonic drive produces membrane depolarization that holds the (voltage-dependent) I_NaP current in a significantly inactivated state In contrast in the pre-BötC–VRG model, with a reduction of the total drive the I_NaP essentially contributes to the cellular firing behavior and the reduction of ḡ_NaP progressively decreases the frequency of PN bursts and finally abolishes the rhythm when ḡ_NaP becomes less than 2.5 nS (Fig. 7C). These modeling results are fully consistent with our experimental data (Fig. 2A1–C1).

Fig. 7.

Effect of reduction of maximum conductance for the persistent sodium channels (ḡ_NaP) in all neurons of the pre-I population of pre-BötC on frequency (solid lines) and amplitude (dashed lines) of PN bursts in the intact (A), medullary (B), and pre-BötC–VGR (C) models. Note that the frequency of PN bursts does not change in the intact and medullary models (A and B), but dramatically decreases with the reduction of ḡ_NaP in the pre-BötC–VGR model and, finally, the PN activity is abolished at ḡ_NaP = 2.5 nS (C). Compare with the corresponding graphs in Fig. 2A1–C1. See explanations in the text.

Recent studies in vitro and in vivo (Mellen et al., 2003; Janczewski and Feldman, 2006) have demonstrated that a blockade of activity of inspiratory neurons in the pre-BötC, e.g., by administration of opioids, can produce spontaneous deletions or “quantal” skipping of individual or series of inspiratory bursts in the pre-BötC and/or in PN, while a rhythmic activity persists in a more rostral compartment of the brainstem, the para-facial (pF) region. In this regard, it is interesting to consider the behavior of our model when the activity of the pre-I population of pre-BötC is suppressed. The results are shown in Fig. 8A, B. The pre-I population activity was suppressed by setting the maximal conductance for fast sodium current to zero (Fig. 8A) for some period shown by a horizontal bar at the top of Fig. 8B. During this period, the pre-I population of pre-BötC as well as the PN and XII nerves show no activity. At the same time, despite the complete blockade of the output inspiratory activity, “expiratory” oscillations persist in the network. This expiratory rhythm results from mutual inhibitory interactions between the post-I, aug-E(1) and early-I(1) populations (see marked by gray in Fig. 8B).

Fig. 8.

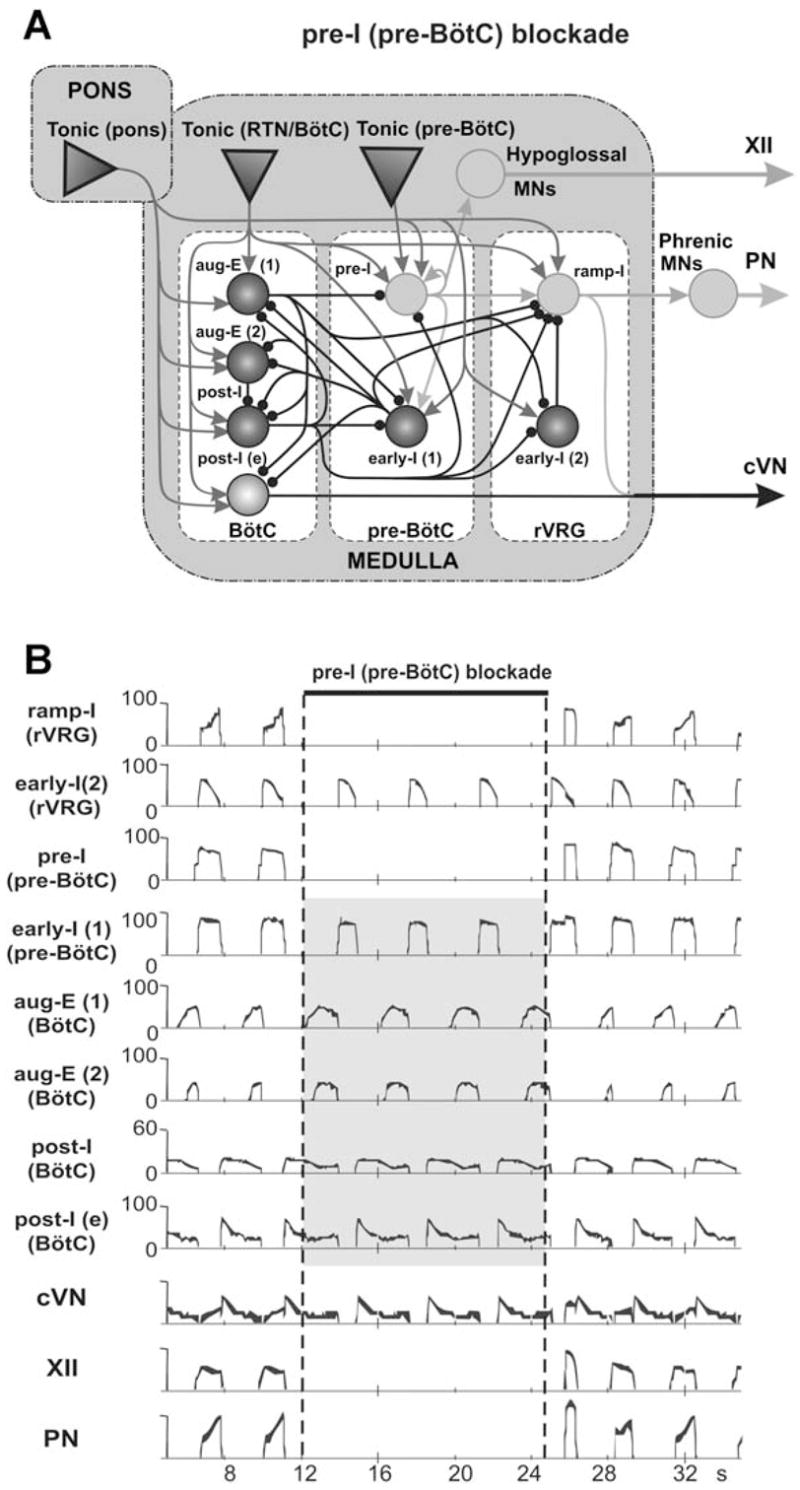
Neuronal activity patterns in the intact model (Fig. 3A) when the activity of the pre-I population of pre-BötC is suppressed. Activity of pre-I population was suppressed by setting the maximal conductance for fast sodium current to zero for the period shown by a horizontal bar at the top. During this period the pre-I population of pre-BötC as well as the phrenic (PN) and hypoglossal (XII) nerves show no activity. At the same time, an “expiratory” rhythm continues despite of the blockade of inspiration.

Discussion

Our experimental studies have demonstrated that the intact in situ perfused rat brainstem–spinal cord preparation under normal conditions generates a three-phase respiratory rhythm with an augmenting shape of PN discharges, temporal delay between the XII and PN bursts, and prominent post-inspiratory activity (as seen in the cVN bursts). Removal of the pons converts this rhythm into a two-phase rhythm with a square-like shape of PN discharges and lack of the post-I activity. Our data show that administration of riluzole, an I_NaP blocker (10–20 μM), does not slow down or abolish these two rhythms (see also Paton et al., 2006). This implicitly supports the conclusion that both these rhythms are generated by network mechanisms without significant contribution of an I_NaP-dependent intrinsic mechanism. Another conclusion drawn from these studies is that the input from the pons is necessary for the expression of the post-inspiratory activity in the network and the three-phase rhythm (at least in the absence of pulmonary stretch receptor inputs as in the in situ preparation), which supports previous findings (Rybak et al., 2004a; Dutschmann and Herbert, 2006).

Based on our experimental studies we also conclude that removal of neural circuits rostral to pre-BötC decreases the role of inhibitory network interactions (provided by the expiratory populations of BötC) and increases the role of the endogenous I_NaP-dependent rhythmicity in the pre-BötC network. Specifically, the medullary transections between pre-BötC and BötC produce switching to a one-phase inspiratory rhythm that is characterized by a decrementing shape of PN discharges. Application of riluzole produces dose-dependent reduction of the oscillation frequency and finally abolishes this rhythm, as predicted from modeling of heterogeneous populations of excitatory neurons with I_NaP (Butera et al., 1999b; Rybak et al., 2003b).

Our experimental and modeling studies reveal a novel spatial and functional organization within the brainstem “respiratory column” that extends from the VRG to the rostral pons. Each functional compartment within this spatial network structure operates under control of more rostral compartments. Specifically, the premotor (bulbospinal) inspiratory neurons of rVRG located caudal to pre-BötC cannot generate rhythmic activity themselves. Their activity is defined by inputs from rostral compartments including excitatory input from pre-BötC and phasic inhibition from expiratory neurons of BötC. In contract, the pre-BötC can, in certain states, intrinsically generate inspiratory bursting activity. However, in the intact system, the pre-BötC is functionally embedded within a more spatially distributed network, and its state and operating conditions are controlled by the more rostral compartments: BötC, inhibiting pre-BötC during expiration, and RTN and pontine nuclei, providing excitatory drives to pre-BötC as well as to BötC and more caudal compartments. Activation of the expiratory populations of BötC (post-I and aug-E), which provide a widely -distributed inhibition within the network during expiration, is critical for the expression of rhythm-generating and pattern-formatting network mechanisms operating in the intact system under normal conditions. In turn, activation of these populations also requires excitatory drives from pons, RTN and other medullary sources as well as a certain balance between these drives. Therefore, both the rhythmogenic mechanism operating in the system under certain conditions (e.g., a network-based, or a pacemaker-driven) and the type of the respiratory pattern generated (e.g., three-phase, two-phase, or one-phase) depend upon the functional states of the system, and specifically, upon the state of BötC (the excitability of post-I and aug-E population, defining the expression of expiratory inhibition within the respiratory network), and the state of the pre-BötC (the expression of the intrinsic I_NaP-dependent mechanisms).

We therefore confirm a critical role of the pre-BötC in the generation of respiratory rhythm. In any state of the system, the pre-BötC plays a central role as the major source of inspiratory activity in the network. However, since this complex is embedded in a wider functionally and spatially distributed network, its state, performance, and the expression of endogenous rhythmogenic bursting properties depend upon (and hence are defined by) inputs from other respiratory compartments and external drives (which can be different in different preparations and under different conditions).

Our modeling studies have also demonstrated that a complete suppression of excitatory (pre-I) activity in the pre-BötC does not necessarily eliminate “expiratory” oscillations. Rhythmic expiratory activity may persist due to reciprocal inhibitory interactions within the BötC and between the BötC and inhibitory populations (e.g., early-I) within the pre-BötC region (see Fig. 8). These simulation results may be relevant to the recent findings of the continuing (presumably expiratory) rhythmic activity in the pF region following a suppression (or quantal deletion) of inspiratory activity in pre-BötC (e.g., by administration of opioids) (Mellen et al., 2003; Janczewski and Feldman, 2006). The pF region appears to be adjacent to BötC and functionally may be considered as an extension of BötC. We therefore suggest that similar to our simulations, the expiratory rhythmic activity in pF may be produced by network interactions within the pF/BötC region, and do not necessarily imply the existence of an independent pF expiratory generator normally interacting with a pre-BötC inspiratory oscillator as was recently suggested (Janczewski and Feldman, 2006).

As described above, the pre-I population of pre-BötC and the post-I and aug-E populations of BötC receive multiple drives from the pons, RTN, and other undefined medullary sources. These drives and their balances define a relative excitability and the states of the above key populations and hence implicitly define the operating rhythmogenic mechanism and the respiratory pattern generated. In our experimental and modeling studies, extreme manipulations (transections) were applied to fully eliminate some parts of the network and their influences on the remaining structure in order to uncover the possible states of the system and rhythmogenic mechanisms engaged in each state. Such extreme changes would never happen in real life. At the same time, system states, similar to those uncovered by the transections may occur as a result of alterations in external drives and/or their balances. These drives originate in multiple brainstem regions involved in central chemoreception (such as RTN, raphe, etc.) or come from peripheral chemoreceptors and hence are dependent on the metabolic state of the system. Therefore, specific changes in the metabolic conditions, such as levels of carbon dioxide/pH, or oxygen may alter the balance between the above drives, change interactions between the key respiratory populations, and finally produce transformations to the two- or one-phase rhythms described above. Specifically, hypocapnia (a reduced level of carbon dioxide) can convert the eupneic three-phase rhythm to a two-phase rhythm that appears identical to that obtained by the pontine transection described above (Sun et al., 2001; Abdala et al., 2007). Severe hypoxia (a strong reduction of the oxygen level) can switch the system to a gasping state driven by a one-phase rhythm similar to that obtained by a transaction between pre-BötC and BötC (Paton et al., 2006). In contrast to the intact rhythm and similar to the one-phase rhythm described here, this gasping rhythm is characterized by a decrementing burst shape and can be abolished by the I_NaP blocker riluzole (Paton et al., 2006).

In summary our results lead to the conclusion that the neural organization in the respiratory CPG supports multiple rhythmogenic mechanisms. The CPG appears to contain multiple functionally embedded oscillators with rhythmogenic mechanisms ranging from (primarily) inhibitory network-based circuits, resembling classical half-center-type structures, to excitatory networks of neurons with conductance-based endogenous rhythmicity. In the intact system, these circuits are organized in a hierarchy that can be understood in terms of spatially and functionally defined, interacting neuroanatomical compartments. This arrangement makes the respiratory CPG a robust, flexible neural machine for respiratory rhythm generation and control of breathing that can easily adapt to current metabolic demands as well as to various changes in internal and external environment, which would be expected for a rhythmic motor system as vital as the respiratory network.

Appendix

Single neuron descriptions

All neurons were modeled in the Hodgkin–Huxley style as single-compartment models:

$$\begin{array}{l}C\cdot \frac{\text{d}V}{\text{d}t}=-I_{\text{Na}}-I_{\text{NaP}}-I_{\text{K}}-I_{\text{CaL}}\\ -I_{\text{K},\text{Ca}}-I_{\text{L}}-I_{\text{SynE}}-I_{\text{SynI}}\end{array}$$ (A.1)

where V is the membrane potential, C the membrane capacitance, and t the time. The terms in the right part of this equation represent ionic currents: I_Na — fast sodium (with maximal conductance ḡ_Na); I_NaP — persistent (slow inactivating) sodium (with maximal conductance ḡ_NaP); I_K — delayed-rectifier potassium (with maximal conductance ḡ_K); I_CaL — high-voltage activated calcium-L (with maximal conductance ḡ_CaL); I_K,Ca —calcium-dependent potassium (with maximal conductance ḡ_K,Ca), I_L — leakage (with constant conductance g_L); I_SynE (with conductance g_SynE) and I_SynI (with conductance g_SynI) — excitatory and inhibitory synaptic currents, respectively.

Currents are described as follows:

$$\begin{array}{l}{I}_{\text{Na}}={\overline{g}}_{\text{Na}}\cdot m_{\text{Na}}^3\cdot h_{\text{Na}}\cdot (V-E_{\text{Na}});\\ I_{\text{NaP}}={\overline{g}}_{\text{NaP}}\cdot m_{\text{NaP}}\cdot h_{\text{NaP}}\cdot (V-E_{\text{Na}});\\ I_{\text{K}}={\overline{g}}_{\text{K}}\cdot m_{\text{K}}^4\cdot (V-E_{\text{K}});\\ I_{\text{CaL}}={\overline{g}}_{\text{CaL}}\cdot m_{\text{CaL}}\cdot h_{\text{CaL}}\cdot (V-E_{\text{Ca}});\\ I_{\text{K},\text{Ca}}={\overline{g}}_{\text{K},\text{Ca}}\cdot m_{\text{K},\text{Ca}}^2\cdot (V-E_{\text{K}});\\ I_{\text{L}}=g_{\text{L}}\cdot (V-E_{\text{L}});\\ I_{\text{SynE}}=g_{\text{SynE}}\cdot (V-E_{\text{SynE}});\\ I_{\text{SynI}}=g_{\text{Synl}}\cdot (V-E_{\text{SynI}}),\end{array}$$ (A.2)

where E_Na, E_K, E_Ca, E_L, E_SynE, and E_SynI are the reversal potentials for the corresponding channels.

Variables m_i and h_i with indexes indicating ionic currents represent, respectively, the activation and inactivation variables of the corresponding ionic channels. Kinetics of activation and inactivation variables is described as follows:

$$\begin{array}{l}{\tau }_{m_i}(V)\cdot \frac{\text{d}}{\text{d}t}{m}_i=m_{\infty i}(V)-m_i;\\ {\tau }_{h_i}(V)\cdot \frac{\text{d}}{\text{d}t}{h}_i=h_{\infty i}(V)-h_i.\end{array}$$ (A.3)

The expressions for steady state activation and inactivation variables and time constants are shown in Table 1. The value of maximal conductances for all neuron types are shown in Table 2.

Table 1.

Steady state activation and inactivation variables and time constants for voltage-dependent ionic channels

Ionic channels	m∞(V), V in mV
	τm(V), ms
	h∞(V), V in mV
	τh(V), ms
Fast sodium, Na	m∞Na = 1/(1 + exp(−(V + 43.8)/6))
	τmNa = τmNa max/cos h((V + 43.8)/14), τmNa max= 0.252
	h∞Na = 1/(1 + exp((V + 67.5)/10.8))
	τhNa = τhNa max/cos h((V + 67.5)/12.8), τhNa max = 8.456
Persistent sodium, NaP	m∞NaP = 1/(1 + exp(−(V + 47.1)/3.1))
	τmNaP = τmNaP max/cos h((V + 47.1)/6.2), τmNaP max = 1
	h∞NaP = 1/(1 + exp((V + 59)/6))
	τhNaP = τhNaP max/cos h((V + 59)/6), τhNaP max = 7000
Delayed rectifier potassium, K	α∞K = 0.01 · (V + 44)/(1 − exp(− (V + 44)/5))
	β∞K = 0.17 · exp(−(V + 49)/40)
	m∞K = α∞K/(α∞K + β∞K)
	τmK = τmK max/(α∞K + β∞K), τmK max =1
High-voltage activated calcium, CaL	m∞CaL = 1/(1 + exp(−(V + 27.4)/5.7))
	τmCaL = 0.5
	h∞CaL = (1 + exp((V + 52.4)/5.2))
	τhCaL = 18
Calcium-dependent potassium, K(Ca2+)	${\alpha }_{\infty }\text{K},\text{Ca}=1.25\times {10}^8·{[\text{Ca}]}_i^2$, β∞K,Ca = 2.5
	m∞K,Ca = α∞K,Ca/(α∞K,Ca + β∞K,Ca)
	τmK,Ca = τmK,Ca max · 1000/(α∞K,Ca + β∞K,Ca), τmK,Ca max= 1–8

Table 2.

Maximal conductances of ionic channels in different neuron types

Neuron type	ḡNa, nS	ḡNaP, nS	ḡK, nS	ḡCaL, nS	ḡK,Ca, nS	gL, nS
pre-I	300	5.0	180			2.5
ramp-I	400		250			6.0
All others	400		250	0.05	3.0–6.0	6.0

The kinetics of intracellular calcium concentration Ca is described as follows (Rybak et al., 1997a):

$$\frac{\text{d}}{\text{d}t}\text{Ca}=k_{\text{Ca}}\cdot I_{\text{Ca}}\cdot (1-P_B)+\frac{({\text{Ca}}_0-\text{Ca})}{{\tau }_{\text{Ca}}}$$ (A.4)

where the first term constitutes influx (with the coefficient k_Ca) and buffering (with the probability P_B), and the second term describes pump kinetics with resting level of calcium concentration Ca₀ and time constant τ_Ca.

$$P_B=\frac{B}{(\text{Ca}+B+K)}$$ (A.5)

where B is the total buffer concentration and K the rate parameter.

The calcium reversal potential is a function of Ca:

$$\begin{array}{l}{E}_{\text{Ca}}=13.27\cdot ln\left(\frac{4}{\text{Ca}}\right)\\ (\text{at rest Ca}={\text{Ca}}_0=5\times {10}^{-5}\text{mM}\\ \text{and }{E}_{\text{Ca}}=150\hspace{0.17em}\text{mV})\end{array}$$ (A.6)

The excitatory (g_SynE) and inhibitory synaptic (g_SynI) conductances are equal to zero at rest and may be activated (opened) by the excitatory or inhibitory inputs, respectively:

$$\begin{array}{l}{g}_{\text{SynEi}}(t)={\overline{g}}_{\text{E}}\cdot \sum _{j}S\{w_{ji}\}\cdot \sum _{t_{kj}<t}exp\left(\frac{(t-t_{kj})}{{\tau }_{\text{SynE}}}\right)\\ +{\overline{g}}_{\text{Ed}}\cdot \sum _{m}S\{w_{\mathit{dmi}}\}\cdot d_{mi};\\ g_{\text{SynIi}}(t)={\overline{g}}_{\text{I}}\cdot \sum _{j}S\{-w_{ji}\}\cdot \sum _{t_{kj}<t}exp\left(-\frac{(t-t_{kj})}{{\tau }_{\text{SynI}}}\right)\\ +{\overline{g}}_{\text{Id}}\cdot \sum _{m}S\{-w_{\mathit{dmi}}\}\cdot d_{mi},\end{array}$$ (A.7)

where the function S{x} = x, if x≥0, and 0 if x<0. In Eq. (A.7), each of the excitatory and inhibitory synaptic conductances has two terms. The first term describes the integrated effect of inputs from other neurons in the network (excitatory and inhibitory, respectively). The second term describes the integrated effect of inputs from external drives d_mi. Each spike arriving to neuron i from neuron j at time t_kj increases the excitatory synaptic conductance by ḡ_E · w_ji if the synaptic weight w_ji>0, or increases the inhibitory synaptic conductance by −ḡ_I · w_ji if the synaptic weight w_ji<0. ḡ_E and ḡ_I are the parameters defining an increase in the excitatory or inhibitory synaptic conductance, respectively, produced by one arriving spike at|w_ji| = 1. τ_SynE and τ_SynE are the decay time constants for the excitatory and inhibitory conductances, respectively. In the second terms of equations (A.7), ḡ_Ed and ḡ_Id are the parameters defining the increase in the excitatory or inhibitory synaptic conductance, respectively, produced by external input drive d_mi = 1 with a synaptic weight of |w_dmi| = 1. All drives were set equal to 1. The relative weights of synaptic connections (w_ji and w_dmi are shown in Table 3).

Table 3.

Weights of synaptic connections in the network

Target population (location)	Source population (one neuron) or drive {weight of synaptic input}
ramp-I (rVRG)	drive(RTN/BötC) {0.1}; drive(pons) {2.8}; early-I(2) {−0.25}; pre-I {0.12}; early-I(1) {−0.15}; aug-E(1){−1.5}; post-I {−0.5}.
early-I(2) (rVRG)	drive(pons) {1.7}; aug-E(1) {−0.25}; post-I {−0.5}.
pre-I (pre-BötC)	drive(pre-BötC) {0.32}; drive(RTN/BötC) {0.1}; drive(pons) {0.6}; pre-I {0.03}; aug-E(1) {−0.035}; post-I {−0.09}.
early-I(1) (pre-BötC)	drive(RTN/BötC) {0.9}; drive(pons) {1.3}; pre-I {0.026}; aug-E(1) {−0.145}; post-I {−0.185}.
aug-E(1) (BötC)	drive(RTN/BötC) {1.0}; drive(pons) {0.9}; early-I(1) {−0.125}; post-I {−0.16}.
aug-E(2) (BötC)	drive(RTN/BötC) {0.1}; drive(pons) {1.4}; early-I(1) {−0.4}; post-I {−0.16}.
post-I (BötC)	drive(RTN/BötC) {0.1}; drive(pons) {2.9}; early-I(1) {−0.13}; aug-E(1) {−0.03}; aug-E(2) {−0.05}.
post-I (e) (BötC)	drive(RTN/BötC) {0.1}; drive(pons) {2.0}; early-I(1) {−0.2}; aug-E(1) {−0.075}.

Note: Values in brackets represent relative weights of synaptic inputs from the corresponding source populations (w_ji) or drives (w_dmi), see Eq. (A.7).

Neuronal parameters

Capacitance: C = 36.2 pF. Reversal potentials: E_Na = 55 mV; E_K = −94 mV; E_SynE = 0 mV; E_SynI = E_Cl = −75 mV.

To provide heterogeneity of neurons within neural populations, the value of E_L was randomly assigned from normal distributions using average value ±SD. Leakage reversal potential for all neurons (except for pre-I) E_L = −60±1.2 mV; for pre-I neurons E_L = −68±1.36 mV.

Synaptic parameters: ḡ_E = ḡ_l = ḡ_Ed = ḡ_ld = 1.0 nS; τ_SynE = 5 ms; τ_SynI = 15 ms.

Parameters of calcium kinetics:

$$\begin{array}{l}{\text{Ca}}_0=5\times {10}^{-5}\text{mM};k_{\text{Ca}}=5.18\times {10}^{-8}\text{mM}/\text{C};\\ {\tau }_{\text{Ca}}=500\text{ ms},B=0.030\text{ mM};K=0.001\text{ mM}\end{array}$$

The motoneuron populations have not been modeled. Integrated activities of the ramp-I and pre-I population were considered as PN and XII motor outputs, respectively. The weighted sum of integrated activities of the ramp-I (1/3) and the post-I(e) (2/3) populations was considered as cVN motor output.

Modeling neural populations

In the present model, each functional type of neuron is represented by a population of 50 neurons. Connections between the populations were established so that, if a population A was assigned to receive an excitatory or inhibitory input from a population B or external drive D, then each neuron of population A received the corresponding excitatory or inhibitory synaptic input from each neuron of population B or from drive D, respectively. The heterogeneity of neurons within each population was set by a random distribution of E_L (mean values ±SD, see above) and initial conditions for values of membrane potential, calcium concentrations and channel conductances. In all simulations, initial conditions were chosen randomly from a uniform distribution for each variable, and a settling period of 20 s was allowed in each simulation before data were collected. Each simulation was repeated 20–30 times, and demonstrated qualitatively similar behavior for particular values of the standard deviation of E_L and initial conditions.

The model was developed using a custom simulation package NSM 2.0, developed at Drexel University by S. N. Markin, I. A. Rybak, and N. A. Shevtsova. Differential equations are solved using the exponential Euler integration method (MacGregor, 1987) with a step of 0.1 ms (for details see Rybak et al., 2003b).