MOSQUITOES DO SENESCE: DEPARTURE FROM THE PARADIGM OF CONSTANT MORTALITY

Abstract

Although variation in mortality is considered by virtually all vector-borne disease specialists to be one of the most important determinants of an arthropod’s capacity to transmit pathogens, the operational assumption often is that insect vector mortality is independent of age. Acceptance of the non-senescence assumption leads to the erroneous conclusion that mosquito age is unimportant, results in misleading predictions regarding disease reductions after vector control, and represses study of other aspects of mosquito biology that change with age. We brought large-scale laboratory life table techniques (N > 100,000) to bear on the question of age-dependent mortality in the mosquito vector of dengue virus, Aedes aegypti. Mortality was highly age dependent in both sexes. Mortality was low at young ages (< 10 days old), steadily increased at middle ages, and decelerated at older ages. A newly derived age-dependent model of pathogen transmission shows the importance of young mosquitoes and population age structure to transmission dynamics. Departure from the age-independent mortality paradigm encourages research on overlooked complexities in mosquito biology, the need for innovative methods to study mosquito population dynamics, and the need to study age-dependent changes for an accurate understanding of mosquito biology and pathogen transmission.

INTRODUCTION

Daily mortality is the most important determinant of a mosquito’s ability to transmit pathogens, such as those causing malaria, dengue, lymphatic filariasis, and viral encephalidites.¹ The longer a mosquito lives, the more likely she is to encounter an infectious host, survive the incubation period, and transmit an infectious agent during subsequent feeding attempts. Because of the important effect of mortality at several stages in the pathogen transmission cycle, small changes in daily mortality can result in relatively large changes in mosquito-borne pathogen transmission.²

Since the 1950s, the assumption that mosquitoes do not senesce (i.e., that mosquito mortality remains constant with age) has been used to assess the role of mosquitoes in pathogen transmission and predict public health consequences of vector control strategies. This assumption was first articulated by MacDonald,³ who reasoned that environmental insults, disease, and predation would kill mosquitoes before they had an opportunity to die of old age. Although evidence from a few studies^4,5 seemed to support this assumption, many others suggest that senescence occurs in both captive and free-ranging mosquito populations.^6–10 For purposes of this discussion, we define senescence as an increased probability of mortality with advancing age. In one notable study, published reports of mosquito mortality were reanalyzed, showing that many species exhibit age-dependent mortality consistent with a Gompertz mortality function, and that substantial error was introduced into pathogen transmission models when age-dependent mortality was not applied.² In addition to increased mortality rates, adverse age-related changes in mosquito flight,¹¹ immune function,¹² salivary gland structure,¹³ and detoxification mechanisms^14,15 have been reported, suggesting that mosquitoes are no different from most other organisms in experiencing deleterious functional and structural changes with age.

Over a decade ago, Gillies¹⁶ advocated that the assumption of age-independent mortality be “buried” because resulting estimates were, “at best, approximations.” Despite this admonition and growing evidence that mosquitoes senesce, non-senescence has continued to be assumed in even the most recent disease transmission models.^17–20 This reluctance to change can be attributed to two factors. First, there are no published reports that provide the detailed mortality trajectory necessary to properly test the assumption. Laboratory studies have generally used populations too small (N < 1,000) to detect differences, and data from field mortality studies are imprecise. Large populations are essential to characterize mortality early in life when few mosquitoes are dying and later in life when few mosquitoes remain alive.²¹ Second, the assumption of age-independent mortality greatly simplifies the mathematics of models and reduces the number and complexity of variables that need to be considered.²²

The major limitation of assuming non-senescence is that it leads to the unrealistic, simplified view that the vector potential of all mosquitoes is the same, regardless of their age. This age-independent assumption applies not only to mortality but also to other determinants of pathogen transmission; for example, biting rate, host preference, vector competence, dispersal, resistance to insecticides, and pathogen-induced adverse effects.²² The pervasiveness of the assumption is shown by the fact that, in the last 50 years, only a few publications have considered the effect of mosquito age on transmission factors.^{11,12,15,23–27} Moreover, because vector mortality is a particularly sensitive component of pathogen transmission, quantitative models that assume non-senescence produce results with substantial errors.²

To rigorously test the hypothesis that mosquitoes do senesce, we carried out two mortality studies, including the largest mosquito mortality study to date (N > 100,000) and a mortality study of blood-fed and reproductively active mosquitoes. To determine the epidemiologic implications of our results, we modified the vectorial capacity²⁸ model to include age-dependent survival and life expectancy values. Our study subject was Aedes aegypti, the most important vector worldwide of dengue virus and an urban vector of yellow fever.²⁹

MATERIALS AND METHODS

Large-scale mortality study

We used a colony of Ae. aegypti that was collected from Chachoengsao Province, Thailand, and had been in continuous culture for 1 year. Immature mosquitoes were raised on a standardized diet of a 1:1 mixture of liver powder and puppy chow (Day 1, 7.5 mg/larva; Day 2, 1 mg; Day 3, 0.5 mg; Day 4, 1 mg; Day 5, 2 mg; Day 6, 2 mg; Day 7, 1 mg) to produce large, robust adults. Pupae were collected, and adults were allowed to emerge into a 15 × 60 × 90-cm screened cage for 24 hours. Twenty-nine replicate cages, with a mean density of 3,500 mosquitoes, were established over a 15-month period. Larval and adult mosquitoes were maintained under semi-controlled climatic conditions (25–30°C; ~1°C daily fluctuations, 5°C drift in mean daily temperature; 25–50% RH, 12:12 L:D). Water and 10% sucrose solution were continuously available from cotton wicks introduced through ports in each cage. Each cage was inspected daily at the same time (±1 hour), and dead mosquitoes were removed. Censored deaths (accidental deaths and escapees) were similarly reported. To estimate adult body size,³⁰ intact wings were removed from dead mosquitoes, mounted on glass slides with double-sided tape, and measured as described in Scott and others.³¹ Cohort life tables were constructed according to Carey.³²

Fitting data to mortality models

We used the software WinModest 1.0³³ to determine the mortality model that best fit observed mortality patterns and to estimate model parameters. Standard mortality models are based on age-specific hazard, u_x, an instantaneous measure of mortality that can be estimated from empirical data with the approximation

$$u_x=-\text{ln}(p_x)$$ (1)

where p_x is the probability that an individual alive at age x survives to age x + 1.³² Briefly, the software fit a series of semi-hierarchical models to the data and calculated the log-likelihood for each model (Table 1). A large log-likelihood indicates a better fit. A test statistic of twice the difference in the log-likelihoods of the nested models was used to determine if the increase was significant.

TABLE 1.

Hazard functions for four semi-hierarchical mortality models used to fit observed mortality data^*

Model	Hazard function
Gompertz	ux = aebx
Gompertz-Makeham	ux = aebx + c
Logistic	$u_x=\frac{a{e}^{bx}}{1+\left(\frac{as}{b}\right)(e^{bx}-1)}$
Logistic-Makeham	$u_x=\frac{a{e}^{bx}}{1+\left(\frac{as}{b}\right)(e^{bx}-1)}+c$

^*Models are semi-hierarchical because with no mortality deceleration (s = 0), the logistic model can be simplified to a Gompertz model, and the logistic-Makeham model can be simplified to a Gompertz-Makeham model.

u_x, age-specific hazard rate; a, initial mortality rate; b, exponential mortality increase with age; x, age; c, age-independent mortality; s, degree of mortality deceleration.

We compared mortality parameters of male and female cohorts by calculating the difference between male and female parameters for each cage and performing the Wilcoxon signed-rank test (PROC UNIVARIATE).³⁴ This test was used to account for potential cage effects.

Mortality study of blood-fed mosquitoes

We conducted a second mortality study to determine the effect of blood feeding and reproduction on mortality. The F₂–F₄ generations of an Ae. aegypti colony obtained from pupae collected in Mae Sot Province, Thailand, were used. Immature mosquitoes were raised as described above. Pupae were collected, and adults were allowed to emerge into a 30 × 30 × 30-cm screened cage for 24 hours. Approximately 100 2-day-old adult males and 100 2-day-old females were placed into each of six 15 × 60 × 90-cm screened cages containing an oviposition cup and maintained under semi-controlled climatic conditions (25–30°C; ~1°C daily fluctuations, 5°C drift in mean daily temperature; 25–50% RH, 12:12 L:D). Oviposition cups consisted of a 60-mm petri dish containing a water-soaked sponge covered with two layers of filter paper. Each cage was assigned to one of three treatments (two cages per treatment): 10% sucrose, human blood, or human blood plus 10% sucrose. Mosquitoes in the blood treatments were given an opportunity to feed on a human forearm introduced into the appropriate cages for 15 minutes every day. The use of human subjects for feeding mosquitoes was approved and conducted in accordance with the University of California at Davis Human Subjects Protocol 991781. Water and 10% sucrose solution (if provided) were continuously available from cotton wicks introduced through ports in each cage. Each cage was inspected daily, dead mosquitoes were removed, censored deaths were recorded, oviposition cups were collected, and life tables were constructed. Oviposition data and its relation to mortality are discussed in another publication.³⁵ We used the software WinModest 1.0³³ to determine the mortality model that best fit observed mortality patterns and to estimate model parameters.

Age-dependent vectorial capacity model

To determine the epidemiologic implications of mosquito senescence for pathogen transmission, we derived an age-dependent vectorial capacity model and used it to compare the vectorial capacity²⁸ (predicted number of new infectious mosquito bites that result from one infectious host entering a naïve population) of simulated mosquito populations exhibiting age-independent versus age-dependent mortality with two age structures (stable age distribution and synchronous adult emergence). Specifically, the model considers the effect of mosquito age when first imbibing an infectious blood meal on subsequent vectorial capacity of that age cohort. The model defines three vectorial capacity concepts: 1) C_x = age-specific vectorial capacity: the daily number of potentially infective bites resulting from a mosquito of age x biting one infectious host; 2) C_x × Ω_x = age class-specific vectorial capacity: the daily number of potentially infective bites resulting from all mosquitoes of age class x biting one infectious host; and 3) C_t = total population vectorial capacity: the sum of age class-specific vectorial capacities over all biting age classes. C_x (age-specific vectorial capacity) is similar to the concept of individual vectorial capacity (IC) defined by Saul and others³⁶ as a function of age.

The modified model is described by the equation,

$$C_t={\displaystyle \sum _{x=\sigma }^{\mathrm{\omega }}[C_x\times {\mathrm{\Omega }}_x]={\displaystyle \sum _{x=\sigma }^{\mathrm{\omega }}\left[\left(m{a}^2{\displaystyle \prod _{i=x}^{x+n}{p}_i\times e_{x+n}}\right)({\mathrm{\Omega }}_x)\right]}}$$ (2)

where σ age at which mosquitoes begin biting hosts; ω = oldest biting age class of mosquitoes in the population; Ω_x = fraction of the population in age class x; m = mosquito density; a = mosquito daily biting rate; n = extrinsic incubation period; ${\displaystyle {\prod }_{i=x}^{x+n}{p}_i}$ = product of mosquito daily survival rates from age x when first biting an infectious host to age x + n, which is the end of the extrinsic incubation period; and e_x+n = expectation of remaining infectious life at age x + n. Model simulations were performed in Excel (Microsoft, Redmond, WA). The following values were used in the model and assumed to remain constant: σ = 3 days,²⁹ m = 1.5 mosquitoes/person,³⁷ a = 0.75 bites/d,³⁸ and N = 10 days.³⁷ The mean female mortality pattern from the large-scale study plus the best fitting logistic (a = 0.0018, b = 0.1416, s = 1.0730), Gompertz (a = 0.0066, b = 0.0623), and exponential (u_x = a, where a = 0.0313) mortality models were used in the modified vectorial capacity model; all mortality patterns had a mean lifespan of 32 days. We used two population age structures in our simulations: stable age distribution (derived from the Lotka equation³²) and synchronous emergence (total population was distributed equally among age classes 3, 4, 5, and 6 days). We calculated the stable age distribution separately for each mortality model, using the same birth rate (estimated from a laboratory reproductive study) and the appropriate mortality schedule.

We examined sensitivity of the vectorial capacity model to changes in overall mortality levels by adjusting parameters of the exponential, Gompertz, and logistic mortality patterns to achieve mean life spans of 5, 10, 16, 20, and 25 days and using this adjusted mortality data in the model.

RESULTS

Large-scale mortality study

We recorded the deaths of 101,051 Ae. aegypti (55,997 males and 45,054 females) housed in 29 experimental cages. Mean adult wing length was 3.14 ± 0.02 (SE) mm for females and 2.38 ± 0.03 mm for males.

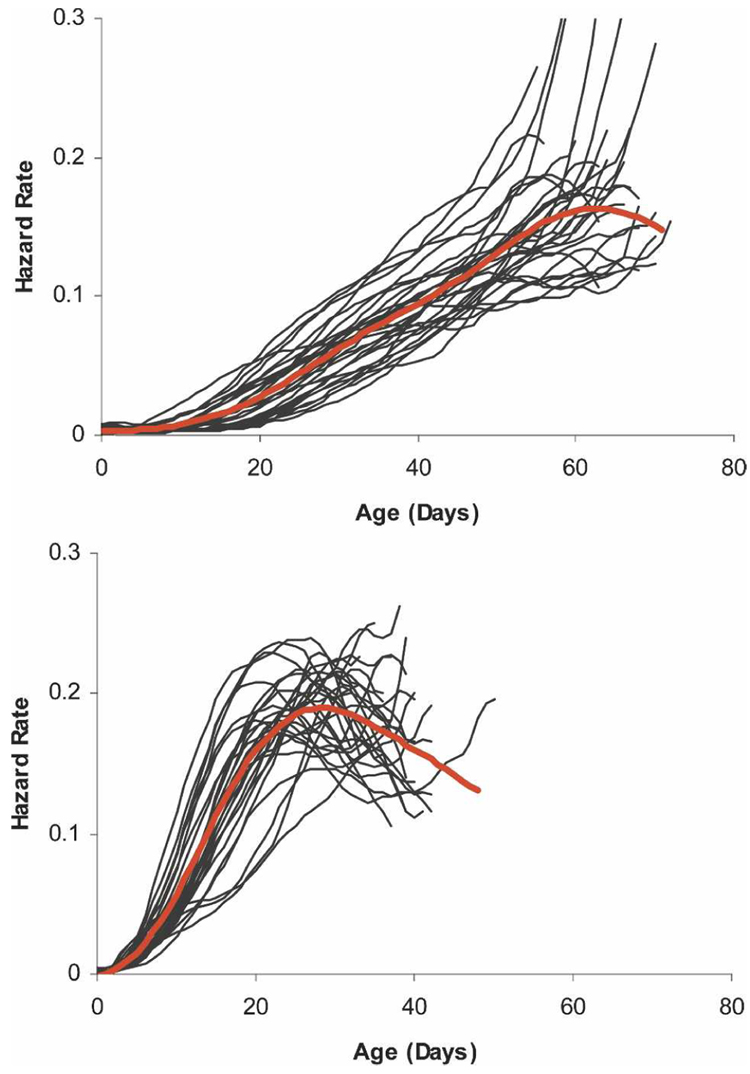
Although mortality patterns differed among cohorts, all cohorts exhibited age-dependent mortality. In general, mortality was low for young mosquitoes (< 10 days old), increased with age, and decelerated or declined at the oldest ages (Figure 1). Young mosquitoes are defined by very low mortality, which, in this laboratory study, was observed in mosquitoes < 10 days old.

FIGURE 1.

Smoothed hazard rate of 45,054 female and 55,997 male sucrose-fed Ae. aegypti housed in 29 cages (thin black lines). Thick red lines designate mean hazard rates for each sex. Hazard curves were derived and smoothed using local least squares regression.⁴⁹ Hazard curves were cut off at the point when 10 females or 10 males remained alive in each cage.

There were striking mortality and survival differences between the sexes. Female mortality was lower overall. Mean and median life span for females (31.69 ± 0.06 days; 31 days) was almost twice as long as males (16.39 ± 0.03 days; 16 days). Female maximum age (92 days) was nearly a third higher than the male maximum age (71 days).

Fitting data to mortality models

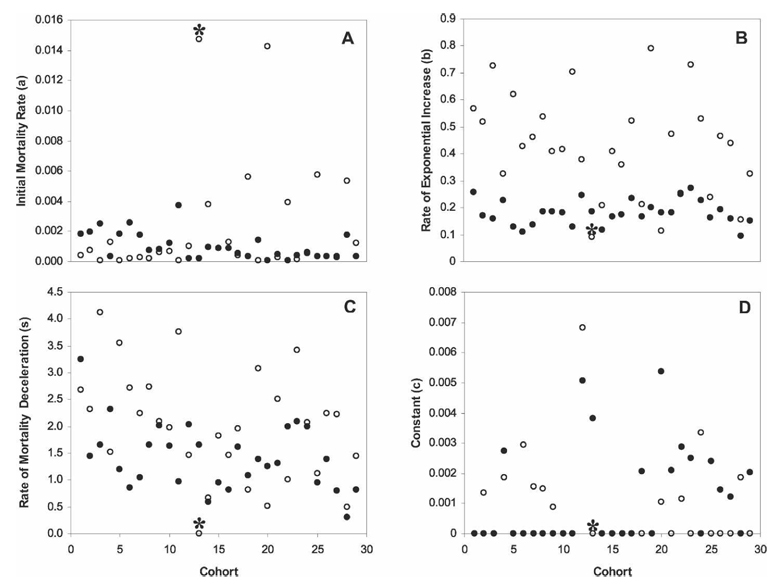
Logistic or logistic-Makeham models provided the best fit for mortality patterns of all female cohorts and 28 of 29 male cohorts (1 was best fit by the Gompertz model). Best-fit models for the combined data of all cohorts were similar: logistic-Makeham for males and logistic for females. Mortality model parameter values varied significantly between the sexes. Mean rate of exponential mortality increase (b) for female cohorts was less than one half that of male cohorts (0.163 ± 0.017 versus 0.357 ± 0.071, respectively; Wilcoxon signed rank = −206.5; P < 0.0001; Figure 2B). Similarly, mean rate of mortality deceleration (s) was significantly lower for females than males (1.417 ± 0.234 versus 2.001 ± 0.392, respectively; Wilcoxon signed rank = −123.5; P = 0.0053; Figure 2C). Other parameter values (a and c) did not vary significantly by sex (a: Wilcoxon signed rank = −16, P = 0.74; c: Wilcoxon signed rank = 25, P = 0.37; Figure 2A and D).

FIGURE 2.

Parameter values of best-fit mortality models for 29 cohorts of sugar-fed males (○) and females (●). All female cohorts and all but one cohort of males (best fit by Gompertz model, marked with an *) were best fit by a logistic or logistic-Makeham mortality model. Parameter values include initial mortality rate (a), rate of exponential increase (b), rate of mortality deceleration (s), and a constant term (c). Mortality models (Gompertz, Gompertz-Makeham, logistic, and logistic-Makeham.) were fit to the observed mortality data by WinModest 1.0.³³

Mortality study of blood-fed mosquitoes

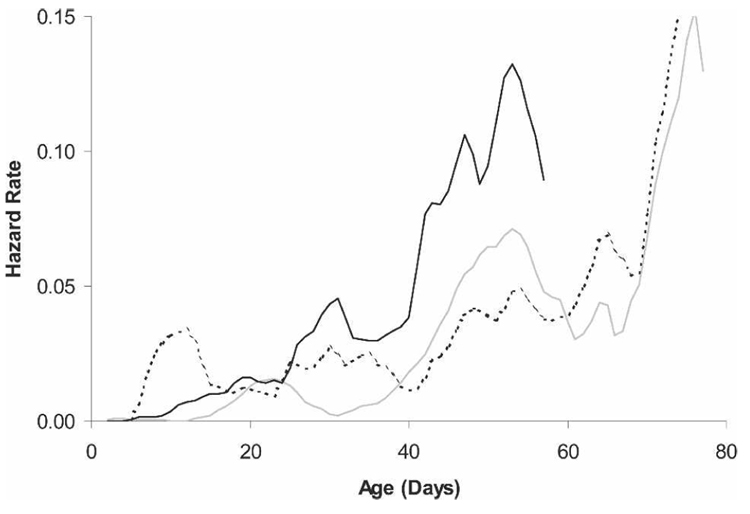
Female mosquitoes in all treatments exhibited age-dependent mortality with a pattern similar to that seen for females in the initial, large-scale experiment (Figure 3). Female mortality rates were lower in this study because of lower density (mean density, ~200 mosquitoes/cage) compared with the initial large-scale experiment (mean density, ~3,500 mosquitoes/cage). Mean (median) age of death for females in the sugar, blood, and blood plus sugar treatments was 37.4 ± 1.1 (38) days, 39.6 ± 1.8 (39) days, and 50.4 ± 1.4 (49) days, respectively. Similar to the large-scale experiment, female mortality patterns in all treatments were best fit by the logistic model.

FIGURE 3.

Smoothed hazard rate of female Ae. aegypti fed human blood (N = 187; dashed line), human blood plus 10% sucrose (N = 188; gray line), or 10% sucrose (N = 197; black line). Each line represents the combined data from two cohorts. Mortality curves were smoothed using a running geometric mean (width = 7).

Modeling age-dependent mortality

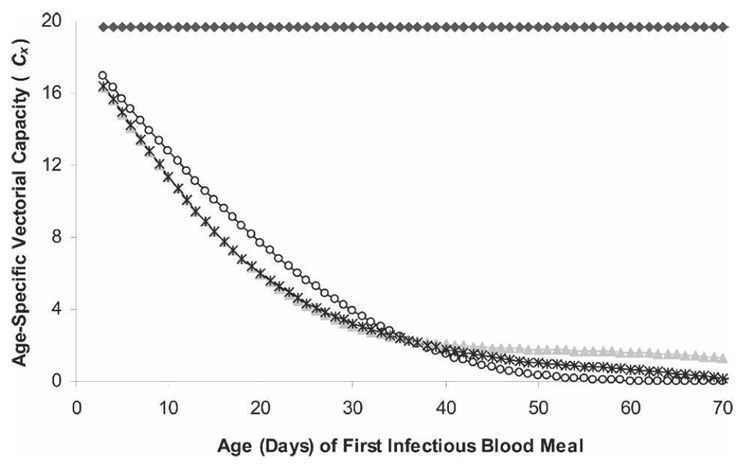
Mosquitoes exhibiting age-dependent mortality patterns (mean large-scale data, logistic and Gompertz) are more likely to transmit pathogens if they bite an infectious host when they are young (Figure 4). This occurs because 1) young mosquitoes are more likely to survive the extrinsic incubation period because of their lower mortality rate and 2) young mosquitoes have a longer life expectancy than old mosquitoes; thus, once infectious, they will likely transmit pathogens to more hosts than old mosquitoes (if other entomologic components of transmission remain constant with age). In contrast, under the assumption of age-independent mortality, a mosquito’s ability to transmit pathogens remains constant across all ages and results in a higher overall level of pathogen transmission (Figure 4).

FIGURE 4.

Vectorial capacity of mosquitoes at the age when first biting an infectious host (age-specific vectorial capacity). Mosquitoes exhibited one of four mortality patterns: exponential (♦), Gompertz (○), logistic (▲), or mean mortality from large-scale study (*). The number of mosquitoes in each age class is held constant for this simulation.

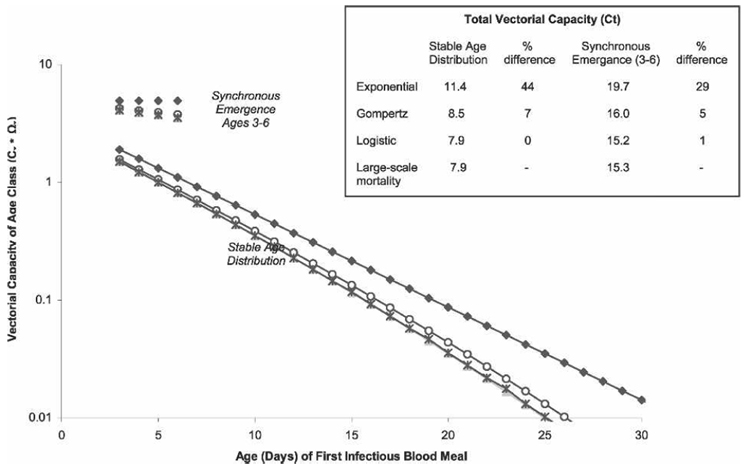
The conceptual shift from age-independent to age-dependent mortality requires knowledge of mosquito population age structure to fully understand pathogen transmission dynamics. Under the stable age distribution assumption, young mosquitoes contribute heavily to pathogen transmission, regardless of mortality pattern, because young individuals constitute the largest portion of the population (Figure 5). Having a population composed entirely of young individuals (synchronous adult emergence) increases total population vectorial capacity by 73–94%, regardless of mortality pattern compared with the stable age distribution (Figure 5, inset). The older this synchronous emergence population is before first being exposed to pathogens, the lower its predicted vectorial capacity (data not shown). Vectorial capacity of aging synchronous emergence populations decreases in direct proportion to the decrease in age-specific vectorial capacity (Figure 4).

FIGURE 5.

Vectorial capacity contributed by each age class of mosquito based on the age when they first bite an infectious host. Populations exhibited either synchronous emergence or stable age distribution age structures. Four mortality patterns were used: exponential (♦), Gompertz (○), logistic (▲), and mean mortality from large-scale study (*). Inset, Total population vectorial capacity (C_t) for each model/age structure combination and percent difference from mortality data from large-scale study.

For both age structures, the three mortality models (exponential, Gompertz, and logistic) differed in their ability to accurately predict vectorial capacity based on the large-scale mortality study. In both cases, using the simpler exponential model caused total vectorial capacity to be overestimated by 29–44%. The Gompertz model, while not the best fit to our data, performed much better, resulting in total vectorial capacity being overestimated by 5–7%. The best-fitting logistic model performed the best, producing an error rate of < 1% (Figure 5, inset).

Our sensitivity analysis indicated that as overall mortality increases (average lifespan [E₀] decreases), the potential for mosquito populations to transmit pathogens declines (Table 2). At all mortality levels, synchronous emergence populations have higher total vectorial capacity (C_t) values than stable age distribution populations because of the greater numbers of young mosquitoes. When lifespan is held constant (16 days), predicted vectorial capacity (C_t) can vary 2-fold depending on specific mortality parameters used. In general, total vectorial capacity is more sensitive to changes in b (exponential mortality increase with age) than a (initial mortality rate), which is understandable because b is exponentially, whereas a is multiplicatively related to overall mortality (Table 1).

TABLE 2.

Sensitivity of total vectorial capacity to changes in overall mortality and mortality parameter values

	Exponential			Gompertz				Logistic
E0	a	Ct SAD	Ct Syn	a	b	Ct SAD	Ct Syn	a	b	s	Ct SAD	Ct Syn
5	0.2	0.2	0.6	0.04	0.469	0.0	0.0	0.0237	0.8	1	0.0	0.0
10	0.1	1.5	3.1	0.018	0.231	0.1	0.3	0.007	0.44	1	0.1	0.3
16	0.0625	3.8	7.2	0.011	0.143	1.4	3.3	0.002	0.332	1	1.1	2.5
16	–	–	–	0.018	0.1006	1.7	3.9	0.00589	0.22	0.5	1.2	2.9
16	–	–	–	0.0228	0.08	2.0	4.3	0.00815	0.22	1	1.5	3.3
16	–	–	–	0.028892	0.06	2.2	4.7	0.01168	0.22	1.5	1.8	3.8
16	–	–	–	0.04	0.0331	2.7	5.5	0.0221	0.14	1	2.2	4.5
20	0.05	5.6	10.2	0.01	0.1047	3.0	6.4	0.003	0.2238	1	2.6	5.6
25	0.04	8.0	14.1	0.00848	0.08	5.2	10.4	0.002	0.187	1	4.6	9.5
32	0.0313	11.4	19.7	0.00662	0.06234	8.5	16.0	0.00182	0.1416	1.073	7.9	15.2

E₀, expectation of life at birth (in days); a, initial mortality rate; b, exponential mortality increase with age; s, degree of mortality deceleration; c_t-SAD, total vectorial capacity for population at the stable age distribution; C_t-Syn, total vectorial capacity for synchronous emergence population (population evenly dispersed in age classes 3, 4, 5, and 6).

DISCUSSION

Our results show that both male and female Ae. aegypti senesce, exhibiting mortality that increases initially with age and decelerates or declines at the oldest ages. We detected senescence in laboratory populations of sugar-fed and blood-fed (and thus reproductively active) mosquitoes. In addition, there were large sex-specific differences in mortality. Males exhibited higher overall mortality rates than females, had increased rates of mortality acceleration early in life, and a greater mortality decline late in life.

Importantly, the companion paper to this one³⁹ shows senescence in free-ranging Ae. aegypti in Thailand. That study used a novel synthetic cohort technique in which mosquitoes of different ages were released simultaneously into homes in a Thai village and subjected to recapture over a short period of time (2 days). Recapture rates decreased with mosquito age, which was consistent with the hypothesis that mortality increases with age. Age-dependent recapture rates could not be explained by differences in mosquito dispersal by age.

Logistic or logistic-Makeham models provided the best fit to female mortality data from both laboratory mortality studies. This result is similar to other large-scale studies on a variety of organisms including yeast, nematodes, flies, and humans, in which mortality deceleration was seen at the oldest ages.⁴⁰ Previous studies reported that female mortality of several mosquito species follows a Gompertz function.^2,6 Those earlier studies, however, generally used small sample sizes (< 1,000) and did not fit results to mortality models other than the Gompertz model.

Our results indicate that the age at which a mosquito bites an infectious host is critical for determining the probability that it will transmit a pathogen. The importance of old mosquitoes has long been recognized because they are the only ones that could have survived long enough to become infectious (i.e., survived to an epidemiologically dangerous age). Our simulations show that young mosquitoes are more important than may have been generally appreciated. Because of increasing risk of mortality with advancing age, a mosquito that first imbibes pathogen-infected blood when it is young has a greater potential to transmit pathogens to more hosts during its lifetime than one that first takes an infected meal when it is old. Younger mosquitoes have lower mortality and thus are more likely to survive through the pathogen incubation period to become infectious than old conspecifics.

Because of the impact of mosquito age on pathogen transmission rates, understanding mosquito population age structure is important. In our simulations, mosquito populations of the same size but with different age structures were predicted to produce significantly different levels of pathogen transmission. For example, when a pathogen, such as West Nile virus or Plasmodium falciparum, first enters an area because of migration of infectious vertebrate hosts or initiation of seasonal transmission, a young mosquito population is epidemiologically most “dangerous” because it consists entirely of individuals with low mortality rates. They have the highest probability of a few surviving long enough to become infectious after biting an infectious host. This type of age structure can be created if large numbers of adult mosquitoes emerge synchronously, an event that can be triggered by seasonally heavy rainfall or temperature increases. Several mosquito species including Anopheles dirus,⁴¹ a vector of malaria in Thailand, and Ochlerotatus provocans,⁴² a vector of Jamestown Canyon virus, have been shown to exhibit large synchronous emergences caused by heavy seasonal rainfall and the seasonal appearance of temporary aquatic development sites. All else being equal, vectorial capacity of populations composed of synchronously emerged adults will be high initially, decrease as the number of young mosquitoes declines, and increase again as the next generation emerges. Populations with a stable age distribution—which is our general expectation for the subject of our study, Ae. aegypti^31,43—will tend, over time, to have more constant vectorial capacity because of continuous adult emergence. Other factors, such as temperature, which can affect pathogen transmission by expanding or contracting extrinsic incubation, may have more of an impact on intra-annual or seasonal fluctuations in dengue transmission than age structure of Ae. aegypti populations. Without perturbations in Ae. aegypti density caused by vector control, over longer periods of time, inter-annual or between-year fluctuations in endemic dengue transmission are most likely associated with shifts in herd immunity.⁴⁴

Our results have three important implications. First, departure from the paradigm of constant mortality frees us to view mosquitoes and the diseases they transmit as complex, dynamic systems, not ones that can be easily described by static age-independent models. At the organismal level, this opens up a plethora of largely unexplored topics like those regarding physiologic processes that cause senescence, the effect of senescence on mosquito behavior, and the large mortality differential between the mosquito sexes. At a larger scale, mosquito senescence leads to unanswered questions concerning the effect of variable death rates on life history and evolution of insect vectors and the pathogens they transmit. At a molecular level, previously unconsidered age-dependent changes in the genetic underpinnings of a mosquito’s role in pathogen transmission (i.e., gene expression) merit study.

Second, within the paradigm of age-dependent mortality, existing methods to study mosquito populations are no longer adequate. New innovative methods must be developed to better understand mosquito population dynamics. Currently the most widely used age-grading technique for Ae. aegypti can only separate mosquitoes into two age classes (parous, > 5 days old; non-parous, < 5 days old).⁴⁵ New age-grading techniques with greater discriminatory power need to be developed, as well as novel means to study aging in wild mosquitoes. Techniques such as cuticular hydrocarbon age-grading^46,47 and the synthetic cohort method^39,48 are examples of such new methods.

Third, our results indicate that age-dependent factors should be included in vector-borne disease transmission models to accurately describe and predict the dynamics of pathogen transmission. Many vector-borne diseases have no clinical cure or vaccine; vector control is the primary option available to contain and prevent pathogen transmission. A more complete and accurate description of pathogen transmission will improve the efficiency by which control measures are developed, administered, and evaluated.

We expect that the phenomenon of mosquito age-dependent mortality is not limited to Ae. aegypti. Because of the important effects of mortality on pathogen transmission, patterns of mortality for virtually all arthropod vectors merit review within the context of their significance to disease in humans and other animals.