Hind limb scaling of kangaroos and wallabies (superfamily Macropodoidea): implications for hopping performance, safety factor and elastic savings

Abstract

The aim of this study was to examine hind limb scaling of the musculoskeletal system in the Macropodoidea, the superfamily containing wallabies and kangaroos, to re-examine the effect of size on the locomotor mechanics and physiology of marsupial hopping. Morphometric musculoskeletal analyses were conducted of 15 species and skeletal specimens of 21 species spanning a size range from 0.8 to 80 kg that included representatives of 12 of the 16 extant genera of macropodoids. We found that unlike other groups, macropodoids are able to match force demands associated with increasing body size primarily through a combination of positive allometry in muscle area and muscle moment arms. Isometric scaling of primary hind limb bones suggests, however, that larger species experience relatively greater bone stresses. Muscle to tendon area ratios of the ankle extensors scale with strong positive allometry, indicating that peak tendon stresses also increase with increasing body size but to a lesser degree than previously reported. Consistent with previous morphological and experimental studies, large macropodoids are therefore better suited for elastic strain energy recovery but operate at lower safety factors, which likely poses an upper limit to body size. Scaling patterns for extant macropodoids suggest that extinct giant kangaroos (∼250 kg) were likely limited in locomotor capacity.

Introduction

Terrestrial mammals encompass a vast size range and employ a number of different gaits to move through the environment. Studies of scale effects on locomotion have predominantly focused on quadrupedal mammals (Alexander et al. 1981; Biewener, 1989, 1990; Pollock & Shadwick, 1994), although a few have investigated the effect of body size on bipedal hopping mammals (Bennett & Taylor, 1995; Bennett, 2000). The mechanical demands of bipedal hopping suggest that animals using this gait may scale differently from other mammals. Biomechanical challenges posed by increasing body size have long been recognized. As animals become larger, the gravitational forces they must resist increase in direct proportion to their body mass, whereas the capacity of musculoskeletal structures to support these forces increases in proportion to cross-sectional area. For geometrically similar animals (Schmidt-Nielson, 1984), stresses (force/area) are therefore predicted to increase proportional to body mass (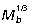). Because the material properties of the musculoskeletal structures are relatively consistent among vertebrates (Close, 1971; Wainwright et al. 1976; Biewener, 1982; Bennett et al. 1986; Curry, 2002), allometric scaling of musculoskeletal geometry and changes in posture likely play an important role in enabling animals to operate over a wide range of sizes (Biewener 1989, 1990).

Within hopping mammals, locomotor performance in relation to body size has been linked to a trade-off between the capacity for elastic energy storage and tendon safety factor. Analysis of tendon design and acceleration capacity has shown that the ankle extensors of kangaroo rats, small heteromyid rodents (∼0.10 kg), are more robust for their size, compared to larger wallabies (∼10 kg). This appears to reflect their need to withstand relatively high forces during the large accelerations used to escape predators (Kenagy, 1973; Biewener et al. 1981; Biewener & Blickhan, 1988). Conversely, larger macropodoid marsupials, such as wallabies and kangaroos (> 5 kg), are capable of storing substantial amounts of elastic strain energy in their long, relatively thin Achilles tendons (Alexander & Vernon, 1975; Ker et al. 1986; Biewener et al. 1995). Indeed, a comparison between kangaroo rats and kangaroos suggests that kangaroos would likely rupture their tendons if they were to accelerate at the magnitudes achieved by kangaroo rats (Biewener & Bertram, 1991).

Species of Macropodoidea, the superfamily containing kangaroos, wallabies and rats kangaroos, span a broad size range from ∼0.5 to 85 kg. All macropodoids appear to maintain similar limb dimensions and employ bipedal hopping as their primary mode of locomotion (Windsor & Dagg, 1971). An anatomical scaling study of ankle extensor musculature of macropodoids supports the conclusion that elastic energy storage capacity increases with body size (Bennett & Taylor, 1995). Because skeletal muscles produce force in proportion to their recruited fiber cross-sectional area, following an approach developed by Ker et al. (1988), Bennet & Taylor (1995) used the ratio of muscle fiber area to tendon area (A_m/A_t) to estimate maximal tendon stress, strain energy storage capacity, and tendon safety factor (failure stress/maximum functional stress) for the ankle extensor tendons in macropodoid marsupials. Largely due to strong positive allometry in muscle fiber area, these workers found that A_m/A_t scales with strong positive allometry in macropodoids (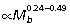), indicating that larger animals generate larger ankle extensor tendon stresses, enabling them to store more elastic strain energy (∝stress²). However, the capacity for elastic energy savings is traded off against a reduced tendon safety factor at larger size. A similar, but less strong, pattern of positive A_m/A_t allometry has also been observed at the ankle in quadrupedal mammals (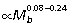; Pollock & Shadwick, 1994).

As quadrupedal mammals become larger, they tend to shift from a more crouched to a more upright posture, which decreases the requirements of force transmission in musculoskeletal structures by increasing the effective mechanical advantage (EMA = muscle moment arms/external moment arms) of the muscles. Biewener (1989) found that limb muscle EMA scales 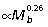in quadrupedal mammals. Over a similar range of mammals, muscle moment arms (r) scale 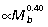(Alexander, 1981), suggesting that external moment arms of the ground reaction force (R) scale with strong negative allometry (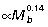). In contrast to the general pattern observed for quadrupedal mammals, macropodoid ankle extensor EMA has been shown to be independent of body size (Bennett & Taylor, 1995), consistent with the strong positive allometry of muscle area (and force) measured for these muscles. This suggests the skeletal elements of the hind limb must also experience higher forces. Based on measurements of macropodoid tibia section modulus and second moment of area, Bennett (2000) concluded that larger macropodoids likely operate with higher bone stresses but have a greater resistance to bending than similarly sized quadrupedal mammals.

In this study, we examine how the entire hind limb musculoskeletal system of macropodoids scales to accommodate increasing force demands due to increasing body size. We revisit the proposed functional trade-off between elastic energy storage capacity and tendon safety factor to assess whether this may limit body size within this group. An anatomical survey including cadaveric and/or skeletal specimens from 30 of the 50–60 extant species of macropodoids was conducted to examine scaling patterns of the principal long bones and primary extensor musculature of the hind limb.

Materials and methods

Cadaveric measurements

Fresh specimens of 15 species from the superfamily Macropodoidea, ranging from 0.60 to 27 kg, were examined in this study (Table 1). These include representatives from both subfamilies, Potoroidae and Macropodidae, and cover a wide range of body size and phylogenetic diversity. All fresh specimens were obtained from wildlife and zoological parks in South Australia and New South Wales, Australia, with the approval of the University of Adelaide Animal Ethics Committee. Some specimens were eviscerated when obtained and intact body masses were estimated based on a value for gut content of 18% of body mass, which was the mean measured for five intact specimens. All specimens were collected after the animals had died or been killed for other purposes and were either dissected fresh or stored frozen until used.

Table 1.

List of species used for soft tissue and skeletal measurements

	Cadavers		Skeletons
	n	body mass (kg ± sd)	n	body mass (kg)†
Potoroidae
Aepyprymnus rufecsens			2	2.3
Bettongia lesueur	1	1.36
Bettongia penicillata	2	0.86 ± 0.11	3
Hypsiprymnodon moschatus			1
Potorous tridactylus	4	0.79 ± 0.13	2
Macropodidae
Dendrolagus bennettainus			1
Dendrolagus lumholtzi			1
Dorcopsis luctosa			2
Dorcopsis sp.			1
Lagorchestes hirsutus			3
Macropus agilus	2	10.46 ± 2.74*
Macropus dorsalis	2	6.31 ± 0.08*	1
Macropus eugenii	5	6.64 ± 0.52	2
Macropus eugenii flindersi			3
Macropus fuligenosus			1	80.0
Macropus giganteus	3	23.47 ± 0.91*
Macropus irma			1
Macropus perryi			1	15.7
Macropus robustus	2	15.15 ± 3.61	1
Macropus rufogrisius	3	13.76 ± 6.28*
Macropus rufus	1	27.30
Petrogale lateralis			2	3.5
Petrogale lateralis pearsoni	1	2.59*
Petrogale xanthopus	6	5.78 ± 1.64	2
Setonix brachyurus			1	3.0
Setonix sp.	2	2.89 ± 1.46
Thylogale billardierri			2
Thylogale thetis	2	4.66 ± 0.58*
Wallabia bicolor	3	11.77 ± 6.04	3	18.0

^*Body mass estimated for gutted specimens assuming gut contents constituted 18% body weight (see Materials and methods).

^†Body mass data from museum records for a single specimen.

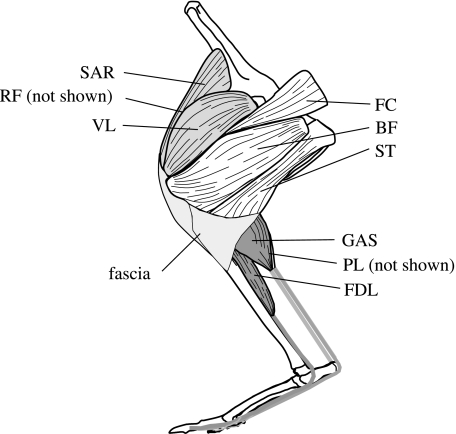
During dissection, hind limb segment length measurements were made of the femur, tibia, metatarsals and longest toe using digital calipers. Measurements were also taken from the major extensor muscles of the hind limb (Fig. 1) as determined from the literature (Badoux, 1965; Lodder, 1991). Hip extensors included the biceps femoris (BF), femorococcygeus (FC), and semitendinosus (ST); knee extensor muscles included the vastus lateralis (VL), rectus femoris (RF) and sartorius (SAR); and ankle extensor muscles included the medial and lateral heads of the gastrocnemius (GAS), plantaris (PL) and flexor digitorum longus (FDL). All muscles were dissected free and weighed to the nearest 1.0 mg on a digital balance. Muscles were then sectioned in a plane parallel to the muscle fibers using a scalpel or sharp knife, depending on the size of the muscle. Muscle fascicle length and pennation angle were measured at regular intervals (∼five per muscle) with digital calipers and a protractor (Alexander, 1983; Roberts et al. 1998).

Fig. 1.

Schematic drawing of the left hind limb of a macropodoid showing the muscles examined in this study. Hip extensors (light grey): femorococcygeus (FC), biceps femoris (BF), and semitendinosus (ST). Knee extensors (white): sartorius (SAR), rectus femoris (RF) and vastus lateralis (VL). Ankle extensors (dark grey): gastrocnemius (GAS), plantaris (PL) and flexor digitorum longus (FDL).

As an estimate of each muscle's force producing capacity, physiological cross-sectional area (PCSA) was calculated based on the following equation:

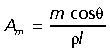(1)

where A_mis the cross-sectional area of the muscle in cm³, m is the muscle mass in g, θ is pennation angle in degrees, ρ is muscle density in g cm⁻³ and l is muscle fascicle length. A value of 1.06 g cm⁻³ was assumed for muscle density (Mendez & Keys, 1960). The calculation of PCSA corrects for the fact that not all of the force in a pennate muscle is directed parallel to the line of action of the muscle.

Prior to removal from the animal, the average extensor moment arm (r) was measured for each muscle. Moment arms were measured as the perpendicular distance from the line of action of the muscle to the joint center of rotation, with the joint angle held in approximately a mid-stance position (when peak forces are most likely to occur). As an estimate of a muscle group's combined action at joint, a weighted mean moment arm (r¯) was calculated based on each muscle's moment arm (r), PCSA (Am) and the combined area of the muscles acting at that joint (Biewener, 1989).

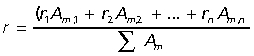(2)

To estimate tendon safety factors and their capacity for elastic energy storage, the tendons of the GAS, PL and FDL were dissected free, measured and weighed to the nearest 0.1 mg wet weight. The PL and FDL tendons were removed at the phalanges. The regions of these tendons that pass over the calcaneus and ankle joint have been shown to have a lower elastic modulus than the rest of the tendon (Ker et al. 1986) and were thus removed before weighing. Tendon cross-sectional area was calculated from mass, length and density, assuming a density of 1.12 g cm⁻³ (Ker, 1981). Tendon volume was determined by assuming a uniform cross-sectional area and multiplying by total tendon length (calculated by subtracting muscle fascicle length from the total length of the muscle–tendon unit: Alexander & Vernon, 1975; Biewener, 1995).

Tendon safety factors were estimated based on the ratio of muscle PSCA to tendon cross-sectional area (A_m/A_t) following Ker et al. (1988). Because muscles and tendons act in series, the maximal force experienced by the tendon cannot be greater than that produced by the muscle. Thus, maximal tendon stress can be calculated as the product of the area ratio and the maximal stress of the muscle (Ker et al. 1988; Pollock & Shadwick, 1994). In mammalian muscles, maximal isometric stress ranges between 200 and 300 kPa (Biewener, 2003). To facilitate comparisons with previous studies and because muscles can exert greater stress when actively stretched, a value of 300 kPa was assumed and maximal tendon stress (σ_t) was calculated as:

(3)

Tendon safety factor was calculated by dividing the failure strength of tendon, assumed here to be 100 MPa (Bennett et al. 1986), by maximal stress (σ_t). However, other results suggest the failure strength of tendon may be 20–40% higher (Wang & Ker, 1995).

In addition to calculating safety factors, maximal tendon stress (σ_t) was used to estimate the capacity for elastic energy storage and recovery in ankle extensor tendons. To calculate elastic energy recovery, we assumed an elastic modulus of 1.0 GPa, following Biewener & Baudinette (1995). This is lower than values reported for wallabies and other mammalian tendons stressed to rupture (1.2–1.7 GPa; Ker et al. 1986; Bennett et al. 1986; Pollock & Shadwick, 1994), but corresponds to the elastic modulus of tendons operating over the functional stress range observed in vivo for tammar wallabies (Biewener & Baudinette, 1995). Elastic strain energy return was calculated using the following equation:

(4)

where σ_t is the peak stress in the tendons in MPa, E is the elastic modulus (1.0 GPa) and V_t is the total volume of the tendons in m³. The constant 0.93 accounts for a 7% loss in energy recovery due to tendon hysteresis (Bennett et al. 1986; Shadwick, 1990).

Fiber length factor

Muscle fiber length factor (L) is the ratio of muscle fiber length to tendon length change when the tendon is maximally loaded (Ker et al. 1988; Pollock & Shadwick, 1994). Tendon length change (ΔL_t) was calculated from tendon length (L_t), maximal tendon stress (σ_t) and elastic modulus (E) according to the following equation:

(5)

Fiber length factor has been used to characterize muscle tendon units that favor elastic energy storage (L < 2) vs. those that are better suited for force transmission and control of joint displacement (L > 4) (Ker et al. 1988; Pollock & Shadwick, 1994).

Skeletal measurements

Measurements were made on the postcranial skeletons of 21 species of macropodoids in the collection at The Museum of South Australia (Table 1). Skeletal dimensions were measured using digital calipers or a measuring tape (for measurements over 200 mm). For each specimen, measurements of bone length and midshaft diameter were made on the femur, tibia, the largest (4th) metatarsal and longest phalanx (4th). However, many specimens were incomplete, and the distal elements were not available for more than two-thirds of those sampled. Femur length was measured from the most proximal point of the greater trochanter to the distal-most point of the femoral condyles. Tibia length was measured from the most proximal point on the tibial tuberosity to the inferior articular surface. Metatarsal length was measured from the most proximal point on the articular surface with the cuboid to the most distal point on the articular surface with the phalanx. Femoral, tibial and metatarsal diameters were measured in the anterior–posterior (A–P) or dorsoventral (metatarsal) direction, at each bone's midshaft. Limb segments were measured for all cadaveric specimens and the five skeletal specimens for which body mass (M_b) data were available. Phalanx measurements from the skeletons were considered unreliable and thus only the phalanx measurements from the cadavers were included in the final analysis.

Statistical analysis

Scaling coefficients (a) and exponents (b) were determined using model I (least squares) and model II (reduced major axis, RMA) regressions of log transformed data. All variables were regressed against body mass unless otherwise noted. Model I regression slopes are reported in the text to facilitate comparison with previously published work; however, RMA regression is generally considered a more reliable method of determining regression slopes as neither variable can be considered to be independent and without measurement error (LaBarbera, 1989). In most cases there was little difference between slopes generated by model I and model II regression due to high correlation coefficients. Instances where there were differences are noted and discussed. When multiple specimens were available, means were generated for individual species and are reported as means ± standard deviations.

Results

Limb segment scaling

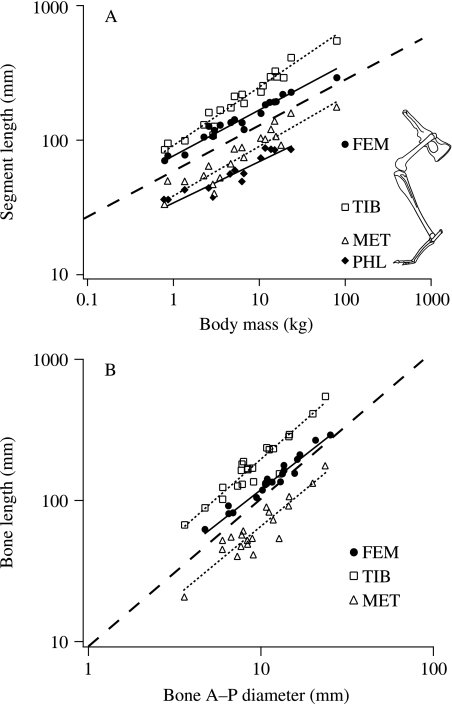
Measurements of limb segment length show that the overall length of the macropodoid hind limb scales with positive allometry (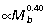), predominantly due to strong positive allometry of the tibia (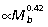, Fig. 2A). The metatarsal segment also tends to scale with positive allometry (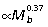) but is not significantly different from isometry (slope of 1/3). The femur scales isometrically (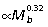), whereas the 4th phalanx tends to be relatively smaller in larger animals (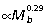), although also not significantly different from isometry. Due to the uniformly high correlation coefficients, reduced major axis regression does not significantly change limb segment scaling relationships.

Fig. 2.

(A) Scaling relationships for individual hind limb segment lengths vs. body mass (M). The inset shows the four segments measured: femur (FEM), tibia (TIB), metatarsals (MET) and the longest phalanx (PHL). (B) Length–diameter plots for the three principal long bones of the hind limb. Solid and dotted lines represent least-squares regression lines. The broken line represents the predicted isometric slope of 1/3 and 1 in (A) and (B), respectively. Least-squares regression equations: (A) FEM l = 79.68M^0.32, r² = 0.95; TIB l = 92.06M^0.42, r² = 0.95; MET l = 39.88M^0.37, r² = 0.85; PHL l = 35.38M^0.29, r² = 0.87. (B) FEM l = 14.26d^0.93, r² = 0.96; TIB l = 17.49d^1.04, r² = 0.90; MET l = 6.64d^0.99, r² = 0.84.

Bone scaling

Scaling of bone length to bone diameter provides a measure of the relative robustness of individual bones. For the skeletal specimens (Table 1), all hind limb long bone length versus diameter measurements scale with exponents close to the isometric slope of 1.0 (Fig. 2B). Only the femur tends to be more robust in larger animals (l∝d^0.93), but is not significantly different from isometry. On average, long bone dimensions scale as l∝d^0.99. RMA exponents are slightly higher for all regressions, but again not significantly different from isometry.

Muscle scaling

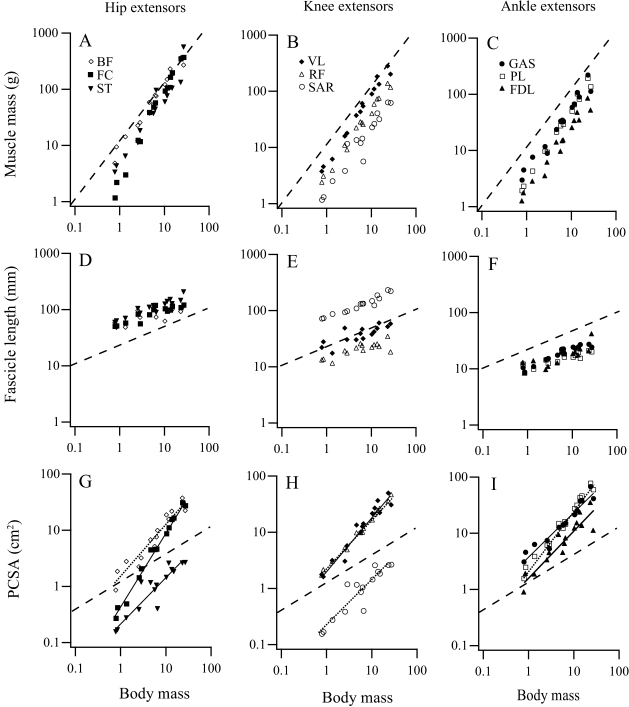
Results from least-squares regressions of muscle mass vs. body mass indicate that for all muscles, except the sartorius and the combined heads of the gastrocnemius, muscle mass scales with significant positive allometry (Fig. 3A–C,Table 2). Reduced major axis regression, however, indicates that the exponent for the gastrocnemius is also significantly greater than the isometric slope of 1.0. Collectively, hind limb extensor muscle mass scales 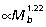in macropodoids. Across all sampled muscles, fascicle length tends to scale with negative allometry (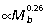). Least-squares regression exponents are significantly less than geometric similarity in four of the nine muscles measured. However, RMA regression indicates that only the plantaris muscle scales with significant negative allometry (Fig. 3D–F,Table 2).

Fig. 3.

Scaling of muscle mass (A–C), fascicle length (D–F) and physiological cross-sectional area (PCSA; G–I) for the principal extensor muscles of the hind limb. Muscles are grouped in columns by joint and include hip extensors (A,D,G): biceps femoris (BF), femorococcygeus (FC), and semitendinosus (ST); knee extensors (B,E,H): vastus lateralis (VL), rectus femoris (RF) and sartorius (SAR); and ankle extensors (C,F,J): gastrocnemius (GAS), plantaris (PL) and flexor digitorum longus (FDL). Broken lines represent isometric slopes for each of the conditions (mass, b = 1; length, b = 1/3; PCSA, b = 2/3). Regression equations and statistics are provided in Table 2.

Table 2.

Constants for allometric equations describing the hind limb muscles of the Macropodoidae

	Muscle mass (g)					Fascicle length (mm)					PCSA (cm2)
	a	b	r2	RMA b	± 95 % C.I.	a	b	r2	RMA b	± 95 % C.I.	a	b	r2	RMA b	± 95 % C.I.
Hip extensors
Biceps femoris	8.6	1.14	0.98	1.15	0.10	57.4	0.19	0.57	0.25	0.10	1.43	0.94	0.93	0.98	0.16
Femorococcygeus	2.3	1.61	0.99	1.62	0.11	55.5	0.25	0.82	0.27	0.07	0.43	1.33	0.99	1.34	0.09
Semitendinosus	4.6	1.22	0.94	1.26	0.18	65.1	0.29	0.89	0.31	0.06	0.66	0.95	0.91	1.00	0.18
Knee extensors
Vastus lateralis	5.1	1.23	0.99	1.24	0.09	23.7	0.26	0.67	0.32	0.11	2.06	0.96	0.94	0.99	0.14
Rectus femoris	3.2	1.14	0.99	1.15	0.07	10.1	0.21	0.64	0.26	0.09	2.17	0.90	0.99	0.90	0.05
Sartorius	1.7	1.11	0.93	1.15	0.19	73.3	0.31	0.93	0.33	0.05	0.22	0.81	0.85	0.88
Ankle extensors
Gastrocnemius	4.3	1.11	0.97	1.14	0.12	10.7	0.31		0.33	0.06	3.84	0.78	0.94	0.81	0.12
Plantaris	2.8	1.28	0.99	1.28	0.08	10.6	0.21	0.73	0.24	0.08	2.41	1.04	0.98	1.05	0.09
Flexor digitorum longus	1.8	1.13	0.97	1.15	0.12	10.0	0.29	0.67	0.36	0.12	1.60	0.84	0.87	0.90	0.20
Mean exponents		1.22		1.24			0.26		0.30			0.95		0.98

The equations are in the form y = aM^b where M is body mass in kg. Data are plotted in Fig. 3.

Bold values indicate a significant difference from isometric exponents (mass = 1.0, length = 0.33, PCSA = 0.67).

PCSA = physiological cross-sectional area.

RMA b = reduced major axis regression exponent.

Strong positive allometry for muscle mass and a tendency towards negative allometry for muscle fascicle length results in extremely strong positive allometry for all hind limb muscle PCSA, 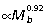(Fig. 3G–I). Least-squares regression indicates that nearly all muscles scale with exponents significantly greater than predicted by geometric similarity. Based on RMA regression, only scaling of the sartorius PCSA fails to differ from isometry (Table 2).

Ankle extensor muscle-tendon scaling

The major ankle extensors – gastrocnemius (GAS), plantaris (PL) and flexor digitorum longus (FDL) – are relatively short fibered muscles with long thin tendons, which likely play the predominant role in elastic strain energy storage and recovery during hopping (Alexander & Vernon, 1975; Biewener et al. 1995). Tendon cross-sectional area of the GAS (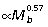) and FDL (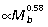) scale with negative allometry, becoming relatively thinner with increased body size, whereas the PL scales with positive allometry (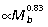) (Table 3). The overall lengths of the ankle extensor muscle–tendon units closely match size-related changes in tibial length (Fig. 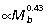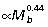2A), scaling with strong positive allometry (GAS , PL , FDL ).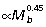

Table 3.

Constants for allometric equations describing the ankle extensor muscle–tendon units of the Macropodoidae

	Gastrocnemius					Plantaris					Flexor digitorum longus
	a	b	r2	RMA b	± 95 % C.I.	a	b	r2	RMA b	± 95 % C.I.	a	b	r2	RMA b	± 95 % C.I.
Tendon area (mm2)	3.24	0.57	0.93	0.60	0.09	2.06	0.84	0.95	0.86	0.12	3.72	0.58	0.88	0.62	0.13
MTU length (mm)	80.3	0.46	0.93	0.47	0.08	137.9	0.42	0.94	0.44	0.07	126.2	0.42	0.95	0.43	0.07
Area ratio (Am/At)	118.6	0.21	0.69	0.25	0.08	117.1	0.21	0.46	0.30	0.13	43.0	0.26	0.36	0.43	0.21
Safety factor	2.8	–0.21	0.69	–0.25	0.08	2.8	–0.21	0.46	–0.30	0.13	7.7	–0.26	0.36	–0.43	0.21
Elastic strain energy (J)	0.16	1.48	0.93	1.54	0.26	0.17	1.69	0.95	1.74	0.24	0.03	1.70	0.94	1.75	0.29
Fiber length factor	4.15	–0.40	0.68	–0.48	0.17	2.36	–0.42	0.51	–0.59	0.26	7.01	–0.54	0.66	–0.67	0.27

The equations are in the form y = aM^b where M is body mass in kg. Data are plotted in Figs 3 and 4.

Bold values indicate significant difference from isometric exponents (area = 0.67, length = 0.33, area ratio, safety factor and fiber length factor = 0.0, strain energy = 1.0).

RMA b = reduced major axis regression exponent. MTU = maximum transmission unit.

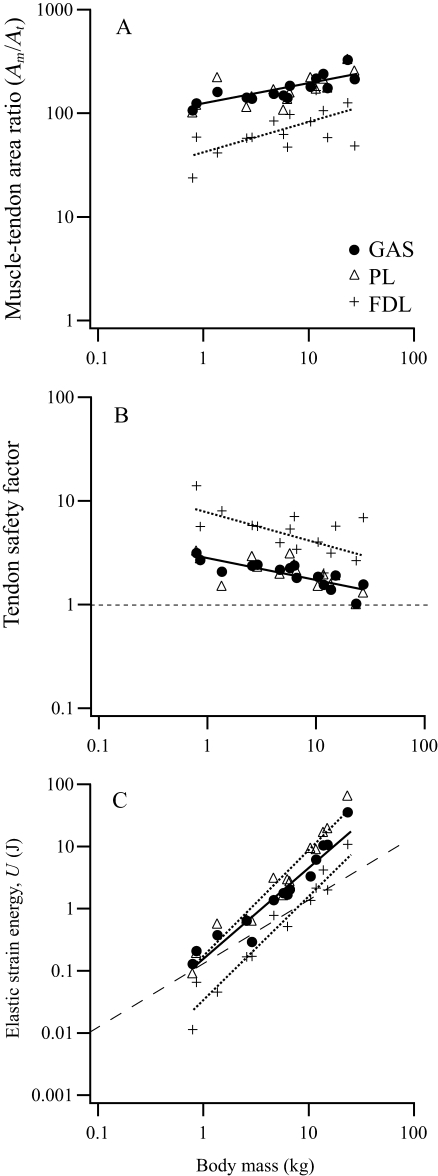
Muscle PCSA vs. tendon cross-sectional area ratios (A_m/A_t) were calculated for the ankle extensors to estimate tendon safety factors and their capacity for elastic energy savings (Table 3). Geometric similarity predicts A_m/A_t ratios to be independent of body size. However, due to the strong positive allometry of muscle area (Fig. 3I,Table 2), A_m/A_t also increases with increasing body size in all three muscles (Fig. 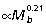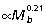3A; GAS , PL , FDL 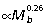). Estimates of maximum tendon safety factor based on A_m/A_t, therefore, decline with increasing size (Fig. 3B). Because A_m/A_t and tendon volume increase with size, the capacity for elastic energy savings is much greater in larger animals, scaling 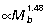, 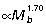and 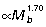for the GAS, PL and FDL muscle–tendon units, respectively (Fig 3C).

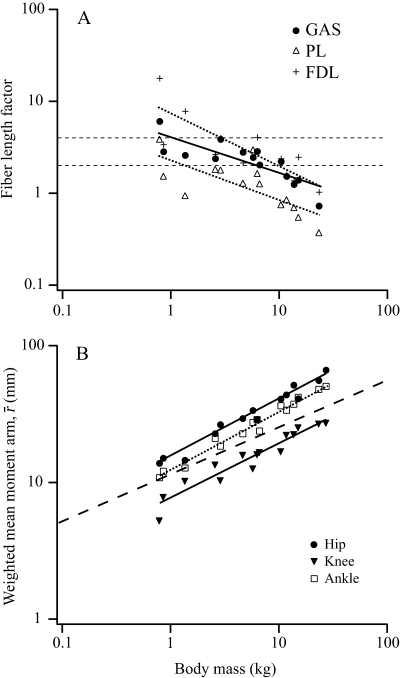
Fiber length factor (FLF) was found to scale with negative allometry in all three ankle extensors (Fig. 5A,Table 3), indicating their predominant role in elastic savings (FLF < 2) in larger animals. PL_FLF indicates a role in elastic energy recovery in all but the smallest macropodoids, whereas GAS_FLF is predicted to fall below 2 at ∼6 kg in body mass. FDL_FLF indicates a shift from control of joint position (FLF > 4) for animals under 2.5 kg to providing substantial elastic energy savings for animals over 10 kg.

Fig. 5.

(A) Scaling of fiber length factor (FLF) for the ankle extensors muscles. Muscles with FLF < 2 (lower dotted line) are considered to be well suited for elastic energy storage, whereas muscles with FLF > 4 (upper dotted line) likely play a more important role in controlling joint displacement. Regression equations are provided in Table 3. (B) Scaling relationships for weighted mean extensor muscle moment arms (r¯) at each joint. The broken line represents the isometric slope of 1/3. Solid and dotted lines represent least squares regression lines. Least-squares regression equations: hip r¯ = 14.97M^0.43, r² = 0.97, C.I. ± 0.04; knee r¯ = 7.51M^0.40, r² = 0.92, C.I. ± 0.07; ankle r¯ = 12.17M^0.43, r² = 0.98, C.I. ± 0.05.

Moment arms

Weighted mean moment arms (r¯), calculated at each joint based on muscle PSCA, assess each agonist muscle group's ability to counteract external joint moments. At all joints, r¯ scales with positive allometry relative to geometric similarity (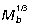; Fig. 5B), with hip and ankle both scaling 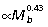and the knee 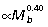. Thus in larger animals, forces produced by each muscle group generate relatively larger joint moments.

Discussion

This study sought to determine how body size affects the structure–function relationship of the hind limb musculoskeletal system of macropodoids (superfamily Macropodoidea). Nearly all members of this group hop bipedally at moderate to fast speeds and have comparable hind limb geometry. Previous studies of distal musculoskeletal structure of macropodoids and other bipedal hoppers indicate that these species do not fit the scaling patterns observed across comparably sized quadrupedal mammals, suggesting that larger macropodoids may operate with unusually high musculoskeletal stresses (Biewener & Bertram, 1991; Bennett & Taylor, 1995; Bennett, 2000). Additionally, we sought to re-evaluate trade-offs in musculoskeletal design for acceleration vs. elastic energy recovery relative to body size, for which tendon safety factor might be a limiting factor of body mass or performance within this group.

The results of our analysis indicate that, unlike quadrupedal mammals and birds, macropodoids meet increasing force demands associated with increasing body size primarily through a combination of positive allometry of muscle area (A_m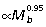) and muscle moment arms (r¯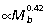). This is most apparent at the knee and ankle where scaling of joint moment capacity, estimated from muscle area and moment arm relations (knee: 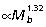, ankle: 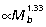), matches well the external (gravitational) moments predicted by isometry (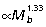). In contrast, hip muscle moments scale 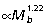, indicating the capacity of larger macropodoids for generating proportionately more torque for their size. The strong positive allometry observed for muscle area results from positive allometry in muscle mass (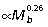) and negative allometry in fascicle length (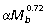) and is similar to results reported for the ankle by Bennett & Taylor (1995) for a comparable group of macropodoids. The negative allometry of muscle fiber length in larger animals is similar to that reported for quadrupedal mammals (Alexander, 1981). However, muscle mass scales isometrically with body size in quadrupeds, so that the increase in muscle area (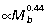) is not nearly as great as observed in macropodoids.

Segment scaling and limb muscle EMA

Over a broad size range, quadrupedal mammals reduce external moments through changes in joint angles, which lead to more upright postures that reduce ground reaction force (GRF) moment arms (R; Biewener, 1989, 1990). In contrast, larger macropodoids do not appear to hop with a more erect posture than smaller species (Bennett & Taylor, 1995; McGowan, 2006). Nevertheless, the analysis here of skeletal allometry suggests that differential scaling of individual hind limb segment lengths likely leads to non-isometric scaling of GRF joint moments. Larger macropodoid species have relatively longer hind limbs due to strong positive allometry of the tibia (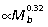, Fig. 2A); whereas the femur (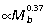) and the foot (metatarsals: 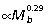and toes: 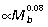) scale close to isometry. Consequently, if joint angle ranges during ground support remain similar across body size, R would be largely unaffected at the ankle but would tend to increase at the knee and decrease at the hip in larger animals. Based on segment scaling and positive allometry of r¯ (Fig. 5B), we would expect ankle EMA (r¯/R) to scale with positive allometry, knee EMA to scale close to isometry, and hip EMA to scale with strong positive allometry. Data from EMA scaling patterns calculated from GRF and muscle impulse measurements over a limited sample and size range of animals (four species, 1.0 to 6.5 kg) are largely consistent these expectations (ankle: 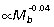, knee: 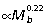, hip: 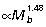, McGowan, 2006). This scaling prediction for ankle EMA differs from that of Bennett & Taylor (1995), who observed no change in EMA with increasing body mass, based on calculations for a single mid-stance limb position and assumed vertical GRF. Ground reaction force and muscle impulse data for a wider size range of species will be required to resolve this difference and to determine whether preliminary scaling trends for the hind limb joints observed by McGowan (2006) are maintained in larger hopping animals.

Bone scaling

Isometric scaling of long bone length vs. diameter suggests larger macropodoids experience greater bone stresses than smaller species. This is consistent with the calculations of Alexander & Vernon (1975), who estimated tibial stresses to be 1.75× greater in an adult red kangaroo (42 kg) than in a juvenile red kangaroo (6.6 kg) hopping at comparable speeds. Their calculations were based on the assumption of geometric similarity, although the authors commented this assumption may be unlikely due to the high stresses calculated for the larger animal. In a later study, Bennett (2000) reported positive allometric scaling for the second moment of area (I) of macropodoid tibiae (∝M^1.52). Results reported here for the five species for which skeletal and body mass measurements were available (Table 1) indicate that tibial diameter scales isometrically with body size (d = 5.56M^0.33; r² = 0.98). These patterns suggest that bone cortical thickness may increase with size, which would counter the increase in bone stress predicted from length and diameter alone. The scaling of the muscle cross-sectional area of macropodoids suggests that musculoskeletal forces are relatively greater in larger animals. Measurements of limb loading in combination with recordings of in vivo bone strain would provide experimental data to test whether skeletal stresses do in fact increase, and safety factors decrease, with increasing size.

Functional role of macropodoid ankle extensors and the scaling of elastic energy storage

Mammalian ankle extensors are typically short fibered muscles connected in series with relatively long thin tendons, a design well suited for the storage and recovery of elastic strain energy during bouncing gaits such as running, trotting and hopping (Alexander 1988; Biewener & Roberts, 2000). Consistent with previous studies of hopping (Bennett & Taylor, 1995) and non-hopping mammals (Pollock & Shadwick, 1994), our results suggest that the capacity for elastic energy savings in the three primary ankle extensor tendons scales strongly with body size (mean ∝M^1.62; Table 3;Fig. 4C). Due to their larger size and longer moment arm at the ankle, the GAS and PL are likely to play the greatest role, consistent with what has been observed in vivo for tammar wallabies (Biewener et al. 1995). Scaling of elastic energy storage capacity for the tendons of these two muscles is much greater than reported for quadrupedal mammals (∝M^1.28; Pollock & Shadwick, 1994) but less than reported previously for macropodoids (∝M^1.89, Bennett & Taylor, 1995).

Fig. 4.

Scaling of (A) muscle/tendon area ratios, (B) tendon safety factor and (C) elastic energy storage capacity for the major ankle extensors; gastrocnemius (GAS), plantaris (PL) and flexor digitorum longus (FDL). Isometry predicts area ratios and tendon safety factor to be independent of body mass (lines not shown), so that elastic energy storage capacity is predicted to scale in proportion to body mass (C, broken line). The dashed horizontal line in (B) indicates the level at which the estimate of peak muscle stress would cause tendon rupture (i.e. a stress > 100 MPa). Solid and dotted lines represent least-squares regression lines. Regression equations are provided in Table 3. Note: GAS and PL regressions lines overlap in (A) and (B).

Scaling of fiber length factor (FLF) reinforces the strong size-dependent change in the functional role of the ankle extensors (Fig. 5A) Above ∼10 kg body mass, all of the ankle extensors have a FLF < 2, indicating that they are well suited for elastic energy storage (Ker, 1988; Pollock & Shadwick, 1994). Below this size, only the PL appears to remain predominantly adapted for elastic energy recovery. The scaling of muscle–tendon architecture suggests that the GAS and FDL are likely to play a more intermediate role between spring-like energy savings and joint control. In the smallest macropodoids, the potoroids (< 3 kg), the FDL and GAS are predicted to contribute mainly to joint control and favor acceleration capacity, rather than elastic savings during steady speed hopping.

Tendon safety factor and limits on body size

Because the capacity to store and recover elastic strain energy in tendons requires high tendon stresses, selection for this design necessarily must be traded-off against a lower safety factor. The scaling relationship of muscle vs. tendon cross-sectional area (Fig. 4A) observed across macropodoids indicates that within this group, larger species are better able to utilize elastic energy recovery, but also operate with lower tendon safety factors. Our results indicate that safety factors for the GAS and PL tendons scale ∝M^−0.21 (Fig 3B,Table 3), suggesting that hopping macropodoids could reach a size of ∼140 kg before safety factors would fall below one. This is considerably higher and perhaps more realistic than the 35–40 kg limit proposed by Bennett & Taylor (1995). By our calculations, the largest extant species (male red kangaroos Macropus rufus∼85 kg) operate with safety factors possibly as low as 1.1 assuming an ultimate tendon strength of 100 MPa. However, other studies suggest tensile rupture strengths may be as high as 150 MPa (Bennett et al. 1986; Wang & Ker, 1995). Even so, the yield strength of a tendon likely represents a more realistic functional limit, especially for repeated locomotor loading. Regardless which value of tendon strength is used, it is clear that tendon safety factor substantially limits the largest body size of hopping macropodoids.

The fact that tendon safety factor poses an upper limit on body size in macropodoids raises the interesting question as to how extinct giant kangaroos moved. Fossil evidence suggests that several extinct species of macropodoids likely reached sizes of 150 kg or more, and the largest, Procoptodon goliah, is estimated to have weighed as much as 250 kg (Johnson & Prideaux, 2004; Murray, 1991; Helgen, et al. 2006). All of these species exhibit the same limb skeletal morphology associated with bipedal hopping in extant species (Szalay, 1994). Based on our analysis, P. goliah would be predicted to have a tendon safety factor of ∼0.89. Consequently, if this group followed the scaling trajectory of modern species, it is unlikely that they would have been capable of saltatory hopping as a locomotor gait, even at moderate speeds. These extremely large fossil forms would also likely have been severely limited in their ability to accelerate. Interestingly, nearly all large Australian mammal species (> 45 kg), including giant macropodoids, became extinct at about the time humans are believed to have reached Australia. One prevailing theory for this extinction event is human impact, possibly from over-hunting (Flannery, 1990; Roberts, et al. 2001; Johnson & Prideaux, 2004). If giant kangaroos were indeed limited in locomotor performance, as our study suggests, they would have likely made easy prey for early hunters.

Alternatively, extinct massive kangaroos may not have scaled with the same trajectory predicted by modern species. A recent study (McGowan et al. 2006) shows that at least one species of rock wallabies (Petrogale xanthopus, yellow footed rock wallaby) have significantly thicker tendons than similarly sized tammar wallabies. The thicker tendons of this species appear well suited to withstanding the high forces associated with negotiating the steep, rocky terrain of their native habitat. To the extent that tendon thickness represents a phenotypically plastic trait that is selected for, giant kangaroos may have had relatively thicker tendons, which would have enabled them to exert the higher forces needed for acceleration and saltatory hopping at their large size.

In conclusion, the increasing biomechanical demands of support and locomotion associated with larger body size within extant species of Macropodoidea are met by substantial allometric scaling of the hind limb musculoskeletal system. Unusually strong positive allometry of muscle physiological cross-sectional area coupled with positive allometry of muscle moment arms enable larger species to support greater joint torques with relatively little change in limb posture. This mechanism for dealing with the demands of increasing body size is thus far unique to macropodoids and differs from other groups of animals that have been investigated. Consistent with previous observations, larger macropodoid species have a relatively greater capacity for elastic energy recovery but operate with relatively lower tendon safety factors.