Evoked brain responses are generated by feedback loops

Abstract

Neuronal responses to stimuli, measured electrophysiologically, unfold over several hundred milliseconds. Typically, they show characteristic waveforms with early and late components. It is thought that early or exogenous components reflect a perturbation of neuronal dynamics by sensory input bottom-up processing. Conversely, later, endogenous components have been ascribed to recurrent dynamics among hierarchically disposed cortical processing levels, top-down effects. Here, we show that evoked brain responses are generated by recurrent dynamics in cortical networks, and late components of event-related responses are mediated by backward connections. This evidence is furnished by dynamic causal modeling of mismatch responses, elicited in an oddball paradigm. We used the evidence for models with and without backward connections to assess their likelihood as a function of peristimulus time and show that backward connections are necessary to explain late components. Furthermore, we were able to quantify the contribution of backward connections to evoked responses and to source activity, again as a function of peristimulus time. These results link a generic feature of brain responses to changes in the sensorium and a key architectural component of functional anatomy; namely, backward connections are necessary for recurrent interactions among levels of cortical hierarchies. This is the theoretical cornerstone of most modern theories of perceptual inference and learning.

Event-related potentials (ERPs) or event-related fields (ERFs) in electroencephalography (EEG) and magnetoencephalography (MEG) are among the mainstays of noninvasive neuroscience. Typically, the response evoked by a stimulus evolves in a systematic way, showing a series of waves or components. Many of these components are elicited so reliably that they are studied in their own right. These include very early sensory-evoked potentials, observed within a few milliseconds; early cortical responses such as the N1 and P2 components; and later components expressed several hundred milliseconds afterward. Broadly speaking, ERP components can be divided into early and late (1). Early- or short-latency stimulus-dependent (exogenous) components reflect the integrity of primary afferent pathways. Late stimulus-independent (endogenous) components entail long-latency (>100 ms) responses thought to reflect cognitive processes (1, 2). Early components have been associated with exogenous bottom-up stimulus-bound effects, whereas late components have been ascribed to endogenous dynamics involving top-down influences. Indeed, the amplitude and latency of early (e.g., P1 and N1) and late (e.g., N2pc) components have been used as explicit indices of bottom-up and top-down processing, respectively (3). Here, we demonstrate that late components are mediated by recurrent interactions among remote cortical regions; specifically, we show that late components rest on backward extrinsic corticocortical connections that enable recurrent or reentrant dynamics.

This enquiry has been enabled by recent advances in the analysis of EEG data, specifically, dynamic causal modeling (DCM). A detailed description of DCM can be found elsewhere (4–8). DCM represents a departure from conventional source reconstruction or inverse solutions to the EEG problem by using a full spatiotemporal forward model that embodies known constraints in the way EEG sources are generated. Put simply, these constraints require that electrical activity in one part of the brain be caused by activity in another. This is modeled explicitly in terms of neuronal subpopulations that influence each other through intrinsic and extrinsic corticocortical connections. The parameters of these models cover not only the expression of cortical sources at the electrodes but also the time constants and coupling parameters that define the network of sources. Model inversion by using DCM allows us to estimate these key parameters.

The focus of this article is on the role of backward connections in the elaboration of long-latency ERP responses. We compared models with and without backward connections and looked at the contribution of forward and backward connections to predicted responses at the source level, as a function of peristimulus time. In brief, we recorded EEG from healthy subjects while listening to a stream of auditory tones embedded in an oddball paradigm. Here, we analyze only the ERP elicited by the deviant stimulus and report our results at both the subject and group levels, by using the ERP averaged over trials within-subject and over all subjects. In all analyses, we compared two models; both had the same source architecture but were distinguished by the presence of backward connections among sources (see Fig. 1).

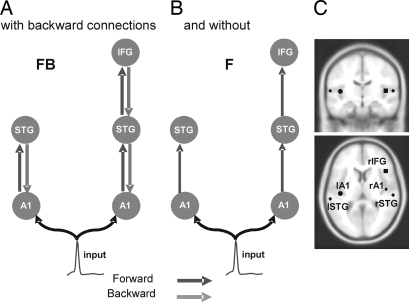
Fig. 1.

Model specification. The sources comprising the network are connected with backward (gray) and/or forward (dark gray) connections as shown. A1, primary auditory cortex; STG, superior temporal gyrus; IFG, inferior temporal gyrus. Two different models were tested within the same architecture, with and without backward connections (A and B, respectively). (C) Sources of activity, modeled as equivalent dipoles (estimated posterior moments and locations), are superimposed in an MRI of a standard brain in MNI space and their prior mean locations are: lA1 [−42,−22, 7], rA1 [46, −14, 8], lSTG [−61, −32, 8], rSTG [59, −25, 8], rIFG [46, 20, 8], in millimeters.

Results

Dynamic Causal Models Specification.

The network architecture was motivated by recent electrophysiological and neuroimaging studies looking at the sources underlying Mismatch Negativity (MMN), an event-related response to violations in the regularity of an auditory sequence (9, 10). We assumed five sources, modeled as equivalent current dipoles (ECD), over left and right primary auditory cortices (A1), left and right superior temporal gyrus (STG), and right inferior frontal gyrus (IFG). Our mechanistic model attempts to explain the generation of responses to deviants. Left and right A1 were chosen as cortical input stations for processing auditory information. Opitz et al. (9) identified sources for the differential response, with functional MRI (fMRI) and EEG measures, in both left and right STG and right IFG. Here, we use the coordinates reported in ref. 9 (for left and right STG and right IFG) and in ref. 11 (for left and right A1) as prior source location means, with a prior variance of 16 mm² (see Fig. 1C). We converted these coordinates, given in the literature in Talairach space, to MNI space by using the algorithm described in http://imaging.mrc-cbu.cam.ac.uk/imaging/MniTalairach. The dipole moment parameters had prior mean of zero and a variance of 256 mm² in each direction.

By using these sources and prior knowledge about functional anatomy, we constructed the following DCM: An extrinsic input entered bilaterally to primary auditory cortex (A1), which were connected to their ipsilateral STG. Right STG was connected with the right IFG. Given this connectivity graph, specified in terms of its nodes and connections, we tested two models. These differed in terms of the presence of reciprocal or recurrent connections: model FB had reciprocal, i.e., forward and backward connections, and model F lacked backward connections, having forward connections only (Fig. 1 A and B). In other words, model FB resembles recurrent dynamics or parallel bottom-up and top-down processing, whereas model F emulates a simple bottom-up mechanism.

ERPs and Bayesian Model Comparison.

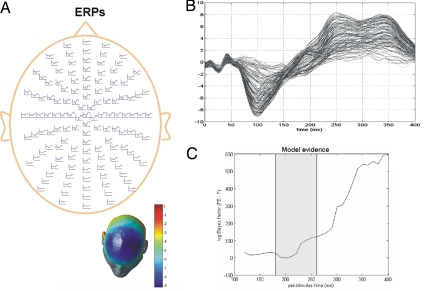
We modeled the ERP elicited by the deviants by using a DCM with these five sources (compare equivalent current dipoles), as in previous analyses of mismatch differences (5, 8). The evoked response to the deviant peaked on average at ≈100 ms and had a widespread negative topography at the frontal electrodes, in agreement with previous studies (Fig. 2A). The free parameters of these models included the location and orientation of each dipole, excitatory and inhibitory rate constants, and postsynaptic densities for the (three) subpopulations of neurons within each source, intrinsic (within-source) coupling strengths and extrinsic (between-sources) coupling. Extrinsic connections were divided into forward and backward and conformed to the connectivity rules described in refs. 7 and 12. These rules allow one to build a network of coupled sources linked by extrinsic connections. Within this model, bottom-up or forward connections originate in the infragranular layers and terminate in the granular layer; top-down or backward connections link agranular layers, and lateral connections originate in infragranular layers and target all layers. All these extrinsic corticocortical connections are excitatory and are mediated through the axons of pyramidal cells. To test the hypothesis that backward connections mediate late components selectively, we evaluated the model-evidence L_i = p(y|θ, m_i) ≈ exp(F_i) for models m₁ and m₀, with and without backward connections as a function of peristimulus time; FB and F, respectively (see Fig. 2C). This involved inverting the model by using data, from stimulus onset to a variable poststimulus time, ranging from 120 to 400 ms, in 10 ms steps. A difference in log-evidence of ≈3 is usually taken as strong evidence for one model over the other (i.e., the likelihood of one model is ≈20 times the other). We compared the evidence, or marginal likelihood (13), of the two models as a function of increasing peristimulus time windows both for the grand average ERP across subjects and for each subject individually (Figs. 2C and 3, respectively). Both analyses revealed the same result. The longer evoked responses evolve, the more likely backward connections appear. For the group data, this is evident in Fig. 2C, which shows that the model with backward connections (FB) supervenes over the model without (F). This is particularly clear later in peristimulus time (220 ms poststimulus or later).

Fig. 2.

Bayesian model comparison among DCMs of grand mean ERPs. (A) Grand mean ERP responses, i.e., averaged over all subjects, to the deviant tone overlaid on a whole-scalp map of 128 EEG electrodes. (B) Overlapped ERP responses to deviant tones from all 128 sensors over the peristimulus interval [0, 400] (in milliseconds). (C) Differences in negative free-energy or log-evidence comparing the model with backward connections (FB) against the model without (F). The gray patch indicates the interval chosen to model the ERPs for each individual subject (see Fig. 3).

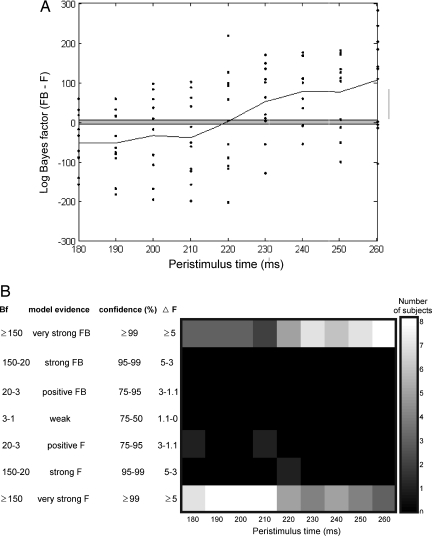
Fig. 3.

Bayesian model comparison across subjects. (A) Comparison of the model with backward connections (FB) against the model without (F), across all subjects over the peristimulus interval 180–260 ms. The dots correspond to differences in log-evidence for 11 subjects over time. The solid line shows the average log-evidence differences over subjects [this is proportional to the log-group Bayes factor (Bf) or to the differences in the free energy of the two models (ΔF); see Materials and Methods for details]. The points outside the gray zone imply very strong inference (≥99% confidence that one model is more likely), i.e., model FB supervenes over F for positive points and the converse for negative points. (B) Histogram showing the number of subjects in each of seven levels of inference on models with and without backward connections across the peristimulus interval 180–260 ms.

At the suggestion of one of our referees, we also evaluated a backward connection-only model for completeness (and to further ensure the validity of our model selection procedure). As anticipated, this model had much lower evidence than either the forward or forward and backward models considered here (over all peristimulus times examined).

Motivated by these results, we selected a window of interest; 180–260 ms for expediency, to perform an identical analysis for each subject. Our results for individual subjects recapitulated the group analysis (Fig. 3). For the majority of subjects (8 of 11), the forward model supervenes over the model with backward connections, when explaining the data in the first half of peristimulus time. Conversely, in the second half, for most subjects (8 of 11), the model with backward connections supervenes over the model without. This means that forward connections are sufficient to explain ERP generation in early periods, but backward connections become essential in later periods. This effect occurs after 220 ms and is more evident for longer latencies. In short, backward connections are not necessary to explain early data and only incur a complexity penalty, without increasing accuracy. This does not mean backward connections are “switched off;” it simply means their effects are not manifest until later in peristimulus time, by which time activity has retuned from higher levels. At this point, backward connections become necessary to explain the data. This can be seen quantitatively in a plot of the log-evidence over time and qualitatively in terms of the number of subjects supporting each model at larger peristimulus time (Fig. 3 A and B, respectively).

Conditional Contribution of Extrinsic Coupling.

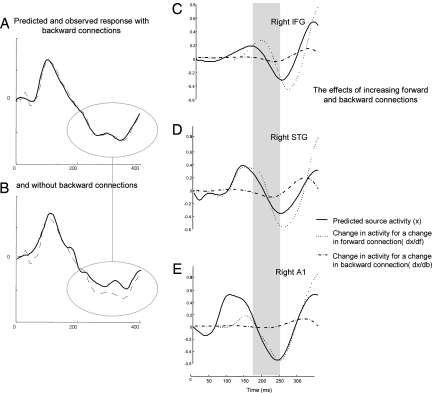
Finally, we evaluated the contribution of forward and backward connections to predicted responses at the channel and source levels, by using the conditional mean of the model parameters, μ, from the model with backward connections for the group data (see Fig. 4). We quantified the change in predicted responses, ∂x(μ,t)/∂θ, at the source level, x, for a change in θ, for selected forward or backward connections. The model parameter θ quantifies the extrinsic coupling in the forward or backward connections linking two remote areas; it encodes how much the activity in one area influences the activity of another. Fig. 4 C–E show traces of how source activity would change at right A1, STG, and IFG, because of increment changes in forward and backward connections. It can be seen that unit changes in forward connections have a profound effect on responses throughout peristimulus time, whereas backward connections show a temporal selectivity, in that they modulate the expression of late components (dx/db is mostly flat for early peristimulus time, <200 ms). In other words, an increment change in the connectivity of a forward connection will cause the source activity to change throughout the whole peristimulus time, whereas an increment change in a backward connection will cause the source activity to change considerably for long latencies but will have no effect early in time. The idea that backward connections are necessary to explain late ERP components is also supported by the remarkable improvement of model fit later in peristimulus time for model FB (afforded by backward connections). Conversely, both models provide an equally good fit when modeling ERP responses at early latencies (see Fig. 4 A and B). This means the backward connections add unnecessary complexity, which is why the forward model has a greater log-evidence in, and only in, early phases of the ERP (see Fig. 3A). These graphs show predicted and observed responses with and without backward connections projected onto the first eigenmode of a principal component analysis (PCA). It is evident that the model fit improves later in time, after ≈200 ms, by adding backward connections to the network. This is coincident with the time interval for which Bayesian model comparison revealed that the model with backward connections explains the data much better at both group and individual subject levels.

Fig. 4.

Contribution of extrinsic coupling to source activity. The graphs show predicted (solid) and observed (broken) responses in measurement space for the first spatial mode, which was obtained after projection of the scalp data onto eight spatial modes, for (A) FB model and (B) F model. The first mode accounts for the greatest amount of observed variance. The improvement of model fit due to backward connections for later components is evident. Predicted responses at each source (solid line) and changes in activity with respect to a unit change in forward (dotted line) and backward connection (dash-dotted line) for (C) right IFG, (D) right STG, and (E) right A1. The gray bar covers the same period of peristimulus time as in Fig. 2.

Discussion

Having established face (4) and predictive validity (8) of DCM, we use it here to provide direct evidence for the theoretical prediction that evoked brain responses are mediated by reentrant dynamics or top-down effects in cortical networks and therefore rest on backward connections. This is an explicit statistical test of the hypothesis that evoked responses depend on top-down effects (1, 2). Furthermore, we hoped to quantify the relative contribution of bottom-up and top-down effects under a biologically informed model. Our results show that backward connections are necessary to explain late neuronal responses. This evidence was furnished by comparison of models of oddball responses with and without backward connections. Bayesian model comparison revealed that the model with backward connections explains both group and individual data better than the model with forward connections only. This was particularly evident for long latencies (>200 ms; see Figs. 2 C and 3). Furthermore, we were able to quantify the contribution of backward connections to evoked responses (in both channel and source space) as a function of peristimulus time. As expected, our results show that forward connections have a profound effect on responses throughout peristimulus time, whereas backward connections show a temporal specificity, in that they mediate the expression of late components (>200 ms).

Backward connections are an important part of functional brain architectures, both empirically and theoretically. The distinction between forward and backward connections rests on the notion of cortical hierarchies and the laminar specificity of their cells of origin and termination (14). Anatomically, backward connections are more abundant than forward connections (in the proportion of ≈1:10/20) and show greater divergence and convergence. Forward connections have sparse axonal bifurcations and are topographically organized, whereas backward connections show abundant axonal bifurcation and diffuse topography transcending various hierarchical levels. Functionally, backward connections have a greater repertoire of synaptic effects: whereas forward connections mediate postsynaptic effects through fast AMPA and GABA_A receptors (constant decay of ≈1–6 ms), backward connections also mediate synaptic effects by slow NMDA receptor, which are voltage-sensitive and therefore show nonlinear dynamics or modulatory effects (with time constants ≈50 ms) (15, 16). Furthermore, the deployment of backward synaptic connections on the dendritic tree can endow them with nonlinear and veto-like properties (17). Backward connections play a central role in most theoretical and computational formulations of brain function (18, 19), ranging from the role of reentry in the theory of neuronal group selection (20) to recurrent neural networks as universal nonlinear approximators (21). Several previous studies have highlighted the functional role of backward connections, especially in the visual domain. It has been suggested that visual perception or awareness emerges from neuronal activity in ascending and descending pathways that link multiple cortical areas (22). Accordingly, recurrent processing or cortical feedback is necessary for object recognition (23) and has been found to be important in differentiation of figure from ground, particularly for stimuli with low salience (24). Modern-day formulations of Helmholtz's ideas about perception suggest that backward connections play a critical role in providing top-down predictions of bottom-up sensory input (25). Indeed, the hypothesis that the brain tries to infer the causes of its sensory input refers explicitly to hierarchical models that may be embodied by cortical hierarchies (26). In these formulations, the brain suppresses its free energy or prediction error to reconcile predictions at one level in the hierarchy with those in neighboring levels. This entails passing prediction errors up the hierarchy (via forward connections) and passing predictions down the hierarchy (via backward connections), which is in conformity with a predictive coding framework based on hierarchical Bayes (25–27). Experimental evidence consistent with predictive coding models has arisen from fMRI studies (28–30). It has been shown that activity in early visual areas is reduced through cortical feedback from high- to low-level areas, which simplifies the description of a visual scenery (28) and facilitates object recognition (29). A recent study has also used DCM to test predictive coding models in the context of perceptual decisions and found an increase in top-down connectivity from the frontal cortex to face visual areas, when ambiguous sensory information is provided (30). In predictive coding, evoked responses correspond to prediction error that is explained away (within trial) by self-organizing neuronal dynamics during perception and is suppressed (between trials) by changes in synaptic efficacy during learning. The recurrent dynamics that ensue are a plausible explanation for the form of evoked responses observed electrophysiologically and the theoretical cornerstone of most modern theories of perceptual inference and learning.

Materials and Methods

Experimental Design.

We chose to study evoked responses known to comprise substantial late components; these were elicited by using a pure-tone oddball paradigm. In this report, we analyze only the responses to the oddball tones. We acquired electroencephalographic data from 13 healthy volunteers aged 24–35 years (five female) while they were listening to a stream of auditory tones at 1,000 HZ (standards, occurring 80% of the time for 480 trials). Occasionally, the tone had a frequency of 2,000 Hz, corresponding to oddball stimuli (deviant, occurring 20% of the time for 120 trials). The stimuli were presented binaurally via headphones, in a pseudorandom sequence, for 15 min every 2 seconds. The duration of each tone was 70 ms, with 5-ms rise and fall times. Subjects sat on a comfortable chair in front of a desk in a dimly illuminated room and were instructed not to move, to keep their eyes closed, and to count the deviant tones. We report our results at both the subject and group levels, by using the ERP averaged over trials within-subject and the ERP averaged over all subjects. Each subject gave signed informed consent before the study, which proceeded under local ethical committee guidelines.

Data Acquisition and Processing.

EEG was recorded with a Biosemi system with 128 scalp electrodes. Data were recorded at a sampling rate of 512 Hz. Vertical and horizontal eye movements were monitored by using electrooculogram (EOG) electrodes. The data were epoched offline, with a peristimulus window of −100–400 ms, down-sampled to 200 Hz, band-pass-filtered between 0.5 and 40 Hz, and rereferenced to the average of the right and left ear lobes. Trials in which the absolute amplitude of the signal exceeded 100 μV were excluded. Two subjects were eliminated from further analysis due to excessive trials containing artifacts. In the remaining subjects, an average 18% of trials were excluded. For computational expediency, the dimensionality of the data was reduced to eight channel mixtures or spatial modes. These were the principal modes of a singular-value decomposition of the channel data from trials with responses to deviant tones. The use of eight principal eigenvariates preserved >90% of the variance in each subject.

Dynamic Causal Modeling.

Most approaches to connectivity in the MEG/EEG literature use functional connectivity measures, such as phase synchronization, temporal correlations, or coherence, that establish statistical dependencies between activities in two sources. Functional connectivity is useful, because it rests on an operational definition and is therefore independent of how the dependencies are caused. However, there are cases where we are precisely interested in the causal architecture of the interactions. Here, DCM plays a determinant role, because it uses the concept of effective connectivity, as opposed to functional connectivity. Effective connectivity refers explicitly to the influence one neuronal system exerts over another and can be estimated by perturbing the system and measuring the response by using Bayesian model inversion (31). DCM is described elsewhere (4–8, 31). In brief, DCM provides an account of the interactions among cortical regions and allows one to make inferences about the parameters of the system and investigate how these parameters are influenced by experimental factors. Furthermore, by taking the marginal likelihood over the conditional density of the model parameters, one can estimate the probability of the data, given a particular model. This is known as the marginal likelihood or evidence and can be used to compare different models.

In the context of EEG/MEG, DCM furnishes spatiotemporal, generative or forward models for evoked responses (4, 5, 7). DCM entails specification of a plausible model of electrodynamic responses. This model is inverted by optimizing a variational free energy bound on the model evidence to provide the conditional density of the model parameters and the model evidence for model comparison. This is an important advance over conventional analyses of evoked responses, because it places natural constraints on the inversion; namely, activity in one source has to be caused by activity in another. DCMs for MEG/EEG use neural mass models (6) to explain source activity in terms of the ensemble dynamics of the interacting inhibitory and excitatory subpopulations of neurons, based on the model of Jansen and Rit (32). This model emulates the activity of a source by using three neural subpopulations, each assigned to one of three cortical layers; an excitatory subpopulation in the granular layer, an inhibitory subpopulation in the supragranular layer, and a population of deep pyramidal cells in the infragranular layer. A hierarchical model described in ref. 7 uses extrinsic connections among multiple sources that conform to the connectivity rules reported in ref. 12. These rules allow one to build a network of coupled sources linked by extrinsic connections. Within this model, bottom-up or forward connections originate in the infragranular layers and terminate in the granular layer; top-down or backward connections link agranular layers, and lateral connections originate in infragranular layers and target all layers. All these extrinsic corticocortical connections are excitatory and are mediated through the axons of pyramidal cells. The exogenous input, u, models afferent activity to subcortical structures. The input is modeled with a gamma and a cosine function and has the same characteristics as forward connections, i.e., exogenous sensory input is delivered to the granular layer.

The DCM is specified in terms of some state equations that summarize the average synaptic dynamics in terms of spike-rate-dependent current and voltage changes, for each subpopulation

This means that the evolution of the neuronal state, x, is a function (parameterized by θ) of the state itself and the input u. An output equation couples specific states (the average depolarization of pyramidal cells in each source), x₀, to the MEG/EEG signals y by using a conventional linear electromagnetic forward model.

Eq. 1 summarizes the state equations specifying the rate of change of the potentials as a function of the current and how currents change as a function of the currents and the potentials (see refs. 4, 6, and 7 for details). The state equations embody the connection rules described above, where θ includes the parameters for forward, backward, and lateral connections and their modulation. These are the parameters we want to estimate. Eq. 2 links the neuronal states to observed channel data. In this application, the lead field L(θ) was parameterized in terms of the location and orientation of each source as described in ref. 5.

Source Localization and DCM.

Source localization refers to inversion of an electromagnetic forward model that maps sources to observed channels. This electromagnetic forward is part of the DCM, so Bayesian inversion of the DCM implicitly performs source localization. In practice, priors on dipole locations or moments (i.e., spatial parameters) are derived from classical source reconstruction techniques or the literature. The latter approach was taken in this study, and we let DCM estimate the conditional density of the locations (under relatively informative priors; 16 mm² Gaussian dispersion) and orientation (under uninformative or flat priors).

Statistical Analysis: Bayesian Model Comparison.

Inversion of a specific DCM, m, corresponds to approximating the posterior probability on the parameters, which is proportional to the probability of the data (the likelihood) conditioned on the model and its parameters, times the prior probability on the parameters

This approximation uses variational Bayes that is formally identical to expectation-maximization (EM), as described in ref. 33. The EM can be formulated in analogy to statistical mechanics as a coordinate descent on the free energy, F, of a system. The aim is to minimize the free energy with respect to a variational density q(θ). When the free energy is minimized q(θ) = p(θ|y,m), the free energy F = −ln p(y|m) is the negative marginal log-likelihood or negative log-evidence. After convergence and minimization of the free energy, the variational density is used as an approximation to the desired conditional density, and the log-evidence is used for model comparison.

One often wants to compare different models and select the best before making statistical inferences on the basis of the conditional density. The best model, given the data, is the one with highest log-evidence ln p(y|m) (assuming a uniform prior over models). Given two models, m₁ and m₀, one can compare them by computing their Bayes factor (13) or, equivalently, the difference in their log-evidences ln p(y|m₁) − ln p(y|m₀). If this difference is greater than ≈3 (i.e., their relative likelihood is >20:1), then one asserts there is strong evidence in favor of the first model.