Protein Structure Fitting and Refinement Guided by cryoEM Density

SUMMARY

For many macromolecular assemblies, both a cryoEM map and atomic structures of its component proteins are available. Here, we describe a method for fitting and refining a component structure within its map at resolutions better than ∼14 Å. The atomic positions are optimized with respect to a scoring function, which includes the cross-correlation coefficient between the structure and the map as well as stereochemical and non-bonded interaction terms. A heuristic protocol that relies on a Monte Carlo search, a conjugate-gradients minimization, and simulated annealing molecular dynamics is applied to a series of subdivisions of the structure into progressively smaller rigid bodies. The method was benchmarked on 13 proteins of known structure with simulated maps; at 10 Å resolution, Cα RMSD between the initial and final models was reduced on average by 41%. Its application to 3 experimental maps (of GroEL and EF-Tu at 6.0, 9.0, and 11.5 Å resolution) resulted in an improvement of 77-88%. The method is automated and can refine both experimental and predicted atomic structures.

INTRODUCTION

High-resolution structures of macromolecular assemblies, such as ribosomes, viruses, ion channels and chaperons, are needed for studying their function and evolution (Sali, et al. 2003). While a number of assembly structures were determined by X-ray crystallography and NMR spectroscopy, thousands of complexes remain to be structurally undefined. Thus, improved methods are needed for structure characterization of assemblies at near atomic resolution, providing approximate positions of the mainchain and sidechains.

Single particle cryo-electron microscopy (cryoEM) has already proven useful for determining macromolecular assembly structures at resolutions lower than approximately 5 Å (Jiang and Ludtke 2005, Chiu, et al. 2005). With very small sample amounts, it can determine the single particle structures of assemblies with molecular weights larger than approximately 150 kDa. A particularly important advantage of cryoEM is its ability to visualize different functional states (Saibil 2000, Mitra and Frank 2006). However, cryoEM is often hampered by its relatively low resolution that does not yield direct determination of atomic structures.

Fortunately, atomic-resolution structures of the isolated assembly components (eg, domains, proteins, and complexes of a subset of all proteins in the assembly) are often available from crystallography, NMR spectroscopy, or comparative protein structure modeling (Eswar, et al. 2006). By fitting the structures of these components into a cryoEM density map of the whole assembly, a more detailed picture of the intact assembly can be provided (Rossmann, et al. 2005, Topf and Sali 2005). This task can be performed by a manual adjustment of the components in the map using interactive visual tools (Goddard, et al. 2007). However, a better alternative is to use an automated computational method to decrease the level of subjectivity as well as increase the accuracy and efficiency (Chiu, et al. 2005, Fabiola and Chapman 2005).

Most such methods attempt to find an optimal position and orientation of a rigid component in the density map by optimizing a quality of fit measure (rigid fitting), such as the cross-correlation coefficient between the component and the map. However, the atomic structure of the isolated component is often not the same as that in the assembly. The variations can originate from the different conditions under which the isolated component and assembly structures are determined and from errors in the experimental methods (Alber, et al. 2004). Common conformational differences are shear and hinge movements of domains and secondary structure elements, as well as loop distortions and movements. Furthermore, when an experimentally-determined structure of the component is unavailable, the use of protein structure prediction methods (Baker and Sali 2001) can also introduce additional errors, such as the misassignment of secondary structure elements to incorrect sequence regions, which will cause their shifts in space in comparative modeling.

To address the problem of fitting an inaccurate component structure into a cryoEM map, the conformation of the component needs to be optimized simultaneously with its position and orientation in the cryoEM map (flexible fitting). Several such methods have been developed. The Situs package relies on a reduced representation of the component structure and the density map to deform the structure while fitting the map (Wriggers, et al. 1999). NMFF-EM and other programs (Tama, et al. 2002, Ming, et al. 2002, Tama, et al. 2004, Suhre, et al. 2006) use Normal Mode Analysis (NMA) (Brooks and Karplus 1983) to follow the dynamics of the components in the context of a cryoEM map. RSRef performs real-space refinement to simultaneously optimize the stereochemistry and the fit of the structure into the density map (Fabiola and Chapman 2005, Chen and Champman 2001). Our Mod-EM and Moulder-EM methods consider the flexibility of the component structures via the fitting of alternative comparative models based on different sequence-structure alignments and different loop conformations (Topf, et al. 2005, Topf, et al. 2006). A similar use of a cryoEM map as a filter was applied to ab initio models (Baker, et al. 2006). The S-flexfit method exploits the structural variability of protein domains within a given superfamily (Velazquez-Muriel, et al. 2006).

The input for almost all flexible-fitting methods is the initial structure of the component rigidly fitted into the approximate position and orientation in the density map. This task is often performed by a separate rigid-body fitting program. Most of the these methods also require a one-to-one correspondence between the fitted component and the density map (ie, the map has to be segmented or masked around the region of interest). Furthermore, except for RSRef, current methods do not explicitly take into account the stereochemistry and non-bonded interactions of proteins during deformation and fitting into the map. Instead, they employ a final step of energy minimization to “fix” potential non-physical geometries introduced during deformation and fitting.

Here, we present a method (Flex-EM) that integrates rigid and flexible fitting of a component structure into the cryoEM density map of their assembly. The component structure can originate from either an experiment (eg, in a different chemical state) or a modeling calculation. The method combines the identification of the position and orientation of the component in the larger map with the refinement of its atomic conformation (Theory). We test the method on a benchmark of 13 protein structures consisting of one or two domains in a non-native conformation; these structures are fitted and refined in the context of their native density maps simulated at 4-14 Å resolution. We also apply it to two structures with experimentally-determined cryoEM maps at this resolution range (Results). Finally, we discuss our approach and its implications for refining structures and models of assembly components using cryoEM density maps (Discussion).

THEORY

The goal is to refine an atomic structure of a protein, given an initial structural model and a cryoEM-derived density map. The refined structure needs to optimally fit into the density map as well as satisfy the general rules of protein structures. We express this task as an optimization problem. Thus, we need to specify (i) the representation of the protein structure; (ii) the scoring function; and (iii) the optimization protocol.

Representation of the protein structure

The input to our protocol are an atomic structure of a protein (probe, P) and a density map at intermediate resolution (< 15 Å) (Figure 1). The density map is represented by intensities at points i on a cubic grid (ρ^EM_i). The spacing between the grid points is equal to the sampling of the input density map (Å/voxel). The probe is defined by its N atomic coordinates and corresponding atomic numbers in real space, using the same coordinate system as for the grid. In addition, the probe density of atom j at position $\stackrel{I}{r_i}$ is

$${\rho }_{i,j}^P=\frac{Z_j}{\sqrt{2\pi \sigma }}\exp \left[-\frac{1}{2}{\left(\frac{\stackrel{\mathrm{r}}{r_j}-\stackrel{\mathrm{r}}{r_i}}{\sigma }\right)}^2\right]$$ (1)

where ${\overrightarrow{r}}_j$ is the position of atom j, Z_j is its atomic number, and σ is 0.425 times the resolution of the density map. This value was calculated based on the ‘full width at half maximum’ criterion (ie, the resolution equals to $2(\stackrel{\mathrm{r}}{r_j}-\stackrel{\mathrm{r}}{r_i})$ when ${\rho }_{i,j}^P$ is equal to half of its maximum value).

Figure 1.

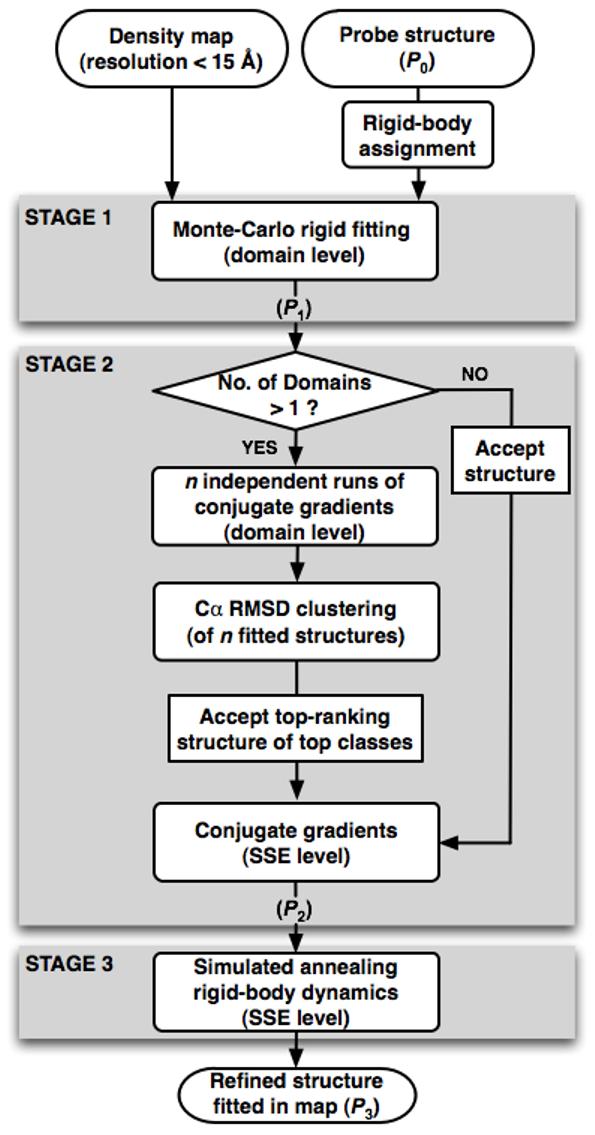
The Flex-EM protocol for fitting and refining an atomic structure within its cryoEM density map. The inputs to the protocol are an atomic structure and a density map at intermediate resolution (<15 Å). The protocol includes 3 stages: rigid fitting by an MC optimization (stage 1, MC); refinement by a CG minimization (stage 2, CG); and simulated annealing rigid-body MD (stage 3, MD). For multiple-domain structures, the CG stage is performed n times at the domain level (typically n=20). For single-domain structures the CG stage is applied only once (ie, at the SSE level).

A major problem that needs to be overcome is the large size of the search space. To reduce the number of degrees of freedom, the structure is partitioned into L rigid bodies, b_l. A rigid body $b_l(\stackrel{\mathrm{r}}{r},\stackrel{\mathrm{I}}{Z},\stackrel{\mathrm{r}}{m})\in B$ can be any set of atoms, including a single atom, a secondary structure element, a domain, or the whole protein; $\overrightarrow{r}$, $\stackrel{\mathrm{I}}{Z}$, and $\stackrel{\mathrm{I}}{m}$ represent the coordinates, atomic numbers, and atomic masses in this set, respectively. B is a set of rigid bodies that covers the whole probe structure (P) such that each atom is a member of exactly one rigid body. The two extreme cases correspond to either the entire structure or each atom being a rigid body. It is up to the user to define these rigid bodies.

Scoring function

The scoring function for a given probe structure P is:

$$E=W_1\cdot E^{\mathrm{CCF}}\left(P\right)+W_2\cdot E^{\mathrm{SC}}\left(P\right)+W_3\cdot E^{\mathrm{NB}}\left(P\right)$$ (2)

where E^CCF(P) quantifies the fit between the probe density, ρ^p, and the density map, ρ^EM; E^SC(P) quantifies the stereochemistry of the model; and E^NB(P) quantifies the non-bonded atom-atom contacts. The weights w₁, w_2, and w₃ determine the relative importance of the corresponding terms. E^CCF(P) is defined as the negative sum of cross-correlation coefficients (CCFs) between the density map and the rigid bodies. For a rigid body b_l, CCF is:

$$\mathrm{CCF}\left(b_l\right)=\frac{\sum _{i\in Vox\left(b_l\right)}{\rho }_i^{\mathrm{EM}}\left(\sum _{j=1}^{\mathrm{N}}{\rho }_{i,j}^{\mathrm{P}}\right)}{\sqrt{\sum _{i\in Vox\left(b_l\right)}{\left({\rho }_i^{\mathrm{EM}}\right)}^2\sum _{i\in Vox\left(b_l\right)}{\left(\sum _{j=1}^{\mathrm{N}}{\rho }_{i,j}^{\mathrm{P}}\right)}^2}}$$ (3)

where Vox(b_l) represents all the voxels in the density grid that are within two times the resolution of the map from any of the atoms of rigid body b_l; and where the total density of P at grid point i is ${\sum }_{j=1}^{\mathrm{N}}{\rho }_{i,j}^{\mathrm{P}}$.

The gradient of the cross-correlation term is:

$${\overrightarrow{F}}^{\mathrm{CCF}}\left(b_l\right)=-\sum _{j\in \text{Atom}\left(b_l\right)}\frac{\partial \mathrm{CCF}\left(b_l\right)}{\partial \stackrel{\mathrm{r}}{r_j}}$$ (4)

where

$$\frac{\partial \mathrm{CCF}\left(b_l\right)}{\partial \stackrel{\mathrm{r}}{r_j}}=A\frac{Z_j}{\sqrt{2\pi \sigma }}\sum _{i\in Vox\left(b_l\right)}{\rho }_i^{EM}\left(\frac{\stackrel{\mathrm{r}}{r_j}-\stackrel{\mathrm{r}}{r_i}}{\sigma }\right)\exp \left[-\frac{1}{2}{\left(\frac{\stackrel{\mathrm{r}}{r_j}-\stackrel{\mathrm{r}}{r_i}}{\sigma }\right)}^2\right].$$ (5)

j is the atom index and i is the EM density voxel index, both of which are associated with b_l. For computational efficiency, A is considered a constant. It is equal to 10,000 divided by the denominator in Eq. 3 for the starting conformation and position. The factor 10,000 was chosen empirically to balance the magnitude of the fitting term relative to the other two terms in the scoring function.

E^SC(P) and E^NB(P) represent the general conformational preferences of proteins and thus ensure that an optimized structure is physically realistic. E^SC(P) restrains the stereochemistry. It is a sum of the harmonic terms of all the chemical bonds, bond angles, dihedral angles, and improper dihedral angles that involve atoms from more than one rigid body. The mean values and force constants were obtained from the CHARMM22 molecular mechanics force field (MacKerell, et al. 1998). E^SC(P) also includes the two-dimensional (Φ,Ψ) dihedral-angle restraints based on the Ramachandran plot (Fiser, et al. 2000). E^NB(P) restrains the non-bonded atom-atom contacts. It is a sum of the harmonic lower bounds of all non-bonded atom pairs from different rigid bodies; the lower bound is the sum of the two atomic van der Waals radii (MacKerell, et al. 1998) and the force constant is 400 kcal/mole/Ų.

The rigid-body gradients of E^SC(P) and E^NB(P) with respect to the Cartesian coordinates ($\stackrel{\mathrm{I}}{F_j^{\mathrm{SC}}}$ and $\stackrel{\mathrm{I}}{F_j^{\mathrm{NB}}}$, respectively) are the sums of the gradients for the individual atoms in the rigid body. The gradient of the scoring function is the sum of all 3 gradient types with the corresponding weights (Eq. 2).

Optimization protocol

The optimization of the scoring function positions, orients, and refines the initial structure so that it satisfies the conformational preferences and fits the density map. We apply a heuristic hierarchical optimization protocol that includes both rigid-body fitting and conformational refinement (Figure 1). The protocol consists of three stages. In the first stage, only the cross-correlation with the cryoEM map is optimized by rigid fitting of the whole structure or its domains, using a Metropolis Monte-Carlo (MC) method. The conformational refinement is performed in the second and third stages, with a conjugate-gradients (CG) minimization and a simulated annealing rigid-body molecular dynamics (MD) protocol, respectively. During the refinement, the coordinates of the rigid bodies into which the structure is dissected are displaced in the direction that maximizes their cross-correlation with the cryoEM density map and minimizes the violations of the stereochemical and non-bonded terms (Figure 1). As the optimization progresses and the value of the scoring function decreases, we divide the structure into progressively smaller rigid bodies. The rigid bodies can be manually assigned by the user at any stage of the optimization. Here, to make our benchmark automated, the structure is first optimized at the “domain level” (ie, the rigid bodies correspond to the domains and the individual atoms that connect the domains), followed by the “SSE level” (ie, the rigid bodies correspond to the secondary structure elements in the initial structure and the individual atoms that connect them) (Figure 1).

Stage 1 (MC): Rigid fitting with an MC method

In the first stage of optimization, the user begins by deciding whether to fit the whole initial probe structure (P₀) or any of its domains independently (with the linkers absent). The corresponding rigid bodies are then placed randomly (or in a specified position) in the density map. Next, the rigid-body positions and orientations are optimized independently in 200 steps of a Metropolis MC optimization protocol using Mod-EM (the density.grid_search method in MODELLER-9.0) (Topf, et al. 2005). The scoring function at this stage includes only the E^CCF(P₀) term; it does not include the stereochemical and non-bonded terms (w₁=1, w₂=0, w₃=0). Therefore, if multiple domains are fitted independently, the resulting structure P₁ can have clashing atoms between the domains. Finally, the linkers that connect the domains are added as follows. Each linker in the initial structure (P₀) is cut at its mid-residue. Each of the P₀ domains attached to a half-linker is then superposed onto the corresponding domain in P₁, to obtain the complete P₁ structure including all domains and linkers. While the linkers in P₁ are generally grossly distorted at their mid-point, they are refined in the next stage.

Stage 2 (CG): Conformational refinement with CG minimization

In the second stage, we perform a CG refinement of P₁. If the probe structure contains more than one domain, the refinement is performed first at the domain level. A set of 20 random initial structures is obtained from P₁ by rotating and translating each rigid body by a random value ranging from 0° to 30° and from -10 Å to 10 Å, respectively; the user has an option not to randomize the position of a specific rigid body. A CG minimization (Shanno and Phua 1980) of each of the randomized initial structures is then performed in 6 iterations, with each iteration progressively increasing the three weights for the individual terms in the scoring function from 0 or small values to 1. Each iteration terminates after 200 CG steps or when the maximum atomic shift is less than 0.01 Å. Next, solutions are clustered in an iterative manner as follows. The structure with the lowest score seeds the first cluster. All the structures with Cα RMSD less than 3.5 Å from the seed structure are included in the cluster. The seeding procedure is repeated for the remaining structures until all structures are clustered. The best-scoring structure in each of the top 5 clusters is then optimized at the SSE level, using the 6-iteration CG protocol described above. The structure with the best value of the scoring function is P₂. If the probe structure is composed of a single domain, the 6-iteration CG protocol is applied to P₁ only once at the SSE level, to get the refined structure P₂.

Stage 3 (MD): Refinement with simulated annealing rigid-body MD

In the third stage, we optimize P₂ by refining positions and orientations of its rigid bodies with a simulated annealing rigid-body MD protocol (Goldstein 1980, Brooks, et al. 1988). We use the same rigid-body definition as in the final level of stage 2 (ie, the SSE level) and the same scoring-function weights (w₁=w₂=w₃=1). The state of each rigid body is specified by the position of the center of mass, $\stackrel{\mathrm{I}}{r_{com}}$, and an orientation quaternion, q. At each step, the forces on each atom are summed to give a total force on the center of mass and a torque on the body. $\stackrel{\mathrm{I}}{r_{com}}$ is then updated using a standard Verlet integrator and q is updated by converting the torque to a quaternion angular acceleration. Three cycles of 5,600 simulated annealing MD steps are performed (gradually increasing the temperature from 0K to 1000K and decreasing it back to 0K). The optimization is terminated if the change in CCF is < 0.001. Finally, to ‘relax’ the structure, we perform 200 CG steps with w₁=w₂=w₃=1 and 200 CG steps with w₁=0 and w₂=w₃=1, resulting in P₃.

Applicability of the method

Flex-EM is an automated method for refining experimentally-determined atomic structures that undergo conformational changes in the context of the assembly cryoEM map as well as comparative models that suffer from modeling errors. The assignment of the rigid bodies is given as an input to the program at each step of the optimization protocol. For a 200 residue target sequence and a density map at ∼10 Å resolution, the typical running times are less than a minute for the MC stage on one CPU, less than 4 hours for the CG stage on 20 CPUs, and less than 12 hours for the MD stage on one CPU. The Flex-EM software and the benchmark (below) are available at http://salilab.org/Flex-EM/.

RESULTS

Benchmark

To test the fitting and refinement protocol, we created a benchmark of 13 proteins in a non-native conformation (P₀) and a density map (ρ^EM) calculated from the corresponding native structure. To make the test more realistic, we generated the non-native conformations with the aid of comparative protein structure modeling (Eswar, et al. 2006). This procedure resulted in variations in domain orientations, loop conformations, positions of secondary structure elements, as well as distortions and shifts of secondary structure elements. Ten of the 13 proteins were selected from the Molecular Movement Database (Flores, et al. 2006) that stores experimentally-determined structures of macromolecules in two distinct conformations. For each of the ten proteins, one conformation was defined as the “target”. Using the DBAli database (Marti-Renom, et al. 2007), a structure of a protein that is closer to the other conformation was defined as the “template”. The remaining three target-template pairs were selected from known sets of homologs containing domains that interact through different surfaces (Han, et al. 2006) and DBAli. Next, we calculated sequence-structure alignments and built corresponding models using the align method and automodel class in MODELLER-9.0 (Eswar, et al. 2006, Sali and Blundell 1993), respectively. The resulting 13 comparative models were used in the benchmarking as the initial probe structures in the non-native conformation (P₀). The native structures were used to calculate the corresponding “native” density maps (ρ^EM) at the resolution of 10 Å with grid spacing of 1 Å/Voxel. To minimize bias, the maps were not produced with our program, zbut with pdb2vol in SITUS (Wriggers, et al. 1999), which uses a different Gaussian smoothing technique. Furthermore, the use of comparative modeling for building the initial benchmark structures introduced test cases that are more challenging for refinement than experimentally-determined atomic structures (which tend to be less distorted). By construction, the native structure has the best value of CCF among all structures produced during the optimization process.

In summary, the benchmark consists of eight single-domain and five two-domain protein structures in a non-native conformation (probes), generated based on homologous structures sharing between 26% and 52% sequence identity (Table 1). The average number of residues per structure is 211. The benchmark contains representatives from all major fold classes (ie, α, β, α+β, and α/β). Domain assignment was based on the domain definition in the Pfam database (Bateman, et al. 2004). Secondary structure elements were determined based on the initial probe structures with DSSP (Kabsch and Sander 1983).

Table 1.

a. Single-domain protein structures fitted and refined within their native density maps at 10 Å resolution, b. Two-domain protein structures fitted and refined within their native density maps at 10 Å resolution

Probea (Name, range)	Templatea (Name, range)	Fold type	seq. Id.a	-ECCF(b)		ESC(b)		ENB(b)		OSc (Å, deg)	Cα RMSDd (Å)				NO3.5d (%)
				P0e	P3e	P0	P3	P0	P3	P3	P0	P3	PBestee	PMine	P0	P3	PE
1akeA 1-213	1dvrB 5-217	α/β	46	0.938	0.969	803	796	1.5	3.4	0.4, 3.1	4.5	2.2	2.2	0.9	75	91	9
1c1xA 8-345	1gtmA 31-407	α/β	30	0.951	0.977	1482	1187	5.8	7.9	0.0, 3.3	6.6	4.6	4.5	1.4	53	66	6
1cll 4-146	2ggmB 25-168	α	52	0.875	0.958	531	490	1.1	3.4	0.2, 3.6	5.0	3.1	3.0	0.6	51	74	7
syD 231-442	3erdA 310-534	α	30	0.933	0.945	768	677	4.4	2.2	0.4, 6.1	5.4	5.1	4.9	1.5	56	67	6
mA 531-711	1ex7A 531-711	α/β	33	0.890	0.967	837	754	1.6	4.8	0.4, 5.7	5.4	3.3	3.3	0.9	43	80	8
1ozoA 1-84	1a03B 2-83	α	42	0.940	0.966	250	242	1.0	2.9	0.3, 6.4	4.7	4.1	4.0	1.3	56	71	7
1uwoA 1-90	1k9pA 3-89	α	41	0.948	0.960	243	308	0.4	23.2	0.3, 5.8	4.7	4.0	4.0	1.3	69	70	7
1cczA 1-170	1hnf 1-170	β	37	0.934	0.973	948	892	323.0	11.9	0.2, 8.3	5.2	5.1	4.9	1.2	64	66	7
Average			39	0.926	0.964	733	668	42.7	7.5	0.3, 5.3	5.2	3.9	3.8	1.1	58	73	7

Probea (Name, range)	Templatea (Name, range)	Fold type	% Seq. Id.a	-ECCF(b)		ESC(b)		ENB(b)		OS (Å, deg)	DOSc Å, deg)		Cα RMSDd (Å)				NO3.5d (%)			NO5.0d (%)
				P0e	P3e	P0	P3	P0	P3	P3	P0	P3	P0	P3	PBeste	PMine	P0	P3	PBest	P0	P3	PBes
1ffgAB 2-226	1u0sAY 2-260	α/β, α +β	26	0.959	0.970	896	796	13.2	5.3	0.6, 15.0	4.8, 123.3	5.0, 6.4	9.1	3.6	3.5	1.1	35	72	76	60	88	89
1iknA 19-273	1svc 43-335	β	46	0.913	0.961	1300	1110	1.9	9.7	0.8, 1.0	12.8, 100.7	2.5, 46.8	10.4	4.4	3.9*	0.8	57	57	65	62	78	80
1a45A 1-172	1blb 1-172	β	35	0.771	0.973	996	965	3.8	3.3	1.3, 161.2	37.8, 168.9	39.3, 141.0	28.9	12.2	11.5	0.9	47	24	52	50	41	55
1ckmA 60-319	1p16 44-366	α +β, β	32	0.903	0.960	1311	1414	3.7	6.1	0.7, 7.9	10.7, 41.6	4.0, 9.8	8.3	6.6	6.5	1.2	42	62	70	62	74	81
1hrdC 22-446	1hwzA 7-491	α/β, α/β	28	0.925	0.961	2313	2151	13.2	17.5	1.6, 8.0	6.7, 23.9	3.4, 10.7	8.2	4.9	4.9	0.9	49	67	67	65	83	84
Average			33	0.894	0.965	1363	1287	1.0	8.4	1.0, 38.6	14.6, 91.7	10.9, 42.9	13.0	6.3	6.1	1.0	46	57	66	59	73	77

^a“Probe” is the structure being refined. The initial coordinates of each probe structure were generated based on the “template” structure using comparative modeling with MODELLER-9.0 (Sali and Blundell 1993). The target-template sequence identity (Seq. Id.) is calculated from their sequence alignment.

^b-E^CCF, E^SC, and E^NB are the 3 terms of the scoring function with equal weights (w₁=w₂=w₃=1, Eq. 2): the cross-correlation coefficient (CCF) between a probe structure and the native density map (which is multiplied by 10,000 during refinement, Eq. 3 and 5, respectively), the stereochemical restraints, and the non-bonded interactions restraints.

^cOS and DOS are the orientation and domain-orientation scores, respectively. For the multi-domain proteins, the OS score was calculated for the N-terminal domain only.

^dCα RMSD is the root-mean-square deviation between the Cα atoms of the probe structure and their corresponding atoms in the native structure, and NO3.5 and NO5.0 are the percentages of Cα atoms in a probe structure that are positioned within 3.5 Å and 5.0 Å, respectively, from their corresponding atoms in the native structure. These scores are calculated upon superposition of the initial or a refined structure onto the corresponding native structure using a rigid-body least-squares minimization.

^eP₀, P₃, P_Best, and P_Min refer respectively to the initial structure (before the refinement); the final structure (following the MC, CG and MD refinement protocol); the structure with the best score (for Cα RMSD, NO3.5 and NO5.0) found in the simulation; and the best possible structure (based on MinRMSD for fitting and refining a model with secondary structure elements as rigid bodies). The corresponding best possible NO3.5 is always equal or higher than 97% (99% on average) and NO5.0 is 100%.

^*This score is for a structure found in the second cluster obtained at the CG stage.

Measures of model accuracy

Model accuracy is measured through two types of scores: (i) a rigid-body shift and rotation of a fitted component relative to its correct position in the density (ie, the orientation score (OS) and the domain-orientation score (DOS)); and (ii) a distortion of the conformation of the probe structure relative to the native structure (ie, the Cα root-mean-square deviation (RMSD) and native overlap (NO)).

OS score

The orientation score quantifies the difference between the orientation and position of a given rigid body fitted in the density, and the orientation of the equivalent rigid body in the native structure, which by construction is positioned correctly in the map. To calculate the score, we first translate the center of mass of the rigid body onto the center of mass of the equivalent rigid body in the native structure. The first component of the OS score, “dist” (Å), is then defined as the magnitude of the corresponding translation vector. We then rotate the rigid body in the refined structure to optimally superpose it onto the equivalent rigid body in the native structure (using the superpose method of MODELLER-9.0). The second component of OS, “ang” (degrees), is then defined as the angle of rotation.

DOS score

DOS is similar to OS, except that it is used for multi-domain proteins. It quantifies the difference between the relative orientations and positions of two rigid body domains in the refined structure and the two equivalent rigid bodies in the native structure. First, the two compared structures are brought into the same frame of reference by superposing the first pair of equivalent domains. Next, the “dist” and “ang” scores are calculated for the second rigid body using the same procedure as for OS.

RMSD and NO

Cα RMSD is calculated between the Cα atoms of a structure (ie, the initial structure or a structure being refined) and the corresponding atoms in the native structure. NO3.5 and NO5.0 of the refined structure are the percentage of its Cα atoms that are within 3.5 Å and 5.0 Å of the corresponding atoms in the native structure, respectively. Both scores are calculated upon superposition of the refined structure onto the corresponding native structure using a rigid-body least-squares minimization, as implemented in the superpose method of MODELLER-9.0.

We also calculated a “minimal” Cα RMSD (MinRMSD) for each structure, corresponding to the best possible model, given that the secondary structure elements are treated as rigid bodies. The best possible model has all loop atoms overlapping perfectly with the equivalent native positions and each rigid body in the initial probe structure (an α-helix or a β-strand, as determined by DSSP) superposed independently onto the corresponding region in the native structure.

Accuracy of the refined structures

Single-domain proteins

The optimization protocol was able to accurately fit and refine all 8 single-domain benchmark proteins: the average OS was [0.3 Å, ∼5.3 degrees] and both Cα RMSD and NO3.5 were improved relative to their initial values (Table 1a). This improvement is correlated with the increase in CCF. The values of the stereochemical and non-bonded terms (E^SC(P) and E^NB(P), respectively) were either reduced or increased by less than a factor of 3 (E^NB in 7 out of 8 structures and E^SC in 8 out of 8). The average Cα RMSD was reduced from 5.2 to 3.9 Å. Given the average MinRMSD of 1.1 Å, the average Cα RMSD corresponds to ∼32% (ie, (5.2-3.9) / (5.2-1.1)) of the maximum possible improvement. The average NO3.5 improved from 58% to 73%, which is 37% of the maximum possible improvement (the average maximum possible NO3.5 is 99%). According to the Ramachandran plots of the final structures (calculated using MOLprobity (Lovell, et al. 2003)), the average percentage of residues in the allowed (Φ,Ψ) dihedral angle regions is 98.9% (eg, Figure S1).

Two-domain proteins

For all 5 final structures (P₃) of the two-domain proteins, the Cα RMSD was better than for the initial structures, correlating with the increase in CCF (Table 1b). For these proteins, the values of E^SC(P) and E^NB(P) were either reduced or increased by less than a factor of 2 (E^SC in 5 out of 5 structures and E^NB in 4 out of 5). The average Cα RMSD was reduced significantly, from 13.0 to 6.3 Å, which is ∼56% of the maximum possible improvement (given that the average MinRMSD is 1.0 Å). The average number of residues in the allowed regions of the Ramachandran plot was above 98% in all structures (eg, Figure S1). The average NO3.5 and NO5.0 increased from 46% to 57% and from 59% to 73%, respectively.

A closer look at the different scores of the 5 structures reveals that while Cα RMSD has improved significantly for all proteins, NO3.5 improved for 3 out of the 5 proteins (1ffgAB, 1ckmA, and 1hrdC) and NO5.0 for 4 out of 5 (1ffgAB, 1iknA, 1ckmA, and 1hrdC). The latter result is also reflected in OS and DOS (Table 1b). The final values of both scores for 1ffgAB, 1ckmA, and 1hrdC were better than [5 Å,15°], respectively. For 1iknA, the DOS ang score could be reduced further (ie, although the orientation between the domains in the final structure is more accurate than in the initial structure, it is still far from the orientation in the native structure). For 1a45A, however, both final OS ang and DOS scores were high, showing that the protein was not fitted correctly in the map.

Sample model optimization

For all initial probe structures except 1a45A (for which the two domains were fitted separately), the first stage of the optimization protocol (rigid fitting by MC) was able to identify the approximate position and orientation in the 10 Å resolution native density maps (as reflected in the OS score, Table 1). Therefore, we focus on stages 2 and 3 (CG and MD) using five sample proteins, each of which represents a different refinement scenario (Figure 2). Generally, most improvement for the two-domain proteins was achieved in the domain-level CG minimization (CG stage), while the SSE-level MD was most beneficial for the single-domain proteins (MD stage). This result is a consequence of the differences between the initial and native structures being dominated by domain and secondary structure element repacking for the two- and single-domain proteins, respectively.

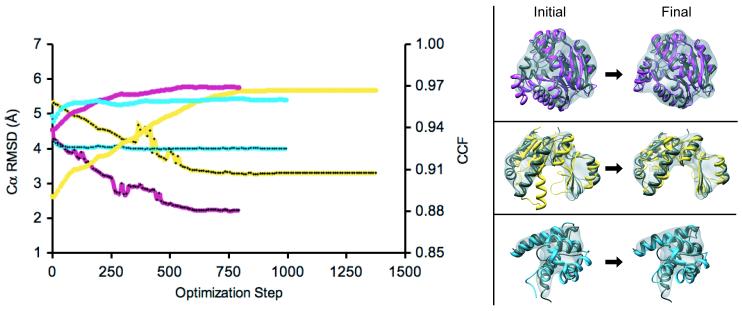
Figure 2.

a. CCF (plain lines) and Cα RMSD (lines with black dots) of 3 non-native single-domain structures during the rigid-body MD refinement within their native 10 Å resolution density maps (MD stage, P₂→ P₃, see Figure 1): 1jxmA (yellow), 1akeA (magenta), and 1uwoA (light blue). The scores were recorded every 10 steps. b. CCF (plain lines) and Cα RMSD (lines with dots) of 2 non-native two-domain structures during the CG and rigid-body MD refinement within their native 10 Å resolution density maps (CG and MD stages, P₁→P₂→ P₃, see Figure 1): 1iknA (magenta) and 1ckmA (light blue). The scores were recorded every 10 steps. The arrow indicates the end of the CG stage.

For the 3 sample single-domain proteins, the improvement in the accuracy of the structure during the MD stage (P₂) was highly correlated with the improvement in CCF (Figure 2a) (ie, Cα RMSD of the probe structure decreased with the increase in CCF and reached a minimum when CCF reached a maximum). For 1akeA, Cα RMSD was reduced from 4.5 to 2.2 Å, pushing the final structure close to the native structure (MinRMSD is 0.9 Å). For 1jxmA, Cα RMSD also decreased significantly, from 5.4 to 3.3 Å, with a MinRMSD of 0.9 Å (Supplemental Movie 1). However, there is room for further improvement, especially in the loop regions and to a smaller degree in the orientations of secondary structure elements. For 1uwoA, the refinement process improved CCF only slightly, primarily due to an incorrect assignment of some of the rigid bodies, caused by a misplacement of secondary structure elements in the probe structure with respect to the native structure: helix 43-46 corresponds to a loop in the native structure, and helices 50-54 and 56-62 correspond to helix 51-59; these mistakes are due to errors in the comparative modeling of 1uwoA based on the 1k9pA template. As a result of these errors, Cα RMSD was reduced only from 4.7 to 4.0 Å and NO3.5 improved only slightly, from 69% to 70%.

The sample two-domain proteins illustrate the impact of correct and incorrect secondary structure element assignments. For 1iknA, the decrease in Cα RMSD was highly correlated with the increase in CCF throughout the CG and MD stages (P₁ and P₂, Figure 2b, Supplemental Movie 2). Cα RMSD improved from 10.4 Å for the initial structure to 4.4 Å for the final structure, with MinRMSD of 0.8 Å. In contrast, Cα RMSD of 1ckmA slightly increased during the MD stage (P₂), despite the small increase in CCF. This contrasting result can be attributed to two different problems with secondary structure element assignments. First, there were missing secondary structure elements in the refined structure (eg, its loop 196-209 corresponds to an α-helix in the native structure and loop 255-266 to a β-sheet). In these regions, the atoms were fitted individually, which turned out to be too large a burden for the optimizer to handle correctly. Second, assignment of the secondary structure elements to incorrect segments of the sequence led to the opposite situation in which the atoms in loops that should have been fitted individually were in fact fitted as rigid helices and strands (eg, helices 178-180 and 182-186 in the structure being refined are loops in the native structure). As a result of the secondary structure element misassignments, Cα RMSD improved only marginally from 8.3 to 6.6 Å, with MinRMSDs of 1.2 Å.

The effect of map resolution on model accuracy

For four proteins in the benchmark, we tested Flex-EM with “native” density maps simulated at a range of resolutions from 4 to 14 Å (Figure 3). In all cases, both Cα RMSD and NO3.5 of the final structures were better than those for the initial structures, at all tested resolutions, from 4 to 14 Å. For all 4 tests, NO3.5 of the final structure at 4 Å resolution was higher than 87% and Cα RMSD was lower than 2.5 Å. Furthermore, for 1jxmA, 1akeA, and 1cll, the results suggest a strong correlation between the accuracy of the final structure and the map resolution (Pearson correlation coefficient (R²) > 0.9). However, for 1uwoA, the correlation is weak due to the incorrect rigid-body assignment (as described above).

Figure 3.

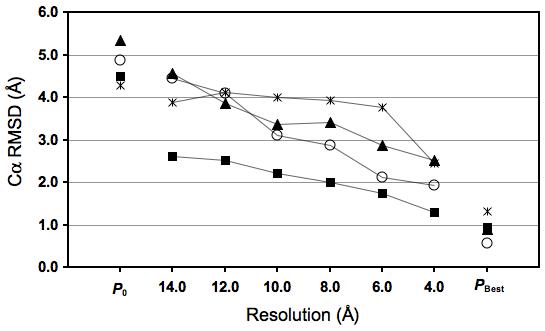
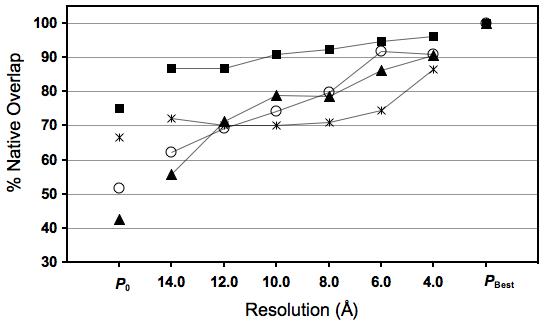
Accuracy of the final structures of four single-domain proteins: 1akeA (square), 1cll (circle), 1jxmA (triangle), and 1uwoA (asterisk), refined in their corresponding density maps at different resolutions (ranging between 4 and 14 Å). (a) The Cα RMSD from of the initial structure (P₀), final structure (at each resolution), and the best-possible structures from the native structures. (b) The native overlap within 3.5 Å (NO3.5). P₀ and P_Best refer to the initial structure (prior to the refinement) and the structure based on which MinRMSD was calculated (Results), respectively.

Modeling conformational changes using experimentally-determined cryoEM maps

To test the refinement of atomic structures using maps with noise not captured in the simulated maps, we applied Flex-EM to two multi-domain proteins with experimentally-determined maps: a monomer of the bacterial chaperonin complex GroEL and the bacterial elongation factor EF-Tu. For GroEL, the initial structure was a comparative model based on 63% sequence identity to a monomer in the bound state (GroEL-GroES-ADP) of a homologous archaebacterial complex, Thermosome (PDB code: 1we3B (Shimamura, et al. 2004)). Density maps for Flex-EM were segmented with Chimera (Goddard, et al. 2007) from cryoEM maps of the double-ring GroEL complex in the unbound state at 11.5 Å (EMDB code: 1080) (Ludtke, et al. 2001) and 6.0 Å (1081) (Ludtke, et al. 2004). For EF-Tu, the initial structure was a comparative model based on 55% sequence identity to a mitochondrial homolog complexed with GDP (PDB code: 1d2eA (Andersen, et al. 2000)). The density map was segmented from the 9.0 Å resolution cryoEM map of E. coli 70S ribosome complexed with tRNA-EF-Tu-GDP-kirromycin (EMDB code: 1055) (Valle, et al. 2003). Both the GroEL monomer and EF-Tu were assigned three domains each, based on SCOP (Murzin, et al. 1995). The secondary structure elements in the initial structures were determined with DSSP (Kabsch and Sander 1983). Each of the initial structures was then fitted and refined in the corresponding density (GroEL in the 11.5 and 6.0 Å resolution maps and EF-Tu in the 9.0 Å resolution map).

In the first stage (MC), we fitted the equatorial domain (I) of GroEL jointly with the small intermediate domain (II), and the apical domain was treated as a separate rigid body (III). In the case of EF-Tu, domain I was fitted individually and domains II and III jointly. Next, we refined each of the structures in the following order: domain-level CG (3 domains), SSE-level CG, and SSE-level MD. To evaluate the accuracy of the refined structures at each stage of the protocol, we compared them to the corresponding known structures: an unbound GroEL (2.8 Å resolution) (PDB code: 1oelD (Braig, et al. 1995)) and an E. coli EF-Tu-GDP-kirromycin (3.4 Å resolution) (PDB code: 1ob2).

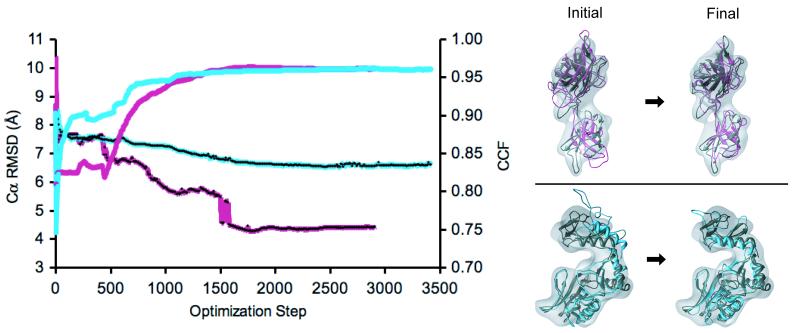
In all 3 cases, the refined structures were significantly more accurately positioned and modeled than the initial structure (Figure 4, Table 2). The largest improvement in the accuracy of the structures occurred during the MC or CG stage, in correlation with the increase in CCF. However, the largest improvement in the stereochemical and non-bonded terms occurred during the CG stage. For GroEL, Cα RMSD was reduced from 16.2 Å to 3.8 and 1.9 Å in the 11.5 and 6.0 Å maps, respectively. For EF-Tu, Cα RMSD was reduced from 28.6 to 4.0 Å. In the 6.0 Å map of GroEL, the final NO3.5 was 96% (ie, almost all atoms in the structure were within 3.5 Å from the crystal structure).

Figure 4.

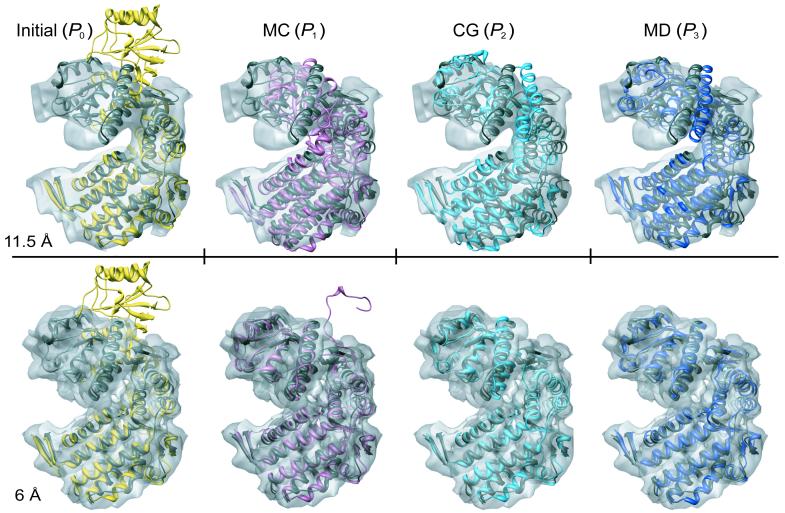
A comparative model of a monomer of the bacterial GroEL in the GroES-ADP-bound conformation (based on the archaeal homolog, PDB code: 1we3B) fitted and refined within the segmented experimental cryoEM maps of the unbound conformation, determined at 11.5 Å (top) and 6.0 Å (bottom) resolution. The known native structure (PDB code: 1oelD) is shown as a reference in grey. The input comparative model is shown in yellow (P₀). The structures shown in pink, light blue, and dark blue, are the final structures resulting from the MC stage (P₁), CG stage (P₂), and MD stage (P₃) of the optimization protocol, respectively. The initial Cα RMSD (left) is 16.2 Å from the native structure, and the final Cα RMSDs (right) are 3.8 and 1.9 Å in the 11.5 Å and 6.0 Å resolution maps, respectively. The figures were generated with Chimera (Pettersen, et al. 2004).

Table 2.

Non-native structures of GroEL monomer and EF-Tu fitted and refined in their experimental cryoEM maps

Protein name, Resolution (Å), Domain definition	Probea	-ECCF(b)	ESC(b)	ENB(b)	OSc (Å, deg)	DOS1c (Å, deg)	DOS2c (Å, [deg])	Cα RMSDd (Å)	NO3.5d (%)	NO5.0′ (%)
GroEL, 11.5, I (3-138, 409 527), II (190- 373), III (139-189, 374- 408)	P0 (Initial)	0.771	1759	2.6	2.0, 7.8	7.2, 30.5	12.3, 106.7	16.2	49	53
	P1 (MC)	0.824	192786	896	2.0, 7.8	7.2, 30.5	12.6, 63.1	13.0	49	53
	P2 (CG)	0.848	175950	22.7	4.3, 5.6	7.1, 26.2	3.8, 19.4	6.0	50	80
	P3 (MD)	0.894	1517	3.3	2.3, 2.6	6.7, 26.3	2.3, 12.1	3.8	61	86
GroEL, 6.0, I (3-138, 409 527), II (190- 373), III (139-189, 374-408)	P0 (Initial)	0.554	1759	2.6	0.3, 2.5	7.2, 30.5	12.3, 106.7	16.2	49	53
	P1 (MC)	0.673	500194	2.6	0.3, 2.5	7.2, 30.5	5.5, 19.9	7.4	75	84
	P2 (CG)	0.710	1896	22.6	0.4, 2.3	2.6, 17.4	4.3, 13.5	2.2	90	96
	P3 (MD)	0.745	1496	5.9	0.5, 2.1	1.6, 8.6	1.7, 4.3	1.9	96	98
EF-Tu, 9.0, I (1-202), II (203-300), III (301-393)	P0 (Initial)	0.659	1629	8.0	1.1, 7.8	24.4, 91.1	0.8, 12.4	28.6	47	48
	P1 (MC)	0.851	20393	5472.5	0.5, 2.8	3.4, 14.4	0.8, 12.4	4.4	84	93
	P2 (CG)	0.856	1712	13.2	1.3, 7.8	6.2, 7.5	3.1, 9.8	4.1	84	94
	P3 (MD)	0.867	2172	9.6	1.7, 5.0	5.4, 5.2	4.5, 8.0	4.0	86	94

^a“Probe” is the structure being refined. P₀,P₁,P₂, and P₃ refer to the initial structure, and the structures resulting from the MC, CG, and MD stages of optimization protocol, respectively.

^b-E^CCF, E^SC, and E^NB are the 3 terms of the scoring function with equal weights (w₁=w₂=w₃=1, Eq. 2): the cross-correlation coefficient (CCF) between a probe structure and the native density map (which is multiplied by 10,000 during refinement, Eq. 3 and 5, respectively), the stereochemical restraints, and the non-bonded interactions restraints.

^cOS, DOS1 ad DOS2 are the orientation and two domain-orientation scores, respectively (the OS score was calculated for the domain I, and DOS1 and DOS2 where calculated for domains I-II and II-III, respectively).

^dCα RMSD is the root-mean-square deviation between the Cα atoms of a probe structure and their corresponding atoms in native structure, and NO3.5 and NO5.0 are the percentages of Cα atoms in a probe structure that are positioned within 3.5 Å and 5.0 Å, respectively, from their corresponding atoms in the native structure. These scores are Calculated upon superposition of the initial or a refined structure onto the corresponding native structure using a rigid-body least-squares minimization.

DISCUSSION

Method

We present a method for flexible fitting of atomic structures of assembly components into the cryoEM density map of the whole assembly (Flex-EM). The method, which is applicable to both experimental structures and models, outputs the position and orientation of the component in the density map (MC stage) as well as its refined coordinates (CG and MD stages) (Figure 1). The optimization is applied to the component rigid bodies, specified by the user, and is driven by the quality of their fit into the density (CCF) as well as stereochemistry and non-bonded interactions. The method is fully automated, while also allowing user intervention in the fitting process, including assigning and refining rigid bodies. For example, some components may be fixed at certain positions while others are refined in their context.

Conceptually, Flex-EM is similar to RSRef, a real-space refinement method that was originally developed for X-ray crystallography (Chapman 1995) and has recently been adopted to cryoEM and applied to maps at resolutions better than 20 Å (Chen and Champman 2001, Chen, et al. 2003). RSRef uses torsion-angle MD to improve the fit of an atomic model to a density map by optimizing a scoring function that includes a CCF term as well as the stereochemical and non-bonded interaction terms. However, there are significant differences between the two methods. RSRef was designed to refine an atomic model within a cryoEM density map once it is already fitted in the approximate position in the map. Flex-EM, in contrast, performs both the initial approximate fitting of the model in the map and its further refinement. During the refinement, Flex-EM, like RSRef, improves the positions and orientations of the domains. Flex-EM has also been shown here to improve the positions and orientations of secondary structure elements within the domains (Table 1a). The ability to treat the secondary structure elements of the structure being refined as individual rigid bodies even at ∼14 Å resolution is partly due to the inclusion of the two-dimensional (Φ,Ψ) dihedral angle term in the scoring function. This term allows better modeling of the loops or linkers connecting the rigid bodies, whether domains or secondary structure elements, resulting in high quality Ramachandran plots for the refined models (Figure S1). Lastly, our method is based on satisfaction of spatial restraints in real space. Therefore, it can be combined relatively easily with additional restraints that provide information about the configuration and conformation of the assembly components, such as footprinting, chemical cross-linking, and various bioinformatics analyses (Russell, et al. 2004).

Previously, Normal Mode Analysis (NMA) relying on the scoring function corresponding to CCF was successfully applied to explore deformations of the structure in the search for an optimal solution (Tama, et al. 2004, Ma 2005). The approach relies on the assumption that a few of the lowest-frequency modes are sufficient to represent the changes needed to refine the initial structure. Although this assumption is often warranted, it does not always apply. For example, a ligand can “stretch” the protein in ways that involve higher frequency modes (Petrone and Pande 2006). In addition, high-frequency deformations that occur due to modeling errors may not be corrected using this method. The advantage of the current method implemented in Flex-EM is that it can in principle produce any kind of molecular deformations (including high-frequency), such as shear and hinge movements of whole domains, sub-domains and secondary structure elements as well as loop distortions and movements.

Accuracy of the modeled structures

Almost all existing cryoEM flexible-fitting methods can lead to artificial distortions in the refined atomic structure. One of the advantages of our method is the ability to optimize the fit of the structure within the density map while maintaining correct stereochemistry. This goal is achieved during the refinement stages of the optimization (CG and MD) by optimizing a scoring function that is driven by a CCF term, but that also includes stereochemical and non-bonded interaction terms.

We demonstrate the ability of the method to improve the accuracy of structures using a benchmark of non-native structures and their corresponding native density maps at 10 Å resolution. While the method does not allow us to predict to what extent a given structure can be refined, none of the initial structures became worse in terms of Cα RMSD as a result of its refinement (Table 1). On average, Cα RMSD improved from 5.2 to 3.9 Å for the single-domain proteins and from 13.0 to 6.3 Å for the two-domain proteins. NO3.5 increased from 58% to 73% and from 46% to 57%, respectively. Furthermore, the values of the stereochemical and non-bonded terms were either reduced or remained comparable to those in the initial structure (Table 1). The final average number of residues in the allowed (Φ,Ψ) regions of the Ramachandran plot was higher than 97.5% for all final structures (Figure S2), indicating that none of the final structures is distorted.

Although the improvement in the accuracy of the benchmark structures was generally high for both single- and two-domain proteins (Table 1), the improvement was higher for the single-domain proteins (as reflected in the NO3.5 score). This result can be explained by the nature of the benchmark, considering that the refinement stages of the optimization are primarily depended on the rigid-fitting stage. For the single-domain proteins, the initial rigid fitting at the domain level was very accurate (as reflected in the OS score), enabling successful refinement at the SSE level (as reflected in the NO3.5 score). For the two-domain proteins, the SSE-level refinement was successful only when the domains were sufficiently accurately positioned in the map by the CG domain-level optimization (as reflected in the DOS, NO3.5, and NO5.0 scores). If, however, there was initially only partial improvement in the domain positions, the subsequent SSE-level refinement failed due to the inability of the sampling to benefit from the map.

A further indicator of the accuracy of the method was provided by testing it at a range of resolutions between 4 and 14 Å (Figure 4). The method was shown to improve the structures significantly at 6 and 4 Å resolutions, decreasing Cα RMSD below 2.5 Å at 4 Å resolution (for 4 of the 4 test cases) and below 3.0 Å at 6 Å resolution (for 3 of the 4 test cases). In addition, for all 4 proteins, both Cα RMSD and NO3.5 of the final structures were better than those of the initial structures, even at 14 Å resolution, indicating that the method is certainly useful for the refinement of secondary structure elements and loops even at resolutions where secondary structure elements cannot be identified directly from the density. The method might be helpful even at resolutions worse than 14 Å, as long as the rigid bodies are large enough (ie, not smaller than domains), a possibility that we will test in the future.

To demonstrate the ability of the method to refine atomic structures in more realistic cases, we applied it to experimentally-determined cryoEM maps of GroEL at 6.0 and 11.5 Å resolution (Table 2, Figure 4) and of EF-Tu at 9.0 Å resolution. Despite the noise in these maps that is not present in the simulated maps, the results were similar to the benchmark average. For GroEL, Cα RMSD was reduced from 16.2 to 1.9 and 3.8 Å using the 6.0 and 11.5 Å maps, respectively; for EF-Tu, the improvement was from 28.6 to 4.0 Å using the 9.0 Å map. In addition, when the initial rigid fitting is accurate and Cα RMSD is thus significantly decreased in the MC stage (GroEL - 11.5 Å and EF-Tu - 9 Å cases), further refinement significantly reduces the distortions in bond distances and angles in the linkers connecting the domains (Table 2). These realistic test cases demonstrate that the method can significantly improve structures with ∼12 Å resolution maps, as well as approach the atomic resolution with 6 Å resolution maps.

Scoring function and sampling

In all tested cases (including GroEL and EF-Tu), the change in CCF is highly correlated with the change in Cα RMSD and NO (Figure 2), and the native structure has the highest score (CCF = 1). Thus, the scoring function of Flex-EM appears to be sufficiently accurate for the current degree of sampling at the tested map resolutions. Correspondingly, the main shortcoming of the current method is its relatively limited sampling. (If the sampling becomes more thorough in the future, the scoring may also become limiting in terms of achieving higher accuracy.) There are two underlying reasons for the limited sampling:

First, on the way to the approximately “correct” solution there are many structures that have a similar score, especially if they have similar shapes. For example, for 1iknA, the most accurate structure, which was found in the second cluster at the CG stage of the optimization, did not have the highest CCF, even following the MD refinement (Table 1b). Another example is 1a45A, for which CCF of the final structure was 0.973, even though Cα RMSD was only 12.2 Å due to a mis-orientation of one of the domains by [39 Å,141°]. This domain is a globular β-sandwich fold for which CCF of the final orientation was similar to CCF of the correct orientation (in the crystal structure). To overcome this problem, we need to add other types of information to the scoring function, such as statistical potentials (Shen and Sali 2006) and geometric complementarity between domains (Lasker, Topf, Sali and Wolfson, submitted).

Second, an incorrect definition of the rigid bodies can “trap” the structure in a local minimum. A good example of this problem is the single-domain protein 1uwoA, where a helix that corresponds to a loop in the native structure was defined as a rigid body, preventing the refinement of the structure towards more accurate conformations. To tackle this problem, we need to assign the rigid bodies more accurately. Possible rigid body assignments may rely on structural variation within the family of the structures related to the component or within a group of independently calculated models of the component. They might also be obtained using graph theory, neural networks, and other approaches based on energetic interactions within and between the proteins (Alexandrov, et al. 2005, Flores and Gerstein 2007).

Implications for comparative protein structure modeling

Experimentally-determined atomic-resolution structures of molecular components are frequently not available and most cryoEM maps are generally still insufficient for atomic structure determination on their own. In such cases, it may be possible to identify a structure (template) that is homologous to the component (target) based on its amino-acid sequence, and construct a useful model using comparative modeling (Eswar, et al. 2006). Currently, ∼1.3 million of the ∼4.5 million known proteins sequences (Bairoch, et al. 2005) have at least one domain that can be modeled based on its similarity to one or more of the ∼47,000 known protein structures (Pieper, et al. 2006). However, sequence-structure alignments between the target and the template are a major source of errors in comparative models, especially in models of sequences that are only remotely related to their templates (ie, at less than 30% sequence identity, which includes most detectably related protein sequences) (Eswar, et al. 2006). Other errors include distortions and shifts of the backbone and sidechains.

We recently showed that CCF between a comparative model and the corresponding density map is highly correlated with the accuracy of the model (Topf, et al. 2005). We then built upon this correlation by adopting our Moulder genetic algorithm protocol that reduces alignment errors through the iteration over alignment, model building, and model assessment (John and Sali 2003). For the application to EM (Moulder-EM), the iteration is guided by a fitness function corresponding to a combination of CCF and statistical potentials (Topf, et al. 2006). The method was able to reduce by ∼19% the Cα RMSD of 20 comparative models (which were based on less than 30% sequence identity to their homologs) using their 10 Å resolution native density maps. As expected, the improvement in the accuracy of the models was due mainly to a reduction in alignment errors and partly due to better loop modeling. However, errors in comparative modeling that occur due to target-template differences in the correctly aligned regions, such as those in the relative positions of secondary structure elements and domains, could not be addressed. As with alignment errors, these types of errors can occur even when the sequence identity is high (ie, higher than 30%), but become more significant at lower sequence identity (Eswar, et al. 2006).

The Flex-EM method can address errors that occur due to target-template differences, because it relies on structure refinement that is guided by the restraints provided by the native density map. Indeed, the benchmark demonstrated that most of the improvement in accuracy was achieved by minimizing errors in the initial non-native structures that resulted from target-template differences in the correctly aligned regions (the benchmark structures were based on an average sequence identity of 37%, resulting in accurate alignments; data not shown). A potential future direction is to combine Moulder-EM with Flex-EM to obtain an iterative procedure that can simultaneously address alignment errors and target-template differences in the correctly aligned regions.

CONCLUSION

We presented a method for fitting and refining atomic protein structures in a density map of their assembly at intermediate resolution. The inclusion of the stereochemical and non-bonded interaction terms during the refinement process enables a more realistic sampling of the conformational space. The method is likely to yield insights into the mechanisms of proteins within macromolecular assemblies for which the structure can often only be obtained at low- to intermediate-resolutions by cryoEM techniques.