Abstract
Many central pattern generating networks are influenced by synaptic input from modulatory projection neurons. The network response to a projection neuron is sometimes mimicked by bath applying the neuronally-released modulator, despite the absence of network interactions with the projection neuron. One interesting example occurs in the crab stomatogastric ganglion (STG), where bath applying the neuropeptide pyrokinin (PK) elicits a gastric mill rhythm which is similar to that elicited by the projection neuron MCN1, despite the absence of PK in MCN1 and the fact that MCN1 is not active during the PK-elicited rhythm. MCN1 terminals have fast and slow synaptic actions on the gastric mill network and are presynaptically inhibited by this network in the STG. These local connections are inactive in the PK-elicited rhythm, and the mechanism underlying this rhythm is unknown. We use mathematical and biophysically-realistic modeling to propose potential mechanisms by which PK can elicit a gastric mill rhythm that is similar to the MCN1-elicited rhythm. We analyze slow-wave network oscillations using simplified mathematical models and, in parallel, develop biophysically-realistic models that account for fast, action potential-driven oscillations and some spatial structure of the network neurons. Our results illustrate how the actions of bath-applied neuromodulators can mimic those of descending projection neurons through mathematically similar but physiologically distinct mechanisms.
Keywords: Model, Central Pattern Generator, Stomatogastric Ganglion, Neuromodulation, Phase Plane
INTRODUCTION
Neuromodulatory substances modify the properties of neurons and synapses, thereby reconfiguring networks and altering their activity. Neuromodulators modify the output of many oscillatory neuronal networks, such as those that control locomotion (Grillner, 2006), respiration (Lieske et al., 2000) and the sleep/wake cycle (Dzirasa et al., 2006). Additionally, network activity is often conditional upon the presence of neuromodulators, which are typically released as circulating hormones or as neurotransmitters of projection neurons (Nusbaum and Beenhakker, 2002; Skiebe, 2001). Elucidating the mechanisms through which neuromodulators shape network output requires an understanding of their cellular and synaptic targets (Dickinson, 2006; LeBeau et al., 2005). For example, different neuromodulators can affect a network by targeting the same ionic mechanisms (Nusbaum et al., 2001) or synaptic properties (Marder and Thirumalai, 2002). Alternatively, neuromodulators that produce similar effects may act through distinct targets (Marder and Bucher, 2007; Prinz et al., 2004).
Bath application of neuromodulators affects network properties in a manner that is often similar to the actions of modulatory projection neurons (Morgan et al., 2000; Nusbaum and Beenhakker, 2002). One distinction, however, between circulating and neuronally released modulators is that the latter are also subject to complex synaptic interactions with their target networks (Coleman et al., 1995; Marder et al., 2005; Norris et al., 1994; Wood et al., 2004). These synaptic interactions cannot be duplicated by bath applying the appropriate neuromodulators. Therefore, bath-applied neuromodulators do not generally produce identical network effects as stimulation of neuromodulatory projection neurons (Nusbaum and Beenhakker, 2002; Nusbaum et al., 2001).
We use both low-dimensional analytically tractable and higher-dimensional biophysically-realistic models, in parallel, to compare the network effects produced by stimulating a descending projection neuron and by bath applying a neuromodulator on the gastric mill (chewing) motor network. This network is a central pattern generator (CPG) that is located within the stomatogastric ganglion (STG) of the crab, Cancer borealis (Marder and Bucher, 2007). The gastric mill rhythm is generally not spontaneously active, but stimulating the projection neuron modulatory commissural neuron 1 (MCN1) faithfully elicits this rhythm in vitro (Coleman et al., 1995). At the heart of the gastric mill rhythm is an asymmetric, half-center oscillator that is composed of reciprocal inhibition between interneuron 1 (Int1) and the lateral gastric (LG) neuron (Nusbaum and Beenhakker, 2002). Both excitatory synaptic input from MCN1 axon terminals within the STG and presynaptic inhibition of these terminals by the LG neuron are necessary for eliciting the gastric mill rhythm (Calabrese, 1999; Coleman et al., 1995). However, recent experiments showed that bath application of the neuropeptide pyrokinin (PK) to the STG elicits a similar gastric mill rhythm in the absence of MCN1 participation (Saideman et al., 2007a; Saideman et al., 2007b). PK is not released by MCN1, and it is the first known neuromodulator to elicit a gastric mill rhythm when bath applied to the crab STG. However, the mechanism that underlies the PK-elicited rhythm is unknown.
Using our models, we propose mechanisms by which PK can elicit a gastric mill rhythm that is similar to the MCN1-elicited rhythm. Previously, a detailed compartmental model (Nadim et al., 1998) was used to show that the frequency of the MCN1-elicited rhythm (freq: ∼ 0.1 Hz) is strongly regulated by a local synaptic input from the coactive pyloric rhythm (freq: ∼ 1 Hz), as later confirmed by experiments (Bartos et al., 1999). This compartmental model was then reduced to a simpler 3-dimensional mathematical model that was used to analyze the synaptic mechanisms that underlie the MCN1-elicited rhythm (Manor et al., 1999).
In this paper, we use a separation of time scales to reduce the 3-dimensional model of Manor et al., (1999) down to 2 dimensions where both state variables are directly involved in generating network oscillations. This allows us to completely describe the network dynamics of the MCN1-elicited rhythm via a phase-plane analysis. We then use this 2-dimensional model to propose potential mechanisms by which PK can elicit a similar gastric mill rhythm in the absence of MCN1 participation. In particular, we propose three physiologically distinct, but mathematically similar, mechanisms through which the induction of voltage-gated ionic currents (potentially by PK) in the LG neuron can elicit a gastric mill rhythm that is similar to the MCN1-elicited rhythm. In parallel, we assess the predictions of our 2-dimensional model with a more biophysically-realistic model. In particular, we show that each PK mechanism proposed in the 2-dimenisonal model also elicits a gastric mill rhythm that is similar to the MCN1-elicited rhythm in the context of the biophysically-realistic model. Thus, our results provide insight into how the complex synaptic interactions between a descending projection neuron and its target network can be mimicked by a bath-applied neuromodulator onto the network through mathematically similar but biologically distinct mechanisms.
METHODS
1. The reduced mathematical models
Our 2-dimensional mathematical model of the MCN1-elicited gastric mill rhythm was developed as a reduction of a previously-published 3-dimensional model (Manor et al., 1999). Before describing the reduction, we briefly summarize the 3-dimensional model below. In the 3-dimensional model, the reciprocally inhibitory CPG neurons Int1 and LG, which comprise the half-center oscillator that determines the activity pattern of the gastric mill rhythm, are treated as passive neurons and only the graded component of synaptic transmission between them is involved. All action potentials and action-potential-mediated transmission were ignored in this model. Thus, the model only accounted for the slow envelope of network oscillations, in order to simplify the network interactions and perform a mathematical analysis. The state variables in the model are the membrane potential of Int1 (VI), the membrane potential of the LG neuron (VL), and the slow, synaptic input (s) from MCN1 to the LG neuron which are governed by the following equations:
| (1) |
| (2) |
| (3) |
The parameters CI and CL represent the membrane capacitance of Int1 and the LG neuron, respectively, and are set to 1. The parameter IExt represents external current injected in the LG neuron, which is set to zero unless stated otherwise. The terms ILeak,I in Equation (1) and ILeak,L in Equation (2) model the leak current in each neuron with gLeak and ELeak representing the leak conductance and reversal potential, respectively. We note that when projection neuron input is absent in the biological system (equivalent to ḡs = 0 here), Int1 remains active and exhibits a high membrane potential while the LG neuron remains inactive and exhibits a low membrane potential (Bartos et al., 1999). This asymmetry between Int1 and the LG neuron is accounted for by assigning a high value to ELeak,I and a low value to ELeak,L (see Table 1).
Table 1.
Parameters for the 2-Dimensional Model of the MCN1-Elicited Gastric Mill Rhythm
| Int1 | Pyloric | LG | MCN1 |
|---|---|---|---|
| gLeak,I = 0.75 mS/cm2 | ḡP = 0.85 mS/cm2 | gLeak,L = 1 mS/cm2 | ḡs = 3 mS/cm2 |
| ELeak,I = 10 mV | EP = −60 mV | ELeak,L = −60 mV | Es = 50 mV |
| ḡL→I = 2 mS/cm2 | per = 1 sec | ḡI→L = 5 mS/cm2 | vpre = −33 mV |
| EL→I = −80 mV | dur = 0.5 | EI→L = −80 mV | ⊺LO,MCN1 = 14 sec |
| vL→I = −30 mV | vq = −35 mV | vI→L = −30 mV | ⊺HI,MCN1 = 5 sec |
| kL→I = 5 mV | kq = 3 sec | kI→L = 5 mV |
The terms IL→I and II→L model the reciprocally inhibitory synapses between Int1 and the LG neuron with ḡL→I and EL→I (ḡI→L and EI→L) denoting the maximal conductance and reversal potential, respectively, of the LG to Int1 (Int1 to LG) synapse. These reciprocally inhibitory synapses are controlled by the gating functions mL→I(VL) and mI→L (VI), which depend only on the membrane potential of the presynaptic neuron and are modeled by the sigmoids
| (4) |
| (5) |
The parameters vL→I and kL→I (vI→L and kI→L) specify the half-activation voltage and steepness of the sigmoid, respectively.
The term IP in Equation (1) models the inhibitory synaptic input from the pacemaker of the pyloric circuit (the AB neuron) to Int1. The parameters ḡP and EP represent its maximal conductance and reversal potential, respectively. Because the frequency of the pyloric rhythm is much faster than the frequency of the gastric mill rhythm in the biological system (Bartos et al., 1999), P(t) in Equation (1) is modeled by a fast periodic half-sine forcing function:
| (6) |
where per and dur represent its period and duty cycle while mod and H designate modulo and Heaviside functions, respectively.
The term Is in Equation (2) models the slow, excitatory synaptic input from MCN1 axon terminals to the LG neuron, where ḡs and Es represent its maximal conductance and reversal potential, respectively. The excitatory MCN1 input to LG (controlled by the variable s in Equation (3)) is gated by VL via presynaptic inhibition: s builds up towards 1 with time constantΤLO,MCN1 when VL is below the threshold voltage vpre for presynaptic inhibition while s decays with time constant ΤHI,MCN1 when VL > vpre.
Previous experiments (Coleman et al., 1995) and modeling (Nadim et al., 1998) indicate that the frequency of the MCN1-elicited rhythm is controlled by the excitatory synapse from MCN1 to the LG neuron, which acts with a slower time scale than all other synapses in the network (Coleman et al., 1995). The time constants ΤLO,MCN1 and ΤHI,MCN1 in Equation (3) are set to large values in order to account for the slow synaptic time scale of the MCN1 to LG synapse. This slow time scale is revealed by rewriting Equation (3) in the form
| (7) |
where ΤMCN1(VL)=ΤHI,MCN1+(ΤLO,MCN1−ΤHI,MCN1)H(vpre−VL), and . As a result, since ε is small, the state variable s in Equation (3) evolves much more slowly than the other state variables.
Reduction to a 2-Dimensional Model of the MCN1-Elicited Gastric Mill Rhythm
During the MCN1-elicited rhythm, we note that the dynamics of the LG neuron are influenced by the slow synaptic input from MCN1. In contrast, Int1 is only influenced by synaptic inputs that occur on a much faster time scale. We exploit this difference in synaptic time scales in order to reduce the 3-dimensional model of (Manor et al., 1999) down to 2 dimensions. In particular, since Int1 is only influenced by fast synaptic inputs, its membrane potential (VI) can be assumed to adjust instantaneously to its steady state compared to that of the other state variables VL and s. Thus, dividing through Equation (1) by the leak conductance gLeak,I gives
| (8) |
where is the membrane time constant of Int1. Then, setting ΤI = 0 makes the left hand side of Equation (8) equal to zero and allows for an explicit solution of the Int1 membrane potential given by
| (9) |
In this equation VI is expressed in terms of the state variable VL and the periodic forcing function P(t,VL). In the biological system, the pyloric-timed inhibition of Int1 does not affect the gastric mill rhythm during the active state of the LG neuron (Bartos et al., 1999). This biological fact was not accounted for in the model of Manor et al (1999), but it is incorporated into our 2-dimensional model by making the pyloric-timed forcing function P dependent upon the membrane potential of the LG neuron:
| (10) |
where P(t) is as in Equation (6), while q(VL) is a decreasing sigmoid given by
| (11) |
whose inflection point voltage and steepness are governed by the parameters vq and kq, respectively. As a result, the pyloric-timed, voltage-dependent, forcing function of Equation (10) only influences the gastric mill rhythm during the inactive state of the LG neuron (see Results).
Substituting the expression for VI given by Equation (9) into the mI→L(VI) term of Equation (2) gives a 2-dimensional model of the MCN1-elicited gastric mill rhythm:
| (12) |
Hence, in reducing to 2 dimensions, we have absorbed the dynamics of VI into the dynamics of the state variable VL. Moreover, the effects of the fast inhibitory synapses that influence Int1, namely the LG to Int1 inhibition and the pyloric-timed inhibition of Int1, are mathematically absorbed into the Int1 to LG synapse via the term mI→L(vI(VL;P(t,VL))) of Equation (12). Thus, we have reduced the 3-dimensional model of (Manor et al., 1999) down to 2 dimensions where both state variables (VL and s) are directly involved in generating network oscillations. This enables a complete description of the network dynamics of the MCN1-elicited gastric mill rhythm via a phase-plane analysis in the VL-s phase plane.
Next, we describe the phase-plane geometry of the 2-dimensional model which is used for the analysis of this model in the Results. First, we compute the VL- and s-nullclines. However, note that the 2-dimensional model is non-autonomous due to the forcing function P(t,VL) in Equation (12). We will treat this forcing term as a parameter and describe a one-parameter family of VL-nullclines indexed by the forcing parameter values p (=P(t,VL)) in [0,1]:
| (13) |
where ILeak,L and II→L are as in Equation (12). Equation (13) describes a cubic VL-nullcline for a given value of p, where the extreme values of p = 0 (p = 1) correspond to the unforced (maximally forced) system. The s-nullcline is given by the step function
| (14) |
and the line connecting its two discontinuous branches.
Note that the cubic shape of the VL-nullcline is not due to any intrinsic properties of the LG neuron (or Int1), which is passive in this model, but rather arises from the reciprocally inhibitory synapses between LG and Int1. The fact that this reciprocal inhibition can give rise to dynamics that are similar to excitability is described by Manor et al (1999).
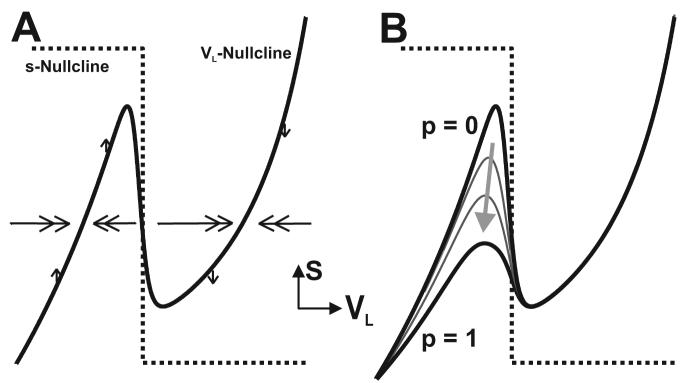
The parameter vpre of Equation (14) can be chosen so that the s-nullcline intersects either (i) the middle branch of the cubic VL-nullcline (as in Figure 1), thus giving rise to an unstable fixed point and a stable oscillatory trajectory, or (ii) the outer branches of the VL-nullcline, thus giving rise to a globally-stable fixed point. In both cases dVL/dt > 0 (< 0) above (below) the VL-nullcline while ds/dt > 0 (< 0) below (above) the s-nullcline within the VL-s phase plane.
Figure 1.
Phase-plane geometry of the 2-dimensional model. A, The cubic-shaped and step-function-shaped nullclines represent the steady-state behavior of the state variables VL and s, respectively. The nullclines intersect along the middle branch of the cubic to allow for a stable oscillatory trajectory. In addition, the 2-dimensional model resides in a relaxation regime. As a result, the flow in the horizontal (VL) direction (double arrows) is much faster than the flow in the vertical (s) direction (single arrows). In the phase plane, dVL/dt > 0 (<0) above (below) the cubic VL-nullcline, while ds/dt > 0 (<0) below (above) the s-nullcline. In the absence of the pyloric input (p = 0 in Eq. (13)), a single cubic VL-nullcline exists in the phase plane. B, In the presence of the pyloric input, a family of cubic VL-nullclines exists in the phase plane. The unforced cubic (p = 0) and maximally forced (p = 1: the peak of the pyloric input) cubic are shown in bold and the arrow indicates increase in the forcing parameter p.
The fact that ε is small (see description of Equation (7)) puts the system (12) in the relaxation (or fast-slow) regime. At the limit of ε = 0, a general trajectory in the VL-s phase plane consists of fast and slow portions where the slow portions track the outer branches of the cubic nullcline to which they are strongly attracted by the fast horizontal flow. It is known that trajectories of fast-slow systems such as system (12) for the case of 0 < ε ⪡ 1 stay close to the limiting trajectories defined by the ε = 0 system (Mishchenko and Rozov, 1980).
Since 0 ≤ p ≤ 1 in Equation (13), a family of cubic VL-nullclines exists in the phase plane (Figure 1B) which lie between the indexed values of p = 0 (the unforced system) and p = 1 (the maximally forced system at the peak of the pyloric input). In particular, the pyloric-timed forcing function shifts the VL-nullcline as p varies in [0,1], which causes the slow portion of any trajectory to shift back and forth between the higher and lower cubics. These shifts between cubics are impulsive since the peak of the forcing is short in duration compared to its period. Thus, when p = 0 in Equation (13), the trajectory in the VL-s phase plane tracks the higher (unforced) cubic, but quickly shifts through a family of lower cubics for nonzero values of p and touches the lowest (maximally forced) cubic when p = 1.
Note that the pyloric forcing function P only affects the inactive state of the LG neuron (as in the biological network; see Equation (10)) and therefore only shifts the left branch of the VL-nullcline. The right branch of the VL-nullcline, which corresponds to the active state of the LG neuron, remains stationary since the effect of the pyloric forcing is not effectively transmitted through the Int1 to LG synapse during the active state of the LG neuron (see Results).
All simulations for the 2-dimensional models in this work were performed using the software package XPPAUT (Ermentrout, 2002). Parameter values for the MCN1-elicited rhythm are given in Table 1. The simulations for the unforced MCN1-elicited rhythm were performed by setting the maximal conductance ḡP for the pyloric-timed forcing to 0.
The 2-Dimensional Model of the PK-Elicited Gastric Mill Rhythm
Three reduced models were used for the PK-elicited oscillations. These three models were based on the 2-dimensional model of the MCN1-elicited rhythm as given in Equations (12). However, the influence of MCN1 through the synaptic variable s was replaced by three alternative PK-induced intrinsic currents in the LG neuron as described below:
1. IPlat in the LG Neuron
In this model PK can elicit a gastric mill rhythm in the absence of MCN1 participation via the induction of a plateau current in the LG neuron, as modeled by a low threshold, slowly-inactivating inward current given by
| (15) |
The parameters ḡplat and Eplat designate its maximal conductance and equilibrium potential, respectively. In addition, we set Eplat above the resting potential of the LG neuron, which is given by ELeak,L in Equation (12), to model IPlat as an inward current. The activation of IPlat is assumed to be instantaneous and given by
| (16) |
where the parameters va and ka specify the inflection point voltage and steepness of the sigmoid, respectively. Inactivation of IPlat is governed by the slow variable n. The 2-dimensional model of the PK-elicited rhythm involving the induction of IPlat in the LG neuron is given by
| (17) |
with Τn(VL)=ΤHI,inact+(ΤLO,inact−ΤHI,inact)H(vinact−VL), where the parameter vinact designates the inactivation voltage threshold of IPlat. ILeak,L and II→L are as in Equation (12). The additional parameters for this model are given in Table 2.
Table 2.
Additional Parameters for Each 2-Dimensional Model of the PK-Elicited Rhythm
| IPlat | IProc | IK | Ih |
|---|---|---|---|
| ḡplat = 6 mS/cm2 | ḡproc = 12 mS/cm2 | ḡK = 4 mS/cm2 | ḡh = 3 mS/cm2 |
| Eplat = 20 mV | Eproc = 12 mV | EK = −80 mV | Eh = 30 mV |
| va = −40 mV | vb = −20 mV | vK = −33 mV | vhyp = −33 mV |
| ka = 17 mV | kb = 19 mV | ⊺LO,K = 3.5 sec | ⊺LO,hyp = 10.5 sec |
| vinact = −33 mV | ⊺HI,K = 5.5 sec | ⊺HI,hyp = 6 sec | |
| ⊺LO,inact = 5 sec | |||
| ⊺HI,inact = 4 sec |
2. IProc + IK in the LG Neuron
A second mechanism by which PK is proposed to elicit a gastric mill rhythm is via the induction of two non-inactivating currents in the LG neuron, a fast inward current IProc and a slow outward current IK. The inward current IProc is modeled by
| (18) |
The parameters ḡProc and EProc designate its maximal conductance and reversal potential, respectively, and EProc is set above the resting potential of the LG neuron to model IProc as an inward current. Physiologically, IProc is a current with fast kinetics (Golowasch and Marder, 1992). Therefore, we approximate its activation by an instantaneous sigmoidal function of the LG membrane potential given by
| (19) |
where the parameters vb and kb designate the inflection point voltage and steepness, respectively. The outward current IK is modeled by
| (20) |
where the parameters ḡK and EK designate its maximal conductance and reversal potential, respectively. However, we set EK below the resting potential of the LG neuron in order to model IK as an outward current. Activation of IK is governed by the slow variable w.
Thus, the 2-dimensional model of the PK-elicited gastric mill rhythm involving PK-induction of both IProc and IK in the LG neuron is given by
| (21) |
with ΤK(VL)=ΤHI,K+(ΤLO,K−ΤHI,K)H(vK−VL), where the parameter vK designates the activation voltage threshold of the outward current IK. ILeak,L and II→L are as in Equation (12). The additional parameters for this model are given in Table 2.
3. Ih in the LG Neuron
A third mechanism by which PK is proposed to elicit a gastric mill rhythm is via the induction of a slow, hyperpolarization-activated, inward current Ih in the LG neuron that is modeled by
| (22) |
The parameters ḡh and Eh designate its maximal conductance and reversal potential, respectively, and Eh is set above the resting potential of the LG neuron to model Ih as an inward current. Physiologically, Ih has slow kinetics, but, unlike the currents proposed in the previous two mechanisms, the conductance of Ih is activated by hyperpolarization (Angstadt and Calabrese, 1989). Activation of Ih is governed by the slow variable c in the model. Thus, the 2-dimensional model of the PK-elicited gastric mill rhythm involving PK-induction of Ih in the LG neuron is given by
| (23) |
with Τhyp(VL)=ΤHI,hyp+(ΤLO,hyp−ΤHI,hyp)H(vhyp−VL), where the parameter vhyp designates the activation voltage threshold of Ih. ILeak,L and II→L are as in Equation (12). The additional parameters for this model are given in Table 2. We note that the family of cubic VL-nullclines in this model is given by:
| (24) |
where p = 0 (p = 1) again corresponds to the unforced (maximally forced) system due to the effect of the pyloric input.
2. The Biophysically-Realistic Models
The biophysically-realistic models are based upon the updates we performed on a previously-published, compartmental model of the MCN1-elicited gastric mill rhythm (Nadim et al., 1998). Before describing these updates, we briefly summarize the original compartmental model of (Nadim et al., 1998). This compartmental model was used to show that the frequency of the MCN1-elicited rhythm is strongly regulated by a local synaptic input from the pacemaker of the pyloric circuit (the AB neuron) to Int1, as later confirmed by experiments (Bartos et al., 1999). Unlike our 2-dimensional mathematical models, the compartmental model of (Nadim et al., 1998) accounts for both action potential generation and some spatial structure of the neurons. In particular, MCN1, Int1, and LG were all treated as Hodgkin and Huxley-type neurons to account for action potential generation. Moreover, all three neurons were represented with a multiple-compartment structure in which adjacent compartments were separated by an axial resistance to separate the neuronal sites of synaptic input from that of action potential generation. However, the compartmental model of (Nadim et al., 1998) did not reproduce the biological fact that MCN1 still elicits a gastric mill rhythm (albeit slower) when the inhibitory synaptic input from the AB neuron to Int1 is removed, as occurs in the biological system (Bartos et al., 1999).
We have updated the compartmental model of (Nadim et al., 1998) to more accurately reproduce the features of the biological system. In particular, we have: (i) modeled MCN1 with only axon and axon terminal compartments, (ii) made the activity of MCN1 dependent upon brief axonal stimulations, rather than a depolarization of its soma as in (Nadim et al., 1998), in order to be consistent with the experimental methods (Bartos et al., 1999), (iii) explicitly included the AB neuron in the compartmental model, (iv) retuned the model so that it now produces a slow gastric mill rhythm in the absence of the AB to Int1 synapse, as occurs in the biological system (Bartos et al., 1999). We refer to this updated model as the biophysically-realistic model of the MCN1-elicited rhythm.
Biophysically-Realistic Model of the MCN1-Elicited Gastric Mill Rhythm
MCN1 is represented with four axon and two axon terminal compartments in the biophysically-realistic model. The axon compartments of MCN1 include voltage-gated ionic conductances to account for action potential generation while the axon terminal compartments are passive. As in (Nadim et al., 1998), an axon compartment of MCN1 is electrically coupled to the LG neuron, while an axon terminal compartment accounts for the sites of both MCN1 synaptic release and presynaptic inhibition of MCN1 by the LG neuron (Fig. 2.C). Int1 and the LG neuron were each modeled with three compartments, which represent the soma, neurite, and axon from left to right (Figure 2.C). As in (Nadim et al., 1998) the soma and neurite compartments of these neurons are passive, while action potential generation occurs in the axon compartment of each neuron. The AB neuron is modeled as a single compartment that includes a voltage-gated conductance to produce oscillations in this pacemaker neuron.
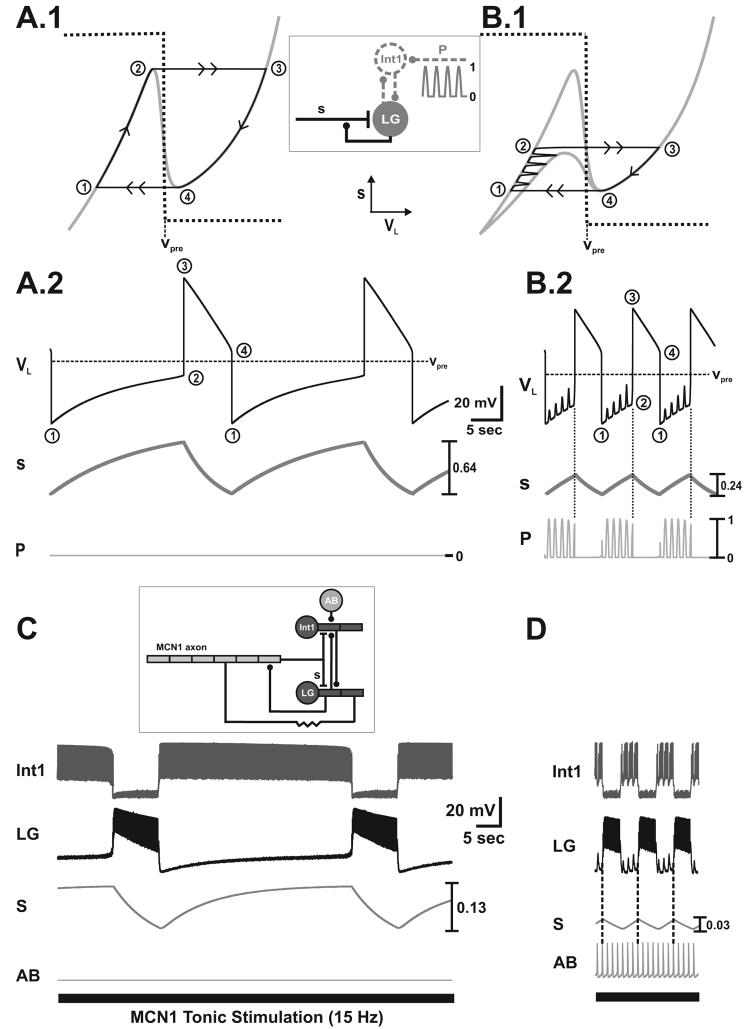
Figure 2.
The buildup and decay of MCN1 excitation (s) in the LG neuron drives the MCN1-elicited gastric mill rhythm. A.1-A.2, Network dynamics in the absence of pyloric input (p = 0). During the inactive state of the LG neuron, the trajectory slowly climbs up the left branch of the VL-nullcline from point 1 to point 2 (A.1), and s builds up in the LG neuron as the LG membrane potential (VL) slowly rises (A.2). At point 2 the trajectory jumps to point 3 on the right branch of the cubic, since dVL/dt > 0 above the VL-nullcline. During the active state of the LG neuron, the trajectory slowly falls down the right branch of the VL-nullcline from point 3 to point 4 (A.1) due to LG presynaptic inhibition of MCN1, and s decays in the LG neuron as VL slowly falls (A.2). At point 4, the trajectory jumps back to point 1 on the left branch of the cubic, since dVL/dt < 0 below the VL-nullcline. Schematic inset shows the circuit diagram corresponding to the 2-dimensional model in which the dynamics of Int1 are absorbed into the equations for LG. B.1-B.2, Network dynamics in the presence of pyloric input. During the LG inactive state, the trajectory slowly climbs up the left branch of the VL-nullcline as it is moved back and forth between the unforced (p = 0) and maximally forced (p = 1) cubics by the pyloric input (B.1). Transitions between the left branches of the VL-nullcline correspond to the small depolarizations in VL (B.2). After sufficient buildup of s, the next pyloric peak (p = 1) shifts the VL-nullcline below the phase point and initiates the jump the right branch at point 2 (B.1). The dynamics on the right branch are similar to that of the unforced system in A.1, since the pyloric input does not affect the active state of the LG neuron. The pyloric input increases the frequency of the MCN1-elicited rhythm (compare A.2 and B.2) and a pyloric peak determines the onset of the LG active phase (vertical dotted lines in B.2). Most hyperpolarized LG membrane potential: −67 mV. C-D, Predictions of the 2-dimensional model are duplicated in the biophysically-realistic model (schematic circuit diagram shown in inset), which accounts for action potential generation and for some of the spatial structure of the network neurons. The MCN1-elicited rhythm is again driven by the buildup and decay of MCN1 excitation (s) in the LG neuron (C, D). The pyloric input increases the frequency of the MCN1-elicited rhythm (compare C and D) and determines the onset of the LG burst phase (vertical dotted lines in D). Most hyperpolarized membrane potentials: Int1 −61 mV (C-D); LG −55 mV (C-D); AB −66 mV (C), −64 mV (D).
The membrane potential of a given neural compartment in our biophysically-realistic model is obtained by numerical integration of a first-order differential equation of the form
| (25) |
where V designates the membrane potential of the given compartment. The parameters C and IExt designate membrane capacitance and external current, respectively. ILeak designates the leak current of the given compartment, while each Iaxial represents the axial current due to a voltage difference with adjacent compartments. The sum of axial currents that affect the ith compartment of a neuron is modeled by
| (26) |
where V represents the membrane potential of the ith compartment. The parameter gi+1 (gi−1) represents the axial conductance due to the voltage difference with the adjacent compartment.
Each voltage-gated ionic current (Iion) in Equation (25) is modeled by
| (27) |
where the parameters ḡion and Eion designate its maximal conductance and reversal potential, respectively. The variables m and h designate activation and inactivation of the ionic conductance, respectively, where p and q are non-negative integers. Moreover, activation and inactivation are modeled by the equations
| (28) |
| (29) |
| (30) |
where x = m (x = h) for activation (inactivation). The steady-state behavior of each ionic conductance is modeled by the sigmoidal function in Equation (29), where the parameters k and vk represent its steepness and inflection point voltage, respectively. We note that k < 0 (k > 0) for activation (inactivation). The corresponding time constant is described by the voltage-dependent sigmoid in Equation (30), where the parameters l and vl represent its steepness and inflection point voltage, respectively while Τ1 and Τ2 are used model the extreme values of this sigmoid.
Each synaptic conductance (Isyn) in Equation (25) is modeled by
| (31) |
where the parameters ḡsyn and Esyn designate its maximal conductance and reversal potential, respectively. The synaptic gating function S is dependent upon the membrane potential of the presynaptic compartment (Vpre), and the dynamics of the synapse are governed by the equations
| (32) |
| (33) |
| (34) |
The steady-state behavior of the synapse is modeled by the sigmoid in Equation (33), whose steepness and inflection point voltage are given by the parameters α and vα, respectively. The corresponding synaptic time constant is modeled by the voltage-dependent sigmoid in Equation (34), whose steepness and inflection point voltage are similarly represented by the parameters β and vβ while Τ3 and Τ4 are used model the extreme values of this sigmoid.
In the biological system, MCN1 is electrically coupled to the LG neuron locally within the STG (Coleman et al., 1995). This electrical coupling is accounted for in the biophysically-realistic model by coupling an MCN1 axon compartment with the LG axon compartment (Fig 2.C). Electrical coupling between compartments is modeled by
| (35) |
where V designates the membrane potential of a neural compartment and Vcouple represents the membrane potential of the coupled compartment. We subtract Equation (35) from the right hand side of Equation (25) for electrically coupled compartments.
Parameter values for the biophysically-realistic model of the MCN1-elicited rhythm are given in Tables 3 and 4.
Table 3.
Parameters for Intrinsic Currents in the Biophysically-Realistic Model of the MCN1-Elicited Gastric Mill Rhythm
| Cell | Current | Site | ḡ | Eion | St. | k | vK | l | vl | ⊺1 | ⊺2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MCN1 | Axon | 8.98 | −80 | ||||||||
| ILeak | Term | 3.59 | −70 | ||||||||
| Axon | 565.47 | 45 | m3 | −0.25 | −62 | 0 | 0 | ||||
| INa | h | 0.24 | −64 | −0.24 | −64 | 1 | 5 | ||||
| Axon | 565.47 | −80 | m4 | −0.24 | −54 | 0.24 | −54 | 8 | 20 | ||
| IK | |||||||||||
| Axon-Axon | 13.09 | ||||||||||
| Iaxial | Axon-Term | 6.23 | |||||||||
| Term-Term | 4.09 | ||||||||||
| Int1 | ILeak | Soma | 0.31 | −34 | |||||||
| Neurite | 0.08 | −34 | |||||||||
| Axon | 0.02 | −34 | |||||||||
| Ih | Axon | 0.63 | −20 | m | 2 | −65 | 2 | −65 | 200 | 2500 | |
| INa | Axon | 11.00 | 45 | m3 | −0.08 | −26 | 0 | 0 | |||
| h | 0.13 | −38 | −0.12 | −67 | 0 | 5 | |||||
| IK | Axon | 18.85 | −80 | m4 | −0.045 | −25 | 0.065 | −30 | 4 | 150 | |
| Iaxial | * | 0.12 | |||||||||
| LG | ILeak | Soma | 0.31 | ||||||||
| Neurite | 0.08 | −40 | |||||||||
| Axon | 0.02 | −40 | |||||||||
| −60 | |||||||||||
| INa | Axon | 18.00 | |||||||||
| 45 | m3 | −0.08 | −21 | 0 | 0 | ||||||
| h | 0.13 | −33 | −0.12 | −62 | 0 | 5 | |||||
| IK | Axon | 12.57 | |||||||||
| −80 | m4 | −0.045 | −33 | 0.065 | −5 | 4 | 100 | ||||
| Iaxial | * | 0.12 | |||||||||
| AB | ILeak | Soma | 0.31 | −63 | |||||||
| ICa | Soma | 1.26 | 120 | m3 | −0.24 | −61 | 0 | 0 | |||
| h | 0.12 | −88 | 0.14 | −84 | 40 | ** | |||||
gaxial for soma-neurite and neurite-axon axial currents have the same value: ḡ = 0.12 nS
⊺2 = 300*exp(0.03(V+162)).
The units for the parameter values of the intrinsic currents are given as follows: ḡ (nS); Eion, vk, vl (mV); k, l (mV−1); ⊺1, ⊺2 (msec).
Table 4.
Parameters for Synaptic Currents in the Biophysically-Realistic Model of the MCN1-Elicited Gastric Mill Rhythm
| Synapse | Pre Site |
Post Site |
ḡsyn | Esyn | α | vα | β | vβ | ⊺3 | ⊺4 |
|---|---|---|---|---|---|---|---|---|---|---|
| MCN1→Int1 | Term. | Neurite | 0.002 | 45 | −1 | −50 | 30 | 0 | ||
| MCN1→LG (chemical) |
Term. | Neurite | 2.14 | 45 | −2 | −68 | −2 | −68 | 8000 | 9000 |
| MCN1→LG (electrical) |
Axon | Axon | 0.021 | |||||||
| LG→MCN1 | Neurite | Term. | 150 | −80 | −2 | −35 | 2 | −35 | 5 | 270 |
| Int1→LG | Soma | Neurite | 1.40 | −80 | −0.5 | −49 | 100 | 0 | ||
| LG→Int1 | Neurite Axon Axon |
Soma Neurite Axon |
0.13 1.30 1.30 |
−80 −80 −80 |
−0.5 −1 −1 |
−45 −25 −25 |
1 1 |
−25 −25 |
50 3 3 |
0 97 97 |
| AB→Int1 | Soma | Neurite | 2.00 | −70 | −1 | −55 | 80 | 0 |
Units for the parameter values of the synaptic currents are given as follows: ḡsyn (nS); Esyn, vα, vβ (mV); α, β (mV−1); ⊺3, ⊺4 (msec).
Biophysically-Realistic Model of the PK-Elicited Gastric Mill Rhythm
Three biophysically-realistic models of the PK-elicited rhythm were developed. Each was based upon the biophysically-realistic model of the MCN1-elicited rhythm. However, all synapses involving MCN1 were replaced by each of the proposed PK mechanisms from the 2-dimensional models. Thus, we assess the efficacy of each PK mechanism for eliciting a gastric mill rhythm in the absence of MCN1 participation with the biophysically-realistic models.
PK Mechanism 1
A low threshold, slowly-inactivating, inward current IPlat was proposed to be induced in the LG neuron as modeled by
| (36) |
to allow for PK to elicit a gastric mill rhythm. The parameters ḡPlat and EPlat designate its maximal conductance and reversal potential. The dynamics of activation (x = a) and inactivation (x = n) for IPlat are modeled by Equations (28) - (30). The additional parameters for this PK-elicited rhythm (involving IPlat in the LG neuron) are given in Table 5.
Table 5.
Additional Parameters for Ionic Currents in the Biophysically-Realistic Models of the PK-Elicited Rhythms
| Cell | Current | Site | ḡion | Eion | State | k | vk | l | vl | ⊺1 | ⊺2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| LG | Mechanism 1: | ||||||||||
| IPlat | Neurite | 0.65 | 0 | a | −0.05 | −65 | 50 | 0 | |||
| n | 2 | −55 | −2 | −55 | 2000 | 6000 | |||||
| Mechanism 2: | |||||||||||
| IProc | Neurite | 0.9 | 0 | b | −0.05 | −45 | 50 | 0 | |||
| IK | Neurite | 0.3 | −80 | w | −1 | −45 | −1 | −45 | 4000 | 4000 | |
| Mechanism 3: | |||||||||||
| Ih | Neurite | 0.75 | 0 | c | 0.1 | −45 | 8000 | 0 |
PK Mechanism 2
Two non-inactivating currents were proposed to be induced in the LG neuron; in particular, a fast, inward current IProc for depolarization of LG and a slow, outward current IK for repolarization. The inward current is modeled by
| (37) |
where ḡProc and EProc designate its maximal conductance and reversal potential. The dynamics of activation (x = b) for IProc are modeled by Equations (28) - (30), where the parameters Τ1 and Τ2 are given small values to model the fast kinetics of IProc in the biological system (Golowasch and Marder, 1992). The slow, outward current in this mechanism is modeled by
| (38) |
with ḡK and EK designating its maximal conductance and reversal potential. The parameters Τ1 and Τ2 are given large values in Equation (30) to model the slow activation dynamics (x = w) of IK. The additional parameters for this PK-elicited rhythm are given in Table 5.
PK Mechanism 3
A slow, hyperpolarization-activated, inward current Ih was proposed to be induced in the LG neuron as modeled by
| (39) |
with ḡh and Eh designating its maximal conductance and reversal potential. The dynamics of activation (x = c) for Ih are modeled by Equations (28) - (30), and the additional parameters for this PK-elicited rhythm are given in Table 5.
All simulations for the biophysically-realistic models were performed with the software package NETWORK, which is freely available at http://stg.rutgers.edu/software/network.htm.
RESULTS
We use both the 2-dimensional and biophysically-realistic models, in parallel, to investigate how the neuromodulator PK can elicit a gastric mill rhythm that is similar to the MCN1-elicited rhythm via a different functional circuit, as occurs in the biological system (Saideman et al., 2007a; Saideman et al., 2007b). First, we use our 2-dimensional model, where both state variables are directly involved in generating network oscillations, to fully describe the network dynamics of the MCN1-elicited rhythm via a phase-plane analysis. Then, we use this model to propose potential mechanisms by which the neuromodulator PK can elicit a similar gastric mill rhythm in the absence of MCN1 participation. Each proposed mechanism involves PK-induction of voltage-gated ionic currents in the LG neuron to elicit a gastric mill rhythm. We further show that, in the context of the biophysically-realistic model which accounts for action potential generation and some spatial structure of the neurons, each of our proposed PK mechanisms also elicits a gastric mill rhythm that is similar to the MCN1-elicited rhythm.
1. Network Dynamics of the MCN1-Elicited Gastric Mill Rhythm
We first examine the network dynamics of the MCN1-elicited rhythm using the 2-dimensional model in Equations (12) (see Methods). The state variable s, which describes the slow excitation from MCN1 to the LG neuron, drives the network dynamics for this gastric mill rhythm (Figure 2). In addition, the time constants of s in (12) are chosen to be large so that the system operates in a relaxation regime (see Methods). In the VL-s phase plane, the left branch of the cubic VL-nullcline corresponds to the inactive state of the LG neuron, where LG is inhibited by Int1 and receives a slow, modulatory, excitation from MCN1 (see Methods). On the other hand, the right branch of the VL-nullcline corresponds to the active state of the LG neuron, where LG inhibits Int1 and presynaptically inhibits MCN1.
The forcing function P(t,VL) in (12) makes the 2-dimensional model non-autonomous so that a family of cubic VL-nullclines exists in the phase plane. This family of cubics is given by Equation (13), while the s-nullcline is given by Equation (14). Physiologically, the P(t,VL) forcing function describes the local inhibitory synapse from the pacemaker (AB) neuron of the pyloric circuit to Int1 (see Methods).
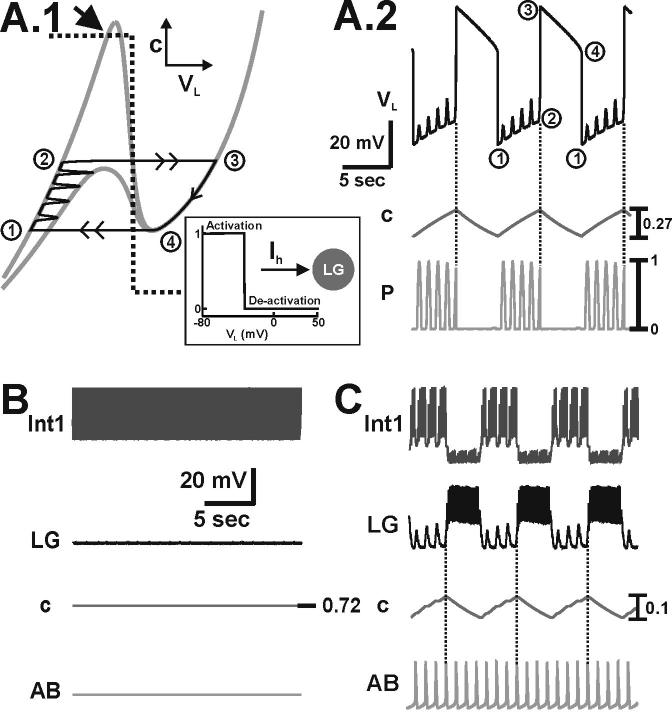
First, we examine the network dynamics of the unforced MCN1-elicited rhythm, which corresponds to when the forcing function P(t,VL) = 0 in (12). The 2-dimensional model is autonomous in the absence of this forcing function so that a single cubic VL-nullcline exists in the phase plane (see Methods). During the inactive state of the LG neuron where it is inhibited by Int1, s, the slow excitation from MCN1 slowly builds up in LG. As a result, the trajectory slowly climbs up the left branch of the cubic VL-nullcline from point 1 to point 2 (Figure 2.A.1). Moreover, the slow buildup of s causes the LG membrane potential VL to slowly rise (Figure 2.A.2). When the trajectory reaches the left knee of the cubic at the point 2 (Figure 2.A.1) it jumps to the right branch of the cubic at point 3 (Figure 2.A.1), because dVL/dt > 0 above the VL-nullcline. Physiologically, LG begins to inhibit Int1 as s increases, and the jump to the right branch of the cubic corresponds to when the slow buildup of MCN1 excitation is sufficient to allow the LG neuron to escape from Int1 inhibition. As a result, the LG neuron jumps into its active state, where it inhibits Int1 and presynaptically inhibits MCN1. The presynaptic inhibition of MCN1 causes s to slowly decay in the LG neuron so that the trajectory slowly falls down the right branch of the cubic, which in turn causes VL to slowly fall (Figure 2.A.2). When the trajectory reaches the right knee of the cubic at the point 4 (Figure 2.A.1), it jumps back to the left branch of the cubic at the point 1 (Figure 2.A.1), since dVL/dt < 0 below the VL-nullcline, and the cycle repeats. Physiologically, LG inhibition of Int1 decreases with VL and s, and the jump back to the left branch corresponds to when the fall in VL is sufficient to release Int1, which pushes the LG neuron back down into its inactive state and in turn removes the LG presynaptic inhibition of MCN1. The trajectory in the VL-s phase plane, which consists of two fast and two slow portions, describes the network dynamics that underlie the MCN1-elicited rhythm in the absence of the local inhibitory synapse from the pyloric circuit (Figure 2.A).
In the presence of the pyloric input, the periodic forcing function P(t,VL) varies in [0,1] and allows for a family of cubic VL-nullclines to exist in the phase plane (see Methods). In Figure 2.B.1, the higher (unforced) cubic occurs when p = 0 in Equation (13) and corresponds to the unforced system of Figure 2.A.1, while the lower (maximally-forced) cubic occurs when p = 1 in Equation (13) and corresponds to the maximally forced system at the peak of the pyloric-timed input (Figure 2.B.1). During the inactive state of the LG neuron where s slowly builds up in LG, the trajectory slowly climbs up the left branch of the VL-nullcline as it moves back and forth between the unforced and maximally-forced cubics due to the pyloric-timed input (Figure 2.B.1). In particular, each pyloric peak shifts the unforced cubic down to the maximally forced cubic (see Methods). In addition, the fast, pyloric-timed transitions between left branches of the VL-nullcline correspond to the small-amplitude depolarizations in VL during the inactive state of the LG neuron (Figure 2.B.2). Physiologically, the pyloric-timed AB to Int1 inhibition interrupts the Int1 to LG inhibitory synapse in turn (circuit diagram of Figure 2.A-B), which effectively disinhibits the LG neuron and causes the small pyloric-timed depolarizations in VL. When the trajectory reaches the level of the lower left knee in the VL-s phase plane, the next pyloric peak shifts the cubic below the phase point and initiates the jump to the right branch at point 2 (Figure 2.B.1). Thus, in the presence of the pyloric-timed forcing, the jump to the right branch of the VL-nullcline occurs below the higher left knee of the unforced cubic (Figure 2.B.1). As a result, compared to the unforced system, less buildup of s is required in the LG neuron before it jumps into its active state (compare s traces in Figures 2.A.2 and 2.B.2).
During the active state of the LG neuron, the dynamics are similar to the unforced system and the trajectory slowly moves down the right branch of the VL-nullcline as s decays and VL slowly falls (Figure 2.B.2). There is only one right branch for the family of VL-nullclines because the pyloric input P(t,VL) does not affect the active state of the LG neuron (Bartos et al., 1999) (see Methods). Thus, the termination of the active state of the LG neuron (point 4 in Figure 2.B.1) is similar to the unforced case and the cycle repeats.
Physiologically, the onset of the LG active state is triggered by the AB to Int1 inhibition (Figure 2.B.2 see also (Bartos et al., 1999)). In the VL-s phase plane, this is shown by the fact that the jump to the right branch of the VL-nullcline is initiated by a pyloric forcing peak (Figure 2.B.1). In addition, the AB to Int1 inhibition increases the frequency of the gastric mill rhythm (compare Figures 2.A.2 and 2.B.2) by reducing the duration on the left branch of the VL-nullcline. This occurs because the jump from point 2 to point 3 occurs below the higher left knee of the unforced cubic (Figure 2.B.1), thus reducing the duration on the right branch of the VL-nullcline. We note that the effects of the AB to Int1 inhibition on the MCN1-elicited rhythm were also reported in a biophysical model (Nadim et al., 1998) and an experimental study (Bartos et al., 1999).
Next, we observe that the predictions of the 2-dimensional model for the MCN1-elicited gastric mill rhythm can also be reproduced in the biophysically-realistic model. In particular, the MCN1-elicited rhythm in the biophysically-realistic model is also driven by the buildup and decay of MCN1 excitation (s) in the LG neuron (Figure 2.C and 2.D). Note that, in contrast to our models, the original compartmental model of Nadim et al. (1998) did not produce rhythmic activity in the absence of the pyloric input, despite the fact that it does so in the biological system (Bartos et al., 1999).
We also note that the additional synapses in the biophysically-realistic model (circuit diagram of Figure 2.C-D) do not significantly affect the frequency of the MCN1-elicited rhythm. In particular, MCN1 excitation of Int1, which occurs on a much faster time scale than the MCN1 to LG excitation (s), has no significant effect on the frequency of the MCN1-elicited rhythm, as suggested by previous modeling results (Nadim et al., 1998). The electrical coupling between MCN1 axon terminals and the LG neuron is not affected by LG presynaptic inhibition of MCN1 (Coleman et al., 1995). Moreover, this electrical coupling increases the number of spikes per LG burst, but its effect on the frequency of the MCN1-elicited rhythm is not well understood (Coleman et al., 1995).
The Gastric Mill Rhythm is Not Spontaneously Active
In the biological system, the gastric mill rhythm is inactive without MCN1 input to the STG (Bartos et al., 1999). This was also the case with both our 2-dimensional and biophysically-realistic models. First in the 2-dimensional model, MCN1 input is removed by setting its maximal conductance to ḡs = 0 in (12) (see Methods). As a result, the denominator of the equation describing the VL-nullcline approaches 0 as ḡs → 0 in Equation (13) (see Methods). Consequently, the VL-nullcline becomes a straight line (Figure 3.A.1) that corresponds to the stable left branch of the cubic (from Figure 2.B.1). Thus, the VL- and s-nullclines intersect at a stable fixed point to which the trajectory settles so that there are no network oscillations in the absence of MCN1 input. Two VL-nullclines are shown in Figure 3.A.1 to illustrate the unforced and maximally forced systems due to the effect of the pyloric-timed forcing that underlies the subthreshold depolarizations in the LG membrane potential (Figure 3.A.2). Physiologically, Figure 3.A illustrates that the gastric mill rhythm is not spontaneously active due to the asymmetry within the Int1-LG reciprocally inhibitory network. In particular, the LG neuron is strongly inhibited by Int1 and remains inactive. Figure 3.B demonstrates the same phenomenon in the biophysically-realistic model.
Figure 3.
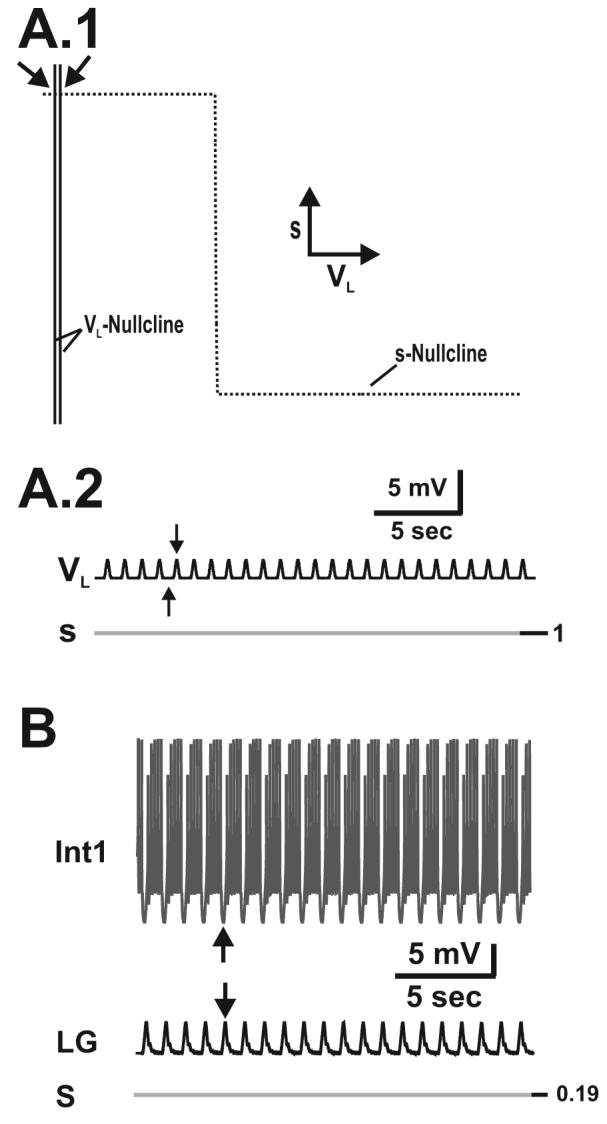
The gastric mill rhythm is not spontaneously active. A.1, Without MCN1 input in the 2-dimensional model, the VL-nullcline becomes a vertical line and intersects the s-nullcline at a stable fixed point (arrows) so that network oscillations can not occur. The left-most and right-most VL-nullclines correspond to the unforced (p = 0) and maximally forced (p = 1) system. A.2, VL exhibits small depolarizations due to the effect of the pyloric input, but the LG neuron remains in its inactive state. Arrows correspond to the VL-nullclines in A.1. Most hyperpolarized LG membrane potential: −77 mV. B, In the biophysically-realistic model, the LG neuron remains in its inactive state without MCN1 input. The pyloric-timed hyperpolarizations in Int1 and corresponding depolarizations in the LG neuron (arrows) are due to the AB-induced disinhibitions of the LG neuron. Most hyperpolarized membrane potentials: Int1 −52 mV; LG −60 mV; AB −64 mV.
2. Proposed Mechanisms by which PK can Elicit an MCN1-like Gastric Mill Rhythm
Recent experiments showed that bath application of the neuromodulator PK to the STG elicits a gastric mill rhythm that is similar to the MCN1-elicited rhythm (Saideman et al., 2007a; Saideman et al., 2007b). This result was surprising because the PK-elicited rhythm generally occurs in the absence of MCN1 participation and MCN1 does not release PK in the biological system (Saideman et al., 2007a; Saideman et al., 2007b). Moreover, no combination of MCN1 co-transmitters elicits a gastric mill rhythm when bath applied to the STG (Wood et al., 2000)(M.P. Nusbaum, Unpublished Observations). Thus, PK is the first known neuromodulator that elicits a gastric mill rhythm upon bath application to the C. borealis STG. Currently, the mechanisms that underlie the PK-elicited rhythm are unknown.
We use clues from the biological system to propose potential mechanisms by which PK can elicit a gastric mill rhythm in the absence of MCN1 participation. Our hypothesis is that PK induces voltage-gated ionic currents in the LG neuron to balance the asymmetry in the Int1-LG pair that exists in the absence of MCN1 input (see Figure 3). The first clue we used from the biological system is that bath application of PK generates plateau properties in the LG neuron (Saideman, 2006). Specifically, a brief depolarizing current pulse in the LG neuron elicits a prolonged depolarization that outlasts the pulse (Figure 4.A). Such a plateau property is not present in the LG neuron in the absence of PK bath application (Saideman, 2006). This indicates that PK induces a slow conductance in the LG neuron that can support the prolonged depolarization (Figure 4.A). A second fact we used from the biological system is that the MCN1-elicited and PK-elicited gastric mill rhythms behave differently when the pyloric-timed AB to Int1 inhibitory synapse is removed. In particular, the cycle period of the MCN1-elicited rhythm increases upon removal of the AB to Int1 synapse (Bartos et al., 1999). This phenomenon is reproduced by our 2-dimensional and biophysically-realistic models (see Figure 2). In contrast, the PK-elicited rhythm is suppressed when the AB to Int1 inhibitory synapse is removed in the biological system and the LG neuron remains in its inactive state, where it is strongly inhibited by Int1 (Saideman et al., 2007a).
Figure 4.
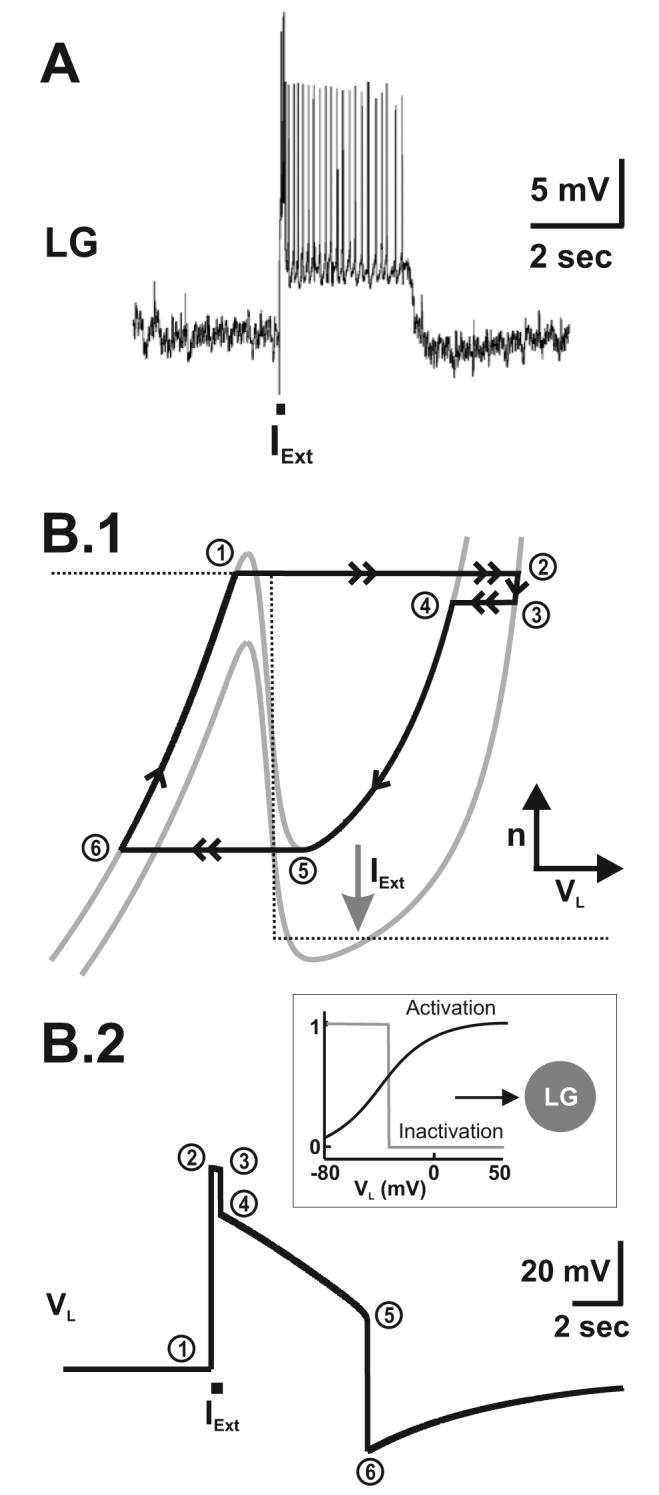
PK generates plateau properties in the LG neuron. A, In the biological system, a brief depolarizing current pulse (IExt) in the LG neuron elicits a prolonged depolarization that outlasts the brief pulse. Most hyperpolarized LG membrane potential: −80 mV. Reproduced from (Saideman, 2006). B.1-B.2, In the 2-dimensional model, a plateau potential can be generated by the induction (potentially by PK) of a plateau current (IPlat) in the LG neuron (as indicated in the schematic inset). In the VL-n phase plane (B.1), a brief current pulse shifts down the VL-nullcline (as indicated by the arrow) resulting in a jump in the trajectory (point 1 to point 2), which shifts back at the end of the brief pulse (point 3 to point 4). The slow inactivation variable (n) of IPlat sustains the prolonged active state of the LG neuron in that the trajectory can not jump back to the left branch of the VL-nullcline until it falls all the way down to point 5 (B.1). As a result, the depolarized state in the model LG neuron long outlasts the brief current pulse (B.2). The plateau potential is generated in the absence of pyloric input in order to mimic the conditions in the biological system (pyloric-timed depolarizations are absent in A). Most hyperpolarized LG membrane potential: −75 mV.
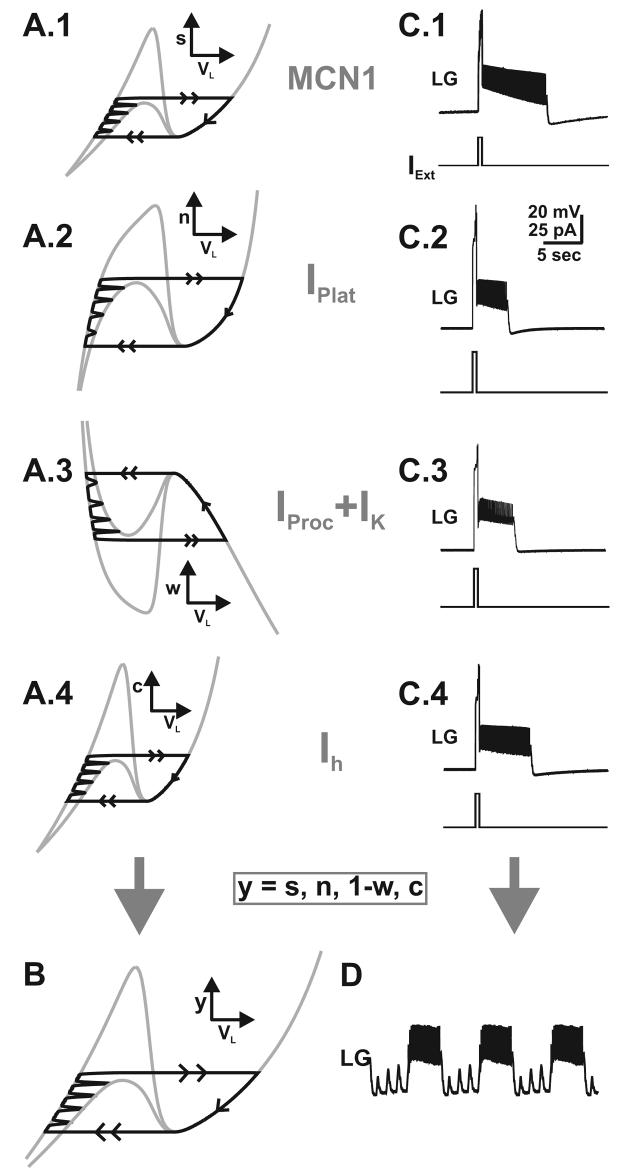
In the remainder of the Results section, we propose three distinct mechanisms by which PK can elicit an MCN1-like gastric mill rhythm, via the induction of voltage-gated ionic currents in the LG neuron to generate plateau properties. These three mechanisms include a (1) low-threshold, slowly-inactivating, inward current (IPlat), (2) fast, non-inactivating, inward current (IProc) plus a slow, non-inactivating, outward current (IK), and (3) slow, hyperpolarization-activated, inward current (Ih) in the LG neuron. All three mechanisms allow for the production of an MCN1-like gastric mill rhythm in the absence of MCN1 participation, in both the 2-dimensional and biophysically-realistic models.
PK Induction of IPlat in the LG Neuron Generates Plateau Properties that Underlie an MCN1-like Gastric Mill Rhythm
One mechanism by which PK can elicit an MCN1-like gastric mill rhythm is via the induction of a plateau current (IPlat) in the LG neuron. IPlat is a low-threshold, slowly-inactivating, inward current. Physiologically, it is similar to the low-threshold, slowly-inactivating, Ca2+ current (ICaS) found in the CPG circuit that controls heartbeat in the medicinal leech (Angstadt and Calabrese, 1991; De Schutter et al., 1993). In our model, IPlat is a low-threshold current that depolarizes the LG neuron during its inactive state. Moreover, inactivation of IPlat occurs on a much slower time scale than activation of IPlat in our model (see Methods).
To mimic the output of the LG neuron as shown in Figure 4.A, we introduced IPlat into this neuron in the 2-dimensional model. A brief depolarizing current pulse in the model LG neuron allows for the slow dynamics of IPlat to sustain the prolonged active state in LG for a duration that outlasts the brief depolarizing current pulse IExt (Figure 4.B.2). Specifically, the depolarizing current pulse pushes the LG neuron to its active state, after which the trajectory can only jump back to the left branch of the VL-nullcline after it falls all the way down to the right knee due to the slow inactivation of IPlat, which is represented by the state variable n (Figure 4.B.1).
We found that PK induction of IPlat in the LG neuron can elicit an MCN1-like gastric mill rhythm using both our 2-dimensional model in Equations (17) and our biophysically-realistic model (see Methods). This PK-elicited rhythm is driven by the slow inactivation dynamics of IPlat in the LG neuron (represented by the state variable n in Figure 4.B). The mechanism underlying the oscillations produced by IPlat are mathematically and computationally similar to those obtained in the model with IProc + IK as described below and for brevity are not explained in detail.
PK Induction of IProc + IK in the LG Neuron Elicits an MCN1-like Gastric Mill Rhythm
A second, but similar, mechanism by which PK can elicit an MCN1-like gastric mill rhythm is via the induction of two non-inactivating currents in the LG neuron. In particular, we show that PK induction of a fast, inward current (IProc) plus a slow, outward current (IK) in the LG neuron can elicit an MCN1-like gastric mill rhythm (Figure 5). In the crab stomatogastric neurons, the inward current IProc, which is a regenerative non-specific cation current (Golowasch and Marder, 1992), is induced by several different neuropeptides (Swensen and Marder, 2000, 2001). Accordingly, because PK is also a neuropeptide it is plausible to assume that it too induces IProc in the LG neuron. IProc is modeled by Equation (18), while the slow current (IK) is modeled by Equation (20). Physiologically, IK is similar to the slow, non-inactivating, K+ current (IKF) found in the heartbeat CPG of the medicinal leech (Nadim and Calabrese, 1997).
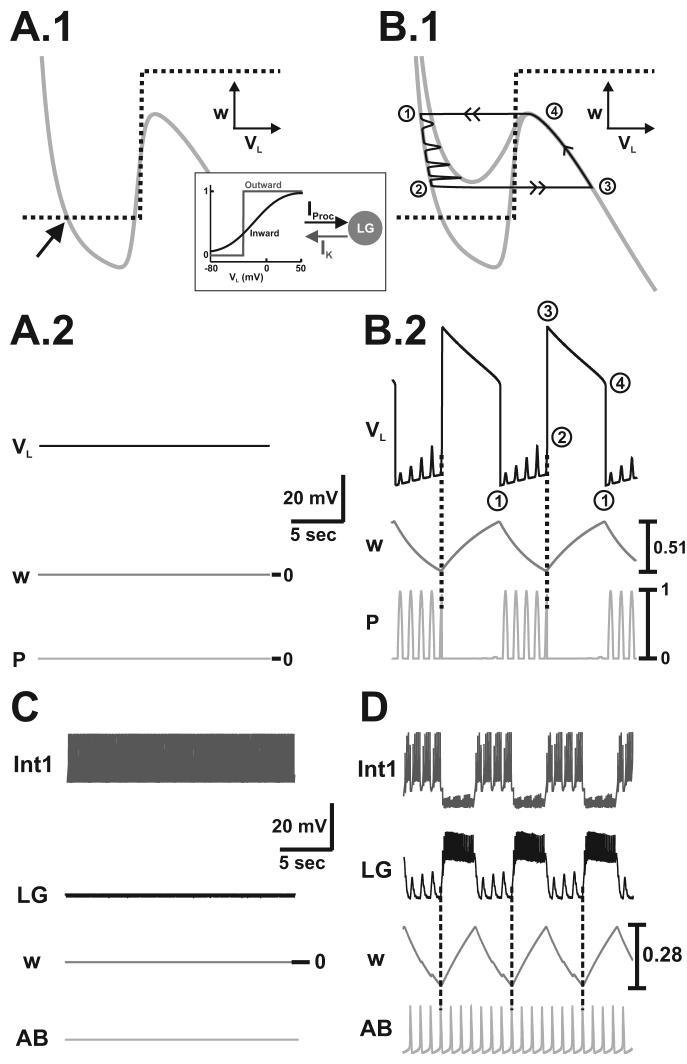
Figure 5.
PK-elicited gastric mill rhythm (mechanism 2: PK induces IProc and IK in the LG neuron as shown in the schematic inset). IProc is a fast inward current while IK is a slow outward current. Both currents are non-inactivating. Network oscillations are driven by the slow activation variable (w) of IK. A.1-A.2, The cubic shape of the VL-nullcline is inverted in the VL-w phase plane (A.1). In the absence of the pyloric input, the VL- and w-nullclines intersect at a stable fixed point along the left branch of the cubic in the VL-w phase plane (indicated by arrow in A.1). As a result, the LG neuron remains in its inactive state, and network oscillations can not be elicited without the pyloric input (A.2; most hyperpolarized LG membrane potential: −55 mV). B.1-B.2, In the presence of the pyloric input, PK-induction of IProc and IK in the LG neuron elicits a gastric mill rhythm that is similar to the MCN1-elicited rhythm. During the inactive state of the LG neuron, the trajectory slowly falls down the left branch of the VL-nullcline as it is moved between the unforced (lower) and maximally forced (higher) cubics by the pyloric input (B.1). Moreover, w slowly decreases (deactivation of the outward current IK from the LG neuron) and facilitates depolarization of VL (B.2). At point 2, the VL-nullcline is shifted above the phase point by a pyloric peak, which initiates the jump to the right branch of the cubic (B.1), and determines the onset of the LG active state (dotted lines in B.2). Then, the trajectory slowly climbs up the right branch of the VL-nullcline (B.1). As a result, w slowly increases (activation of the outward current IK in the LG neuron) and slowly repolarizes VL (B.2). At point 4, the trajectory jumps back to the left branch (B.1) and the cycle repeats. Most hyperpolarized LG membrane potential: −71 mV. C-D, Predictions of the 2-dimensional model are duplicated in the biophysically-realistic model. Hyperpolarization of the AB neuron inactivates the AB to Int1 synapse and prevents the generation of a gastric mill rhythm (C). In the presence of this synapse, the induction of IProc and IK in the LG neuron elicits a gastric mill rhythm that is similar to the MCN1-elicited rhythm (compare 5.D to 2.D). The slow activation variable w of IK drives this gastric mill rhythm, and the AB to Int1 inhibition determines the onset of the LG burst phase (vertical dotted lines in D). Most hyperpolarized membrane potentials: Int1 −48 mV (C), −61mV (D); LG −54 mV (C), −55mV(D); AB −65mV (C), −64 mV (D).
The gastric mill rhythm that is elicited by this mechanism occurs in the absence of MCN1 participation and is governed by the 2-dimensional model in Equations (21) (see Methods). The network oscillations that are produced by PK-induction of IProc+IK in the LG neuron are shown in Figure 5. We note that unlike the MCN1-elicited rhythm which is driven by the synaptic interactions between MCN1 and the LG neuron (Figure 2), the PK-elicited rhythm in this mechanism is controlled by the activation (w) kinetics of the (slow) outward current IK in the LG neuron.
We use the geometrical properties in the VL-w phase plane to examine the network dynamics of this PK-elicited rhythm (Figure 5.A and 5.B). The VL-nullcline is an inverted N-shaped cubic in the VL-w phase plane, where dVL/dt > 0 (< 0) below (above) the VL-nullcline while dw/dt > 0 (< 0) below (above) the w-nullcline. Thus, as occurs in the MCN1-elicited rhythm, the outer branches of the cubic VL-nullcline are again stable while its middle branch is unstable. Moreover, the forcing function P(t,VL) again models the pyloric-timed inhibition of Int1 (see Methods) and allows for a family of cubic VL-nullclines to exist in the VL-w phase plane.
First, we examine the network dynamics of the unforced system. As occurs in the MCN1-elicited rhythm, the 2-dimensional model in (21) is autonomous when the pyloric-timed forcing function P(t,VL) is absent from the system (see Methods). As a result, a single cubic VL-nullcline exists in the VL-w phase plane (Figure 5.A.1). However, unlike the MCN1-elicited rhythm where the nullclines intersect along the unstable middle branch of the cubic to allow for network oscillations to occur (Figure 2.A.1), the nullclines in the VL-w phase plane of the PK-elicited rhythm intersect along the stable left branch of the cubic (Figure 5.A.1) and, as a result, the trajectory tends to a stable fixed point (Figure 5.A.2). Thus, PK-induction of IProc+IK does not elicit a gastric mill rhythm without the pyloric-timed inhibition of Int1. This result agrees with the experimental data, where PK does not elicit a gastric mill rhythm in the absence of the AB to Int1 inhibitory synapse (Saideman et al., 2007a).
In the forced system, the pyloric input function P(t,VL) produces a family of cubic VL-nullclines in the VL-w phase plane. The lower (unforced) cubic in Figure 5.B.1 occurs when p = 0 (and is equivalent to the unforced cubic in Figure 5.A.1), while the higher (maximally forced) cubic occurs when p = 1 and corresponds to the maximally forced system. Thus, in the presence of the pyloric-timed forcing, PK-induction of IProc+IK in the LG neuron elicits a gastric mill rhythm that is similar to the MCN1-elicited rhythm (compare Figures 5.B and 2.B). However, the PK-elicited rhythm is controlled by different network components. In particular, during the inactive state of the LG neuron where it is inhibited by Int1, IK slowly deactivates in LG (from point 1 to point 2 in Figure 5.B). This in turn allows for activation of the fast inward current (IProc) which depolarizes the LG neuron. When the phase point reaches the level of the higher left knee, the next forcing peak shifts the cubic above the phase point and initiates the jump to the stable right branch (from point 2 to point 3 in Figure 5.B). Physiologically, this jump corresponds to when the LG neuron transitions into its active state, where it inhibits Int1 (Figure 5.B.2). As a result, the trajectory slowly climbs up the right branch of the VL-nullcline as IK slowly activates in the LG neuron. When the trajectory reaches the right knee of the cubic it jumps back to the stable left branch (from point 4 to point 1 in Figure 5.B) and the cycle repeats. Physiologically, this jump corresponds to the end of the LG neuron active state. Thus, in the presence of the AB to Int1 inhibition, the presence of IProc+IK in the LG neuron can elicit a gastric mill rhythm that is similar to the MCN1-elicited rhythm.
Next, we show that the prediction of the 2-dimensional model carries over to the biophysically-realistic model as well. In particular, PK elicits an MCN1-like gastric mill rhythm via the induction of IProc+IK in the LG neuron (Figure 5.D). In the absence of the AB to Int1 inhibitory synapse, PK does not elicit a gastric mill rhythm (Figure 5.C), as occurs in the biological system (Saideman et al., 2007a) and in our 2-dimensional model. However, in the complete model, the PK-elicited gastric mill rhythm is similar to the MCN1-elicited rhythm and it is driven by the slow dynamics (w) of the outward current IK in the LG neuron (Figure 5.D). We note that, as in the 2-dimensional model, activation of the inward current IProc occurs on a much faster time scale and does not control the dynamics of the PK-elicited rhythm. Yet, during the LG interburst phase of the PK-elicited rhythm, IK slowly deactivates (decrease in w – Figure 5.D) which allows for IProc to depolarize the LG neuron. The pyloric-timed, subthreshold depolarizations in the LG membrane potential are due to the effect of the AB to Int1 inhibitory synapse (Figure 5.D) and correspond to the effect of the forcing term in the 2-dimensional model. These subthreshold depolarizations are similar in size amplitude and mechanism to those seen in the MCN1-elicited rhythm (Figure 2.D). We note that the state variable w of IK also exhibits small pyloric-timed fluctuations during the LG interburst phase due to the disinhibitions of the LG neuron during the AB neuron active phase (Figure 5.D). These pyloric-timed fluctuations are not present in the 2-dimensional model since the state variable w is governed by the simplified dynamics of Equation (21). During the LG burst phase of the PK-elicited rhythm, the outward current IK slowly activates (w increases) resulting in the decay of the LG neuron membrane potential and eventually the termination of its burst (Figure 5.D).
In the IProc+IK mechanism, the inward current IProc is necessary for the depolarization of the LG neuron during the gastric mill rhythm. However, this rhythm is controlled by the slow dynamics (w) of the outward current IK (Figure 5). Therefore, we investigate if PK-induction of IProc is absolutely necessary to elicit a gastric mill rhythm. To examine the role of these two currents, we first remove IProc from the system by setting its conductance in (21). As a result, with no inward current for depolarization of the LG neuron, the VL- and w-nullclines intersect at a stable fixed point so that network oscillations cannot occur (Figure 6.A.1). In particular, the LG neuron remains in its inactive state, where it is inhibited by Int1. The unforced (lower) and maximally forced (higher) VL-nullclines are shown in Figure 6.A.1. We find that even in the absence of the inward current IProc, the VL-nullcline still retains a cubic shape due to the reciprocal inhibition between Int1 and LG. As a result, the reciprocally-inhibitory circuit still has the potential for exhibiting network oscillations if the stability of the fixed point is changed. For example, when we inject external current (IExt) into the model LG neuron, the VL- and w-nullclines intersect along the unstable middle branch of the cubic so that the system can exhibit network oscillations (Figure 6.B.1). Moreover, the resulting gastric mill rhythm is still controlled by the slow dynamics (w) of the outward current (IK) in the LG neuron (Figure 6.B.2).
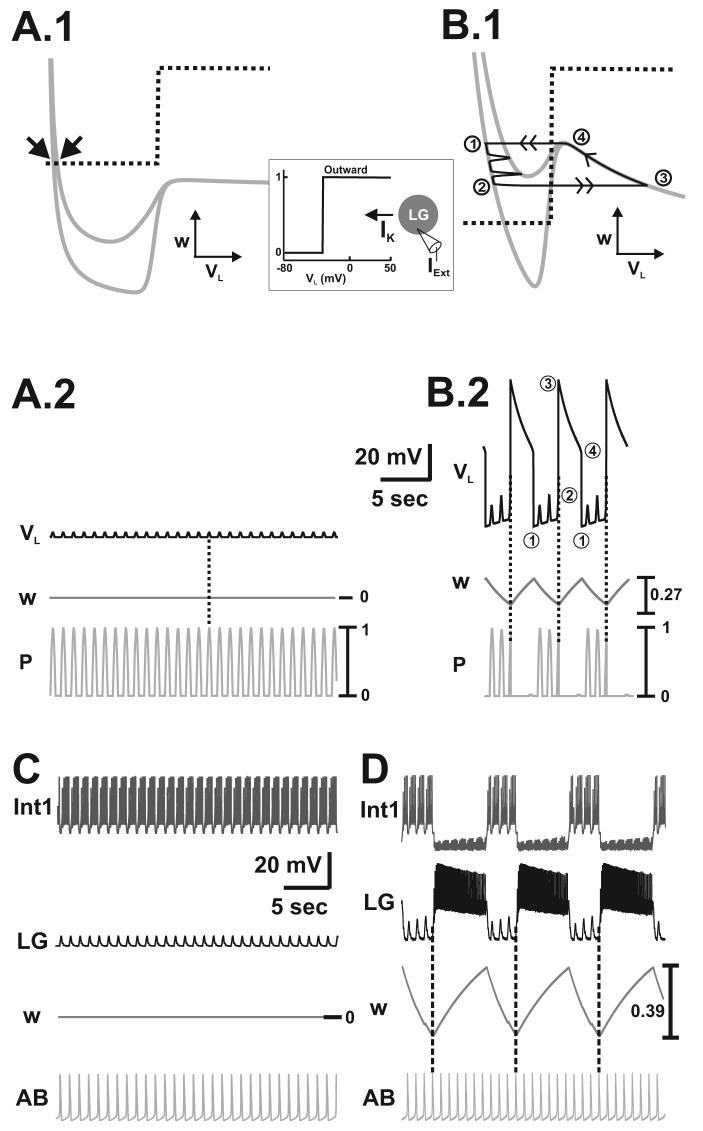
Figure 6.
Network oscillations with only IK in the LG neuron (as shown by schematic inset) induced by depolarizing DC current injection. A.1-A.2, When IProc is removed from the model (by setting ḡProc = 0 mS/cm2 in Equations (21): PK mechanism 2) the VL- and w-nullclines intersect at stable fixed points (arrows in A.1) so that network oscillations can not occur. VL exhibits small, pyloric-timed depolarizations (dotted line in A.2), but the LG neuron remains in its inactive state. Most hyperpolarized LG membrane potential: −77 mV. B.1-B.2, Injecting external current (IExt= 150 μA/cm2) into the LG neuron moves the intersection of the VL- and w-nullclines to the middle branch of the cubic so that network oscillations occur (B.1). As in Figure 5, the slow activation variable w of IK controls the network oscillations and the onset of the active state of the LG neuron is still determined by a pyloric peak (vertical dotted lines in B.2). Most hyperpolarized LG membrane potential: −59 mV. C-D, In the biophysically-realistic model, removal of IProc similarly disrupts the gastric mill rhythm (C). Injecting IExt into the LG neuron elicits a gastric mill rhythm that is controlled by the slow activation variable w of IK (D). Thus the induction of IProc is not absolutely necessary for eliciting a gastric mill rhythm in this mechanism. Simulations were performed by setting ḡion = 0 nS for IProc in Table 5 and IExt = 31 pA while leaving all other parameters unchanged. Most hyperpolarized membrane potentials: Int1 −52 mV (C), −61 mV (D); LG = −60 mV (C), −16 mV (D); AB = −64 mV (C-D).
A similar result can be obtained in the biophysically-realistic model by producing gastric mill-like oscillations without the induction of IProc in the LG neuron (Figures 6.C - 6.D). Thus, although the fast IProc and the slow IK are sufficient to elicit the gastric mill rhythm that is similar to the MCN1-elicited rhythm, IProc is not absolutely necessary to elicit the network rhythm with the proposed mechanism. In particular, the results shown in Figure 6 suggest that neuromodulator-elicited oscillations can be induced in an asymmetric, reciprocally-inhibitory circuit via the induction of only a slow, noninactivating, outward current in one of the circuit neurons.
PK Induction of Ih in the LG Neuron Elicits an MCN1-like Gastric Mill Rhythm
In this section we propose a simple mechanism by which PK can elicit an MCN1-like gastric mill rhythm. In particular, we show that the presence of a slow, hyperpolarization-activated, inward current (Ih) in the LG neuron can elicit this rhythm (Figure 7). Physiologically, Ih is a mixed cation current that is activated by hyperpolarization and has been shown to play an important role in rebound from inhibition and the generation of rhythmic activity (Angstadt and Calabrese, 1989; Marder and Bucher, 2007).
Figure 7.
PK-elicited gastric mill rhythm (mechanism 3: PK induces Ih in the LG neuron). A.1-A.2, Network oscillations do not occur in the unforced system since the VL- and c-nullclines intersect along the stable left branch of the higher cubic (arrow in A.1). In the forced system, the induction of Ih in the LG neuron (as indicated in the schematic inset) elicits a gastric mill rhythm (A.2) controlled by the activation variable c of Ih. In the VL-c phase plane, the trajectory slowly climbs up the left branch of the VL-nullcline as it is moved back and forth between the unforced and maximally forced cubics by the pyloric input (A.1). As a result, c slowly increases during the inactive state of the LG neuron and slowly depolarizes VL (A.2). At point 2, the VL-nullcline is shifted below the phase point by a pyloric peak, which initiates the jump to the right branch of the cubic (A.1) and determines the onset of the LG active state (dotted lines in A.2). During the active state of the LG neuron, the trajectory slowly falls down the right branch of the VL-nullcline (A.1) and c slowly decreases in the LG neuron to repolarize VL (A.2). At point 4, the trajectory jumps back to the left branch (B.1) and the cycle repeats. Most hyperpolarized LG membrane potential: −66 mV. B-C, In the biophysically-realistic model, hyperpolarizing the AB neuron inactivates the AB to Int1 synapse which does not allow for the generation of a gastric mill rhythm (B). In the presence of this synapse, the gastric mill rhythm is driven by the dynamics of Ih in the LG neuron (C). Vertical dotted lines in C indicate the onsets of LG bursts. Most hyperpolarized membrane potentials: Int1 −48 mV (B), −61 mV (C); LG −49 mV (B), −52 mV (C), AB −65 mV (B), −64 mV (C).
The 2-dimensional model in Equations (23) incorporates the inward current Ih into the LG neuron in which the Ih activation variable c has slow dynamics. The geometrical properties of this model in the VL-c phase plane are shown in Figure 7.A.1. The N-shaped cubic of the VL-nullcline results from the interaction between the LG-Int1 reciprocal inhibition, as incorporated in the term II→, together with the contribution of the Ih term (see Equation (24)). It is important to note that neither term alone would have produced the cubic shape of the VL-nullcline, which is necessary for the existence of oscillations (not shown). The existence of the family of cubic VL-nullclines which depend on the pyloric forcing function P(t,VL) results in a network oscillation (Figure 7.A) that is similar to those described with the previous two mechanisms (Figures 4 and 5). In this case, the network oscillations are controlled by the kinetics of the slow Ih activation variable c.
In the biophysically-realistic model, the addition of Ih in the LG neuron also elicits a gastric mill rhythm that is similar to the MCN1-elicited rhythm (Figure 7.C). As in the previous mechanisms, PK does not elicit a gastric mill rhythm in the absence of the AB to Int1 inhibitory synapse (Figure 7.B). However, in the intact system, PK induction of Ih in the LG neuron elicits a similar gastric mill rhythm that is driven by the slow dynamics of the hyperpolarization-activated current (Figure 7.C). In particular, during the LG interburst phase when LG is hyperpolarized, activation of Ih results in the slow depolarization of the LG neuron (increase in c - Figure 7.C). As in the 2-dimensional model, the AB disinhibition of the LG neuron determines the onset of the LG burst phase (Figure 7.C), and induces the small, pyloric-timed, depolarizations in the LG membrane potential. Moreover, the Ih activation variable c exhibits small pyloric-timed fluctuations during the LG interburst phase due to the effect of the AB to Int1 inhibition. These fluctuations are not present in the 2-dimensional model since the state variable c is governed by the simplified dynamics in (23). When the LG neuron escapes from Int1 inhibition and transitions into its burst phase Ih begins to slowly deactivate, resulting in the decay of the LG neuron membrane potential and the eventual termination of the burst (Figure 7.C).
DISCUSSION
Descending projection neurons can initiate, terminate, or regulate the activity of CPGs through release of neuromodulatory substances and fast synaptic interactions with the target networks (Blitz et al., 2004; Deliagina et al., 2002; Jing and Weiss, 2005; Kiehn, 2006; Rossignol et al., 2006). Despite the complexity of interactions between projection neurons and their target CPGs, the pattern of network activity resulting from bath application of neuromodulators is often quite similar to that resulting from the actions of the relevant projection neuron (Morgan et al., 2000; Nusbaum and Beenhakker, 2002). Recent experimental results have shown that the gastric mill CPG in the crab is elicited by bath application of the neuropeptide pyrokynin (PK) and the resulting gastric mill rhythm is quite similar to that elicited by the projection neuron MCN1 (Saideman et al., 2007a; Saideman et al., 2007b). Yet, all fast synaptic interactions between MCN1 and the gastric mill CPG are absent in the PK-elicited rhythm. In this study, we examined potential mechanisms through which bath applied PK can elicit an MCN1-like gastric mill rhythm, despite the absence of the local circuit interactions that normally involve this projection neuron. Starting with the clue from the biological system that PK elicits a plateau potential in the LG neuron, we proposed three mechanisms that can elicit the PK-rhythm. Our results indicate that, at a fundamental level, these physiologically distinct mechanisms are mathematically equivalent to those underlying the MCN1-elicited rhythm.
Although a bath applied neuromodulator is sufficient to duplicate the effects of the appropriate projection neuron in some cases, this is not true in general. One reason is because a bath applied neuromodulator cannot account for the complex synaptic interactions between a projection neuron and its target network. For example, a projection neuron influences the different neurons in its target network via distinct synaptic strengths and/or time courses and by gap-junctional interactions (Nusbaum and Beenhakker, 2002; Stein et al., 2007). Moreover, local synaptic feedback from the rhythmic target network can shape the pattern of neurotransmitter release from the projection neuron (Beenhakker et al., 2005; Coleman et al., 1995; Norris et al., 1994; Wood et al., 2004).
In addition, projection neurons often co-release several modulatory substances to influence their target networks (Blitz et al., 1999; Wood et al., 2000). Yet, each of the co-released modulators does not have an effect downstream due to synaptic interactions within the target network (Marder et al., 2005; Nusbaum et al., 2001; Stein et al., 2007). As a result, it is not possible to mimic projection neuron actions with bath applied neuromodulators in such cases.
Modeling the MCN1-Elicited and PK-Elicited Gastric Mill Rhythms
We used phase plane analysis to study the slow-wave oscillations of the MCN1-elicited rhythm and to propose mechanisms by which PK can elicit a similar gastric mill rhythm. In parallel, we assessed the efficacy of these proposed mechanisms for the PK-elicited rhythm with the biophysically-realistic models. The latter models account for (i) the slow-wave oscillations and the fast oscillations due to action potentials and (ii) some of the spatial structure of the network neurons. Moreover, the output of the realistic models can be directly compared to the activity patterns of the biological neurons.
The original biophysical model of the MCN1-elicited gastric mill rhythm as described by Nadim et al. (1998) did not produce rhythmic activity in the absence of pyloric timed inputs. Later experimental results showed that this rhythm was significantly slower, but was not disrupted, when the pyloric activity was abolished (Bartos et al., 1999). Due to the complexity of the biophysical model, it was unclear what model parameters led to this discrepancy. Our reduction to a 2-dimensional model of the MCN1-elicited rhythm allowed us to isolate the important network properties responsible for the production of oscillations and therefore provided a simple mechanism for tuning the biophysically-realistic model to match the biological activity. Specifically, by moving the threshold for the presynaptic inhibition of MCN1 by LG (vpre in the 2-d model is moved between points 2 and 4 in Figure 2.A.1), the biophysically-realistic model produced oscillations without the pyloric-timed inputs.
While the MCN1-elicited rhythm is driven by the synaptic interactions between the MCN1 terminals and the LG neuron in the biological system, these interactions do not drive the PK-elicited rhythm because it occurs without MCN1 participation (Saideman et al., 2007a; Saideman et al., 2007b). Using clues from the biological system, we proposed three physiologically distinct, but mathematically similar mechanisms by which PK elicits an MCN1-like gastric mill rhythm. In developing these mechanisms, we used the facts that (i) bath applied PK unmasks plateau properties in LG and (ii) the PK-elicited rhythm is suppressed when the AB to Int1 inhibitory synapse is removed (Saideman et al., 2007a; Saideman et al., 2007b). Our phase-plane analysis of the 2-dimensional models, which accounted for slow-wave oscillations, allowed us to examine how PK, via the induction of voltage-gated ionic currents in the LG neuron, could produce a gastric mill rhythm that is similar to the MCN1-elicited rhythm (Figure 8A-B). Moreover, each of the proposed mechanisms for the PK-elicited rhythm generates LG plateau properties in the biophysically-realistic models and generates an MCN1-like gastric mill rhythm (Figure 8C-D).
Figure 8.
Common properties of the MCN1- and PK-elicited gastric mill rhythms. A-B, In the 2-dimensional models, the MCN1-elicited rhythm was analyzed using geometrical properties in the phase plane (A.1), and three physiologically distinct but mathematically similar mechanisms were proposed by which PK can elicit a similar gastric mill rhythm in the absence of MCN1 participation (A.2-A.4). Each of these individual models can be generalized into a single 2-dimensional model (B), where the individual slow variables are represented by a general variable (y), to study the network dynamics of the generalized system. C-D, Physiologically distinct mechanisms underlie similar plateau properties in the LG neuron during the MCN1- and PK-elicited gastric mill rhythms. In the MCN1-elicited rhythm, the MCN1 to LG excitatory synapse plus LG presynaptic inhibition of MCN1 underlie the plateau potential (C.1). In the PK-elicited rhythm, the plateau potential is generated by: the fast activation plus slow inactivation of IPlat in the LG neuron for the first mechanism (C.2), the fast dynamics of IProc plus slow dynamics of IK in the second mechanism (C.3), or the slow dynamics of Ih in the third mechanism (C.4). The physiologically distinct mechanisms that underlie these plateau properties generate similar LG neuron activity in the MCN1- and PK-elicited gastric mill rhythms (D).
In the first mechanism, we introduced a plateau current (low-threshold, slowly-inactivating inward current – IPlat) into the LG neuron, which produced plateau properties in LG that are similar to those observed in the biological system and elicited an MCN1-like gastric mill rhythm without MCN1 participation in our model. Next, we proposed a similar mechanism for the PK-elicited rhythm that had two separate components: an inward current (IProc) that initiated a plateau potential in LG and a slow outward current (IK) that terminated the plateau. Moreover, our analysis showed that network oscillations in this model still occurred when the voltage-gated inward current (IProc) was replaced by DC current injection (IExt). In particular, an MCN1-like gastric mill rhythm was elicited simply by depolarizing the LG neuron in the presence of a slow, voltage-gated, outward current (IK). In the last mechanism, we showed that PK-induction of a slow, hyperpolarization-activated, inward current (Ih) in LG also elicited an MCN1-like gastric mill rhythm. It is important to note that Ih generally does not support plateau potentials because it is not a regenerative current. However, in the reciprocally inhibitory Int1-LG neuron pair, the activation of Ih in the LG neuron depolarizes LG, thereby inhibiting Int1 and removing Int1 inhibition of LG. This interaction between Ih activation and reciprocal inhibition results in a plateau property that is indistinguishable from that produced by a regenerative current such as IPlat. In this mechanism, the time course of the plateau is determined by the deactivation time constant of Ih. Because reciprocal inhibition is a universal building block in many neuronal networks, especially rhythmic networks (Grillner et al., 2005; Marder and Bucher, 2007), it would be interesting to investigate the occurrence of plateau potentials due to the presence of Ih in such networks.
Although we did not explore PK actions on Int1 in detail, our analysis of the 2-dimensional model suggests that hyperpolarization of Int1 or, equivalently, PK induction of a slow, voltage-gated outward current in Int1 may also enable a gastric mill rhythm. However, experimental results indicate that PK does not elicit an outward current in Int1. Instead, PK action on Int1 is similar to that of MCN1, which depolarizes Int1 through synaptic excitation (Saideman et al., 2007a).
Some of the proposed mechanisms by which PK can elicit an MCN1-like gastric mill can be addressed experimentally, for example, by utilizing pharmacological blockers. In particular, because in this system Ih is selectively blocked by bath application of Cs+ (Peck et al., 2006), disruption of the PK-elicited rhythm in Cs+ would strongly support the Ih-dependent mechanism. Yet, due to a lack of specific blockers for IProc and low-threshold Ca2+ currents in this system, alternative techniques such as voltage-clamp measurements are necessary to check for any PK-induced voltage-gated ionic currents as proposed in the other two mechanisms.
Consequences of Simplified Steady-State Behavior in the 2-Dimensional Models
For each of the 2-dimensional models in this work, we made the simplifying assumption that the steady-state behavior of the slow variable, which drives the network oscillations, is well-represented by a step function. This assumption was only made to simplify the network dynamics and mathematical analysis in the 2-dimensional models. We note that relaxing this simplifying assumption in the biophysically-realistic models did not change the qualitative behavior of the MCN1-elicited or PK-elicited gastric mill rhythms.
Our 2-dimensional models can also be used to compute bounds on the gastric mill cycle period that are based upon the parameters of the system, similar to the calculations done by Ambrosio-Mouser et al. (2006). Physiologically, these bounds account for the cycle-to-cycle variability in the gastric mill cycle period that is due to the effect of the pyloric-timed AB to Int1 inhibitory synapse (Bartos et al., 1999).
Comparison with Previous Modeling Studies of Neuromodulation
Previous modeling has uncovered potential intrinsic and synaptic mechanisms by which neuromodulators can alter network activity (Baxter et al., 1999; Bertram, 1994; Butera et al., 1995; Canavier et al., 1994; Guckenheimer et al., 1993; Zhou et al., 2007). Each of these studies, however, examined how different modulatory inputs can elicit distinct activity patterns in the same neural network. In contrast, our focus was to propose mechanisms by which different neural inputs can elicit similar activity patterns from distinct functional networks. A somewhat similar perspective is supported by other recent modeling studies where different combinations of intrinsic and synaptic properties can lead to similar activity in the same neuronal network (Goldman et al., 2001; Prinz et al., 2004).
Future Modeling of the PK-Elicited Gastric Mill Rhythm
As with most CPGs, the gastric mill network involves many distinct types of neurons. Although the MCN1- and PK-elicited gastric mill rhythms have similar rhythm generating mechanisms, including the LG-Int1 reciprocal inhibition, they may differ in their locus of coordination with the participating network neurons. In the biological system, LG presynaptic inhibition of MCN1 importantly coordinates the MCN1-elicited rhythm (Coleman et al., 1995). For example, the follower gastric mill motor neurons, such as the dorsal gastric (DG) neuron, are coordinated with the LG-Int1 oscillations by the waxing and waning of the MCN1 influence that result from the LG presynaptic inhibition.
Because the PK-elicited rhythm does not involve presynaptic inhibition of projection neurons, other mechanisms must coordinate the follower motor neurons with the alternating LG-Int1 activity pattern. One such mechanism may be enhancement of synaptic actions by PK. For example, bath applied PK strengthens an inhibitory synapse from the DG neuron to the LG neuron (Saideman et al., 2007a). Using a biophysically-realistic model, we recently showed that the PK-strengthened DG to LG synapse can play an important role in coordinating the activity of the PK-elicited rhythm, but not the MCN1-elicited rhythm (Kintos et al., 2006).
Further modeling may help elucidate whether the MCN1- and PK-elicited rhythms involve different mechanisms for coordinating the network motor neurons and thus shed light on the behavioral consequences of two comparable motor patterns which are produced by similar underlying mechanisms but coordinated through distinct pathways.
Acknowledgments
This work was supported by NIH grants MH60605 (FN) and NS29436 (MPN).
References
- Ambrosio-Mouser C, Nadim F, Bose A. The effects of varying the timing of inputs on a neuronal oscillator. SIAM J Applied Dynamical Systems. 2006;5:108–139. doi: 10.1137/050625795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angstadt JD, Calabrese RL. A hyperpolarization-activated inward current in heart interneurons of the medicinal leech. J Neurosci. 1989;9:2846–2857. doi: 10.1523/JNEUROSCI.09-08-02846.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angstadt JD, Calabrese RL. Calcium currents and graded synaptic transmission between heart interneurons of the leech. J Neurosci. 1991;11:746–759. doi: 10.1523/JNEUROSCI.11-03-00746.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartos M, Manor Y, Nadim F, Marder E, Nusbaum MP. Coordination of fast and slow rhythmic neuronal circuits. J Neurosci. 1999;19:6650–6660. doi: 10.1523/JNEUROSCI.19-15-06650.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baxter DA, Canavier CC, Clark JW, Jr., Byrne JH. Computational model of the serotonergic modulation of sensory neurons in Aplysia. J Neurophysiol. 1999;82:2914–2935. doi: 10.1152/jn.1999.82.6.2914. [DOI] [PubMed] [Google Scholar]
- Beenhakker MP, DeLong ND, Saideman SR, Nadim F, Nusbaum MP. Proprioceptor regulation of motor circuit activity by presynaptic inhibition of a modulatory projection neuron. J Neurosci. 2005;25:8794–8806. doi: 10.1523/JNEUROSCI.2663-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertram R. Reduced-system analysis of the effects of serotonin on a molluscan burster neuron. Biol Cybern. 1994;70:359–368. doi: 10.1007/BF00200333. [DOI] [PubMed] [Google Scholar]
- Blitz DM, Beenhakker MP, Nusbaum MP. Different sensory systems share projection neurons but elicit distinct motor patterns. J Neurosci. 2004;24:11381–11390. doi: 10.1523/JNEUROSCI.3219-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blitz DM, Christie AE, Coleman MJ, Norris BJ, Marder E, Nusbaum MP. Different proctolin neurons elicit distinct motor patterns from a multifunctional neuronal network. J Neurosci. 1999;19:5449–5463. doi: 10.1523/JNEUROSCI.19-13-05449.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butera RJ, Jr., Clark JW, Jr., Canavier CC, Baxter DA, Byrne JH. Analysis of the effects of modulatory agents on a modeled bursting neuron: dynamic interactions between voltage and calcium dependent systems. J Comput Neurosci. 1995;2:19–44. doi: 10.1007/BF00962706. [DOI] [PubMed] [Google Scholar]
- Calabrese RL. Taking the lead from a model. Curr Biol. 1999;9:R680–683. doi: 10.1016/s0960-9822(99)80438-2. [DOI] [PubMed] [Google Scholar]
- Canavier CC, Baxter DA, Clark JW, Byrne JH. Multiple modes of activity in a model neuron suggest a novel mechanism for the effects of neuromodulators. J Neurophysiol. 1994;72:872–882. doi: 10.1152/jn.1994.72.2.872. [DOI] [PubMed] [Google Scholar]
- Coleman MJ, Meyrand P, Nusbaum MP. A switch between two modes of synaptic transmission mediated by presynaptic inhibition. Nature. 1995;378:502–505. doi: 10.1038/378502a0. [DOI] [PubMed] [Google Scholar]
- De Schutter E, Angstadt JD, Calabrese RL. A model of graded synaptic transmission for use in dynamic network simulations. J Neurophysiol. 1993;69:1225–1235. doi: 10.1152/jn.1993.69.4.1225. [DOI] [PubMed] [Google Scholar]
- Deliagina TG, Zelenin PV, Orlovsky GN. Encoding and decoding of reticulospinal commands. Brain Res Brain Res Rev. 2002;40:166–177. doi: 10.1016/s0165-0173(02)00199-6. [DOI] [PubMed] [Google Scholar]
- Dickinson PS. Neuromodulation of central pattern generators in invertebrates and vertebrates. Curr Opin Neurobiol. 2006;16:604–614. doi: 10.1016/j.conb.2006.10.007. [DOI] [PubMed] [Google Scholar]
- Dzirasa K, Ribeiro S, Costa R, Santos LM, Lin SC, Grosmark A, Sotnikova TD, Gainetdinov RR, Caron MG, Nicolelis MA. Dopaminergic control of sleep-wake states. J Neurosci. 2006;26:10577–10589. doi: 10.1523/JNEUROSCI.1767-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermentrout GB. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to Xppaut for Researchers and Students (Software, Environments, Tools) SIAM; Philadelphia: 2002. [Google Scholar]
- Goldman MS, Golowasch J, Marder E, Abbott LF. Global structure, robustness, and modulation of neuronal models. J Neurosci. 2001;21:5229–5238. doi: 10.1523/JNEUROSCI.21-14-05229.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golowasch J, Marder E. Proctolin activates an inward current whose voltage dependence is modified by extracellular Ca2+ J Neurosci. 1992;12:810–817. doi: 10.1523/JNEUROSCI.12-03-00810.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grillner S. Biological pattern generation: the cellular and computational logic of networks in motion. Neuron. 2006;52:751–766. doi: 10.1016/j.neuron.2006.11.008. [DOI] [PubMed] [Google Scholar]
- Grillner S, Markram H, De Schutter E, Silberberg G, LeBeau FE. Microcircuits in action--from CPGs to neocortex. Trends Neurosci. 2005;28:525–533. doi: 10.1016/j.tins.2005.08.003. [DOI] [PubMed] [Google Scholar]
- Guckenheimer J, Gueron S, Harris-Warrick RM. Mapping the dynamics of a bursting neuron. Philos Trans R Soc Lond B Biol Sci. 1993;341:345–359. doi: 10.1098/rstb.1993.0121. [DOI] [PubMed] [Google Scholar]
- Jing J, Weiss KR. Generation of variants of a motor act in a modular and hierarchical motor network. Curr Biol. 2005;15:1712–1721. doi: 10.1016/j.cub.2005.08.051. [DOI] [PubMed] [Google Scholar]
- Kiehn O. Locomotor circuits in the mammalian spinal cord. Annu Rev Neurosci. 2006;29:279–306. doi: 10.1146/annurev.neuro.29.051605.112910. [DOI] [PubMed] [Google Scholar]
- Kintos N, Nadim F, Saideman S, Nusbaum MP. Comparing projection neuron and neuromodulatory effects on network activity using a computational model; SfN 36th Annual Meeting; Atlanta, GA. 2006. [Google Scholar]
- LeBeau FE, El Manira A, Griller S. Tuning the network: modulation of neuronal microcircuits in the spinal cord and hippocampus. Trends Neurosci. 2005;28:552–561. doi: 10.1016/j.tins.2005.08.005. [DOI] [PubMed] [Google Scholar]
- Lieske SP, Thoby-Brisson M, Telgkamp P, Ramirez JM. Reconfiguration of the neural network controlling multiple breathing patterns: eupnea, sighs and gasps [see comment] Nat Neurosci. 2000;3:600–607. doi: 10.1038/75776. [DOI] [PubMed] [Google Scholar]
- Manor Y, Nadim F, Epstein S, Ritt J, Marder E, Kopell N. Network oscillations generated by balancing graded asymmetric reciprocal inhibition in passive neurons. J Neurosci. 1999;19:2765–2779. doi: 10.1523/JNEUROSCI.19-07-02765.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Bucher D. Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu Rev Physiol. 2007;69:291–316. doi: 10.1146/annurev.physiol.69.031905.161516. [DOI] [PubMed] [Google Scholar]
- Marder E, Bucher D, Schulz DJ, Taylor AL. Invertebrate central pattern generation moves along. Curr Biol. 2005;15:R685–699. doi: 10.1016/j.cub.2005.08.022. [DOI] [PubMed] [Google Scholar]
- Marder E, Thirumalai V. Cellular, synaptic and network effects of neuromodulation. Neural Netw. 2002;15:479–493. doi: 10.1016/s0893-6080(02)00043-6. [DOI] [PubMed] [Google Scholar]
- Mishchenko EF, Rozov NK. Differential Equations with Small Parameters and Relaxation Oscillators. Plenum Press; New York: 1980. [Google Scholar]
- Morgan PT, Perrins R, Lloyd PE, Weiss KR. Intrinsic and extrinsic modulation of a single central pattern generating circuit. J Neurophysiol. 2000;84:1186–1193. doi: 10.1152/jn.2000.84.3.1186. [DOI] [PubMed] [Google Scholar]
- Nadim F, Calabrese RL. A slow outward current activated by FMRFamide in heart interneurons of the medicinal leech. J Neurosci. 1997;17:4461–4472. doi: 10.1523/JNEUROSCI.17-11-04461.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadim F, Manor Y, Nusbaum MP, Marder E. Frequency regulation of a slow rhythm by a fast periodic input. J Neurosci. 1998;18:5053–5067. doi: 10.1523/JNEUROSCI.18-13-05053.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norris BJ, Coleman MJ, Nusbaum MP. Recruitment of a projection neuron determines gastric mill motor pattern selection in the stomatogastric nervous system of the crab, Cancer borealis. J Neurophysiol. 1994;72:1451–1463. doi: 10.1152/jn.1994.72.4.1451. [DOI] [PubMed] [Google Scholar]
- Nusbaum MP, Beenhakker MP. A small-systems approach to motor pattern generation. Nature. 2002;417:343–350. doi: 10.1038/417343a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusbaum MP, Blitz DM, Swensen AM, Wood D, Marder E. The roles of co-transmission in neural network modulation. Trends Neurosci. 2001;24:146–154. doi: 10.1016/s0166-2236(00)01723-9. [DOI] [PubMed] [Google Scholar]
- Peck JH, Gaier E, Stevens E, Repicky S, Harris-Warrick RM. Amine modulation of Ih in a small neural network. J Neurophysiol. 2006;96:2931–2940. doi: 10.1152/jn.00423.2005. [DOI] [PubMed] [Google Scholar]
- Prinz AA, Bucher D, Marder E. Similar network activity from disparate circuit parameters. Nat Neurosci. 2004;7:1345–1352. doi: 10.1038/nn1352. [DOI] [PubMed] [Google Scholar]
- Rossignol S, Dubuc R, Gossard JP. Dynamic sensorimotor interactions in locomotion. Physiol Rev. 2006;86:89–154. doi: 10.1152/physrev.00028.2005. [DOI] [PubMed] [Google Scholar]
- Saideman S. Neuroscience. University of Pennsylvania; Philadelphia, PA: 2006. Circuit-specific Modulation by Neuroactive Peptides. [Google Scholar]
- Saideman SR, Blitz DM, Nusbaum MP. Convergent motor patterns from divergent circuits. J Neurosci. 2007a;27:6664–6674. doi: 10.1523/JNEUROSCI.0315-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saideman SR, Ma M, Kutz-Naber KK, Cook A, Torfs P, Schoofs L, Li L, Nusbaum MP. Modulation of rhythmic motor activity by pyrokinin peptides. J Neurophysiol. 2007b;97:579–595. doi: 10.1152/jn.00772.2006. [DOI] [PubMed] [Google Scholar]
- Skiebe P. Neuropeptides are ubiquitous chemical mediators: Using the stomatogastric nervous system as a model system. J Exp Biol. 2001;204:2035–2048. doi: 10.1242/jeb.204.12.2035. [DOI] [PubMed] [Google Scholar]
- Stein W, DeLong ND, Wood DE, Nusbaum MP. Divergent cotransmitter actions underlie motor pattern activation by a modulatory projection neuron. Eur J Neurosci. 2007 doi: 10.1111/j.1460-9568.2007.05744.x. In Press. [DOI] [PubMed] [Google Scholar]
- Swensen AM, Marder E. Multiple peptides converge to activate the same voltage-dependent current in a central pattern-generating circuit. J Neurosci. 2000;20:6752–6759. doi: 10.1523/JNEUROSCI.20-18-06752.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swensen AM, Marder E. Modulators with convergent cellular actions elicit distinct circuit outputs. J Neurosci. 2001;21:4050–4058. doi: 10.1523/JNEUROSCI.21-11-04050.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood DE, Manor Y, Nadim F, Nusbaum MP. Intercircuit control via rhythmic regulation of projection neuron activity. J Neurosci. 2004;24:7455–7463. doi: 10.1523/JNEUROSCI.1840-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood DE, Stein W, Nusbaum MP. Projection neurons with shared cotransmitters elicit different motor patterns from the same neural circuit. J Neurosci. 2000;20:8943–8953. doi: 10.1523/JNEUROSCI.20-23-08943.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou L, Zhao S, Nadim F. Neuromodulation of short-term synaptic dynamics examined in a mechanistic model based on kinetics of calcium currents. Neurocomputing. 2007;70:2050–2054. doi: 10.1016/j.neucom.2006.10.084. [DOI] [PMC free article] [PubMed] [Google Scholar]