Controlling the efficiency of an artificial light-harvesting complex

Abstract

Adaptive femtosecond pulse shaping in an evolutionary learning loop is applied to a bioinspired dyad molecule that closely mimics the early-time photophysics of the light-harvesting complex 2 (LH2) photosynthetic antenna complex. Control over the branching ratio between the two competing pathways for energy flow, internal conversion (IC) and energy transfer (ET), is realized. We show that by pulse shaping it is possible to increase independently the relative yield of both channels, ET and IC. The optimization results are analyzed by using Fourier analysis, which gives direct insight to the mechanism featuring quantum interference of a low-frequency mode. The results from the closed-loop experiments are repeatable and robust and demonstrate the power of coherent control experiments as a spectroscopic tool (i.e., quantum-control spectroscopy) capable of revealing functionally relevant molecular properties that are hidden from conventional techniques.

Artificial photosynthesis is an important challenge of science and technology today. Numerous applications include solar cells and other artificial power sources, light-emitting materials, sensor systems, and other electronic and photonic nanodevices that use the conversion of light energy into chemical potentials (1). Over the last decade, major technological advances have been made by using biomimicry, an approach that makes use of teachings from studies on nature's wide-ranging selection of highly efficient pigment–protein complexes (2). It has been shown that integrating light-harvesting antennae with electron-transfer relay systems is a potent way to emulate photosynthesis (3). Thus, biomimicry has inspired systems based on complicated natural light-harvesting complexes (LHCs) reduced to their basic elements, and efficient antenna systems based on polymer polyenes covalently attached to tetrapyrroles have been synthesized (4, 5).

The antennae are responsible for the first step of photosynthesis, capturing energy of the sun and transferring it to subsequent photosynthetic structures where the energy is transformed in chemical potential. Within various natural and synthetic LHCs, blue-green photons are absorbed by carotenoid molecules, from which the energy is transferred to neighboring porphyrin molecules (6). This energy transfer (ET) step from the carotenoid donor to the accepting molecular species is the primary process in using energy in the 450- to 550-nm window and contributes significantly to the functioning of the complex. The efficiency of ET over competing loss processes, such as internal conversion (IC), is a crucial factor in the overall quantum yield of (artificial) photosynthesis. Hence, a high priority is given to understanding the mechanisms of energy flow and mediating processes to allow development of more efficient artificial systems.

In this study, we use adaptive femtosecond pulse shaping in a learning loop (7, 8) to control the pathways of energy flow in an artificial LHC. This closed-loop optimization technique has produced several successful examples in obtaining control over various physicochemical reactions in complex molecules in liquid phase without previous knowledge of the molecular Hamiltonian (8, 9). Examples extend from control of ET (10), fluorescence yield (11), population transfer (PT) (12), selective excitation of vibrational modes (13), and isomerization reactions (14–16). However, in such complex systems the algorithm has to navigate through a multidimensional parameter space, and the search often results in a complicated, highly modulated pulse shape that eludes interpretation and leaves the physical mechanism unresolved. Here we show how coherent control techniques can teach us more about the intrinsic properties and interactions of molecular systems; that is, we perform quantum-control spectroscopy with pulse shaping (8, 17, 18). For artificial photosynthesis, the goal is to reveal mechanisms and related design criteria that underlie optimal performance for light harvesting.

The system we study was inspired by the LH2 complex from the purple bacterium Rhodopseudomonas acidophila, in which many carotenoid and porphyrin pigments are embedded in a ring structure within a protein (19). Our bioinspired dyad molecule consists of a single donor (carotenoid) and single acceptor (purpurin) moiety; thus, the structural complexity is reduced significantly. Previously, detailed ultrafast studies revealed that the dyad mimics the salient features of the photophysics of the natural photosynthetic complex (20, 21).

Our study also expands on previous work in which coherent control was used to manipulate the branching ratio between two competing energy-flow pathways in LH2 (10). In that study the relative efficiency of the loss channel (IC) was improved over the functional pathway (ET) by 30%. The proposed control mechanism (22) involves an excitation of a specific low-frequency C-C-C bending mode enhancing the energy flow to the IC channel. According to this mechanism, a multipulse laser field is synchronized to a critical vibrational frequency (≈160 cm⁻¹) on the electronic ground state, the activation of which leads to more rapid IC, thus increasing the energy flow to the loss channel (22).

To control the pathways of energy flow in the dyad molecule, we start “blindly” without restricting the optimization to any particular region of the search space. We then extract recognizable features from the resulting pulse shapes, simplify the parameter space accordingly, and test whether a similar result is available by using a smaller number of parameters (23, 24). This strategy provides a powerful spectroscopic tool that is sensitive to the function of the artificial LHC, thereby revealing important characteristics that affect the efficiency of the light-harvesting process. Furthermore, we show that it is possible to enhance or suppress the functional channel by pulse shapes exploiting different control mechanisms. Ultimately, this approach may lead to the discovery of new design principles to aid the development of more efficient artificial light-harvesting systems.

Results

For the blind optimization, a large search space described by 208 parameters was chosen to not limit the complexity of the pulse shape. The search space was described by a basis having three different frequency ranges (10, 20, and 40 pixels) over the pulse-shaper window, and the spectral phase was interpolated between these frequencies. The shaping was done only to the phase, and no amplitude shaping was used.

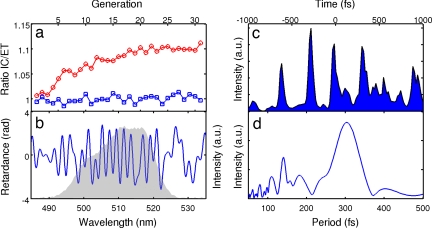
Fig. 1 shows a learning curve of a blind optimization in which the target was to maximize the IC/ET ratio, the pathway successfully optimized in LH2 (10). A total of 15% increase of the ratio was obtained after 108 generations. The fitness values of the best pulse shapes (red circles) reveal that after an initial jump of ≈5%, the algorithm explores the search space for ≈20 generations before finding a feasible route on the fitness landscape, which gradually results in a further ≈10% increase of the IC/ET ratio, although the optimization likely has not yet converged. The fitness value of the transform-limited (TL) pulse (blue squares) was determined before each new generation, providing an excellent indicator that the experimental conditions remained constant during the optimization.

Fig. 1.

A closed-loop optimization of IC/ET. The learning curve shows an improvement of ≈15% in the fitness value of the best individuals (red dots) compared with the fitness of the TL pulse measured before each new generation (blue squares). (Inset) Cross-correlation (Upper) and fast Fourier transform of the cross-correlation (Lower) of the best pulse of generation 108.

The optimal pulse shape of the generation 108 (Fig. 1 Inset) spreads as a complicated pulse-train-like structure over several picoseconds. The power spectrum of the cross-correlation of the pulse (Fig. 1 Inset) shows a major peak at a period of ≈300 fs corresponding to a frequency within the complex pulse-train structure of ≈110 cm⁻¹. The initial jump between the first and the second generation is attributable to an artifact, as will be discussed further in the following section.

According to our strategy, the following step was to move to a more restricted parameter space. Because the first results hinted that pulse trains were a key characteristic, we then used a Fourier-series parameterization consisting of 20 sinusoidal and 20 cosine functions. In this optimization, the number of parameters was 40, still sufficiently large to allow for complex pulse shapes. The results of this optimization are shown in Fig. 2; now the learning is much faster, such that with just 31 generations an ≈10% increase of the fitness value IC/ET is found again (Fig. 2a). Fig. 2b shows the optimal phase pattern (blue line) overlapping the pump spectrum (gray area), and Fig. 2c shows the corresponding experimental cross-correlation of the resulting optimal control field. The power spectrum of the cross-correlation of the optimal pulse is shown in Fig. 2d. The figure indicates that the major feature responsible for the increase of the IC/ET ratio is, indeed, a pulse train with a subpulse spacing of ≈300 fs. This result is in agreement with that of the aforementioned experiment on LH2 (10), in which the optimized pulse shape showed a strong periodic modulation with spacing of 220 fs.

Fig. 2.

Optimization of the IC/ET ratio using the Fourier-series parameterization. (a) The learning curve shows an improvement of ≈10% in the fitness value of the best individual (red circles). Blue squares indicate the fitness of the TL pulse, measured before each new generation. The initial (from TL to the first generation) increase of the fitness value caused by the stretching of the pulse is subtracted from the data. (b) The optimal phase pattern (blue line) and the pump spectrum (gray area). (c) Cross-correlation of the optimal pulse shape. (d) The power spectrum of the cross-correlation. a.u., arbitrary units.

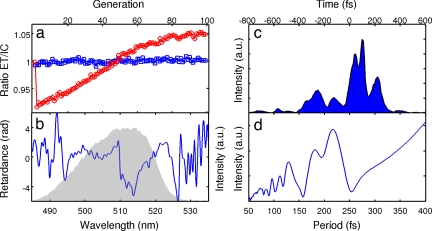
We also explored a target objective aimed to improve the relative yield of the ET by using fitness function ET/IC. Fig. 3a shows an example of a learning curve of an ET/IC optimization. Initially, the fitness jumps downward ≈8% but grows to a final improvement of ≈13% higher. It should be noted that during the learning process a nonflat phase pattern having an equal fitness value as the TL pulse is found at approximately the halfway point of the optimization. However, after the crossing point, more favorable pulse shapes are found that lead to an improvement of the efficiency of the ET process over the competing IC process by 5%, compared with the TL pulse. As in the case of the IC/ET optimization, the optimal phase pattern shown in Fig. 3b (blue line) results in a multipulse structure shown in Fig. 3c. The four-pulse structure has a total duration that is significantly shorter than the best pulse from the IC/ET optimization, and the most pronounced subpulse spacing is ≈200 fs. The power spectrum of the cross-correlation of the best-found pulse shape in Fig. 3d shows a major peak at a period of ≈200 fs.

Fig. 3.

The closed-loop optimization of the ET/IC ratio. (a) The learning curve shows an improvement of ≈5% in the fitness value of the best individual (red circles). The blue squares indicate the fitness of the TL pulse, measured before each new generation. (b) The optimal phase function (blue line) and the pump spectrum (gray area). (c) Cross-correlation of the optimal pulse shape. (d) The power spectrum of the cross-correlation. a.u., arbitrary units.

Discussion

The experiments show that both product channels (ET and IC) in the artificial LHC are susceptible to coherent control. Using the strategy of sequentially moving from blind optimizations to a restricted parameter space and analyzing the optimizations using Fourier analysis, we find that for both product channels a pulse-train structure with varying subpulse spacings (≈300 fs for IC and 200 fs for ET) is responsible for the control. The large parameter space provides a lot of freedom for the learning process, but the result is very difficult to interpret. We show that a simpler parameterization makes optimizations faster while preserving the amplitude of the learning process (10%). Thus, we have found important directions on the fitness landscape describing a smaller search space still containing the optimal solution.

The initial jump observed in the optimizations is attributable to a trivial and incoherent control mechanism that simply avoids saturation by pulse stretching, a phenomenon previously discussed for LH2 by Papagiannakis et al. (25). The effect stems from the fact that the signals for IC and ET have very different life times. Effectively, this means that when the excitation pulse gets longer, we observe more signal in IC compared with a transform-limited pulse that can readily saturate the carotenoid S₀-to-S₂ transition. We used the measured saturation curves (data not shown) in combination with the kinetic model of the system (26) and the measured cross-correlations of the pulse shapes along the learning curve to model the effect. The simulations show that compared with the TL pulse the first shaped pulse is invariably stretched in time, resulting in a higher fitness value for IC/ET (or lower in the ET/IC optimization). This contribution remains constant (fluctuating <0.5%) over the course of the optimization, creating a step that underlies the exponential growth curve attributable to real learning. In addition, we experimentally tested the recorded pulse shapes from the IC/ET optimization in a repeat measurement by using only half the energy. According to the data (not shown), the jump and the “learning” part have very different intensity dependencies; the initial jump decreased by approximately half of its amplitude, whereas the learning part remained the same (≈10%). We conclude that the initial jump observed in the optimizations is caused by a trivial and incoherent control mechanism that simply avoids saturation and that the learning originates from an active control mechanism over the branching of the energy flow in the dyad.

The control mechanism may involve dynamics in an excited and/or the ground state of the dyad. After excitation of the carotenoid moiety to its S₂ state, a rapid IC via a conical intersection competes with the ET to the porphyrin (26). This competition results in a very short lifetime of the S₂ state (<40 fs). Considering that the pulse separations in the found pulse shapes are substantially longer, control mechanisms involving wave-packet dynamics in the S₂ state during the interaction with the pulse can be excluded, because population (and thereby also the electronic coherence) decays completely between the subpulses. On the other hand, the S₁ lifetime of the carotenoid is 7.8 ps, and one possibility is that the found pulse shapes are promoting constructive (destructive) interferences between wave packets that are evolving on the S₁ potential energy surface. Although in some systems vibrational coherence may be preserved during a relaxation between electronic states (27, 28), previous reports on carotenoids show that passage through the conical intersection between the S₂ and S₁ occurs most likely incoherently (18, 29, 30). The observations in the pump-probe experiments show vibrational coherence only in ground-state potential energy surface, indicating that the vibrational wave packet created in the S₂ state does not survive the IC process to the S₁ potential energy surface (30).

In a recent study on all-trans-β-carotene in solution, Lustres et al. (31) described a strongly overdamped oscillation between the S₂ and S₁ states that causes a recurrence of population in the S₂ potential energy surface with a 300-fs period. It is interesting to note that this recurrence time matches the separation of subpulses in the found pulse train in the IC/ET optimization. Involvement of such a dynamical feature cannot be excluded entirely, but again, the lifetime of the S₂ state suggests that influence of the recurring feature would be very small. Only a minor part of the carotenoid still has excitation, because 70% flows to the purpurin with ultrafast time scales. In addition, it is uncertain whether this recurrence exists in the dyad and with what efficiency.

We now consider a mechanism that incorporates impulsive stimulated Raman scattering (ISRS) of low-frequency skeletal modes in the ground state (32). In the following, we use a pathway approach with potential energy surfaces and wave packets to describe the multidimensional photophysics of the dyad. Wave-packet generation on specific vibrational modes by shaped pulses (33–35), which turns into enhancement of vibrational coherence under near-electronic resonant condition (36–38), has been demonstrated in various molecules including carotenoids. By periodically modulating the phase of the laser pulse over its spectrum, it is possible to prepare wave packets selectively and, under near-resonant conditions, to enhance wave-packet excitation of Raman-active modes. The leading pulses prepare a wave packet in the vibrationally hot ground state of the carotenoid. By matching the frequency of the pulse train to a ground-state vibrational mode (e.g., a low-frequency twisting of the backbone), we introduce momentum along a trajectory that may take the wave packet toward Franck–Condon regions not accessed by a Fourier-limited pulse. Subsequently, this push leads to an altered evolution on the excited state, either toward or away from the conical intersection between S₂ and S₁. In the former case, an excitation of vibrationally hot ground-state modes could lead to a more efficient IC process, averting the ET pathway.

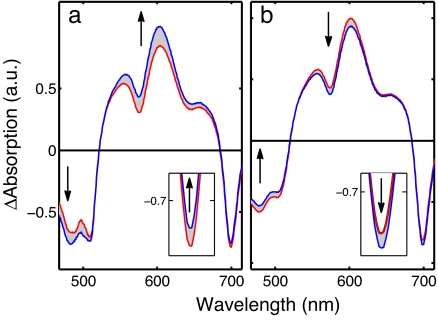
Observing the PT from S₀ to S₂ for the two investigated control scenarios, namely IC/ET or ET/IC optimizations, substantiates this mechanism. The former case (IC/ET) brings on an increased PT compared with Fourier-limited excitation (see Fig. 4a). The pulse optimal for the ET/IC shaping goal results in a reduction of PT to S₂ (Fig. 4b), which can be attributed to a modulation of the PT from ground to excited state because of the multipulse interaction (36). In the case of IC/ET, the increased population has momentum along the reaction coordinate, leading to wave-packet propagation along a trajectory that brings the wave packet faster to the conical intersection between S₂ and S₁; hence, the improved PT almost entirely flows to the S₁ state. This mechanism is mediated by a pulse-train-like structure with a dominant subpulse spacing of ≈300 fs that matches to a Raman-active mode according to b = n·T_vib, with T_vib as the vibrational period of the mode and n as an integer number. The opposite holds for the ET/IC optimization: the pulse train with an ≈200-fs pulse separation is out of phase with the multipulse optimal for the other scenario. It avoids the aforementioned build-up of momentum along the low-frequency mode. Such an excitation laser field is more favorable for the ET process by lacking momentum along the trajectory toward the conical intersection. Therefore, through the reduced PT we gain a slight increase of ET as illustrated in Fig. 4. The amount of total PT can be estimated from the blue-most region of the bleach, where no pump scattering is observed. In the case of IC/ET optimization, PT and IC are increased and ET slightly reduced. In ET/IC optimization, ET is increased and IC and PT are decreased.

Fig. 4.

The transient spectra at an 8-ps probe delay using TL pulse (red line) and the found optimal shapes (blue line). (a) IC/ET optimization: PT increases, IC increases, and the ET reduces slightly. (b) ET/IC optimization: PT decreases, IC decreases, and the ET increases. (Insets) Zoom-in views of ET signals at ≈700 nm. The arrows indicate the change from the TL to the optimal pulse shapes. a.u., arbitrary units.

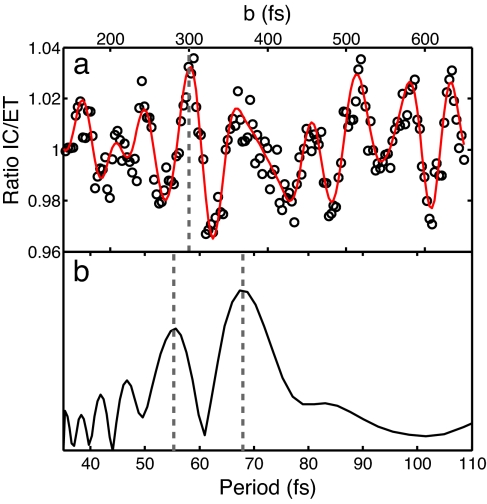
As another test of the ISRS mechanism, we monitor how the IC/ET ratio evolves when the parameter b of a periodic phase function, Φ(x) = asin[(2πx/b) + c], is scanned. In time domain, this so-called b scan renders a pulse train with varying time separation b between the subpulses. In the b scan, the parameters a and c are kept constant at π and 0, respectively, producing a pulse envelope profile having 11 subpulses. Fig. 5a shows the result of the b scan after the aforementioned incoherent contribution caused by the pulse lengthening has been removed from the data. As expected for the ISRS hypothesis, we observe a maximum at the pulse separation of 300 fs. The power spectrum of the b-scan trace (Fig. 5b) reveals two major contributions with periods of 55 and 68 fs, which suggests that the optimal control field found in the closed-loop optimizations uses higher harmonics of more than one Raman active modes, most pronounced having frequencies of ≈500 and ≈600 cm⁻¹. These periods may correspond to low-frequency structural modes, as proposed in the work on LH2 (10, 22). We note that the control amplitude at b = 300 fs is lower than the 10% that was found in the closed-loop optimizations, which may be because of the lower pulse energy used in the b scan, reducing the amount of ISRS. Also, the possible interplay between several modes in the control mechanism might be better used by the optimal control field found in the closed-loop experiments than the “clean” and the equidistant pulse train used in the b scan. The underlying physics are likely to incorporate quantum interferences whose manipulation requires more sophisticated pulse shapes than are available when using a simple sinusoidal phase function.

Fig. 5.

Results of the pulse-train scan. (a) IC/ET ratio as a function of the subpulse separation (black circles). To guide the eye, a frequency-filtered trace is shown (red line). (b) The power spectrum of the pulse-train scan. The two major contributions are at periods of 55 and 68 fs.

Conclusions

We have shown how the energy flow in the artificial LHC can be manipulated by femtosecond pulse shaping to both suppress and enhance the ET yield. Many repeated runs of the recorded phase shapes from the optimizations were performed, indicating that the results are robust. The efficiency of ET in the dyad depends strongly on the photophysics of the carotenoid moiety. By reducing the parameter space in combination with a Fourier analysis of obtained results, we were able to track down the functionally important features of this molecular system. A mechanism based on the periodic excitation pulse enhancing the vibrational coherence of low-frequency wave packets via the ISRS process is most likely responsible for the control, analogous to that proposed earlier for the control in LH2 (22). However, in the dyad, the observed effect is smaller, perhaps illustrating the fact that the dyad in solution has more degrees of freedom and possible conformations in the ground and/or excited states (39, 40). The low-frequency mode that is involved is not restricted by the environment and may gain energy attributable to intramolecular vibrational redistribution freely, hence leaving the effect of the selective excitation smaller than in the LH2 complex, in which such a mode is probably more inhibited. In nature, the protein environment/structure seems to aid the ET by posing restrictions to the carotenoid conformational degrees of freedom. This is an important point when considering the design of artificial light-harvesting systems. It seems that coupling to the environment and the restricted conformation and movement have influence on the quantum yield. In the future, this insight will lead to novel design principles for building more efficient artificial solar energy-harvesting systems for various applications.

Materials and Methods

The control measurements were made by using a tailored pump pulse and an unmodulated probe pulse. The transient absorption setup was based on an amplified femtosecond laser system (Clark CPA2001; Clark–MXR) and noncollinear optical parametric amplifier (Clark–MXR), as described (26). The pulse-shaper comprises a liquid-crystal spatial light modulator (SLM) (Cambridge Research Instruments) placed in the Fourier plane of a 4-f (f = 500 mm) zero-dispersion compressor with two 1800 grooves per mm gratings and cylindrical mirrors. The SLM had 640 pixels, leading to the resolution of 0.11 nm per pixel. In this study, only phase shaping is used. A robust calibration method, in which each SLM pixel is calibrated and correction for any phase distortion is made by optimizing second-harmonic generation in a nonlinear crystal, ensured that the shaping introduced no effect on the amplitude of the pump pulse; the fluencies of the excitation pulses were kept moderate at ≈10¹⁴ to 10¹⁵ photons cm⁻² at a 510-nm excitation wavelength.

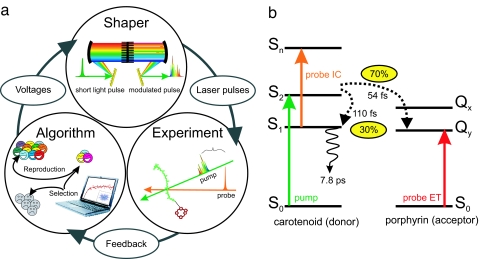
The control experiments used a closed-loop optimization strategy (7, 8), the basic elements of which are presented in Fig. 6a. The optimization is blind in that it begins with no initial guess but, rather, a set of random phases that corresponds to a generation of different pulse shapes. The individual phase patterns are applied to the SLM, which modulates the dispersed spectrum of the femtosecond laser, tuned to the first optically allowed transition of the carotenoid (S₀ → S₂ in Fig. 6b) at 510 nm. The resulting pulse shapes are then successively tested on the sample, and a feedback signal is derived by using transient absorption. On the basis of this signal, a fitness function is evaluated according to the target of the optimization, and the individual pulse shapes are ranked. A learning algorithm then selects the best pulse shapes for reproduction and creates a new generation of pulse shapes. Another iteration of the cycle begins, and the loop proceeds to search for pulse shapes that further increase the value of the feedback function, thus closing in on the target objective.

Fig. 6.

Optimization of the energy flow in a learning loop. (a) Elements of a learning-loop experiment. (b) Simplified energy-flow diagram. After excitation, ET from the carotenoid S₂ state to porphyrin takes place in 54 fs. Simultaneously, the first excited state (S₁) of the carotenoid is populated via hot S₁ state by a competing IC process in 110 fs, resulting in a 30/70 branching ratio between IC and ET. The S₁ state decays to the ground state in 7.8 ps. The lowest excited energy level of the porphyrin is deactivated on nanosecond time scales.

The target objective is to manipulate the pathways of energy flow in the dyad (Fig. 6b). Two competing channels, labeled (ET) and (IC), are resolved from the transient spectrum at an 8-ps time delay and used as feedback for the optimization. A 10-nm band centered at 610 nm corresponding to the excited-state absorption of the S₁ state was used to monitor the loss channel (IC), and a 10-nm band at ≈700 nm corresponding to the bleach of the acceptor was used to monitor the functional channel (ET). The pump spectrum was centered at 510 nm and had a full width of ≈45 nm. The algorithm used was a covariance-matrix adaptation of the derandomized evolutionary strategy (26, 41).