The evolution of urban sprawl: Evidence of spatial heterogeneity and increasing land fragmentation

Abstract

We investigate the dynamics and spatial distribution of land use fragmentation in a rapidly urbanizing region of the United States to test key propositions regarding the evolution of sprawl. Using selected pattern metrics and data from 1973 and 2000 for the state of Maryland, we find significant increases in developed and undeveloped land fragmentation but substantial spatial heterogeneity as well. Estimated fragmentation gradients that describe mean fragmentation as a function of distance from urban centers confirm the hypotheses that fragmentation rises and falls with distance and that the point of maximum fragmentation shifted outward over time. However, rather than outward increases in sprawl balanced by development infill, we find substantial and significant increases in mean fragmentation values along the entire urban–rural gradient. These findings are in contrast to the results of Burchfield et al. [Burchfield M, Overman HG, Puga D, Turner MA (2006) Q J Econ 121:587–633], who conclude that the extent of sprawl remained roughly unchanged in the Unites States between 1976 and 1992. As demonstrated here, both the data and pattern measure used in their study are systematically biased against recording low-density residential development, the very land use that we find is most strongly associated with fragmentation. Other results demonstrate the association between exurban growth and increasing fragmentation and the systematic variation of fragmentation with nonurban factors. In particular, proximity to the Chesapeake Bay is negatively associated with fragmentation, suggesting that an attraction effect associated with this natural amenity has concentrated development.

The subject of urban sprawl—its prevalence, causes, and effects—has been hotly debated in the United States for several decades. For many, sprawl is a judgment about one or more aspects of excessive urban development, e.g., cities that are too extensive (1), employment that is too dispersed (2), or urban areas that are not sufficiently dense (3). A dearth of fine-scale land use data has prevented spatially explicit quantification of urban land use patterns beyond the extent of a single county or urban area. Yet it is precisely this fine-scale pattern with which the debate over sprawl and its impacts is principally concerned—the lack of contiguous residential development that increases public service costs; the spatial diffusion of households and jobs that magnifies traffic congestion and increases greenhouse gas emissions; and the fragmentation of undeveloped land that alters habitat, degrades natural resources, and eliminates functional open spaces.

This paper is principally concerned with testing key propositions regarding the pattern and evolution of urban sprawl. To do so, we would ideally use highly detailed data for multiple regions of the United States. However, as we demonstrate in the next section, the only consistent data that are available at a spatially disaggregate level, the National Land Cover Dataset (NLCD), are systematically biased against recording low-density residential development, particularly in nonurban areas. Even if these data did record low-density urban land accurately, we would still be faced with the dilemma of translating land cover data into meaningful estimates of sprawl. Although land cover, defined in terms of physical characteristics, can be observed with aerial photography and often interpreted successfully from satellite imagery, it is land use, defined in terms of human activity, that is most relevant for the study of urban patterns. Changes in land use often lead to changes in land cover, but there is no one-to-one mapping (4–6). Nowhere is this ambiguity more severe than for low-density development, as the ratio of impervious surface to vegetative cover is exceedingly small.

Because consistent, fine-scale data on land use are not available for the United States, we turn to a more limited geographical area, the state of Maryland, for which land use/land cover data are available for two points in time, 1973 and 2000 [supporting information (SI) Fig. 2]. Maryland underwent rapid urbanization during this time period. The proportion of developed land in the State of Maryland increased from 8.9% to 18.2% of the State's total land and of the 2,211 km² of new development, low-density residential land accounted for 62%. These large proportionate gains in low-density development mirror development trends in urbanizing regions across the United States (7).

Describing and explaining landscape patterns are two separate endeavors, each posing their own difficulties. The latter involves untangling the myriad of factors evolving at different spatial and temporal scales, many of which are endogenously determined within the same system that determines land use change. This challenge is beyond the scope of our paper. Attempts to identify causal mechanisms, however, depend first on careful measurement and description. Thus, a goal of this paper is to identify important empirical regularities with respect to land fragmentation that can be used to guide and test process-based models of land use change. Here our analysis underscores the importance of a spatially explicit approach in which the full heterogeneity of land use patterns can be explored.

Results

Dataset Comparisons.

Our contention that the NLCD data are inappropriate for measuring low-density development is based in part on published literature (8, 9). Researchers (10, 11) have found that NLCD accuracy declines significantly as the number of contiguous cells of the same land cover class within a 3 × 3 cell window around a target cell declines and as the number of different land cover classes occurring in that 3 × 3 cell window increases. Low-density, fragmented development at the urban–rural fringe is characterized by both of these features. According to one study (7), 75% of residential development between 1994 and 1997 in the United States occurred on lots of >1 acre. Given that the size of an NLCD grid cell is 900 m² (≈0.22 acre) and the average house leaves a footprint of ≈200 m², picking up low-density residential development even at densities of one dwelling unit per acre requires recognition of an impervious surface patch of no more than a quarter of a cell in a field of 4.5 cells. Thus in theory, NLCD should encounter difficulties in recognizing low-density development.

To investigate this claim empirically, we compare the 2001 NLCD satellite imagery data with planimetric data that represent the major sources of constructed surfaces (hereafter, HCP) for Howard County, Maryland, an urbanizing county located between Washington, D.C., and Baltimore (SI Fig. 2). By overlaying the NLCD and HCP data, the amount of building footprint, road footprint, and parking lot footprint intersecting each NLCD 30 × 30 m cell is calculated.^§Table 1 reports a comparison of developed cells according to the HCP data and the percentage of those cells that the 2001 NLCD data record as belonging to any developed category. Success rates are reported by development density categories, where the development density of each cell is determined by Howard County parcel boundary data. The correspondence between NLCD and HCP data is quite good for high-density development and for major roads and parking lots, with the NLCD correctly reporting development for at least 80% of the developed cells. However, the lower the development density, the lower is the success rate. In particular, for the low-density development category (0.5- to 5-acre housing lots), the NLCD recognizes only 26% of developed cells. Errors of omission (those labeled developed by the HDP data but not by the NLCD) exceed errors of commission (those labeled developed by the NLCD but not by the HDP data) by more than 2 to 1, suggesting that large amounts of development are simply missed by the NLCD. Success rates by distance from the nearest major city (Baltimore in this case) reveal that within 20 miles of the city center, errors of omission exceed those of commission by only ≈30%, but between 20 and 32 miles from Baltimore, the errors of omission exceed those of commission by more than 4 to 1.

Table 1.

Comparison of 2001 NLCD land cover and HCP data

Actual land use*(density or road type)	No. of developed cells (from 2001 HCP data)†	% labeled developed by 2001 NLCD
Nonresidential development, high-density residential	19,639	83
Medium-density residential (0.125- to 0.5-acre lots)	28,297	62
Low-density residential (0.5- to 5-acre lots)	26,836	26
Very low density, including farmsteads (>5 acres)	6,720	8
Federal and state roads, parking lots	35,792	80
County and smaller roads	57,494	56
Undeveloped (530,494 cells)		6

*Cells with multiple land uses are attributed to the dominant category; 5% minimum impervious surface.

^†Grid cells are 30 × 30 m.

As an alternative to the NLCD data, we consider Maryland Department of Planning (MDP) land use/land cover data from 2000, developed through a combination of aerial photography and geocoded tax data. To assess its ability to recognize low-density development, we compare MDP's map for Howard County with the HCP data and with Howard County's digitized parcel boundary map. The latter reflects the boundaries of owned parcels, not just building footprints and, as such, land use can be ascribed to the landscape.

This comparison must be based on a different approach, as the MDP maps are made up of polygons drawn around land uses of similar type. The third column of Table 2 reports the percentage of buildings (using HCP data) found within any developed-use polygon in the MDP maps, by type of land use. Almost 90% of all buildings on residential lots of ≤0.5 acre and on commercial, industrial, and institutional land (rows 1 and 2) are located within MDP “developed” land use polygons. A full 80% of low-density residential houses are similarly recorded as developed by MDP.

Table 2.

Comparison of 2000 MDP land use data with HCP and Howard County parcel boundary data

Actual land use*(density)	No. of buildings (from 2000 HCP data)	% labeled developed by MDP	Acres developed (from 2000 Howard County parcel boundary data)	% labeled developed by MDP
Nonresidential development, high-density residential	10,830	86	17,259	61
Medium-density residential(0.125- to 0.5-acre lots)	30,434	91	9,043	91
Low-density residential (0.5- to 5-acre lots)	20,701	80	28,309	69
Very low density, including farmsteads (>5 acres)	7,451	29	9,099	39
Undeveloped (85,614 acres)				11

*Roads are not an MDP category and are omitted from the analysis.

A comparison of Howard County parcel boundaries with the MDP land use polygons provides an alternative means of evaluating the latter. Almost 70% of acreage in low-density residential parcels is identified as developed by the MDP maps. Surprisingly only 61% of high-intensity acres is identified as developed by MDP, principally because several very large parcels made up almost entirely of open space are actually owned by institutions or the public sector. In terms of parcel acres, MDP errors of omission are twice as large as errors of commission. However, the errors are largely due to an inability to recognize from aerial photography the extent of parcels in a particular use, as compared with a high reliability in correctly registering the location of the structures on these large parcels.

Measuring Fragmentation.

To examine the spatial pattern of sprawl and its change over time, we identify a set of pattern metrics that capture different dimensions of land fragmentation (Table 3): (i) patch density, (ii) mean patch size, (iii) mean perimeter-to-area ratio, (iv and v) contrasting edge length between developed and undeveloped land, and (vi) mean dispersion of developed and undeveloped land within a local area.^¶ The first is a straightforward measure of fragmentation at the patch level. The next two capture the mean size and shape of patches, holding constant the total number of patches. Decreases in the mean patch size of a given (focal) land use reflect increases in the fragmentation when the total amount of the focal land use is nondecreasing. Increases in the mean perimeter-to-area ratio of a focal land use reflect either increasing complexity of patch shapes or the addition of smaller-than-average patches to the landscape. The fourth and fifth metrics measure the interspersion of a focal and contrasting land use (e.g., developed and undeveloped land) by measuring the total length of their shared border. Because the total edge increases with the total focal land use area, regardless of its pattern, the measure is normalized, first by the length of like edges of the focal land use (contrasting edge ratio) and then by the total length of contrasting and like edges (contrasting edge proportion).^‖ The final metric measures the mean proportion of a contrasting land use within a given neighborhood of a focal land use cell. To measure development dispersion, the relative number of undeveloped (contrasting) cells within a given neighborhood of each developed (focal) cell is summed, and the mean value across all developed cells is taken. We also reverse the contrasting edge and dispersion measures, defining undeveloped land as the focal and development as the contrasting land use. The entire set of pattern statistics is applied to the 1973 and 2000 MDP maps for the state of Maryland. Residential and nonresidential developed land uses are grouped into a single developed category and agricultural and forest land uses comprise the undeveloped use. In addition, the fragmentation of low- and higher-density residential land uses is measured by using a land use map in which patches belonging to each of these classes are treated as distinct.

Table 3.

Explanation of pattern measures

Land conversion in the state of Maryland subsequent to 1973 led to a substantially more complex land use pattern by 2000**(Table 4). The first three measures of pattern reveal substantial increases in fragmentation, with higher-density residential development exhibiting even more dramatic changes in mean patch size and shape complexity than low-density development. The contrasting edge measures also show dramatic increases in fragmentation, but here low-density residential changes dominate. These results reflect a key difference between the patch- and edge-based measures, as the former do not capture the relative spatial distribution of patches. The smaller changes in the contrasting edge of high-density residential land indicate that new high-density residential development often occurred contiguous to other development and thus, despite its substantially smaller patch size, conversion of land to high-density residential development did not contribute substantially to increases in fragmentation between developed and undeveloped land. Just the opposite is true of low-density residential land. The high level of contrasting edges in 1973 indicates that the then existing pattern of low-density residential development was already much less contiguous than the high-density pattern. Relatively small changes in patch size combined with the substantial increases in contrasting edges show that new low-density residential development occurred in an even less contiguous pattern than it did previously. In contrast to the patch- and edge-based measures, the dispersion statistic does not reflect dramatic changes in the development pattern and, if anything, indicates that the relative dispersion of residential land diminished somewhat over time. Although undeveloped land is much less fragmented than developed land, precipitous declines in the mean size of undeveloped land patches and large percentage increases in the relative amount of contrasting edges point to rapid changes in the pattern of agricultural and forest land. In contrast to the mean dispersion of development, the mean dispersion of undeveloped land relative to neighboring development increased markedly. Taken together, the statistics reported in Table 4 are consistent with a fixed landscape filling up with more distinct and complex patches, demonstrating increasing fragmentation.

Table 4.

Aggregate land use pattern measures

Pattern measure	Developed land use pattern									Undeveloped land use pattern
	All development			High-density residential			Low-density residential
	1973	2000	% change	1973	2000	% change	1973	2000	% change	1973	2000	% change
Patch density	0.14	0.33	132.0	0.04	0.11	157.2	0.12	0.33	172.9	0.03	0.06	86.5
Mean patch size	0.60	0.52	−14.3	0.94	0.56	−40.4	0.27	0.25	−4.3	25.74	12.24	−52.4
Mean perimeter-to-area ratio	13.23	15.02	13.5	11.31	14.46	27.8	13.68	16.10	17.7	13.78	17.27	25.4
Contrasting edge ratio*	0.51	0.81	60.5	0.13	0.16	25.8	0.53	0.86	63.1	0.03	0.09	177.8
Contrasting edge proportion*	0.22	0.35	54.9	0.06	0.08	37.2	0.21	0.35	63.6	0.03	0.06	138.8
Mean dispersion* (1 km2)	0.37	0.38	2.7	0.23	0.21	−10.1	0.57	0.53	−6.3	0.03	0.08	131.9
Mean dispersion* (25 km2)	0.52	0.50	−3.0	0.39	0.33	−15.4	0.70	0.65	−7.2	0.07	0.12	62.5

*For developed (residential) land use measures, focal land use = developed (residential), and contrasting land use = undeveloped; for the undeveloped land use measures, focal land use = undeveloped, and contrasting land use = developed. Refer to Table 3 for pattern measure definitions.

Spatial Heterogeneity.

Because we are primarily interested in the spatial distribution of fragmentation and its changes over time, we use the contrasting edge proportion metric (Table 3), which when differenced over time, quantifies both infill, defined here as new development that is contiguous to existing development (negative values), and increased fragmentation (positive values) for a given area. The statistic is calculated for each nonoverlapping 2 × 2 km window in the landscape, yielding 6,647 observations for a given point in time. This measure is regressed on distance to the nearest urban center, measured as the distance (km) along the roads network from the window centroid to the edge of the nearest city with 10,000 or more population. Because our fragmentation measure reflects the interspersion between developed and undeveloped land uses, it will reach a maximum where the mix of undeveloped and developed land is highest: the urban–rural fringe. A squared term is included to account for this nonlinear association. By using both spatial sampling and a parametric correction to account for spatial error dependence in this and all subsequent estimations, the model is estimated separately for 1973, 2000, and the change in fragmentation during this time period (n = 2,007). Fragmentation is found to vary significantly and nonlinearly with distance from urban centers. The null hypothesis of equality between the 2000 and 1973 parameter estimates is rejected by using standard t tests (Table 5).

Table 5.

Spatial error models of fragmentation and distance to urban centers

Variable	Estimate (SE)			t statistic
	2000	1973	2000 – 1973
Constant	0.21299 (0.01857)	0.1900 (0.0193)	0.0218* (0.0208)	30.9
Distance to nearest urban center	0.0064 (0.00083)	0.0028 (0.0009)	0.0037 (0.00094)	109.6
(Distance to nearest urban center)2	−0.00006 (0.00001)	−0.00003 (0.000007)	−0.00002 (0.000008)	−77.5
Spatial error correlation coefficient	0.3470 (0.0274)	0.3642 (0.0270)	0.2669 (0.0293)	—
Moran's I with residuals	−0.0126 (P = 0.208)	−0.0116 (P = 0.240)	−0.0066 (P = 0.336)	—
R2	0.154	0.139	0.078	—

Dependent variable: proportion of contrasting edges within a 2 × 2 km window; n = 2,007; W = inverse distance weighting function with 5,000-m maximum cutoff; all coefficients are significant at the 0.005 level except for ∗, which is not significant. t test of null hypothesis: β̂₂₀₀₀ − β̂₁₉₇₃ = 0.

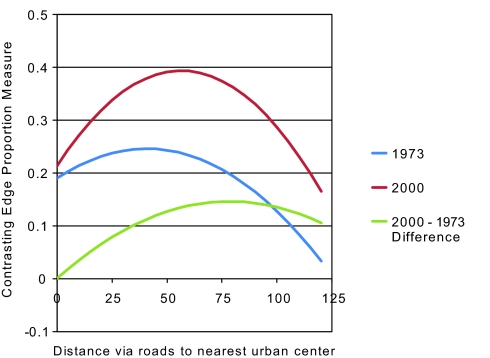
The specific shapes of the estimated gradients are plotted by using the predicted fragmentation values as functions of distance to the nearest city boundary (Fig. 1). The mean level of fragmentation is higher in 2000 than in 1973 along the entire distance gradient. The level of peak fragmentation is 60% greater in 2000 as in 1973 and shifted outward from a distance of 40 km in 1973 to 55 km in 2000. Fragmentation increased the most between 1973 and 2000 in nonurban areas located ≈80 km from the nearest city.

Fig. 1.

Predicted fragmentation gradients.

To investigate the link between fragmentation and land use, we regress the change in fragmentation on the percentage change between 1973 and 2000 in selected land use categories (n = 2,007). With the exception of nonresidential urban changes, which is not significant at the 0.05 level, the estimates (SI Table 6) are all statistically significant at the 0.001 level and demonstrate the importance of low-density residential land: A 1% increase in the amount of low-density residential land within a 2 × 2 km area is associated with an average 0.14 increase in the proportion of contrasting edges, as quantified by our fragmentation measure. In comparison, a 1% increase in high-density residential land is associated with an average 0.04 reduction in the proportion of contrasting edges.

Finally, we investigate the association of the 2000 fragmentation pattern with other spatially heterogeneous landscape features by using a multiple regression model, estimated with a spatial subsample of 2 × 2 km windows that contained any developed land as of 2000 (n = 697). In addition to distance from urban centers, two other distance variables measure proximity to potentially important features of the built and natural landscape: distance to the nearest major road (clearly an endogenous variable) and distance to the Chesapeake Bay coastline. Binary indicator variables are included to represent land with soils that are well suited for development, poorly draining soils, and slopes steeper than 15% grade. Lastly, we include the minimum lot size required for residential development as determined by zoning, a variable that is likely endogenous. The model explains 25% of the total variation in the 2000 fragmentation pattern (SI Table 7). Fragmentation is found to increase significantly with distance from the Chesapeake Bay coastline (significant at the 0.001 level) and with distance to the nearest road (although significant only at the 0.07 level). Two of the three physical land attributes, land that is well suited for development (0.01 level) and poorly draining soils (0.001 level), are found to be positively and significantly associated with fragmentation, as is minimum lot size zoning (0.001 level).

Discussion

Our investigation of sprawl, measured as the fragmentation of developed and undeveloped land use patches, suggests two critical characteristics of areas that experienced the largest gains in fragmentation: (i) they are located relatively far from urban areas and (ii) they experienced concomitant increases in their proportion of low-density residential land. The results underscore the linkages among fragmentation, low-density development, and exurban growth and the limitation of measuring sprawl with data that do not fully capture these features. Our comparison of the HCP data and the 2001 NLCD data provides strong support for what others have found at a more general level by using the 1992 NLCD data: the inability of these data to recognize low-density development, which we find to be the essential footprint of sprawl.

In examining the usefulness of various pattern measures intended to measure fragmentation, we find some distinct differences in the trends reported by the patch, edge, and dispersion measures (Table 4). Unlike the patch metrics, the edge and dispersion statistics are similar in that both consider a focal land use relative to a contrasting one. However they differ in their implicit weighting of the landscape. The dispersion statistic measures the amount of undeveloped land within a local neighborhood of each developed cell and is thus conditional on the location of development. The implication is that the mean value of this statistic is weighted toward higher-density areas that contain a greater number of developed cells. However, the edge-based measures do not weight any particular area of the landscape, as each edge length is counted only once regardless of its location. Thus, the contrasting edge measures are more likely to reflect changes in land use patterns in low-density areas, precisely the areas that are most strongly associated with fragmentation increases.

These results call into question the analysis by Burchfield et al. (22) and their conclusion that “the extent of sprawl remained roughly unchanged between 1976 and 1992.” Their analysis relies on NLCD data that are systematically biased against recording low-density development and on the mean dispersion measure, which, when applied to developed land, undercounts the pattern of low-density development. Any such assessment of sprawl is, at best, incomplete and the question remains: How has the extent of sprawl changed over time?

Our analysis (Table 5 and Fig. 1) reveals systematic variation in fragmentation with distance from urban centers and a significant upward and outward shift in the peak level of fragmentation. The nonlinear shape of the fragmentation gradient is consistent with the basic urban economic model's prediction of a negative density gradient (23–25) and the outward shift in peak fragmentation is consistent with the application of this model to a growing region. However, we find very little evidence that the evolution of sprawl conforms to the dynamic extension of this basic model (e.g., refs. 26 and 27), which predicts temporary patterns of leapfrog development that diminish over time because of development infill. Rather than outward increases in sprawl balanced by infill development, the results show large and statistically significant increases in the fragmentation gradient at every distance except those areas that are within or immediately adjacent to a city boundary. In addition, we find that the largest increases in fragmentation occurred in areas located far, ≈80 km, from urban centers. These results are consistent with the hypothesis that the diminished pull of urban centers, e.g., due to declining transportation costs (3), relocation of jobs to suburban areas (28), central city fiscal and social problems (29), and advances in communications and information technologies (30), as well as the subsequent growth in exurban areas (31–33), has led to a substantial increase in the amount and spatial extent of sprawl.

Other explanations of land use fragmentation center on physical land heterogeneity (34–36), land use externalities (14, 37–40), and government policies, including roads (41) and large-lot zoning (42, 43). Results from the multiple regression model (SI Table 7) confirm the significance of heterogeneous soil and slope characteristics and the importance of large-scale natural features. Proximity to the Chesapeake Bay is negatively associated with fragmentation. Because the Bay is located away from most of the urban areas, this suggests an attraction effect associated with the coastline that has concentrated development, a result that is consistent with other empirical evidence of large-scale natural amenities (44–46).

In examining the influence of roads and zoning, two policy variables that are clearly endogenous to the development process, we find that proximity to roads is associated with reduced fragmentation, but the estimate is not significant at the 0.05 level. However, larger minimum-lot-size zoning is associated with increases in fragmentation. We use the term “endogenous” to indicate that with these covariates in particular, we are unable to identify the direction of causality. Because roads follow development and development follows roads (47), a positive estimate is consistent with concentrated development attracting roads as well as roads spurring concentrated development. Likewise, although zoning affects the pattern and likelihood of development (48, 49), zoning changes are also responsive to the land market (50). Here we find a result that is consistent with minimum lot size increasing fragmentation, but it's unclear whether this result would hold once the endogeneity of zoning is controlled. It is possible, for example, that large-lot zoning may actually reduce fragmentation among land parcels because with larger lots each house provides its own open space amenity (51), thus reducing the “repelling” effects of neighboring development that induce fragmentation (38).

Given that Maryland is one of the most urbanized states in the United States, is it reasonable to extrapolate our results to other regions of the United States? As we have discussed, the factors that we find to be significantly related to land use fragmentation are consistent with much of the related empirical evidence on urbanization. These findings provide grounds for hypothesizing that the dynamics of sprawl and its correlates in other regions of the United States may be similar to those we document here, but ultimately this remains an empirical question.

Data and Methods

Data Description.

For a complete description of the data, see the SI Appendix.

1973 and 2000 MDP land use data.

These are vector data derived from aerial photography (52, 53). Developed categories include residential densities of 0.2–2 dwelling units per acre (low density); 2–8 dwelling units per acre (medium density); >8 dwelling units per acre (high density); and nonresidential development. Although the published minimum mapping unit for the 1973 and 2000 MDP data is 10 acres, the 2000 data were augmented by tax assessment data, which resulted in a substantial number of land use polygons <10 acres. For comparison purposes, we adjusted the minimum polygon size by dissolving all polygons <10 acres and replacing them with their majority neighboring land use. This adjustment reduces the absolute level of fragmentation recorded by the 2000 data but is necessary for comparability of the datasets.

2001 NLCD land cover data.

These are raster data derived from remotely sensed Landsat Thematic Mapper (TM) satellite imagery with a spatial resolution of 30 × 30 m² (54). Urban land is classified as developed open space (<20% impervious cover), low-intensity developed (20–49% impervious cover), medium-intensity developed (50–79% impervious cover), and high-intensity developed (≥80% impervious cover). The analysis reported in Table 1 aggregates these into one “developed” category.

2003 Howard County parcel boundary and 2003 HCP data.

The parcel boundaries (55) are geocoded versions of the county's tax maps that delineate the boundaries of all privately and publicly owned parcels. These vector maps are linked to the tax assessment database that includes an array of attribute data. Given the parcel size and use, each parcel is assigned to one of the following categories: nonresidential or high-density (more than eight dwelling units per acre) residential use, medium-density residential (two to eight dwelling units per acre), low-density residential use (fewer than two dwelling units per acre), very low density (houses on >5 acres), and undeveloped. The HCP data (56) include footprints of all structures, parking lots, and roads in the county. In both cases, the data can be linked with construction dates, allowing adjustment of the datasets to be comparable with the 2001 NLCD and 2000 MDP data. For comparison, both datasets were overlaid with the 2001 NLCD 30 × 30 m grid. A minimum of 5% impervious surface was required for a cell to be classified as “developed” according to the HCP source.

Statistical Methods.

We follow well established methods from landscape ecology (12–15) to quantify land use patterns based on patches, where a “patch” refers to a discrete and contiguous area of the same land use. The measures of contrasting edge are normalized versions of total edge contrast statistics. This normalization requires a raster representation of the landscape, so that the edges between contiguous cells belonging to the same focal land use can be summed to derive a measure of like edges. We used a 100 × 100 m grid to perform the calculations for both the contrasting edge proportion and mean local dispersion statistics. ArcInfo software (57, 58) was used to perform all landscape metric calculations. As detailed elsewhere (e.g., ref. 59), landscape metrics are subject to certain limitations, including reliance on categorical data, scale dependence, and aggregation bias. Our measure of contrasting edge is subject to these same limitations. In addition, because it is based on raster data, the length of edge is biased upward (12). However, the normalization by “like” edges offsets this bias.

Spatial error autocorrelation is found to be highly significant in all three of the regression models (Table 5 and SI Tables 6 and 7). To control for this dependence, a subsample is drawn in which the nearest neighbors of randomly drawn observations are omitted from the sample. Despite this, moderate levels of spatial error dependence persist, and thus we control for the remaining spatial error autocorrelation using a spatial error model. We also estimated spatial error models with the full sample, but the parametric correction did not fully eliminate the error correlation. The form of the spatial error dependence is assumed to follow a first-order, autoregressive process: ε = λWε + μ, where ε is a vector of spatially correlated errors, λ is a spatial error autocorrelation coefficient that is estimated, W is an N × N inverse distance weights matrix defined with a maximum cutoff of 5 km, and μ is a vector of i.i.d. errors. We consider different distance decay specifications of the elements of W and also estimate the model with different spatial subsets and find the results to be robust to both. In each case, a test of the residuals using Moran's I indicates no further spatial error dependence. GeoDa spatial analysis software (60) was used to construct spatial weights matrices, estimate the spatial error models, and perform Moran's I tests of significance.