Sensitivity and Bias Under Conditions of equal and Unequal Academic Task Difficulty

Abstract

We conducted an experimental analysis of children's relative problem-completion rates across two workstations under conditions of equal (Experiment 1) and unequal (Experiment 2) problem difficulty. Results were described using the generalized matching equation and were evaluated for degree of schedule versus stimulus control. Experiment 1 involved a symmetrical choice arrangement in which the children could earn points exchangeable for rewards contingent on correct math problem completion. Points were delivered according to signaled variable-interval schedules at each workstation. For 2 children, relative rates of problem completion appeared to have been controlled by the schedule requirements in effect and matched relative rates of reinforcement, with sensitivity values near 1 and bias values near 0. Experiment 2 involved increasing the difficulty of math problems at one of the workstations. Sensitivity values for all 3 participants were near 1, but a substantial increase in bias toward the easier math problems was observed. This bias was possibly associated with responding at the more difficult workstation coming under stimulus control rather than schedule control.

Matching theory predicts that the relative rate of responding across two alternatives should match the relative rate of reinforcement associated with those alternatives (Herrnstein, 1961, 1970). Shifts in the allocation of behavior across response alternatives away from perfect matching are regarded as biased responding (Baum, 1974). Research into biased responding suggests several reasons for these shifts, including (a) discrepancies between the number of obtained and programmed reinforcers, (b) qualitatively different schedules of reinforcement (i.e., fixed interval vs. fixed ratio; LaBounty & Reynolds, 1973), and (c) preference for a particular dimension of reinforcement associated with one response alternative (e.g., Neef & Lutz, 2001).

Not surprisingly, the role of response effort has been discussed as an explanation for biased responding across response alternatives. Previous research has suggested that children's choice in response allocation, particularly academic engagement, is often a function of the effort required to complete a task as well as competing sources of reinforcement for each alternative (e.g., Lannie & Martens, 2004; Neef & Lutz, 2001; Neef, Shade, & Miller, 1994; Weeks & Gaylord-Ross, 1981). For example, Cuvo, Lerch, Leurquin, Gaffaney, and Poppen (1998) found that when participants were asked to engage in a number of choices involving work requirements with equal schedules of reinforcement, they consistently chose the less effortful alternative. Similarly, Bradshaw, Ruddle, and Szabadi (1981) demonstrated that when participants were asked to pull levers in exchange for points, they demonstrated an increase in response rate for the less effortful alternative despite equal rates of reinforcement programmed across both levers.

One way to evaluate biased responding between concurrent alternatives is to fit the generalized matching equation to log ratios of behavior (B) and contingent reinforcement (R) across two response alternatives (Baum, 1974, 1979):

The parameter a represents sensitivity to reinforcement, or the extent to which unit changes in reinforcer ratios are accompanied by unit changes in response shifting. The parameter b represents bias toward a particular response not accounted for by the reinforcement schedules in place.

Both experimental and descriptive research has shown the generalized matching equation to provide a good description of children's choice behavior (e.g., Borrero & Vollmer, 2002; Mace, Neef, Shade, & Mauro, 1994; Martens, Halperin, Rummel, & Kilpatrick, 1990; Martens & Houk, 1989; Shriver & Kramer, 1997). For example, Mace et al. arranged concurrent variable-interval (VI) schedules of reinforcement contingent on math problem completion for 3 adolescents with learning and behavior problems. The percentage of time allocated to problems on the richer schedule was related to the percentage of reinforcers obtained on that schedule for each participant using the generalized matching equation. A linear function provided a good fit to the data, accounting for 56% to 98% of the variance in relative time allocation. Despite the use of modeling, changeover delays, signaled reinforcement, and equivalent sets of math problems, significant undermatching (mean slope  =  .19) and biased responding (mean intercept  =  .65) was observed for each participant.

Although apparently robust as a description of behavior–environment relations, no applied studies have systematically investigated the effects of task difficulty on responding in applied situations through use of the generalized matching equation's bias parameter. Given that children typically are expected to complete assigned work of varying difficulty during different instructional activities, it is important to understand how task difficulty interacts with competing sources of reinforcement to affect response allocation across concurrent alternatives. Thus, the purpose of the present study was twofold. First, we evaluated the sensitivity and bias parameters of the generalized matching equation with typically developing, elementary-aged students using procedures similar to those of Mace et al. (1994, Experiment 1). This analysis was conducted to establish a baseline description of the distribution of behavior across a two-alternative choice arrangement of math problems in which response effort was constant across alternatives. In Experiment 2, we manipulated response effort for one alternative using the same participants and methods as Experiment 1. The goal of this manipulation was to evaluate the effects of response effort on the relative rate of math problem completion through the bias parameter of the generalized matching equation.

Method

Participants and Setting

Children from three third-grade regular public education classrooms were recruited to participate in Experiments 1 and 2. Criteria for participation in the study included (a) the absence of any formally diagnosed disability, no prescribed medications, and no teacher-reported behavior problems or identified problems with off-task behavior; and (b) demonstration that problem-completion rates were sensitive to a simple reinforcement contingency as measured by a brief experimental analysis (described below). Three children met criteria for the study and participated in both experiments: Gina, a girl aged 8 years 9 months, and Andy and Nate, boys aged 9 years 2 months. In addition, all children were behind grade level for fluency in math, based on curriculum-based assessment (Shapiro, 1996) screening probes, and principal report.

Each 4-min session was conducted in an empty conference room located in the participants' school building. Two workstations, comprised of two tables, were used as response alternatives along with reinforcers in the form of tokens. One workstation was termed the blue workstation, and the other was termed the orange workstation. Each participant was seated at a swivel stool between the two workstations, which were placed approximately 1 m apart. Sessions were conducted individually for a minimum of eight times per week for approximately 2 weeks for both Experiments 1 and 2, with a 5-day break following completion of Experiment 1.

Preliminary Assessments

Curriculum-based assessment probes (Shapiro, 1996) were administered to assess each participant's fluency (i.e., digits correct per minute) in grade-level math computation skills. During these probes, a series of worksheets was administered, each assessing a different mathematics skill (e.g., 1-digit by 1-digit addition, sums to 9) for 2 min. Following the initial baseline assessment, a brief experimental analysis (Daly, Martens, Hamler, Dool, & Eckert, 1999) was conducted to identify those children whose math fluency was likely to increase with reinforcement. This analysis consisted of one administration of a “beat your score” contingency in which participants were given the opportunity to beat their initial baseline math fluency score. If the participant beat his or her score (even if by only one problem correct in a minute), the participant was allowed to choose one reinforcer from the project store (described below). The brief analysis was used to assess the sensitivity-to-reinforcement criterion for inclusion in the study.

Based on the results of the initial baseline assessment, both easy and difficult math problems were identified for use in the study. Easy problems consisted of those identified as instructional (10 to 19 digits correct per minute) from the initial probes described above screenings in accordance with the guidelines described by Shapiro (1996). Difficult problems consisted of those identified as frustrational (0 to 9 digits correct per min) from the initial probes. For all participants, 2-digit by 2-digit addition sums to 18 were identified as easy math problems. For both Gina and Nate, difficult math problems consisted of 3-digit by 3-digit subtraction with no regrouping. For Andy, difficult math problems consisted of 3-digit by 3-digit subtraction with regrouping in the tens column. Experiment 1 featured easy problems at both workstations, and Experiment 2 featured easy problems at the blue workstation and difficult problems at the orange workstation. With the exception of the effort manipulation, the procedures for Experiment 2 were identical to those of Experiment 1.

Materials and Procedure

Math Problems

Two stacks of math problems were placed on the table at each workstation and within reach of the participant. Each stack contained 100 unlined note cards (7.6 cm by 12.7 cm) with one math problem arranged vertically and centered in the upper half portion of the card. The math cards in the two stacks for each participant were identical (i.e., same vertical arrangement, range of digits, and operation); however, in both Experiments 1 and 2, the math problems were sorted randomly to prevent the possibility that participants could identify sequences in the problem presentation. That is, both stacks of problems were unique in the order in which problems were presented. Located between the stacks of cards on each of the two desks were sharpened pencils.

Reinforcers and Tokens

All 3 participants were administered a group-based paired-choice pictorial assessment (adapted from Berkowitz & Martens, 2001) to identify both moderately and highly preferred items for inclusion in the project store. Specifically, eight picture cards of various stimuli were created for the preference assessment. All possible pairs of picture cards (N  =  28) were presented to the group of 3 participants who were told to choose by pointing to the item each child preferred. For each item pairing, the item receiving the most choices (i.e., at least 2 children pointing to the item picture) was identified as the preferred item. Preferred items were ranked in terms of most to least chosen. The top three items were identified as highly preferred, with the median three of the remaining five items identified as moderately preferred. These moderately and highly preferred items were pooled to constitute the project store (i.e., the back-up reinforcers in which obtained tokens may be exchanged for later in the study). Pens, pencils, and Skittles were identified as the most preferred items, with M&Ms, stickers, and erasers identified as the moderately preferred items. During experimental sessions, the highly preferred items had a token exchange rate of eight tokens per item, and the items identified as moderately preferred had an exchange rate of four tokens. Tokens were delivered by placing a bead on an upright wooden dowel according to concurrent VI VI schedules. Both the token and dowel were color-coordinated with the workstation (blue or orange).

Concurrent Reinforcement Schedules

Participants were allowed to choose which stack of math problems to complete and to switch between workstations at any time. Three paired VI schedules were prepared as follows: VI 100 s VI 20 s, VI 60 s VI 60 s, and VI 20 s VI 100 s, with the first value in each pair representing the schedule value for the blue workstation and the second value representing the schedule value for the orange workstation. At the end of each session, participants were given the opportunity to redeem any tokens earned for their choice of items from the project store.

Each workstation was equipped with a compact disc (CD) player programmed to signal the availability of reinforcement for completing problems at that workstation. The sound of a cash register opening was recorded on the orange workstation CD according to a random number generator based on each of the three VI schedules (4 min for each schedule). The sound of clapping was recorded on the blue workstation CD. The sounds at the two workstations were offset by a minimum of 5 s to allow participants time to switch workstations and complete a problem. Auditory signals were used to help students discriminate reinforcer availability at each workstation and to bring responding under schedule control.

Instructions and Pretraining

Prior to each session, the experimenter read the directions explaining that each participant would have an opportunity to earn tokens by completing math cards at each workstation, as well as the maximum number of tokens possible at each alternative. Immediately following the directions and prior to the first session, the experimenter demonstrated the procedures for 1 min. For Gina, an additional coaching session was conducted between Sessions 9 and 10 due to increasing variability in responding across the initial nine sessions. During the coaching session, Gina was told by the experimenter that she could switch between the workstations whenever a tone sounded (these data were not included in any analyses and are not reported in the Results).

Procedural Fidelity and Interscorer Agreement

An additional observer collected data on procedural fidelity (occurrence and nonoccurrence of each step of the experimental protocol) and interscorer agreement during 94% of sessions. Agreement was assessed by having two observers independently score each problem and count the total number of reinforcers delivered upon the completion of each experimental session. In addition, agreement as to whether the stability criteria were met in the time-series figure (see below) was assessed based on independent judgments (both occurrence and nonoccurrence) by the researchers. This was done by having two researchers review the time-series plots after the primary researcher graphed each session's data and then independently check a box on a data sheet if stability criteria had or had not been met. Procedural fidelity and interscorer agreement were determined by calculating the number of instances of agreements, dividing by the number of instances of agreements plus instances of disagreements, and multiplying by 100%. For all participants, agreement was 100% and procedural fidelity was 99% (range, 96% to 100%).

Data Analysis

Stability Criteria

Data collection began under the VI 100-s VI 20-s schedule, and participants remained exposed to this schedule until responding met stability criteria of three consecutive data points that favored responding toward the richer schedule (e.g., above 50% of problems completed at the blue workstation when the blue workstation had the richer reinforcement; Mace et al., 1994), with all three data points having a range of 10% or less. When the schedules were equal, the required range was still 10% or less for variability, but all three data points had to fall above the range of the three stable data points for the leaner (blue) alternative from the previous condition. These stability criteria were applied to all phases of the study for both experiments.

Fitting the Generalized Matching Equation

To fit the generalized matching equation to the data, the number of reinforcers obtained from the blue workstation was divided by the number of reinforcers obtained from the orange workstation. In addition, a blue response ratio was calculated by taking the number of digits correct at the blue workstation divided by the number of digits correct at the orange workstation. We chose digits correct rather than digits attempted as the primary dependent variable for two reasons. First, digits correct involves a combination of accuracy and fluency and has been shown in previous research to be a meaningful (i.e., sensitive and valid) measure of academic performance (e.g., Shapiro, 1996). Second, through the preliminary assessments, we were able to identify instructional level math problems that students were able to complete with high accuracy but low fluency. Similar to other concurrent-operants research with humans, only terminal data (final three data points in each phase that met the stability criteria) were used in fitting the generalized matching equation in an effort to ensure analysis of steady-state responding (e.g., Baron & Perone, 1998; Critchfield, Paletz, MacAleese, & Newland, 2003; Johnston & Pennypacker, 1993).

Discrimination Indexes

To assess if participants' responding was under stimulus control of the reinforcement signals at each workstation, discrimination indexes (Pierce & Epling, 1999) were computed. Because auditory tones signaled when the next problem completed would be reinforced for either schedule, respective discrimination indexes were calculated by dividing the number of reinforced problem completions at a given workstation by the total number of problems completed at that workstation during each session.

Results

Experiment 1

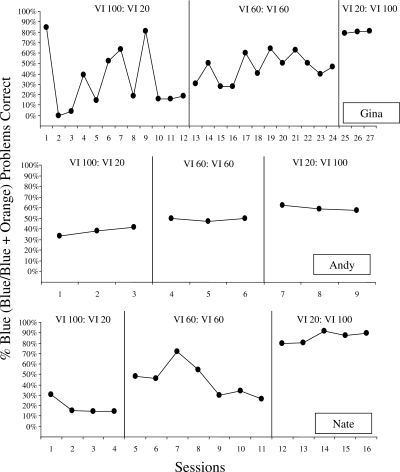
Figure 1 depicts the percentage of behavior allocated toward the blue workstation during each experimental session of Experiment 1 for each participant. The percentage of behavior allocated toward the blue alternative was calculated by dividing the number of correctly completed math problems at the blue workstation by the total number of correct problems completed during the session (orange plus blue). Recall that for each schedule requirement, the first VI schedule value refers to the schedule in place for the blue alternative and the second VI schedule value refers to the schedule in place for the orange alternative. Gina and Nate completed a higher percentage of problems correctly at the blue workstation during each 4-min session as the relative rate of reinforcement for completing these problems increased. The mean percentage of behavioral allocation towards the blue alternative for Gina was 34% (range, 0% to 85%) under the VI 100-s VI 20-s schedule, 46% (range, 28% to 64%) under the VI 60-s VI 60-s schedule, and 80% (range, 79% to 81%) under the VI 20-s VI 100-s schedule. Nate's mean percentages of behavioral allocation towards the blue alternative followed a similar trend, with values of 19% (range, 14% to 31%), 45% (range, 27% to 72%), and 86% (range, 80% to 92%), respectively. During the initial VI 100-s VI 20-s condition, Gina demonstrated a high degree of variability in her performance. Gina verbally reported to the experimenters that she could not distinguish the tones on the CD player. Thus, a coaching session between Sessions 9 and 10 was conducted in an effort to associate the tones with the workstations and thereby reduce the variability in her responding.

Figure 1.

Time-series data of the percentage of behavior allocated toward the blue alternative for each participant in Experiment 1. For each phase, the first schedule value represents the blue workstation. Phase changes were applied after three data points met the stability criteria and are denoted as solid vertical lines.

In contrast to the results obtained for Gina and Nate, Andy (Figure 1) allocated approximately 50% of his responses to problems at the blue workstation regardless of the schedules in effect. Mean percentage values were 38% (range, 33% to 42%), 49% (range, 47% to 50%), and 60% (range, 57% to 62%), respectively. Anecdotally, Andy was observed to switch workstations after completing each problem, a strategy that he adopted for unknown reasons. This response pattern may explain the relatively limited differentiation of responding across phases.

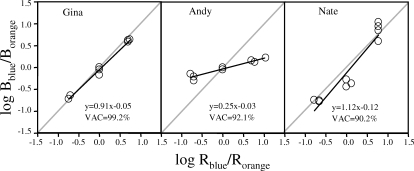
Figure 2 illustrates each participant's adherence to matching theory by fitting the generalized matching equation to the final three data points of each condition (Baum, 1974). The log ratio of correct problem completion (blue or orange, y axis) was plotted against the log ratio of tokens earned (blue or orange, x axis), with each terminal data point depicted as an open circle in a scatter plot. The parameters of the regression line are presented along with the variance accounted for by the generalized matching equation in the lower right corner of each panel.

Figure 2.

Results of fitting the generalized matching equation to participant data from Experiment 1. Each data point represents one session after meeting the stability criteria. Gray diagonal lines indicate strict matching.

Both Gina's and Nate's performances approximated strict matching, with sensitivity-to-reinforcement parameters of 0.91 and 1.12, respectively. Moreover, Gina and Nate demonstrated little or no bias to either alternative, with bias parameters of −.05 and −.12, respectively. These data suggest that there were no systematic preferences toward either alternative not accounted for by the programmed schedules of reinforcement. Finally, the generalized matching equation accounted for a high proportion of the variance in responding for Gina and Nate (99% and 90%, respectively). Andy's responding yielded a low sensitivity-to-reinforcement parameter of 0.25, which suggested indifference to the schedules. These data suggested that Andy's relative problem completion rates were not under schedule control, consistent with his undifferentiated pattern of responding (Figure 1).

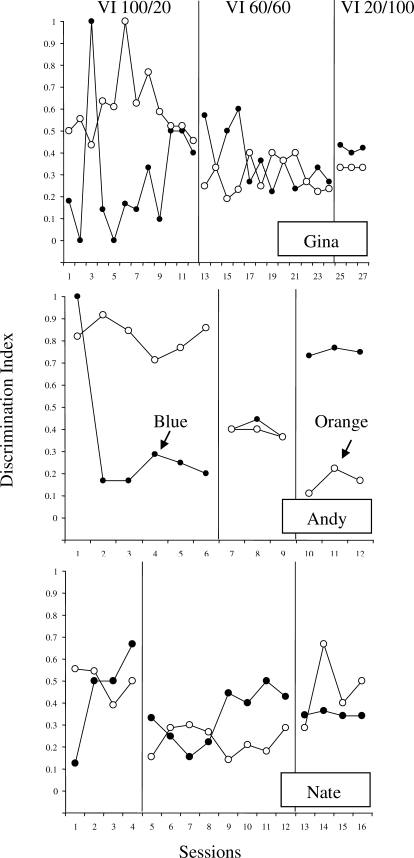
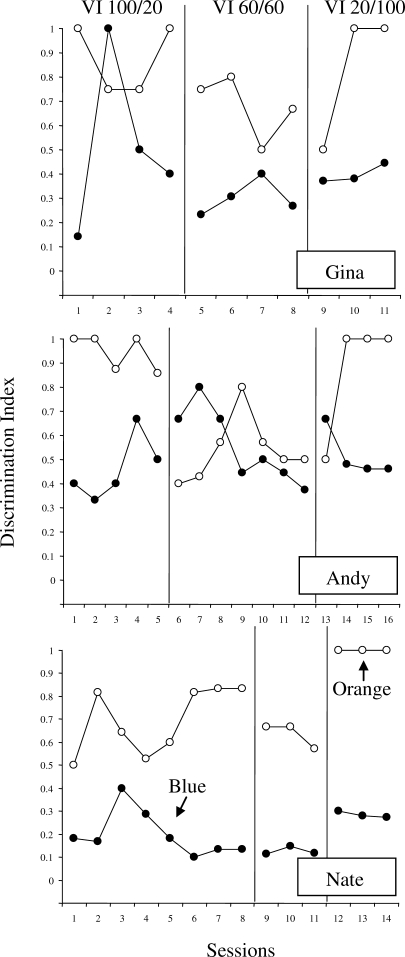
Figure 3 shows discrimination indexes of responding to each workstation by each participant across all sessions in Experiment 1. If the participants' responding was under stimulus control (via the auditory signals), increasing discrimination index values that approached 1.0 across sessions in each phase would be likely, suggesting that the participants essentially sit and wait for the reinforcement signal before working a problem. Gina and Nate revealed relatively low discrimination index values under all conditions, with the exception of Sessions 7 and 9 for Gina. Thus, relative problem-completion rates by these 2 students appeared to be under schedule control rather than stimulus control. By contrast, Andy's discrimination index values reflected indifference at the concurrent VI 60-s VI 60-s values; however, when completion of either problem set was reinforced on the VI 20-s schedule, Andy's responding shifted accordingly. Given Andy's strategy of switching after each problem and his relative-problem completion rates approximating 50% under all conditions (see Figure 1), it is possible that his high discrimination index values under the rich VI 20-s schedules resulted from a higher number of contiguous behavior–reinforcer pairings as a function of his switching strategy. That is, the pattern of switching workstations after each problem completion in combination with a rich reinforcement schedule likely produced a higher proportion of reinforced problems by chance.

Figure 3.

Discrimination indexes for each participant in Experiment 1. Indexes near 1.0 suggest high degrees of stimulus control, and indexes near .5 or below suggest indifference. The blue workstation was associated with the leaner schedule (VI 100 s; filled circles) in the first phase and the denser schedule (VI 20 s) in the last phase.

Experiment 2

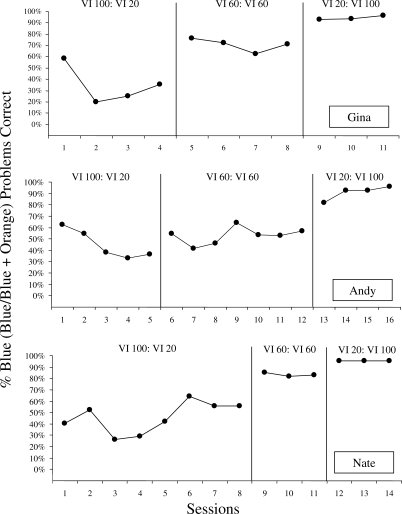
Experiment 2 consisted of a response-effort manipulation in which easy math problems were presented at the blue workstation and difficult math problems were presented at the orange workstation. Figure 4 depicts the percentage of behavior allocated toward the blue alternative during each experimental session in Experiment 2 for Gina, Andy, and Nate. All participants demonstrated fairly immediate and clear increases in responding toward the easier blue alternative in accordance with the concurrent-operants design. Specifically, Gina had mean percentages of allocation towards the blue problems of 35% (range, 20% to 58%), 71% (range, 62% to 76%), and 94% (range, 93% to 96%) across the VI 100-s VI 20-s, VI 60-s VI 60-s, and VI 20-s VI 100-s schedules, respectively. Andy and Nate responded with similar patterns of allocation towards the blue workstation, with mean percentages of blue problems correct of 45% (range, 33% to 62%), 53% (range, 42% to 64%), and 91% (range, 82% to 96%) for Andy; and 46% (range, 26% to 64%), 83% (range, 83% to 85%), and 95.5% (range, 95.2% to 95.7%) for Nate, respectively, across the three schedule pairings.

Figure 4.

Time-series data of the percentage of behavior allocated toward the blue alternative for each participant in Experiment 2. For each phase, the first schedule value represents the blue workstation. Phase changes were applied after three data points met the stability criteria and are denoted as solid vertical lines.

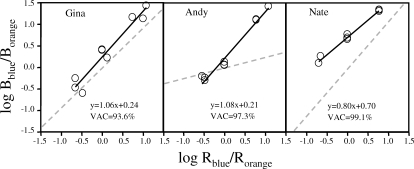
The matching plots of Gina, Andy, and Nate are presented in Figure 5. Least squares linear regression lines are presented in each panel as black lines, indicating the degree to which each participant matched behavior to scheduled reinforcement rates as predicted by the generalized matching equation. In addition to the regression lines, a dotted gray line representing the regression line of Experiment 1 is included in each plot to allow within-subject comparisons of matching parameters across Experiments 1 and 2. For Gina, a slight increase in sensitivity to reinforcement was observed from Experiment 1 (0.91) to Experiment 2 (1.06). Andy's sensitivity to reinforcement increased greatly from Experiment 1 (0.25) to Experiment 2 (1.08), shifting to near-perfect matching. A slight decrease in sensitivity to reinforcement was observed for Nate, decreasing from 1.12 in Experiment 1 to 0.80 in Experiment 2. However, Nate's sensitivity-to-reinforcement parameter of 0.80 was still in the typical range for human participants (Kollins, Newland, & Critchfield, 1997).

Figure 5.

Results of fitting the generalized matching equation to participant data from Experiment 2. The regression lines from Experiment 1 are included as gray dotted lines to allow within-subject comparisons between Experiments 1 and 2.

More important, all 3 participants' matching analyses suggested a positive shift in bias towards responding at the easier blue workstation as a function of the effort manipulation. The bias parameters for Gina, Nate, and Andy were .24, .21, and .70, respectively (see Figure 5). Compared to the near-zero bias parameters of Experiment 1, this suggests a reallocation of responding away from perfect matching and towards the less effortful alternative.

Figure 6 shows the discrimination indexes for the easy math problems at the blue workstation and the difficult math problems at the orange workstation for each participant. The discrimination indexes were relatively high for the difficult problems for all 3 participants except under the VI 60-s VI 60-s schedule for Andy. Conversely, discrimination index values for the easier problems at the blue workstation were generally low under all conditions, suggesting that behavior at this alternative was schedule controlled, as in Experiment 1. Thus, the results of Experiment 2 suggested that all 3 participants' relative problem-completion rates showed near-unit sensitivity to increases in relative reinforcement rates across workstations. The manipulation to problem difficulty, however, produced a positive bias for completing problems at the easier blue workstation that was not accounted for by the reinforcement schedules. This bias was associated with responding that may have been influenced by the schedule-correlated discriminative stimuli at the more difficult orange workstation, in that participants completed problems at this workstation only when reinforcement was signaled.

Figure 6.

Discrimination indexes for each participant in Experiment 2. Indexes near 1.0 suggest high degrees of stimulus control, and indexes near .5 or below suggest indifference. The blue workstation was associated with the leaner schedule (VI 100 s; filled circles) in the first phase and the denser schedule (VI 20 s) in the last phase.

Discussion

Experiments 1 and 2 investigated the degree to which children's academic behavior conformed to the generalized matching equation. In addition, Experiment 2 investigated the role of response effort in influencing the bias parameter of the generalized matching equation. In Experiment 1, relative rates of correct problem completion closely approximated the relative rates of reinforcement across workstations for 2 participants (Gina and Nate), whereas the 3rd participant (Andy) showed little sensitivity to relative reinforcement rates. In addition, in Experiment 1 all 3 participants displayed high variance-accounted-for estimates and little to no evidence of stimulus control, suggesting that the generalized matching equation provided an accurate description of the data. These data support a small body of research on the applicability of matching theory to academic performance (Mace, McCurdy, & Quigley, 1990; Mace et al., 1994; Neef et al., 1994).

In Experiment 2, response effort was manipulated by increasing the difficulty of math problems at the orange workstation. This manipulation increased the bias parameter of the generalized matching equation (in the direction of the easy blue workstation) for all 3 participants relative to Experiment 1, although the obtained discrimination indexes suggested that responding at the more difficult orange workstation was under stimulus control of the reinforcement signal as opposed to the programmed schedule and effort manipulations. These results lend further evidence that response effort contributes to deviations from matching in applied settings (Baum, 1979; Kollins et al., 1997; Neef et al., 1994). In addition, these results suggest that increases in response effort may lead to discriminated responding at the more effortful alternative. Interestingly, the participants appeared to complete difficult problems only when reinforcement for that response was signaled.

A comparison of responses allocated to the blue workstation between Experiments 1 and 2 (Table 1) revealed a definitive shift during the effort manipulation for each of the 3 participants. Specifically, across participants the mean increase in responding to the blue workstation from the schedule conditions in Experiment 1 to Experiment 2 was 17.5% (SD  =  13.4). This increase constitutes a significant difference in allocation between the two experiments, t(8)  =  3.92, p  =  .004 (one tailed). In light of the increase in the bias parameter of the generalized matching equation and the discrimination indexes, these data provide further evidence that the effort manipulation successfully biased responding toward the less effortful alternative in accordance with previous behavioral accounts of effort manipulations (Bradshaw et al., 1981; Cuvo et al., 1998; Lannie & Martens, 2004; Neef & Lutz, 2001; Neef et al., 1994; Weeks & Gaylord-Ross, 1981).

Table 1.

Comparison of Responses Allocated to the Blue Alternative across Experimental Conditions

	% blue problems (Experiment 1)			% blue problems (Experiment 2)
	VI 100 s VI 20 s	VI 60 s VI 60 s	VI 20 s VI 100 s	VI 100 s VI 20 s	VI 60 s VI 60 s	VI 20 s VI 100 s
Gina	34	46	80	35	701	94
Andy	38	49	60	45	53	91
Nate	19	45	86	46	83	95

Matching theory assumes that alternative sources of reinforcement are highly discriminable (Davison & McCarthy, 1988). Although auditory cues were used to enhance discrimination in the present study, reinforcer delivery alone also can acquire discriminative properties (Ferster & Skinner, 1957). The role of discriminated responding in the bias parameter of the generalized matching equation might be clarified in future research by examining within-session distributions of responding under conditions of unequal effort.

Approaching academic performance and related behaviors with an understanding of the influence of task effort on responding may prove to be beneficial for instructional design as well as for behavioral programming. For example, when students are assigned work to complete, they are placed in a choice situation that is partly under the control of task difficulty as well as the reinforcement contingencies associated with each alternative (e.g., Lannie & Martens, 2004). Previous research has shown that children choose not to complete difficult tasks when given less effortful alternatives (e.g., Berkowitz & Martens, 2001; Neef & Lutz, 2001). Conversely, assigning work that is appropriate to students' ability level in terms of difficulty can promote high levels of task engagement (Daly, Martens, Kilmer, & Massie, 1996; Gickling & Armstrong, 1978).

The current study provides further evidence that instructionally matched assignments (e.g., Experiment 1) may result in higher rates of work completion and possibly foster greater motivation for academic success (Martens & Witt, 2004). On the contrary, when students are provided with instructionally mismatched work (e.g., Experiment 2), they may be more likely to find the academic environment aversive, possibly leading to increased frustration and avoidance of the assigned task (Martens & Witt). Matching theory predicts that if instructionally mismatched work is aversive, more behavior will be allocated toward less effortful alternatives (e.g., engaging in off-task behavior). Thus, the current findings extend research in the application of matching theory to the understanding of academic behavior. In particular, these results suggest that the presentation of difficult academic tasks (i.e., those at a student's frustration level) may bias responding toward other available options and that such biases may not be easily overcome with reinforcement. Moreover, the current results suggest that the generalized matching equation can be used to detect biases in responding related to task difficulty.

Several limitations mitigate the generality of the present findings. First, students were provided with explicit discriminative stimuli such as color-coded workstations and information on the maximum number of reinforcers available. Moreover, students were provided specific, workstation-correlated tones to signal reinforcer availability at each alternative. Because reinforcement delivery at each workstation was signaled, it is possible that the combination of schedules and signals functioned as a multiple VI extinction schedule at each station. Specifically, the first problem completed correctly following the signal was reinforced at each workstation on a VI schedule, whereas all other problems completed between signals at each workstation were on extinction (i.e., the absence of a signal during the session served as an S^Δ). By conceptualizing our experimental arrangement in this way, we were able to calculate discrimination indexes as a means of evaluating the possibility of stimulus control versus schedule control over responding. These analyses revealed, however, that children continued to complete problems at each workstation between reinforcer signals (with the possible exception of the difficult workstation in Experiment 2), a pattern that is consistent with responding under typical VI schedules. These techniques are not readily applicable to classroom instruction, and as noted above, likely increased the discriminability of reinforcer sources.

Second, given the increased difficulty of the math problems in Experiment 2, biased responding may have resulted from students learning to avoid the difficult workstation rather than from nonreinforced problem completion due to incorrect responding. The calculation of discrimination indexes confirmed that participants did indeed learn to avoid the more effortful alternative except when the availability of reinforcement was signaled. Little research exists concerning the role of avoidance in choice behavior (Bradshaw, Szabadi, & Bevan, 1979; Critchfield et al., 2003), which limits one's ability to analyze response distribution in the context of aversive conditions (e.g., high effort, punishment). In studies such as this, in which response effort is manipulated within a choice arrangement, a model of matching that incorporates punishment may better account for the variance in the observed distribution of behavior.

Third, although we used a concurrent-operants design to demonstrate experimental control over relative response rates, there was no within-subject replication of effects due to the effort manipulation. That is, the effects of increased problem difficulty on the bias parameter of the generalized matching equation were compared across experiments. Similarly, the schedule comparisons progressed in an identical manner for all participants (i.e., VI 100 s VI 20 s, VI 60 s VI 60 s, VI 20 s VI 100 s). The effects of this history as a threat to the internal validity of the obtained results cannot be ruled out in the current investigation. Future research should evaluate different schedule progressions either within or across participants.

Fourth, the present study employed the relative rate of correct math problem completion as the dependent variable in all analyses. Although the problems were designed to be at students' instructional level (i.e., completed with high accuracy but low fluency), the more difficult math problems in Experiment 2 required more time and effort to complete. As a result, using the number of correct math problems may have underestimated each participant's ability to match responding to reinforcement. For example, a participant may have allocated responding toward one alternative for a relative amount of time that matched the relative rate of reinforcement but did not complete any math problems correctly, rendering the assumption that no behavior towards that alternative was emitted. Thus, using time spent at each alternative as a response output may have provided a more accurate description of behavior compared to either digits correct or digits attempted. Direct analyses of these different response types as the target behavior in matching analyses may prove to be beneficial in future investigations.

Future research into the use of the generalized matching equation to evaluate academic performance should perhaps investigate time allocation in addition to discrete task completion to allow a more precise description of choice (see Baum & Rachlin, 1969). In addition, basic research using the generalized matching equation with human participants should consider the generality of its methods and interpretations to applied settings. Specifically, more research into the influence of punishment and aversive control should be investigated in basic laboratory settings to better equip applied researchers with equations to describe the effects of punishment on choice in natural settings. Finally, basic research on choice should address the roles in which instructions (i.e., rules), feedback, and discriminative stimuli contribute to deviations in matching, in both within-subject and between-subjects designs. Such information would provide researchers and practitioners alike with valuable information about the factors that contribute to behavior change and sensitivity to reward.