Contingency Space Analysis: An Alternative Method for Identifying Contingent Relations from Observational Data

Abstract

Descriptive assessment methods have been used in applied settings to identify consequences for problem behavior, thereby aiding in the design of effective treatment programs. Consensus has not been reached, however, regarding the types of data or analytic strategies that are most useful for describing behavior–consequence relations. One promising approach involves the analysis of conditional probabilities from sequential recordings of behavior and events that follow its occurrence. In this paper we review several strategies for identifying contingent relations from conditional probabilities, and propose an alternative strategy known as a contingency space analysis (CSA). Step-by-step procedures for conducting and interpreting a CSA using sample data are presented, followed by discussion of the potential use of a CSA for conducting descriptive assessments, informing intervention design, and evaluating changes in reinforcement contingencies following treatment.

Functional behavior assessment refers to a set of procedures for describing antecedent–behavior–consequence relations in the natural environment, the goal of which is to generate hypotheses about potential maintaining variables (e.g., Mace & Lalli, 1991; Repp & Karsh, 1994; Witt, Daly, & Noell, 2000). By identifying the potential functions of problem behavior from a descriptive assessment, interventions can be developed to eliminate, reverse, or weaken the reinforcement contingencies believed to support its occurrence (Martens, Witt, Daly, & Vollmer, 1999).

In practice, strategies for collecting descriptive data about behavior and events surrounding its occurrence have included both indirect and direct assessment methods. Informant reports via interviews (e.g., Bergan & Kratochwill, 1990) or questionnaires (Durand & Crimmins, 1988) represent indirect methods, whereas scatterplot analyses (Touchette, MacDonald, & Langer, 1985), narrative A-B-C recordings (Bijou, Peterson, & Ault, 1968), and sequential recordings of behavior and its consequences constitute direct methods (e.g., Lerman & Iwata, 1993). Because indirect methods rely on retrospective accounts of behavior, the resulting data are limited by the informant's previous opportunities to observe behavior, memory, and potential biases. Direct methods involve observations of actual behavior at the time and place of its natural occurrence (Cone, 1977). Although time consuming, direct observations can provide more accurate descriptions of behavior and events surrounding its occurrence and, therefore, are the sine qua non of descriptive assessment.

Observing behavior and its consequences in the natural environment may be useful in designing interventions for several reasons. First, one may observe consequences for behavior that are idiosyncratic to the individual or setting, or that are delivered on schedules difficult to evaluate in standard functional analysis test conditions (Anderson & Long, 2002). Second, descriptive assessments do not require experimental manipulations that may be perceived by typically developing individuals or those with mild disabilities as artificial or contrived, thereby compromising the validity of such analyses. Third, observational methods are extremely flexible in application and can be tailored to address a wide range of target behaviors and social consequences in a variety of settings.

We begin by discussing different types of behavior–consequence relations and review various analytic strategies that have been used to identify events contingent on behavior from observational data. We then describe an alternative strategy known as a contingency space analysis (CSA; Gibbon, Berryman, & Thompson, 1974; Matthews, Shimoff, & Catania, 1987; Schwartz, 1989), and illustrate how to conduct and interpret a CSA using sample observational data. We conclude by discussing the potential use of a CSA for conducting descriptive assessments, informing intervention design, and evaluating changes in reinforcement contingencies following treatment.

Types of Behavior–consequence Relations

Vollmer, Borrero, Wright, Van Camp, and Lalli (2001) distinguished among three classes of consequences, those that are contiguous with behavior, those that are contingent on behavior, and those that are dependent on behavior. Dependent consequences follow some or all instances of behavior but never occur in its absence, thereby exhibiting a perfect contingency. Dependent consequences are the goal when arranging functional analysis test conditions or implementing reinforcement-based programs with high levels of integrity. Contingent consequences occur more often following behavior than in its absence (i.e., show a positive contingency), whereas contiguous consequences simply follow behavior sometimes. If contiguous consequences are also no more likely to occur in the absence of behavior, then they occur independent of behavior (i.e., show neither a positive or negative contingency). Vollmer et al. suggested that these distinctions may be useful when conducting descriptive assessments in that consequences may be contingent on behavior to varying degrees yet still produce reinforcement effects.

Determining degree of contingency from behavior–consequence data requires the evaluation of four possible sequences: (a) Behavior occurred and was followed by a consequence, (b) behavior occurred and was not followed by a consequence, (c) behavior did not occur but the consequence was still delivered, and (d) neither behavior nor the consequence occurred (Schachtman & Reed, 1998). Consideration of (a) alone reveals contiguity, with nonzero values indicating that the consequence at least sometimes followed behavior. Consideration of (a) and (b) together provides an indication of schedule or the proportion of behavior occurrences that were followed by a consequence (Gibbon et al., 1974). In essence, this value corrects contiguity for the base rate of behavior. Thus, if a consequence was observed to follow behavior five times (contiguity value) but behavior occurred 10 times, then the conditional probability of the consequence occurring given behavior would be .50 (schedule value). Note that these same interpretations can be applied to sequences (c) and (d) to indicate the conditional probability of a consequence occurring in the absence of behavior. Finally, the two conditional probability values can be considered simultaneously to define degree of contingency from an operant perspective. Specifically, an operant contingency is defined as the difference between the conditional probability of reinforcement given behavior and the conditional probability of reinforcement given the absence of behavior (Hammond, 1980; Schwartz, 1989). Within this framework, positive values indicate a consequence that is contingent on the target behavior, and negative values indicate a consequence that is contingent on absence of the target behavior. Although our focus here is on an operant definition of contingency, it should be noted that several statistical indexes of association can be computed from 2 × 2 tables containing these same four cells (e.g., Bakeman, McArthur, & Quera, 1996; Symons, Hoch, Dahl, & McComas, 2003).

It is axiomatic in behavior analysis that a positive contingency is necessary for reinforcement effects to occur (Schwartz, 1989; Vollmer et al., 2001). Typically, positive contingencies are arranged experimentally, but these also may arise accidentally when events are delivered independent of behavior. Depending on the conditional probabilities of such events actually following behavior or its absence, a positive contingency may develop followed by a reinforcement effect. For example, Vollmer, Ringdahl, Roane, and Marcus (1997) provided access to tangible reinforcers independent of behavior in an attempt to reduce aggression in a girl with mental retardation. When the fixed-time (FT) schedule was thinned to FT 1 min, aggression actually increased (i.e., a reinforcement effect occurred). Cumulative records of within-session responding revealed increased rates of responding just prior to reinforcement delivery, resulting in a positive contingency value and an adventitious reinforcement effect.

How much of a positive contingency is required to produce a reinforcement effect? Hammond (1980) addressed this issue in a basic operant study in which water reinforcements were delivered with varying degrees of contingency for lever pressing. Animals were exposed first to conditions in which the probability of reinforcement given a lever press was very high (1.0), high (.20), or moderate (.05) and the probability of reinforcement given the absence of a lever press was 0. Thus, a moderate to high positive contingency existed in all conditions. This situation also might be labeled as a dependency, because the probability of reinforcement given the absence of behavior was always 0. Next, using an ABAB design, the animals were shifted from the .05, 0 condition (i.e., a moderate positive contingency or dependency) to a .05, .05 condition (i.e., independence or a zero contingency). Reinforcement effects were observed with positive contingency values as low as .05 but not during the zero contingency condition.

Analytic Strategies for Identifying Contingent Relations

Sequential recording involves the scoring of participant behavior and caregivers' responses to that behavior each time they occur in immediate sequence throughout an observation period. Doing so requires that categories of participant and caregiver behavior be defined in advance and that occurrences of each be recorded using partial-interval procedures or in real time using frequency counts. Regardless of recording procedure, it is important to preserve the sequences of events as they occur for the resulting data to be meaningful. Sequential recordings have been conducted during regularly scheduled activities (e.g., McKerchar & Thompson, 2004) and in the context of structured antecedent conditions (e.g., attention deprivation) designed as motivating operations for the reinforcement of behavior (e.g., Anderson & Long, 2002). Once the data have been collected, one or more conditional probabilities are calculated, graphed, and analyzed for evidence of a potential contingency.

To date, at least three different analytic strategies have been reported in the literature for identifying possible contingent relations based on conditional probabilities from behavior–consequence recordings. The first approach involves simply computing the conditional probability of each consequence given the occurrence of behavior (e.g., Lalli, Browder, Mace, & Brown, 1993; Mace & Lalli, 1991; Repp & Karsh, 1994). Those consequences that follow behavior at least sometimes (i.e., exhibit contiguity) are hypothesized to function as potential reinforcers. Consequences with the highest conditional probabilities (i.e., those delivered on the richest schedule) are viewed often as the most likely candidates. For example, teacher attention followed between 20% and 52% of problem behavior occurrences on average for 3 students in Lalli et al., whereas discontinuation of the task and access to tangible items were never observed to follow problem behavior for 2 of the students. Similarly, approximately 40% of tantrum occurrences in Repp and Karsh were followed by teacher attention. In both studies, these data led to hypotheses of an attention function for problem behavior. Mace and Lalli found that high percentages of bizarre speech occurrences were followed by task disengagement (40% to 100%) and a low percentage were followed by staff attention (5% to 20%). Based on these data, Mace and Lalli hypothesized both escape and attention functions.

The second approach involves computing the conditional probability of each consequence given the occurrence of behavior (as above) and comparing it to the base rate or “background” probability of each consequence (McKerchar & Thompson, 2004; Vollmer et al., 2001). This approach has been used in verbal interaction research to determine if one person's statements are constrained by or statistically dependent on another person's statements (Lichtenberg & Heck, 1986; Martens, Deery, & Gherardi, 1991; Patterson & Forgatch, 1985). Vollmer et al. applied this strategy to identify events with a positive, negative, or neutral contingency on problem behavior exhibited by 11 individuals with mental retardation. Real-time sequential recordings were collected on problem behavior and its consequences (i.e., attention, escape, access to materials) during times when access to these same reinforcers was restricted (i.e., potential motivating operation conditions). The base rate probability of each consequence occurring at randomly selected points in time was computed and compared to the conditional probability of the same consequence occurring given the occurrence of problem behavior within 5-, 10-, 15-, and 20-s time windows. Conditional probabilities higher than base rate were taken as evidence of a positive contingency, those lower than base rate as a negative contingency, and those equal to base rate as no contingency.

McKerchar and Thompson (2004) adopted a similar strategy by comparing base rate and conditional probabilities of various teacher responses to children's problem behavior in inclusive preschool programs. Using 10-s partial-interval sequential recording, a positive contingency was identified between teacher attention and problem behavior for all the children observed.

The third approach to identifying possible contingent relations from conditional probabilities involves computing the conditional probability of each consequence given the occurrence of behavior (also as above), but taking into account the proportion of consequences preceded by the target behavior (Anderson & Long, 2002; Lerman & Iwata, 1993). This is accomplished by calculating the conditional probability of behavior occurring given occurrence of the consequence. Note that this quantity differs from the conditional probability used to determine schedule in that the number of behavior–consequence pairs is divided by the number of times the consequence was observed, not the number of times the behavior was observed. In so doing, this value indicates the proportion of consequence deliveries that were immediately preceded by the target behavior rather than the proportion of behavior occurrences that were immediately followed by the consequence.

For example, in both Anderson and Long (2002) and Lerman and Iwata (1993), the conditional probability of each consequence given the occurrence of problem behavior (i.e., the schedule value) was depicted in the bottom right panel of each figure. The proportion of consequence intervals immediately preceded by the problem behavior was depicted in the bottom left panel of each figure. For Drew in Figure 1 of Anderson and Long, a high proportion of problem behavior was followed by the consequence of escape in both task (53%) and play (67%) conditions. Thus, escape was delivered on a moderate to rich schedule for the occurrence of problem behavior. In addition, most occurrences of the escape consequence were preceded by occurrences of problem behavior in both the task and play conditions (over 90% and over 70%, respectively). These latter quantities indicate that problem behavior had just occurred in most of the intervals in which escape was allowed. Taken together, these data were interpreted as evidence of a possible escape contingency.

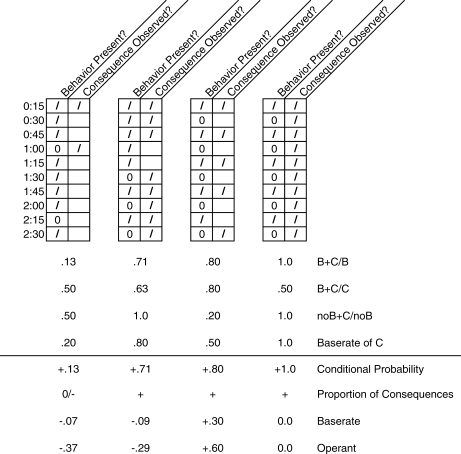
Figure 1.

Hypothetical data illustrating the computations involved in applying conditional probability, proportion of consequences, base rate, and operant analyses. Decision about degree of contingency using each approach is indicated by sign (+, −, 0) along with a contingency value where applicable.

Presented in Figure 1 are four hypothetical data sets illustrating negative, positive, and zero contingencies between behavior and a consequence. Probabilities required to apply each of the four decision approaches described above appear in the top four rows. The direction of contingency (+, −, 0) or contingency value based on each approach (i.e., operant, conditional probability, base rate, and proportion of consequences) appears in the bottom four rows. The conditional probability approach is based on the B+C/B values and identifies consequences that are contiguous with at least a proportion of behavioral occurrences. Because it says nothing about the extent to which consequences occur in the absence of behavior, nonzero values will always be interpreted as a positive contingency by this approach. The base rate strategy can be used to determine if consequences are more likely to occur following behavior than independent of behavior, thereby satisfying statistical definitions of contingency (Bakeman & Gottman, 1986). This approach yields contingency estimates that have the same direction or sign as an operant approach, but different values. The values differ because the base rate probability of a consequence used for comparison is computed independent of whether behavior occurred or not. By contrast, the comparison value used in the operant approach is computed as the conditional probability of a consequence given the absence of behavior (i.e., no B+C/no B).

Interpreting the data in Figure 1 using the proportion-of-consequences strategy is less clear cut, although Lerman and Iwata (1993) applied the following two-step sequence. First, if even a small proportion of consequences were preceded by behavior (i.e., nonzero values of B+C/C), then a contingency may exist. Additional evidence is provided by a high conditional probability of the consequence given behavior (i.e., B+C/B). Although high was not defined, we adopted .50 as a cutoff when evaluating the data in Figure 1. This approach can actually lead to decisions that are inconsistent with both operant and base rate definitions of contingency (Figure 1). This is the case because knowing the percentage of consequences that occur in the absence of behavior says nothing about the conditional probability of a consequence occurring in the absence of behavior.

A Contingency Space Analysis

An alternative strategy that addresses the limitations discussed above is suggested by operant definitions of contingency. As noted previously, a contingent relation between behavior and a consequence can be defined as the difference between two conditional probabilities: (a) the probability of a consequence given behavior (p[C/B]) and (b) the probability of a consequence given the absence of behavior (p[C/no B]). Graphed together in coordinate space (i.e., the contingency space), these two probabilities can be used to evaluate contiguity, conditional probability or schedule, and degree of contingency between behavior and one or more social consequences simultaneously (Eckert, Martens, & DiGennaro, 2005; Gibbon et al., 1974; Matthews et al., 1987; Schwartz, 1989).

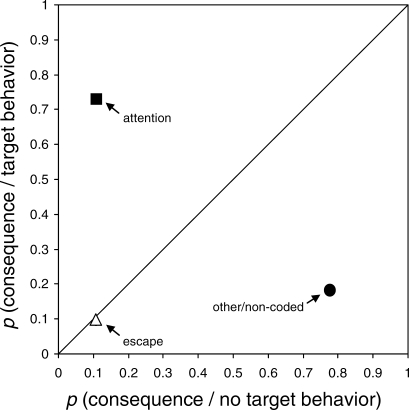
Consider the data displayed in Figure 2. The probability of attention, escape, or other or noncoded (i.e., the absence of an overt consequence) given occurrences of target behavior appears on the y axis. The probability of these same consequences given behavior exclusive of the target appears on the x axis. The diagonal line represents the unity diagonal and indicates where on the graph the two conditional probabilities would be plotted if they were identical. Thus, the unity diagonal indicates situations in which a given consequence is just as likely to occur given occurrence or nonoccurrence of target behavior (i.e., the consequence is independent of the two behavior categories).

Figure 2.

A contingency space analysis of attention, escape, and other or noncoded consequences for target behavior and its absence.

Data plotted in the operant contingency space can be evaluated with respect to the y axis, the x axis, or both. Relative position along the y axis indicates the proportion of target behavior occurrences that were followed by the consequence. This probability can be interpreted as an approximation of a schedule with an upper limit of 1 (continuous reinforcement). For example, the conditional probability of attention given occurrence of target behavior in Figure 2 is .73 (a rich schedule). By contrast, target behavior was infrequently ignored with a conditional probability of .18 for other or noncoded. Relative position along the x axis indicates the proportion of behavior occurrences exclusive of the target that were followed by the same consequence. This value also approximates a reinforcement schedule with an upper limit of 1 but for all behavior other than the target. In Figure 2, the conditional probability of escape given no target behavior is .11, with the conditional probability of attention given no target behavior also equal to .11.

With respect to relative position in coordinate space, points falling above the unity diagonal represent consequences that are more likely to occur given occurrence of the target behavior (as with attention in Figure 2). These events, therefore, are contingent on the target behavior to some degree and may serve a reinforcing function. Points falling below the unity diagonal represent consequences that are more likely to occur given occurrences of behavior exclusive of the target (as with the other or noncoded category in Figure 2). In the case of other or noncoded, behaviors exclusive of the target behavior may be on a lean schedule of reinforcement or mostly ignored. Escape is plotted below, but close to, the unity diagonal, indicating nearly equal probabilities of occurrence given the presence or absence of the target behavior. Finally, points falling closer to the origin represent events that follow target behavior or its absence relatively infrequently regardless of degree of contingency, such as escape.

Based on sequential recordings of two mutually exclusive behaviors and their consequences, a CSA can depict events that are dependent on target behavior (on the y axis above the diagonal), contingent on target behavior (above the diagonal), independent of behavior (on the diagonal), contingent on behavior exclusive of the target (below the diagonal), or dependent on behavior exclusive of the target (on the x axis below the diagonal).

Data Requirements for a Csa

A CSA can be conducted from partial-interval or real-time sequential recordings of behavior and its consequences, assuming that (a) the experimenter defines two mutually exclusive and exhaustive behavior categories directly (i.e., on task or off task, engagement or disruption) or by exclusion, (b) the delivery of consequences for both behavior categories is recorded within or across adjacent intervals (partial-interval recording) or dichotomously rescored on an interval basis (real-time recording), and (c) occurrences of behavior and its consequences are recorded in sequence to retain temporal integrity. As with any form of direct observation, samples of coded two-event sequences must be large enough so as to be representative of behavior in a given setting. Obtaining these samples will depend in part on base rates of the target behavior and caregiver responses, interval length, total number of observation sessions conducted, and individual session length. Previous studies involving sequential recordings have included 50 to 300 min of observation per participant, resulting in 600 to 1,800 intervals (Anderson & Long, 2002; Lalli et al., 1993; Lerman & Iwata, 1993; McKerchar & Thompson, 2004; Symons et al., 2003). McKerchar and Thompson suggested that observations be continued until at least 10 intervals with coded target behavior are obtained. Behavioral base rates in their study, however, were typically less than 5%, requiring up to 1,440 observed intervals for 1 participant. When collecting data for a CSA, one must consider base rates of both the target behavior and behavior exclusive of the target. That is, at very low or very high base rates of target behavior, more intervals need to be observed in order to attain the 10-interval criterion for both behavioral occurrences and nonoccurrences. Conversely, for target behaviors that occur with higher base rates (i.e., 15% to 25% of intervals), three 15-min observations using 10-s partial-interval sequential recording would result in 40 to 67 intervals of coded target behavior and 202 to 229 intervals of coded behavior exclusive of the target.

We also have found that including the other or noncoded category can be helpful in data interpretation and routinely include it when conducting the observations. Because data collection is restricted by the categories of consequences defined by the experimenter, including other or noncoded allows an analysis of consequences that are not immediately obvious to the experimenter. In addition, in many instances behavior may not receive a consequence (i.e., planned ignoring). In these cases, coding “other or noncoded” allows us to capture this sequence.

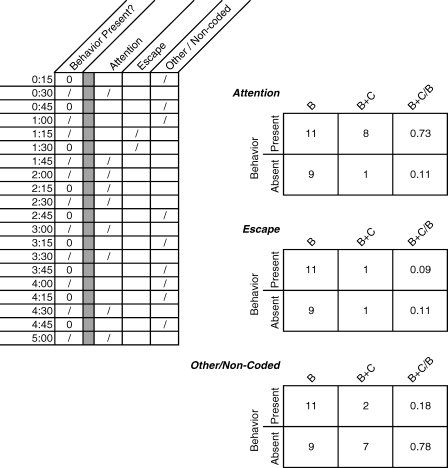
A sample data sheet showing computation of the various conditional probabilities plotted in Figure 2 based on 20 intervals of data is presented in Figure 3. Using these data, a CSA would involve the calculation of conditional probabilities as proportions of intervals in which each consequence occurred (i.e., attention, escape, other or noncoded) given both the occurrence and nonoccurrence of target behavior. For example, the conditional probability of attention given target behavior would be computed as the total number of intervals containing target behavior that were followed by attention divided by the total number of intervals containing target behavior. Attention was delivered in 8 of the 11 intervals in which target behavior was present (8/11  =  73%). These data indicate that most intervals of target behavior (73%) were followed by attention, a situation that might be interpreted as a rich reinforcement schedule. Third, we also would compute the conditional probability of attention given that target behavior did not occur as the total number of intervals in which attention occurred absent target behavior divided by the total number of intervals in which target behavior was absent. Here we see that attention was provided on one of the nine intervals in which no target behavior was present (1/9  =  11%). This value indicates that attention was delivered in only 11% of the intervals in which the target behavior did not occur. To complete the analysis, these two conditional probabilities (.73 and .11) would be plotted in the operant contingency space to reveal the positive contingency for attention, as shown in Figure 2.

Figure 3.

A sample completed partial-interval sequential recording sheet for use in calculating conditional probabilities (B is the number of intervals in which target behavior was present or absent, B+C is the number of intervals in which consequences occurred given the presence or absence of target behavior, B+C/B is the conditional probability of the consequence given the presence or absence of target behavior).

Commonly, more than one event will follow an individual's response within the same interval. To best capture the naturally occurring contingencies, all consequences should be recorded in sequence. Consider the data presented in Figure 3 at interval 0:30 s. Suppose that in addition to attention, an escape consequence also was observed. In this circumstance, the conditional probability of attention given the target behavior would be the same. However, adding an instance of escape during this interval would alter the conditional probability of escape given the target behavior to 2/11 or .18. If the clinician observes a pattern of multiple consequences per interval, the data-collection procedures allow flexibility to create a new compound-consequence category for analysis. One such compound consequence could be the delivery of a verbal reprimand paired with the withdrawal of a demand. If this were observed repeatedly, the experimenter may choose to code this pairing as one category.

Identifying Contingent Consequences from a Descriptive Assessment

The purpose of this case example is to show how a CSA can be used to identify events contingent on problem behavior that might subsequently inform the design of a function-based intervention. For example, consider again the data shown in Figure 2. Suppose the problem behavior targeted was disruptive verbalizations, defined as any vocalization that was not preceded by hand raising or a teacher question. As outlined above, a CSA of these data indicates that attention was positively contingent on disruptive verbalizations and delivered on a rich schedule (.73 and .11). On the other hand, the absence of disruptive verbalizations was more likely to be ignored (.18 and .78), suggesting that appropriate behavior was on extinction. Given these data, the clinician might hypothesize that attention is the function of the disruptive verbalizations (i.e., serves as the reinforcer for this individual in this setting). Thus, an effective intervention might consist of differential reinforcement of alternative behavior. In this case, hand raising may be targeted as an alternative to disruptive verbalizations, using attention as the programmed reinforcer. Conversely, disruptive verbalizations would be put on an extinction schedule (i.e., planned ignoring).

Evaluating Changes in Reinforcement Following Treatment

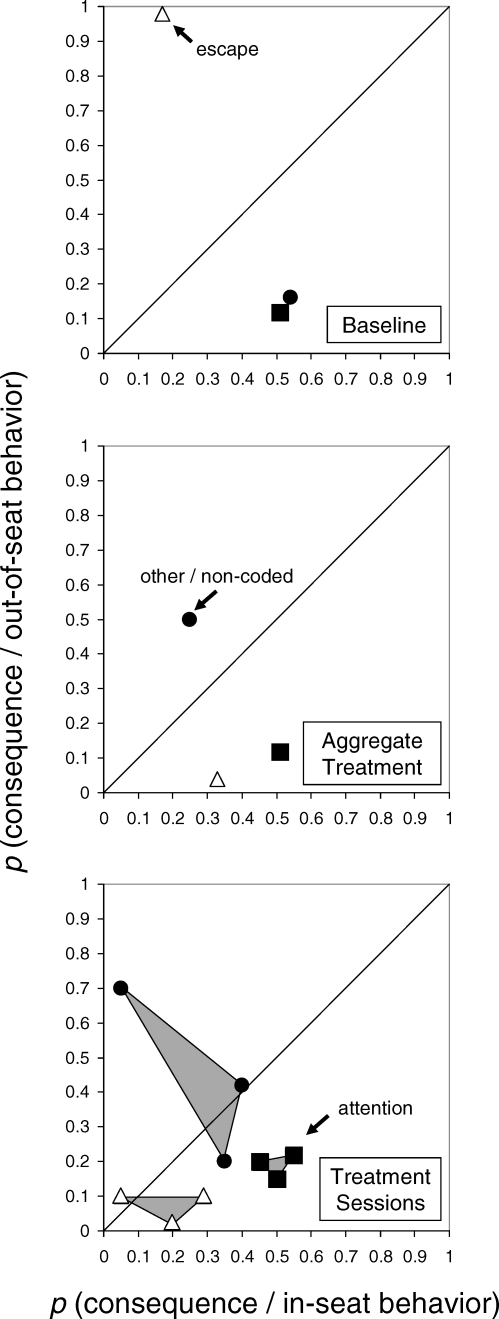
The purpose of the second case example is to demonstrate a novel application of CSA by verifying that a behavioral intervention produced the intended changes in reinforcement delivery. In school settings it is common for students to be referred for high levels of out-of-seat behavior, defined as leaving their seat or seated position or their weight not being supported by the chair (e.g., Ardoin & Martens, 2000). Suppose that baseline observations of the classroom were graphed in aggregate format as in the top panel of Figure 4. In this example, escape falls above the unity diagonal and therefore is positively contingent on out-of-seat behavior. However, both attention and other or noncoded consequences fall below the unity diagonal and are contingent on in-seat behavior. These data suggest that out-of-seat behavior may be maintained by escape from task demands even though the student receives attention (e.g., assistance, praise) contingent on in-seat behavior. Thus, differential negative reinforcement of incompatible behavior (DNRI), using escape from task demands as the reinforcer, would be one treatment option to target out-of-seat behavior.

Figure 4.

A case example of a contingency space analysis of escape, attention, and other or noncoded consequences for out-of-seat and in-seat behavior during baseline and following intervention.

Imagine that function-based DNRI consisting of a 30-s break from work after every 1.5 min of in-seat behavior (i.e., a .33 negative reinforcement schedule) was implemented by the teacher. In addition, task demands continued to be presented when the child was out of seat (i.e., escape extinction), but out-of-seat behavior was otherwise ignored. Finally, assume also that attention for in-seat behavior in the form of assistance or praise remained unchanged. If the intervention was implemented with 100% accuracy, one would expect the resulting CSA to look similar to the aggregated data presented in the middle panel of Figure 4. These data suggest that, following intervention, escape was allowed contingent on appropriate, in-seat behavior and at a probability consistent with the programmed .33 schedule. Attention occurred as before, whereas out-of-seat behavior was largely ignored when tasks were not being presented, as shown by the now positive contingency for other or noncoded consequences. Based on this information, it would be easy to conclude that the hypothesized negative reinforcer was delivered as intended with high levels of treatment integrity.

Given that these data are aggregated, variability across sessions may be masked. As an index of treatment integrity, the experimenter also may choose to present these data separately for each observation session on the same graph and conduct a cluster analysis. These sample data are presented in the bottom panel of Figure 4. Similar consequences across observation sessions are depicted with the same symbol (e.g., filled squares for attention) and connected to form a cluster of data points for each consequence. In the bottom panel of Figure 4, these clusters are shaded gray. Smaller clusters represent more consistent implementation across sessions, whereas larger clusters represent more variable implementation. The cluster analysis in Figure 4 shows that during one observation session, escape was not provided as intended when the student exhibited in-seat behavior. Moreover, during one of the observation sessions, escape was delivered less frequently than the planned schedule of reinforcement would dictate. A cluster analysis of attention reveals that this consequence continued to be delivered consistently contingent on in-seat behavior. This is not surprising, given that the teacher already was providing contingent attention at baseline. Conversely, the teacher was more variable in her contingent ignoring of out-of-seat behavior, being more likely to ignore in-seat behavior on one occasion. Thus, ongoing training and consultation regarding this component of plan implementation would be warranted.

Conclusions

Despite the relative ease and potential effectiveness of conducting a CSA, a number of limitations warrant further discussion. As with all forms of naturalistic observation, a CSA relies solely on descriptive data-collection techniques. That is, when conducting a CSA the observer is simply recording behavior without experimental manipulation of antecedent or consequential variables. Thus, by failing to create situations in which particular consequences are delivered contingent on the target behavior, the observer can never be assured fully that he or she has accounted for all possible functional reinforcers. On a similar note, failing to manipulate environmental conditions may cause the observer to arrive at false conclusions concerning the degree of contingency of a particular behavior–consequence relation. This is especially true in situations in which target behaviors occur infrequently, resulting in small samples of behavior–consequence pairings. Thus, practitioners may want to consider alternative or supplemental descriptive assessment methods in cases in which low-frequency behaviors are targeted (e.g., interviews, anecdotal recording).

A CSA can be conducted only for two mutually exclusive behavior categories at a time. Depending on the size of the “target” and “absence of target” response classes, the latter may include other aberrant behaviors that potentially serve the same function as the target problem behavior. Relatedly, scoring consequences contingent on the absence of problem behavior may seem counterintuitive. However, as noted by Schoenfeld and Farmer's (1970) notion of the “behavior stream,” individuals are always doing something, and the absence of target behavior automatically defines the presence of alternative behavior.

Although analyzing the degree of contingency between target behaviors and natural consequences has yielded positive results in our clinical work, a number of questions concerning the utility of this analysis remain unanswered. First, we typically collect data on behavior–consequence relations that occur within the same 10-s interval and do not record immediate antecedent influences on the occurrence of target behavior. The extent to which the same contingency patterns would be obtained if data were coded across adjacent intervals or in conjunction with antecedents is a direction for future research. Second, the partial-interval coding system imposes structure to the observation system in a way that may result in erroneous interpretation of the data. For example, in a continuous time-based recording system, the observer is knowledgeable about the time interval between the behavior and its corresponding consequence. In partial-interval recording, this information is not always apparent. Given the limited amount of research in this area, we do not know which time window is most appropriate for coding the occurrence and nonoccurrence of consequences. Information also may be lost with partial-interval recording when multiple behavior–consequence sequences occur in the same interval. For example, appropriate behavior may receive attention in the same interval that escape from task demands follows problem behavior. Although this occurs infrequently with short intervals (i.e., 10 s), one way to handle this limitation is to score all sequences, note this in an observation summary, and adjust the interval length in subsequent observation sessions. It is important for professionals to continue to use good clinical judgment and tailor recording techniques and data collection to each individual case. Third, due to the limited applied research on CSA, we are unaware of any decision rules concerning degree of contingency. For example, how might one determine whether a deviation from the unity diagonal represents a weak versus strong contingency? How many occurrences need to be sampled to obtain statistically reliable estimates of dependency, and once obtained, does a statistically significant difference in conditional probabilities (e.g., Lichtenberg & Heck, 1986; Martens et al., 1991) correspond to a difference in reinforcer function? Clearly, the most logical approach to answering these questions lies in continued research on the applicability of CSA to descriptive assessments. More specifically, future research should examine the degree to which CSA outcomes match the findings of more traditional descriptive and experimental analyses, as well as the successful translation of CSA outcomes into effective treatment strategies.