Is redshift-dependent evolution of galaxies a theoretical artifact?

Abstract

The physical validity of the hypothesis of (redshift-dependent) luminosity evolution in galaxies is tested by statistical analysis of an intensively studied complete high-redshift sample of normal galaxies. The necessity of the evolution hypothesis in the frame of big-bang cosmology is confirmed at a high level of statistical significance; however, this evolution is quantitatively just as predicted by chronometric cosmology, in which there is no such evolution. Since there is no direct observational means to establish the evolution postulated in big-bang studies of higher-redshift galaxies, and the chronometric predictions involve no adjustable parameters (in contrast to the two in big-bang cosmology), the hypothesized evolution appears from the standpoint of conservative scientific methodology as a possible theoretical artifact.

The big-bang theory of the universe, known in its modern form as Friedman–Lemaitre cosmology (FLC) (e.g., refs. 1 and 2), appeared both confirmed and shaken by two observational developments of the middle 1960s. On the one hand, the discovery of the cosmic microwave background radiation (CBR) (3) gave greater credence to the possible occurrence of a primeval explosion, but on the other, the discovery of quasars (4) raised questions about the nature of the redshift. Later observations on the CBR, notably the discovery of its precise isotropy and the closeness of its spectrum to the Planck law, raised questions about the consistency of these phenomena with the putative big bang.

Both questions have been addressed by hypothesizing somewhat ad hoc mechanisms, such as “inflation” in the case of the CBR, and “luminosity evolution” in the case of quasars, that appear incapable of direct and precise observational substantiation. Such mechanisms are not required in the chronometric cosmology (CC) (e.g., ref. 5), which moreover restores the law of conservation of energy to a global principle (lacking in FLC, but required in the derivation of the Planck law for photon ensembles such as the CBR), and appears to predict the results of direct observations in objectively selected and statistically analyzable samples of low-redshift normal galaxies, quasars, active galactic nuclei, and radio sources, with greater exactitude than FLC (see, e.g., refs. below), notwithstanding that it has two fewer adjustable fundamental constants. In CC the universe is fixed in size and conformally equivalent to the model proposed by Einstein in the first modern paper on cosmology (6).

Strong evolution in one form or another has long been adduced in FLC for quasars, but to do so for normal galaxies would undermine the scientific basis for the linear redshift–distance law from which FLC derives, and which represents its principal empirically falsifiable implication. The hypothesis of evolution in FLC eliminates its quantitative predictive power regarding the relations between directly observable quantities such as the redshifts and energy fluxes of the class of sources subject to the assumed evolution. In the context of observational cosmology, the term “evolution” refers not to temporal development of individual objects, of which there is no question, but rather to a hypothetical redshift-dependent effect, according to which the characteristics of a galaxy population depend on its location in the universe. For example, the supposition that galaxies at higher redshifts (or presumptive greater distances) are typically intrinsically brighter represents “luminosity evolution,” or the supposition that they are less numerous represents “density evolution.”

The latter may appear a more natural form of evolution from a general standpoint, but the literature has typically focused on luminosity evolution, the evidence for which has generally been represented as compelling, although there exists observational evidence for variants such as luminosity-dependent density evolution [e.g., see Green (7)]. However, the testing of density evolution requires an additional physical hypothesis, in the nature of spatial homogeneity for the spatial distribution of sources, which is not required for tests of luminosity evolution. These require only the absence of discrimination in the selection of samples on the basis of flux, down to a given limiting flux, and in particular do not require that the redshifts of all selected objects be determined. Tests regarding luminosity evolution thus provide a more conservative basis for possible rejection of cosmological hypotheses than tests involving density evolution, which are observationally more demanding and theoretically involve an additional assumption.

The question of whether and to what extent normal galaxies may evolve has been intensively disputed and investigated in recent literature, particularly with regard to qualitative indications from Hubble Space Telescope images. The situation at low redshifts has also been subject to dispute and investigation, but has often been represented as inconclusive by virtue of the possible existence of local irregularities and perturbations that would not affect the generic higher-redshift regime. To address the question of evolution in normal galaxies beyond the presumed local (low-redshift) region, a substantial objectively specified and observed sample of such galaxies at higher redshifts is required [e.g., see Lilly (8)].

The sample of Brinchmann et al. (9) has been carefully selected toward this end. However, intensive morphological analysis based on Hubble Space Telescope imaging (10) has indicated that one of the best-observed classes of galaxies “have, as a set, properties consistent with the idea that they are similar galaxies observed at different cosmic epochs.” This is unexpected within the frame of FLC because of its contrast with its apparent luminosity evolution. It may, however, be explained by the result of the present investigation, to the effect that the hypothesized luminosity evolution is quantitatively consistent with the predictions of CC for the [unadjusted] results of analysis predicated on FLC.

Analysis of the Basic Sample

The sample of ref. 9 will here be subjected to parallel statistical analyses within the frames of both FLC and CC on the basis of conservative and statistically efficient methodology. As with any two hypotheses with statistical implications regarding the same quantitative phenomena, it is relevant to test not only the predictive fits of each to the observations but also the implications of each for the results of analysis predicated on the other. To this end, nonparametric maximum likelihood estimation (NPMLE) is used here to determine the predictions of each cosmology regarding the directly observed magnitude–redshift relation reported in ref. 9. Specifically, the sample range from the brightest to the faintest absolute magnitude is divided into equal-sized bins within each of which possible variations in the differential luminosity function (LF) appear inconsequential, with the same number of bins for each cosmology, relative to which the absolute magnitude is defined. The assumed constant values of the LF within each bin are then the parameters to be estimated by maximum likelihood, subject to the given apparent magnitude limit of the sample. The NPMLE of the LF may be expressed in a closed form known as ROBUST (11).

In observational practice, bins fixed in magnitudes of the order of ≥∼1 magnitude are used, or in especially refined work, 1/2 magnitude. For statistical equitability, it is necessary to allow both cosmologies the same number of adjustable parameters. Ten parameters results in bin sizes of a conventional observational order of magnitude, and will be used here except in Table 6.

Table 6.

Predictions using 4 or 40 adjustable parameters

Statistic	1	2	3	4	5	6	7
sm	0.95	1.58  ± 0.06	1.52  ± 0.06	0.99  ± 0.04	9.7	−0.3	1.2
		1.36  ± 0.06	1.45  ± 0.08	0.94  ± 0.05	6.6	0.9	−0.1
〈m〉	21.28	20.97  ± 0.08	21.02  ± 0.07	21.21  ± 0.05	−3.9	1.1	−1.4
		21.22  ± 0.05	21.12  ± 0.07	21.28  ± 0.05	−1.2	0.9	−0.1
β	1.56	3.43  ± 0.33	3.30  ± 0.30	1.60  ± 0.21	5.6	−0.3	0.2
		2.71  ± 0.31	3.11  ± 0.37	1.54  ± 0.19	3.7	0.8	−0.1
ρ1	−0.78	−0.39  ± 0.06	−0.43  ± 0.06	−0.77  ± 0.02	6.6	−0.4	1.1
		−0.55  ± 0.05	−0.48  ± 0.07	−0.79  ± 0.02	4.9	0.9	−0.1
ρ2	−0.10	0.34  ± 0.07	0.33  ± 0.06	−0.08  ± 0.07	6.5	−0.6	0.3
		0.21  ± 0.08	0.30  ± 0.03	−0.11  ± 0.06	4.1	1.0	0.1
σ1	1.36	1.35  ± 0.07	1.33  ± 0.05	1.38  ± 0.08	−0.1	0.7	0.4
		1.34  ± 0.07	1.31  ± 0.06	1.36  ± 0.05	−0.3	0.3	0.1
σ2	0.84	1.31  ± 0.05	1.26  ± 0.05	0.89  ± 0.04	9.0	−0.1	1.1
		1.14  ± 0.05	1.20  ± 0.06	0.84  ± 0.04	6.2	0.8	−0.1

For each statistic, the results for N = 4 are shown directly above those for N = 40. 

The sample of ref. 9 is the conjunction of two samples of slightly different selection criteria, the CFRS (12, 13), augmented by a small number of galaxies considered by Groth et al. (14), and the LDSS (15). To treat the combined sample, common magnitude and redshift limits will be imposed that appear appropriate for both samples. The “basic sample” considered here consists of all 269 objects listed in table 1 of ref. 9 in the redshift range 0.05 < z ≤ 1.65, m ≤ 23, where m denotes the Hubble Space Telescope F814W magnitude given there.

Directly observed quantities, whose definitions are independent of any assumption as to cosmological theory, will be predicted from the NPMLE estimates for this basic sample of the respective LFs. The quantities considered here are the mean 〈m〉 and standard deviation s_m of the apparent magnitudes and the slope β of the apparent magnitude–redshift relation. It is convenient to denote FLC and CC as C1 and C2, respectively; here 1 and 2 indicate the powers of the distance to which sufficiently low redshifts are predicted to be basically proportional, in the respective theories. In addition, the following cosmology-dependent quantities, which are commonly reported in the literature, and are directly observable, will be predicted: the standard deviations σ_p of the absolute magnitudes in the range observed by the sample, and the correlations ρ_p of the absolute magnitude with log redshift, where p = 1 or 2 according as the cosmology in question. The two parameters on which FLC depends will be given the representative values q_o = 1/2 and Λ = 0 considered in refs. 9 and 10, if not otherwise indicated.

Table 1 summarizes the comparison of the resulting predictions with observation. Column 1 gives the observed value of the statistic in question. Column 2 is the predicted value according to C1, as determined from SLF1, where SLFp denotes the sample LF according to NPMLE, as given in closed form in ref. 11, for cosmology p. Column 3 is the predicted value, according to C2, of the predicted value according to C1, as determined from SLF2. Column 4 is the predicted value according to C2, as determined from SLF2. Columns 5, 6, and 7 are the corresponding prediction errors in units of standard deviations. The standard deviations of the C1 predictions are of the order of 40% larger than those for C2, whence the absolute errors of C1 relative to those of C2 are ∼40% larger than indicated in columns 5 and 6.

Table 1.

Observations and predictions for the basic sample

Statistic	1	2	3	4	5	6	7
sm	0.95	1.54  ± 0.06	1.54  ± 0.08	0.95  ± 0.04	9.7	0.1	0.1
〈m〉	21.28	20.93  ± 0.07	20.92  ± 0.07	21.43  ± 0.05	−4.9	−0.1	−1.0
β	1.56	3.46  ± 0.28	3.47  ± 0.38	1.58  ± 0.19	6.7	0.0	0.1
ρ1	−0.79	−0.40  ± 0.05	−0.44  ± 0.06	−0.78  ± 0.02	9.1	−0.8	0.1
ρ2	−0.10	0.36  ± 0.06	0.36  ± 0.08	−0.09  ± 0.06	7.8	0.0	0.1
σ1	1.36	1.29  ± 0.06	1.29  ± 0.06	1.35  ± 0.05	1.0	0.0	0.1
σ2	0.84	1.27  ± 0.05	1.27  ± 0.06	0.84  ± 0.04	8.1	0.0	0.0

Here and in Tables 2–6, column 1 gives the observed value of the statistic in question. Column 2 is the predicted value according to C1, as determined from SLF1, where SLFp denotes the sample LF according to NPMLE, as given in closed form in ref. 11, for cosmology p. Column 3 is the predicted value, according to C2, of the predicted value according to C1, as determined from SLF2. Column 4 is the predicted value according to C2, as determined from SLF2. Columns 5, 6, and 7 are the corresponding prediction errors in units of standard deviations. 

For mathematical convenience as well as direct physical interpretability, all predictions were determined by Monte Carlo analysis, in which samples are drawn at random from the appropriate SLFp, subject to the given limiting magnitude, and placed at the observed redshifts. The statistics in question were determined for each random sample. One hundred such samples were constructed, and the predictions and standard deviations represent the mean and standard deviation of the corresponding 100 predictive estimates, which tests showed were quite stable.

With the exception of s₁, whose corresponding prediction is typically accurate within ∼2σ for a general class of cosmologies, all of the C1 predictions are highly deviant. The C2 predictions for the directly observable quantities in column 4 are quite accurate. The C2 predictions for the results in column 3 of statistical analysis predicated on C1 were derived from the C2 prediction for the C1 LF, consisting of the average of the C1 LFs for the 100 random samples constructed assuming C2. Following this, 100 random samples drawn from this C2 prediction for the C1 LF were constructed, subject to the magnitude limit, and placed at the observed redshifts, and the corresponding C1 predictions were made and averaged, as for the direct C1 and C2 predictions. These predictions of C2 for the results of analysis predicated on C1 are also quite accurate. The standard errors shown are the square roots of the sum of squares of the standard errors of the C1 self-prediction and the C2 prediction of the C1 self-prediction. In view of the deviations of the C1 predictions from observation, it appears supererogatory to show the deviations of the C1 predictions for the results of analysis predicated on C2, apart from those for ρ₂ and σ₂.

As with any putatively complete sample, there can be no absolute assurance of completeness, and the empirical reliability of the statistical results may be enhanced by the analysis of subsamples defined by more stringent limits. To this end, Table 2 shows the same results as Table 1 for the subsample of 242 galaxies apparently brighter than magnitude 22.5 (upper line), and with 0.1 < z ≤ 1.65, and for the subsample of 237 galaxies further limited by the constraint z ≤ 1.1 (lower line). In statistical summary, there is no significant difference from the indications of Table 1, although with the successive reductions in sample size and dynamic range, the statistical significance of the C1 deviations is naturally reduced.

Table 2.

Observations and predictions for bright subsamples

Statistic	1	2	3	4	5	6	7
sm	0.79	1.11  ± 0.06	1.15  ± 0.06	0.78  ± 0.04	5.3	0.5	−0.4
	0.79	1.06  ± 0.05	1.13  ± 0.06	0.77  ± 0.04	4.9	0.9	−0.8
〈m〉	21.29	21.08  ± 0.06	21.05  ± 0.08	21.25  ± 0.05	−3.7	−0.4	−1.0
	21.29	21.14  ± 0.05	21.06  ± 0.06	21.23  ± 0.05	−2.8	−0.9	−1.1
β	1.34	2.58  ± 0.30	2.70  ± 0.44	1.26  ± 0.20	4.1	0.3	−0.3
	1.43	2.53  ± 0.37	2.78  ± 0.32	1.32  ± 0.25	3.0	0.5	−0.5
ρ1	−0.78	−0.58  ± 0.05	−0.53  ± 0.07	−0.79  ± 0.02	4.5	−0.4	0.2
	−0.77	−0.57  ± 0.05	−0.52  ± 0.06	−0.79  ± 0.02	3.7	0.8	−0.7
ρ2	−0.13	0.20  ± 0.07	0.22  ± 0.10	−0.15  ± 0.06	4.7	0.2	−0.4
	−0.10	0.19  ± 0.09	0.23  ± 0.07	−0.14  ± 0.08	3.2	0.4	−0.5
σ1	1.17	1.13  ± 0.05	1.15  ± 0.07	1.18  ± 0.04	−0.8	0.2	0.3
	1.13	1.09  ± 0.06	1.11  ± 0.04	1.14  ± 0.05	−0.8	0.3	0.2
σ2	0.74	0.96  ± 0.05	0.99  ± 0.07	0.73  ± 0.04	4.4	0.5	−0.3
	0.74	0.91  ± 0.04	0.97  ± 0.05	0.71  ± 0.03	4.4	1.0	−0.8

For each statistic, the upper line is for the subsample of 242 galaxies apparently brighter than magnitude 22.5 and with 0.1 < z ≤ 1.65, and the lower line is for the subsample of 237 galaxies further limited by the constraint z ≤ 1.1. 

Within FLC there has long been a question as to the value of q_o. The value used above, q_o = 1/2, represents the original de Sitter model, appears theoretically relatively attractive, and is favored in much current theoretical analysis. Moreover, it interpolates between the values q_o = 0 and 1 that bracket the values traditionally considered in the literature. The precise presumptive value for q_o would appear unlikely to significantly affect the present results, but for conservatism the empirically favored value q_o ∼ 0 is also treated here. Table 3 summarizes the results on the same basis as Table 1 under the assumption that q_o = 0. The deviations of the FLC predictions from observation are slightly less than those assuming q_o = 1/2, but they remain at a statistically quite significant level.

Table 3.

Predictions under the assumption that q_o = 0

Statistic	1	2	3	4	5	6	7
sm	0.95	1.48  ± 0.08	1.56  ± 0.07	0.95  ± 0.04	6.2	1.1	−0.1
〈m〉	21.28	21.15  ± 0.07	21.01  ± 0.08	21.23  ± 0.04	−1.9	−1.3	−1.4
β	1.56	2.86  ± 0.36	3.38  ± 0.31	1.61  ± 0.19	3.7	1.1	0.3
ρ1	−0.82	−0.57  ± 0.54	−0.49  ± 0.05	−0.82  ± 0.02	4.6	1.2	0.1
ρ2	−0.10	0.24  ± 0.08	0.33  ± 0.06	−0.08  ± 0.06	4.3	1.0	0.3
σ1	1.47	1.44  ± 0.07	1.41  ± 0.06	1.45  ± 0.05	−0.3	−0.4	−0.3
σ2	0.84	1.22  ± 0.06	1.29  ± 0.06	0.83  ± 0.03	6.0	0.9	0.4

The conjunction of distinct samples, even when painstakingly done as in ref. 9, is a potential source of a statistical fluke. To deal with this possibility, analyses were made for two individual subsamples, one consisting of the CFRS with the Groth objects (213 galaxies), and the other with the LDSS (56 galaxies). In Table 4 the results for the CFRS are shown above those for the LDSS; both analyses appear quite consistent with the analysis for the combined sample.

Table 4.

Observations and predictions for the CFRS and LDSS subsamples

Statistic	1	2	3	4	5	6	7
sm	0.93	1.48  ± 0.08	1.56  ± 0.08	0.92  ± 0.04	7.1	0.1	−0.2
	1.02	1.41  ± 0.14	1.51  ± 0.13	1.03  ± 0.08	2.8	0.5	−0.1
〈m〉	21.32	21.04  ± 0.08	21.01  ± 0.10	21.28  ± 0.06	3.7	0.1	−0.7
	21.09	20.98  ± 0.16	20.90  ± 0.14	21.05  ± 0.14	−0.7	−0.4	−0.3
β	1.65	3.29  ± 0.38	3.31  ± 0.38	1.59  ± 0.21	4.3	0.1	−0.3
	1.24	2.79  ± 0.82	3.61  ± 0.63	1.62  ± 0.59	1.9	0.7	0.7
ρ1	−0.79	−0.45  ± 0.07	−0.45  ± 0.07	−0.80  ± 0.02	4.1	0.1	−0.2
	−0.74	−0.47  ± 0.13	−0.34  ± 0.12	−0.71  ± 0.06	2.1	0.7	−0.4
ρ2	−0.08	0.34  ± 0.08	0.34  ± 0.08	−0.08  ± 0.02	5.0	0.0	−0.2
	−0.17	0.19  ± 0.17	0.35  ± 0.12	−0.07  ± 0.16	2.1	0.8	0.6
σ1	1.31	1.27  ± 0.08	1.27  ± 0.07	1.44  ± 0.06	−0.5	0.0	−0.5
	1.43	1.37  ± 0.14	1.26  ± 0.11	1.34  ± 0.12	−0.5	−0.6	−0.9
σ2	0.80	1.21  ± 0.06	1.21  ± 0.08	0.80  ± 0.04	7.1	0.0	0.1
	0.99	1.23  ± 0.11	1.25  ± 0.11	0.94  ± 0.07	2.3	0.1	−0.7

For each statistic, the results for the CFRS are shown on the upper line and those for the LDSS are on the lower line. 

The 10 LF parameters are estimated from the same data as those used for testing, which in statistical principle may equitably enhance the predictive precision of both cosmologies. The estimation of 10 parameters from a sample of size 269 would appear generally unlikely to greatly affect statistical significance levels, and because of observational sample size limitations there is no entirely satisfactory alternative. But the matter may be elucidated by further analysis.

At the cost of a large reduction in sample size, the problem of the estimation of the LF from the same data as those whose collective statistics are predicted can be eliminated, by testing one random half-sample on another. The LF estimated from the one sample is then statistically independent of the data in the other sample. The results are summarized in Table 5. As was to be expected from the reduction in sample size, the C1 deviations are reduced when measured in units of standard deviation, but they remain significantly deviant and consistent with the predictions of C2 for the results of analysis predicated on C1.

Table 5.

Observations and predictions for a random half-sample

Statistic	1	2	3	4	5	6	7
sm	0.99	1.40  ± 0.07	1.54  ± 0.09	0.95  ± 0.06	5.5	1.6	1.3
〈m〉	21.19	21.05  ± 0.09	21.19  ± 0.09	21.33  ± 0.08	−1.6	1.6	1.8
β	2.05	3.34  ± 0.44	3.21  ± 0.38	1.58  ± 0.28	2.9	−0.3	−1.7
ρ1	−0.74	−0.46  ± 0.08	−0.36  ± 0.08	−0.80  ± 0.03	3.8	1.3	1.5
ρ2	0.07	0.37  ± 0.11	0.32  ± 0.08	−0.9  ± 0.09	3.5	0.6	1.9
σ1	1.22	1.18  ± 0.09	1.27  ± 0.07	1.33  ± 0.07	−0.4	0.9	1.7
σ2	0.82	1.13  ± 0.05	1.18  ± 0.07	0.83  ± 0.05	5.9	1.7	0.2

Table 6 shows the same quantities as in Table 1 when the numbers N of adjustable parameters are taken as 4 or 40, rather than 10, resulting respectively in unusually large or small magnitude bins; the results for N = 4 are shown directly above those for N = 40. Whether with 4 or 40 parameters, the predictions of C2 remain consistent with the observations, while the predictions of C1 remain significantly deviant, although to a somewhat lesser degree with 40 adjustable parameters, as was to be expected. Indeed, in the same tests for the extreme value N = 200, the predictions of C1 remain deviant from observation by >5σ.

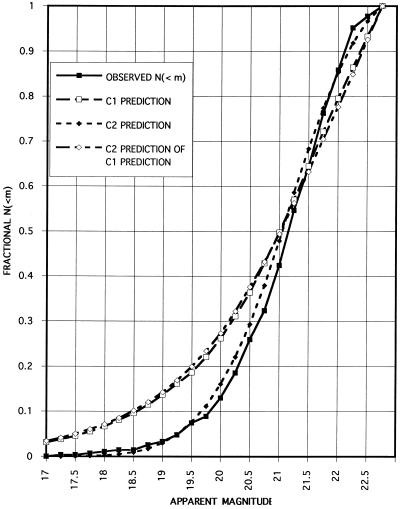
The moments of the observed bivariate magnitude–redshift distribution, and the standard deviation of the absolute magnitudes and their correlation with log redshift, form the natural statistics from the standpoint of general statistics and traditional cosmological analysis; moreover, they are adapted to the determination of quantitative probabilistic significance levels. The prediction of observed distributions, rather than of individual statistics, adds, however, a measure of perspective. Fig. 1 shows the simplest such distribution, that of the overall distribution of apparent magnitudes in the basic sample. This prediction is made by averaging the distributions of apparent magnitudes in each of the 100 random samples constructed to compute the predictions of the individual statistics given above. The prediction is thus independent of any assumption as to the spatial distribution of the galaxies, and thereby of the assumption of completeness in redshift, within the given limits. The distribution predicted by C1 seems clearly to disagree with observation, but appears consistent with the distribution predicted by C2 for the results of analysis predicated on C1. The C2 prediction itself appears in very good agreement with observation.

Figure 1.

Observed and predicted N(<m) relations for the basic sample.

Discussion

I thank E. E. Salpeter for comments on the above results and the suggestion that because of possible observational limitations the subsample at redshifts below 0.3 should be more appropriate for statistical purposes than the full sample. Table 7 summarizes the results of analysis of the subsample of 64 galaxies, consisting of those constrained by the limits 0.05 < z ≤ 0.3, m < 23, by the same procedure as used above. The results appear entirely consistent with those for the full sample.

Table 7.

Observations and predictions for the subsample at redshifts ≤ 0.3

Statistic	1	2	3	4	5	6
sm	1.23	1.51  ± 0.12	1.23  ± 0.10	0.28	0.00	−0.01
〈m〉	20.70	20.62  ± 0.15	20.67  ± 0.13	−0.08	−0.03	0.35
β	2.07	3.79  ± 0.82	2.08  ± 0.73	1.72	0.01	0.01
ρ1	−0.52	−0.25  ± 0.12	−0.52  ± 0.09	0.27	0.00	0.01
ρ2	−0.02	0.26  ± 0.13	−0.02  ± 0.13	0.28	0.00	0.01
σ1	1.35	1.32  ± 0.11	1.34  ± 0.12	−0.03	−0.01	0.19
σ2	1.15	1.32  ± 0.10	1.15  ± 0.09	0.17	0.00	−0.02

Column 1 gives the observed value of the indicated statistic; column 2, the C1 prediction; column 3, the C2 prediction, columns 4 and 5, the respective errors; and column 6, the ratio of the C2 to the C1 error. 

Inevitably, in a complex statistical context, there are factors that are not controlled, known, or observed, which will add dispersion to the observed data. Because such factors are not included in the theoretical prediction, which takes into account only the theoretical magnitude–redshift relation in conjunction with the LF, the corresponding theoretical prediction may underestimate s_m, to the extent that such factors may be present, but would appear unlikely to significantly overestimate s_m if the underlying cosmology is correct. Yet, significantly, such overestimates have been found for C1 not only in the present sample but in all substantially complete samples in which such predictions have been made. There is otherwise a common pattern of C1 deviations, such as the prediction that the lowest-redshift objects in the sample will appear much brighter than is observed, and that the correlation of C1 absolute magnitude with redshift will be much greater in absolute value than is observed.

The samples exhibiting these statistical phenomena include low-redshift samples of normal galaxies, such as those of Nilson (16), Visvanathan (17), and de Vaucouleurs et al. (18); cf. refs. 19–21. At higher redshifts, there have been analyses of substantially complete samples of quasars observed by Schmidt and Green (22), Warren, Hewett, and Osmer (23), and Foltz et al. (24) (cf. refs. 25–27); of active galactic nuclei observed by Gioia et al. (28) and Stocke et al. (29) (cf. ref. 30); and radio sources reported in updated form by Spinrad et al. (31) (cf. ref. 32). The apparent luminosity evolution in the frame of FLC for these higher-redshift samples has been shown to be statistically coincident with the predictions of C2 for the results of analysis predicated on C1. These types of objects are, however, commonly viewed in the frame of FLC as presently somewhat mysterious and not necessarily quite representative of the basic cosmic redshift phenomenon.

The present sample consists of objects selected for close apparent resemblance to local normal galaxies, but it shows precisely the same general pattern of deviations of prediction from observation. These deviations are not quite as striking as in the case of quasars; this was to be expected from the substantially greater dispersion in magnitude than for quasars, together with the lesser redshift range. From the standpoint of C1, the evolution accordingly appears less rapid than for quasars. But the deviations are again quite significant, and statistically coincident with those predicted by the rational alternative cosmology C2 on the basis of the simple magnitude–redshift relation m = 2.5 log[z/(1 + z)] + constant, which is devoid of adjustable cosmological parameters such as the q_o and L of FLC, for the results of analysis predicated on C2. In the absence of direct observational means to substantiate the assumption of luminosity evolution, this hypothesis would appear to be flawed scientifically by a deficiency of falsifiability and inability to explain the predictive accuracy of CC.

Abbreviations

FLC

Friedman–Lemaitre cosmology (also denoted C1)

CC

chronometric cosmology (also denoted C2)

NPMLE

nonparametric maximum likelihood estimation

LF

luminosity function

SLFp

sample LF for cosmology p