Case study of the effects of atmospheric aerosols and regional haze on agriculture: An opportunity to enhance crop yields in China through emission controls?

Abstract

The effect of atmospheric aerosols and regional haze from air pollution on the yields of rice and winter wheat grown in China is assessed. The assessment is based on estimates of aerosol optical depths over China, the effect of these optical depths on the solar irradiance reaching the earth’s surface, and the response of rice and winter wheat grown in Nanjing to the change in solar irradiance. Two sets of aerosol optical depths are presented: one based on a coupled, regional climate/air quality model simulation and the other inferred from solar radiation measurements made over a 12-year period at meteorological stations in China. The model-estimated optical depths are significantly smaller than those derived from observations, perhaps because of errors in one or both sets of optical depths or because the data from the meteorological stations has been affected by local pollution. Radiative transfer calculations using the smaller, model-estimated aerosol optical depths indicate that the so-called “direct effect” of regional haze results in an ≈5–30% reduction in the solar irradiance reaching some of China’s most productive agricultural regions. Crop-response model simulations suggest an ≈1:1 relationship between a percentage increase (decrease) in total surface solar irradiance and a percentage increase (decrease) in the yields of rice and wheat. Collectively, these calculations suggest that regional haze in China is currently depressing optimal yields of ≈70% of the crops grown in China by at least 5–30%. Reducing the severity of regional haze in China through air pollution control could potentially result in a significant increase in crop yields and help the nation meet its growing food demands in the coming decades.

Atmospheric aerosols are a complex chemical mixture of solid and liquid particles suspended in air. They range in size from the smallest superfine mode, with diameters of a few nanometers, to large coarse mode particles, with diameters of a few micrometers or more. Between the superfine and the coarse mode particles are the fine mode particles, with diameters ranging from 0.1 μm to a few micrometers.

Fine mode particles have two important characteristics. The first is their association with regional-scale air pollution (1). While atmospheric fine particles are produced naturally, the natural sources are often overwhelmed by anthropogenic sources in polluted areas. These sources include the direct emission of fine particles into the atmosphere during the burning of fossil fuels and biomass and other anthropogenic processes, as well as the production of fine particles in the atmosphere from the oxidation and gas-to-particle conversion of gaseous pollutants such as sulfur dioxide, nitrogen oxides, and volatile organic compounds. Because fine particles typically reside in the atmosphere for days to weeks, they can be transported over thousands of kilometers before being removed. As a result, large regions of the globe with sufficient industrial activity and urbanization and/or biomass burning can be covered by a contiguous layer of air containing enhanced concentrations of fine particles. Under the appropriate meteorological conditions, the affected area can extend over 10⁶ square kilometers or more (1).

The second important characteristic of fine particles is their ability to affect the flux of solar radiation passing through the atmosphere. This can occur in two ways: (i) directly, by scattering and absorbing solar radiation; and (ii) indirectly, by acting as cloud condensation nuclei and thereby influencing the optical properties of clouds (2–4). Both effects tend to reduce the amount of solar radiation reaching the earth’s surface; however, the magnitude of the indirect effect is far more uncertain than that of the direct effect (5, 6).

Collectively, these two characteristics lead to the phenomenon known as regional haze. The characteristic of regional haze that is most apparent to the naked eye is a reduction in visibility. Another effect of regional haze is a reduction in the flux of solar radiation reaching the earth’s surface over large geographic areas. The magnitude of the effect can be significant. For example, it has been estimated that regional haze diminishes surface solar visible radiation over the eastern United States by ≈8% (7). The reduction in surface UV-B radiation from sulfate-containing aerosols has been estimated at 5–18% (8).

A vigorous scientific effort is currently underway to assess the effect of atmospheric aerosols on surface temperatures and climate (9). Concerns about the impact of regional haze on visibility (as well as their effect on human health) has led to proposals to reduce the concentration of fine particles through regulation and emissions control (10). In this work we examine a different but potentially significant environmental impact of regional haze: namely, the effect on the yields of crops due to a reduction in the solar radiation reaching the earth’s surface. Considerable research has already been carried out on the effects of air pollutants on crop yields and the mechanisms by which these effects are induced. While it has been found that crop losses from air pollutants can be significant, the research has focused almost exclusively on the effects induced by phytotoxic compounds: e.g., ozone (11–13). Moreover, while previous investigators have noted the significant reduction in solar radiation that can occur as a result of regional haze (7, 14), and others have found crop yields to be sensitive to the amount of sunlight they receive (15–21), this work attempts to connect these separate findings by assessing the direct impact of regional haze on crop yields.

China as a Case Study.

To examine whether regional haze can affect crop yields, we adopt a case study approach and focus on China. We do this for two reasons. In the first place, observations suggest that regional haze over China is especially severe (22, 23), and thus it represents an opportune region for an initial assessment of regional-haze effects.

Secondly, agricultural productivity is generally recognized to be a critical factor in determining the future economic trajectory of China. China is the most populous nation in the world, with one of the most rapidly developing economies (24). The question of whether China will be able to feed its growing population and at the same time sustain a rapid pace of economic development has been the subject of considerable debate (25–27). It is generally agreed that China’s food demand will increase by ≈1%⋅yr⁻¹ over the next two decades. Less certain is whether China will be able to meet this growing demand internally or will have to import increasing amounts of foodstuffs from other nations. One aspect of resolving this question is understanding the extent to which air pollution affects the yields of crops grown in China and how this effect may change in the coming decades.

Given China’s heavy reliance on coal, its burgeoning industrial sector, and its growing use of automobiles (28, 29), regional air pollution may already be affecting crop yields in China. In fact, recent analyses of non-urban air quality data from China and regional air quality model simulations indicate that agricultural areas in China are exposed to potentially harmful amounts of phyotoxic pollutants such as O₃ and acidic precipitation (30, 31). However, because of a lack of data on the effect of these pollutants on crops grown in China, it has not yet been possible to quantitatively assess their impact on agricultural productivity.

In contrast to phyotoxic pollutants, the amount of solar radiation reaching the earth’s surface is a standard input variable in so-called crop-response models, used to simulate the yields of specific crops as a function of environmental conditions (32). Moreover, these models have been tested and applied to agricultural systems throughout the world, including those in China (33–37). Thus, these models can be used to calculate the effect of changes in surface solar radiation on the yields of specific crops grown in China. By combining these calculations with estimates of the effect of regional haze on solar radiation in China, it should be possible to derive a rough lower limit estimate of the impact of regional air pollution on China’s agricultural productivity.

Atmospheric Aerosols and Solar Radiation.

The amount of solar radiation reaching the earth’s surface is quantified here in terms of I_s(λ), the surface solar irradiance as a function of wavelength, λ. I_s has units of W⋅m⁻²⋅μm⁻¹ and is defined as the number of watts of solar radiation having wavelengths between λ and λ + dλ (in units of micrometers) that impinge on a square meter of the earth’s surface. The total surface solar irradiance, I_s^tot, has units of W⋅m⁻² and is obtained by integrating I_s over the solar spectrum:

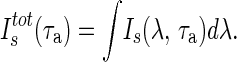1

In general, I_s can be divided into two components: (i) I_s^dir, the direct irradiance representing the direct beam of light from the sun; and (ii) I_s^diff, the diffuse irradiance or skylight representing the radiation from the sun that reaches the surface after having been scattered by atmospheric gases, aerosols, and/or clouds.

As noted above, atmospheric aerosols can reduce I_s via the direct effect, whereby solar photons are scattered and absorbed by the aerosols themselves, and the indirect effect, whereby aerosols enhance the ability of clouds to scatter and absorb solar photons (2, 3). Because the magnitude of the indirect effect is far more uncertain than that of the direct effect (4, 5), only the direct effect is considered here.

The direct effect of aerosols on I_s can be described in terms of the three unitless parameters: the aerosol optical depth, τ_a, the aerosol single scattering albedo, w_a, and the aerosol asymmetry factor, g_a. Like I_s, all three of these parameters vary with wavelength, λ. The optical depth is given by

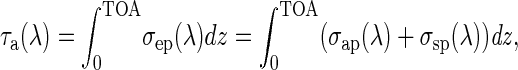2

where TOA is used to represent the top of the atmosphere, and σ_ep is the aerosol (or particulate) extinction coefficient: i.e., the sum of σ_ap and σ_sp, the aerosol absorption and scattering coefficients, respectively. These coefficients have units of m⁻¹ and represent the inverse of the e-folding length for attenuation of an incident beam of radiation by aerosols due to absorption and/or scattering. Note that since τ_a is obtained by integrating a quantity having units of m⁻¹ over height, it is unitless.

Values for τ_a are usually reported for λ = 550 nm. Extrapolation of this value to other wavelengths is often made by using an empirically derived parameter, a, referred to as the Angstrom exponent (38):

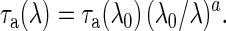3

When most of the aerosol scattering is due to submicron-sized fine particles, the Angstrom exponent in the visible range of the spectrum is typically ≈1. However, values as large as 2 or more can apply if the scattering is due to superfine mode aerosols and as small as 0 (or even slightly <0) if the scattering is due to fine particles >1 μm and/or coarse particles (32, 33). What little data from China that is available suggests that an Angstrom exponent of ≈1 is appropriate for anthropogenic aerosols (see, for example, ref. 41).

The physical meaning of the optical depth can be understood in terms of its relationship to I_s^dir. For example, in a cloudless atmosphere,

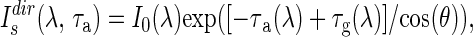4

where I_o(λ) is the solar irradiance at wavelength λ entering the top of the atmosphere, θ is the solar zenith angle, and τ_g is the optical depth due to (Rayleigh) scattering by atmospheric gases. Thus we see that the optical depths, τ_a and τ_g, are the values needed in the exponent of Eq. 4 to calculate the direct surface irradiance when the sun is directly overhead. The “cos θ” term is used to correct for the longer path length needed to traverse the atmosphere when the sun is not overhead.

From Eq. 4, it follows that the magnitude of I_s^dir relates exponentially and inversely to τ_a. By contrast, I_s^diff tends to increase with τ_a. (This occurs because an increase in τ_a increases the amount of light scattered and, hence, the amount of diffuse radiation reaching the surface.) I_s^diff also depends on w_a and g_a. The single scattering albedo, w_a, is the ratio of scattering to total extinction by the aerosols: i.e.,

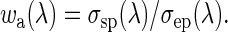5

The asymmetry factor, g_a, is used to define the fraction of scattered radiation that is scattered in the forward direction. This fraction can be approximated by (1 + g_a)/2; when g_a = 1, all radiation is scattered in the forward direction, and when g_a = −1, all is scattered in the backward direction.

I_s^diff tends to increase with increasing w_a and g_a, as well as τ_a. However, because of the possibility of multiple scattering (by gases, cloud droplets, and aerosols), as well as the fact that σ_sp, σ_ep, w_a, and g_a can vary with height, I_s^diff is a complicated function of the relevant parameters, and numerical simulations are generally required to calculate its magnitude.

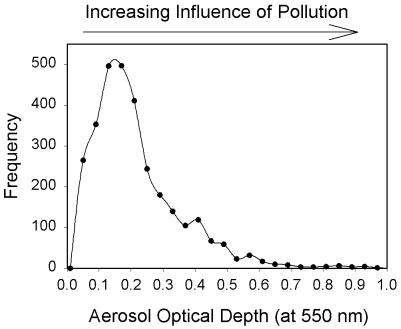
Under unpolluted conditions over continents, τ_a is generally ≈0.05 or less, w_a is >0.9, and g_a is ≈0.7 (9). By comparison, τ_g is ≈0.06. Thus, in clean air, most of the scattering of visible radiation from the sun is generally caused by Rayleigh scattering. As conditions become more polluted and the fine particle concentrations in the lower 1- 2 km of the atmosphere increase, τ_a increases. If the particles contain a significant amount of elemental carbon, w_a decreases. As a result, aerosol scattering and absorption can dominate over Rayleigh scattering in the polluted atmosphere. This is, in fact, the case over much of the eastern half of the United States, where annually averaged values of τ_a generally range from ≈0.2 to 0.5 (1, 42). At a site in Oklahoma, for example, observations during 1998 yielded a τ_a of 0.2 ± 0.14 (see Fig. 1).

Figure 1.

Frequency distribution of aerosol optical depth at 550 nm observed at the U.S. Department of Energy Southern Great Plains Atmospheric Radiation Measurement Site in Oklahoma during 1998 (43). (Data courtesy of R. Halthore and A. Cronet.)

Model-Calculated Aerosol Optical Depths Over China.

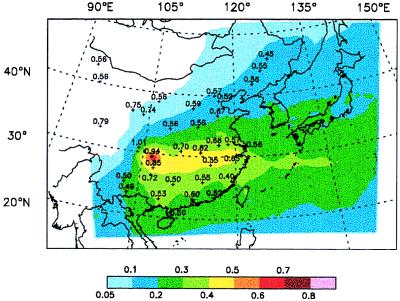
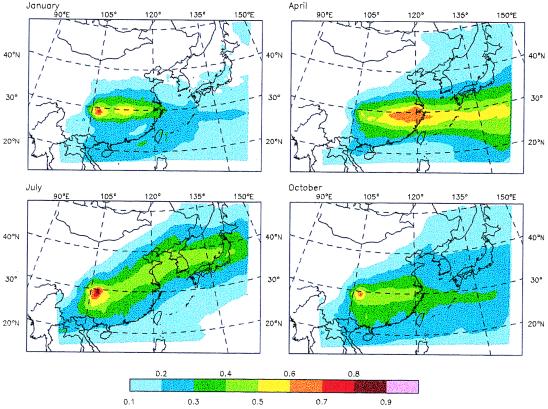
Fig. 2 depicts annually averaged values for τ_a (at 550 nm) over China derived from a 12-month (August, 1994–July, 1995) simulation of the regional distribution of anthropogenic sulfate aerosols in East Asia using the coupled, regional climate/air quality model of Chameides et al. (30). (Also depicted in Fig. 2 are τ_a values derived from surface solar irradiance measurements at 35 sites in China; these will be discussed later.) In Fig. 3, model-based τ_a values are illustrated for 4 months of the year, each representative of one of the four seasons.

Figure 2.

Annually averaged values for τ_a (550 nm) over China: model-estimated values are indicated by color coding; numbers and crosses indicate measurement-based values from Zhou et al. (23) and the locations where the data were collected.

Figure 3.

Average model-estimated values for τ_a (550 nm) over China for the months of January, April, July, and October.

The model-based τ_as in Figs. 2 and 3 were calculated from Eq. 2, with the aerosol extinction coefficient given by

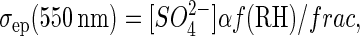6

where [SO₄²⁻] is the model-calculated aerosol sulfate concentration (in g⋅m⁻³), α = 5.3 m²⋅g⁻¹ is the specific extinction coefficient for dry sulfate aerosols (4), f(RH) ≥ 1 and accounts for the increase in scattering as relative humidity, RH, increases due to deliquescence (5), and frac is the ratio of the extinction due to the sulfate portion of the aerosols to the total aerosol extinction. Measurements in urban-source regions in northeastern China indicate that sulfate is responsible for ≈ 50% of the total aerosol scattering (44). We therefore assumed a value of 0.5 for frac.

Inspection of Fig. 2 reveals annually averaged τ_as ranging from 0.05 or less in western China (where anthropogenic emissions are relatively small) to almost 0.7 in the Sichuan area. In the eastern part of the country, annually averaged optical depths tend to be largest in the central portion of the nation (i.e., Sichuan and the Yangtze Delta) relative to areas lying to the north and south. From Fig. 3, we see that the region of maximum optical depths tends to move northward and southward with the seasons, reflecting the changing wind patterns and actinic fluxes. It should be noted that the springtime is the period when China (especially northern China) experiences significant loadings of wind-blown dust. However, since our estimates were derived from model simulations of anthropogenic sulfate aerosol, the influence of wind-blown dust is not reflected in the figures.

Comparison with Aerosol Optical Depths Inferred from Radiation Measurements.

The τ_a values derived from radiation measurements in Fig. 2 are from Zhou et al. (23). These investigators retrieved aerosol optical depths from data collected over a 12-year period (1979–1990) at meteorological stations located near the outskirts of various cities throughout China. The τ_as were derived by using the method of Qiu (45), in which the total extinction of the direct beam of sunlight by aerosols is inferred from measurements at each site of I_s^dir under cloud-free conditions, the number of sunshine hours, and surface water vapor partial pressure, as well as the appropriate ozone column abundance from the Total Ozone Measurement Satellite (TOMS) Version 7. Zhou et al. (23) reported τ_as for a wavelength of 750 nm. In Fig. 2, we have scaled these values to a wavelength of 550 nm (which is a more conventional wavelength for reporting τ_a), assuming an Angstrom exponent of 1. However, this scaling does not introduce any additional uncertainty since Zhou et al. assumed the same value for the Angstrom exponent in their original derivation.

Inspection of Fig. 2 reveals some qualitative consistency between the model-based and measurement-based τ_as; for example, both have maximum values in the Sichuan area and generally lower values to the north and south of the Yangtze Delta region. However, there are significant quantitative differences, with the measurement-based τ_as being larger than the model-based values at all locations. The smallest relative difference is found in the Sichuan area, where the measurement-based τ_as are ≈30–40% larger than the model-based values. In southeastern China, they differ by a factor of ≈2, in northeastern China the difference is as much as a factor of 5, and to the west of Sichuan the difference is a factor of 10 or more.

There are a number of possible explanations for the discrepancies. For example, the measurement-based values may be essentially correct and the model-based values too low, either because of an under-prediction in SO₄²⁻ or an overestimation in frac. There is in fact some evidence in support of this view. The measurement-based τ_as are about a factor of 2 larger than those typically observed in the eastern United States (i.e., 0.5–0.9 in China and 0.2–0.5 in the United States). This is qualitatively consistent with the particle emission inventories for the two countries estimated by Wolf and Hidy (46): 46 × 10¹² g⋅year⁻¹ in China and ≈22 × 10¹² g⋅year⁻¹ in the United States. The measurement-based τ_as are also about a factor of 2 larger than those inferred from similar measurements made between the late 1950s and 1980 (47). This is also qualitatively consistent with emissions inventories, which indicate that anthropogenic emissions in China increased by a factor of ≈2 from the 1970s to the 1980s (48).

It is also possible that the measurement-based τ_as are too large, perhaps because of an improper filtering of cloud-influenced data. The rather large τ_a values reported by Zhou et al. (23) in the western part of China, where anthropogenic emissions are relatively low, suggest that this may have occurred for at least some of the sites.

A third possibility is that both the measurement-based and model-based τ_as are correct but reflect different spatial scales. Since the radiance measurements were made in suburban locations, these data may have been affected by local pollution sources and thus are not representative of the surrounding region. The model results, on the other hand, were obtained by using a 60- × 60-km grid and are, by definition, regional in scale.

In the calculations presented below, we use the model-estimated τ_a values to evaluate the effect of regional haze in China on surface solar irradiance and, in turn, on crop yields. Since the model-estimated τ_a values are the smaller of the two sets of τ_as, this approach provides us with a more conservative measure of the regional-haze effect.

Calculations of I_s Over China.

To estimate the direct effect of the aerosol loadings discussed above on solar radiation, a broad-band, one-dimensional radiative transfer model (49) was used to calculate the surface solar irradiance as a function of wavelength. The solar spectrum from 200 nm to 4 μm (i.e., the wavelengths that encompass ≈99% of the total solar irradiance reaching the top of the atmosphere) was divided into 15 bands. The radiative transfer equation for each band was then solved by using the Δ four-stream approximation, an approach that has been shown to be well suited for calculating solar radiative fluxes and heating rates in an atmosphere containing aerosols and clouds (50).

The magnitude of direct effect on the surface solar irradiance for a given value of τ_a was obtained by carrying out two sets of calculations—one with τ_a equal to the model-estimated value and another with τ_a set to zero—and then calculating ΔI_s^tot(τ_a), the relative change in the total surface irradiance, where

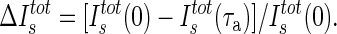7

Note that, given the above definition, a positive value in ΔI_s^tot denotes a reduction in the surface irradiance due to the aerosol direct effect.

The calculations were made by using July-averaged τ_as and July 15 solar zenith angles appropriate for each location. We have chosen summertime conditions because, although not shown here, the discrepancies between model-estimated and measurement-based τ_as tended to be smallest during July. The profiles for atmospheric temperature, pressure, water vapor, and ozone used in the model calculations were taken from the mid-latitude summer atmospheric conditions reported by McClatchey et al. (51). A flat surface with an albedo of 20% at 0 km above sea level was also assumed for all calculations. In addition to the above, the model calculations require the specification of a number of input parameters. These are discussed below and summarized in Table 1.

Table 1.

Assumptions and input parameters used in radiative transfer model

General conditions

All calculations: Appropriate for mid-July

Asymmetry Factor, ga

All calculations: ga = 0.67

Cloud parameterization

Cloud Free: None

Thin Cloud Case: 100% cloud cover, cloud transmissivity = 80%*

Thick Cloud Case: 100% cloud cover, cloud transmissivity = 40%*

Aerosol single scatter albedo, wa

Low Absorption Case: wa = 0.95

High Absorption Case: wa = 0.75

^*Clouds were assumed to be absorbing in the 250- to 350-μm range with a single scattering albedo of ≈0.65, weakly absorbing in the 350- to 400-μm range with a single scattering albedo of ≈0.9, and non-absorbing (i.e., only reflecting) at other wavelengths. 

The model calculations have a relatively weak dependence on the altitude profile for the aerosol scattering and absorption. This was defined by assuming that the aerosol scattering and absorption were linearly proportional to the total aerosol mixing ratio (with an altitude independent proportionality constant) and, in turn, specifying an altitude profile for the aerosol mixing ratio. In all calculations, the aerosols were assumed to be well mixed from the surface to the top of the boundary layer, which was set to a height of 2 km, a value appropriate for summer clear sky conditions. [Fine mode aerosols, as well as particles in the smaller-sized fraction of the coarse mode, are expected to be well mixed in the boundary layer because their atmospheric residence times are significantly longer than the few-hour mixing time of the boundary layer. Aircraft measurements of aerosol concentrations tend to support this inference (52).] Above the boundary layer, aerosol mixing ratios were assumed to decrease exponentially with altitude using a scale height of 1 km, similar to that of Liu et al. (8).

Clouds are highly variable in space and time and have a strong interaction with solar radiation. Thus our assumptions concerning clouds may have a significant effect on our model calculations. To assess the uncertainty in our calculations that might arise from clouds, we have carried out calculations with three different assumptions concerning cloud cover and the transmissivity of the clouds. In our base model calculations, we assume cloud free conditions. In addition, sensitivity calculations are presented for a “Thin Cloud Case” in which 100% cloud cover is assumed with a cloud transmissivity at all wavelengths of 80% and for a “Thick Cloud Case” in which 100% cloud cover is assumed with a cloud transmissivity of 40%. In each of these cases, ΔI_s^tot was calculated from Eq. 6 by using the value for I_s^tot(0) appropriate to that case.

The optical properties of the aerosols (i.e., w_a, g_a) depend on the chemical composition and size distribution of the aerosols over China (which have yet to be characterized and most likely vary with time and location). The model results are relatively insensitive to the asymmetry factor, g_a, and thus the specification of this parameter is not critical to our conclusions (53, 54). We have adopted a value of 0.67 and assumed that the angular distribution of the scattering could be represented with a Henyey-Greenstein phase function (55, 56).

Unlike the asymmetry factor, the model calculations are quite sensitive to the single scattering albedo, w_a. Recall from Eq. 6 that this factor decreases as the absorptivity of the aerosols increases. Absorption of solar radiation by aerosols is generally due to the presence of elemental carbon (e.g., in soot) or mineral aerosols. In the United States, a w_a of ≈0.9 is often observed (14). However, in China, where emissions of soot and dust may very likely be substantially higher, a value for w_a of 0.9 may be too high. Recent measurements made continuously over a 2-week period in Beijing by one of the authors (M.B.) indicated a mean w_a of 0.80 ± 0.06. To bracket the possible range in the single scattering albedo, we have carried out model calculations using two values for w_a: a “Low Absorption Case” with w_a = 0.95 and a “High Absorption Case” with w_a = 0.75.

Model results.

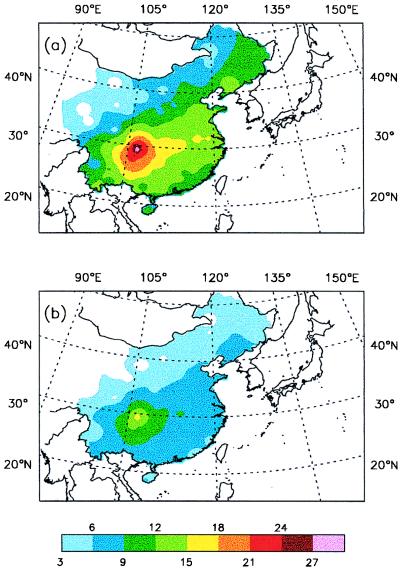
Fig. 4 illustrates the model-calculated spatial distribution in ΔI_s^tot(τ_a), the relative change in the total surface irradiance, for the Low and High Absorption Cases, assuming cloud free conditions and the model-estimated τ_a values. In both cases, the distribution closely mimics that of τ_a for the month of July illustrated in Fig. 3. In the Low Absorption Case, the reductions in I_s range from a few percent in western China to a little >15% in the Sichuan area, while in the High Absorption Case the maximum reduction approaches 30%. The larger reduction in I_s^tot for the High Absorption Case occurs because absorbing aerosols remove photons from the direct and diffuse beams while scattering aerosols only redirect the photons.

Figure 4.

Calculated ΔI_s^tot (in percent), the percent reduction in the total surface irradiance over China for summertime conditions using model-estimated τ_as. (a) The Cloud-Free, High Absorption Case. (b) The Cloud-Free, Low Absorption case.

Table 2 summarizes the sensitivity of our results to cloud cover and transmissivity. We find that the effect of these parameters depends on the absorptive properties of the aerosol. In the Low Absorption Case, the presence of a cloud deck tends to keep radiation that had been backscattered by aerosols in the boundary layer, thereby increasing the likelihood that it will eventually reach the surface. Thus, the aerosol effect is decreased somewhat by the presence of clouds in this case. In the High Absorption Case, on the other hand, aerosols cause greater absorption of photons that had been reflected back toward the surface by clouds. In either case, the uncertainty introduced into the calculations of ΔI_s^tot by the possible presence of clouds is relatively modest: i.e., ≈20%. If conditions in China correspond to that the Thick Cloud/Low Absorption Case, the appropriate ΔI_s^tot values can probably be approximated by dividing those calculated for the Cloud Free/Low Absorption Case by a factor of 1.2. If, on the other hand, the Thick Cloud/High Absorption Case is more applicable, then ΔI_s^tot can be approximated by multiplying the ΔI_s^tot value calculated for the Cloud Free/High Absorption Case by 1.2. [The modest impact of clouds calculated here contrasts with similar estimates related to the direct effect of aerosols on surface temperature and climate; in the later case, clouds are found to significantly reduce the climatic cooling caused by aerosols (4). The reason for this difference is that aerosols generally lay below clouds and our calculations relate to the change in the solar irradiance that reaches the earth’s surface, whereas the climate calculations are based on the change in the irradiance reflected back to space.]

Table 2.

Sensitivity of radiative model simulations to cloud cover

Cloud Parameterization	ΔIstot, %
Low absorption case and τa = 0.3
Cloud-free	6.5
Thin cloud	6.1
Thick cloud	5.3
Low absorption case and τa = 0.6
Cloud-free	12.4
Thin cloud	11.7
Thick cloud	10.4
High absorption case and τa = 0.3
Cloud-free	11.7
Thin cloud	12.5
Thick cloud	13.7
High Absorption case and τa = 0.6
Cloud-free	21.5
Thin cloud	22.8
Thick cloud	24.7

In summary, our radiative transfer model calculations suggest that surface irradiances over China are reduced by a few percent to as much as 30% during the summer season as a result of the direct effect of regional haze. The highest reductions are found to occur in the portion of China that is east of ≈105°E latitude and bordered on the north by a line running in a northeasterly direction from about 35°N 105°E to ≈40°N 120°E. Within this area, ΔI_s^tot is ≥5% in the Low Absorption Case and ≥10% in the High Absorption Case. This is significant because this area encompasses some of China’s most productive agricultural regions, including those found in the Yellow, Yangtze, and Pearl River valleys. In the 1980s, ≈70% of China’s total grain production was harvested within this area (57).

The magnitude of the calculated reduction depends most strongly on the absorptive properties of the aerosols that make up the haze. Even under the most favorable of conditions (consistent thick clouds and very low absorption), surface irradiance reductions in excess of 5% would likely apply for much of China’s agriculturally important regions. Under highly unfavorable conditions, reductions in excess of 10% for these regions and >30% in the Sichuan Basin appear to be possible. It seems reasonable to expect that these reductions in surface irradiance could have a number of significant climatic and ecological impacts. In the next section, we examine whether the reductions in I_s^tot might have an impact on crop yields.

Effect of Reductions in Surface Irradiance on “Optimal” Crop Yields Grown in China.

To assess the likely impact of reductions in I_s^tot on crop yields in China, we carried out a series of sensitivity calculations using a crop response model for both rice and winter wheat. Before describing the specifics of these calculations, a brief discussion of the role of sunlight in limiting photosynthesis rates in agricultural systems is useful. In general, photosynthesis depends on a variety of inputs, including water and nutrients as well as sunlight (58). Any one of these inputs can limit the rate at which green plants carry out photosynthesis and store carbon. In natural or unmanaged ecosystems, nutrients and/or water are often limiting, and thus reductions in surface solar irradiance may not have a significant impact on photosynthesis rates. In managed ecosystems such as those in cultivation for food crops, on the other hand, conditions are often manipulated to maximize crop yields through irrigation and the application of fertilizers. Thus the possibility that surface irradiance can affect net yields of crops is far greater.

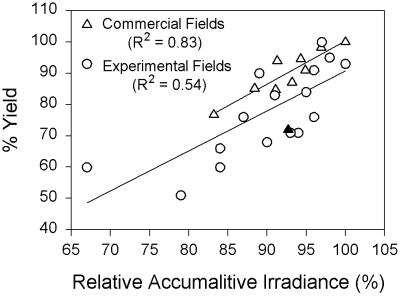
In the specific case of rice, field observations tend to confirm that yields are, in fact, affected by the amount of solar radiation received by the crops (15–17, 20). For example, Fig. 5 illustrates data gathered on rice grown in commercial and experimental fields in Texas. In both datasets, there is a statistically significant positive correlation between the rice yields and the cumulative surface solar irradiance received during a 40-day period when rice has its greatest sunlight requirement. On the basis of these and other data, Stansel and Huke (15) posited a strong linear relationship between solar radiation and the yields of rice. Wheat yields are more often limited by moisture or temperature than by solar radiation. However, when these conditions are not limiting, yields can be affected by variations in solar radiation receipt (18).

Figure 5.

Scatterplots of measured yields of rice cultivated in Texas as a function of accumulated surface solar irradiance received during a 40-day critical sunlight-requiring period for rice beginning with panicle differentiation and ending 10 days before maturity. The triangles represent annual data from commercial fields in Orange and Jefferson Counties cultivated with rice from 1964 to 1973. The closed triangle is the datum obtained in 1969, a year with adverse weather conditions; this datum was not included in the calculation of the indicated R² value. The circles represent annual data obtained from experimental fields in Texas cultivated from 1963 to 1967 with varying planting dates. For the commercial-field data, 100% accumulated solar irradiance is equal to 1.3 × 10⁸ J⋅m⁻² (and was observed in 1971) and 100% yield is equal to 4,784 kg⋅ha⁻¹ (and was observed in 1971). For the experimental-field data, 100% accumulated irradiance is equal to 1.6 ×10⁸ J⋅m⁻² (and was observed in one of three fields tested in 1964) and 100% yield is equal to 5,988 kg⋅ha⁻¹ (and was observed in one of three fields tested in 1965). Data are taken from Stansel and Huke (15).

In the crop response model calculations presented here, we assume a sufficiency of water and nutrients for the crops so that they are never subjected to water and/or nutrient stress. For this reason, our results represent the effect of reductions in I_s^tot on optimal crop yields as opposed to crop yields grown under a specific set of conditions during a specific year. Depending on the actual conditions under which the crops are grown in China, these optimal yields may or may not reflect the actual yields.

Crop response model.

Our crop response simulations were carried out by using the ceres 3.1 Rice and Wheat models (59, 60) with the Priestley-Taylor method of estimating potential evapotranspiration. The models use mathematical functions to simulate the growth and yield of rice and wheat as a function of plant genetics, weather, soil, and management factors. Processes modeled include phenological development, vegetative and reproductive plant development stages, production and partitioning of photosynthates, growth of leaves and stems, senescence, biomass accumulation, and root system dynamics. (Respiration is not explicitly treated in this class of crop model.) Soil and management inputs include soil characteristics, cultivar type, row spacing, fertilizer amount, sowing and harvest dates, and irrigation. Weather inputs include daily maximum and minimum temperature, precipitation, and total surface solar irradiance.

As is the case with many quasideterministic crop models, production of biomass in the ceres models is treated as a linear function of incoming photosynthetically active radiation. Photosynthetically active radiation at the top of the plant canopy is assumed to be 50% of the total surface solar irradiance and is attenuated through the plant canopy as an exponential function of leaf area index. Under optimal conditions, the production of photosynthate increases with increasing photosynthetically active radiation up to the point of light saturation (58).

Our simulations were carried out for rice and winter wheat crops grown in Nanjing. Table 3 lists the input data for each crop simulation, as well as the yields obtained assuming 100% of the observed surface solar irradiance. For each crop, we carried out five simulations: the base case, using 100% of the observed I_s^tot, as well as cases with I_s^tot increased and decreased by 10 and 20%. In the ceres models, changes in solar radiation affect photosynthesis and potential evapotranspiration. An increase in solar radiation increases carbohydrate accumulation due to increased photosynthesis, and increases potential evapotranspiration. (The opposite is true for a decrease in solar radiation.) The increase in carbohydrate accumulation over an entire growing season leads to an increase in yield. On the other hand, the increase in potential evapotranspiration may potentially cause water stress and negatively affect yield. Since our calculations were conducted assuming no water stress, this effect was not considered. Another process not considered is the effect of changes in solar radiation on temperature. Under real-world conditions, an increase in surface solar irradiance would tend to cause an increase in temperature (particularly maximum temperature), which would also affect crop growth and yield (58).

Table 3.

Crop model inputs and base results for wheat and rice yields in Nanjing

	Weather data*	Sow date	Harvest date	Mean yield for base model†, kg/ha
Wheat	1969–1979	November 9	June 8	4,053
Rice	1970–1979	May 10	September 25	12,138

^*Input weather data consisted of averages of observations made during the indicated years. The data were obtained from Nanjing Agricultural Sciences (courtesy of Jin Zhiqiang). 

^† Base model represents the simulation using 100% of the observed total surface solar irradiance. 

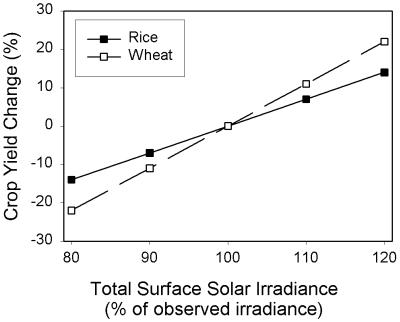
The model-calculated rice and wheat yields are illustrated in Fig. 6. Similar to the observations illustrated in Fig. 5, the simulated yields for both crops responded linearly to changes in surface solar irradiance. In the case of wheat, we found a little more than a 1% increase (decrease) in yields for each 1% increase (decrease) in solar irradiance. For rice, the sensitivity was somewhat lower; i.e., an ≈0.7% increase (decrease) for each 1% increase (decrease) in solar irradiance. Similar results were found in sensitivity analyses of the simriw rice model (21).

Figure 6.

Model-calculated percentage change in crop yields as a function of the assumed total surface solar irradiance, with 100% representing the observed irradiance. The calculations were carried out by using conditions appropriate for Nanjing (see Table 3).

Because our crop-response model calculations were carried out for only one site, our results should not be viewed as being definitive for Chinese agriculture as a whole. Such a definitive understanding of the relationship between solar radiation and crop yields in China will require region-specific field studies, as well as more comprehensive crop-model simulations. With this caveat in mind, we address the implications of our model calculations for Chinese agriculture in the next section.

Implications for Agriculture in China: An Opportunity for Increased Crop Yields.

If the crop yield model calculations discussed in the previous section for rice and wheat grown in Nanjing are generally applicable to Chinese agriculture, then our calculations suggest that air pollution and regional haze in China are having a significant impact on the optimal yields of crops grown in the nation. The predicted reduction in yields for China’s highly productive eastern agricultural regions ranges from a little less than 5 to more than 30% and depends most critically on the absorptive properties of the aerosols. However, it is likely that this range represents a lower limit because (i) the indirect effect of aerosols on solar radiation was neglected; (ii) the radiative transfer calculations were carried using the smaller, model-estimated τ_as; (iii) the possible reduction in surface irradiance by the pollutant nitrogen dioxide was not considered (61); and (iv) the effects on crops of phytotoxic air pollutants typically associated with regional haze such as ground-level ozone (30) were not considered.

One implication of our results is that mitigation of regional haze over China could have the benefit of significantly increasing the optimal yields of crops grown in the nation. Translating these optimal-yield increases into actual increases in agricultural productivity would of course require sufficient supply of water and nutrients. However, given China’s plans to boost agricultural productivity by ≈30% over the next three decades (27), this would not appear to be a problem.

Conclusion.

A rudimentary assessment of the direct effect of atmospheric aerosols on agriculture in China suggests that optimal crop yields are significantly affected by regional-scale air pollution and its associated haze. This in turn implies that the mitigation of this pollution could help boost crop yields in China. Our calculations suggest that, under optimal growing conditions, crop yields in eastern China could be enhanced by ≈5–30%, possibly more if the indirect effect by aerosols and other air pollutants also significantly affect crop yields.

Whether such a scenario is feasible and economically realistic is a question whose answer will require a good deal of further study—including more detailed measurements of the chemical and optical properties of aerosols over agricultural areas of China. Nevertheless, given the projections of a rapidly rising food demand in China in the coming decades, and concerns about whether this rising demand can be met internally through enhanced agricultural productivity, further study may prove to be a worthwhile endeavor.

More generally, it should be noted that regional haze is not unique to China. It occurs in virtually all heavily populated regions, those that are developing economically as well as those that are already economically developed (4, 14). While a good deal of effort is being made to characterize the climatic impact of this reduction, further investigation of the direct ecological impacts, especially those occurring within agricultural systems, may also prove to be worthwhile.