Systems biology of embryonic morphogens

Abstract

A network of secreted proteins that interact with each other in the extracellular space regulates embryonic morphogenesis. Mathematical modeling offers an excellent opportunity to understand how morphogens signal and self-regenerate pattern.

The regulatory nature of embryonic development

The ways and means by which orders for different developmental pathways are handed out in proper spatial coordination to the parts of a developing system constitute one of the central problems of developmental biology. (Klaus Sander, 1976)

A central problem of systems biology is to understand the chemical reactions of living organisms as a whole, rather than as a reductionist sum of individual reactions. One way of overcoming this challenge is through mathematical modeling. Developmental biology presents a special challenge, since the building of an animal is one of the most complex tasks performed by a biological system. Animal embryos develop into a huge diversity of morphologies adapted to a wide range of ecological environments, yet all use a conserved set of molecular mechanisms to coordinate morphogenesis. Here we explain how the network of extra-cellular signals that controls dorsal–ventral (back-to-belly) patterning in the embryo of the clawed African frog Xenopus provides, in our opinion, one of the best opportunities for understanding in physicochemical terms how patterning signals are coordinated spatially over an entire organism.

Embryonic development requires great robustness, for perfect offspring must be produced time after time despite environmental and genetic variations. While embryologists lacked for most of the last century any knowledge of the chemistry of development, they were able to capture fundamental concepts on the resilient embryo through ablation, cutand-paste transplantation techniques, and genetic analyses. From the very beginnings of experimental embryology it was realized that embryos have an astounding capacity to self-regulate.¹ If an early embryo is cut in half along the antero-posterior axis, each part can regenerate a complete half-sized identical twin, regardless of whether the hapless subject is a cricket² or an amphibian embryo.³ Groups of cells capable of such regenerative feats are called morphogenetic fields, and are found not only in early embryos, but also in developing organs (such as limbs, heart, eyes, lens, and many others) and in some animals even in the adult.⁴ Embryological studies culminated with the realization that transplantation of a small tissue fragment, the amphibian dorsal gastrula organizer, was able to induce neighboring cells to differentiate into a perfectly patterned Siamese twin after transplantation into a host embyo.³ The discovery of embryonic induction earned the 1935 Nobel Prize of Medicine for Hans Spemann.

Recent progress in molecular biology has revealed that the development of all animals is controlled by a conserved toolkit of signaling pathways and genes.⁵ By using a reductionist approach it has been possible to assign functions to many genes, but we still lack a global understanding of how they work coordinately to organize morphogenetic fields.

The mathematics of development

In experimental physics, chemistry, and engineering, mathematical modeling has generated insights that could not have been reached by intuition alone, providing an invaluable tool to predict and control the behavior of physical systems. Mathematical modeling is currently becoming an area of intense interest also in biology, and may help understand the rules that regulate morphogenetic fields.

Alan Turing, the famous British mathematician credited with the invention of the computer, was the first to model embryonic patterning.⁶ In 1952 he proposed that a system of chemical substances capable of reacting together and diffusing through a tissue would be able to generate pattern. He coined the new term “morphogen” for the mysterious diffusing chemical, a name that is still in use by biologists today. In his landmark paper⁶ Turing formulated a general partial differential equation to describe quantitatively the changes in morphogen concentration (∂C) over time (∂t):

$$\frac{\partial C}{\partial t}=D\cdot {\nabla }^{2}C+F\left(C\right)$$

The right side of the equation describes that, following Fick's law of diffusion in a fluid medium, the change in concentration of the morphogen at any given point is proportional to its diffusion rate (D) and to the second derivative in space of the morphogen concentration (▽²C). In addition, the change in morphogen concentration is also a function (F) of all the chemical reactions that it undergoes (e.g., its synthesis and its degradation). From this initial insight a large set of “reaction–diffusion” equations have been derived. The mathematical modeling of morphogenesis was greatly advanced by Hans Meinhardt⁷, who demonstrated theoretically that a pair of morphogens composed of an Activator and an Inhibitor diffusing from the same cellular source can generate a stable pattern, provided that the inhibitor diffuses at a faster rate than the activator (Fig. 1). He proposed that the general condition for obtaining pattern stability was local self-enhancement (i.e., the activator drives its own synthesis and that of the inhibitor) coupled to long-range inhibition. Remarkably, these two mathematicians provided a theoretical framework for understanding patterning at a time when the chemical nature of not a single morphogen was known.^6,7

Fig. 1.

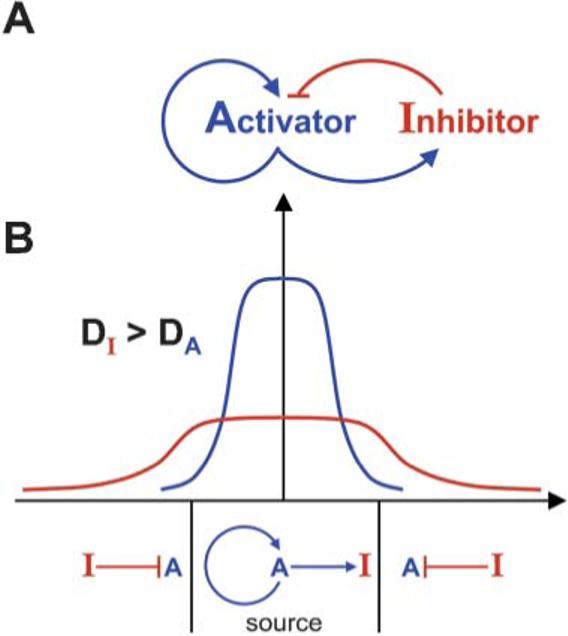
Stable patterning by an Activator/Inhibitor pair according to Meinhardt. (A) The system consists of two diffusible morphogens secreted by the same source. The activator turns on itself and its own inhibitor. (B) A field of cells can be stably patterned into two different zones, provided the inhibitor diffuses faster than the activator. The activator and inhibitor are synthesized in the source at the center, and turned off by a preponderance of the inhibitor in the periphery.

A network of secreted patterning proteins

The frog gastrula embryo is a hollow ball of 1.2 mm containing about 10,000 cells, in which the endoderm and mesoderm cell layers move to the inside through a circular blastopore lip (Fig. 2A). At this stage cells have not formed differentiated tissues yet, and are mainly dedicated to producing signals that communicate their position with respect to the whole. Since frog eggs are available in large numbers and can be dissected into dorsal and ventral regions, many cDNAs encoding dorsal–ventral signals have been cloned in the past 15 years. It was found that many novel secreted proteins emanated from two centers at the dorsal and ventral poles^1,8 (Fig. 2). The biochemical activities of these proteins have been investigated, and some have been found to encode growth factors (such as Bone Morphogenetic Proteins, BMPs) that signal by binding to cell surface receptors, which in turn phosphorylate transcription factors (such as Smad1) that move into the nucleus and activate gene transcription. Many other secreted proteins turned out to be inhibitors that bind to growth factors in the extracellular space and prevent them from binding to receptors (such as the secreted antagonists Chordin, Noggin, Follistatin, Cerberus, Frzb-1 and sFRPs).⁸ The frog embryo has the advantage that it can be readily manipulated, not only by cut-and-paste surgical experiments, but also by knocking down multiple genes simultaneously via micro-injection of the recently developed anti-sense Morpholino oligos. These reagents block mRNA translation and are similar to oligonucleotides, except that the ribose or deoxyribose moiety is replaced by a morpholine heterocyclic ring resistant to cellular nucleases.⁹

Fig. 2.

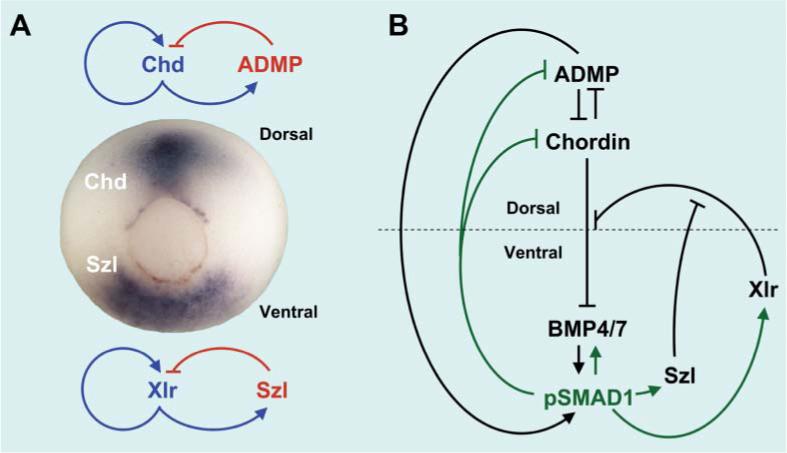
Patterning of the Xenopus gastrula. (A) The Xenopus gastrula has dorsal and ventral signaling centers, marked here by the expression of Chordin (Chd) and Sizzled (Szl) mRNA, respectively. Each center is regulated by an Activator/Inhibitor pair. The circular structure seen is the blastopore, which eventually becomes the anus. (B) An extracellular network of proteins that regulates the transcription factor Smad1 in the Xenopus gastrula. This self-regulating circular system controls embryonic patterning.¹⁰,¹¹

Fig. 2B shows the genetic network required for dorsal–ventral patterning, as determined by loss-of-function experiments in Xenopus.^10,11 The dorsal center secretes the BMP antagonist Chordin and a BMP-like molecule¹⁰ called ADMP (an acronym for Anti-Dorsalizing Morphogenetic Protein). Dorsal genes are expressed when levels of Smad1 signaling are low, so Chordin serves as the activator and ADMP as the inhibitor in this case (Fig. 2A). In the ventral center, gene expression is driven by high phospho-Smad1 levels caused by binding of BMP4/7 to its receptors. An important ventral center component is a zinc metalloproteinase of the Tolloid/Astacin family called Xolloid-related (Xlr) in Xenopus. Tolloids are proteinases that cleave Chordin at two specific aspartates, causing the release of ADMP or BMP4/7 and therefore increased BMP signaling.⁸ Another interesting component of this molecular machinery is Sizzled (Szl), a Frizzled domain-containing protein that works as an inhibitor of the Xlr/Tolloid metalloproteinase.¹¹ Thus, in the ventral center Xlr serves as activator and Sizzled as its inhibitor (Fig. 2).

Remarkably, the dorsal and ventral centers communicate with each other through a chemical reaction in which Xlr/Tolloid catalyzes the digestion of Chordin. We have measured the kinetic properties of this reaction and determined that the enzyme has a K_m (Michaelis–Menten constant) of 25 nM for its Chordin substrate and a K_i (Inhibition constant) of about 20 nM for its inhibitor Sizzled. The inhibition is competitive, which means that both proteins bind to the same active site.¹² Large amounts of Chordin and Sizzled are secreted during Xenopus gastrulation that were measured, using specific antibodies, to be in the range of 30 nM each if they were uniformly distributed in the extracellular space; at the dorsal and ventral centers they must reach much higher concentrations.¹¹

Ventrally, digestion by Xlr serves as a sink for Chordin. In Drosophila, the homologue of Chordin (Short gastrulation) has been shown to flow in the embryo in a process driven by diffusion from its site of synthesis and degradation by the Tolloid protease in the opposite side of the embryo.¹³ Presumably Chordin in Xenopus also diffuses, carrying along inactive ADMP and BMP4/7 that are released by Xlr/Tolloid ventrally. Sizzled provides the brakes for the proteinase since it is transcribed at high phospho-Smad1 levels, serving as a negative feedback regulator when BMP levels are high.¹¹ When BMP levels are lowered, transcription of ADMP increases, as does its transport by Chordin to the ventral side where it restores BMP levels.¹⁰ In this view, the self-regulating BMP gradient is maintained by the continued flux of Chordin from its dorsal site of synthesis to its degradation sink in the ventral side. Importantly, this cycle of synthesis and degradation of Chordin is adjusted both by opposite transcriptional regulation intracellularly (dorsal genes switched off and ventral genes turned on by phospho-Smad1) and by regulated proteolysis extracellularly.

The electronic frog

This circular network of proteins^10,11 provides a molecular explanation for how a self-regulating morphogenetic field might be established in Xenopus (Fig. 2B). It is noteworthy that most components are extracellular proteins that directly interact with each other and that their chemical affinities can be quantified biochemically. Mathematical modeling has been applied to oocyte,¹⁴ antero–posterior¹⁵ and dorsal–ventral¹⁶ axial patterning in Drosophila. These studies have already demonstrated the power of the Turing–Meinhardt approach. However, the molecular mechanisms by which a morphogenetic field can self-regenerate pattern after experimental perturbations have not yet been investigated mathematically in this organism. Recent work in Xenopus suggests that the robustness of vertebrate development results from having a double gradient of BMPs originating from opposite poles of the embryo. The key to understanding self-regulation is the realization that the synthesis of these gradients is under opposite transcriptional control by the transcription factor activated by BMP signals.¹⁰

We are currently constructing an “electronic frog” mathematical model based on the observation that while the extracellular network is very complex, it has a very simple output: the intracellular levels of phospho-Smad1, which regulate the rate of synthesis of all other components of the system (Fig. 2B). In this model, which is still in its embryonic stages, the Turing reaction–diffusion equation has been fleshed out so that the function F includes all known chemical reactions of each component, such as its associating to and dissociating from other proteins, as well as its synthesis, and its degradation. All these partial differential equations are coupled, and the synthesis of each component dictated locally by the phospho-Smad1 input. The hope is that this modeling will provide an estimate of the diffusion constants that are difficult to measure in vivo for technical reasons, and perhaps yield unexpected surprises as well. We have not yet included other known components (e.g., Noggin and Follistatin). However, the Chordin–BMP axis provides the conserved core circuit that regulates dorsal–ventral patterning in all bilateral animals.¹⁷

If one could build a mathematical model capable of self-regeneration after it is cut in half, this may have applications for stem cell and organ regeneration studies, and perhaps engineering in general.

Conclusion

It is almost ironic that the study of one of the most complicated biological processes imaginable has provided physico-chemical insights into how a network of interacting proteins self-regulates in space. Developmental biology has historically attempted to understand the embryo as a complete system that develops seamlessly into an integrated organism.^2,3 This vocation may now be paying off as embryology intersects systems biology.

Biography

Jean-Louis Plouhinec is an Associate of the Howard Hughes Medical Institute at the University of California, Los Angeles. He studied mathematics and computer science at the Ecole Polytechnique, France, receiving the degree of Ingénieur. He received a PhD in evolutionary biology from the Paris XI University in 2005.

Edward M. De Robertis is Norman Sprague Professor of Biological Chemistry at UCLA and a Howard Hughes Medical Institute Investigator. He studied Medicine at the University of Uruguay and received a PhD in Chemistry at the Leloir Institute in Buenos Aires. He was a postdoctoral trainee in Embryology with Sir John Gurdon in Cambridge for six years.