Skip to main content
NCBI home page
Biology Letters logoLink to Biology Letters
. 2007 Nov 20;4(1):57–59. doi: 10.1098/rsbl.2007.0481

The effect of spatial structure on adaptation in Escherichia coli

Lilia Perfeito 1,*,†, M Inês Pereira 1,†, Paulo RA Campos 2, Isabel Gordo 1
PMCID: PMC2412928  PMID: 18029298

Abstract

Populations of organisms are generally organized in a given spatial structure. However, the vast majority of population genetic studies are based on populations in which every individual competes globally. Here we use experimental evolution in Escherichia coli to directly test a recently made prediction that spatial structure slows down adaptation and that this cost increases with the mutation rate. This was studied by comparing populations of different mutation rates adapting to a liquid (unstructured) medium with populations that evolved in a Petri dish on solid (structured) medium. We find that mutators adapt faster to both environments and that adaptation is slower if there is spatial structure. We observed no significant difference in the cost of structure between mutator and wild-type populations, which suggests that clonal interference is intense in both genetic backgrounds.

Keywords: adaptation, spatial structure, mutation rate, clonal interference

1. Introduction

Natural populations are often dispersed over a spatial environment where individuals compete locally. The effect of spatial structure on evolution and adaptation has been studied in several theoretical models (Rousset (2004) and for a recent review see Charlesworth et al. (2003)). A recent study has predicted that if mutation rates to new beneficial alleles are high, adaptation proceeds more slowly in a spatially structured environment than in one where competition is global (Gordo & Campos 2006). We can therefore say that there is an adaptive cost of spatial structure. The reason for this relates to an important phenomenon that limits adaptation in asexuals—the Hill–Robertson effect (1966) or clonal interference (Gerrish & Lenski 1998). In asexual organisms, clones with different beneficial mutations will compete with each other and only one will fix in the population. This leads to a reduction in the rate of adaptation and to an increase in the mean effect of fixed mutations (Campos & De Oliveira 2004). This interference is more important the higher the product of population size and beneficial mutation rate, that is, the higher the number of segregating mutations. If competition is local, the time to fixation is longer and the chance that another beneficial mutation will appear in a different individual, and compete with the first one, is higher (Gordo & Campos 2006). Therefore, adaptation in asexuals when there is spatial structure is slower than if there is no structure.

In nature, the spatial organization of individuals in a population is probably variable. Periodic changes in spatial structure have been modelled and it has been shown that these changes impose an even higher adaptive cost of spatial structure. This is so because newly arising mutations that have not yet risen in frequency at the time of the spatial rearrangement have a higher probability of being lost (Perfeito et al. 2006). Therefore, the biggest difference in adaptation rates should be seen between populations with a fluctuating spatial structure and populations with no spatial structure.

There are a few studies on adaptation of organisms in structured environments using experimental evolution in micro-organisms (Chao & Levin 1981; Korona et al. 1994; Rainey & Travisano 1998; Dionisio et al. 2005; Habets et al. 2006). However, none of these studies addressed differences in adaptation dynamics specifically.

In this work we use an experimental system with Escherichia coli to directly test the theoretical prediction that a structured environment has a high adaptive cost. We compare the rates of adaptation to a medium with no spatial structure and to a structured medium with periodical changes in spatial structure (Perfeito et al. 2006). We studied a wild-type E. coli strain and a mutator strain, where the impact of clonal interference is expected to be higher (Cooper 2007). We find that mutators adapt faster than wild-type populations in both environments. We also show that adaptation proceeds more slowly in a structured environment than in one where each individual competes with every other, for both mutators and wild-type. We therefore observe a cost of structure on the rate of adaptive evolution in both genetic backgrounds. This is expected theoretically when clonal interference plays a major role in the evolution of these populations.

2. Material and methods

(a) Bacterial strains

The E. coli strains used were K12 MG1655 srl::Tn10 MutS+ ara+, K12 MG1655 srl::Tn10 MutS+ Δara, K12 MG1655 srl::Tn10 MutS− ara+ and K12 MG1655 srl::Tn10 MutS− Δara, which were constructed by P1 transduction (Miller 1992) from strains K12 MG1655 Δara, K12 srl::Tn10 MutS− StrR and K12 srl::Tn10 MutS+ StrR kindly provided by I. Matic. When plated on rich medium supplemented with arabinose, the ara+ strains create white colonies, while the Δara strains give rise to red colonies, so the initial and final number of each strain can be readily assessed (Levin et al. 1977). The mutator strain has a mutation rate which is 60-fold higher than the wild-type (Trindade et al. in preparation).

(b) Experimental evolution

All populations were derived from single clones (either mutator or non-mutator) which were grown from stocks in 50 ml tubes with 10 ml of M9 minimal medium supplemented with 5% glucose (MM), at 37°C. Every day, the cultures were diluted and grown in a 60 mm diameter Petri dish with MM supplemented with agar (structured environment where the structure was randomized every day) or in a tube with liquid MM incubated at 230 RPM in an Infors HT Unitron Shaker (unstructured environment) so that approximately 6×106 bacteria were allowed to propagate for approximately 11 generations, reaching a final number of colony-forming units (CFUs) of 1010. The final CFU number was the same on either the Petri dishes or the tubes (Student's t-test: t90=0.43, p=0.67). The effective population size is Ne=B·G (Haldane 1927; Wahl et al. 2002), where B is the initial number of bacteria and G is the number of generations between bottlenecks. Ne was approximately 7×107 in both environments and the evolution occurred during approximately 275 generations. In the structured environment, five independent wild-type populations and six independent mutator populations were allowed to evolve. In the case of the unstructured environment, six independent populations of both wild-type and mutator were evolved. There was no significant difference either in liquid or solid medium in the adaptation rate of ara+ and Δara (Student's t-tests: p>0.05) strains, so they were grouped and analysed together. After 25 days (approx. 275 generations), all populations were competed with the ancestor in the same environment used in the evolution experiment to assess their fitness increase (see electronic supplementary material).

3. Results

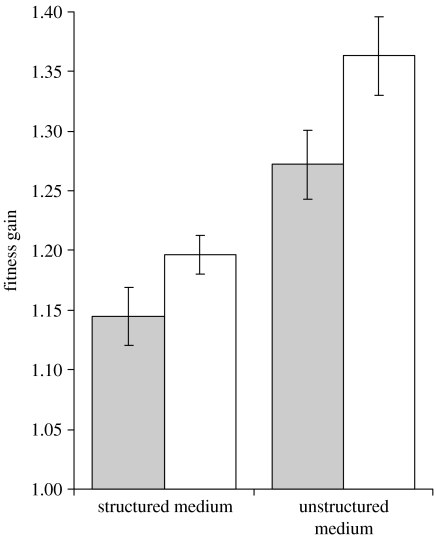
Replicate populations of both mutator and wild-type strains were allowed to adapt to either structured (liquid) or unstructured (solid) media and after 275 generations their fitnesses were measured. The results are summarized in figure 1. As expected, in both environments, the fitness was higher for the mutator strains than for the wild-type. This agrees with previous experiments in unstructured environments (de Visser et al. 1999) and we show here that the same is true for a structured environment (two-way ANOVA, p<0.001). Owing to their high mutation rate, the probability that a mutator will have a beneficial mutation is higher than the wild-type. Mutators also suffer from an increased probability of accumulating deleterious mutations (Funchain et al. 2000; Trindade et al. in preparation). Although the accumulation of deleterious mutations in our experiment is more likely in mutators, given our large population size, empirical estimates of deleterious mutation rate and effect and the mutator strength, these are probably purged in our populations (Crow & Kimura 1970).

Figure 1.

Figure 1

Open in a new tab

Mean fitness relative to the ancestral after 275 generations of evolution in either structured (solid) or unstructured (liquid) media. Grey bars represent the wild-type results and white bars represent the mutator populations. The error bars show twice the standard error.

Despite the fact that fitness increased in all cases, the augment was bigger in the unstructured environment, for both mutators and wild-type populations (two-way ANOVA, p<0.001 for both strains). So, as predicted theoretically, there is a cost on the speed of adaptation when there is spatial structure (Gordo & Campos 2006; Perfeito et al. 2006).

It was also predicted that the adaptive cost of structure (measured by the difference between the rate of adaptation in the unstructured and the structured environments, normalized by the rate in the unstructured environment) should increase with the rate to advantageous mutations (Ua) but have a limit for high Ua, in conditions where clonal interference has a major impact during adaptation (Gordo & Campos 2006). This limit is also observed when we consider a spatial structure that fluctuates in time (Perfeito et al. 2006; electronic supplementary material). We observe that after 275 generations of adaptation, the cost for the wild-type was 10% and for mutators it was 12%. Since this difference is not significant (two-way ANOVA, p=0.42), this suggests that the beneficial mutation rate is so large that further increases in the mutation rate do not lead to higher costs of structure. Nevertheless, the adaptation rate still increases with the beneficial mutation rate, which is expected under models that postulate intense clonal interference (Desai et al. 2007). In fact, a high Ua is compatible with recent estimates for E. coli on the order of 10−5 beneficial mutations per genome per generation (Perfeito et al. 2007).

To estimate the rate and effects of beneficial mutations that best describe the data, we used stochastic simulations of the process of adaptation in the unstructured environment during 275 generations (further details of the simulations are available on the electronic supplementary material). We find that a Ua∼10−6 (for the wild-type strain), and a mean selective effect of 2% can explain the observed fitness increases in the unstructured environment. Given an effective population size of 107 and an estimated Ua of 10−6, this implies that the effect of clonal interference is strong which can explain the observed cost of structure in both the genetic backgrounds, provided the beneficial mutation rates are similar in both environments.

4. Discussion

We study the adaptation of E. coli in structured and unstructured environments using strains with different mutation rates. Our results can be compared with recent predictions of theoretical models (Perfeito et al. 2006), which studied adaptation in fluctuating spatial environments. We show that mutator populations adapt faster than wild-type populations in both environments and that, independently of the mutation rate, the increase in fitness in the structured environment is smaller than in the unstructured one. This can be explained because, on one hand the effect of clonal interference is higher when there is structure (Gordo & Campos 2006), and on the other hand, the effect of genetic drift is higher when the spatial structure is not stable (Perfeito et al. 2006). We do not observe a significantly higher cost of structure for the mutators, which is expected if the adaptive mutation rate is very large in both genetic backgrounds.

Previously, Miralles et al. (1999) found that increasing population structure reduced the rate of adaptation in an RNA virus. Recently, Habets et al. (2006) used E. coli evolving in a structured environment with the aim of studying how spatial structure affects the emergence and maintenance of diversity in an ecological perspective. For this purpose, they analysed diversity parameters by comparing single clones from the evolved populations with the ancestor. In particular, they found that in an environment with a fixed spatial structure, frequency-dependent selection is very common, whereas in a mixed structure environment, as the one we use, frequency dependence is not detected. Importantly, they observed that adaptation is slower when there is no spatial structure, which is opposite to what we found. The discrepancy between the results may be due to a difference in methodology, because we measured fitness of a large sample of the evolved populations whereas these authors measured fitness of single clones (for more details, see electronic supplementary material).

In natural environments, there will always be some spatial structure. In particular, for bacterial communities, individuals are likely to compete locally and the spatial structure is likely to change in time. Bacteria biofilms are one such example. Biofilms show a high capacity to develop virulence and antibiotic resistance (Costerton et al. 1981). Although there may be a selective advantage in growing as groups in a spatial structure, there is also a cost due to a slower adaptation rate. Understanding the dynamics of adaptation in such structured environments might shed some light into how these structures evolve and what might be the best way to fight them.

Acknowledgments

This work was supported by project POCTI/BSE/46856/2002 through Fundação para a Ciência e Tecnologia. L.P. was supported by fellowship SFRH/BD/18161/2004 and P.R.A.C. by Conselho Nacional de Desenvolvimento Científico e Tecnológico. We thank the editor and anonymous reviewers for their helpful comments.

Supplementary Material

Details of the fitness measurements and Monte Carlo simulations, results of the Monte Carlo simulations and supplementary discussion

rsbl20070481s13.doc (33.5KB, doc)

References

  1. Campos P.R.A, De Oliveira V.M. Mutational effects on the clonal interference phenomenon. Evolution. 2004;58:932–937. doi: 10.1111/j.0014-3820.2004.tb00427.x. doi:10.1111/j.0014-3820.2004.tb00427.x [DOI] [PubMed] [Google Scholar]
  2. Chao L, Levin B. Structured habitats and the evolution of anticompetitor toxins in bacteria. Proc. Natl Acad. Sci. USA. 1981;78:6324–6328. doi: 10.1073/pnas.78.10.6324. doi:10.1073/pnas.78.10.6324 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Charlesworth B, Charlesworth D, Barton N. The effects of genetic and geographic structure on neutral variation. Annu. Rev. Ecol. Evol. Syst. 2003;34:99–125. doi:10.1146/annurev.ecolsys.34.011802.132359 [Google Scholar]
  4. Cooper T.F. Recombination speeds adaptation by reducing competition between beneficial mutations in populations of Escherichia coli. PLoS Biol. 2007;5:e225. doi: 10.1371/journal.pbio.0050225. doi:10.1371/journal.pbio.0050225 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Costerton J.W, Irvin R.T, Cheng K.J. The bacterial glycocalyx in nature and disease. Annu. Rev. Microbiol. 1981;35:299–324. doi: 10.1146/annurev.mi.35.100181.001503. doi:10.1146/annurev.mi.35.100181.001503 [DOI] [PubMed] [Google Scholar]
  6. Crow J.F, Kimura M. Harper and Row; New York, NY: 1970. An introduction to population genetics theory. [Google Scholar]
  7. de Visser J, Zeyl C, Gerrish P, Blanchard J, Lenski R. Diminishing returns from mutation supply rate in asexual populations. Science. 1999;283:404–406. doi: 10.1126/science.283.5400.404. doi:10.1126/science.283.5400.404 [DOI] [PubMed] [Google Scholar]
  8. Desai M.M, Fisher D.S, Murray A.W. The speed of evolution and maintenance of variation in asexual populations. Curr. Biol. 2007;17:385–394. doi: 10.1016/j.cub.2007.01.072. doi:10.1016/j.cub.2007.01.072 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dionisio F, Conceicao I, Marques A, Fernandes L, Gordo I. The evolution of a conjugative plasmid and its ability to increase bacterial fitness. Biol. Lett. 2005;1:250–252. doi: 10.1098/rsbl.2004.0275. doi:10.1098/rsbl.2004.0275 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Funchain P, Yeung A, Stewart J.L, Lin R, Slupska M.M, Miller J.H. The consequences of growth of a mutator strain of Escherichia coli as measured by loss of function among multiple gene targets and loss of fitness. Genetics. 2000;154:959–970. doi: 10.1093/genetics/154.3.959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gerrish P, Lenski R. The fate of competing beneficial mutations in an asexual population. Genetica. 1998;102–103:127–144. doi:10.1023/A:1017067816551 [PubMed] [Google Scholar]
  12. Gordo I, Campos P.R. Adaptive evolution in a spatially structured asexual population. Genetica. 2006;127:217–229. doi: 10.1007/s10709-005-4012-9. doi:10.1007/s10709-005-4012-9 [DOI] [PubMed] [Google Scholar]
  13. Habets M, Rozen D, Hoekstra R, de Visser J. The effect of population structure on the adaptive radiation of microbial populations evolving in spatially structured environments. Ecol. Lett. 2006;9:1041–1048. doi: 10.1111/j.1461-0248.2006.00955.x. doi:10.1111/j.1461-0248.2006.00955.x [DOI] [PubMed] [Google Scholar]
  14. Haldane J.B. A Mathematical theory of natural and artificial selection, part V. Selection and mutation. Proc. Camb. Philos. Soc. 1927;23:838–844. [Google Scholar]
  15. Hill W, Robertson A. Effect of linkage on limits to artificial selection. Genet. Res. 1966;8:269–294. [PubMed] [Google Scholar]
  16. Korona R, Nakatsu C.H, Forney L.J, Lenski R.E. Evidence for multiple adaptive peaks from populations of bacteria evolving in a structured habitat. Proc. Natl Acad. Sci. USA. 1994;91:9037–9041. doi: 10.1073/pnas.91.19.9037. doi:10.1073/pnas.91.19.9037 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Levin B, Stewart F, Chao L. Resource-limited growth, competition, and predation—a model and experimental studies with bacteria and bacteriphage. Am. Nat. 1977;111:3–24. doi:10.1086/283134 [Google Scholar]
  18. Miller J.H. Cold Spring Harbor Laboratory Press; Plainview, NY: 1992. A short course in bacterial genetics a laboratory manual and handbook for Escherichia coli and related bacteria. [Google Scholar]
  19. Miralles R, Moya A, Elena S.F. Effect of population patchiness and migration rates on the adaptation and divergence of vesicular stomatitis virus quasispecies populations. J. Gen. Virol. 1999;80:2051–2059. doi: 10.1099/0022-1317-80-8-2051. [DOI] [PubMed] [Google Scholar]
  20. Perfeito L, Gordo I, Campos P. The effect of spatial structure in adaptive evolution. Eur. Phys. J. B. 2006;51:301–306. doi:10.1140/epjb/e2006-00222-x [Google Scholar]
  21. Perfeito L, Fernandes L, Mota C, Gordo I. Adaptive mutations in bacteria: high rate and small effects. Science. 2007;317:813–815. doi: 10.1126/science.1142284. doi:10.1126/science.1142284 [DOI] [PubMed] [Google Scholar]
  22. Rainey P, Travisano M. Adaptive radiation in a heterogeneous environment. Nature. 1998;394:69–72. doi: 10.1038/27900. doi:10.1038/27900 [DOI] [PubMed] [Google Scholar]
  23. Rousset F. Princeton University Press; Princeton, NJ: 2004. Genetic structure and selection in subdivided populations. [Google Scholar]
  24. Trindade, S., Perfeito, L. & Gordo, I. In preparation. Rates and effects of spontaneous fitness-affecting mutations in mutator Escherichia coli [DOI] [PMC free article] [PubMed]
  25. Wahl L, Gerrish P, Saika-Voivod I. Evaluating the impact of population bottlenecks in experimental evolution. Genetics. 2002;162:961–971. doi: 10.1093/genetics/162.2.961. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Details of the fitness measurements and Monte Carlo simulations, results of the Monte Carlo simulations and supplementary discussion

rsbl20070481s13.doc (33.5KB, doc)

Articles from Biology Letters are provided here courtesy of The Royal Society

RESOURCES