Abstract
Considering the biological importance of heparan sulfate (HS) and the significant activity of its highly-sulfated regions (S-domains), the paucity of known functions for the non-sulfated NA-domains is somewhat puzzling. It has been suggested that chain dynamics within the NA-domains are the key to their functional role in HS. In this study, we investigate this hypothesis using state-of-the-art nuclear magnetic resonance (NMR) experiments at multiple frequencies. To resolve the problem of severe overlap in 1H-NMR spectra of repetitive polysaccharides from proteoglycans, we have prepared oligosaccharides with the chemical structure of HS NA-domains containing the 15N nucleus, which has enough chemical shift dispersion to probe the central residues of octasaccharides at atomic resolution using 600 MHz NMR. By performing NMR relaxation experiments at three magnetic-field strengths, high quality data on internal dynamics and rotational diffusion was obtained. Furthermore, translational diffusion could also be measured by NMR using pulse field gradients. These experimental data were used, in concert with molecular dynamics simulations, to provide information on local molecular shape, greatly aiding our relaxation analyses. Our results, which are more accurate than those presented previously, confirm the higher flexibility of the NA-domains as compared with reported data on S-domains. It is proposed that this flexibility has two functional roles. First, it confers a greater area of interaction from the anchoring point on the core protein for the bioactive S-domains. Secondly, it allows multiple interactions along the same HS chain that are dynamically independent of each other.
Electronic Supplementary Material
The online version of this article (doi:10.1007/s10719-007-9081-9) contains supplementary material, which is available to authorized users.
Keywords: Carbohydrate, Polysaccharide, Glycosaminoglycan, Heparin, Proteoglycan, N-acetyl heparosan, Nuclear magnetic resonance (NMR), Dynamics
Introduction
Heparan sulfate (HS), a member of the glycosaminoglycan (GAG) family, is thought to have appeared early in metazoan evolution [1, 2]. It is ubiquitous in vertebrate extracellular matrices as a constituent of proteoglycans and its extensive repertoire of biological roles, via interactions with hundreds of proteins, make it the most intensely studied of the GAGs. In particular, HS has been implicated in several important biological functions that involve binding to anti-thrombin (AT), fibroblast growth factors (FGFs), cytokines and chemokines [3]. Chemically, the HS biopolymer consists of repeating disaccharide units of variably-sulfated uronic acid (d-glucuronic or l-iduronic acid) and glucosamine (N-acetylated or N-sulfated) monosaccharides. It is this variability in chain epimerization and sulfation (see Fig. 1) that appears to be responsible for the specificity of interactions between HS and proteins [4], rather than the basic linkage pattern of the polymer, which is conserved in all forms.
Fig. 1.
The basic disaccharide repeating unit of heparan sulfate. In the compounds studied here, the number of repeats (n) is 2, 3 and 4, for compounds 1, 2 and 3 respectively. In these compounds, R1 = COCH3 and R2 = R3 = R4 = OH, the uronic acid residue is glucuronic acid and the terminal uronic acid residue is 4–5 unsaturated
In some cases, such as the interaction between anti-thrombin (AT) and a HS pentasaccharide sequence (which includes the rare 3-O-sulfated glucosamine) [5], the local spatial arrangement of sulfo groups is postulated to be the major driver of specificity. Furthermore, the internal and global conformation and dynamics of the chains also play important roles in HS bioactivity [6–8]. These conformational contributions to function are not easy to separate from the others, since the density and arrangement of the opposing sulfo groups may profoundly influence the local dynamics of HS-chains, creating an ambiguity in relating HS structure to function. However, solution-state nuclear magnetic resonance (NMR) studies can be used to resolve this ambiguity by directly measuring molecular conformation and dynamics on the nanosecond time scale with atomic resolution [9, 10].
Numerous NMR studies have been conducted to gain insight into the 3D-structure of HS chains. Much of the early literature was concerned with the conformation and dynamics of the l-iduronate residues [7, 11–13], and not without controversy [14]. From these studies, which used NMR coupling-constants and basic relaxation data, a picture emerged of iduronic acid residues that have high internal flexibility, but their dynamic segmental motions are decoupled from neighboring residues [6]. More recent studies of HS chain dynamics using model-free analysis [15] of NMR relaxation data have attempted to describe the internal and overall motion of the various residues of HS [16–18]. Interpretation of these data has not been without controversy either. Hricovini et al. [18] compared the dynamics of the non-sulfated region of HS (NA-domain) with those from a highly sulfated HS fragment (S-domain) using the model-free analysis and found that the NA-domain was more rigid. This was ascribed to the lack of flexible iduronic acid residues in the NA-domains. However, a more recent publication by Angulo et al. [16] (also using the model-free approach) showed very restricted motion of the internal iduronic acid residues, in contrast to earlier investigations. At the heart of these conflicting results lies: (a) the difficulty in separation of internal motion due to inter-converting ring conformations of the flexible iduronic acid residue and motion due to flexibility of the glycosidic linkages, (b) problems associated with gathering of high quality data for these nearly linear biopolymers, and (c) interpretation of NMR data from polydisperse samples [11]. These difficulties can be overcome by: (a) restricting the analysis to rigid glucosamine rings (which are not epimerized), (b) increasing the NMR chemical shift dispersion using isotopic enrichment, and (c) improved purification protocols.
In protein NMR, isotopic labeling in conjunction with modern heteronuclear filtering experiments (which remove all proton resonances not correlated to a labeled nucleus) are used to overcome issues of signal overlap. In particular, 15N-enrichment is frequently used because the nitrogen atom is highly sensitive to changes in its local environment and consequently has a large range of NMR chemical shifts. The fact that there is often only one nitrogen atom per residue, as opposed to several protons, further adds to spectral simplicity. For dynamic molecular studies, the 15N-nucleus is also desirable since the 1H-15N system within an amide moiety can be considered as an isolated spin-pair for relaxation purposes, simplifying the analysis. Furthermore, 15N has a small negative gyromagnetic ratio, making it more sensitive to dynamics compared to the 13C nucleus (which has a larger and positive gyromagnetic ratio). For example, recent use of 15N-labeling in the GAG hyaluronan has permitted full residue-specific NMR signal assignment and dynamical studies of oligosaccharides of up to eight residues, with unprecedented accuracy [19].
In this study, isotopic 15N-labeling of the glucosamine residues was used to overcome the difficulties associated with previous NMR relaxation analyses of HS dynamics. The polymer used here was the capsular polysaccharide from E. coli K5 bacteria, which is chemically identical to the NA-domains from HS. By growing the bacteria in 15N-enriched media, quantitative isotopic labeling of the polysaccharide can be achieved on the milligram scale, as described previously [20]. The polysaccharide was degraded using K5-lyase enzymatic digestion and separated into pure oligosaccharides using large-scale ion-exchange chromatography to facilitate the study of dynamics at the atomic level. Three 15N-labeled oligosaccharides (see Fig. 1) were purified to homogeneity and used for NMR studies: a tetrasaccharide (1), a hexasaccharide (2) and an octasaccharide (3). 1H-15N NMR relaxation experiments (T1 and heteronuclear nOe experiments) were fitted to both isotropic and anisotropic models of molecular diffusion to assess the validity of assuming isotropic overall motion in these non-sulfated molecules. The libration of the amide group (which contributes to the measured dynamics) was taken into consideration using experimental J-coupling data. Furthermore, diffusion ordered spectroscopy (DOSY) [21, 22] and molecular dynamics (MD) simulations were used to assist in evaluating the models of molecular shape.
The approach presented here can easily be extended to the various modified forms of HS, as these can be produced by chemical and enzymatic modification of the K5 capsular polysaccharide [23]. Our novel findings shed light upon the role of dynamics in HS, and it is intended that these approaches will be adopted more generally, leading to higher quality dynamic data with atomic precision for these most interesting and important biomolecules.
Theory
15N NMR relaxation and rotational diffusion
The dynamic behavior of biomolecules on the sub-nanosecond timescale can be probed by NMR relaxation, by measuring T1- and T2- relaxation rates and the nOe enhancement (η) at multiple magnetic fields [9] and interpreting the results using the Lipari–Szabo model-free approach [15]. For small molecules (as described here) the T1-and T2-relaxation rates are similar for the 1H-15N system, thus in this case only T1 and η are considered [19]. Several (often confusing) treatises of these equations are present in the literature, thus the basic theory is briefly reconsidered here.
Relaxation rates for an isolated N–H spin-pair are related to the spectral density function, J(ω), through Eqs. 1 and 2, where γ is the gyromagnetic ratio, ħ is Planck’s constant over 2π, ω is the relevant nuclear Larmor frequency, ΔσN is the difference between the axial symmetric 15N chemical shift tensor (estimated to be −135 ppm for N-acetylglucosamine see also methods section) and rNH is the N–H inter-nuclear distance (a value of 1.01 Å is used here, see also methods section).
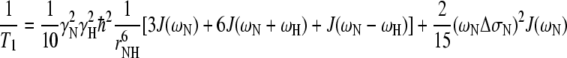 |
1 |
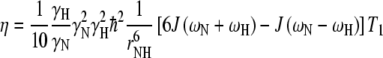 |
2 |
For an isotropic (spherical) model of molecular diffusion the spectral density function is given by Eq. 3, where τ is the average rotational correlation time (radians s−1) and D is the rotational diffusion coefficient. In the case of a symmetric top (cylindrical) model of molecular diffusion the anisotropic spectral density function is given by the Eqs. 4 and 5, where 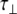 and
and 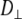 are the correlation time and rotational diffusion coefficient perpendicular to the symmetry axis,
are the correlation time and rotational diffusion coefficient perpendicular to the symmetry axis, 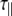 and
and 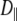 are the corresponding variables parallel to the symmetry axis (by this definition
are the corresponding variables parallel to the symmetry axis (by this definition 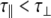 ), and α is the angle between the N–H vector and the cylindrical axis of symmetry.
), and α is the angle between the N–H vector and the cylindrical axis of symmetry.
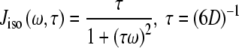 |
3 |
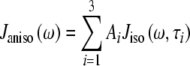 |
4 |
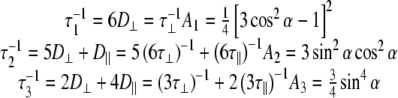 |
5 |
When the internal motion (τe) is much faster than the global rotational correlation time (τM), these two phenomena can be separated using the model free approach of Lipari and Szabo [15]. In their treatment, if it is assumed that molecular tumbling is isotropic, the spectral density function is represented by Eqs. 6 and 7, where S2 is the generalized order parameter. The corresponding anisotropic relationship is shown in Eq. 8, where Janiso(ω) is described by Eq. 4 and the 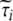 are given in Eq. 9.
are given in Eq. 9.
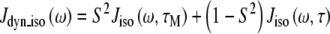 |
6 |
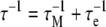 |
7 |
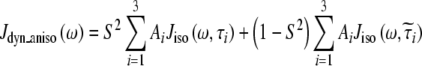 |
8 |
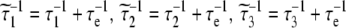 |
9 |
It should be noted that this derivation (resulting in Eq. 8) is consistent with the original proposal of Lipari and Szabo [15] and slightly different to a recent and broadly-used implementation of that theory [24].
Diffusion measurements
The average translational diffusion rate can be measured by pulsed-field-gradient (PFG) NMR [25], often referred to as diffusion ordered spectroscopy (DOSY) [21, 22]. In this experiment, the diffusion coefficients can be estimated by varying the gradient amplitude (g) and fitting the experimental data to the theoretical Stejskal–Tanner Eq. 10 [26].
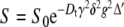 |
10 |
In Eq. 10, S is the signal amplitude, S0 is the echo amplitude that would have resulted had there been no diffusion, Dt is the translational diffusion coefficient (not to be confused with the rotational diffusion rates described above), δ is the gradient pulse width and Δ′ is the diffusion time corrected for the effects of a finite gradient pulse width.
Often the relative diffusion coefficient is sought, but when the absolute value is of interest, a more correct value of Dt can be obtained by taking the systematic errors (due to non-uniform field gradients) into account by fitting to a different expression, which compensates for this, Eqs. 11 and 12 [27], where the coefficients cn are probe and pulse-sequence dependent.
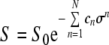 |
11 |
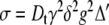 |
12 |
The hydrodynamic radius of a molecule can be shown to be related to the translational diffusion coefficient, Dt. This radius, and thus Dt for an isolated polymer in solution, scales (via an exponent, v) with molecular mass (M), Eq. 13. The value of v can be shown to be 3/5 and 1/3 for fully solvated and collapsed polymer chains, respectively [28]. A polymer is fully solvated in a solvent where its interactions with the solvent are favored over self-association—the converse is true for a collapsed polymer. In a so-called Flory or θ solvent, the polymer behaves as a random coil, where v = 1/2 [28].
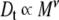 |
13 |
Results
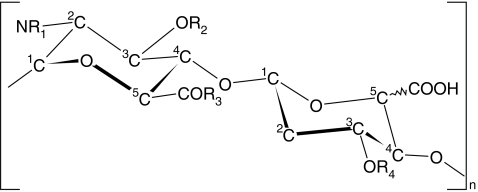
15N-labeled polymer with a chemical structure identical to the non-sulfated domains of heparan sulfate (HS) was prepared from E. coli. K5 capsular polysaccharide and enzymatically digested. The resulting oligomers were purified and three samples were prepared that had 4, 6 and 8 sugar units (see experimental section for details). 1D 1H-NMR spectra and mass spectrometry (not shown) determined that the oligosaccharides were uniformly 15N-labeled and 1H-15N-HSQC spectra (see Fig. 2) confirmed that the samples contained no major contaminants.
Fig. 2.
15N-1H HSQC spectrum of the tetra-, hexa- and octa-saccharides (from top to bottom) of the NA-domain of heparan sulfate at a proton-resonant frequency of 900 MHz. The abscissa shows 1H chemical shift [ppm]. Labels on the spectrum correspond to amide groups, labeled according to their position within the oligosaccharide, using Greek nomenclature. Variability in the line shapes are due to acquisition and processing of the NMR spectra
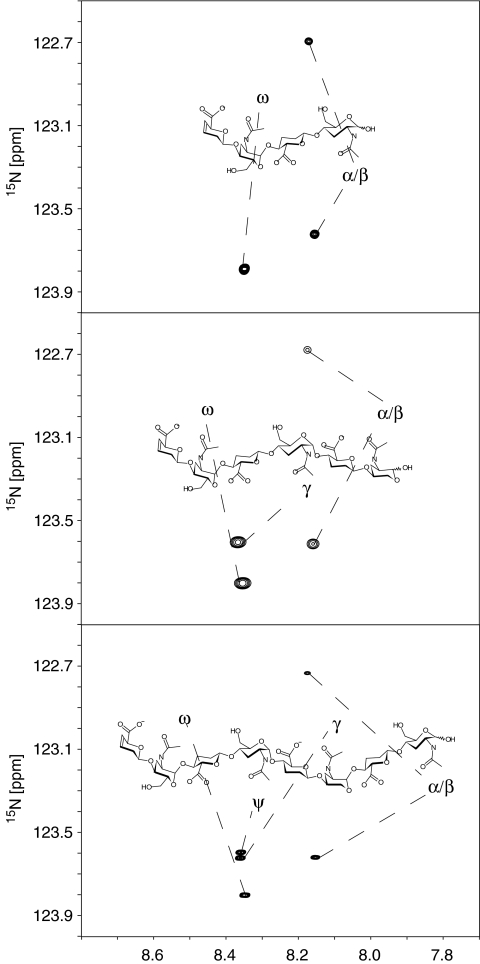
Relaxation experiments (1H-15N T1 and heteronuclear nOe) were measured for each of the oligosaccharides (1, 2 and 3) at three magnetic field strengths (14.1, 18.1 and 21.1 T). In each case the 1H-15N HSQC-based T1-relaxation experiments were repeated 12 times with a variable relaxation delay and the resultant peak heights were fitted to exponential curves (relaxation curves for the octasaccharide at 14.1 T are shown in Fig. 3). The heteronuclear nOes were calculated from the ratio of peak heights in 1H-15N spectra, recorded with and without 1H-presaturation.
Fig. 3.
T1-relaxation curves for an octasaccharide unit from the NA-domain of heparan sulfate at the lowest magnetic field strength used in this study (14.1 T). The resonances from the amide groups of the central residues (ψ and γ) are resolved and have slightly different relaxation times. For the specific assignments see Fig. 2
Table 1 shows the calculated exponential decay constants (T1) and the corresponding nOe ratios (η). The errors in the tabulated T1 values were taken to be twice the exponential curve fitting errors, while the errors in the nOe ratios were estimated by calculating the ratio of the sum of the amplitudes (A) of the two HN signals from the anomeric amide group (α/β) and the same signal in the ω-amide group (clearly resolved in all spectra, see Fig. 2), according to Eq. 14.
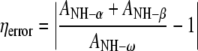 |
14 |
Table 1.
Fitted 1H-15N T1-relaxation data and measured nOe (η) ratios for three lengths (4-, 6- and 8-saccharide units denoted 1, 2 and 3 respectively) of the NA-domain from heparan sulfate at three magnetic-field strengths (14.1, 18.1 and 21.1 T)
| 14.1T | 18.1T | 21.1T | |||||
|---|---|---|---|---|---|---|---|
| η | T1[ms] | η | T1[ms] | η | T1[ms] | ||
| 1 | α | −1.35 | 1,790 | −1.23 | 1,625 | −0.42 | 1,526 |
| β | −1.63 | 1,614 | −1.22 | 1,524 | −0.56 | 1,445 | |
| ω | −1.89 | 1,255 | −0.95 | 1,183 | −0.39 | 1,116 | |
| 2 | α | −0.96 | 1,613 | −0.85 | 1,473 | −0.28 | 1,400 |
| β | −1.12 | 1,456 | −0.79 | 1,368 | −0.34 | 1,310 | |
| γ | −1.07 | 995 | −0.33 | 942 | 0.14 | 889 | |
| ω | −1.17 | 1,050 | −0.38 | 978 | −0.01 | 939 | |
| 3 | α | −0.81 | 1,437 | −0.84 | 1,362 | −0.14 | 1,342 |
| β | −0.99 | 1,318 | −0.75 | 1,278 | −0.33 | 1,252 | |
| γ | −0.58 | 755 | 0.04 | 797 | 0.50 | 803a | |
| ψ | −0.77 | 831 | −0.17 | 824 | 0.40 | 803a | |
| ω | −0.92 | 946 | −0.18 | 910 | 0.25 | 908 | |
aHigh resolution spectrum not collected—value estimated from a low-resolution spectrum (see experimental section).
The heteronuclear experiments for the octasaccharide (3) were collected using two different sweep-widths. In the first experiment a larger sweep width was used, where all nuclei were present and unfolded, but in which the γ- and ψ-amide groups could not be resolved. These resonances were resolved using a second, narrower spectral width (not shown). The spectral width of the second experiment was chosen so that aliased peaks did not interfere with the resonances of interest.
Conversion of the resultant relaxation measurements into 3D-molecular information was performed via the model-free method for calculating the spectral density function (as needed by relaxation Eqs. 1 and 2). Due to the potential shape anisotropy of the oligosaccharides, two methods were used to estimate the spectral density functions, one that assumed spherical symmetry and one that incorporated cylindrical symmetry, see Eqs. 6 and 8. Fitting the relaxation data to these equations resulted in order parameters, overall and internal tumbling times, and in the case of anisotropy, a set of angles. It was found that the relaxation data was not sensitive to the internal correlation time (τe) and thus it varied significantly when allowed to change during the fitting process. However, this parameter is of secondary interest, and by fixing the internal correlation time at 30 ps (consistent with molecular dynamics simulations), higher quality and more robust fits to the experimental data could be produced, as noted previously [29]. The uncertainty in this variable is reflected in previous literature data for similar compounds, where τe ranges from a few picoseconds to several hundred picoseconds in similar compounds (15–50 ps for a HS pentasaccharide and 110–290 ps for a HS hexasaccharide) and with large errors (±25–85 ps) [16–19, 30]. The results, given in Table 2, therefore assume a constant internal correlation time of 30 ps and clearly show the expected trend in generalized order parameter (S2), where the amide groups at the central residues are more ordered (higher S2 values) than those at the terminal residues. Also, the overall correlation times increase as the oligosaccharides get longer, as expected a priori.
Table 2.
Calculated model-free parameters for the tetra-, hexa- and octa-saccharides (1, 2 and 3 respectively) of the NA-domain of heparan sulfate, using a constant internal correlation time of 30 ps, fitted to isotropic and anisotropic models of rotational diffusion
| Models of rotational diffusion | ||||||
|---|---|---|---|---|---|---|
| Isotropic | S2 | S2calc | ||||
| 1 | ||||||
| τM [ns] | 0.57 | α | 0.32 | 0.46 | ||
| τe [ns] | 0.03 | β | 0.35 | 0.59 | ||
| ω | 0.48 | 0.62 | ||||
| 2 | ||||||
| τM [ns] | 0.71 | α | 0.35 | 0.49 | ||
| τe [ns] | 0.03 | β | 0.36 | |||
| γ | 0.60 | 0.70 | ||||
| ω | 0.55 | 0.61 | ||||
| 3 | ||||||
| τM [ns] | 0.74 | α | 0.32 | |||
| τe [ns] | 0.03 | β | 0.34 | |||
| γ | 0.87 | |||||
| Ψ | 0.82 | |||||
| ω | 0.67 | |||||
| Anisotropic | S2 | α[°] | S2calc | αcalc[°] | ||
| 1 | ||||||
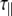 [ns] [ns] |
0.35 | α | 0.33 | 15.4 | 0.46 | 64.2 |
 [ns] [ns] |
0.65 | β | 0.36 | 40.1 | 0.59 | 62.1 |
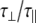 |
1.88 | ω | 0.56 | 58.6 | 0.62 | 63.1 |
| τe [ns] | 0.03 | |||||
| 2 | ||||||
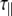 [ns] [ns] |
0.57 | α | 0.31 | 3.8 | 0.49 | 62.8 |
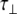 [ns] [ns] |
0.79 | β | 0.36 | 49.5 | ||
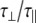 |
1.39 | γ | 0.62 | 58.6 | 0.70 | 64.4 |
| τe [ns] | 0.03 | ω | 0.61 | 84.7 | 0.61 | 63.3 |
| 3 | ||||||
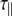 [ns] [ns] |
0.39 | α | 0.39 | 75.0 | ||
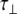 [ns] [ns] |
1.00 | β | 0.41 | 66.7 | ||
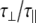 |
2.59 | γ | 0.65 | 2.2 | ||
| τe [ns] | 0.03 | Ψ | 0.66 | 23.2 | ||
| ω | 0.54 | 31.1 | ||||
These values were calculated from experimental data collected at three magnetic-field strengths (14.1, 18.1 and 21.1 T). The S2calc and αcalc values were calculated by averaging data extracted from 50 ns molecular dynamics simulations
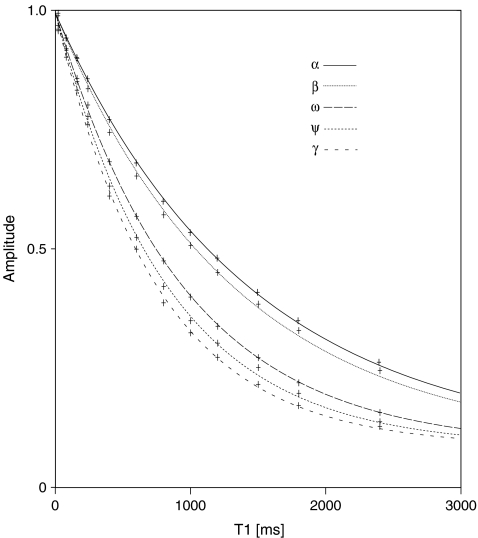
Molecular shape was probed using the DOSY experiment, applied to the three samples. The diffusion coefficients were estimated from their respective methyl peaks at 2.03 ppm (Table 3) using the Stejskal–Tanner Eq. 10. The resulting diffusion values were used to calculate the scaling-factor exponent (ν) in Eq. 13, which provides information about the overall molecular shape. Figure 4 shows a plot of log(Dt) against log(M), showing the slope of the fitted line (ν) to be 0.48 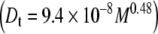 .
.
Table 3.
Calculated translational diffusion times using the methyl resonance of the various oligomers (tetra-, hexa- and octasaccharides labeled in table as 1, 2 and 3 respectively) of the NA-domain from heparan sulfate at a proton frequency of 400 MHz
| Compound | D [10−6 cm2/s] |
|---|---|
| 1 | 3.08 ± 0.0004 |
| 2 | 2.55 ± 0.0007 |
| 3 | 2.22 ± 0.0007 |
Fig. 4.
Plot of log(Dt) vs. log(M) for three different lengths of the NA-domain of heparan sulfate, consisting of 4, 6 and 8 sugar units (Dt is the translational diffusion time and M the weight-averaged molecular mass). The dotted line is the best-fit to a straight line (as described in the theory section, Eq. 13)
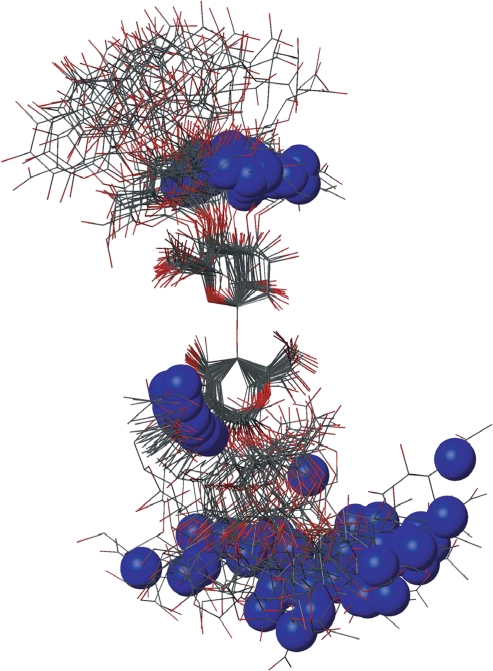
Molecular dynamics (MD) simulations were performed on the tetra- and hexa-saccharides in water boxes. Figure 5 shows 40 snapshots from the simulation of the hexasaccharide (stripped of ions and water molecules), superimposed on the atoms from the central linkage. The simulation data were analyzed to give theoretical values of both S2 and the angle (α), defined as the angle between the molecular axis and the N–H vector (see Table 2). The calculated S2 values show similar trends to the experimental data, but are generally higher. The α values for both the tetra- and hexa-saccharide show nearly random behavior, consistent with an isotropic model.
Fig. 5.
Overlay of 40 snapshots from 50 ns of molecular dynamics simulations of the hexasaccharide of unsulfated heparan sulfate. The molecules are superimposed using the atoms in the adjacent linkages. The position of the nitrogen atom (blue sphere) in each structure is highlighted
The coupling constants of 1 and 2 were measured from 1D 1H spectra except for the central residues of 2 where there was overlap in the 1D spectrum. In this case, cross-peaks in the 1H-15N HSQC were fitted to 2D Lorentzian line-shapes using a non-linear fitting scheme (these data are given in Table 4).
Table 4.
3J(H2−HN)-coupling constant (in Hz) of the tetra- and hexa-saccharides (1 and 2 respectively) from the NA-domains of heparan sulfate
| 3J(α− [H2−HN]) [Hz] | 3J(β− [H2−HN]) [Hz] | 3J(γ− [H2−HN]) [Hz] | 3J(ω− [H2−HN]) [Hz] | |
|---|---|---|---|---|
| 1 | 8.43 | 8.55 | 9.14 | |
| 2 | 8.30 | 8.65 | 9.14 | 9.24 |
All values have an estimated error of ±0.05 Hz.
Discussion
Analysis of the NMR relaxation data
The results clearly show the advantages of 15N-labeling, where even the amide groups in the central residues of an octasaccharide are well resolved (Fig. 2). In addition to the gain resolution, an excellent spread of relaxation data is found due to the use of the 15N-nucleus (Table 1). The average change in nOe enhancement (η) over the different fields is 1 unit, with some of the η-values passing through zero. In addition, much more precise measurements can be made of the longer T1-relaxation times in the 1H-15N system (compared to 1H-13C). The data follows a clear trend and even without further analysis the difference in relaxation properties of the central and terminal residues of the octasaccharide can be appreciated, as well as the difference between the various lengths of the polymer.
The experimentally measured relaxation datasets were interpreted using the model-free approach [15], which relates the measured relaxation values at multiple fields to dynamic conformational properties. In the model-free approximation it is assumed that internal motion (libration) and global motion (diffusion) are uncoupled and on significantly different timescales. Furthermore, it is assumed that molecular dynamics occurs with respect to a rigid diffusing molecular frame. While neither of these assumptions are entirely true for biomolecules, they yield good results if an appropriate model for molecular diffusion is chosen. The two simplest models for diffusion are based on the isotropic sphere and the anisotropic symmetric top (rod or cylindrical shape) [15]. In proteins, for example, the simpler isotropic spherical shape usually suffices, but this model may not be accurate for rod-shaped carbohydrate polymers [18], which are expected to become more anisotropic (rod shaped) with increasing length of the polymer chain. Previous studies on HS analogues have modeled diffusion using an anisotropic model, improving the agreement with experimental data [6, 11, 16–18, 30, 31]. In such a symmetric-top model, the correlation time about the symmetry axis of the rod shape 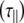 is separated from that perpendicular to the symmetry axis
is separated from that perpendicular to the symmetry axis 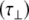 . Values of the parallel correlation time
. Values of the parallel correlation time 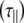 tend to be similar in linear carbohydrates (~0.5 ns) and (by definition) are always smaller than the perpendicular correlation time
tend to be similar in linear carbohydrates (~0.5 ns) and (by definition) are always smaller than the perpendicular correlation time 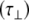 ; the ratio of the two correlation times can be used as a measure of anisotropy. Other parameters in the model-free approach are the internal correlation time (τe), the generalized order parameter (S2) and, in the anisotropic model, an angle (α).
; the ratio of the two correlation times can be used as a measure of anisotropy. Other parameters in the model-free approach are the internal correlation time (τe), the generalized order parameter (S2) and, in the anisotropic model, an angle (α).
Isotropic or anisotropic model of rotational diffusion?
From the diffusion ordered spectroscopy (DOSY) data in Table 3 and Fig. 4 it is apparent that the overall polymeric shape of the NA-domain of HS is not consistent with a rigid rod. In fact, the slope of the line in Fig. 4 is almost equal to the theoretical value for a random coil (ν = 1/2), which indicates that even the oligosaccharides have significant segmental motion. This is supported by the model-free analysis of the tetra- and hexa-saccharides (using an isotropic model of diffusion), where relatively low values of S2 are found. However, when similar analysis was used to interpret relaxation measurement from the octasaccharide, relatively higher S2-values were found at the central amide groups. In contrast, the corresponding parameters, calculated using the anisotropic model of diffusion, are consistent with a random coil. These data therefore suggest that the tetra- and hexa-saccharides undergo nearly isotropic diffusion, whereas the octasaccharide diffuses anisotropically (all with high internal and segmental motion). It is likely that it is the α-linkages within the oligosaccharides that are responsible for a compact dynamic shape at shorter lengths, which only starts to behave anisotropically as an octasaccharide.
The lower order parameters calculated using an anisotropic diffusional model are due to the introduction of an additional parameter (α) that is the angle between the inter-nuclear N–H vector and the molecular cylindrical-symmetry axis. This parameter adds another dimension of complexity, providing a more accurate interpretation of the experimental data than using isotropic diffusion. For example, in the isotropic diffusional model, if there is a large amplitude motion along an N–H vector that is coincident with the long axis of the molecule, the T1 and η values will be interpreted as low amplitude motion, which will be compensated for by an increase in the overall rotational diffusion. However, in the anisotropic model, the angular dependence of the internal motion with respect to the molecular frame is taken into account, and the data fitted so that the angle (α) is also optimized. Inspection of Table 2 reveals that the amide groups at the central residues in the octasaccharide are indeed coincident with long axis of the molecule (small α), explaining the decrease in order parameter compared to the isotropic model. Further inspection shows that whenever the N–H vector is along the long axis, the anisotropic model predicts more motion and, when the vector is pointing along the short axis (large α), the converse is true.
More importantly, the anisotropic interpretation indicates that the two amide groups in the central residues of the octasaccharide have similar dynamics, as inferred from their S2 values (Table 1), in contrast to the results from the isotropic analysis, where the γ-amide group appears to be more ordered (higher S2) than the more central ψ-amide group. Furthermore, naïve interpretation of the raw experimental relaxation values (see Fig. 3, for example) would agree with the conclusion of the analysis via the isotropic model. However, this initial inspection is likely to be erroneous, because one would logically expect that the amide group in the most central residue (i.e., ψ in Fig. 2) would be more ordered (or at least similarly ordered) than that in a neighboring residue, which is in agreement with the initially counterintuitive results from the anisotropic diffusional model. Therefore, these findings (in addition to the DOSY data) substantiate the use of an anisotropic model in the analysis of octasaccharide dynamics.
Considering now analysis of the shorter oligosaccharides using an anisotropic model of diffusion, it is found that both the parallel 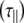 and perpendicular
and perpendicular 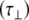 diffusional rates increase, whereas one would expect only
diffusional rates increase, whereas one would expect only 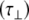 to increase. This suggests that there is no well-defined anisotropic interpretation and the simpler isotropic model is preferable. Such an observation is further substantiated by molecular dynamics simulations performed for the tetra- and hexa-saccharide (see Fig. 5 and Table 2). In these simulations it was found that the angle α is nearly random for all amides, consistent with an isotropic model.
to increase. This suggests that there is no well-defined anisotropic interpretation and the simpler isotropic model is preferable. Such an observation is further substantiated by molecular dynamics simulations performed for the tetra- and hexa-saccharide (see Fig. 5 and Table 2). In these simulations it was found that the angle α is nearly random for all amides, consistent with an isotropic model.
Microscopic interpretation of S2
NMR scalar coupling constants (J-couplings) [32] can also be used to measure dynamics due to bond librations (via a suitable empirical equation) and the 3J(H2−HN) coupling constant is a direct reporter of amide dynamics in these oligosaccharides. Theoretical calculations have shown that, given the same chemical environment, a decrease in the coupling constant is associated with increased amide librations. From Table 4, it can be seen that in 2 the central γ-amide group has a higher coupling constant compared to that of the terminal ω-amide group. This is contrary to expectation, as the central amide group is regarded to be more rigid. In this case, it appears that the change in chemical environment causes the unexpected observation. This is not expected to be the case when comparing coupling constants measured in 1 and 2 from amides in similar chemical environments, i.e., those at the α-, β- and ω-positions, where a variability of 0.1 Hz is observed in the coupling constants. This can be attributed to slight changes in amide libration of a few degrees (using a previously derived relationship between coupling constants and torsional libration [32]). A similar relationship between dihedral angle and S2 indicated that these angular variabilities would correspond to deviations in S2 of less than 0.01 [15]. Furthermore, the expected differences in amide group librations across individual molecules are less than 5° (using the above mentioned relationship), which would result in small changes in S2 of less than 0.05. Therefore, differences in amide libration are not responsible for the more dramatic change in S2 observed at specific amide positions (Table 2). The major remaining site-specific contributor to S2 in the NA-domains from HS (which contain relatively rigid 4C1-puckered sugar rings) must thus be due to segmental motions induced by linkage librations. The S2-values reported here can therefore be seen as direct reporters of the chain dynamics in these polymers.
Role of dynamics in HS
The S-domains of HS have previously been investigated using relaxation data from C–H vectors and an interpretation based on an anisotropic diffusional model (see Angulo [16] and references therein). The values reported for 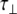 of such domains are 1.6, 1.7 and 2.6 ns for penta-, hexa- and hepta-saccharide fragments, respectively. In addition, these fragments show a much higher degree of anisotropy compared to the NA-domain analyzed here. This would suggest that the S-domains are comparatively more rigid, as reflected in the higher S2 values reported: 0.91, 0.91 and 0.93 for central residues of the penta-, hexa- and hepta-saccharide fragments, respectively (cf. ~0.65 for the NA-domains found here).
of such domains are 1.6, 1.7 and 2.6 ns for penta-, hexa- and hepta-saccharide fragments, respectively. In addition, these fragments show a much higher degree of anisotropy compared to the NA-domain analyzed here. This would suggest that the S-domains are comparatively more rigid, as reflected in the higher S2 values reported: 0.91, 0.91 and 0.93 for central residues of the penta-, hexa- and hepta-saccharide fragments, respectively (cf. ~0.65 for the NA-domains found here).
From the findings presented here it thus appears that the NA-domains of HS are much more dynamic than the S-domains. At the molecular level, the only chemical difference between the NA- and S-domains of HS is sulfation and epimerization, and it has been suggested previously that both share a similar local 3D-chain conformation [33]. Therefore, it is more likely that the major contributor to chain rigidity of S-domains is the repulsion of multiple negative charges, rather than specific cross-residue intramolecular interactions, but this remains to be validated by further experimentation.
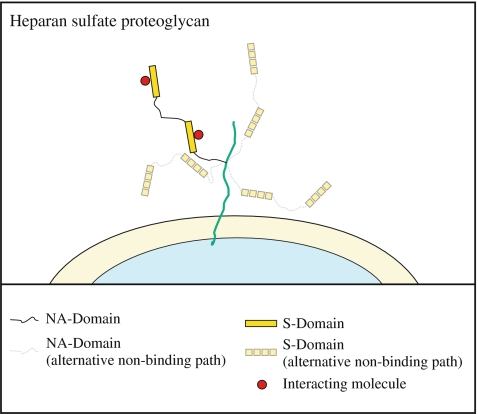
From a biological viewpoint this confirms the hypothesis that the primary function of the NA-domains is to give the HS chains flexibility, since the S-domains are significantly stiffer. This would give proteoglycan HS chains the ability to rapidly and effectively explore space around their tethering points on the core protein (Fig. 6). It would also allow them to dynamically adapt their shapes and present themselves effectively to a range of protein targets. In addition, this would permit HS chains to interact in a multivalent fashion, without the dynamics of one interaction greatly affecting others. This may explain the omnipresence of functional S-domains in HS, which are separated by completely unsulfated NA-domains [34]. Supporting evidence is provided by Stringer and Gallagher [8], who found an HS fragment with specifically high affinity for the platelet factor 4 (PF4) tetramer. This HS fragment consisted of two S-domains separated by an NA-domain long enough to allow for interaction of the two S-domains with each side of the PF4 tetramer. This argument is also consistent with the diversity of molecules that HS interacts with and the picture that its primary role is in regulation and control [2, 4, 35].
Fig. 6.
Schematic diagram illustrating the proposed increase in flexibility due to the NA-domains of heparan sulfate and the concomitant increase in spatial range that can be covered together with the potential for mediating multivalent interactions
Conversely, the current study would suggest that the S-domain rich heparin proteoglycans do not have the local plasticity of HS proteoglycans. Therefore, in order to provide the same effective local concentration of sulfo-groups, heparin may be required at higher concentrations than HS. This is supported by the fact that when mast cells are activated their cytoplasmic granules (where heparin is thought to act as a depository for cationic molecules i.e. histamines, serotonin, etc.) are released into the extracellular matrix resulting in a high concentration of highly active (S-domain rich) heparin molecules [36]. Such action would allow heparin to quickly interact with proteins at the site of release, a response which is important in inflammatory processes, where heparin acts as an anticoagulant [36]. However, as its concentration falls due to diffusion from the point of release its highly potent effects would drop-off rapidly.
Conclusions
Heparan sulfate (HS) NA-domains have been investigated using NMR and computational methods, to determine whether their dynamic properties are consistent with previous hypotheses, suggesting that NA-domains add flexibility to HS. For these nearly-linear biomolecules conventional 1H-NMR methods yield poor spectra with overlapping resonances that are difficult to interpret. We have demonstrated that these difficulties can be overcome by use of 15N-labeling and efficient purification protocols. This approach, which could easily be extended to sulfated domains, allows the dynamical properties of NA-domains of HS to be studied with unprecedented accuracy.
In this study, three lengths of the enzymatically-digested polymer (consisting of 4, 6 and 8 sugar units, respectively) were isolated, purified and high-quality 15N-NMR relaxation data was collected for each at three magnetic-field strengths. The resultant data was analyzed using the model-free approach using both isotropic and anisotropic models of rotational diffusion. To complement these studies, and to ease their interpretation, molecular shape was further probed by measuring translational diffusion (using NMR pulse field gradients) and by performing solvated molecular dynamics simulations. The resultant order parameters (S2) from the model-free analysis reveal a high degree of disorder in the oligosaccharide chains, with S2-values that are similar in the hexa- and octa-saccharide, suggesting that these values represent polymer behavior. Following these analyses, it was determined that the NA-domains of HS behave as random coils and that for shorter oligosaccharides their rotational diffusion can be approximated to be isotropic, whereas for the octasaccharide the results are more consistent with anisotropic diffusion.
The flexibility exhibited by the NA-domains is contrary to literature data on the sulfated S-domains of HS, which appear to be much more rigid [16]. It is proposed that the NA-domains primarily serve a motional role in HS, consistent with reports of the domain structure of HS. It is therefore argued that the motional properties of the NA-domains increase the efficiency of HS in control and regulation. These findings also suggest that heparin does not have this flexibility, a view consistent with the known roles of heparin, which include storage of ionic molecules and involvement in processes requiring a fast, local response.
Methods and materials
Biochemical preparation of oligosaccharides
K5 capsular polysaccharide was prepared from cultures of Escherichia coli Bi8337/41 [O10:K5:H4], originally supplied by Professor Ian S. Roberts. Cells were grown in a starter culture of 50 ml of LB broth, 1 ml of that media was pelleted and resuspended in 500 ml of M9-minimal media containing 1g/l 15N-ammonium chloride (15N>99%) as the only nitrogen source. The polysaccharide purification procedure was similar to that described previously and is summarized here [37]. After 16 h of growth the cells were harvested (5,000 g, 10 min) and washed once with 50 ml of phosphate-buffered saline (pH 7.2). Cell pellets were resuspended and incubated (30 min, 37°C) in 50 ml extraction buffer (50 mM Tris–Cl, 5 mM EDTA, pH 7.3) four times, retaining the supernatants. Polysaccharide was precipitated from the pooled supernatants by addition of sodium cetyl-3-ethyl ammonium bromide to 0.1% (w/v) followed by a 16 h incubation at room temperature. The precipitate was recovered by centrifugation (10,000 g, 20 min), re-suspended in 1 M NaCl, precipitated by addition of ethanol to 80% (v/v) and again recovered by centrifugation. Following dissolution in distilled water (5 ml), the preparation was dialysed against distilled water, centrifuged (100,000 g, 1 h) and the supernatant containing purified polydisperse K5 polysaccharide (20 mg/l) was lyophilized.
Lyophilized 15N-enriched K5 polysaccharide (~30 mg) was dissolved in 5 ml of digest buffer (100 mM Tris–HCl, 100 mM Na-acetate, pH 8.5) and incubated at 37°C for 16 h with 180 U of K5-lyase enzyme (kindly supplied by Professor Ian S. Roberts). The reaction was stopped by incubation in a boiling water bath for 5 min and the precipitated enzyme was removed by centrifugation (13,000 g, 2 min).
Differing lengths of oligosaccharides from the K5-polysaccharide digest were separated using anion exchange FPLC on an ÄKTA system (GE Healthcare). Briefly, digest supernatant was loaded onto a Sepharose-Q HR column (GE Healthcare), equilibrated in Milli-Q H2O at flow rate of 10 ml/min, and eluted with a gradient of 0–100 mM NaCl over 90 min. The eluent was monitored at both 214 and 232 nm. Following lyophilization, each oligosaccharide was desalted using a Bio-Gel P2 column (BioRad) running in 50 mM HN4Ac, and then repeatedly lyophilized to remove residual NH4Ac by sublimation. Purity was confirmed by analytical ion-exchange chromatography using a Mono-Q HR 5/5 (GE Healthcare), NMR and mass spectrometry.
Sample preparation
Samples of oligosaccharides for NMR spectroscopy were prepared from lyophilized material reconstituted in 5% (v/v) D2O, 0.02% (w/v) NaN3, 0.3 mM DSS, pH 6.0; pH 6.0 was chosen to allow amide HN protons to be observed. The final concentration of all samples was calculated to be approximately 5 mM.
NMR spectroscopy
The T1-relaxation and nOe experiments were performed at 24.5°C, using standard pulse sequences [40]. All experiments were repeated at three different magnetic-field strengths: 14.1, 18.1 and 21.1T. The T1-relaxation delays were: 4, 12, 16, 32, 48, 80, 120, 160, 240, 300, 360 and 480 ms, performed in a random order to avoid systematic errors. 1024 complex data points were acquired in the direct (1H) dimension and 18 complex points in the indirect (15N) dimension, using a spectral window of 10 ppm in the direct dimension and 2.2 ppm in the indirect dimension. In addition, a second spectrum was collected for three (for all experiments), which had a narrower spectral width of 0.35 ppm in the indirect dimension.
The data was processed using the NMRPipe processing software [41]. The data was typically zero-filled in the acquisition dimension to 16,384 complex points and 1,024 complex points in the indirect dimension. The acquisition dimension was apodized using an exponential window function (typically with 15 Hz line-broadening) and the indirect dimension was apodized using a Lorentzian to Gaussian apodization function, in which the line broadening and narrowing parameters were adjusted as appropriate for the spectrum. The various peaks were picked using the peak-picking algorithm within the NMRPipe software and the peaks heights were used in all cases. The nonlinLS line shape fitting algorithm within the NMRPipe software was used on a subset of the peaks to validate this approach, and the agreement between the two approaches was found to be excellent (with the zero-filling used here). The J-couplings were measured by finding the difference between peak frequencies, determined also using the nonlinLS algorithm.
The assignment of the NH resonances follow the strategy employed by Blundell et al. [38, 39], applied to the oligosaccharides of hyaluronan. The full assignment of these oligosaccharides will be published elsewhere, the assignment of the resonances of interest, however, is given here. The assignment of the tetrasaccharide is straightforward as there are only three cross-peaks, two of which are weaker than the third. The weaker peaks have intensities equal to 60 and 40% of the intensity of the third peak. Based on their intensities, the weaker peaks were assigned to the anomeric protons (α and β), which are further assigned based on their intensities, since the α-anomer is dominant with preserved ratio in both free GlcNAc [32] and in the terminal GlcNAc of hyaluronan [39] (this assignment is further verified by a NOESY cross-peak between the NH proton and the previously assigned [37] anomeric proton at position 1 of α/β-GlcNAc). The remaining cross-peaks can thus be assigned to the remaining NH atoms in the ω-residue of the tetrasaccharide. In the hexasaccharide all of the cross-peaks present in the tetrasaccharide are observed together with an additional cross-peak. This additional peak is assigned as the more central γ-residue, as it does not experience the same “end effects” (see also references to end effects in Blundell et al. [38, 39]). Finally, the octasaccharide was assigned based on the known assignment of the shorter fragments and the trend towards polymer properties. The cross-peaks for the NHs at α-, β- and ω-positions were nearly identical to those in the hexasaccharide, as these experience the same end-effects and could thus be readily assigned. The position of the NH cross-peaks of the γ- and ψ-residues in the octasaccharide are close to each other. However, one of these resonances has 1H and 15N chemical shifts that are almost identical to γ-residue of the hexasaccharide and is thus assigned as the γ-amide in the octasaccharide. The remaining cross-peak is therefore due to the ψ-amide. These assignments were further verified using the HSQC spectrum of a decasaccharide. In this spectrum, the intensity of the cross-peak corresponding to the ψ-amide increases (not shown), due to convergence to polymer properties and overlap, whereas the intensity of the remaining resonances are unchanged. This tendency towards polymer behaviour was additionally used to verify the assignment of the NH cross-peak in the ψ-residue of the octasaccharide, which experiences the least amount of end-effects.
Model-free NMR relaxation analysis
Computer programs were written in the C-programming language to calculate the relaxation times for an isolated N–H vector, according to the equations presented in the theory section. The internal correlation time at each vector was fixed at 30 ps (as described in the text), with an associated variable S2 at each position and for each molecule a single variable for the isotopic model. For the anisotropic model, the rotational correlation time 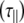 and angles between the long axis and each N–H vector (α) had to be additionally considered. Predictions were compared with experimental data using the χ2 function and optimized using a Monte Carlo algorithm [19]. This process was carried out ten times for each oligosaccharide and the mean and standard deviation values for each fitted parameter were reported.
and angles between the long axis and each N–H vector (α) had to be additionally considered. Predictions were compared with experimental data using the χ2 function and optimized using a Monte Carlo algorithm [19]. This process was carried out ten times for each oligosaccharide and the mean and standard deviation values for each fitted parameter were reported.
The N–H bond length and the chemical shift anisotropy of the amide nitrogen were calculated by ab initio DFT calculations on N-acetyl-d-glucosamine [32] (while the calculations were performed previously these values have not been reported before). Briefly, the computation of the chemical shift anisotropy was performed using the GIAO method in the Gaussian software at the B3LYP/IGLOO-III level of theory, which resulted in a value of −135 ppm, in close agreement with previously-reported values that used similar methods [42, 43]. Similarly, the N–H bond length was taken from quantum mechanical geometry optimization at B3LYP/631G(d,p) level of theory. The N–H distance was found to range from 1.008 to 1.020 Å, depending on solvation model used (1.008, 1.020 and 1.015 Å for calculations performed in vacuo, with implicit solvent and with explicit solvent, respectively), which is in agreement with similar calculations on proteins [42, 44]. Due to this small variability of the N–H distance, the relaxation calculations were performed using a bond length of both 1.01 and 1.02 Å (the results of the latter calculation are included in supplementary Table 2).
Molecular dynamics simulations
Molecular dynamics (MD) simulations were performed using CHARMm and a force-field suitable for glycosaminoglycans, as described previously [45] using an integration time-step of 2 fs. Briefly, oligosaccharides were built in a low-energy conformation consistent with preliminary NOESY measurements (unpublished results) and placed into rhomboidal dodecahedral water-boxes. The boxes had dimensions of 4.0 and 4.5 nm, containing 1504 and 2141 TIP3P water molecules for the tetrasaccharide and hexsaccharide, respectively. Long-range electrostatic interactions were treated using the particle-mesh Ewald approach and truncated to zero between 0.8 and 1.2 nm. Simulations (using the CPT ensemble) were carried out at 298 K on both α and β-anomers of the tetrasaccharide and on the β-anomer of the hexasaccharide, for a total of 50 ns in each case. Coordinates were stored every 5 ps for later analysis.
The S2 values were calculated as the autocorrelation of N–H vectors extracted from the MD simulation. The N–H vectors were extracted by overlaying all frames from the MD simulation on the same set of atoms. These atoms were the linkage atoms adjacent to each amide (O4 of the same residue GlcNAci to C1 of previous residue GlcAi−1 (d-glucuronic acid) and O4 of next residue GlcNAci+1 to C4 of that residue GlcNAci+1). For the GlcNAc residue at the reducing terminus the corresponding anomeric atoms (O1 and its attached proton) were used instead (as there is no i + 1 residue).
Values for cos(α) were calculated from the simulation by alignment (rotation and translation) of each coordinate frame such that the radius of gyration tensor was diagonal. Each N–H vector was normalized and then projected along the unit vector coincident with the long axis of the aligned molecule, which resulted in estimates for cos(α). These values were arithmetically averaged over the whole simulation.
Diffusion ordered spectroscopy (DOSY) experiments
Diffusion measurements were carried out without spinning on a 400 MHz Varian Inova instrument, using a 5 mm diameter indirect detection probe equipped with a z-gradient coil, allowing gradient pulses up to 30 G cm−1. No sample temperature control was used; experiments were carried out at the probe quiescent temperature in a room air-conditioned to about 20°C. Nominal gradient strengths were calibrated according to manufacturer’s recommendations. The Oneshot pulse sequence [46] was used with a diffusion delay Δ of 0.2 s and a net diffusion-encoding pulse width δ of 2 ms (i.e., each bipolar pulse-pair consisted of two 1 ms gradient pulses) with 10 gradient strengths, ranging from 3.0 to 27.3 G cm−1, chosen to give equal steps in gradient squared. A spectral width of 4,000 Hz and 16,384 complex data points were acquired for each gradient strength. Correction for instrumental imperfections by reference deconvolution [25], using the TSP peak as reference, were performed on the DOSY data using the standard instrument software (Vnmr6.1C). The diffusion coefficients were fitted to Eq. 10 using four coefficients in the power series, where the coefficients for correction of the non-uniform field gradients (0.928, −9.78 × 10−3, −3.83 × 10−4 and 2.51 × 10−5) were obtained as previously described [27].
Electronic supplementary material
Below is the link to the electronic supplementary material.
Experimental and calculated nOe ratios (η), and T1 relaxation data for isotopic models of diffusion. (PDF 24.5 kb)
Calculated model-free parameters for the tetra-, hexa-, and octa sacchrides (1, 2, and 3 respectively) of the NA-domain of heparan sulfate, using a constant internal correlation time of 30 ps, fitted to isotopic and anisotropic models of rotational diffusion (PDF 23.5 kb)
Acknowledgements
We would like to thank Professor Ian Roberts for providing the K5-E. coli bacteria, the K5 lyase enzyme and for helpful discussions. We also thank Mr. Andrew Buck for help with the bacterial work. We are deeply indebted to staff of the Swedish NMR center for allowing us to use their high-field spectrometers (600, 800 and 900 MHz) and for their hospitality and technical support. In particular, we would like to thank Dr. Vladislav Orekhov and Dr. Göran Karlsson for their help. We would also like to thank Professor Lu-Yun Lian and Dr. Igor Barsukov for the use of their 800 MHz spectrometer at the Liverpool NMR centre and Dr. Charles Blundell for helpful discussions. This work was funded by a Wellcome Trust project grant, reference number 075489, as well as support from a BBSRC David Phillips Fellowship and the EPSRC (UK), grant references: GR/S90751/01 and EP/E057888/1.
Open Access This article is distributed under the terms of the Creative Commons Attribution Noncommercial Licence which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Abbreviations
- HS
Heparan sulfate
- GlcNAc
N-acetyl-d-glucosamine
- GlcA
d-glucuronic acid
- GAG
Glucosaminoglycan
- nOe
Nuclear Overhauser enhancement
- RDC
Residual dipolar coupling
- DOSY
Diffusion ordered spectroscopy
- MD
Molecular dynamics
Footnotes
Electronic Supplementary Material
The online version of this article (doi:10.1007/s10719-007-9081-9) contains supplementary material, which is available to authorized users.
References
- 1.Esko, J.D., Lindahl, U.: Molecular diversity of heparan sulfate. J. Clin. Invest. 108, 169–173 (2001) [DOI] [PMC free article] [PubMed]
- 2.Nader, H.B., Chavante, S.F., de-Paiva, E.A., Jeronimo, S.M.B., Medeiros, G.F., de-Abreu, L.R.D., Lette, E.L., de-Sousa-Filho, J.F., Castro, R.A.B., Toma, L., Terasariol, I.L.S., Porcionatto, M.A., Dietrich, C.P.: Heparan sulfates and heparins: similar compounds performing the same functions in vertebrates and invertebrates? Braz. J. Med. Biol. Res. 32, 529–538 (1999) [DOI] [PubMed]
- 3.Lamanna, W.C., Kalus, I., Padva, M., Baldwin, R.J., Merry, C.L.R., Dierks, T.: The heparanome—The enigma of encoding and decoding heparan sulfate sulfation. J. Biotechnol. 129, 290–307 (2007) [DOI] [PubMed]
- 4.Bishop, J.R., Schuksz, M., Esko, J.D.: Heparan sulphate proteoglycans fine-tune mammalian physiology. Nature 446, 1030–1037 (2007) [DOI] [PubMed]
- 5.Salmivirta, M., Lidholt, K., Lindahl, U.: Heparan sulfate: a piece of information. FASEB J. 10, 1270–1279 (1996) [DOI] [PubMed]
- 6.Mulloy, B., Forster, M.J.: Conformation and dynamics of heparin and heparan sulfate. Glycobiology 10, 1147–1156 (2000) [DOI] [PubMed]
- 7.Ferro, D.R., Provasoli, A., Ragazzi, M., Torri, G., Casu, B., Gatti, G., Jacquinet, J.C., Sinay, P., Petitou, M., Choay, J.: Evidence for conformational equilibrium of the sulfated L-iduronate residue in heparin and in synthetic heparin monosaccharides and oligosaccharides—NMR and force-field studies. J. Am. Chem. Soc. 108, 6773–6778 (1986) [DOI]
- 8.Stringer, S.E., Gallagher, J.T.: Specific binding of the chemokine platelet factor 4 to heparan sulfate. J. Biol. Chem. 272, 20508–20514 (1997) [DOI] [PubMed]
- 9.Fischer, M.W.F., Majumdar, A., Zuiderweg, E.R.P.: Protein NMR relaxation: theory, applications and outlook. Prog. Nucl. Magn. Reson. Spectrosc. 33, 207–272 (1998) [DOI]
- 10.Clavel, C., Canales, A., Gupta, G., Santos, J., Cañada, F., Penadés, S., Surolia, A., Jiménez-Barbero, J.: NMR studies on the conformation of oligomannosides and their interaction with banana lectin. Glycocon. J. 24, (8), 449–464 (2007) [DOI] [PubMed]
- 11.Mulloy, B., Forster, M.J., Jones, C., Davies, D.B.: N.M.R. and molecular-modelling studies of the solution conformation of heparin. Biochem. J. 293, 849–858 (1993) [DOI] [PMC free article] [PubMed]
- 12.Mulloy, B., Forster, M.J., Jones, C., Drake, A.F., Johnson, E.A., Davies, D.B.: The effect of variation of substitution on the solution conformation of heparin—a spectroscopic and molecular modeling study. Carbohyd. Res. 255, 1–26 (1994) [DOI] [PubMed]
- 13.Ferro, D.R., Provasoli, A., Ragazzi, M., Casu, B., Torri, G., Bossennec, V., Perly, B., Sinay, P., Petitou, M., Choay, J.: Conformer populations of L-iduronic acid residues in glycosaminoglycan sequences. Carbohyd. Res. 195, 157–167 (1990) [DOI] [PubMed]
- 14.Casu, B., Choay, J., Ferro, D.R., Gatti, G., Jacquinet, J.C., Petitou, M., Provasoli, A., Ragazzi, M., Sinay, P., Torri, G.: Controversial glycosaminoglycan conformations. Nature 322, 215–216 (1986) [DOI] [PubMed]
- 15.Lipari, G., Szabo, A.: Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 104, 4546–4559 (1982) [DOI]
- 16.Angulo, J., Hricovini, M., Gairi, M., Guerrini, M., de Paz, J.L., Ojeda, R., Martin-Lomas, M., Nieto, P.M.: Dynamic properties of biologically active synthetic heparin-like hexasaccharides. Glycobiology 15, 1008–1015 (2005) [DOI] [PubMed]
- 17.Hricovini, M., Guerrini, M., Torri, G., Casu, B.: Motional properties of E. Coli polysaccharide K5 in aqueous solution analyzed by NMR relaxation measurements. Carbohydr. Res. 300, 69–76 (1997) [DOI] [PubMed]
- 18.Hricovini, M., Torri, G.: Dynamics in aqueous solutions of the pentasaccharide corresponding to the binding site of heparin for antithrombin III studied by NMR relaxation measurements. Carbohyd. Res. 268, 159–175 (1995) [DOI] [PubMed]
- 19.Almond, A., DeAngelis, P.L., Blundell, C.D.: Dynamics of hyaluronan oligosaccharides revealed by 15N relaxation. J. Am. Chem. Soc. 127, 1086–1087 (2005) [DOI] [PubMed]
- 20.Clarke, B.R., Esumeh, F., Roberts, I.S.: Cloning, expression, and purification of the K5 capsular polysaccharide lyase (kflA) from coliphage K5A: evidence for two distinct K5 lyase enzymes. J. Bacteriol. 182, 3761–3766 (2000) [DOI] [PMC free article] [PubMed]
- 21.Morris, G.A.: In: Grant, D.M., Harris, R.K. (ed.) Encyclopedia of Nuclear Magnetic Resonance, pp. 35–44. Wiley, Chichester (2002)
- 22.Johnson Jr, C.S.: Diffusion ordered nuclear magnetic resonance spectroscopy principles and applications. Prog. Nucl. Magn. Reson. Spectrosc. 34, 203–256 (1999) [DOI]
- 23.Lindahl, U., Li, J.P., Kusche-Gullberg, M., Salmivirta, M., Alaranta, S., Veromaa, T., Emeis, J., Roberts, I., Taylor, C., Oreste, P., Zoppetti, G., Naggi, A., Torri, G., Casu, B.: Generation of “Neoheparin” from E. coli K5 capsular polysaccharide. J. Med. Chem. 48, 349–352 (2005) [DOI] [PubMed]
- 24.Barbato, G., Ikura, M., Kay, L.E., Pastor, R.W., Bax, A.: Backbone dynamics of calmodulin studied by nitrogen-15 relaxation using inverse detected two-dimensional NMR spectroscopy the central helix is flexible. Biochemistry 31, 5269–5278 (1992) [DOI] [PubMed]
- 25.Morris, G.A., Barjat, H., Home, T.J.: Reference deconvolution methods. Prog. Nucl. Magn. Reson. Spectrosc. 31, 197–257 (1997) [DOI]
- 26.Stejskal, E.O., Tanner, J.E.: Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys. 42, 288–292 (1965) [DOI]
- 27.Nilsson, M., Connell, M.A., Davis, A.L., Morris, G.A.: Biexponential fitting of diffusion-ordered NMR data: practicalities and limitations. Anal. Chem. 78, 3040–3045 (2006) [DOI] [PubMed]
- 28.Wilkins, D.K., Grimshaw, S.B., Receveur, V., Dobson, C.M., Jones, J.A., Smith, L.J.: Hydrodynamic radii of native and denatured proteins measured by pulse field gradient NMR techniques. Biochemistry 38, 16424–16431 (1999) [DOI] [PubMed]
- 29.Phan, I.Q.H., Boyd, J., Cambell, I.D.: Dynamic studies of a fibronectin type I module pair at three frequencies: anisotropic modelling and direct determination of conformational exchange. J. Biomol. NMR 8, 369–378 (1996) [DOI] [PubMed]
- 30.Hricovini, M., Guerrini, M., Torri, G., Piani, S., Ungarelli, F.: Conformational analysis of heparin epoxide in aqueous solution. An NMR relaxation study. Carbohyd. Res. 277, 11–23 (1995) [DOI] [PubMed]
- 31.Rundlof, T., Venable, R.M., Pastor, R.W., Kowalewski, J., Widmalm, G.: Distinguishing anisotropy and flexibility of the pentasaccharide LNF-1 in solution by carbon-13 NMR relaxation and hydrodynamic modeling. J. Am. Chem. Soc. 121, 11847–11854 (1999) [DOI]
- 32.Mobli, M., Almond, A.: N-acetylated amino sugars: the dependence of NMR 3J(HNH2)-couplings on conformation, dynamics and solvent. Org. Biomol. Chem. 5, 2243–2251 (2007) [DOI] [PMC free article] [PubMed]
- 33.Mulloy, B., Forster, M.J., Jones, C., Drake, A.F., Johnson, E.A., Davies, D.B.: The effect of variation of substitution on the solution conformation of heparin: a spectroscopic and molecular modelling study. Carbohyd. Res. 255, 1–26 (1994) [DOI] [PubMed]
- 34.Murphy, K.J., Merry, C.L.R., Lyon, M., Thompson, J.E., Roberts, I.S., Gallagher, J.T.: A new model for the domain structure of heparan sulfate based on the novel specificity of K5 lyase. J. Biol. Chem. 279, 27239–27245 (2004) [DOI] [PubMed]
- 35.Lindahl, U., Kusche-Gullberg, M., Kjellen, L.: Regulated diversity of heparan sulfate. J. Biol. Chem. 273, 24979–24982 (1998) [DOI] [PubMed]
- 36.Zehnder, J.L., Galli, S.J.: Cell biology: mast-cell heparin demystified. Nature 400, 714–715 (1999) [DOI] [PubMed]
- 37.Vann, W.F., Schmidt, M.A., Jann, B., Jann, K.: The structure of the capsular polysaccharide (K5 Antigen) of urinary-tract-infective Escherichia-Coli 010-K5-H4—a polymer similar to desulfo-heparin. Eur. J. Biochem 116, 359–364 (1981) [DOI] [PubMed]
- 38.Blundell, C.D., DeAngelis, P.L., Day, A.J., Almond, A.: Use of 15N-NMR to resolve molecular details in isotopically-enriched carbohydrates: sequence-specific observations in hyaluronan oligomers up to decasaccharides. Glycobiology 14, 999–1009 (2004) [DOI] [PubMed]
- 39.Blundell, C.D., Reed, M.A.C., Almond, A.: Complete assignment of hyaluronan oligosaccharides up to hexasaccharides. Carbohyd. Res. 341, 2803–2815 (2006) [DOI] [PubMed]
- 40.Farrow, N.A., Muhandiram, R., Singer, A.U., Pascal, S.M., Kay, C.M., Gish, G., Shoelson, S.E., Pawson, T., Forman-Kay, J.D., Kay, L.E.: Backbone dynamics of a free and a phosphopeptide-complexed Src homology 2 domain studied by 15N NMR relaxation. Biochemistry 33, 5984–6003 (1994) [DOI] [PubMed]
- 41.Delaglio, F., Grzesiek, S., Vuister, G.W., Zhu, G., Pfeifer, J., Bax, A.: NMR pipe: a multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR 6, 277–293 (1995) [DOI] [PubMed]
- 42.Korzhnev, D.M., Billeter, M., Arseniev, A.S., Orekhov, V.Y.: NMR studies of Brownian tumbling and internal motions in proteins. Prog. Nucl. Magn. Reson. Spectrosc. 38, 197–266 (2001) [DOI]
- 43.Walling, A.E., Pargas, R.E., Dios, A.C.d.: Chemical shift tensors in peptides a quantum mechanical study. J. Phys. Chem. A 101, 7299–7303 (1997) [DOI]
- 44.Case, D.A.: Calculations of NMR dipolar couplin strengths in model peptides. J. Bio. NMR 15, 95–102 (1999) [DOI] [PubMed]
- 45.Almond, A., DeAngelis, P.L., Blundell, C.D.: Hyaluronan: the local solution conformation determined by NMR and computer modeling is close to a contracted left-handed 4-fold helix. J. Mol. Biol. 358, 1256–1269 (2006) [DOI] [PubMed]
- 46.Pelta, M.D., Morris, G.A., Stchedroff, M.J., Hammond, S.J.: A one-shot sequence for high-resolution diffusion-ordered spectroscopy. Magn. Reson. Chem. 40, S147–S152 (2002) [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Below is the link to the electronic supplementary material.
Experimental and calculated nOe ratios (η), and T1 relaxation data for isotopic models of diffusion. (PDF 24.5 kb)
Calculated model-free parameters for the tetra-, hexa-, and octa sacchrides (1, 2, and 3 respectively) of the NA-domain of heparan sulfate, using a constant internal correlation time of 30 ps, fitted to isotopic and anisotropic models of rotational diffusion (PDF 23.5 kb)