Skip to main content
PMC home page
Genome Research logoLink to Genome Research
. 2008 Jun;18(6):911–917. doi: 10.1101/gr.074872.107

Power and SNP tagging in whole mitochondrial genome association studies

Allan F McRae 1,1, Enda M Byrne 1, Zhen Zhen Zhao 1, Grant W Montgomery 1, Peter M Visscher 1
PMCID: PMC2413158  PMID: 18356315

Abstract

The application of genetic association studies to detect mitochondrial variants responsible for phenotypic variation has recently been demonstrated. However, the only power estimates currently available are based on the use of mitochondrial haplogroups, which can only tag a small fraction of the common variation in the mitochondrial genome. Here, power estimates are derived for a SNP-based study design for both disease (case-control) and quantitative trait mapping studies. Power is estimated using simulations based on a collection of publicly available mitochondrial sequences of European origin. The power when testing all common mitochondrial SNPs is shown to be equivalent to that when testing only tagging SNPs, despite the relatively high ratio of tagging SNPs to total SNPs resulting from the tagging of all SNPs with a minor allele frequency greater than 1%. The sample size requirements of mitochondrial genome association studies are compared with that of nuclear whole-genome studies. Remarkably, the trade off between the number of tests being performed and the proportion of phenotypic variance explained for a fixed effect size results in approximately equal sample sizes required for both study types, although the per individual cost for the mitochondrial association study is much less. To test the representation of the sequences used in the power simulations, a sample of 3839 individuals from 1037 Australian families was genotyped for 69 tagging SNPs. The strong concordance in allele frequencies and linkage disequilibrium between the European sequences and the Australian sample indicates that the results presented here are transferable across populations of European descent.

The human mitochondria contain a circular, haploid, and maternally inherited genome 16.6 kb in length. The genome encodes 13 genes involved in oxidative phosphorylation, two rRNA genes, and 22 tRNA genes. Mitochondrial DNA (mtDNA) is highly polymorphic, providing an aspect of the human genome that has been thus far widely excluded from studies looking for genetic factors involved in human variation, despite the well-known role of mitochondria in disease (Wallace 1999).

Recently, the use of association studies to detect mitochondrial sequence variants responsible for variation in disease risk has received attention (Samuels et al. 2006; Saxena et al. 2006). Samuels et al. (2006) present an analysis of the power to detect an association between mtDNA haplogroups and disease using simulation-based permutation tests. Their analysis tests for differences in mtDNA haplogroup frequency between cases and control samples using a (2 × N) contingency table, where N is the number of haplogroups in the sample (∼10 in European samples). Saxena et al. (2006) tested a set of tagging mitochondrial single nucleotide polymorphisms (SNPs) for association with diabetes and related metabolic traits. Their analysis used a SNP-based approach, where individual SNPs were tested for association with the trait of interest, effectively using a series of (2 × 2) contingency tables for disease traits and t-tests for continuous variables, with an appropriate correction for multiple testing.

While the approach of Samuels et al. (2006) may appear to be advantageous due to the use of a single test for association, and thereby removing any multiple testing issues, this approach suffers from lack of coverage of the mitochondrial genome. Assuming the 10 common European haplogroups were genetically independent, they could, at most, tag an equivalent number of independent SNPs. This is only a fraction of the 64 SNPs identified by Saxena et al. (2006) as being necessary to tag common mitochondrial variation with an r2 of 0.8, where r2 is the squared correlation of the alleles at two SNPs and 0.8 is the usual tagging threshold. Also, when using a haplogroup-based approach, there is substantial within-haplogroup variation being excluded from testing. For example, sequences of haplogroup H, the most common European haplogroup, taken from mtDB (Ingman and Gyllensten 2006), contain 78 SNPs with minor allele frequency >1%, of which nine have minor allele frequency >5%. To account for this variation when using the haplogroup association approach requires the continued subdivision of haplogroups into smaller units, which, in turn, will reduce the power of the analysis.

In this study, we investigate the properties of the SNP-based approach used by Saxena et al. (2006). Although analogies with nuclear genome association studies may suggest this approach to be advantageous in terms of locating the underlying genetic variant, it should be remembered that the mitochondrial DNA is essentially a recombination “coldspot”, and this prohibits the localization of causal variants through association. (Despite some initial reports [Awadalla et al. 1999], there appears to be little evidence for widespread recombination between mitochondrial genomes [Eyre-Walker and Awadalla 2001; McVean et al. 2002].) Here, the power of the SNP-based approach to mitochondrial association studies is investigated and a comparison of the power of association studies on mitochondrial DNA relative to genome- wide association studies is made. To investigate the representation of the available European mitochondrial genome sequences used in the simulation studies, we genotyped a sample of 3839 individuals from 1037 Australian families for 69 tagging SNPs and compared allele frequencies and linkage disequilibrium patterns.

Results

Linkage disequilibrium between mitochondrial SNPs

The number of SNPs required for tagging mitochondrial genetic variation, and thus the extent of the correction for multiple testing in mitochondrial association studies, depends on the amount of linkage disequilibrium in the mitochondrial genome. Based on the alignment of over 900 mtDNA sequences, Saxena et al. (2006) identified 144 variants with frequency >1% in European populations. These SNPs contain 49 of the 50 SNPs identified as segregating in the founders of the CEU HapMap population (HapMap Data Release 21, July 2006; The International HapMap Consortium 2005). Of the 144 SNPs, 50 had a minor allele frequency (MAF) greater than 5%. Furthermore, seven of the SNPs were triallelic. As the third allele always was present at less than 1% at all loci, occurring only once in the 928 samples for five of the seven loci, SNPs with this allele were considered as missing values for the purpose of this study.

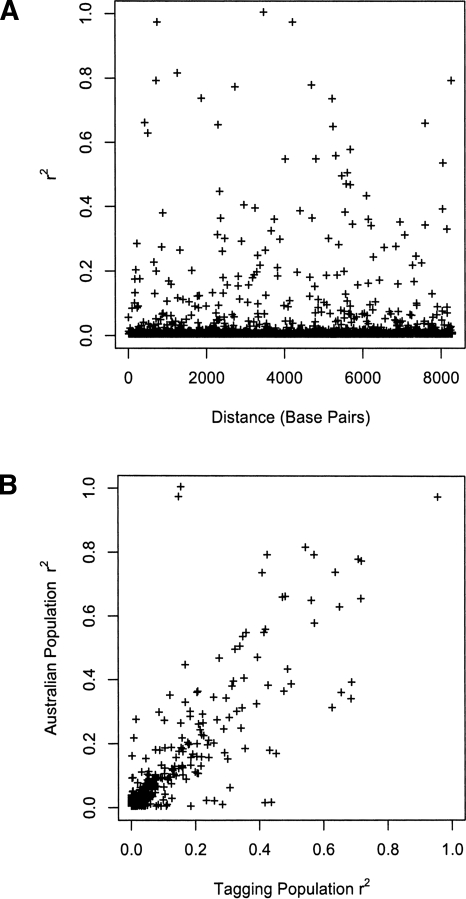
The average r2 value for all pairs of SNPs was 0.04 (SD = 0.14) without a restriction on allele frequency and 0.14 (SD = 0.26) when MAF was restricted to >0.05. Out of the 10,296 pairwise SNP comparisons in the complete data set, only two pairs showed complete linkage disequilibrium (r2 = 1) and 136 pairs (1.3%) show r2 > 0.8. These average r2 values are low when considering that the mitochondrial genome is essentially a recombination “cold-spot” and indicate that the number of tests to be corrected for in a mitochondrial association study will be close to the number of SNPs tested. The average r2 values are smaller that those in the CEU HapMap population, which has an average r2 of 0.12 for all SNPs and 0.22 with the restriction on minor allele frequency being greater than 0.05. This difference can be attributed to an inflation in the average r2 in the HapMap population, due to an increase of sampling variation (Hill and Weir 1994) and the choice of SNPs to be genotyped in the initial phase of the HapMap project resulting in an approximately uniform distribution of minor allele frequency instead of relatively exponential distribution observed when examining all SNPs (The International HapMap Consortium 2005). The correlation between r2 and distance was small and positive (0.005) and thus provided no evidence for mitochondrial recombination.

Power of whole mitochondrial genome association studies

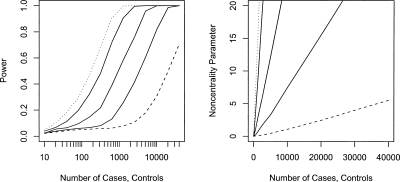
Figure 1 presents estimates of the power of case-control studies to detect risk alleles in the mitochondrial genome. These estimates average power differences over the observed distribution of minor allele frequencies, an approach consistent with the fact that the allele frequency at the causal allele will be unknown during study design. The differing approaches of genotyping all common variants (144 SNPs) and SNPs that tag those variants with an r2 of 0.8 (64 SNPs) result in small differences in the power to detect mitochondrial association, with genotyping of all common variants being ∼2%–3% more powerful when power is in the 0.8–0.9 range. Given the tagging approach requires less than half the genotyping of examining all SNPs, this power difference can readily be overcome by the additional genotyping of individuals that can be achieved for a fixed cost when only using tagging SNPs. For this reason, the only power estimates from the tagging SNP approach are presented in Figure 1. From the power curves, ∼900 cases and controls will be needed to detect an allele with a relative risk of 3 with a power of 0.8. This sample size increases to ∼3000 for a relative risk of 2 and 10,000 for a relative risk of 1.5.

Figure 1.

Figure 1.

Open in a new tab

Power (left) and noncentrality parameter (right) of case-control studies to detect a mitochondrial variant encoding relative risks of 1.2 (dashed line), 1.5, 2, 3, and 4 (dotted line) at a 5% mitochondrial genome-wide significance level. The noncentrality parameter is calculated as the difference in the mean of the distribution of the –log10 of the minimum P-value across all SNPs under the alternative and null hypotheses.

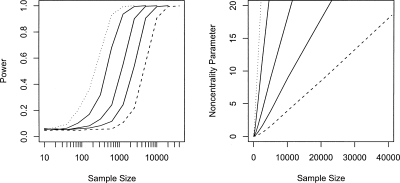
Figure 2 presents the power estimates for the detection of a mitochondrial SNP with an effect on a quantitative trait. As with case-control studies, the differences in power when genotyping all common SNPs or tagging SNPs is small (3%–4%), with genotyping all SNPs being the more powerful approach for a fixed number of individuals. A sample size of ∼8000 is needed to detect a genetic variant explaining 0.25% of the phenotypic variance, reducing to ∼2000 for a locus explaining 1% with a power of 0.8.

Figure 2.

Figure 2.

Open in a new tab

Power (left) and noncentrality parameter (right) of detecting a mitochondrial variant with effect sizes of 0.25 (dashed line), 0.5, 1, 2.5, and 5% (dotted line) of the phenotypic variance of a quantitative trait at a 5% mitochondrial genome-wide significance level. The noncentrality parameter is calculated as the difference in the mean of the distribution of the –log10 of the minimum P-value across all SNPs under the alternative and null hypotheses.

Relative power of mitochondrial and genome-wide association studies

As many association studies have been or are being performed on the entire nuclear genome and with mitochondrial SNPs now being included on some high-throughput genotyping platforms, it is of interest to compare the relative power of mitochondrial association studies with their nuclear counterparts. In general, the sample size (N) required to detect a quantitative trait locus (QTL) explaining a proportion of the trait variance (q2) is

graphic file with name 911equ1.jpg

where α is the type I error rate, 1 − β is the power, and z is the normal score. This formula agrees with the power estimates given in Figure 2. Let zA and zM be the type I error z-scores for nuclear genome and mitochondrial association scans, respectively. For two loci with the same allele frequencies and equal effects on a quantitative trait, one situated on an autosome and the other on the mitochondria, q2 = 2p(1 − p)a2 for the autosomal locus and q2 = p(1 − p)a2 for the mitochondrial locus, where p is the allele frequency at the locus and a is the effect size in phenotypic standard deviation units (acting additively on the nuclear locus). Thus, the autosomal locus explains twice the amount of variance in the trait due to the haploid nature of mitochondria. The ratio of the same sizes required for a given power in mitochondrial (NM) to autosomal association studies (NA) is

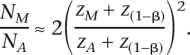graphic file with name 911equ2.jpg

Being conservative with respect to the difference in the number of independent tests performed between the study types, let an autosomal association scan use a Bonferonni correction for 300,000 tests and a mitochondrial scan for 64 tests. Thus, the values for zM and zA for a Type I error of 0.05 are 3.36 and 5.23, respectively. Then, at a power level of 80%, and thus z(1−β) of 0.84, the ratio of sample sizes required for mitochondrial to autosomal scans is approximately one. That is, mitochondrial genome-wide association studies require approximately the same sample size as a nuclear genome association study to achieve 80% power to detect a locus of equivalent effect size.

Efficiency of mtSNP tagging in the Australian population

The maintenance of power while use tagging SNPs requires that the allele frequencies and intermarker linkage disequilibrium in the tagging and sample populations are similar. To address whether the European mitochondrial sequences from public databases formed a suitable tagging population, a sample of 3839 individuals from 1037 Australian families was genotyped at 69 polymorphic SNPs. Genotyping was successful in 260,627 of the 264,891 (98.4%) cases, and a heterozygous genotype call was made for 75 (0.03%) of the called genotypes. Where multiple samples were genotyped from a maternal lineage, 18 of the apparent heteroplasmies were observed only once in the lineage, and five cases were observed multiple times. Apart from heteroplasmy, only eight genotype mismatches within a maternal lineage were observed. For the purposes of this article, heterozygous genotype calls were considered as missing and independent mitochondrial haplotypes were generated by forming a consensus within mitochondrial lineages.

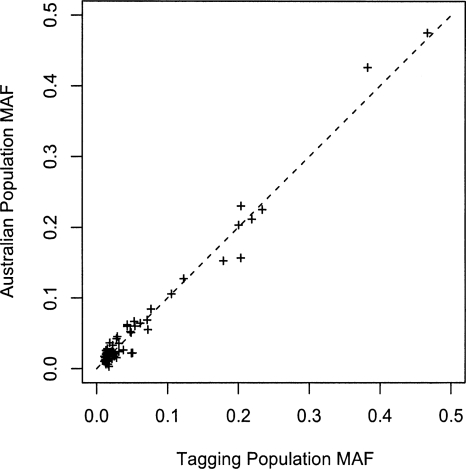
Figure 3 compares the allele frequency at the 69 SNPs genotyped in the Australian population to those from the publicly available European sequence data. As expected, given that the vast majority of mitochondrial lineages in the Australian sample were European, the correlation of allele frequencies in the two samples was very strong (ρ = 0.99). A comparison of the intermarker linkage disequilibrium between the tagging SNPs in the European sequences to that in the Australian samples is given in Figure 4. The distribution of linkage disequilibrium (LD) with distance in the Australian sample (Fig. 4A) shows the low average LD between markers that is expected with tagging SNPs. While several marker pairs have an r2 of >0.8, the overall tagging efficiency appears high. Again, no significant correlation is observed with distance (ρ = 0.86, P = 0.93), providing no evidence for mitochondrial recombination. Figure 4B compares the LD at a pair of markers in the European and Australian samples. Overall, there is a high correlation between the two data sets (ρ = 0.86). The main discordances are due to markers mt11674 and mt15884. These markers are in high LD in both populations and both have minor allele frequencies of 0.05 in the tagging population and 0.02 in the Australian population. The pair of discordant marker-pairs with high LD in the Australian population (r2 > 0.95) and low LD in the tagging samples (r2 ≈ 0.15) is these two markers with marker mt12414. Similarly, the pair of discordant marker-pairs with low LD in the Australian population (r2 ≈ 0.01) and high LD in the tagging samples (r2 ≈ 0.42) is mt11674 and mt15884 with mt5495.

Figure 3.

Figure 3.

Open in a new tab

Allele frequency comparisons between tagging sample and Australian sample. A nearly complete correlation of 0.99 is observed between the two samples.

Figure 4.

Figure 4.

Open in a new tab

Linkage disequilibrium between mitochondrial SNPs in the Australian population. (A) Distribution of linkage disequilibrium with distance. (B) Comparison of LD in the Australian and tagging populations.

Mitochondrial haplogroup prediction from tagging SNPs

We have argued for the use of a tagging SNP approach to mitochondrial association studies, as this approach results in comprehensive coverage of the genetic variation in the mitochondrial genome. However, the traditional approach of using mitochondrial haplogroups has been considered to be superior, as the haplogroup approach uses information on the evolution of the mitochondrial genome (Elson et al. 2007). As mitochondrial haplotypes are defined by genetic variants and a tagging SNP set is chosen to capture most genetic variation, it should be possible to retrieve mitochondrial haplogroups from the use of tagging SNP genotypes.

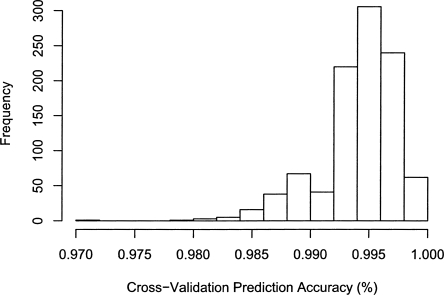
In order to demonstrate this, the genotypes of the tagging SNP set used here for power calculations was determined for all mitochondrial sequences in mtDB from the 10 most common European mitochondrial haplogroups. A linear discriminant function analysis with bootstrap cross-validation (see Methods) was used to assign a haplogroup to each mitochondrial sequence. The predicted haplogroups were compared with the known haplogroup from mtDB for each sequence. Figure 5 shows the high prediction accuracy of this approach, with 95% of all cross-validation replicates having a prediction accuracy of >98.5%. The majority of the misclassified sequences were in rare haplogroups that are nested in larger clades. Obviously, the prediction accuracy could be increased by taking into account haplogroup defining variants when selecting a tagging SNP set.

Figure 5.

Figure 5.

Open in a new tab

Distribution of haplogroup prediction accuracy as determined using bootstrap cross-validation of the linear discriminant function analysis on sequences from the common European haplogroups in mtDB.

Discussion

We investigated the power to detect a causal mitochondrial variant through association for both disease (case-control) and quantitative trait study designs. Remarkably, the sample sizes required to detect loci of moderate effect sizes was shown to be within the range of those that are being deployed in current nuclear whole-genome association studies. This was demonstrated to be due to a trade-off between the number of tests performed and the reduced phenotypic variance explained by a mitochondrial locus compared with a nuclear locus with equivalent effect size. This is an important facet to consider when using the Illumina HumanHap550 Genotyping BeadChip and Affymetrix Genome-Wide SNP Array 6.0, both of which include mitochondrial SNPs, as most studies using these genotyping platforms will be designed with the power of nuclear association in mind. Both the Illumina HumanHap300 Genotyping BeadChip and the Affymetrix GeneChip Human Mapping 500K Array Set contain no mitochondrial SNPs, so any association study performed with these chips is uninformative for a mitochondrial association study. Given that mitochondrial association studies require ∼0.02% of the genotyping required for a nuclear genome association study, the addition of the mitochondrial SNPs to an association study will only trivially increase its overall cost.

On initial inspection, the average r2 between mitochondrial SNPs appears to be low considering it is essentially a 16.6-kb recombination cold-spot. This is confirmed with coalescent simulations using the program “ms” (Hudson 2002), using an effective population size (Ne) of 5000 (Wilder et al. 2004), and mutation rates varying between 10−7 and 10−8 (Ingman et al. 2000; Wilder et al. 2004). For minor allele frequencies of >1%, an average r2 between SNPs of ∼0.16 is obtained, increasing to between 0.32 and 0.34 (depending on mutation rate) when the minor allele frequency is restricted to >5%. However, the observed linkage disequilibrium is within the range of simulation replicates, confirming the consistency of the observed data with estimates of genetic parameters.

In order to compare power estimates to those obtained by Samuels et al. (2006), a conversion is needed to a common measure of disease penetrance. Using the formula given in the Methods section, a relative risk of 2.0 is equivalent to a change in allele frequency of 42%, 80%, and 96% for haplogroups H, I, and J, respectively. From Figure 2D in Samuels et al. (2006) the required sample sizes to detect these differences with 90% power are ∼300, 600, and 3000, respectively. For a relative risk of 2.0, the simulations presented here estimate ∼4000 individuals are needed to gain 90% power. The differences can be attributed to two factors, namely, the number of tests performed and the allele frequency of the causal variant. Samuels et al. perform only one test compared with the 64 or 144 performed here. However, as discussed above, their test only covers a fraction of the variation in the mitochondria, so their assumption that the causal variant will be tagged by the haplogroup is reducing their required sample sizes. Second, the simulations presented here average over the distribution of common allele frequencies. The frequencies of the H, I, and J haplogroups in European populations are 0.41, 0.11, and 0.02, respectively. Given that ∼65% of common mitochondrial polymorphisms have minor allele frequencies in the range of from 0.01 to 0.05, the sample size required for haplogroup J is a more realistic measure of the size required to detect an unknown genetic variant and is in the same order of magnitude as that determined here.

The power estimates given here provide an average measure over the minor allele frequencies of all SNPs. This is consistent with the allele frequency of the causal SNP not being known during study design. However, if an assumption can be made regarding the allele frequency of the causal variant, a simple correction can be made to adjust the required sample size for a given power. From the equation relating required sample size and variance explained by a QTL, it can be seen that N∝1/[p(1 − p)], where p is the allele frequency of the locus. Thus, for a locus with assumed allele frequency pg, the value of N can be adjusted by a factor of 0.042/[pg(1 − pg)], where 0.042 is the average of p(1 − p) over the 64 tagging SNPs.

Saxena et al. (2006) selected 64 tagging SNPs that tagged all 144 mtSNPs with a minor allele frequency of >1% using an r2 of 0.8. The use of these tagging SNPs on a fixed number of individuals was shown to have only a slight loss in power when compared with genotyping all mtSNPs. Thus, for a fixed number of samples, the genotyping budget can be approximately halved with minor loss of power, or equivalently, for a fixed genotyping budget, the number of individuals genotyped can be doubled. The reduction of the numbers of SNPs through tagging by a factor of approximately two appears low compared with the usual numbers used to describe tagging in nuclear genome association studies in European populations (Barrett and Cardon 2006). However, the mitochondrial tagging set covers 94 SNPs with minor allele frequencies between 0.01 and 0.05, a range that is typically not covered in tagging of variation in the nuclear genome.

The power to detect a causal genetic variant on the mitochondria was compared with that of a locus with equivalent effect size on the nuclear genome. This comparison is affected by the different number of tests performed in the two types of studies and the variance explained by the causal variant. The much-reduced number of tests required for a mitochondrial association study results in sample size requirements for a given power in a mitochondrial association scan being approximately half that required for a nuclear genome-wide association scan, when a fixed amount of phenotypic variance is explained by the causal locus. In order to compare the power to detect a locus with defined effect size in the mitochondria to that of a nuclear genome locus, the question of how to define “equivalence” in effect size arises. For example, an argument can be made for either equating the effect size of the mitochondrial locus to the additive effect of the locus in the nuclear genome (a) or to the difference between the two homozygous genotypes of the nuclear locus (2a). When defining the effect size for the nuclear locus as its additive effect size, then the genetic variance explained by the autosomal locus is twice that of a mitochondrial locus with the same allele frequency and effect size. This is the measure of the effect size used in the comparisons made here. However, if instead the mitochondrial effect size is equivalent to the difference between the two homozygous genotypes, then the variance explained by a mitochondrial locus becomes 4p(1 − p)a2, or twice that of an equivalent autosomal locus. With this measure, mitochondrial genome scans would need only a quarter of the sample size required for autosomal genome scans to achieve 80% power of detecting a locus. Empirical data on effect sizes for both nuclear and mitochondrial genetic variants will be required to resolve the correct parameterization.

When appropriate corrections are made for nuclear genetic relationships, familial data will be useful in increasing the power of mitochondrial association studies. As all individuals sharing the same maternal lineage will also share the same mitochondrial genotype (apart from rare mutation events), additional phenotypic information can be used in an analysis without further genotyping. Using this information, more accurate estimates of the genetic effect of a locus can be obtained, increasing the power of the test.

It has been shown that nuclear genome tagging SNPs can be transferred across different population samples with little loss in power (de Bakker et al. 2006). However, the transferability of the mitochondrial tagging SNPs chosen to cover variation in a collection of sequences from European samples to other populations required investigation, since the representation of the sequenced individuals has been questioned due to the high proportion of Finnish sequences and disease samples (Elson et al. 2007). There was a strong correlation between the allele frequencies estimated from the Australian sample and the European sequences. This is in agreement with a previous study that found the frequencies of mitochondrial haplogroups in the Australian population were similar to those in European populations (Manwaring et al. 2006). The Australian population showed similar levels of intermarker linkage disequilibrium between tagging SNPs to that in the European sequences, with major discordances being caused by two markers with low allele frequencies. While these could be genuine differences between the two “populations”, any small nonrandomness in the collection of sequences could cause a difference in LD, as all SNPs with minor allele frequency >0.01 (i.e., occurring in only 10 of the 928 sequences) were tagged.

In summary, mitochondrial genetic association studies are a relatively inexpensive addition to nuclear genome-wide association studies, requiring only 64 SNPs to tag mitochondrial SNPs with an allele frequency of greater than 1% in European populations with an r2 of 0.8. Also, mitochondrial association studies for a trait have been shown to be at least as powerful as their nuclear counterparts for a given effect size. This allows the reuse of previous study sets and provides a potentially valuable addition to ongoing genetic association studies. The success of transferring mitochondrial tagging SNPs across populations of similar ancestry was demonstrated using a sample of Australian individuals. This allows the continued use of the tagging set proposed by Saxena et al. (2006) for mitochondrial association studies in populations of European descent, which will increase the ability to make comparisons across studies.

Methods

Mitochondrial sequences

Saxena et al. (2006) compiled a collection of >1200 mitochondrial sequences from the GenBank and MitoKor databases. From these sequences, 928 sequences of European origin were aligned, identifying 144 SNPs with a minor allele frequency greater than 1% (Saxena et al. 2006). The hypervariable D-loop region was excluded due to the comparatively high mutation rate in this region of the mitochondrial genome, indicating that tagging this region is not an optimal strategy, especially when tagging for use across populations; therefore, direct sequencing should be used instead.

Power estimation

The power to detect loci in both case-control and quantitative trait settings was investigated using simulation. For each simulation replicate, one of the 144 common SNPs was randomly selected as a causal polymorphism affecting the trait of interest. The power of studies examining both case-control and quantitative trait data was investigated with 1000 replicates for sample-sizes of 2i × 10, where i took values from 0 to 12 (n = 10, 20, 40, . . . , 20,480, 40,960).

In the case-control study setting, the control sample was generated by randomly selecting a sample with replacement from the 928 mitochondrial sequences. The case sample was generated by determining the frequency of the minor allele at the causal SNP using the relationship to the relative risk (RR). Assuming that the disease under study is rare, the relative risk of a disease at a mitochondrial locus can be expressed as RR ≈ (pd(1 − p))/(p(1 − pd)), where p is the allele frequency in the control samples and pd is the frequency in the case samples. Using the calculated minor allele frequency in the case samples, the number of samples containing each allele at the causal SNP is determined using a random draw from a binomial distribution. The case sample is then generated by sampling with replacement haplotypes from the subset of the 928 mitochondrial sequences with the relevant allele at the causal SNP to achieve the previously determined number of samples with each allele. Power was estimated for SNPs that confer a relative risk of 1.2, 1.5, 2, 3, and 4 on the disease trait.

The power to detect a locus affecting a quantitative trait was examined by randomly drawing a sample of mitochondrial haplotypes with replacement. A quantitative trait was then simulated by calculating the required effect at the causal SNP by rearranging the formula 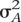Inline graphic = p(1 − p)a2, where 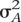Inline graphic is the genetic variance explained by the causal SNP, p is the allele frequency at that SNP, and a is the effect of the SNP in phenotypic standard deviation units. Note that this variance is half the value for an autosomal locus with the same additive effect and allele frequency, due to the haploid nature of the mitochondria. As the samples are considered to be unrelated, the remaining phenotypic variance was simulated as random normal deviates. The power was estimated for SNPs explaining 0.25, 0.5, 1, 2.5, and 5% of the variance in a trait.

The effect of each SNP on the trait of interest was tested using Fisher’s exact test (Fisher 1922) in the case control setting and a two-sample t-test (Student 1908) for quantitative traits. Significance was determined at the 5% experiment-wide level using a threshold obtained using 10,000 simulation replicates under the null hypothesis. The noncentrality parameter for the tests are calculated as the difference in the mean of the distribution of the –log10 of the minimum P-value across all SNPs under the alternative and null hypotheses. The analysis was performed on all 144 common SNPs and results compared with those obtained using the 64 tagging SNPs from Saxena et al. (2006).

Australian sample

A total of 3839 individuals from 1037 Australian families consisting of adolescent twins, their siblings, and parents were genotyped for a panel of mitochondrial SNPs. The vast majority of these samples were of northern European ancestry, primarily Anglo-Celtic, and so are expected to be comparable to the sequence data described above. Further details of this sample, including recruitment strategy, are found in Zhu et al. (2007) and Duffy et al. (2007). Due to the familial relationships, these samples provided 1693 independent mitochondrial haplotypes. The SNP panel consisted of 61 out of the 64 tagging SNPs used by Saxena et al. (2006) supplemented with nine SNPs to tag variation that was captured with an r2 of 0.8 in Saxena’s study only when using multi-SNP haplotypes. Additionally, a common variant in the D loop region, mt16189, was included (Poulton et al. 1998). Two SNPs (mt4928 and mt8251) were monomorphic in our sample, leaving 69 polymorphic SNPs in total.

Prediction of mitochondrial haplogroups

A total of 1074 complete sequences from the 10 most common European haplogroups (H, I, J, K, M, T, U, V, W, and X) were downloaded from mtDB (http://www.genpat.uu.se/mtDB/). From these sequences, the genotypes at tagging SNP loci were determined and used as predictors in a linear discriminant function analysis in the R statistical package (www.r-project.org). The accuracy of prediction of haplogroup was determined using a bootstrap cross-validation approach. For each of 1000 replicates, a bootstrap sample of sequences was chosen to form the prediction model, and the unsampled sequences had their haplogroups predicted. The prediction accuracy was then determined simply as the proportions of sequences whose haplogroups were correctly predicted.

Acknowledgments

We thank Richa Saxena and David Altshuler for providing information on assay conditions used in genotyping the mitochondrial SNPs, David Thornburn for useful discussion on mitochondrial studies, and Nicholas Martin for access to study samples. This work was supported by National Health and Medical Research Council of Australia (NHMRC) grants 389875 and 389892, and Australian Research Council grant DP0770096. G.W.M. and P.M.V. are NHMRC research fellows.

Footnotes

Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.074872.107.

References

  1. Awadalla P., Eyre-Walker A., Maynard Smith J., Eyre-Walker A., Maynard Smith J., Maynard Smith J. Linkage disequilibrium and recombination in hominid mitochondrial DNA. Science. 1999;286:2524–2525. doi: 10.1126/science.286.5449.2524. [DOI] [PubMed] [Google Scholar]
  2. Barrett J.C., Cardon L.R., Cardon L.R. Evaluating coverage of genome-wide association studies. Nat. Genet. 2006;38:659–662. doi: 10.1038/ng1801. [DOI] [PubMed] [Google Scholar]
  3. de Bakker P.I.W., Burtt N.P., Graham R.R., Cuiducci C., Yelensky R., Drake J.A., Bersaglieri T., Penney K.L., Butler J., Young S., Burtt N.P., Graham R.R., Cuiducci C., Yelensky R., Drake J.A., Bersaglieri T., Penney K.L., Butler J., Young S., Graham R.R., Cuiducci C., Yelensky R., Drake J.A., Bersaglieri T., Penney K.L., Butler J., Young S., Cuiducci C., Yelensky R., Drake J.A., Bersaglieri T., Penney K.L., Butler J., Young S., Yelensky R., Drake J.A., Bersaglieri T., Penney K.L., Butler J., Young S., Drake J.A., Bersaglieri T., Penney K.L., Butler J., Young S., Bersaglieri T., Penney K.L., Butler J., Young S., Penney K.L., Butler J., Young S., Butler J., Young S., Young S., et al. Transferability of tag SNPs in genetic association studies in multiple populations. Nat. Genet. 2006;38:1298–1303. doi: 10.1038/ng1899. [DOI] [PubMed] [Google Scholar]
  4. Duffy D.L., Montgomery G.W., Chen W., Zhao Z.Z., Le L., James M.R., Hayward N.K., Martin N.G., Sturm R.A., Montgomery G.W., Chen W., Zhao Z.Z., Le L., James M.R., Hayward N.K., Martin N.G., Sturm R.A., Chen W., Zhao Z.Z., Le L., James M.R., Hayward N.K., Martin N.G., Sturm R.A., Zhao Z.Z., Le L., James M.R., Hayward N.K., Martin N.G., Sturm R.A., Le L., James M.R., Hayward N.K., Martin N.G., Sturm R.A., James M.R., Hayward N.K., Martin N.G., Sturm R.A., Hayward N.K., Martin N.G., Sturm R.A., Martin N.G., Sturm R.A., Sturm R.A. A three–single-nucleotide polymorphism haplotype in intron 1 of OCA2 explains most human eye-color variation. Am. J. Hum. Genet. 2007;80:241–252. doi: 10.1086/510885. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Elson J.L., Majamaa K., Howell N., Chinnery P.F., Majamaa K., Howell N., Chinnery P.F., Howell N., Chinnery P.F., Chinnery P.F. Associating mitochondrial DNA variation with complex traits. Am. J. Hum. Genet. 2007;80:378–382. doi: 10.1086/511652. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Eyre-Walker A., Awadalla P., Awadalla P. Does human mtDNA recombine? J. Mol. Evol. 2001;53:430–435. doi: 10.1007/s002390010232. [DOI] [PubMed] [Google Scholar]
  7. Fisher R.A. On the interpretation of χ2 from contingency tables, and the calculation of P. J. R. Stat. Soc. [Ser A] 1922;85:87–94. [Google Scholar]
  8. Hill W.G., Weir B.S., Weir B.S. Maximum-likelihood estimation of gene location by linkage disequilibrium. Am. J. Hum. Genet. 1994;54:705–714. [PMC free article] [PubMed] [Google Scholar]
  9. Hudson R.R. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics. 2002;18:337–338. doi: 10.1093/bioinformatics/18.2.337. [DOI] [PubMed] [Google Scholar]
  10. Ingman M., Gyllensten U., Gyllensten U. mtDB: Human Mitochondrial Genome Database, a resource for population genetics and medical sciences. Nucleic Acids Res. 2006;34:D749–D751. doi: 10.1093/nar/gkj010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ingman M., Kaessmann H., Paabo S., Gyllensten U., Kaessmann H., Paabo S., Gyllensten U., Paabo S., Gyllensten U., Gyllensten U. Mitochondrial genome variation and the origin of modern humans. Nature. 2000;408:708–713. doi: 10.1038/35047064. [DOI] [PubMed] [Google Scholar]
  12. The International HapMap Consortium A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Manwaring N., Jones M.M., Wang J.J., Rochtchina E., Mitchell P., Sue C.M., Jones M.M., Wang J.J., Rochtchina E., Mitchell P., Sue C.M., Wang J.J., Rochtchina E., Mitchell P., Sue C.M., Rochtchina E., Mitchell P., Sue C.M., Mitchell P., Sue C.M., Sue C.M. Prevalence of mitochondrial DNA haplogroups in an Australian population. Intern. Med. J. 2006;36:530–533. doi: 10.1111/j.1445-5994.2006.01118.x. [DOI] [PubMed] [Google Scholar]
  14. McVean G., Awadalla P., Fearnhead P., Awadalla P., Fearnhead P., Fearnhead P. A coalescent-based method for detecting and estimating recombination from gene sequences. Genetics. 2002;160:1231–1241. doi: 10.1093/genetics/160.3.1231. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Poulton J., Marchington D.R., Scott-Brown M., Phillips D.I., Hagelberg E., Marchington D.R., Scott-Brown M., Phillips D.I., Hagelberg E., Scott-Brown M., Phillips D.I., Hagelberg E., Phillips D.I., Hagelberg E., Hagelberg E. Does a common mitochondrial DNA polymorphism underlie susceptibility to diabetes and the thrifty genotype? Trends Genet. 1998;14:387–389. doi: 10.1016/s0168-9525(98)01529-7. [DOI] [PubMed] [Google Scholar]
  16. Samuels D.C., Carothers A.D., Horton R., Chinnery P.F., Carothers A.D., Horton R., Chinnery P.F., Horton R., Chinnery P.F., Chinnery P.F. The power to detect disease associations with mitochondrial DNA haplogroups. Am. J. Hum. Genet. 2006;78:713–720. doi: 10.1086/502682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Saxena R., de Bakker P.I.W., Singer K., Mootha V., Burtt N., Hirschhorn J.N., Gaudet D., Isomaa B., Daly M.J., Groop L., de Bakker P.I.W., Singer K., Mootha V., Burtt N., Hirschhorn J.N., Gaudet D., Isomaa B., Daly M.J., Groop L., Singer K., Mootha V., Burtt N., Hirschhorn J.N., Gaudet D., Isomaa B., Daly M.J., Groop L., Mootha V., Burtt N., Hirschhorn J.N., Gaudet D., Isomaa B., Daly M.J., Groop L., Burtt N., Hirschhorn J.N., Gaudet D., Isomaa B., Daly M.J., Groop L., Hirschhorn J.N., Gaudet D., Isomaa B., Daly M.J., Groop L., Gaudet D., Isomaa B., Daly M.J., Groop L., Isomaa B., Daly M.J., Groop L., Daly M.J., Groop L., Groop L., et al. Comprehensive association testing of common mitochondrial DNA variation in metabolic disease. Am. J. Hum. Genet. 2006;79:54–61. doi: 10.1086/504926. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Student The probable error of a mean. Biometrika. 1908;6:1–25. [Google Scholar]
  19. Wallace D.C. Mitochondiral diseases in man and mouse. Science. 1999;283:1482–1488. doi: 10.1126/science.283.5407.1482. [DOI] [PubMed] [Google Scholar]
  20. Wilder J.A., Mobasher Z., Hammer M.F., Mobasher Z., Hammer M.F., Hammer M.F. Genetic evidence for unequal effective population sizes of human females and males. Mol. Biol. Evol. 2004;21:2047–2057. doi: 10.1093/molbev/msh214. [DOI] [PubMed] [Google Scholar]
  21. Zhu G., Montgomery G.W., James M.R., Trent J.M., Hayward N.K., Martin N.G., Duffy D.L., Montgomery G.W., James M.R., Trent J.M., Hayward N.K., Martin N.G., Duffy D.L., James M.R., Trent J.M., Hayward N.K., Martin N.G., Duffy D.L., Trent J.M., Hayward N.K., Martin N.G., Duffy D.L., Hayward N.K., Martin N.G., Duffy D.L., Martin N.G., Duffy D.L., Duffy D.L. A genome-wide scan for naevus count: Linkage to CDKN2A and to other chromosome regions. Eur. J. Hum. Genet. 2007;15:94–102. doi: 10.1038/sj.ejhg.5201729. [DOI] [PubMed] [Google Scholar]

Articles from Genome Research are provided here courtesy of Cold Spring Harbor Laboratory Press

RESOURCES