Protein conformational flexibility prediction using machine learning

Abstract

Using a data set of 16 proteins, a neural network has been trained to predict backbone ¹⁵N generalized order parameters from the three-dimensional structures of proteins. The final network parameterization contains six input features. The average prediction accuracy, as measured by the Pearson correlation coefficient between experimental and predicted values of the square of the generalized order parameter is > 0.70. Predicted order parameters for non-terminal amino acid residues depends most strongly on local packing density and the probability that the residue is located in regular secondary structure.

Introduction

Dynamical processes in proteins are believed to be closely related to protein function, including ligand-binding, catalysis, and folding, even though this relationship is not yet understood in great detail [1]. Moreover, information about protein conformational flexibility is becoming important in drug design [2]. Thus, considerable importance exists in the related problems of elucidating the microscopic factors that determine protein conformational flexibility and of predicting flexibility from sequence or structural data.

Theoretical assessments of protein flexibility can derive from computational simulations with atomistic and mechanistic detail [3] or from more abstract approaches [4,5]. Theoretical approaches can be free-standing or aimed at interpretation of experimental measurements of protein flexibility, such as crystallographic B-factors [6,7].

NMR spin relaxation experiments are widely applied for the study of the dynamics of macromolecules [8,9]. NMR spin relaxation data has been collected for various proteins by a number of different research groups, and some of these data have been compiled into publicly accessible data banks [10,11]. Most commonly, laboratory frame relaxation experiments conducted for ¹⁵N [12,13] or ²H [14,15] spins have been used to determine the square of the generalized order parameter, S², [16] for backbone amide or side chain methyl groups, respectively [8].

A number of authors have used the availability of such NMR data as the basis for further studies of conformational flexibility of proteins (for a recent review, see [17]). Order parameters derived from NMR have been compared with other experimental and theoretical measures of protein flexibility, including crystallographic B-factors [18], order parameters obtained from fluorescence anisotropy decay measurements [19,20], and order parameters obtained from molecular dynamics (MD) simulations [21,22]. Correlations have been uncovered between order parameters and molecular features, such as secondary structural elements and amino acid side chain volumes [10,23] and amino acid sequence conservation [24]. Abergel and Bodenhausen used a model comprising a network of coupled rotators to predict generalized order parameters from protein structures [25]. Using a database of backbone amide order parameters, Zhang and Brüschweiler empirically devised a simple analytic method for predicting generalized order parameters from static three-dimensional protein structures [26] and subsequently extended their approach to generalized order parameters for side chain methyl side groups [27] and to a contact-weighted elastic network model [28]. Schlessinger and Rost used a neural network to predict B-factors and generalized order parameters from protein sequences [7].

Our goal in the present work is to devise a systematic knowledge-based method for predicting picosecond to nanosecond protein backbone flexibility as described by generalized order parameters obtained from NMR measurements. We are interested in “learning” S² as a function of structure from “examples” without necessarily looking in detail into the physics of the process. As “examples”, we use backbone ¹⁵N order parameters deposited into the Indiana Dynamics Database (IDD) [10] and the BioMagResBank (BMRB) [11] and the corresponding 3D structures from the Protein Data Bank (PDB) [29]. We use a particular type of neural network typically referred to as a multi-layered feed-forward network (sometimes as a multi-layer perceptron) with one hidden layer [30] to optimize the prediction of S² given the set of “examples”. We anticipate that similar approaches also can be applied to predicting slower time scale dynamic properties accessible to NMR experiments [9].

Methods

Order Parameter

The angular distribution of the orientations of the backbone N-H bond vector on the picosecond to nanosecond time scale is described using the square of the generalized order parameter from the Lipari-Szabo model-free formalism [16]

$$S^2=(4\pi /5)\sum _{m=-2}^2\mid <Y_{2,m}(\mathrm{\Omega })>{\mid }^2,$$ (1)

where Y_2,m(Ω) are the second order spherical harmonics, and Ω describes the orientation of the N-H bond vector in the protein-attached coordinate system. In the limiting case of completely isotropic orientation of the bond vector with respect to the body of the molecule, S² = 0. Alternatively, S² = 1, if the orientation is fixed.

Data Banks

Table 1 lists the PDB, IDD and BMRB entries that were used in the present work. The data set contains two pairs of closely related proteins: 1clb and 1cdn are the apo and (Cd²⁺)₁ forms of calbindin D_9k, and 1xoa and 1xob are oxidized and reduced forms of thioredoxin. As discussed by Goodman et.al. [10], some of the systematic differences in S² between different data sets are due to the differences in the ways the data were collected and analyzed.

Table 1.

Dataset composition

Index	PDB entry	Chain ID	Residues	Database entry	S2 values	Relatives
1	3CI2		66	IDD 1	58
2	1CLB		76	IDD 2	72	1CDN
3	1CDN		76	IDD 3	71	1CLB
4	1STG		149	IDD 4	106
5	2BBN	A	148	IDD 5	114
6	1XOB		108	IDD 7	95	1XOA
7	1XOA		108	IDD 8	96	1XOB
8	1GPR		162	IDD 9	128
9	1BVE	A	99	IDD 10	78
10	1ITM		130	IDD 13	113
11	1KUN		58	IDD 25	51
12	2FSP		124	IDD 31	109
13	1NGL	A	179	BMR 4267	147
14	1VRF	A	147	BMR 4096	138
15	1D2B	A	126	BMR 5154	102
16	1D3Z	A	76	IDD 11	70

Normalization of S² reduces this artificial variation. Goodman et.al. divide each S² by the average value of S² for the protein in which the N-H group resides. We employ a similar linear transformation. However, under the assumption that the true average order parameter of residues in the secondary structure is likely to vary less among different proteins than the order parameter averaged over all residues of the protein, we use the former as the reference point, “normalizing” each database entry so that the average value of S² for residues in the secondary structure becomes 0.86. This value is close to the canonical value measured in proteins for N-H moieties in secondary structure elements when an effective bond length of 1.02 Å is used in the data analysis.

Supervised learning

“Learning from examples” constitutes what is known as the supervised learning or the function approximation problem [30], which is informally stated as follows. Given an unknown function f(x⃗) and a training set ${\{({\overrightarrow{x}}_i,{\overrightarrow{y}}_i)\}}_{i=1}^N$, for which y⃗_i ≈ f(x⃗_i), find an approximation of the unknown function f(x⃗). This approximation is typically obtained from an adequately general parametrization F(x⃗, w⃗) by optimizing parameters w⃗. Supervised learning problems can be solved using artifical neural networks. We use a special kind of a neural network called a multi-layered feed-forward network with one hidden layer [30]. This network architecture corresponds to the parametrization expression:

$$F=s_2({\text{W}}_2{s}_1({\text{W}}_1\overrightarrow{x}+{\overrightarrow{b}}_1)+{\overrightarrow{b}}_2),$$ (2)

where weight matrices W₁, W₂ and bias vectors b⃗₁, b⃗₂ are the parameters adjusted to fit the training data, and s₁(x), s₂(x) are the transfer functions, which we choose to be an elementwise application of the sigmoid function:

$$s_1(x)s_2(x)=\text{sigm}(x)=1/(e^{-x}+1).$$ (3)

The function being approximated is the value of S² for the ith amino acid residue; therefore, f(x⃗) is a scalar. The universal approximation theorem [30] implies that this parametrization can approximate any continuous function with values within [0, 1] to any given accuracy, if sufficiently large dimension-alities of W₁, W₂, b₁ and b₂ are allowed.

Features

Instead of using the 3D structure of the protein in some machine-readable form as inputs in the training set, we extracted features of the 3D structure that appear to be statistically related to conformational flexibility and use those features as inputs. Statistical correlations between features and S² were measured using the Pearson correlation coefficient, defined by

$$C_{xy}=\frac{\overline{xy}-\overline{x}\overline{y}}{{\sigma }_x{\sigma }_y}$$ (4)

for two variables x (= experimental S²) and y (=feature or predicted S²) in which the bars indicate averaging and σ_x and σ_y are the standard deviations in the two variables. These statistics were calculated over the number of generalized order parameters available for each protein. Correlations were considered between S² for the N-H bond vector of the ith residue and features for the ith residue and flanking residues in the amino acid sequence. “Position” denotes the position of the residue in the protein chain for which the feature is calculated relative to the position of the residue for which S² is measured. Thus, a correlation coefficient reported for feature p and position k indicates that the correlation coefficient was calculated using equation 4 with $x=S_i^2$ and y = p_i+k for i = 1, N and N is the number of amino acid residues for which data are available. Ranges of k from −6 to +6 were examined. Correlations between features and S² were calculated both by pooling all data for all proteins and by averaging the correlations obtained for individual proteins. The features examined, which were chosen based on intuition and the work of others [6,26], are described below.

The DSSP (dictionary of secondary structure of proteins) program [31] classifies the secondary structure state of each residue in the protein as helix (3₁₀, G; α, H; π, I), extended sheet (E), β bridge (B), turn (T), bend (S), or “other” (L). The continuum secondary secondary structure assignment DSSPcont [23] extends this method by capturing “uncertainties” of DSSP assignments and assigning an eight-dimensional vector to each residue. The vector can be thought of as the probabilities of the respective DSSP assignments. The sum of all eight elements, therefore, equals 1. Each of the eight DSSPcont probabilities was treated as a feature. In addition, the feature “secondary” was defined as the sum of all DSSPcont values except ’L’ and ’S’.

The feature “BB H-bonds energy” is the energy of the backbone-to-backbone H-bonds that involve a given peptide bond, where the energy is calculated in the same manner as by DSSP.

“D_com” is the distance between the C_α atom and the center of mass of the non-hydrogen atoms of the protein.

“Residue Size” is the number of all non-hydrogen atoms in the residue.

“Tail M” equals 1 if the peptide bond, to which the N-H bond belongs, is M or fewer residues away from N- or C-terminus, and 0 otherwise. For example, in a protein chain with residues numbered from 1 to 100, for residues 3 and 99, “Tail M = 1” will be 0, while “Tail M = 2” will be 1.

“Loop left” and “Loop right” show the extent of the non-secondary (loop) structure towards the N- and C-terminus, respectively. For a given residue, “Loop right” is one-tenth times the relative position towards the C-terminus of the first residue with a “secondary” feature (defined above) greater than 0.95 (or 95%). If the residue currently of interest is in regular secondary structure, “loop right” is 0.0. If such residue is not found (due to a chain break) or is found more than 10 residues away, “loop right” is 1.0. The definition of “loop left” is analogous.

“Bend(−m, 0, m)” is the cosine of the angle formed by vectors C_α(i + k − m)C_α(i + k) and C_α(i + k + m)C_α(i + k), where C_α(n), is the C_α atoms of the nth residue.

Distance dependent features, “ $g(r_k^X)$”, are given by Σ_j f(r_Xi+k,j), where r_Xi+k,j is the distance between the jth atom and the atom X in the (i + k)th residue. The summation extends over all heavy atoms, including hetero-atoms, but not water molecules. When X = H, the reference atom is the amide hydrogen of the (i+k)th residue and heavy atoms in the (i+k)th and (i+k−1)th residues are not included in the summation. When X = O, the reference atom is the carbonyl oxygen of the (i + k)th residue and heavy atoms in the (i + k)th and (i + k + 1)th residues are not included in the summation. When X = C, the reference atom is the C^α atom of the residue. The modifier “(BB)” indicates that the the summation involves only the atoms that are part of the backbone (N, C_α, C′). The modifier “(all)” indicates that the summation exends over all residues. The function hard(x) is defined by,

$$\text{hard}(x)=\{\begin{array}{cc}1,& \text{if }x\ge 0\\ 0,& \text{if }x<0\end{array}$$ (5)

The notation “1/…” indicates the inverse.

Some of these features are similar to quantities used by other authors. For example, “ $exp(-r_0^H/1\mathring{A})$” and “ $1/\text{hard}(7\mathring{A}-r_0^C)$”are the components of formula used by Zhang-Brüschweiler to predict S² [26]. In addition, “ $1/\text{hard}(7\mathring{A}-r_k^C)(\text{all})$” corresponds to the function used by Halle to interpret crystallographic B-factors [6].

Optimization

To find the optimal, in the least-squared sense, values of the parameters W₁, W₂, b⃗₁, and b⃗₂, the Levenberg-Marquardt algorithm was used [32,33]. The learning process was cross-validated by iteratively selecting one of the proteins from the data set, also excluding its relatives from the data set, allowing the network to learn S² from the remaining set and calculating Pearson correlation between experimental and predicted values of S². This step was repeated for all proteins in the dataset. The average correlation was used as a measure of the quality of the prediction process.

Independent data

Experimental generalized order parameters have been reported for B3 domain of staphyloccocal protein G (GB3) [34], the villin headpiece domain (HP67) [35], the holo frenolicin acyl carrier protein (fren ACP) [36], and Escherichia coli ribonuclease H (RNaseH) [37–40]. Generalized order parameters were predicted using the structural coordinates from PDB files 1IGD, 1QQV, 1OR5, and 2RN2, respectively. Experimental generalized order parameters have been reported for wild-type and loop-swap mutants of the tenth fibronectin type III domain of the protein fibronectin (fnfn10) and of the third fibronectin type III domain of the protein tenascin (tnfn3) [41]. The mutants were constructed by interchange of the CC′ and FG loops between fnfn10 and tnfn3. Generalized order parameters were predicted using structural models described elsewhere [41]. GB3, HP67, fren ACP, RNaseH, fnfn10, and tnfn3 are not similar to any of the proteins used to develop the prediction method.

Results

Correlations between some of the features we examined and the normalized squared order parameters for all proteins in the sample set are summarized in table 2. The average correlations determined by analyzing each protein independently are shown in table 3.

Table 2.

Dataset-wide correlations 100C_xy between features and S²

Feature description	Position, k
	−6	−5	−4	−3	−2	−1	0	+1	+2	+3	+4	+5	+6
$exp(-r_k^O/1\mathring{A})$	4.9	12.8	21.8	28.0	33.7	37.1	32.1	23.9	13.7	4.7	−1.7	−8.5	−9.6
$exp(-r_k^O/2\mathring{A})$	8.4	16.9	27.2	34.2	40.8	44.4	39.1	28.1	17.0	6.8	−1.4	−8.4	−9.3
$exp(-r_k^O/3\mathring{A})$	9.9	18.5	28.6	35.6	42.0	45.5	40.6	29.6	18.5	8.2	−0.5	−7.4	−8.4
$exp(-r_k^O/4\mathring{A})$	10.6	19.0	28.8	35.7	41.7	45.1	40.6	30.1	19.2	9.2	0.5	−6.3	−7.5
$exp(-r_k^O/5\mathring{A})$	11.0	19.2	28.5	35.2	41.1	44.3	40.1	30.1	19.6	9.9	1.3	−5.4	−6.7
$exp(-r_k^O/7\mathring{A})$	11.4	18.9	27.4	33.5	38.9	41.9	38.3	29.1	19.4	10.4	2.3	−3.9	−5.5
$exp(-r_k^O/10\mathring{A})$	11.3	17.7	24.8	30.1	34.7	37.3	34.2	26.3	17.8	9.8	2.7	−2.7	−4.4
$1/exp(-r_k^O/1\mathring{A})$	4.9	12.8	21.8	28.0	33.7	37.1	32.1	23.9	13.7	4.7	−1.7	−8.5	−9.6
$1/exp(-r_k^O/2\mathring{A})$	−8.1	−16.6	−25.9	−36.5	−47.7	−54.7	−47.7	−33.6	−21.2	−10.6	−0.1	6.7	8.1
$1/exp(-r_k^O/3\mathring{A})$	−12.1	−20.9	−31.1	−41.9	−52.4	−58.1	−52.3	−38.8	−25.5	−13.1	−1.8	5.5	7.9
$1/exp(-r_k^O/4\mathring{A})$	−14.2	−23.1	−33.6	−44.0	−53.7	−58.7	−53.9	−41.0	−27.3	−14.1	−2.9	4.8	7.5
$1/exp(-r_k^O/5\mathring{A})$	−15.2	−24.2	−34.5	−44.6	−53.4	−58.0	−53.8	−41.2	−27.6	−14.3	−3.2	4.4	7.3
$1/exp(-r_k^O/7\mathring{A})$	−15.5	−24.3	−34.1	−43.3	−51.0	−54.8	−50.7	−38.6	−25.6	−13.0	−2.8	4.3	6.9
$1/exp(-r_k^O/10\mathring{A})$	−13.9	−21.5	−30.0	−37.6	−43.8	−46.7	−42.7	−31.6	−20.4	−9.9	−1.6	4.2	6.2
$exp(-r_k^H/1\mathring{A})$	−4.6	−1.2	3.2	9.8	16.3	26.0	33.6	33.3	31.1	22.3	16.5	10.3	8.2
$exp(-r_k^H/2\mathring{A})$	−1.5	3.9	11.3	20.1	28.4	39.8	46.5	43.0	36.9	27.0	17.9	8.8	5.0
$exp(-r_k^H/3\mathring{A})$	0.4	6.5	14.3	23.3	31.6	41.9	47.4	43.1	35.7	26.6	17.0	7.8	3.5
$exp(-r_k^H/4\mathring{A})$	1.5	7.7	15.3	24.1	32.1	41.6	46.4	42.0	34.5	25.9	16.6	7.6	3.2
$exp(-r_k^H/5\mathring{A})$	2.3	8.4	15.7	24.2	31.9	40.7	45.1	40.8	33.4	25.2	16.2	7.7	3.3
$exp(-r_k^H/7\mathring{A})$	3.6	9.2	15.8	23.4	30.5	38.3	42.0	38.0	31.1	23.7	15.4	7.7	3.4
$exp(-r_k^H/10\mathring{A})$	4.8	9.5	15.1	21.4	27.3	33.9	36.8	33.2	27.1	20.7	13.6	7.1	3.2
$1/exp(-r_k^H/1\mathring{A})$	2.1	−2.0	−7.4	−15.5	−22.7	−33.6	−38.5	−40.2	−34.1	−25.6	−16.3	−11.2	−8.5
$1/exp(-r_k^H/2\mathring{A})$	0.1	−6.2	−14.1	−24.5	−34.9	−48.2	−53.8	−51.6	−43.8	−32.1	−20.8	−11.5	−6.7
$1/exp(-r_k^H/3\mathring{A})$	−1.7	−9.0	−17.9	−29.1	−39.9	−53.1	−58.7	−55.3	−46.6	−34.2	−22.2	−11.3	−5.4
$1/exp(-r_k^H/4\mathring{A})$	−2.8	−10.7	−19.8	−30.9	−41.5	−54.0	−59.4	−55.9	−46.9	−34.5	−22.3	−11.1	−4.9
$1/exp(-r_k^H/5\mathring{A})$	−3.5	−11.6	−20.7	−31.5	−41.7	−53.6	−58.7	−55.1	−45.9	−33.7	−21.6	−10.6	−4.4
$1/exp(-r_k^H/7\mathring{A})$	−4.2	−12.0	−20.7	−30.8	−40.0	−50.7	−55.1	−50.9	−41.4	−29.9	−18.8	−9.0	−3.4
$1/exp(-r_k^H/10\mathring{A})$	−4.6	−10.8	−18.1	−26.3	−33.9	−42.7	−46.2	−41.3	−32.5	−22.7	−13.8	−6.3	−1.9
$\text{sigm}(3\mathring{A}-r_k^H)$	−3.5	0.2	6.0	13.1	20.5	31.6	39.0	37.7	34.2	24.7	17.4	10.3	7.4
$\text{sigm}(4\mathring{A}-r_k^H)$	−2.9	1.3	7.9	15.5	23.3	34.8	41.8	39.7	35.1	25.6	17.5	9.6	6.3
$\text{sigm}(5\mathring{A}-r_k^H)$	−2.0	2.8	10.1	18.2	26.2	37.9	44.2	41.0	35.4	25.9	17.2	8.4	4.9
$\text{sigm}(7\mathring{A}-r_k^H)$	−0.2	5.8	13.4	22.2	30.2	41.0	46.4	41.5	34.1	25.2	15.7	6.2	2.2
$\text{sigm}(10\mathring{A}-r_k^H)$	1.7	7.6	15.3	24.1	31.6	40.7	45.2	39.7	31.9	23.7	14.5	5.5	1.1
$\text{1}/\text{sigm}(3\mathring{A}-r_k^H)$	1.7	−2.9	−8.9	−17.5	−25.8	−37.5	−42.9	−43.4	−37.1	−27.8	−17.7	−11.4	−8.1
$\text{1}/\text{sigm}(4\mathring{A}-r_k^H)$	1.4	−3.7	−10.2	−19.3	−28.4	−40.7	−46.5	−45.8	−39.1	−29.2	−18.6	−11.3	−7.5
$\text{1}/\text{sigm}(5\mathring{A}-r_k^H)$	0.9	−4.8	−12.0	−21.7	−31.5	−44.6	−50.7	−48.5	−41.1	−30.5	−19.5	−10.9	−6.6
$\text{1}/\text{sigm}(7\mathring{A}-r_k^H)$	−0.5	−7.4	−15.6	−26.3	−36.8	−50.7	−56.9	−52.3	−43.4	−31.9	−20.5	−9.8	−4.3
$\text{1}/\text{sigm}(10\mathring{A}-r_k^H)$	−2.6	−10.1	−18.8	−29.9	−40.1	−53.2	−59.2	−54.3	−45.0	−33.1	−21.4	−9.6	−3.0
$\text{hard}(3\mathring{A}-r_k^H)$	−1.7	−1.7	−2.2	2.9	4.7	11.5	16.4	18.7	18.6	13.1	9.9	8.5	9.6
$\text{hard}(4\mathring{A}-r_k^H)$	−5.0	−2.1	1.6	7.0	12.4	21.0	27.9	28.4	27.8	20.1	15.0	9.9	8.0
$\text{hard}(5\mathring{A}-r_k^H)$	−2.6	−0.7	5.3	9.8	16.1	24.8	31.2	31.6	28.4	20.3	14.5	9.3	7.4
$\text{hard}(7\mathring{A}-r_k^H)$	−2.0	4.1	11.9	20.3	28.4	39.8	44.5	40.0	33.0	23.8	14.7	5.7	2.3
$\text{hard}(10\mathring{A}-r_k^H)$	1.7	7.6	14.7	23.1	30.6	39.4	44.3	38.5	31.1	23.3	14.1	5.2	1.0
$exp(-r_k^N/3\mathring{A})(\text{BB})$	2.1	7.6	16.2	25.9	34.9	43.6	48.4	43.4	35.5	25.6	15.7	6.2	0.7
$1/\text{hard}(7\mathring{A}-r_k^C)(\text{all})$	−2.1	−8.9	−18.4	−29.5	−40.5	−52.4	−52.8	−41.3	−29.6	−17.7	−7.3	0.7	4.3
Dcom	−3.4	−10.3	−19.3	−27.9	−33.7	−38.7	−38.8	−32.6	−25.3	−17.4	−8.8	−1.6	2.1
Tail, M = 1	−7.4	−8.7	−10.6	−14.1	−20.5	−21.7	−36.5	−16.3	−9.1	−2.8	2.3	2.8	3.9
Tail, M = 2	−7.4	−9.6	−11.9	−15.1	−21.2	−40.1	−42.3	−22.0	−8.3	−0.5	3.6	4.8	5.5
Tail, M = 3	−6.5	−9.5	−12.4	−15.8	−36.6	−41.9	−41.8	−26.7	−10.9	1.3	5.2	6.2	8.0
Tail, M = 4	−4.7	−8.5	−12.2	−31.2	−38.5	−41.1	−39.3	−26.4	−15.9	−2.2	6.5	8.4	9.2
Tail, M = 5	−2.9	−6.7	−26.3	−33.5	−38.1	−38.7	−36.5	−25.1	−17.0	−8.2	3.5	9.5	10.5
Tail, M = 6	−1.9	−20.0	−27.5	−32.7	−35.8	−35.9	−33.7	−23.6	−17.0	−9.6	−2.7	6.1	10.7
DSSPcont G	−7.2	−9.3	−13.4	−10.2	−4.9	−1.9	−0.1	−2.2	−4.7	−2.6	0.3	3.1	1.2
DSSPcont H	−5.4	0.1	5.7	12.1	16.2	19.1	22.7	21.2	16.9	11.8	6.5	2.6	−1.1
DSSPcont I	−6.4	−14.3	−14.2	−3.4	−0.5	1.0	1.2	0.9	−0.5	−1.7	2.2	3.0	1.4
DSSPcont T	3.3	1.1	−1.5	−6.0	−3.8	0.5	1.4	0.1	2.1	2.3	3.7	7.7	8.9
DSSPcont E	2.7	5.5	7.7	10.7	14.2	16.7	14.9	9.6	5.6	0.6	−2.4	−0.8	−1.4
DSSPcont B	4.2	2.8	2.4	1.8	−0.1	0.9	3.4	−2.9	−0.1	−4.1	−5.7	−4.1	−7.5
DSSPcont S	8.0	2.8	0.8	−8.5	−14.8	−15.6	−20.1	−14.6	−8.4	−4.4	0.9	0.9	2.6
DSSPcont L	−2.1	−4.3	−8.8	−12.7	−21.4	−33.2	−33.8	−26.9	−22.4	−12.4	−8.6	−10.0	−4.9
Secondary	−3.2	1.8	7.0	16.1	27.3	37.7	41.5	32.0	24.3	13.3	6.6	7.8	2.4
Bend (−1, 0, 1)	1.6	0.9	−0.9	−4.2	−8.6	−15.7	−16.7	−14.6	−13.2	−11.1	−9.8	−9.0	−5.1
Bend (−2, 0, 2)	3.3	2.8	1.3	−1.5	−5.1	−8.3	−10.1	−12.2	−12.0	−11.4	−10.8	−10.2	−6.4
loop left	−3.8	−5.8	−9.5	−14.5	−22.6	−28.6	−32.0	−37.6	−35.5	−33.9	−30.3	−30.1	−27.5
loop right	−14.4	−19.0	−25.7	−36.0	−40.4	−37.6	−37.6	−17.4	−5.3	1.1	3.9	3.8	4.3
Residue Size	−6.4	−1.5	−0.2	4.1	6.4	9.0	10.0	7.2	6.4	2.3	−1.2	−4.1	−6.0
BB H-bonds energy	5.1	−2.5	−7.8	−15.3	−22.3	−27.1	−34.1	−31.3	−26.6	−16.0	−10.0	−2.8	0.8

Table 3.

Average correlations 100C_xy between features and S²

Feature description	Position, k
	−6	−5	−4	−3	−2	−1	0	+1	+2	+3	+4	+5	+6
$exp(-r_k^O/1\mathring{A})$	5.0	13.6	23.0	29.1	34.4	38.8	32.8	21.5	12.2	1.8	−3.7	−11.8	−11.7
$exp(-r_k^O/2\mathring{A})$	8.1	16.9	27.2	33.7	40.5	44.8	38.8	24.1	13.6	1.7	−6.5	−14.6	−14.0
$exp(-r_k^O/3\mathring{A})$	9.2	18.0	28.1	34.7	41.6	45.8	40.2	24.9	14.2	2.2	−7.3	−15.2	−14.6
$exp(-r_k^O/4\mathring{A})$	9.5	18.3	28.2	34.9	41.8	45.9	40.7	25.4	14.6	2.7	−7.4	−15.1	−14.7
$exp(-r_k^O/5\mathring{A})$	9.5	18.3	28.1	34.9	41.8	45.9	40.9	25.7	14.9	3.1	−7.2	−14.9	−14.6
$exp(-r_k^O/7\mathring{A})$	9.4	18.2	28.0	34.9	41.7	45.8	41.1	26.1	15.4	3.7	−7.0	−14.4	−14.4
$exp(-r_k^O/10\mathring{A})$	9.3	18.0	27.8	34.8	41.7	45.8	41.3	26.5	15.8	4.2	−6.7	−13.9	−14.2
$1/exp(-r_k^O/1\mathring{A})$	5.0	13.6	23.0	29.1	34.4	38.8	32.8	21.5	12.2	1.8	−3.7	−11.8	−11.7
$1/exp(-r_k^O/2\mathring{A})$	−6.4	−14.0	−23.0	−33.1	−42.3	−51.8	−45.2	−26.1	−16.9	−5.0	4.8	12.2	11.2
$1/exp(-r_k^O/3\mathring{A})$	−8.4	−16.1	−25.9	−36.1	−45.1	−53.9	−48.1	−29.1	−19.2	−6.0	5.0	12.4	12.4
$1/exp(-r_k^O/4\mathring{A})$	−9.2	−17.0	−27.2	−37.2	−45.9	−53.9	−48.7	−30.3	−20.2	−6.7	5.0	12.4	12.9
$1/exp(-r_k^O/5\mathring{A})$	−9.5	−17.4	−27.8	−37.6	−46.1	−53.5	−48.6	−30.7	−20.5	−7.0	5.0	12.4	13.2
$1/exp(-r_k^O/7\mathring{A})$	−9.7	−17.7	−28.3	−37.7	−45.7	−52.4	−47.8	−30.7	−20.5	−7.1	5.0	12.3	13.3
$1/exp(-r_k^O/10\mathring{A})$	−9.6	−17.8	−28.4	−37.4	−45.1	−51.1	−46.6	−30.2	−19.9	−7.0	5.1	12.3	13.4
$exp(-r_k^H/1\mathring{A})$	−4.3	−1.2	2.7	8.1	15.7	26.6	36.0	35.0	33.9	23.0	18.3	9.1	8.7
$exp(-r_k^H/2\mathring{A})$	−3.0	2.5	9.9	17.8	26.2	39.2	48.3	43.0	36.9	24.5	15.4	4.0	1.1
$exp(-r_k^H/3\mathring{A})$	−2.0	4.2	12.4	21.0	29.4	41.5	49.4	42.8	35.1	23.0	12.9	1.6	−2.2
$exp(-r_k^H/4\mathring{A})$	−1.6	4.7	13.2	21.9	30.2	41.7	49.0	42.1	33.9	22.3	11.8	0.9	−3.4
$exp(-r_k^H/5\mathring{A})$	−1.4	4.9	13.4	22.2	30.5	41.6	48.6	41.6	33.3	21.9	11.3	0.7	−3.8
$exp(-r_k^H/7\mathring{A})$	−1.4	4.9	13.5	22.4	30.6	41.4	48.1	41.2	32.8	21.6	10.9	0.7	−4.1
$exp(-r_k^H/10\mathring{A})$	−1.4	4.9	13.4	22.4	30.6	41.3	47.7	40.9	32.5	21.5	10.7	0.8	−4.2
$1/exp(-r_k^H/1\mathring{A})$	2.9	0.2	−4.2	−9.8	−17.8	−31.4	−39.3	−39.0	−37.1	−23.8	−16.9	−8.2	−5.9
$1/exp(-r_k^H/2\mathring{A})$	2.5	−2.5	−9.3	−17.6	−27.4	−43.0	−52.5	−47.9	−42.8	−27.2	−16.2	−5.4	−1.2
$1/exp(-r_k^H/3\mathring{A})$	1.8	−3.9	−11.7	−21.6	−31.3	−46.5	−55.7	−49.5	−42.5	−27.0	−15.0	−3.7	1.5
$1/exp(-r_k^H/4\mathring{A})$	1.5	−4.5	−12.7	−23.0	−32.6	−47.1	−55.8	−49.1	−41.4	−26.7	−14.3	−3.1	2.6
$1/exp(-r_k^H/5\mathring{A})$	1.3	−4.8	−13.1	−23.6	−33.1	−47.0	−55.2	−48.3	−40.4	−26.4	−13.9	−2.8	3.1
$1/exp(-r_k^H/7\mathring{A})$	1.2	−5.0	−13.5	−24.0	−33.2	−46.2	−53.8	−46.9	−38.9	−25.8	−13.4	−2.6	3.4
$1/exp(-r_k^H/10\mathring{A})$	1.3	−5.0	−13.6	−23.9	−32.9	−45.2	−52.3	−45.5	−37.3	−24.9	−12.7	−2.3	3.6
$\text{sigm}(3\mathring{A}-r_k^H)$	−4.2	−0.5	5.1	11.1	19.2	31.9	41.5	38.9	36.2	24.5	18.2	7.9	6.4
$\text{sigm}(4\mathring{A}-r_k^H)$	−4.1	0.3	6.9	13.4	21.6	34.8	44.2	40.4	36.4	24.5	17.2	6.2	4.2
$\text{sigm}(5\mathring{A}-r_k^H)$	−3.6	1.7	9.0	16.1	24.3	37.6	46.4	41.2	35.8	23.8	15.4	4.1	1.5
$\text{sigm}(7\mathring{A}-r_k^H)$	−2.2	4.4	12.3	20.5	28.2	40.5	48.1	41.2	33.3	21.8	11.9	0.6	−2.8
$\text{sigm}(10\mathring{A}-r_k^H)$	−0.1	5.6	13.8	22.4	29.7	40.2	46.9	39.3	30.8	20.0	9.6	−1.0	−5.3
$\text{1}/\text{sigm}(3\mathring{A}-r_k^H)$	3.0	−0.4	−5.5	−11.8	−20.6	−35.1	−44.0	−42.0	−39.5	−25.6	−17.1	−7.5	−4.7
$\text{1}/\text{sigm}(4\mathring{A}-r_k^H)$	3.1	−1.0	−6.8	−13.7	−22.8	−37.9	−47.2	−43.8	−40.6	−26.3	−16.9	−6.6	−3.4
$\text{1}/\text{sigm}(5\mathring{A}-r_k^H)$	3.1	−1.8	−8.4	−16.2	−25.6	−41.2	−50.7	−45.8	−41.2	−26.4	−16.1	−5.3	−1.7
$\text{1}/\text{sigm}(7\mathring{A}-r_k^H)$	2.3	−3.8	−11.3	−21.0	−30.1	−45.7	−55.3	−48.1	−40.8	−25.6	−13.9	−2.8	1.9
$\text{1}/\text{sigm}(10\mathring{A}-r_k^H)$	0.5	−5.2	−13.2	−23.9	−32.4	−46.5	−55.6	−47.9	−39.4	−24.9	−12.7	−1.6	4.3
$\text{hard}(3\mathring{A}-r_k^H)$	−0.2	−0.8	−3.3	0.7	4.4	12.6	17.6	20.8	21.5	14.1	12.3	9.3	12.9
$\text{hard}(4\mathring{A}-r_k^H)$	−5.2	−2.8	0.6	5.6	13.2	22.6	31.5	31.5	32.3	22.7	19.1	10.5	9.8
$\text{hard}(5\mathring{A}-r_k^H)$	−3.7	−1.5	4.6	7.8	15.3	25.5	33.7	32.7	31.4	21.3	16.4	7.3	6.7
$\text{hard}(7\mathring{A}-r_k^H)$	−4.6	3.0	11.2	19.1	26.8	39.3	46.3	39.9	32.7	20.7	11.6	0.8	−2.0
$\text{hard}(10\mathring{A}-r_k^H)$	0.1	5.8	13.3	21.4	28.5	38.8	45.8	38.2	30.1	19.8	9.5	−1.2	−5.0
$exp(-r_k^N/3\mathring{A})(\text{BB})$	−1.9	4.8	13.8	23.5	33.3	44.7	50.6	43.4	34.1	22.1	11.3	0.5	−5.2
$1/\text{hard}(7\mathring{A}-r_k^C)(\text{all})$	−0.1	−7.6	−16.5	−26.8	−38.1	−53.5	−51.1	−36.7	−25.6	−12.8	−1.5	7.4	10.0
Dcom	−3.3	−10.3	−19.3	−28.1	−34.6	−42.2	−42.7	−32.2	−22.8	−12.8	−1.4	7.0	10.1
Tail, M = 1	−5.7	−6.0	−7.6	−10.6	−17.4	−23.4	−40.8	−12.3	−10.8	−5.3	3.1	1.7	4.6
Tail, M = 2	−5.3	−6.5	−8.5	−10.8	−17.3	−41.0	−45.1	−26.1	−9.9	−3.3	2.7	4.3	6.4
Tail, M = 3	−4.8	−6.0	−8.3	−11.1	−33.0	−41.3	−42.1	−29.7	−15.4	−1.2	5.1	6.1	9.6
Tail, M = 4	−3.0	−5.6	−7.7	−27.2	−34.1	−39.7	−38.5	−27.4	−19.4	−6.0	6.7	8.9	11.2
Tail, M = 5	−1.2	−3.9	−22.7	−28.6	−33.9	−36.5	−34.8	−25.1	−18.5	−10.4	2.2	10.6	12.6
Tail, M = 6	−0.9	−17.3	−23.4	−28.4	−31.3	−33.3	−31.7	−22.5	−17.1	−9.7	−2.6	5.3	12.8
DSSPcont G	−5.1	−9.0	−15.2	−11.6	−5.4	−2.8	−0.7	−2.1	−2.7	−0.4	0.8	6.5	4.6
DSSPcont H	−6.4	−0.4	5.9	13.1	17.9	22.0	26.3	25.3	21.4	16.5	10.7	6.5	2.4
DSSPcont I	−3.4	−6.0	−5.7	−2.5	−0.4	−2.4	0.0	0.3	0.9	0.8	2.0	3.5	2.9
DSSPcont T	2.1	−1.4	−3.1	−9.7	−7.5	−1.5	−1.1	−3.7	−0.3	2.3	4.5	9.3	10.2
DSSPcont E	2.7	5.9	7.3	10.1	12.8	14.9	11.6	4.9	−0.1	−6.9	−12.4	−9.4	−9.3
DSSPcont B	5.5	3.9	3.1	1.4	−0.3	−0.0	3.3	0.4	0.6	−2.8	−1.5	1.9	−5.5
DSSPcont S	8.7	3.3	1.0	−7.5	−14.3	−15.1	−19.5	−14.3	−9.0	−3.4	1.1	0.2	4.2
DSSPcont L	−0.3	−1.3	−6.5	−11.4	−21.5	−36.4	−37.0	−27.4	−19.9	−10.7	−1.5	−4.0	1.1
Secondary	−5.4	−0.8	5.0	14.5	26.5	39.2	42.9	31.4	22.0	10.5	0.7	3.5	−3.0
Bend (−1, 0, 1)	2.4	1.6	−0.6	−4.5	−10.0	−21.4	−23.2	−20.3	−18.0	−16.2	−13.0	−11.0	−7.0
Bend (−2, 0, 2)	2.6	2.1	0.5	−2.6	−7.0	−11.8	−15.5	−18.6	−17.7	−17.1	−14.7	−12.7	−9.0
loop left	−0.9	−1.5	−4.5	−8.0	−14.8	−22.4	−24.6	−24.8	−16.0	−12.1	−9.0	−7.2	−6.7
loop right	−8.6	−8.3	−15.4	−20.9	−24.3	−26.4	−34.8	−14.4	−5.7	−0.8	4.7	3.7	5.2
Residue Size	−5.2	−0.6	0.4	4.7	7.6	10.4	9.4	8.5	8.1	1.8	1.1	−6.2	−8.0
BB H-bonds energy	7.4	−1.4	−7.3	−15.3	−23.1	−28.5	−35.5	−32.8	−26.7	−14.6	−6.7	0.9	3.8

Because of the finite size of the training set, supervised learning can be subject to the problem of overfitting/overtraining. Therefore, the number of adjustable parameters and, consequently, the number of features used by the network, must be limited. After some experimentation, we decided to use just six features and no hidden layer, i.e. a simple perceptron that can only capture linear correlations (due to technical issues, this perceptron was realized by using a single hidden unit in a two-layer feed-forward network). The cells of tables 2 and 3 corresponding to the features presently incoportated into the model are marked in bold font and underlined. A feature utilized in the final model may not necessarily correspond to feature the highest correlation in tables 2 and 3 for two reasons. First, the network was trained using least squares minimization of the difference between the experimental and predicted values of S²; the reported correlation coefficients are descriptive statistics. Second, the various features are correlated to different extents and such correlations are not exhibited in the tables.

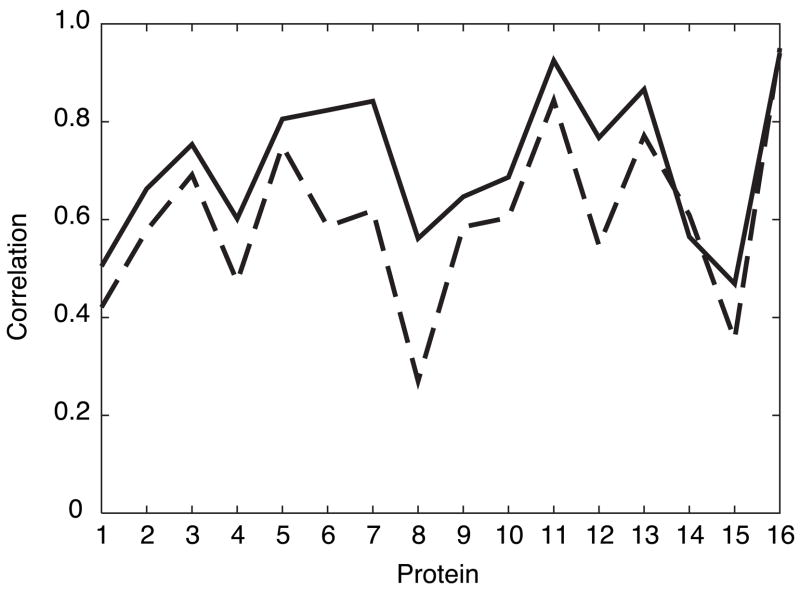
The optimized values of the model parameters are shown in table 4. The results of cross-validating the optimized parameters for these features are shown in figure 1. Although the predictions themselves are affected by the initial normalization of the S², the average correlation used as the measure of the prediction quality is the same, whether we compare the predictions to the normalized S² or the original unnormalized data. The average correlation between experimental and predicted values of S² during the cross-validation procedure equals 0.71 with a sample deviation of 0.15.

Table 4.

Optimized weights and bias parameters

Feature	Parameter	Value
$exp(-r_{-1}^O/3\mathring{A})$	W1(1)	−2.56
$exp(-r_0^H/2\mathring{A})$	W1(2)	−1.94
Secondary, k = 0	W1(3)	−0.821
DSSPcont L, k = 0	W1(4)	−0.270
Bend(−1,0,1), k = 0	W1(5)	0.292
Tail, M = 4, k = 0	W1(6)	0.730
	b⃗1	0.652
	W2	−4.64
	b⃗2	2.01

Fig. 1.

Correlations between predicted and experimental S². (- - -) Zhang-Brüschweiler formula (6); (—) neural network predictions during cross-validation. Abscissa shows the protein index from table 1. As noted in table 1, proteins 2 and 3 and proteins 6 and 7 are closely related.

Sensitivity to Structure

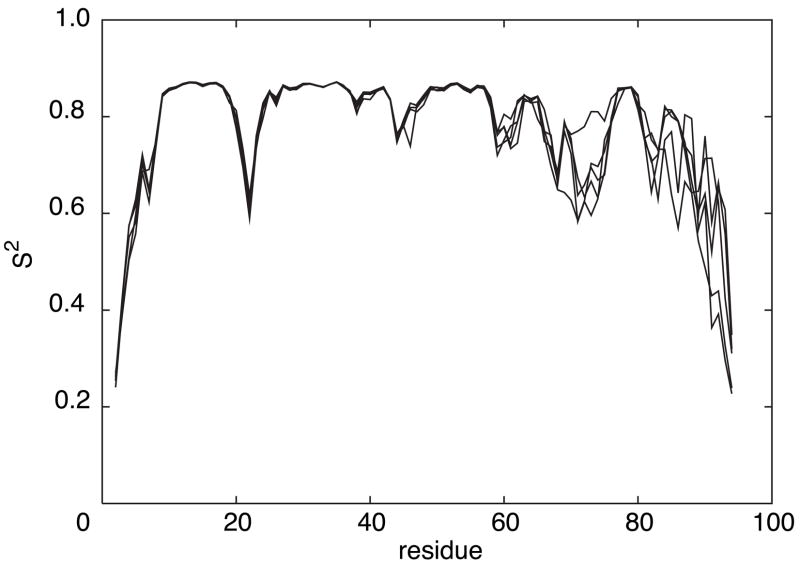
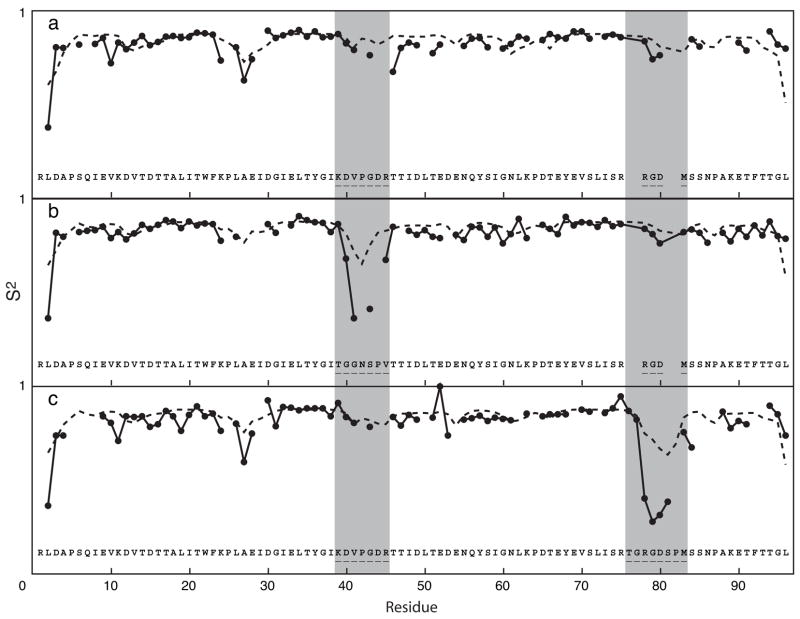
To illustrate the sensitivity of the predictions to details of the protein structure, figure 2 shows the S² predictions for the first 5 NMR models of the forkhead domain of the adipocyte-transcription factor freac-11 (also known as S12) [42]. A superposition of the structures is shown in Figure 3).

Fig. 2.

S² predictions for the first 5 NMR models of the forkhead domain of the adipocyte-transcription factor freac-11 (S12) (PDB code: 1D5V).

Fig. 3.

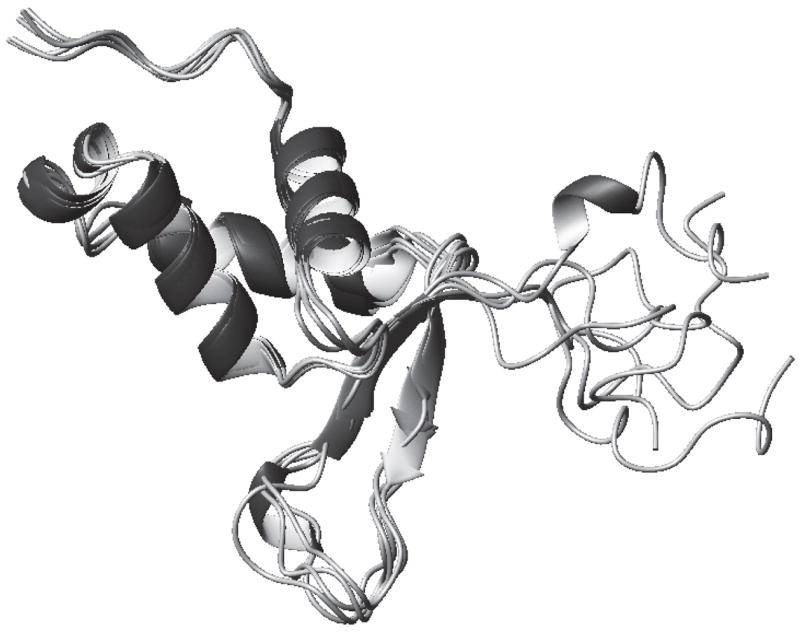
The backbones of the first 5 NMR models of the forkhead domain of the adipocyte-transcription factor freac-11 (S12) (PDB code: 1D5V).

Prediction for additional proteins

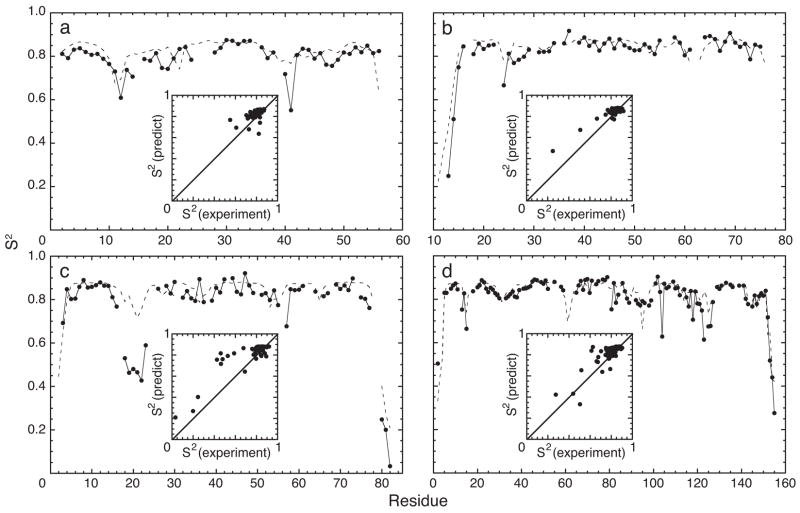
Backbone dynamics of GB3, HP67, fren ACP, and RNaseH have been reported in the literature. None of these proteins, nor any homologs, were included in the training set and consequently this set of proteins provides an independent assessment of the performance of the neural network. The experimental and predicted values of S² are shown in figure 4. The correlation coefficients between the experimental and predicted data are 0.491, 0.925, 0.867, and 0.837 for GB3, HP67, fren ACP, and RNaseH, respectively. The root-mean-square deviations between experimental and predicted values of S² are 0.061, 0.052, 0.104, and 0.053, respectively. The lower correlation for GB3 reflects the absence of residues with markedly low values of S²; however, the root-mean-square-deviation is similar to those for the other proteins. The average correlation coefficient for these four proteins is 0.78 ± 0.20 and is similar to the estimate from the cross-validation experiment (0.71 ± 0.15).

Fig. 4.

S² for (a) GB3 (56 residues, 50 S² values), (b) HP67 (67 residues, 54 S² values), (c) fren ACP (83 residues, 64 S² values) and (d) RNase H (155 residues, 120 S² values). (—) Experimental measurements and (- - -) neural network predictions are plotted as a function of residue number. Insets: Predictions are plotted versus experimental values; the x- and y-coordinates ranges from 0 to 1. Predicted values were calculated using structural coordinates from PDB files (a) 1IGD, (b) 1QQV, (c) 1OR5, and (d) 2RN2.

Prediction for fibronectin type III domains

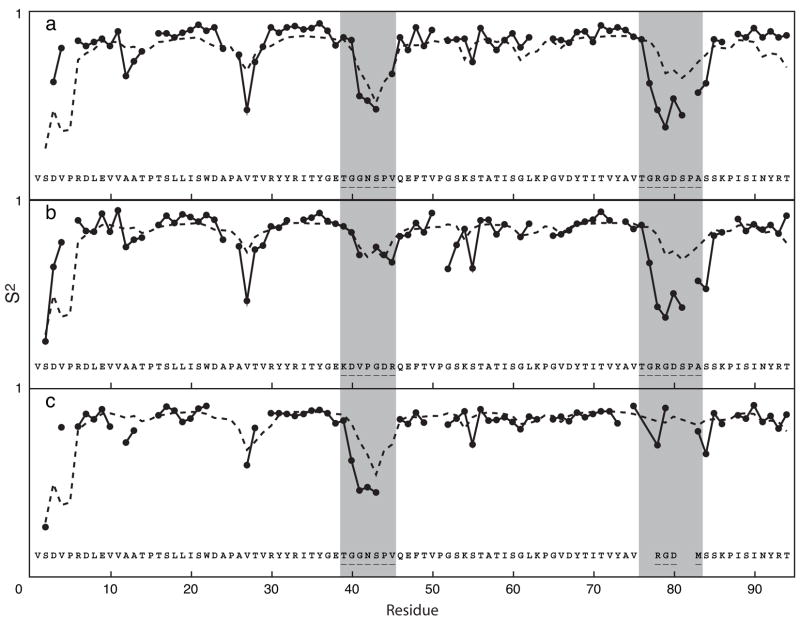
Backbone ¹⁵N S² have been reported for wild-type and two loop swap mutants of fnfn10 and of tnfn3 [41]. The experimental and predicted S² for the wild-type and mutant proteins are shown in figures 5 and 6. The wild-type fnfn10 domain has highly flexible CC′ (residues 39-45) and RGD (residues 76-83), shown in figure 5a, whereas the wild-type tnfn3 domain has relatively rigid CC′ and RGD loops, shown in figure 6a. The first fnfn10 mutant, shown in figure 5b, substitutes the more rigid CC′ loop from tnfn3 for the corresponding loop in fnfn10. The second mutant, shown in figure 5c, substitutes the shorter more rigid RGD loop from tnfn3 for the corresponding loop in fnfn10. The predicted values for the two mutant fnfn10 domains show that the flexibilities of the mutant loops are reduced relative to the native loop sequences. The first tnfn3 mutant, shown in figure 6b, substitutes the more flexible CC′ loop from fnfn10 for the corresponding loop in tnfn3. The second mutant, shown in figure 6c, substitutes the longer more flexible RGD loop from fnfn10 for the corresponding loop in tnfn3. The predicted values for the two mutant proteins show that the flexibility of the mutant loops is increased relative to the native loop sequences. These results are in qualitative agreement with the experimental data, although the predictions tend to overestimate the value of S² for the mutant loops for tnfn3.

Fig. 5.

S² of fnfn10 domain (a) and its mutants (b, c); (—) experimental measurements; (- - -) neural network predictions. The y-coordinate of each figure ranges from 0 to 1. Residue numbering is based on the wild-type sequence. The location of the CC′ and RGD loops is highlighted in gray. The mutations introduced are shown for each variant protein. Structures of the fnfn10 domains used for predictions are described elsewhere [41]. The correlation coefficients between experimental and predicted S² values are (a) 0.620, (b) 0.625, and (c) 0.720.

Fig. 6.

S² of tnfn3 domain (a) and its mutants (b, c); (—) experimental measurements; (- - -) neural network predictions. The y-coordinate of each section ranges from 0 to 1. Residue numbering is based on the longest construct, the RGD loop swap variant. The location of the CC′ and RGD loops is highlighted in gray. The mutations introduced are shown for each variant protein. Structures of the tnfn3 domains used for predictions are described elsewhere [41]. The correlation coefficients between experimental and predicted S² values are (a) 0.512, (b) 0.635, and (c) 0.759.

Discussion and Conclusion

Correlations have been examined for features for residues in positions −6 to +6 relative to the residue for which S² is to be predicted. The correlations shown in tables 2 and 3 are dominated by residues in the −1, 0, and +1 positions. Features for residues in positions further away are much less correlated with S².

In the present case, residue size is much less important than local packing density and secondary structure state. The importance of local packing density agrees with the results reported by Zhang and Brüschweiler [26]. Packing density, parameterized differently, was also found to be critical in determining crystallographic B-factors [6]. The relative unimportance of residue size appears to differ from the results of Goodman and coworkers [10]. However, in that earlier study, average values of S² for each amino acid residue were determined first and then correlated with residue side chain volume. This procedure averages over differences in local packing density and secondary structural state and consequently accentuates the dependence on side chain volume compared to the present approach.

The Zhang-Brüschweiler formula for predicting S² is

$$S^2=tanh[2.656(exp(-r_{-1}^O/1\mathring{A})+0.8exp(-r_0^H/\mathring{A})]-\mathrm{0.1.}$$ (6)

This formula corresponds to the parametrization expression:

$$F=s_2({\text{W}}_2{s}_1({\text{W}}_1\overrightarrow{x})+{\overrightarrow{b}}_2),$$ (7)

and can be thought of as a 2-layer perceptron with two inputs (exp(−r^O/1Å) and exp(−r^H/1Å]). The first layer has a transfer function is s₁(x) = tanh(x), W₁ = [2.656, 2.125], and no bias. The second layer has a transfer function s₂(x) equal to the identity operation, W₂ = 1, and a bias b₂ = −0.1. As can be seen from figure 1, a consistent improvement in prediction is obtained using the neural network model presented herein compared to the Zhang-Brüschweiler formula. Both the present model and the Zhang-Brüschweiler formula use distances to carbonyl oxygen and amide hydrogen atoms as important inputs. The improvement obtained by the neural network results in part from the different characteristic length used, 3 Å and 2 Å, for normalizing carbonyl oxygen and amide hydrogen distances, respectively, and in part from additional features in the neural network. Neither the change of the characteristic lengths, nor the addition of any single feature are responsible for most of the accuracy improvement. As shown by Figures 4–6, the neural network tends to overestimate the rigidity of loops. This observation suggests that other structural features governing protein conformational dynamics remain to be discovered and parameterized in the future.

Few studies of the accuracy of experimental measurements of S² have been reported. Difficulties in controlling for differences in the models used to fit experimental data is a confounding factor in attempts to determine absolute accuracy of experimental values of S² [21]; consequently, whether further improvements in prediction accuracy are limited by the quality of the experimental S² data or merely by the size of the feature set that can be stably parameterized is unknown.

The predictions obtained for GB3, HP67, fen ACP, RNaseH, and the wild-type and mutant fnfn10 and tnfn3 domains suggest that the parameterization of the neural network is transferable to proteins outside the training set. Furthermore, the predictions obtained for the loop-swap mutant fnfn10 and tnfn3 domains suggest that the neural network provides a useful approach for identifying mutant proteins with significantly altered conformational dynamics “in silico” prior to experimental studies.