From calcium blips to calcium puffs: Theoretical analysis of the requirements for interchannel communication

Abstract

In the cytoplasm of cells of different types, discrete clusters of inositol 1,4,5-trisphosphate-sensitive Ca²⁺ channels generate Ca²⁺ signals of graded size, ranging from blips, which involve the opening of only one channel, to moderately larger puffs, which result from the concerted opening of a few channels in the same cluster. These channel clusters are of unknown size or geometrical characteristics. The aim of this study was to estimate the number of channels and the interchannel distance within such a cluster. Because these characteristics are not attainable experimentally, we performed computer stochastic simulations of Ca²⁺ release events. We conclude that, to ensure efficient interchannel communication, as experimentally observed, a typical cluster should contain two or three tens of inositol 1,4,5-trisphosphate-sensitive Ca²⁺ channels in close contact.

One of the pathways for intracellular signaling involves Ca²⁺ mobilization from intracellular stores by agonist-liberated inositol 1,4,5-trisphosphate (InsP₃) (1). In response to stimuli of appropriate levels, InsP₃ induces oscillatory patterns of intracellular Ca²⁺ in individual cells of different types; Ca²⁺ signals also may be spatially organized as Ca²⁺ waves, initiated in certain regions of the cytoplasm and propagating throughout the whole cell (2–7). Recently, taking advantage of enhanced resolution for detection of intracellular Ca²⁺ signals, several groups have described elementary signals evoked by weaker InsP₃ stimuli (reviewed in ref. 8). These Ca²⁺ signals remain confined in a small cytoplasmic region around the Ca²⁺ releasing site, as originally observed in Xenopus oocytes (4). They were initially thought to fall into either one or the other of two stereotypic classes of events, characterized by different amplitudes, time-courses, and spatial spreading of Ca²⁺ signal (9): the so-called blips, which would be true elementary events resulting from transient activation of a single channel, and the so-called puffs, exhibiting amplitudes ≈5-fold higher that would be generated by concerted opening of a few clustered channels. Similar observations also were made in studies dealing with other cell types (10–13). In subsequent work with both Xenopus oocytes and HeLa cells, events involving opening of more than one single channel appeared to exhibit a whole spectrum of amplitudes and thus to be less stereotypic than originally thought (10, 14).

As a first step toward quantitative analysis of the hierarchy of Ca²⁺ signaling events, we previously simulated the behavior of a single channel placed in its cytoplasmic environment (15). That study concluded that a blip could be explained by the repetitive opening of a single channel due to the activatory effect of the high Ca²⁺ concentration transiently reached in the vicinity of the channel mouth. In those simulations, the duration of the simulated burst of channel activity was controlled, on one hand, by the slower inhibitory effect of this high Ca²⁺ concentration and, on the other hand, by a stochastic channel closing of sufficient duration so that the local Ca²⁺ concentration collapsed. The amplitude and duration of Ca²⁺ signals generated by simulated isolated single channels largely varied because of the stochastic nature of gating behavior, so that even predicted blips were not stereotypic. In the present work, we went a step further and aimed at understanding how clusters of InsP₃-sensitive channels could generate blips and puffs, accepting as a basic concept that the fact that blips and puffs form a continuum of events of graded size and variable time course can be thought of within a simple framework: At relatively low InsP₃ concentration, most opening events in a given cluster of InsP₃-sensitive channels are likely to be blips because an active channel is generally not surrounded by other channels with InsP₃ bound to them whereas higher InsP₃ concentrations are able to induce the concomitant opening of several InsP₃-bound channels nearby in the same cluster, and thus generate puffs. The stochastic nature of channel opening as well as simple geometrical proximity considerations then should result in a broad distribution of amplitudes and durations of calcium signaling events.

An additional important fact, however, is that, at concentrations of InsP₃ appropriate for producing Ca²⁺ puffs, the relative occurrence of blips is rather scarce (14, 16), as if, once a channel opened, it readily recruited several other channels in the cluster. Such an efficient channel synchronization requires that, during the burst of activity of the leader channel (i.e., the first one to open), the Ca²⁺ signal is able in most cases to propagate up to a neighboring InsP₃-bound channel of the same cluster and activate it. Because synchronization efficiency obviously depends on the distance between activatable InsP₃-bound channels, this experimental observation implies relatively short interchannel distances. Within a cluster, however, the current spatial definition of confocal microfluorimetry allows to visualize neither the number of channels nor the interchannel distances.

To estimate these parameters, which are not attainable through experiments, we have performed in this study computer stochastic simulations of InsP₃-induced activation of channels, grouped in a cluster and placed in a cytoplasmic-like environment. Following our previous study (15), the kinetic parameters for channel gating and Ca²⁺ diffusion in the cytoplasm were chosen to allow optimal fit to previously published experimental observations, and we searched for geometrical characteristics of the channel cluster allowing appropriate channel synchronization within the cluster. From our simulations, we conclude that a Ca²⁺ releasing site probably consists of a few tens of very closely packed InsP₃-sensitive Ca²⁺ channels: A square-shaped lattice of 25 channels in close contact leads to theoretical distributions of Ca²⁺ signal amplitudes compatible with experimentally observed distributions.

Simulation Procedures

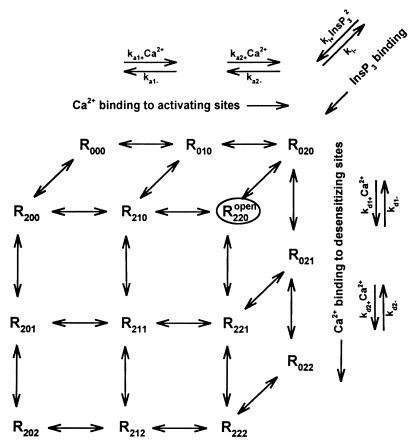
The numerical procedure used to generate Ca²⁺ signals is based on stochastic simulation of the transitions between the various states of the InsP₃-sensitive Ca²⁺ channel and on deterministic calculation of Ca²⁺ diffusion in a buffered cytosolic-like medium. This procedure, elaborated and described in detail in a previous work (15), was based on a gating model (Fig. 1) differing from the original one by the order of the InsP₃ binding reaction (third order instead of second order).

Figure 1.

Working model of InsP₃-sensitive Ca²⁺ channel. The channel exhibits different states, depending on the absence or presence of InsP₃ and Ca²⁺ in the respective specific binding sites: The symbol R_ijk refers to the state of the channel, to which i (0 or 2) InsP₃ molecules, j (0, 1 or 2) Ca²⁺ ions at the activating sites, and k (0, 1 or 2) Ca²⁺ ions at the desensitizing sites are bound. The transitions between the different states may be described by a cubic scheme, partially represented in the figure. All of the simulation results were obtained with the following parameter values: k_i+ = 5 × 10¹² M⁻²⋅s⁻¹; k_i− = 5 s⁻¹; k_a1+ = 1.25 × 10⁷ M⁻¹⋅s⁻¹; k_a1− = 64 s⁻¹; k_a2+ = 4.7 × 10⁹ M⁻¹⋅s⁻¹; k_a2− = 208 s⁻¹; k_d1+ = 2.6 × 10⁵ M⁻¹⋅s⁻¹; k_d1− = 380 s⁻¹; k_d2+ = 5.7 × 10⁸ M⁻¹⋅s⁻¹; k_d2− = 1.9 s⁻¹. Note that, because the binding of InsP₃ is assumed to be positively cooperative (nH = 2), k_i+ is a trimolecular binding rate constant, but the apparent K_d is still 1 μM, as in ref. 15.

The probabilistic approach may be summarized as follows. At any time t, the state of each channel was defined by the numbers of InsP₃ molecules bound to the receptor and the number of Ca²⁺ ions bound to the activating and/or desensitizing sites. Given the InsP₃ and Ca²⁺ concentrations in the channel vicinity and the kinetic constants characterizing the transitions to other states (see scheme in Fig. 1), the probabilities for all possible transitions within a small time interval Δt were computed and were represented in a [0,1] interval by a series of consecutive segments. A random number then was generated between 0 and 1, falling into a segment that defined the channel state at time t + Δt. This procedure was reproduced for each channel at each time step. When a channel was in the open state, R₂₂₀, this was assumed to result in a Ca²⁺ current of 0.1 pA into the corresponding box of the discretized space (see below).

The partial differential equation governing Ca²⁺ diffusion was numerically solved, using one or the other of two different types of discretization of the three-dimensional (3-D) space. A first discretization type was used when the system presented a spherical symmetry: i.e., in the presence of only one point source, representing a single active channel placed in the center of the space, as was the case for Fig. 2A. In this case, the procedure previously described (15) was strictly applied. In contrast, simulation of the behavior of a channel cluster, consisting of multiple point sources distributed on a planar portion of the endoplasmic reticulum, required a 3-D cartesian discretization in small cubic boxes. The 25 channels of the square-shaped cluster (see below) were distributed in a 2-D array of 5 × 5 contiguous boxes placed in the center of the space. The diffusion space extended 1 μm away from the cluster in every direction, the boundary condition consisting of a constant Ca²⁺ concentration equal to 40 nM (basal level). The diffusion equation was solved by the finite difference method applied to this discretized space and according to the rapid buffering approximation (17) (for more details, see ref. 15 and Table 1 therein showing the buffer characteristics used).

Figure 2.

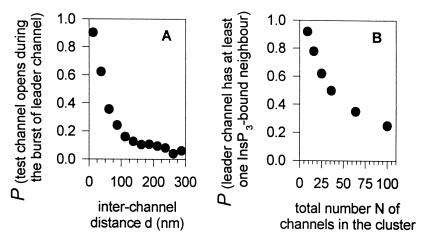
Estimation of cluster characteristics leading to efficient interchannel communication. (A) Probability that a test channel, placed at a distance d from the leader channel and sensing the fluctuations of Ca²⁺ concentration produced by the active leader channel, opens during the activity burst (blip) of the leader channel, as a function of the interchannel distance. For large distances, the probability reaches a small value, reflecting the low probability that a channel opens during bursting of another noncommunicating channel. (B) Probability that the leader channel in a cluster with N channels has at least one InsP₃-bound neighbor, as a function of N, assuming that each channel has a probability of 5/N to be InsP₃-bound.

Results

Preliminary Analysis of the Average Number of Channels Open During a Standard Puff Event.

The amplitudes of InsP₃-induced Ca²⁺ signals produced during elementary events like blips and puffs were previously estimated in Xenopus oocytes (9) and HeLa cells (5): mean Ca²⁺ amplitude of puffs was ≈170 nM above the basal concentration whereas amplitudes of blips reached ≈5-fold lower values (30 nM above basal level). Moreover, Sun and coworkers (14) reported that the rates of rise of “signal mass” (obtained by integrating the fluorescence signal throughout three dimensions) computed for averaged traces was ≈6× higher for puffs than for blips. Therefore, if a blip reflects the opening of a single channel, a puff is likely to involve the concerted opening of only a few channels: say, of about five on average.

Adaptation of Model Parameters to New Kinetic Experimental Constraints.

Another preliminary step in the present work was to make use of newly available information about latencies before channel opening, to refine our previously proposed model of the gating mechanism of InsP₃-sensitive Ca²⁺ channels (see Fig. 1). In this model, the delay observed before opening of any channel is mainly attributable to rate-limiting association of Ca²⁺ with the first activating Ca²⁺-binding site on this channel (15). On the other hand, opening of a channel in a cluster can initiate concerted activation of other channels, and hence a puff, only if the Ca²⁺ signal that reaches these neighboring channels is sufficiently high to allow Ca²⁺ binding to them within the short duration of the transient Ca²⁺ signal. The value of the kinetic parameter describing the rate of Ca²⁺ binding to its first activation site on the channel, k_a1+, is therefore critical for channel synchronization. Experimental information about this kinetic parameter can be derived from recently published measurements of the lag between flash photolysis of caged InsP₃ and the first observed elementary event reflecting the onset of Ca²⁺ liberation by any channel of a Xenopus oocyte Ca²⁺ release site: This latency was found to decrease with increasing InsP₃ concentration, down to a limiting value of 80 ms (18). Under saturating InsP₃ conditions, all channels in the cluster are expected to bind InsP₃ almost immediately, and the minimal 80-ms delay therefore corresponds to the average period of time elapsed before Ca²⁺ binds to an activating site on any one of the channels of the cluster, under conditions of basal Ca²⁺ concentration: i.e., (k_a1+[Ca²⁺]_basal)⁻¹/N. Indeed, the transitions between channel states being considered as Poisson processes, the mean time to observe the first transition R_i0k to R_i1k in the population of N channels is N times lower than the mean time required by a single channel to undergo this transition, which is equal to (k_a1+[Ca²⁺]_basal)⁻¹. Assuming that a Ca²⁺ releasing site consists of 25 channels (see below), the average latency before opening of an isolated single InsP₃-bound channel would thus be ≈2 s (80 × 25 ms) and, for a basal Ca²⁺ concentration of 40 nM, k_a1+ = 1.25 × 10⁷ M⁻¹⋅s⁻¹. Note that the k_a1+ value estimated from these latencies depends on the number of channels in the cluster in a reciprocal way. Therefore, if the cluster contains a larger number of channels, a smaller k_a1+ value will be obtained and, hence, less efficient channel synchronization (see below).

The k_a1+ value estimated above is ≈6.6× smaller than the value we had previously used to simulate the behavior of an isolated single channel (15). To remain in agreement with the other experimental results originally selected as reference, we were led to alter some of the other Ca²⁺ binding parameters (k_a1−, k_d1−, and k_d2− have been divided by 3.9, 0.15, and 10, respectively). In addition, because of the experimentally observed shape of the relationship between latency and InsP₃ concentration (18), InsP₃ binding was now assumed to exhibit positive cooperativity (n_H = 2). The new set of parameter values (see legend of Fig. 1) satisfactorily fitted Besprozvanny’s data (19) about the open probability of isolated channels under bilayer conditions and was also able to generate blip events as resulting from the flickering of a single channel during a few tens of milliseconds (data not shown).

Estimation of the Distance Between InsP₃-Sensitive Ca²⁺ Channels Within a Cluster.

To gain some understanding of synchronization between channels, we analyzed how far the Ca²⁺ signal generated by a leader channel could be expected to propagate in the cytosol and thus activate a neighboring channel. We considered the leader channel as an isolated channel in a cytosolic-like environment, initially in the open R₂₂₀ state and subsequently experiencing a classical activity burst of random duration. Ca²⁺ was considered to diffuse in an hemispherical 3-D space, representing the cytosolic volume adjacent to the endoplasmic reticulum membrane. A test channel also was placed in this space, at a certain distance (d) from the leader channel. Like the leader channel, this test channel also was assumed to be InsP₃-bound initially, but its Ca²⁺ binding sites were initially vacant (R₂₀₀ state). Our simulation procedure (15) was applied, leading to a transient burst of activity of the leader channel. The numerical procedure monitored whether the test channel opened during this burst and stopped the simulation at that moment. After repeating the simulation 300 times, we counted the number of runs for which the test channel had opened during the activity burst of the leader channel. This was an indication for synchronization because, otherwise, the average delay before opening of an isolated channel would have been much longer, ≈2 s, as indicated above. Fig. 2A shows that, under cytosolic-like conditions (with a mobile Ca²⁺-sensitive dye present), activation of the test channel before closure of the leader channel was relatively frequent only when the two channels were rather close to each other: When the interchannel distance was 12 nm, i.e., the minimal value corresponding to the lateral dimensions of the channel (20), synchronization between the two channels took place in ≈90% of the cases, but when the two channels were 50 nm apart, synchronization occurred in less than half of the cases. This very short effective range of Ca²⁺-mediated communication between channels is in fact the consequence of the steep gradient of Ca²⁺ concentration created by a Ca²⁺ point source in a buffered medium (21, 22). Our results were obtained by using a k_a1+ value corresponding to a hypothetical number of 25 channels per Ca²⁺ releasing site, but synchronization efficiency would have been even worse if the cluster had been supposed to be bigger, because of the lower k_a1+ value.

Because synchronization between channels appears to require closely packed channels, the functional Ca²⁺ releasing site must be restricted to a very small portion of the membrane of an endoplasmic reticulum tubule. Thus, for subsequent simulations, we considered that the channel cluster extends over a flat surface as a 2-D pattern, which, for simplicity, we assumed to be a square-shaped lattice.

Estimation of the Number of InsP₃-Sensitive Ca²⁺ Channels Within a Cluster.

Because the amplitude of a mean puff event requires the concerted activation of about five channels, the total number of InsP₃-bound channels in the cluster also has to be close to about five. Indeed, if a cluster of moderate size were to contain many more InsP₃-bound channels, the puff amplitude would be too high because the Ca²⁺ concentration around the cluster would presumably be sufficient to induce the opening of most InsP₃-bound channels (see Fig. 5 for confirmation). Each channel thus has a probability of ≈5/N to be InsP₃-bound, N being the total number of channels in the cluster. We then estimated the probability that, in such a cluster, at least one InsP₃-bound channel is adjacent to the leader active channel, as follows. In square-shaped clusters containing N channels, InsP₃-bound channels were first chosen at random, with a probability of 5/N. If at least two channels turned out to be InsP₃-bound, one of them was randomly chosen as the active leader channel initiating the Ca²⁺ signal. The procedure then checked whether the leader active channel was adjacent to any one of the other InsP₃-bound channels. Analysis of the results obtained by repeating this procedure allowed us to estimate the probability that at least one of the nearest neighbors of the active channel was InsP₃-bound. Fig. 2B shows that this probability rapidly decreases as the total number of channels in the cluster increases: a probability as low as 0.5 is already obtained with a cluster consisting of only 36 channels.

Figure 5.

Efficiency of puff production with a loosely packed channel cluster. A stochastic simulation was performed under the same conditions as for Fig. 3D (d = 40 nm), but with two different InsP₃ concentrations, 0.5 and 1 μM in A and B, respectively.

On the basis of this simple counting procedure, we predict that an upper limit for the cluster content should be 20–30 channels. Indeed, if the cluster were to contain more channels, the probability to generate a puff would vanish for two reasons: first, because the channel activation rate would be too slow (k_a1+ decreases as N increases), and second, because the distance that the Ca²⁺ signal should cover to activate a second channel would be too large (the probability that a direct neighbor is InsP₃-bound being equal to 5/N). On the other hand, the experimental observation that increasing InsP₃ concentrations produce Ca²⁺ puffs with higher amplitudes (Fig. 6 in ref. 16) requires the recruitment of more than 5 channels per cluster under these circumstances and suggests that 10–20 should be a lower limit for the number of channels in the cluster. At this point, we thus propose the tentative guess that a typical cluster contains 25 channels.

One may wonder whether a value of 25 channels per Ca²⁺ releasing site is realistic with respect to actual cells. In Xenopus oocytes, which are thought to contain 3 × 10¹⁴ tetrameric InsP₃ receptors per liter of cytoplasm (23), InsP₃-sensitive Ca²⁺ release sites have been predominantly localized within a 6-μm-thick subplasmalemmal band (24). If all of the receptors are concentrated in this band, a simple calculation indicates that the mean spacing between adjacent clusters of 25 channels is equal to 1.44 μm. This figure should be a lower limit because InsP₃ receptors were immunolocalized not only in this region (24) but also in the perinuclear region (25, 26). Values of 1.6 and 2.25 μm were recently reported for the mean spacing between adjacent Ca²⁺ releasing sites in the animal and vegetal hemispheres of Xenopus oocytes, respectively (27). Thus, defining a cluster as an assembly of 25 densely packed channels is certainly not unreasonable.

Stochastic Simulation of a 25 (5 × 5)-Channel Cluster in a Cytosolic Environment.

The previous simulations aimed at anticipating likely features of the spatial organization of Ca²⁺ releasing site. We have now to demonstrate that a theoretical cluster made of 25 closely packed channels may generate Ca²⁺ signals compatible with experimental observations. We already mentioned a recently reported remarkable experimental observation (14, 16): Despite the fact that a given InsP₃ stimulus always leads to a broad distribution of event amplitudes, when puffs involving the concerted activation of a few channels only were generated, pure blip events were rare. In this case indeed, the amplitude distribution was unimodal with amplitude values corresponding to puffs (Fig. 8 in ref. 14; Fig. 6—0.1 μM histamine—in ref. 16). This reveals highly efficient communication between these few activatable InsP₃-bound channels because weak interchannel communication would rather favor the production of blips. The aim of our next simulation was, therefore, to determine under which conditions the simulated distribution of amplitude has a shape compatible with the experimental observations.

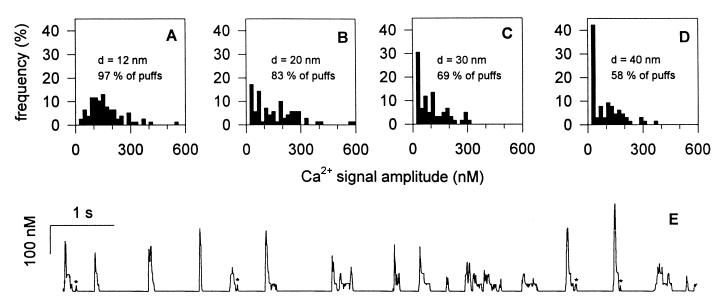
The simulation was performed for a 2-D square-shaped cluster of 25 channels surrounded by a 3-D cytosolic-like space containing a basal Ca²⁺ concentration of 40 nM and in the presence of an InsP₃ concentration of 0.5 μM, leading to an average of 5 InsP₃-bound channels within the cluster. The channels with InsP₃ bound were chosen at random, according to the probability associated with the InsP₃ concentration used, and one of them, at random, was designated as being in the active state (R₂₂₀) at time zero. The stochastic procedure then was initiated to simulate both the state transitions for all channels and the diffusion of Ca²⁺ in the whole cytosolic space. The average Ca²⁺ concentration in a volume of 1 fl, centered on the cluster, was simultaneously calculated, up to the end of the Ca²⁺ release event. The procedure was repeated 100 times, and, each time, the maximal Ca²⁺ concentration was recorded. To analyze the amplitude distribution, the sole events for which the Ca²⁺ concentration rose to >20 nM above the basal level were considered, to account for the existence of a detection threshold compatible with the fact that blips of 30 nM blip amplitude can be detected (16). Fig. 3 shows the amplitude distribution obtained with four different clusters in which adjacent channels were separated by a center-to-center distance (d) of 12, 20, 30, and 40 nm, respectively. A bell-shaped, unimodal distribution can be observed only in the case of the smallest distance, corresponding to the situation in which neighboring channels are in close contact. Blips, i.e., events characterized by a Ca²⁺ concentration increment ranging from 20 to 40 nM and corresponding thus to the opening of a single channel, represent only 3% of all detectable events. When adjacent channels are separated by only a few nanometers (d = 20 nm), the production of puffs is still abundant, but the occurrence of blips is already sufficient (17%) to distort significantly the distribution shape. As anticipated, the situation is even worse for larger interchannel distances. This demonstrates that, within the framework of the proposed model, a cluster of 25 channels must be as compact as possible to generate a Ca²⁺ amplitude distribution of appropriate shape. This distribution exhibits a median amplitude of 149 nM, which is reasonably consistent with experimental observations. This realistic simulation result a posteriori justifies our initial choices concerning the size of the cluster and the number of InsP₃-bound channels required to generate standard puffs.

Figure 3.

Effect of the interchannel distance in a 25-channel cluster on the distribution of Ca²⁺ signal amplitudes in the presence of 0.5 μM InsP₃. Ca²⁺ signals generated by a square-shaped 25-channel cluster placed in a cytosolic environment in the presence of 50 μM Ca²⁺ Green-1 were simulated. The InsP₃ concentration was set to 0.5 μM, and the center-to-center distance (d) between adjacent channels was 12, 20, 30, and 40 nm in A, B, C, and D, respectively. The Ca²⁺ concentration in a 1-fl volume centered on the cluster was followed up to the end of the release event. The amplitude of the Ca²⁺ signal characterizing one event was calculated as the peak Ca²⁺ increase above the basal value. Events with amplitudes between 20 and 40 nM or higher than 40 nM were referred to as blips or puffs, respectively. E shows the time dependence, over 10 s, of the Ca²⁺ concentration simulated under the conditions of A (closely packed channels), exhibiting a series of puffs and a few blips (marked by stars).

The same stochastic simulation procedure was used to simulate, over a long period, successive Ca²⁺ signals generated by the same cluster of 25 closely packed channels stimulated by 0.5 μM InsP₃. The simulated trace of the Ca²⁺ concentration in a volume of 1 fl centered on the cluster exhibits puffs and a few blips, separated by time intervals of random length (Fig. 3E). The rising phase of puffs is quite short, because of fast recruitment of InsP₃-bound channels within the cluster, whereas the subsequent Ca²⁺ decline is generally slower, because this phase is governed by progressive Ca²⁺-induced desensitization of the channels. Interestingly, previous theoretical simulations (15) suggested that the termination of a blip event could result from the dissociation and absence of rebinding of activating Ca²⁺, because of the fast decrease of local Ca²⁺ concentration once the channel closed. On the contrary, our simulation shows that, at the end of a puff, most channels are desensitized, including the InsP₃-free ones that did not open during the puff. The reason is that the Ca²⁺ concentration in the vicinity of the cluster remains high as long as at least one channel is open. Note that, a priori, a subsequent Ca²⁺ release event might then start as soon as resensitization of an InsP₃-bound channel occurs. If this resensitization (i.e., Ca²⁺ dissociation from the desensitizing sites) were to be relatively slow, compared with channel activation (i.e., Ca²⁺ association to the activating sites), the first InsP₃-bound channel resensitized would be able to re-open before a second one is resensitized, and only blips would subsequently be observed. In contrast, as a consequence of a relatively fast resensitization, compared with activation, most channels resensitize before any one of them has an opportunity to re-open again, and simulation results in sequential puffs, as experimentally observed (4).

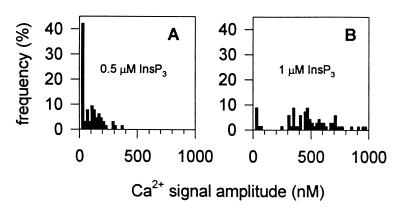
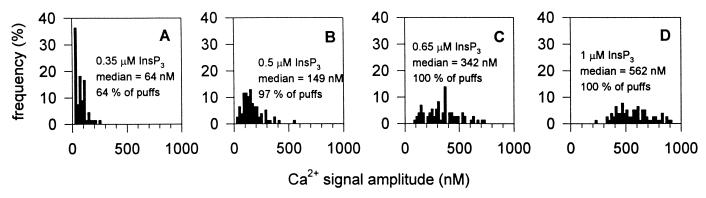
When simulations were repeated for channels in close contact (d = 12 nm) but with increasing InsP₃ concentrations (up to 0.65 μM and 1 μM, corresponding to an average of 7.4 and 12.5 InsP₃-bound channels in the cluster, respectively), the amplitude distribution became broader and shifted to larger values for the Ca²⁺ signal (Fig. 4 C and D), in agreement with the reported distributions of puff amplitudes obtained with stimuli of increasing strength (Fig. 6 in ref. 16). Among the 100 simulation runs with these two higher InsP₃ concentrations, no detectable blip event was obtained, confirming the high degree of synchronization between the channels. On the contrary, in the presence of a distinctly lower InsP₃ concentration, 0.35 μM (leading to an average of only 2.7 InsP₃-bound channels in the whole cluster), 36% of the Ca²⁺ release events were pure blips, the population of which was now clearly detectable in the amplitude distribution (Fig. 4A).

Figure 4.

Effect of InsP₃ concentration on the distribution of Ca²⁺ signal amplitudes with a 25 closely packed channel cluster. A stochastic simulation was performed under the same conditions as for Fig. 3A (d = 12 nm), but with InsP₃ concentrations equal to 0.35, 0.5, 0.65, and 1 μM in A, B, C, and D, respectively.

The previous simulations show that puffs can be mimicked by simulating the concerted opening of about 5 InsP₃-bound channels in a cluster of 25 closely packed channels. Because of their close proximity, virtually all of the InsP₃-bound channels in such a cluster participate in a single event. Despite this analysis, one might wonder whether puffs could not be obtained with clusters consisting of less tightly packed channels but with a number of InsP₃-bound channels larger than five, to allow simultaneous recruitment, partly by chance, of five of them, as required for the production of puffs with an acceptable amplitude. To test this alternative hypothesis, we simulated the behavior of a 25-channel cluster with a 40-nm center-to-center distance in the presence of a higher InsP₃ concentration (1 μM), thus leading to a higher number of InsP₃-bound channels in the cluster (12.5, on average). As expected, increasing the InsP₃ concentration (Fig. 5 A and B) led to more frequent occurrence of puffs, but, then, the average amplitude of the puffs was too high and too many blip events were still observed. It thus appears that too distant and thus functionally independent channels cannot give rise to the appropriate distribution of amplitudes. This confirms our conclusion that a Ca²⁺ releasing site must consist of a quite limited number of efficiently communicating channels, in fact in close contact.

Discussion

Discrete hot spots of InsP₃-sensitive Ca²⁺ release have been observed in the cytoplasm of different cell types (8), but, because of the limitations of microfluorimetric detection methods, neither their spatial dimensions (which are <1 μm³) nor their actual contents could be estimated precisely. Hot spots presumably consist of clusters of InsP₃-sensitive Ca²⁺ channels, in which only a few channels open in a concerted way during a Ca²⁺ release event. The aim of the present study was to deduce from stochastic computer simulations the cluster characteristics required to permit efficient synchronization of the channels and to solve the experimental paradox that, despite the small number of channels open during such release events, blip events, which involve the opening of a single channel, only rarely occur.

The conceptual core of our analysis is that, if a puff is generated by the concerted activation of about five InsP₃-bound channels, these channels must be located in close proximity to permit interchannel communication and, thus, synchronization. We in fact demonstrate that, within the framework of our gating model, and taking into account experimental physiological constraints (diffusion coefficient for cytoplasmic Ca²⁺, unitary channel current, channel activation kinetics, and latencies before opening, etc.), efficient interchannel communication only takes place if the InsP₃-bound channels are in close contact. This implies that channel clusters responsible for puffs might have a spatial arrangement similar to that observed for channels in Purkinje cell dendrites: i.e., a quasicrystalline organization (20). We also demonstrate that the five InsP₃-bound channels required to generate a Ca²⁺ puff of appropriate mean amplitude can be in close proximity only if the cluster does not contain more than two or three tens of channels—i.e., has lateral dimensions of the order of 60 nm. This cluster is therefore a very localized region, whose experimental characterization will presumably only be made possible by electron microscopy, as has been the case for the junctional region in sarcoplasmic reticulum. In the latter case, stochastic simulations have convincingly established the competence of ryanodine receptor and dihydropyridine receptor organized clusters for generating characteristic patterns of calcium release events (28).

The results shown here were obtained by a numerical procedure involving stochastic simulation within a 3-D cartesian space, each channel occupying a certain position inside the cluster on the endoplasmic reticulum membrane and being in contact with the Ca²⁺ concentration in the adjacent small cubic volume of 12 × 12 × 12 nm³. Because of the high level of proximity between these channels, we wondered whether it was possible to reproduce the results by using a numerical procedure based on a more macroscopic view of the cluster: e.g., by considering all channels of this cluster as being homogeneously distributed in a single domain of larger volume and in which a homogenous Ca²⁺ concentration would prevail. We then resorted to a numerical method based on central symmetry (15), in which a central sphere represents the cluster domain. With a diameter of 40 nm, this central sphere has a volume roughly equal to the sum of the 25 small cubic volumes adjacent to the channels in the procedure described above. In these new simulations, we were able to obtain a distribution of Ca²⁺ signal amplitudes similar to that illustrated in Fig. 3A (data not shown). Thus, it appears that the kinetic behavior of a cluster may be satisfactorily simulated by considering a virtual domain, a few tens of nanometers wide, in which all of the channels of a cluster and the Ca²⁺ ions close to them are homogeneously distributed. This result may be viewed as a rational basis for the operational concept of intermediate domain (between the channel cluster and the bulk cytosolic medium), which was previously introduced to permit empirical simulation of the so-called incremental Ca²⁺ detection (29) and of the long-period Ca²⁺ oscillations (30). In this context, such an intermediate domain would be associated with a cluster of closely packed channels. It is thus larger than the microdomains formed around the mouth of single open channels (21) but smaller than the submembrane domains containing distant channels recently described (22). Further simulations are in progress for defining the conditions under which synchronization of Ca²⁺ releasing sites may occur through long range Ca²⁺-mediated communication, leading to Ca²⁺ waves and oscillations.

Abbreviations

InsP₃

inositol 1,4,5-trisphosphate

3-D

three-dimensional