Abstract
Conclusions have differed in studies that have compared vaccine efficacy in groups receiving influenza vaccine for the first time to efficacy in groups vaccinated more than once. For example, the Hoskins study [Hoskins, T. W., Davis, J. R., Smith, A. J., Miller, C. L. & Allchin, A. (1979) Lancet i, 33–35] concluded that repeat vaccination was not protective in the long term, whereas the Keitel study [Keitel, W. A., Cate, T. R., Couch, R. B., Huggins, L. L. & Hess, K. R. (1997) Vaccine 15, 1114–1122] concluded that repeat vaccination provided continual protection. We propose an explanation, the antigenic distance hypothesis, and test it by analyzing seven influenza outbreaks that occurred during the Hoskins and Keitel studies. The hypothesis is that variation in repeat vaccine efficacy is due to differences in antigenic distances among vaccine strains and between the vaccine strains and the epidemic strain in each outbreak. To test the hypothesis, antigenic distances were calculated from historical hemagglutination inhibition assay tables, and a computer model of the immune response was used to predict the vaccine efficacy of individuals given different vaccinations. The model accurately predicted the observed vaccine efficacies in repeat vaccinees relative to the efficacy in first-time vaccinees (correlation 0.87). Thus, the antigenic distance hypothesis offers a parsimonious explanation of the differences between and within the Hoskins and Keitel studies. These results have implications for the selection of influenza vaccine strains, and also for vaccination strategies for other antigenically variable pathogens that might require repeated vaccination.
Keywords: original antigenic sin, vaccine efficacy, repeated vaccination, antigenic distance
Antigenic drift of the influenza virus exposes the human population to new but related influenza variants on an annual basis. Thus, components of the influenza vaccine are updated, sometimes yearly, to maintain a reasonable correspondence between the vaccine and epidemic strains. Public health recommendations are for annual vaccination of at-risk individuals (1).
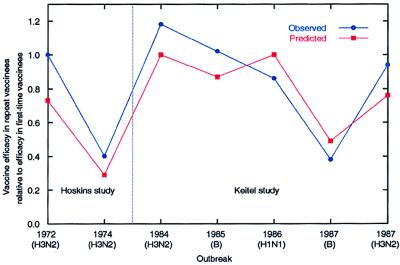
Influenza vaccination works effectively in first-time vaccinees (2). However, efficacy in repeat vaccinees has been difficult to determine definitively. A meta-analysis of 19 repeat vaccination studies showed that on average repeat vaccinees were protected at least as well as first-time vaccinees (3). However, in the 12 studies in which protection was measured serologically, there was statistically significant unexplained heterogeneity: In some years repeat vaccinees were better protected than first-time vaccinees; in other years they had worse protection (3). Similarly, two widely cited vaccine efficacy field studies have reached different conclusions: The “Hoskins study” (4) concluded that repeat vaccination was not effective, whereas the “Keitel study” (5) concluded that repeat vaccination was effective. There was also heterogeneity within the Hoskins (6) and Keitel studies (Fig. 1). Meta-analysis found no factor that explained the heterogeneity among 12 serological studies; among the factors tested were differences in influenza subtype, age, study design, hemagglutination inhibition (HI) assay method, and vaccine type (3).
Figure 1.
Observed vaccine efficacy in repeat vaccinees relative to the efficacy in first-time vaccinees, and predicted vaccine efficacy based on the antigenic distance hypothesis.
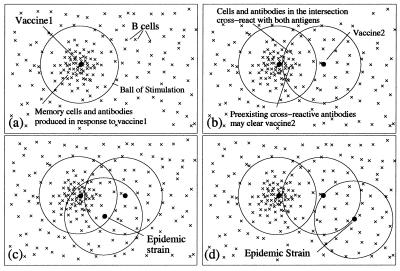
We propose and test a hypothesis to explain the heterogeneity of repeated influenza vaccination. The hypothesis extends the idea that the closeness of the antigenic match between the vaccine strain and the epidemic virus is important for vaccine efficacy in first-time vaccinees, by also considering the closeness of the vaccine and epidemic strains to previous vaccine strains to determine how vaccine efficacy is modulated by prior vaccination. This “antigenic distance” hypothesis is illustrated in Fig. 2.
Figure 2.
An illustration of the antigenic distance hypothesis. Shape space diagrams are a way to illustrate the affinities between multiple B cells/antibodies and antigens, and also the antigenic distances between antigens (7). In these shape space diagrams, the affinity between a B cell or antibody (×) and an antigen (●) is represented by the distance between them. Similarly, the distance between antigens is a measure of how similar they are antigenically. (a) B cells with sufficient affinity to be stimulated by an antigen lie within a ball of stimulation centered on the antigen. Thus, a first vaccine (vaccine1) creates a population of memory B cells and antibodies within its ball of stimulation. (b) Cross-reactive antigens have intersecting balls of stimulation, and antibodies and B cells in the intersection of their balls—those with affinity for both antigens—are the cross-reactive antibodies and B cells. The antigen in a second vaccine (vaccine2) will be partially eliminated by preexisting cross-reactive antibodies (depending on the amount of antibody in the intersection), and thus the immune response to vaccine2 will be reduced (8, 9). (c) If a subsequent epidemic strain is close to vaccine1, it will be cleared by preexisting antibodies. (d) However, if there is no intersection between vaccine1 and the epidemic strain, there will be few preexisting cross-reactive antibodies to clear the epidemic strain quickly, despite two vaccinations. Note, in the absence of vaccine1, vaccine2 would have produced a memory population and antibodies that would have been protective against both the epidemic strains in c and d. For an antigen with multiple epitopes (such as influenza) there would be a ball of stimulation for each epitope.
The experiments reported here were performed in machina. Like any model system (animal or computer), a computer model trades off accuracy for controllability, observability, repeatability, speed, and lower cost. Using a computer model allows us to study a large number of vaccination regimens, and to isolate the effects of antigenic difference from other effects such as dose and antigenicity of the vaccine, immunocompetence of the vaccinee, and virulence and transmissibility of the influenza virus.
Materials and Methods
Computer Model.
The model simulates a repertoire of 107 B cell clones, each with a different specificity for antigen. When antigen is introduced into the model, B cells with sufficient affinity have a chance to bind the antigen, be stimulated to divide, undergo somatic hypermutation, and differentiate into a plasma or memory cell. Secreted antibody has a chance to bind antigen, and antigen–antibody complexes are removed from the system. In the simulation, just as in animals, one sees differences among individuals. This is due to different random number choices for each individual, which result in different repertoires and hence variation in the number and specificity of B cells that are stimulated by an antigen. We are concerned with protection from infection conferred by inactivated influenza vaccine and mediated by circulating antibodies; thus we do not consider mucosal or cell-mediated immunity.
Receptors on B cells, antibodies, and antigens are represented by strings of 20 symbols, each of which can take on one of four values. The reasons for choosing this representation are described in ref. 10. The distance between two antigens is measured by Hamming distance—i.e., the number of point mutations in the string describing one antigen required to make it identical to those of the second antigen. Similarly, the distance between an antibody (or B cell) and an antigen is the number of changes required to make the antibody a perfect match for the antigen. This measurement of the distance between antigens by their Hamming distance allows antigenic difference to be computed in quantitative terms. Antigenic (Hamming) distances vary between 0 and 20, where a distance of 0 implies antigenic identity, and a distance of 7 or more implies no cross-reactivity. Further details of the model are included in the supplemental material (www.pnas.org), and the computer program is available from http://www.cs.unm.edu/∼dsmith/software/PNAS-model.html.
Experimental Design.
The computer experiment considered two influenza seasons and four categories of individuals: (i) those never vaccinated, (ii) those who received “vaccine1” (v1) at the start of the first influenza season and were not vaccinated for the second season, (iii) those not vaccinated for the first season but who received “vaccine2” (v2) at the start of the second season (“first-time vaccinees”), and (iv) those who received v1 at the start of the first season and v2 at the start of the second (“repeat vaccinees”). All simulated individuals were challenged with epidemic virus 2 months into the second influenza season.
The same v2 and epidemic strains were used for all simulated individuals, and v1 was varied. The vaccine2-epidemic strain antigenic distance (v2–e distance) was 2. Since cross-reactive distances vary between 0 and 7, this distance is “close,” but it is not a perfect match. The v1-only category (ii) was split into eight groups with each group receiving a different v1, and with the vaccine1-epidemic strain antigenic distance (v1–e distance) varying between 0 and 7. Similarly, the repeat vaccine category (iv) was split into 31 groups,¶ with each group receiving a different v1, and with the v1–e distance, and different vaccine1–vaccine2 antigenic distances (v1–v2 distances) varying between 0 and 7. Dosage and timing of the vaccinations and epidemic challenge are summarized in Table 1. The vaccine strains were nonreplicating.
Table 1.
Timing and dose of simulated vaccinations and epidemic challenge
| Category | No. of groups | No. in group | v1 dose (day 0) | v2 dose (day 365) | Challenge dose (day 425) |
|---|---|---|---|---|---|
| (i) No vaccines | 1 | 200 | 500 | ||
| (ii) v1 only | 8 | 200 | 1,000 | 500 | |
| (iii) v2 only | 1 | 200 | 1,000 | 500 | |
| (iv) v1 and v2 | 31 | 200 | 1,000 | 1,000 | 500 |
Each category corresponds to a different vaccine strategy, and each group within a category corresponds to different antigenic distances among the vaccine and epidemic strains.
For each member of each group, the viral load, and antibody quantity and affinities for each antigen, were measured every 6 hr. In addition, prior to each vaccination and epidemic challenge, and at the peak of each response, the number, affinity for each antigen, and clonal history of each B cell involved in the response were recorded. If the viral load exceeded 1,500 “units” it was deemed to have passed a “disease threshold” and the simulated individual was considered symptomatic. Every simulated individual was exposed to epidemic virus, and the attack rate within a group was defined as the proportion of the group in which the viral load exceeded the disease threshold.
Statistical Analysis.
Two-sample z tests were used to compare proportions. Two-tailed testing was used for P values.
Results
Table 2 shows the experimental attack rate in each experimental and control group. The attack rate was 1.0 in the group never vaccinated.‖ The attack rate was 0.55 for first-time vaccinees. Attack rates varied from 0.01 to 1.0 in the v1-only groups, and the attack rate increased as the v1–e distance increased. Attack rates varied from 0.0 to 0.78 for repeat vaccinees, and the attack rate depended on the v1–v2 distance and the v1–e distance.
Table 2.
Summary of experimental attack rates
| v1–e distance | Attack rate
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| v1 only | Repeat vaccinees (v1–v2 distance indicated)
|
||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 0 | 0.01** | 0.00** | |||||||
| 1 | 0.46 | 0.06** | 0.01** | 0.04** | |||||
| 2 | 0.87‡ | 0.78‡ | 0.37** | 0.20** | 0.19** | 0.18** | |||
| 3 | 0.96‡ | 0.74‡ | 0.44* | 0.36** | 0.35** | 0.38** | |||
| 4 | 0.99‡ | 0.71‡ | 0.50 | 0.45* | 0.41** | 0.50 | |||
| 5 | 1.00‡ | 0.66† | 0.46 | 0.47 | 0.50 | 0.50 | |||
| 6 | 1.00‡ | 0.65† | 0.54 | 0.45* | 0.54 | ||||
| 7 | 1.00‡ | 0.55 | 0.58 | 0.52 | |||||
The attack rate in the unvaccinated control was 1.0 (not shown). The attack rate for first-time vaccinees (v2-only) was 0.55 (not shown). Attack rates for repeat vaccinees and the v1-only groups are shown in the table. Groups marked with a † or ‡ had higher (P < 0.05 or P < 0.01, respectively) and groups marked with an * or ** had lower (P < 0.05 or P < 0.01, respectively) attack rate than did first-time vaccinees. Attack rates in other repeat vaccination groups did not differ significantly from that for first-time vaccinees, either because v1 was too far from v2 and the epidemic strain to have an effect, or because the effects of positive and negative interference canceled each other out. Attack rates as high as 1.0 are due the large-dose experimental challenge of each simulated individual.
An additional year between vaccination and challenge increased (P < 0.01) the experimental attack rate from 0.55 to 0.87 for first-time vaccinees when the vaccine-epidemic strain antigenic distance (v–e distance) was 2 (see v1-only column in Table 2). This increase in attack rate was due to decay of cross-reactive antibody (data not shown).
Repeat Vaccination Was Beneficial When Given to Previous Vaccinees.
In all groups that received v1, it always lowered experimental attack rates to receive v2. The lowering of attack rates was statistically significant, P < 0.01, other than in the group in which the v1–v2 distance was 0 and the v1–e distance was 2 (P < 0.05), and in the group in which the v1–v2 distance was 2 and the v1–e distance was 0. This can be seen by comparing the experimental attack rates in the v1-only column of Table 2 with the attack rates in the corresponding row of the repeat-vaccine columns (a row corresponds to groups in which the v1–e distance was the same).
Negative and Positive Interference of a Prior Vaccine.
Attack rates for repeat vaccinees were sometimes lower, and sometimes higher, than the attack rate for first-time vaccinees (Table 2)—even though the timing, dose, and v2–e distance were identical. The effect of v1 on the apparent efficacy of v2 can be split into two factors: negative and positive interference. Because of the first vaccination, v2 is partially eliminated by preexisting cross-reactive antibody produced in response to v1 and by v2 stimulating v1 memory clones. These effects, which lead to reduced effectiveness of v2, we call “negative interference.” Negative interference is greater when the v1–v2 distance is small.
The second factor influencing the attack rate in repeat vaccinees is “positive interference,” in which preexisting cross-reactive antibody produced in the response to v1, and boosted by the response to v2, helps to clear the epidemic virus. Positive interference is greater when the v1–e distance is small—this trend can be seen in the columns of Table 2.
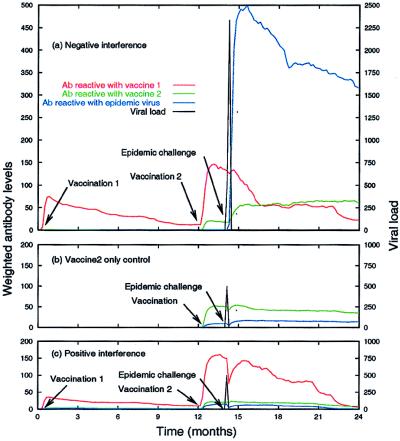
Fig. 3a shows an example of negative interference of v1 on v2. The response to v1 reached levels** typical for the model. The response to v2 caused a 6-fold increase in the antibody cross-reactive with v1. This increase was caused by stimulation of cross-reactive memory B cells produced in the response to v1 (data not shown). After the response to v2, the antibody reactive with v2 was approximately one-half of that usually seen after a primary vaccination (e.g., the level in the response to v2 in Fig. 3b, and the response to v1 in Fig. 3 a and c). Furthermore, the antibody produced in response to v1 and v2 was strongly cross-reactive with v1, but only weakly cross-reactive with the epidemic strain. This absence of protective antibody cross-reactive with the epidemic virus allowed the virus to exceed the 1500 antigen unit threshold and “cause disease” (Fig. 3a). The antibody level reactive to the epidemic strain was large after the epidemic virus was cleared, though the antibody levels to v1 and v2 remained mostly unaffected (Fig. 3a), suggesting a de novo immune response to the epidemic strain. The effects of negative interference are most evident in comparison with the response generated by the v2-only control (Fig. 3b). The antibody produced in this case cross-reacted with the epidemic strain and provided protection against the epidemic challenge.
Figure 3.
An example of negative interference by v1 on v2 (a), a v2-only control for comparison (b), and positive interference by v1 on the epidemic challenge (c). The v1–v2 distance was 2 for the examples in a and c, and the v1–e distance was 4 for the example in a and 2 for the example in c. An enlarged region of a is included in the supplemental material (www.pnas.org).
Fig. 3c shows an example of positive interference of v1 on the epidemic challenge. As in Fig. 3a, the response to v1 was typical, and v1 negatively interfered with v2 by about the same amount (the v1–v2 distance was the same in both cases). The difference between this example and Fig. 3a is that the antibody produced in response to v1, and boosted by v2, was cross-reactive with the epidemic strain, whereas it was not cross-reactive in Fig. 3a (the v1–e distance is 2 in Fig. 3c and 4 in Fig. 3a). The antibodies cross-reactive with the epidemic strain were sufficient in number and affinity to clear the epidemic virus before it caused disease. Because the epidemic virus was cleared quickly, it did not stimulate the production of new antibody and the antibody levels to all three antigens was mostly unaffected by the challenge.
Figure 4.
Homologous vaccination over a range of v–e distances. (a) Comparison of giving the same vaccine in the prior influenza season, the current season, and both seasons. (b) Observed vaccine efficacy in repeat vaccinees relative to the efficacy in first-time vaccinees and predicted efficacy based on the antigenic distance hypothesis. Observed data are from the four outbreaks in the Hoskins and Keitel studies preceded by homologous vaccination [1972, 1984, 1985, and 1987 (B)]. The predicted vaccine efficacy is computed from panel a as 1 − attack rate. In computing the efficacy relative to first-time vaccinees we assumed that first-time vaccinees received the vaccine in the current season.
For some repeat vaccine groups, positive interference dominated over negative interference (entries marked with an ∗ or ∗∗ in Table 2) and the attack rate was lower than for first-time vaccinees. In other repeat vaccine groups negative interference dominated (entries marked with a † or ‡ in Table 2) and the attack rate was higher than for first-time vaccinees.
When the v1–e distance was less than 4, a greater proportion of memory B cells that cross-reacted with the epidemic strain were initially produced in response to v1 than to v2 (data not shown). This observation, the result of negative interference, was more pronounced when the v1–v2 distance was small.
When the v1 and v2 strains were the same, there was a high attack rate (0.78) for repeat vaccinees (Table 2, v1–v2 distance = 0). This finding was investigated further with experiments in which the v–e distances were 0, 1, and 3. In these homologous vaccination experiments, repeat vaccinees had higher attack rates than corresponding first-time vaccinees and lower attack rates than corresponding v1-only groups (Fig. 4a).
Historical Analysis.
The Hoskins and Keitel studies reported vaccine and epidemic strains, together with vaccine efficacies in first-time and repeat vaccinees, for each outbreak (Table 3); thus, they can be used to test the antigenic distance hypothesis. Field study data were accepted according to the definitions in ref. 3: first-time vaccinees were defined as individuals vaccinated immediately before the influenza season in which an outbreak occurred, and not vaccinated in the preceding years; repeat vaccinees were defined as individuals vaccinated immediately before the influenza season in which an outbreak occurred, and also vaccinated in one or more consecutive preceding years. Thus for our study, the Hoskins 1976 (H3N2) outbreak was excluded because there was no strict first-time vaccine group (6), and the outbreaks in the first year (1983) of the Keitel study were excluded because there was no strict repeat vaccine group. The antigenic distances among the vaccine and epidemic strains were determined from historical HI assay tables‡‡ kindly provided by the Centers for Disease Control and Prevention, Atlanta. Differences in HI values were scaled to equate them with our measure of antigenic distance†† and are shown in Table 3. Using our model and the HI derived antigenic distances, we predicted the vaccine efficacy for first-time and repeat vaccinees. No attempt was made to tune parameters of the model to fit the Hoskins and Keitel observations.
Table 3.
Vaccine and epidemic strains, antigenic distances among those strains, and observed and predicted vaccine efficacies for the influenza outbreaks reported in the Hoskins and Keitel studies
| Outbreak | Strains
|
Antigenic
distancesa
|
Predicted
VE,b %
|
Observed
VE,b
%
|
Repeat/firstc
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| v1 | v2 | Epidemic (like) | v2–e | v1–e | v1–v2 | First | Repeat | First | Repeat | Predicted | Observed | |
| 1972 (H3N2) | A/HongKong/X31/68d | A/HongKong/1/68Xd | A/England/42/72 | 1.2 | 1.2 | 0.0 | 98 | 72 | 69e | 69e | 0.73 | 1.0 |
| 1974 (H3N2) | A/HongKong/1/68X | A/England/42/72 | A/PortChalmers/1/73 | 3.2 | 4.4 | 1.2 | 17 | 5 | 81 | 32 | 0.29 | 0.40 |
| 1976 (H3N2) | A/PortChalmers/1/73 | A/PortChalmers/1/73 | A/Victoria/3/75 | 2.0 | 2.0 | 0.0 | 67 | 57 | NAf | NAf | 0.85 | ? |
| A/England/42/72g | A/Scotland/840/74g | 4.0 | 4.0 | 4.0 | ||||||||
| 1983 (B) | B/Singapore/222/79h | B/Singapore/222/79 | B/USSR/100/83 | 2.5 | 2.5 | 0.0 | 31 | 16 | 70 | (57)i | 0.52 | (0.81)i |
| 1983 (H1N1) | A/Brazil/11/78h | A/Brazil/11/78 | A/Victoria/7/83 | 0.4 | 0.4 | 0.0 | 99 | 86 | 24 | (81)i | 0.87 | (3.38)i |
| 1984 (H3N2) | A/Phillippines/2/82 | A/Phillipines/2/82 | A/Phillippines/2/82 | 0.0 | 0.0 | 0.0 | 100 | 100 | 65 | 77 | 1.00 | 1.18 |
| 1985 (B) | B/USSR/100/83 | B/USSR/100/83 | B/AnnArbor/1/86 | 0.6 | 0.6 | 0.0 | 99 | 86 | 55 | 56 | 0.87 | 1.02 |
| 1986 (H1N1) | A/Chile/1/83 | A/Chile/1/83 | A/Taiwan/1/86 | 2.0 | 2.0 | 0.0 | 100 | 100 | 72 | 62 | 1.00 | 0.86 |
| A/Taiwan/1/86g | 0.0 | 2.0 | ||||||||||
| 1987 (B) | B/AnnArbor/1/86 | B/AnnArbor/1/86 | B/Victoria/2/87 | 1.8 | 1.8 | 0.0 | 45 | 22 | 100 | 38 | 0.49 | 0.38 |
| 1987 (H3N2) | A/Mississippi/1/85 | A/Leningrad/360/86 | A/Sichuan/2/87 | 3.3 | 3.8 | 1.3 | 17 | 13 | 49 | 46 | 0.76 | 0.94 |
a Antigenic distances were averages over four HI tables. For prediction using the model, which requires integer antigenic distances, real-valued antigenic distances were usually converted by rounding to the nearest integer [see supplemental methods (www.pnas.org)].
b Vaccine efficacy.
c Ratio of vaccine efficacy in repeat vaccinees to efficacy in first-time vaccinees.
d Both strains assumed to be antigenically equivalent to the A/HongKong/8/68 reference strain (see supplemental methods).
e Hoskins et al. (4) reported a single attack rate and saw no significant difference with the number of vaccinations.
f No first-time vaccine group (6) (see main text).
g In 1976 and 1986 two vaccines of the same subtype were given. In these cases the second vaccine strains and antigenic distances are reported on second row of data in the table. In addition, for the 1976 outbreak, the antigenic distances from A/PortChalmers/1/73 to A/England/42/72 and A/Scotland/840/74 were 2 and 2, respectively.
h Likely strains (see supplemental methods).
i No repeat vaccine group (see main text).
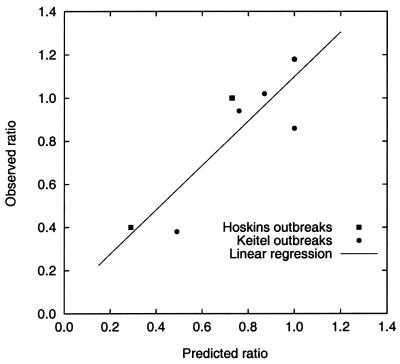
The predictions from the model of vaccine efficacy in repeat vaccinees relative to the efficacy in first-time vaccinees had good correlation (r = 0.87) with that seen in the Hoskins and Keitel studies (Table 3, Figs. 1 and 5). However, the model did not accurately predict absolute vaccine efficacies. Nor was there any correlation between vaccine efficacy in first-time vaccinees and the v2–e distance.
Figure 5.
Predicted and observed vaccine efficacy in repeat vaccinees relative to the efficacy in first-time vaccinees for the outbreaks during the Hoskins and Keitel studies. Correlation 0.87 (P = 0.01); linear regression slope 1.03, intercept 0.07.
Discussion
Our results show that antigenic distances between the first and second vaccines, and between the first vaccine and the epidemic strain, significantly affect attack rates in repeat vaccinees. The model accurately predicted vaccine efficacy in repeat vaccinees, relative to that in first-time vaccinees, for outbreaks during Hoskins and Keitel studies of annual influenza vaccination (Figs. 1 and 5). Thus, the proposed antigenic distance hypothesis offers a parsimonious explanation for the differing observations in the Hoskins and Keitel studies.
In repeat vaccinees, when the v1–v2 distance was small, antibodies produced by the immune response to v1 cross-reacted with v2, eliminating some of v2 before it induced an immune response—a phenomenon we call negative interference. When the v1–e distance was small, antibodies produced by the response to v1 cross-reacted with the epidemic strain and helped clear it—a phenomenon we call positive interference by v1 on the epidemic virus. Thus, attack rates varied in repeat vaccinees depending on the combination of negative and positive interference induced by v1, which in turn depended on the v1–v2 and v1–e distances, respectively. Positive and negative interference are well documented aspects of the cross-reactive immune response (8, 9); in this study we have combined them in a quantitative way to predict vaccine efficacies in first-time and repeat vaccinees.
Homologous Vaccination.
Intuitively, it seems wrong that repeat vaccinees given the same (homologous) vaccine for two successive years could be less protected than first-time vaccinees. However, the model predicts that as the v–e distance increases from 0 to 2, the ratio of vaccine efficacy in repeat vaccinees compared with that in first-time vaccinees will fall monotonically from 1.0 to 0.5. This prediction holds for the four outbreaks in the Hoskins and Keitel studies that were preceded by homologous vaccination (Fig. 4b). Homologous vaccination can result in low vaccine efficacy because it causes maximum negative interference of the first vaccine on the second vaccine, and thus repeat vaccinees are protected only by the positive interference of the first vaccine on the epidemic strain (which depends on the v–e distance).
In two other cases of homologous vaccination [1976 (H3N2) and 1986 (H1N1)], the v–e distance was 2, and thus the model would have predicted poor efficacy in repeat vaccinees. However, in both cases, a second nonhomologous v2 strain was also given and the model predicted approximately equal efficacy in first-time and repeat vaccinees (a good prediction for the 1986 outbreak, and not testable for the 1976 outbreak).
Failure of homologous strain vaccination to boost after 2 weeks (11) and after 6 months (12) has been seen in human trials. We have previously performed simulations, similar to those reported here, but in which antibody levels fell close to zero levels before revaccination (13). In those experiments a homologous revaccination provided good protection. Thus, the results of the model depend on the persistence of antibody and whether that persistence remains above protective levels.
Negative interference of a prior vaccine on a subsequent vaccine has been seen in influenza vaccination in humans (14, 15), as has the preferential production of antibody cross-reactive with the prior vaccine (15, 16). As in the model, the amount of vaccine antigen elimination by preexisting cross-reactive antibody appears to be proportional to the amount of circulating antibody (11, 17).
Historical Analysis.
The ability of the model to predict the ratio of repeat to first-time vaccine efficacies, yet not predict absolute vaccine efficacies, suggests that taking the ratio cancels out a linear factor that affects first-time and repeat vaccinees equally—a factor that has been obscuring the relationship between antigenic distance and vaccine efficacy. This factor (or factors) could be caused by variation in the antigenicity or dose of the vaccine—factors not explored in the current study.
Although the results from the two Keitel study outbreaks in 1983 were excluded from the statistical testing of the hypothesis, the differences between the predicted and observed ratios for these outbreaks support the hypothesis. The outbreaks were excluded because although repeat vaccinees received v1 sometime within the 3 years preceding the study, not all of them had received v1 in the fall of 1981. This would allow antibody levels to decrease before vaccination in the fall of 1982. Lower antibody levels would decrease the negative interference of v1 on v2, and thus favor repeat vaccinees (as was seen). The extreme 4-fold favoring of repeat vaccinees in the 1983 (H1N1) outbreak also supports the hypothesis: The vaccine (A/Brazil/11/78) appears to have been of low antigenicity (observed vaccine efficacy in first-time vaccinees was only 21%) and antibody persistence was less than for concomitant H3N2 and B vaccination (12). Thus negative interference would be likely to be low, and a repeat homologous vaccination would produce a more classic secondary response with high antibody titers, and thus be highly effective (as was seen).
In the Hoskins study it was found that boys who had confirmed influenza infection were better protected against subsequent outbreaks than boys who had not been infected (but who had been vaccinated). The results from the model offer a potential explanation. In the model, antibody levels after the epidemic challenge were different, depending on whether the experimental challenge caused disease. If the challenge caused disease, the antibody levels cross-reactive with the epidemic strain were at least 3-fold higher than after a primary or secondary vaccination (Fig. 3a)—in the model this was due to the antigen stimulating the immune system for a longer time, leading to more plasma cells and antibodies being produced. Thus, antibody levels to the epidemic virus remained higher for longer, and would be protective for longer, than the lower antibody levels in response to vaccination. Conversely, when the epidemic virus was cleared quickly it had little effect on antibody levels (Fig. 3 b and c); thus, we would expect it to have little influence on future protection.
In the model, repeat vaccinees received only two vaccinations, and were exposed to a single experimental epidemic challenge after the second vaccination. However, in both the Hoskins and Keitel studies, some repeat vaccinees were vaccinated more than twice, and individuals might have been exposed to epidemic challenge multiple times; yet the model still made good predictions. This observation suggests that the last two vaccinations are the most important in determining efficacy in repeat vaccinees.
Vaccine Design.
One focus of influenza vaccine strain selection is the selection of a strain that will be close to the (unknown) upcoming epidemic strain. The antigenic distance hypothesis supports this strategy, and adds the following: If there is a choice among otherwise equivalent strains (i.e., strains thought to be equally good guesses of the upcoming epidemic strain and equally appropriate for manufacture), then choosing the strain farthest from the previous vaccine strain would reduce the effects of negative interference and thus potentially increase vaccine efficacy in repeat vaccinees.
Vaccine design strives for persistent high antibody titer and persistent cellular memory. However, this may not be the optimal strategy if the pathogen is antigenically variable and revaccination is necessary. In the case of annual influenza vaccination, if the antibody titer is high for more than a year then it has the potential to negatively interfere with a subsequent revaccination. One option to overcome negative interference would be to increase the vaccine dose; although this could work for one influenza season, the strategy has the danger of resulting in high antibody levels that would increase negative interference in subsequent years. An alternate, counter-intuitive, option would be to design vaccines in which the vaccine specific antibody titer remained high only during the influenza season, and then decreased substantially before revaccination, thus lowering the potential negative interference on subsequent vaccinations.
Skipping vaccination for a year would be another method to allow antibody titers to fall and thus reduce negative interference in the following year. However, while skipping vaccination might benefit repeat vaccinees in the following year, they would suffer in the year they skipped because, even though some repeat vaccination groups in our experiments had significantly higher attack rates than the first-time vaccination group, they still had a lower attack rate than groups that skipped the second vaccination (Table 2).
Summary.
The antigenic distance hypothesis, as tested by comparing the predictions from a computer model to seven influenza outbreaks observed in the Hoskins and Keitel studies, accurately predicted the year-to-year variation in vaccine efficacy of repeat vaccinees relative to that in first-time vaccinees. The hypothesis suggests considering antigenic distance to the previous year’s vaccine strain as part of the vaccine strain selection process, a refinement that has the potential to increase the vaccine efficacy in repeat vaccinees. The methods presented here may also have application to vaccination strategies for other antigenically variable pathogens requiring multiple vaccinations for protection.
Supplementary Material
Acknowledgments
We thank Nancy Arden, Nancy Cox, Henrietta Hall, Ron Hightower, Pentti Kanerva, Jacqueline Katz, Alexander Klimov, Stan Lee, Mihaela Oprea, Francesca Shrady, Paul Stanford, and Bernhard Sulzer. This work was supported by the Office of Naval Research (N00014-95-1-0364, N0014-99-1-0417), the National Science Foundation (IRI-9157644, IRI-9711199), the National Institutes of Health (AI28433), the Joseph P. and Jeanne M. Sullivan Foundation, the Santa Fe Institute, and the Laboratory Directed Research and Development Program of Los Alamos National Laboratory. Portions of this work were performed under the auspices of the U.S. Department of Energy.
Abbreviation
- HI
hemagglutination inhibition
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
Some groups are not possible–e.g., a v1–e distance of 7, a v2–e distance of 2, and a v1–v2 distance of 1.
Experimental challenge of each simulated individual with a large dose of epidemic virus gives higher attack rates than those observed in influenza vaccine field trials.
Assays such as the HI assay implicitly take into account affinity as well as concentration of antibody. This fact is useful in assessing the effectiveness of antibody to clear an antigen. Thus, the antibody levels in Fig. 3 have been weighted by affinity; the details are described in the supplemental material (www.pnas.org).
The HI assay measures the ability of ferret antibodies, raised in response to one influenza strain, to inhibit a second influenza strain from agglutinating red blood cells.
Because the HI assay measures titers, we assume that the difference between log2 of HI values is equivalent to antigenic distance [details in supplemental methods (www.pnas.org)]. For example, a 2-fold difference in HI values is assumed equivalent to antigenic distance 1, and an 8-fold difference, antigenic distance 3.
References
- 1.Centers for Disease Control and Prevention. Morbid Mortal Wkly Rep. 1999;48(RR-4):1–28. [Google Scholar]
- 2.Gross P A, Herrington D, Sachs H S, Laufer J, Levandowski R A. Ann Intern Med. 1995;123:518–527. doi: 10.7326/0003-4819-123-7-199510010-00008. [DOI] [PubMed] [Google Scholar]
- 3.Beyer W E P, DeBruijn I A, Palache A M, Westendorp R G J, Osterhaus A D M E. Arch Intern Med. 1999;159:182–188. doi: 10.1001/archinte.159.2.182. [DOI] [PubMed] [Google Scholar]
- 4.Hoskins T W, Davis J R, Smith A J, Miller C L, Allchin A. Lancet. 1979;i:33–35. doi: 10.1016/s0140-6736(79)90468-9. [DOI] [PubMed] [Google Scholar]
- 5.Keitel W A, Cate T R, Couch R B, Huggins L L, Hess K R. Vaccine. 1997;15:1114–1122. doi: 10.1016/s0264-410x(97)00003-0. [DOI] [PubMed] [Google Scholar]
- 6.Beyer W E P, DeBruijn I A, Westendorp R G J, Osterhaus A D M E. Vaccine. 1998;16:1929–1932. doi: 10.1016/s0264-410x(98)00123-6. [DOI] [PubMed] [Google Scholar]
- 7.Perelson A S, Oster G F. J Theor Biol. 1979;81:645–670. doi: 10.1016/0022-5193(79)90275-3. [DOI] [PubMed] [Google Scholar]
- 8.Davenport F M, Hennessy A V, Francis T. J Exp Med. 1953;98:641–656. doi: 10.1084/jem.98.6.641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fazekas de St. Groth S, Webster R G. J Exp Med. 1966;124:347–361. doi: 10.1084/jem.124.3.347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Smith D J, Forrest S, Hightower R R, Perelson A S. J Theor Biol. 1997;189:141–150. doi: 10.1006/jtbi.1997.0495. [DOI] [PubMed] [Google Scholar]
- 11.Hobson D, Baker F A, Curry R L. Lancet. 1973;ii:155–156. doi: 10.1016/s0140-6736(73)93106-1. [DOI] [PubMed] [Google Scholar]
- 12.Powers R D, Hayden F G, Samuelson J, Gwaltney J M., Jr J Med Virol. 1984;14:169–175. doi: 10.1002/jmv.1890140211. [DOI] [PubMed] [Google Scholar]
- 13.Smith D J, Forrest S, Ackley D H, Perelson A S. In: Artificial Immune Systems and Their Applications. Dasgupta D, editor. Berlin: Springer; 1998. pp. 144–153. [Google Scholar]
- 14.Howells C H L, Evans A D, Vessilinova-Jenkins C. Lancet. 1973;i:1436–1438. doi: 10.1016/s0140-6736(73)91755-8. [DOI] [PubMed] [Google Scholar]
- 15.Masurel N, Ophof P, deJong P. J Hyg (London) 1981;87:201–209. doi: 10.1017/s0022172400069412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Webster R G, Kasel J A, Couch R B, Laver W G. J Infect Dis. 1976;134:48–58. doi: 10.1093/infdis/134.1.48. [DOI] [PubMed] [Google Scholar]
- 17.Robinson H L, Boyle C A, Feltquate D M, Morin M J, Santoro J C, Webster R G. J Infect Dis. 1997;176,(Suppl. 1):50–55. doi: 10.1086/514176. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.