Abstract
We review recent experiments examining whether simple models of the allocation and persistence of operant behavior are applicable to attending. In one series of experiments, observing responses of pigeons were used as an analog of attending. Maintenance of observing is often attributed to the conditioned reinforcing effects of a food-correlated stimulus (i.e., S+), so these experiments also may inform our understanding of conditioned reinforcement. Rates and allocations of observing were governed by rates of food or S+ delivery in a manner consistent with the matching law. Resistance to change of observing was well described by behavioral momentum theory only when rates of primary reinforcement in the context were considered. Rate and value of S+ deliveries did not affect resistance to change. Thus, persistence of attending to stimuli appears to be governed by primary reinforcement rates in the training context rather than conditioned reinforcing effects of the stimuli. An additional implication of these findings is that conditioned “reinforcers” may affect response rates through some mechanism other than response-strengthening. In a second series of experiments, we examined the applicability of the matching law to the allocation of attending to the elements of compound stimuli in a divided-attention task. The generalized matching law described performance well, and sensitivity to relative reinforcement varied with sample duration. The bias and sensitivity terms of the generalized matching law may provide measures of stimulus-driven and goal-driven control of divided attention. Further application of theories of operant behavior to performance on attention tasks may provide insights into what is referred to variously as endogenous, top-down, or goal-directed control of attention.
Keywords: Attention, observing, matching law, behavioral momentum, conditioned reinforcement
1. Introduction
Problems in the allocation and persistence of attention are involved in many psychological disorders. For example, attention is too easily disrupted in those with Attention-Deficit/Hyperactivity Disorder (ADHD; American Psychiatric Association, 1994). In addition, persistent misallocation of attention has been identified in people with schizophrenia (Nestor & O’Donnell, 1998), and as been implicated in educational difficulties with the developmental disabled (i.e., stimulus overselectivity; Dube & McIlvane, 1997; Lovaas, Koegel, & Shreibman, 1979). Finally, persistent and problematic attentional biases to drug cues have been noted with drug abusers (e.g., Ehrman et al., 2002; Johnsen, Laberg, Cox, Vaksdal, & Hugdahl, 1994; Lubman, Peters, Mogg, Bradley, & Deakin, 2000; Townshend & Duka, 2001).
Attention is widely recognized to be governed in part by both stimulus features and the goals of the organism (see Yantis, 2000, for review). In addition, the deployment of attention is considered to be a skill modifiable by experience (e.g., Gopher, 1992). Thus, an understanding of the impact of reinforcement variables on the allocation and persistence of attention may help to suggest improved behavioral interventions for the psychological disorders noted above. Recently, we have been examining the applicability of quantitative models of operant behavior like the matching law and behavioral momentum theory to the allocation and persistence of attending.
In one series of experiments (Section 2 below), we used observing responses of pigeons as an analog of attending. Observing responses bring sensory receptors into contact with stimuli to be discriminated and have long been considered an analog of attending (Wyckoff, 1952). In the typical procedure used to study observing responses, periods in which food is available for a response on some schedule of reinforcement alternate with periods in which the response is not reinforced and food is never available (i.e., extinction). During each session, these alternating periods of food availability versus extinction are not signaled. Observing responses (e.g., pecks on a second key) produce brief discriminative stimuli signaling whether food is available (i.e., S+) or not (i.e., S−). Below we review experiments examining the applicability of the matching law (Section 2.2) and behavioral momentum theory (Section 2.3) to observing behavior. Observing behavior is generally believed to be maintained by the conditioned reinforcing properties of S+ presentations, thus along the way we will examine the implications of these experiments for an understanding of conditioned reinforcement in general.
In a second series of experiments (Section 3 below), we examined the applicability of the generalized matching law to the allocation of attention in a divided attention task. In this task, pigeons are presented with compound samples comprised of a combination of two elements (i.e., a color and a line orientation) and single-element comparison stimuli (i.e., two colors or two line orientations) in a delayed-matching-to-sample procedure. Accurate performance requires attending to both elements of the compound stimuli. We apply the generalized matching law to changes in performance associated with variations in the relative rates of reinforcement for attending to the elements of the compound samples.
2. Observing Responses
2.1. Observing and the Matching Law
First, we examine the applicability of the matching law to changes in absolute rates of observing produced by changes in the rate of primary reinforcement signaled by an S+. Herrnstein’s (1970) single-response version of the matching law states that:
| (1) |
where B is the absolute rate of a target response, R is the rate of reinforcement, and the parameters k and Re correspond to asymptotic response rates and extraneous sources of reinforcement, respectively. To examine the applicability of Equation 1 to observing behavior we reanalyzed data from an experiment presented in Shahan (2002, Experiment 4). The experiment examined the effects of varying the rate of 10% sucrose deliveries on rats’ observing behavior. Sucrose deliveries were arranged on a variable-time (VT) schedule that alternated with periods of extinction. The VT and extinction periods were unsignaled in the absence of observing responses. Each response to an observing lever produced 15-s of access to stimuli correlated with the VT sucrose (i.e., S+) and extinction periods (i.e., S−). The value of the VT schedule was varied across conditions such that the rate of sucrose delivery ranged from 7.2 to 240 per hour. Figure 1 shows the fits of Equation 1 to the data of four rats. Equation 1 did a good job of describing increases in observing rates with increases in the rate of primary reinforcement and accounted for between 79 and 96 percent of the variance. Thus, the absolute response-rate version of the matching law appears to provide a good description of changes in observing behavior with changes in the rate of primary reinforcement signaled by an S+.
Figure 1.
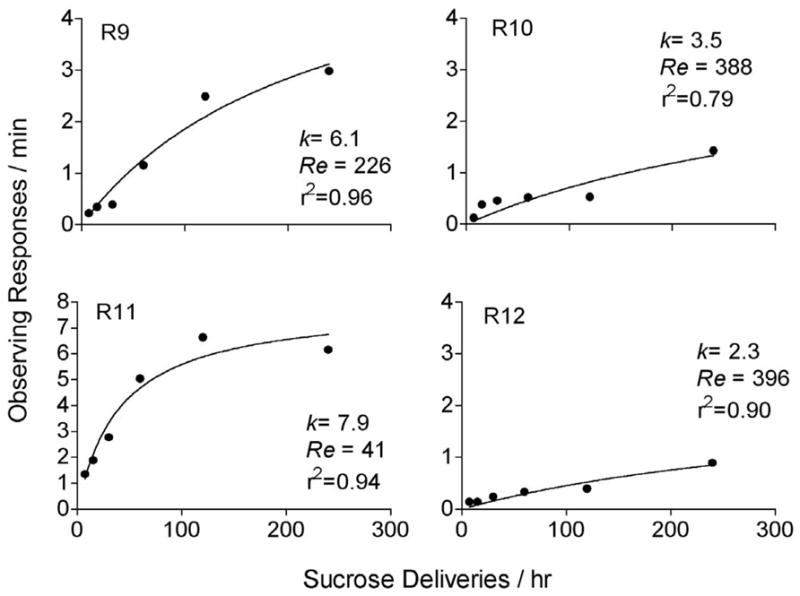
Reanalysis of rats observing as a function of the rate of primary reinforcement associated with an S+ in Shahan (2002). Regressions of Equation 1 and the resultant parameters are shown in each panel.
Second, an experiment by Shahan, Podlesnik, and Jimenez-Gomez (2006) examined the applicability of the generalized matching law to changes in the allocation of two observing responses with changes in the relative rate of S+ delivery (i.e., conditioned reinforcement rate). The generalized matching law (Baum, 1974, 1979) suggests that the ratio of responses at two options is a power function of the ratio of reinforcers obtained at those options. In its logarithmic form that is:
| (2) |
where B1 and B2 are the two responses and R1 and R2 are reinforcers obtained from the two responses. The parameters a and log c represent sensitivity of the behavior ratio to variations in the reinforcement ratio and bias unrelated to variations in the reinforcement ratio, respectively.
Shahan et al. (2006) used a concurrent observing-response procedure with pigeons to vary the relative rate of S+ presentation. Unsignaled periods of a variable-interval (VI) 90-s schedule of primary reinforcement alternated with extinction on a center key (i.e., a mixed schedule of reinforcement). Responses to two observing keys produced 15-s periods of S+ if the VI 90 was in effect on the food key. The ratio of S+ delivery rates on the two observing keys was varied across conditions by changing the VI schedules of S+ delivery on the observing keys. The ratios of S+ deliveries examined were 1:9 (VI 100, VI 11.1), 1:3 (VI 40, VI 13.3), 1:1 (VI 20, VI 20), 3:1 (VI 13.3, VI 40), and 9:1 (VI 11.1, VI 100). Importantly, the overall rate of primary reinforcement remained constant with variations in the relative rate of S+ deliveries. Moreover, the value of S+ deliveries remained constant because the ratio of primary reinforcement obtained in S+ to that obtained in the presence of the non-differential mixed-schedule stimuli remained constant across conditions (see Shahan et al. for more discussion). Figure 2 shows the fits of Equation 2 to the data for the four pigeons with obtained S+ delivery rates for the two observing responses used for R1 and R2. Equation 2 accounted for between 91 and 97 percent of the variance across subjects. Thus, the generalized matching law provides a good account of changes in the allocation of two observing responses with changes in the relative rate of S+ delivery associated with those responses.
Figure 2.
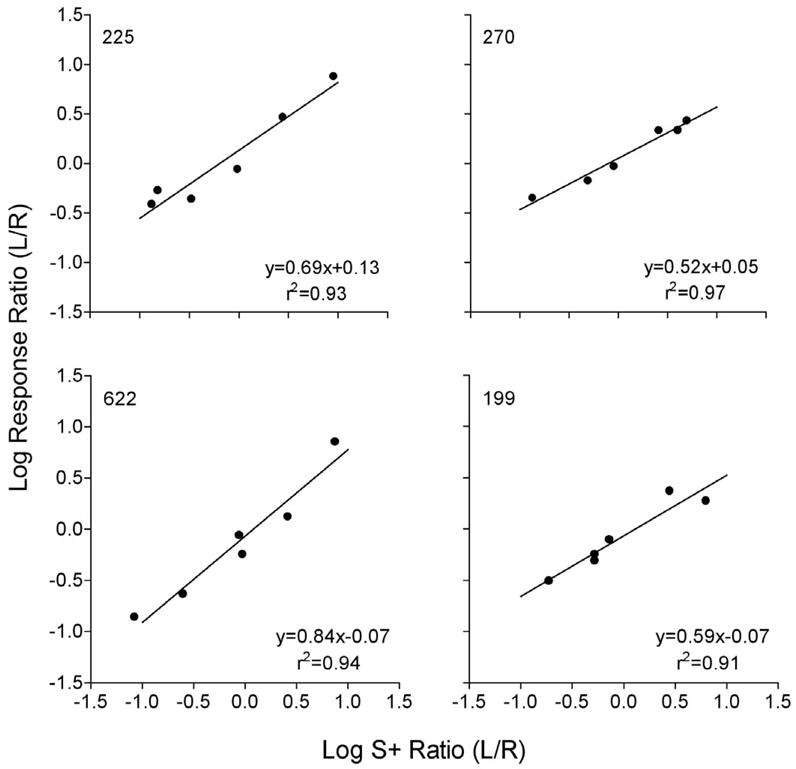
Generalized matching law analysis of changes in the relative allocation of two concurrent observing responses with changes in the relative rate of S+ presentation produced by those responses. Regressions of Equation 2 and the resultant parameters are shown in each panel. The figure is reprinted from Shahan et al. (2006).
To the extent that observing responses are analogous to attending, the concurrent observing-response procedure might be considered a method to study divided attention (i.e., the allocation of attention to two potential sources of stimuli). From this perspective, the present results suggest that the generalized matching law may be useful for describing how attention is allocated when the relative frequency of important signals of forthcoming reinforcement is varied at two locations (cf. Schroeder and Holland, 1969). In Section 3 below we present an alternative approach to studying the applicability of the generalized matching law to divided-attention performance.
2.1.1. Implications for General Choice Theories
The findings of Shahan et al. (2006) also may have implications for our understanding of the role of conditioned-reinforcement rate in general choice theories. Variations in the relative rates of S+ delivery represent variations in the relative rate of conditioned reinforcement. The mean sensitivity value (i.e., a in Equation 2) obtained by Shahan et al. using the concurrent observing-response procedure was 0.66. This value is very close to sensitivities obtained when relative rates of conditioned reinforcement are varied in concurrent-chains procedures by changing relative initial-link values (e.g., Berg and Grace, 2004; Davison, 1983). However, variations in relative rates of terminal-link entry in concurrent-chains schedules are confounded with changes in relative rates of primary reinforcement for the two options. In fact, the interdependent nature of conditioned and primary rates of reinforcement in concurrent chains is formalized in Delay Reduction Theory (DRT; Squires and Fantino, 1971). Specifically, DRT states that:
| (3) |
where B1 and B2 are response rates in the two initial links, R1 and R2 are the rates of primary reinforcement associated with the responses, Ttotal is the overall average delay to reinforcement, and Tt1 and Tt2 are the delays to reinforcement signaled by the onset of the terminal links. DRT includes no role for rate of conditioned reinforcement (i.e., terminal-link entry rate) and attributes the effects of variations in relative initial-link durations to changes in relative primary reinforcement rates or conditioned reinforcement value. The observing-response procedure used by Shahan et al. produced matching to relative rates of conditioned reinforcement in the absence of both changes in primary reinforcement rate and in the conditioned-reinforcing value of S+ deliveries. Thus, the results of Shahan et al. appear to be inconsistent with DRT.
Fantino and Romanowich (2007) argued, however, that the Shahan et al. (2006) data were not inconsistent with DRT because DRT reduces to the matching law when simple VI schedules are used. The conditioned reinforcers in Shahan et al. were indeed presented on simple VI schedules, but the same is true of terminal-link stimulus presentations in concurrent-chains schedules. Thus, it is unclear why variations in conditioned reinforcement rate should not be expected to similarly impact choice in concurrent chains. As noted by Fantino, Freed, Preston, and Williams (1991), DRT makes the odd suggestion that terminal-link stimuli in concurrent-chains are conditioned reinforcers, but variations in their frequency of presentation do not directly impact behavior.
Fantino and Romanowich (2007) also reviewed experiments using a variety of methods to examine the impact of changes in conditioned reinforcement rate on preference in concurrent chains. Many of the studies reviewed examine the impact of arranging additional unreinforced terminal-link stimulus presentations or including additional food-paired stimuli in the terminal links. Based on their review, Fantino and Romanowich concluded that rates of conditioned reinforcement do not affect preference in concurrent chains, an outcome they describe as “not surprising since the additional conditioned reinforers in the terminal links are not correlated with a reduction in time to primary reinforcement or with an increase in value”. Their conclusion succinctly summarizes one major difficulty with examining the effects of conditioned reinforcement rate on choice using concurrent-chains procedures; adding such additional unreinforced stimuli decreases the value of the stimuli, perhaps to the point that they do not function as conditioned reinforcers at all (see also Mazur, 1999).
Fantino and Romanowich also discussed an alternative approach to examining the role of conditioned reinforcement rate in concurrent-chains performance used by Fantino et al. (1991). Fantino et al. examined the effects of increasing the rate of terminal link entry for one option (i.e., decreasing one initial link) with both concurrent-chains and concurrent-tandem (i.e., unsignaled terminal links) schedules. DRT posits no role for conditioned reinforcement rate, thus it predicts that decreasing one of the initial links should impact concurrent-chains and concurrent-tandem performance similarly because the confounded change in primary reinforcement rate is the same for both procedures. Although the experiments supported the predictions of DRT, Fantino et al. noted the difficulty associated with knowing how to scale the value of the conditioned reinforcing effects of the terminal-link stimuli relative to the confounded changes in primary reinforcement. They also noted that it was difficult to know whether any effects of conditioned reinforcement rate were overpowered by the confounded changes in primary reinforcement rate. Thus, it is difficult to definitively conclude that variations in conditioned reinforcement rate do not impact preference based on such procedures.
One can conclude, as did Fantino and Romanowich, that “theories of concurrent chains schedules [italics added] need not include a term reflecting greater preference for higher rates of conditioned reinforcement”, but only because it is difficult to show independent effects of conditioned reinforcement rate in concurrent-chains procedures (but see Berg and Grace, 2004). In addition, it does not seem desirable in our opinion to develop theories of performance on a particular procedure like concurrent-chains schedules, but more general-process oriented theories. One purpose of the Shahan et al. (2006) experiment was to approach the question of the effects of conditioned reinforcement rate on choice using an alternative procedure.
The finding in Shahan et al. (2006) that rates of conditioned reinforcement impact preference in a manner consistent with the matching law is consistent with general choice theories based on the concatenated matching law (e.g., contextual choice model, Grace, 1994; hyperbolic value-added model, Mazur, 2001). Such theories include a role for both relative rate of conditioned reinforcement (i.e., relative terminal-link entries) and relative value of conditioned reinforcement, but differ in how they characterize value. Fantino and Romanowich (2007) noted that DRT could easily be modified to incorporate the effects of conditioned reinforcement (see also Fantino, Preston, and Dunn, 1993; Luco, 1990). Luco (1990) examined such a model in which relative conditioned reinforcement rate is substituted for overall primary reinforcement rate in Equation 3. However, he found that the model performed poorly with existing data sets, especially when relative terminal-link entry rates varied. The model examined by Luco did not include free parameters, thus it remains to be seen how such a model would fare when provided with parameters paralleling those used in the contextual choice and hyperbolic value-added models. It also remains to be seen how such a modified version of DRT would perform with the variety of other phenomena previously captured by DRT as expressed in Equation 3 above.
The discussion above about general choice theories, based largely on data from concurrent-chains schedules, raises two questions for us. First, would phenomena widely studied with concurrent-chains schedules (e.g., initial- and terminal-link effects) also be obtained using the concurrent observing-response procedure? Second, given that our use of the observing-response procedure in the experiments above was based on the notion that observing responses provide an analog of attending to important stimuli, what are the implications of general choice theories and the large body of data from concurrent-chains schedules for our understanding of attention?
2.2. Observing and Behavioral Momentum Theory
Using observing responses as an analog of attending, we also have been examining the applicability of behavioral momentum theory to the persistence of attending under conditions of disruption. Again, because observing responses are believed to be maintained by the conditioned-reinforcing effects of S+ presentations, these experiments also have implications for our understanding of conditioned reinforcement and for the applicability of behavioral momentum theory to responding maintained by conditioned reinforcement. Although a large body of research has been directed at examining the resistance to change of responding maintained by primary reinforcement, little research has examined resistance to change of responding maintained by conditioned reinforcement.
A reliable outcome of experiments on resistance to change is that resistance to disruption is greater in the presence of multiple-schedule stimuli associated with higher rates or magnitudes of primary reinforcement (see Nevin and Grace, 2000, for review). Behavioral momentum theory provides a framework for describing the effects of differential reinforcement conditions on resistance to change. Specifically, the theory suggests that response rates and resistance to change are separable aspects of operant behavior (Nevin, 1992; Nevin & Grace, 2000; Nevin et al., 1983). The response-reinforcer relation governs response rate, but the Pavlovian stimulus-reinforcer relation governs resistance to change. The Pavlovian stimulus-reinforcer relation refers to the relationship between a stimulus in the presence of which a response occurs and the reinforcers obtained in the presence of that stimulus. From the perspective of behavioral momentum theory, resistance to change provides a more appropriate measure of response strength than response rates. This perspective is supported by experiments showing that adding response-independent reinforcers to one component of a multiple schedule decreases response rates but increases resistance to change. (e.g., Ahern et al., 2003; Cohen, 1996; Grimes and Shull, 2001; Harper, 1999; Mace et al., 1990; Nevin et al., 1990; Shahan and Burke, 2004; Podlesnik & Shahan, 2008). Although the added reinforcers decrease response rates by degrading the response-reinforcer relation, they increase response strength as measured by resistance to change by improving the Pavlovian stimulus-reinforcer relation.
Quantitatively, behavioral momentum suggests that relative resistance to change is a power function of the relative rates of reinforcement obtained in the two components of a multiple schedule. Specifically, Grace and Nevin (1997; see also Nevin, 2002) suggested the following equation:
| (4) |
where Bo and Bx are response rates during baseline and disruption, R is reinforcement rate, and the subscripts correspond to the two components of a multiple schedule. The parameters a and log b represent sensitivity of relative resistance to relative reinforcement rates and bias in relative resistance unrelated to relative reinforcement rates, respectively.
In what follows, we will first provide a brief description of the methods and findings from a number of experiments we have conducted examining the resistance to change of observing behavior. Next, we will use Equation 4 to provide a quantitative summary of the effects of conditioned reinforcement and primary reinforcement on resistance to change of observing. Finally, we will further explore the implications of these findings for an understanding of conditioned reinforcement and attention.
2.2.1. Description of Experiments and Results
Shahan, Magee, and Dobberstein (2003) examined resistance to change of observing using a multiple schedule of observing-response procedures. A separate observing-response procedure was arranged in each of two components of a multiple schedule. In both components, unsignaled periods of primary reinforcement on a random-interval (RI) schedule alternated with periods of extinction on a food key. Observing responses produced stimuli correlated with the RI (i.e., S+) and extinction (i.e., S−) periods. The RI schedules in the two observing-response components arranged different rates of primary reinforcement. As a result, the S+ produced by observing responses in one component was associated with a higher rate of primary reinforcement than the S+ in the other component. Consistent with the data from Shahan (2002) presented in Figure 1 above, observing rates were higher in the component arranging the higher rate of primary reinforcement. In addition, observing was more resistant to disruption by presession feeding and extinction in the component arranging the higher rate of primary reinforcement. Shahan et al. suggested that the greater resistance to change of observing in the component with the higher rate of primary reinforcement might be attributable to the greater conditioned reinforcing value of the S+ in that component. In addition, Shahan et al. suggested that behavioral momentum theory appeared to be applicable to observing/attending with little modification.
Two experiments by Shahan and Podlesnik (2005) examined the impact of different rates of conditioned reinforcement on observing rates and resistance to change using a similar multiple schedule of observing-response procedures. Different rates of conditioned reinforcement were arranged by scheduling S+ deliveries on different VI schedules in the two components. The programmed rate of primary reinforcement was the same in the two components. The first experiment examined a four-fold difference in conditioned reinforcement rates and the second experiment examined a six-fold difference in conditioned reinforcement rate. Consistent with the Shahan et al. (2006) matching experiment presented in Figure 2 above, observing rates in both experiments were higher in the component with the higher rate of conditioned reinforcement. Despite the difference in response rates in the two components, rates of conditioned reinforcement had no impact on resistance to disruption by presession feeding, intercomponent food deliveries, or extinction of observing. In fact, in the second experiment, resistance to change was somewhat greater in the component arranging the lower rate of conditioned reinforcement. However, the extreme parameters of the second experiment resulted in a somewhat higher obtained rate of primary reinforcement in that component. Thus, conditioned reinforcement rate appeared to have no impact on resistance to change. Resistance to change of observing only differed when there was a difference in primary reinforcement rates. This finding led Shahan and Podlesnik to speculate that parameters of conditioned reinforcement might have no impact on resistance to change.
In a recent series of three experiments, Shahan and Podlesnik (in press) examined the effects of conditioned reinforcement value and primary reinforcement rate on resistance to change. Each of the experiments used pigeons responding on a multiple schedule of observing-response procedures.
In the first experiment, the conditioned reinforcing value of S+ deliveries was higher in one component, but the rate of primary reinforcement was higher in the other. The component with the lower-valued conditioned reinforcer but higher primary reinforcement rate was arranged by including extra response-independent food deliveries uncorrelated with the conditions of reinforcement signaled by S+. Figure 3 shows a schematic of the procedure. In both components, a VI 60-s schedule of food reinforcement alternated with extinction on the food key. Observing response during the VI 60 periods in both components produced S+ deliveries on a VI 15-s schedule. In one component, VT food deliveries could occur during the mixed-schedule or during S+ presentations. Although the VT food deliveries increased primary reinforcement rate, they would be expected to decrease the conditioned-reinforcing value of S+ deliveries by reducing their predictive relation to food. Thus, we will refer to the components with and without the added food deliveries as the Low-Value and High-Value components, respectively. The results showed that observing rates were either equal in the two components or higher in the High-Value component. On the other hand, resistance to disruption by presession feeding and extinction was higher in the Low-Value component in which the higher rate of primary reinforcement was arranged.
Figure 3.
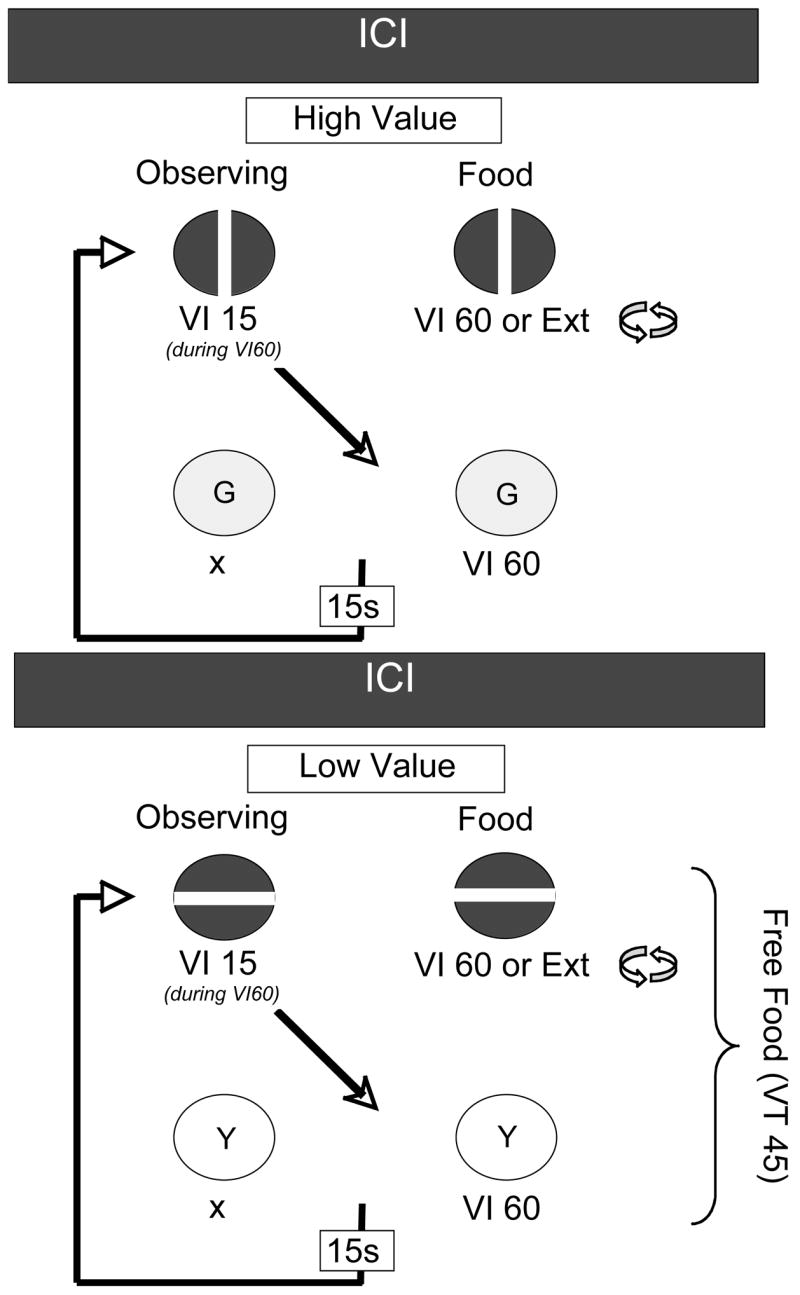
Schematic of the multiple-schedule of observing-response procedures used by Shahan and Podlesnik (in press). ICIs refer to intercomponent interval. Other details available in the text.
The second experiment also placed conditioned-reinforcement value and primary reinforcement rate in opposition to one another using a different method. The same basic multiple schedule of observing response procedures was used as shown in Figure 3 above, except that the VT food deliveries were absent, and the periods of VI food reinforcement and extinction on the food key were arranged probabilistically as opposed to strictly alternating. In one component, VI 30-s food periods occurred with p=.6 (i.e., Low-Value component) and in the other component with p=.1 (i.e., High-Value component). Previous experiments using observing responses and related procedures have shown that observing is an asymmetrical inverted U-shaped function of probability of reinforcement period (e.g., McMillian 1974). Thus, increases in the probability of reinforcement period above.5 produce decreases in observing. Decreases in the probability of reinforcement period below.5, however, first produce an increase and then a decrease in observing at lower probabilities (see also Eckerman, 1973; Hendry, 1965; Kendall, 1973; McMicheal, Lanzetta, & Driscoll, 1967; Wilton & Clements, 1971). These initial effects of decreases in the probability of a reinforcement period are often attributed to an increase in the conditioned-reinforcing effects of S+ (see Dinsmoor, 1983; Fantino, 1977, for reviews). The reason why value of S+ deliveries is thought to increase is that S+ signals a relatively larger improvement in primary reinforcement rate (or reduction in delay to primary reinforcement) when the probability of a reinforcement period is lower. With more probable reinforcement periods, like in the Low-Value component here, the value of S+ is lower because the primary reinforcement rate in the mixed schedule is closer to that arranged during S+. Interestingly, decreases in the probability of a reinforcement period increase observing rates despite the fact that they also decrease both overall primary reinforcement rates and rates of S+ delivery (i.e., conditioned reinforcement rate).
As expected, obtained overall primary reinforcement rates (i.e., based on total foods and time during both S+ and the mixed schedule) and mixed-schedule primary reinforcement rates (i.e., based on reinforcers and time during mixed schedule only) were higher in the Low-Value component than in the High-Value component in our experiment. In addition, rates of S+ delivery were lower in the High-Value component than in the Low-Value component. Value of S+ deliveries in two components may be estimated by calculating the ratio of reinforcement rates during S+ to those during the mixed-schedule. A higher ratio corresponds to a greater signaled improvement in primary reinforcement rate associated with the onset of S+. Based on the obtained primary reinforcement rates, S+ value in the High- and Low-Value components in baseline conditions was 20 (2/0.1 rein per min) and 2.1 (1.9/0.9 rein per min), respectively.
The results showed that observing rates were higher in the High-Value component than in the Low-Value component, despite the fact that rates of primary reinforcement and S+ delivery were higher in the Low-Value component. As in the first experiment above, however, resistance to change as assessed by a variety of disrupters was greater in the Low-Value component. Thus, regardless of the impact of conditioned-reinforcement value on baseline response rates, resistance to change was governed by rates of primary reinforcement. The Shahan and Podlesnik (2005) experiments above showed that rates of S+ delivery do not impact resistance to change when rates of primary reinforcement are similar. Thus, it is unlikely the higher rate of S+ delivery in the Low-Value component was responsible for the present results. Nonetheless, it remains possible that any impact of conditioned-reinforcement value in these experiments was counteracted by the considerably higher rates of primary reinforcement in the Low-Value components.
In a final experiment, we examined the effects of differences in conditioned- reinforcement value when overall rates of primary reinforcement were similar. The procedure was the same as the previous experiment except that the VI schedule of food delivery alternating with extinction differed for the two observing-response components. Specifically, in the Low-Value component periods of VI 51.43-s food reinforcement occurred with p=.6 and extinction periods occurred with p=.4. In the High-Value component, periods of VI 8.57-s food reinforcement occurred with p=.1 and extinction periods occurred with p=.9. Thus, the programmed rate of primary reinforcement in both components was 0.7 foods/min [i.e., food/min = 60/(VI value/p of VI period)]. Obtained value of S+ (i.e., S+/mixed schedule rein per min) was 2.2 (1.1/0.5 rein per min) in the Low-Value component and 13.8 (5.5/0.4 rein per min) in the High-Value component.
As in the previous experiments, observing-response rates were higher in the High-Value component than in the Low-Value component. Nonetheless, there was some tendency for resistance to change of observing to be greater in the Low-Value component, although there were a number of exceptions. Thus, even when rates of primary reinforcement were similar in the two components, the value of S+ deliveries appears not to impact resistance to change. Obtained rates of primary reinforcement were slightly higher in the Low-Value component (i.e., 0.68 rein/min) than in the High-Value component (i.e., 0.57 rein/min), and this difference may have contributed to the sometimes greater resistance to change in the Low-Value component. However, the difference in primary reinforcement rates was small and the resistance to change data were not consistent. As a result, it seems unlikely that differences in primary reinforcement rate were overpowering any effects of S+ value on resistance to change.
2.2.2. Quantitative Summary of Resistance to Change Results
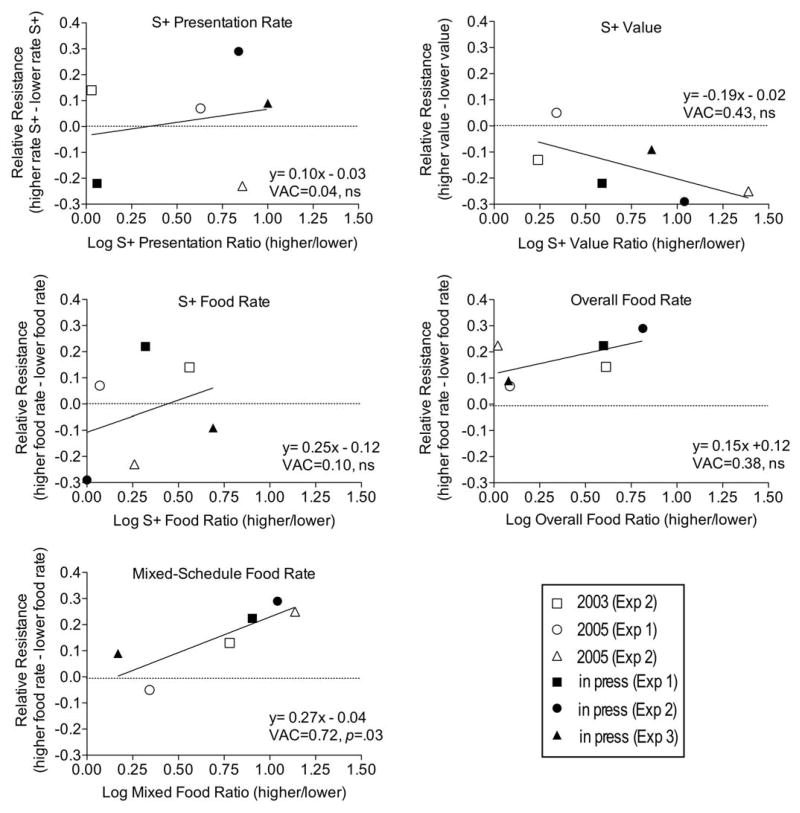
We will use Equation 4 to provide a summary of the results of the experiments on resistance to change of observing described above. In applying the equation to the data of the experiments, we have collapsed the data across subjects and disruptors for each of the experiments. Figure 4 shows relative resistance to change as a function of the reinforcement ratio arranged by the two observing-response components. The panels differ in what they used for the reinforcement terms in Equation 4 (i.e., R1 and R2). Relative resistance is always calculated by subtracting resistance to change [i.e., log(Bx/Bo)] in the component with the lower reinforcement term from resistance to change in the component with the higher reinforcement term for that particular analysis. The ratio of reinforcement terms on the abscissa was similarly constructed with the higher reinforcement term in the numerator. Thus, the log ratio of reinforcement terms on the abscissa is always positive. If the ratio of the reinforcement terms used in the analysis governs relative resistance to change according to Equation 4, one would expect relative resistance to be a positive linear function of the reinforcement ratio.
Figure 4.
Analyses of resistance to change of observing behavior in experiments from Shahan et al. (2003), Shahan and Podlesnik (2005), and Shahan and Podlesnik (in press). Only Experiment 2 from Shahan et al. (2003) was used because, unlike all the other experiments, observing produced S+ on a fixed-ratio schedule. Regressions of Equation 4 and the resultant parameters are shown in each panel. The panels differ in what is used for the reinforcement terms (i.e., R1 and R2) in Equation 4.
The top two panels show that relative resistance to change is not an orderly function of relative rate of S+ presentation (i.e., conditioned reinforcement rate) or relative value of S+ presentations. Neither function accounted for much of the variance and the neither slope was significantly greater than zero. The middle-left panel shows that variations in relative rate of primary reinforcement during S+ do not provide a good account of changes in relative resistance to change of observing and the slope of the function was not significantly different from zero. The middle-right panel shows that relative resistance was always greater for the component associated with the overall higher rate of primary reinforcement, but Equation 4 accounted for only 38% of the variance and the slope was not significantly different from zero. However, the bottom-left panel shows that relative resistance was a positive function of relative rate of primary reinforcement in the presence of the mixed-schedule stimuli in the two components. Equation 4 accounted for 72% of the variance in observing from the six experiments and the slope was significantly greater than zero [F(1,4) = 10.17, p=.03]. We conclude that relative resistance to change of observing is likely governed by the rate of primary reinforcement arranged in the presence of the mixed-schedule stimulus. It is important to note that the mixed schedule provides the context in which observing occurs. Thus, despite the impact of rates of S+ delivery and S+ value on observing rate, resistance to change of observing appears to be governed by the rates of primary reinforcement in the context in which observing occurs.
2.2.3. Implications for Conditioned Reinforcement and Attending
The results of our resistance to change experiments also may have implications for the concept of conditioned reinforcement and for the applicability of behavioral momentum theory to responding maintained by conditioned reinforcement. Maintenance of observing behavior is typically attributed to the conditioned reinforcing effects of S+ presentations (e.g., Fantino, 1977). The experiments above showed that observing rates were higher with higher rates of S+ presentation and higher valued S+ presentations. Thus, parameters of conditioned reinforcement appear to be important in governing observing rates and allocations. However, as noted above, from the perspective of behavioral momentum theory resistance to change is taken as a more appropriate measure of response strength than baseline response rates. If S+ deliveries function as reinforcers in the sense of strengthening behavior, then one might expect that changes in their rate and value would affect resistance to change. The analyses above might be taken to suggest that variations in parameters of conditioned reinforcement do not impact response strength, and that the effects of variations in S+ frequency and value may have their effects on observing rates through some mechanism other than response-strengthening. This issue has been discussed by Shahan and Podlesnik (2005) and Shahan and Podlesnik (in press), so we will not repeat that discussion here. We will note, however, that Schuster (1969) reached a similar conclusion based on the finding that food-paired stimuli added to one terminal link of a concurrent-chains procedure increased response rates in the terminal link but failed to produce a preference for that terminal link. Recently, Davison and Baum (2006) reached a similar conclusion based on the fact that food-paired stimuli did not necessarily produce pulses of preference for one of two options in concurrent schedules of reinforcement. Both Schuster and Davison and Baum concluded that stimuli typically considered to function as conditioned reinforcers were likely having their impact on response rates as a result of a signaling function. Although such information-based accounts of the effects of an S+ on behavior remain controversial, the data from our resistance to change experiments raise further questions about the response-strengthening effects of stimuli predictive of food.
Another interpretation of the results above is that S+ deliveries do function as reinforcers, but that it is difficult to detect their response-strengthening effects with tests of resistance to change. As noted above, behavioral momentum theory suggests that resistance to change is governed by the Pavlovian stimulus-reinforcer relation between the discriminative context and the reinforcers obtained in that context. Because establishing a conditioned reinforcer would require first-order Pavlovian conditioning, second-order conditioning would be required for conditioned reinforcers to affect resistance to change via the discriminative-stimulus context. Schuster’s (1969) failure to find preference for the terminal link with the additional food-associated stimuli could similarly represent a failure of second-order conditioning (cf. Williams and Dunn, 1991). If putative conditioned reinforcers are indeed reinforcers, and such failures of second-order conditioning with conditioned reinforcers are widespread, then it could mean that behavioral momentum theory will have limited applicability to responding maintained by conditioned reinforcement. At present, it is difficult to accept or reject either of these interpretations of why parameters of conditioned reinforcement appear not to impact resistance to change.
The issues above raise questions about our discussion of choice and conditioned reinforcement rate in Section 2.1.1. Based on the results of the Shahan et al. (2006) concurrent observing-response procedure, we suggested that general theories of choice need to include a term for relative conditioned reinforcement rate. As noted in Section 2.1.1., unlike concatenated matching-law based theories, DRT does not include a term for conditioned reinforcement rate. Fantino and Romanowich (2007) concluded that DRT need not include such a term based partially on experiments like Schuster’s showing that added food-associated stimuli do not affect preference for a terminal link. Given that one potential interpretation of the Schuster data and our resistance to change data is that an S+ might not function as a reinforcer at all, it may seem odd to suggest that choice theories should include a term for conditioned reinforcement rate. However, even if it ultimately turns out that the process by which an S+ has its effects on response rates is not response-strengthening per se, the other potential process (whatever it is) produces changes in response rates and allocation that are consistent with the matching law. Thus, unlike DRT, concatenated matching law-based choice theories still capture the impact of relative rates of stimulus presentation with terms reflecting relative terminal-link entries, even if terminal link stimulus presentations affect preference through some mechanism other than conditioned reinforcement.
Finally, considering observing as an analog of attending, the results above suggest that rates of attending may depend upon the rate at which important stimuli are encountered, and the value of those stimuli. However, the persistence of attending appears to be governed by the rate of primary reinforcement in the context in which the attending is occurring. Obviously before this conclusion is considered too seriously, experiments should be undertaken to examine the effects of rates of stimulus presentation, stimulus value, and rates of primary reinforcement on the persistence of attending in other procedures.
3. Divided Attention and the Matching Law
The experiments in Section 2.1 above suggested that the matching law might provide a good account of how reinforcement variables impact the allocation of attention. Although the concurrent observing-response experiment of Shahan et al. (2006) might be considered an analog of divided attention, we sought to examine the applicability of the matching law to performance on a task more typically used to study divided attention of pigeons. We used a modified delayed-matching-to-sample procedure in which pigeons are presented with compound samples comprised of a combination of two elements (i.e., a color and a line orientation). Following the compound samples, the pigeons are presented with a pair of single-element comparison stimuli (i.e., two colors or two line orientations). A correct choice requires responding to the element that had appeared in the compound sample. Previous findings have suggested that compound-sample stimuli produce lower accuracies or require longer sample durations to maintain accuracy than single-element samples because they require a division of attention to the sample elements (see Zentall 2005, and Zentall & Riley, 2000, for reviews).
Shahan and Podlesnik (2006) noted that the allocation of attending to the elements of compound samples might be analogous to the allocation of responding on concurrent schedules of reinforcement. Thus, Shahan and Podlesnik asked whether performance on the divided-attention task varied with changes in relative reinforcement in a manner consistent with the matching law. Figure 5 shows a schematic of the procedure. The pigeons were presented with compound samples that terminated response independently after 5 s. With p=.5, one of two sets of single-element comparison stimuli comprised of two colors (i.e., color trials) or two line orientations (i.e., line trials) were presented. A response to the element that had appeared in the compound sample produced reinforcement with some probability. The relative probability of reinforcement on the two types of comparison trials was varied across conditions to generate reinforcement ratios of 1:9, 1:3, 1:1, 3:1, and 9:1.
Figure 5.
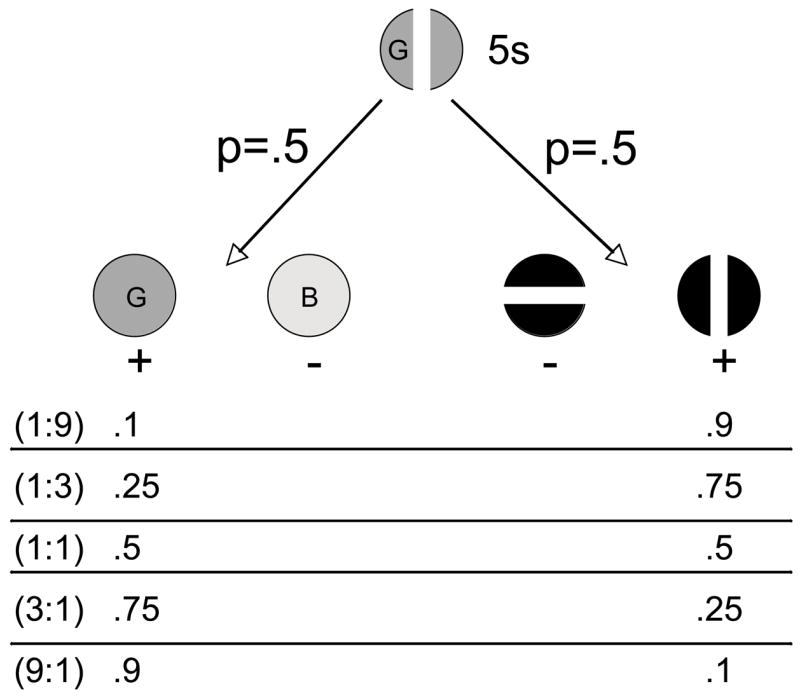
Schematic of the procedure used in Shahan and Podlesnik (2006). Compound color and line-orientation samples were followed by one of two sets of element comparison stimuli (i.e., two colors or two lines) with p=.5. The probabilities at the bottom of the figure represent the probability of reinforcement for a correct choice on each type of element-comparison trial.
In order to apply the matching law to the resulting data, log d was used as the measure of accuracy. Log d has been used widely in applications of the generalized matching law to discriminative performance (e.g., Davison and Tustin, 1978; Davison and Nevin, 1999). This measure of accuracy is useful because, unlike percent correct, it is bias free and shares metric properties with response rates, ranging from 0 at chance performance to infinity at perfect performance. Specifically, log d was calculated separately for color and line trials such that:
| (5) |
where corrS1 and incorrS1 refer to correct and incorrect responses following presentation of one sample (e.g., blue) and corrS2 and incorrS2 refer to correct and incorrect responses following the other sample (e.g., green). To apply the generalized matching law to variations in accuracy with variations in relative reinforcement, Shahan and Podlesnik used the follow expression:
| (6) |
where log dC and log dL refer to log d for color and line trials and RC and RL refer to reinforcers obtained on color and line trials, respectively. The parameters a and log b refer to sensitivity of relative accuracy to relative reinforcement and bias in accuracy for one trial type unrelated to relative reinforcement, respectively. The expression log dC – log dL in Equation 6 replaces log (B1/B2) in the typical version generalized matching law (Equation 2) because log d is already in logarithmic terms and log x – log y is equivalent to log (x/y).
Figure 6 shows the fits of Equation 6 to the data averaged across four pigeons. Equation 6 accounted for 96% of the variance (see Shahan and Podlesnik, 2005, for individual subject data). Sensitivity to relative reinforcement (i.e., a in Equation 6) was 0.57 and bias (i.e., log b in Equation 6) was 0.26. Thus, the effects of variations in relative reinforcement on pigeons’ performance on the divided-attention task were well described by the generalized matching law. The fact that bias was greater than zero reflects the fact that accuracy tended to be higher for color trials than for line trials regardless of the reinforcement ratio arranged.
Figure 6.
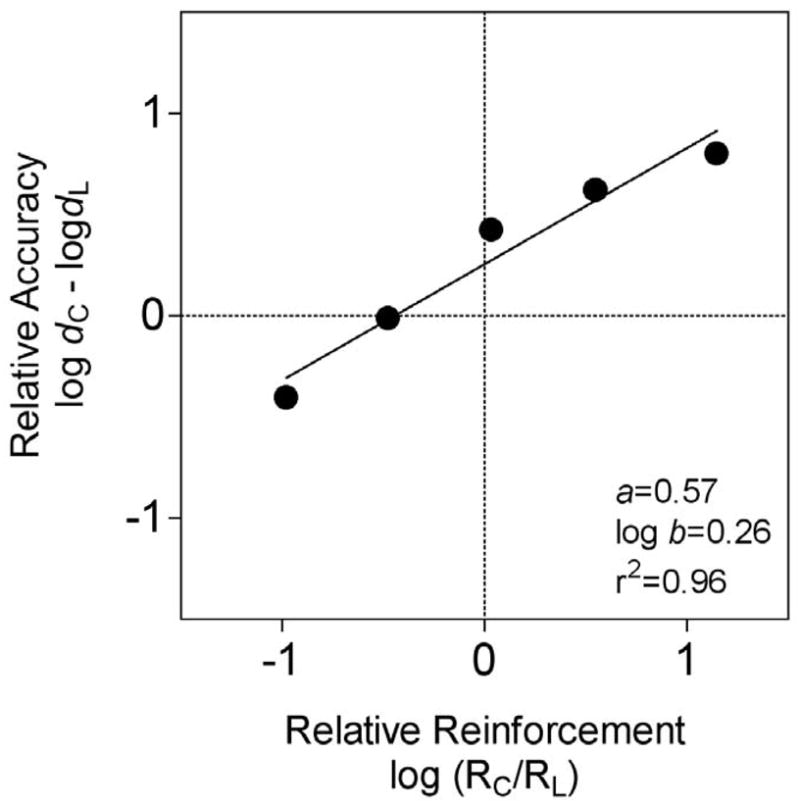
Relative accuracy of pigeons’ performance on the two types of element-comparison trials in a divided-attention task as a function of relative reinforcement for correct choices. Regressions of Equation 6 and the resultant parameters are presented. Data are from Shahan and Podlesnik (2006).
One interpretation of the above result is that variations in relative reinforcement for the two types of trials resulted in changes in the way attention was allocated to the elements of the compound samples. Alternatively, because relative reinforcement was varied by changing the probability of reinforcement at the comparison choice point, it is possible that variations in relative reinforcement had their effects by impacting only behavior at the choice point. For example, the pigeons may have attended equally to the two elements of the compound sample, but they may have been less motivated to choose the correct stimulus at the choice point when faced with the comparison stimuli signaling the lower probability of reinforcement.
A recent experiment by Shahan and Podlesnik (2007) examined whether the effects of differential reinforcement on performance in the divided attention task are mediated by changes in processing of the samples. One of the key features of the divided attention task is that the amount of time available for processing the sample stimuli is limited. Shahan and Podlesnik (2007) asked whether the impact of differential reinforcement on performance in the divided-attention task depends on sample duration. If the effects of differential reinforcement are mediated only by changes in motivation at the choice point, then sensitivity to variations in relative reinforcement would not be expected to be dependent upon sample duration. In addition, Shahan and Podlesnik examined relative comparison choice response speeds (i.e., l/latency) to assess changes in motivation at the comparison choice point.
The procedure was the same as that used by Shahan and Podlesnik (2006), except that half of the trials in the session arranged a 2.25-s sample duration and half arranged a 0.75-s sample duration. Relative reinforcement on color and line trials was varied across conditions to examine the same reinforcement ratios as in the previous experiment. As in Shahan and Podlesnik (2006), performance with both sample durations was sensitive to variations in relative reinforcement for the two types of trials. The top panel of Figure 7 shows sensitivity values (i.e., a in Equation 6) with the short and long samples for individual pigeons. Sensitivity was greater with the longer sample duration for 7 of 8 of the pigeons. Also as in the previous experiment, the pigeons showed a bias for greater accuracy on color trials, but unlike sensitivity to relative reinforcement, this bias was not sample-duration dependent (data not shown here). Although overall accuracy was lower with the short samples, Shahan and Podlesnik (2007) showed that the lower sensitivities with the shorter sample were not likely an artifact of the lower accuracies (see original paper for full discussion). In essence, they showed that sensitivity values could have been similar with the two sample durations if accuracy had been even lower when relative reinforcement rate was lower in the short trials. In other words, the lower sensitivity value with the short sample appeared to result from the pigeons attending to the element associated with the lower probability of reinforcement too much.
Figure 7.
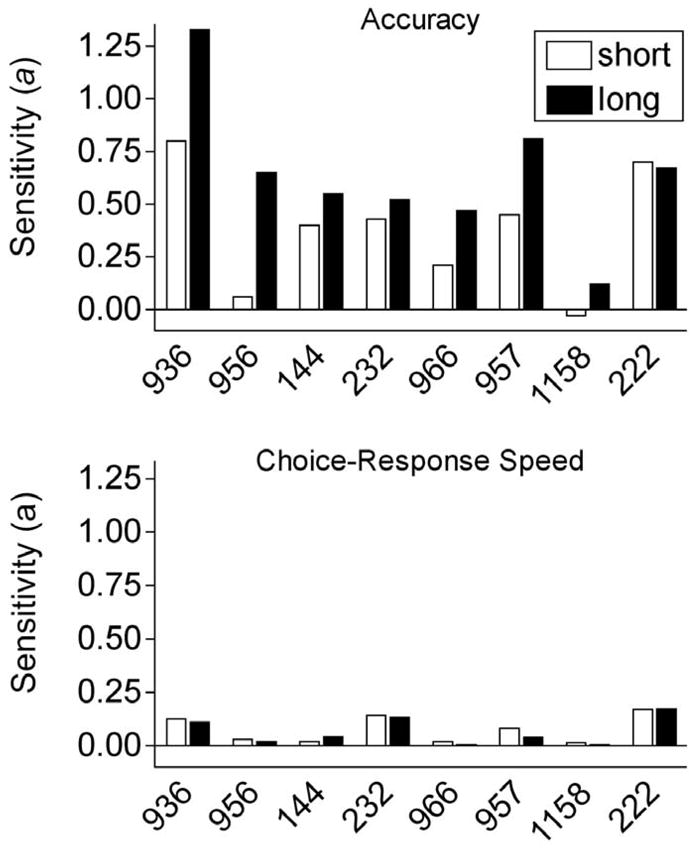
Sensitivity (i.e., a) values for accuracy (top panel) and choice-response speeds (bottom panel) based on the fits of Equations 6 and 2, respectively. Data are from Shahan and Podlesnik (2007).
The bottom panel of Figure 7 shows sensitivity values based on relative choice-response speeds to the comparisons. Sensitivity values were obtained by using response speeds as the behavior terms (i.e., B1 and B2) in a generalized matching law analysis (i.e., Equation 2). Relative choice-response speeds on the color and line trials were somewhat sensitive to changes in relative reinforcement with both sample durations (i.e., a significantly > 0), but sensitivity did not differ for the short and long sample duration trials. Although relative accuracy and relative choice-response speeds were sensitive to relative reinforcement, only changes in relative accuracy were sample dependent. Thus, Shahan and Podlesnik concluded that it was unlikely that changes in motivation at the choice point were mediating the effects of relative reinforcement on accuracy and that the impact of relative reinforcement could be attributed to changes in processing of the sample stimuli.
Shahan and Podlesnik (2007) suggested a “one look” hypothesis to account for the lower sensitivity obtained with the shorter sample duration. They noted that unless the subjects were to completely forgo the reinforcers for the sample-element associated with the lower reinforcement probability, at least one look to each of the elements is required. Based on the assumption that an effective look to an element takes some minimal amount of time, the amount of time remaining for extra attention to be allocated to the higher-reinforcement element is limited with a shorter sample duration. Thus, with a shorter sample duration, the allocation of attention to the elements would be expected to approach equality, resulting in a decrease in sensitivity to reinforcement allocation. If the one-look hypothesis is correct, then sample durations short enough to allow only one look would be expected to produce exclusive attending to the element associated with the higher reinforcement probability.
Finally, as noted in the Section 1 above, both sensory aspects of stimuli and the goals of the organism are widely recognized in cognitive psychology as contributing to the allocation of attention (see Yantis, 2000). Shahan and Podlesnik (2006, 2007) suggested that the sensitivity and bias terms of the generalized matching law might provide a way to describe goal-driven and stimulus-driven control of attention, respectively. Sensitivity might reflect the impact of relative reinforcement on the importance of the stimuli, or what Norman (1968) called pertinence. On the other hand, bias in accuracy independent of reinforcement variations might reflect the impact of the sensory features of the stimuli, or what Norman called sensory activation. Although goal-driven attentional control in humans is typically manipulated via instructions, the matching law might be useful for characterizing how both consequences and stimulus features contribute to the allocation of attention.
4. Conclusions
The research reviewed here was undertaken in an attempt to examine whether models of the allocation and persistence of operant behavior are applicable to attending. The observing experiments presented in Section 2 suggest that the matching law does well as an account of changes in the rate and allocation of observing. In addition, behavioral momentum theory provided a reasonable account of the persistence of observing, but only when rates of primary reinforcement in the context were considered. Despite their impact on rates and allocation of observing, parameters of stimulus presentation usually thought to have their effects as a result of the conditioned reinforcing properties of the stimuli had no detectable impact on resistance to change. There are multiple interpretations of this outcome, some of which raise questions about the nature of conditioned reinforcement. Regardless, the results suggest to us that the frequency with which important stimuli are encountered and the value of those stimuli do not contribute to the persistence of attending, at least as it is measured with observing responses.
The experiments presented in Section 3 represent our first attempts to further examine the utility of models of operant behavior in describing performance on a procedure more directly aimed at studying divided attention. Our initial results suggest that the matching law is applicable to changes in the allocation of attending to the elements of compound stimuli resulting from variations in relative reinforcement. Thus, the matching law might provide a starting point for translating insights about goal-directed action derived from the quantitative analysis of behavior to attention. We are also presently examining the applicability of behavioral momentum theory to the persistence of attending in a divided-attention task. Further applications of more general theories of operant behavior to performance on a variety of traditional attention tasks may provide insights into what is referred to variously as endogenous, top-down, or goal-directed control of attention.
Acknowledgments
Portions of the research reviewed here and preparation of this paper was funded by National Institute of Mental Health grant MH072621. The authors thank Amy Odum, Tony Nevin, and Corina Jimenez-Gomez for their contributions.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahearn WH, Clark KM, Gardenier NC, Chung BI, Dube WV. Persistence of stereotyped behavior: Examining the effects of external reinforcers. J Appl Behav Anal. 2003;36:439–448. doi: 10.1901/jaba.2003.36-439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- American Psychiatric Association. Diagnostic and statistical manual of mental disorders. 4. American Psychiatric Association; Washington, DC: 1994. [Google Scholar]
- Baum WM. On two types of deviation from the matching law: Bias and undermatching. J Exp Anal Behav. 1974;22:231–242. doi: 10.1901/jeab.1974.22-231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum WM. Matching, undermatching, and overmatching in studies of choice. J Exp Anal Behav. 1979;32:269–281. doi: 10.1901/jeab.1979.32-269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berg ME, Grace RC. Independence of terminal-link entry rate and immediacy in concurrent chains. J Exp Anal Behav. 2004;82:235–251. doi: 10.1901/jeab.2004.82-235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen SL. Behavioral momentum of typing behavior in college students. J Behav Anal Ther. 1996;1:36–51. [Google Scholar]
- Davison M. Bias and sensitivity to reinforcement in a concurrent-chain schedule. J Exp Anal Behav. 1983;40:15–34. doi: 10.1901/jeab.1983.40-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison M, Baum WM. Do conditional reinforcers count? J Exp Anal Behav. 2006;86:269–283. doi: 10.1901/jeab.2006.56-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison M, Nevin JA. Stimuli, reinforcers, and behavior: An integration. J Exp Anal Behav. 1999;71:439–482. doi: 10.1901/jeab.1999.71-439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davison MC, Tustin RD. The relation between the generalized matching law and signal-detection theory. J Exp Anal Behav. 1978;29:331–336. doi: 10.1901/jeab.1978.29-331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dinsmoor JA. Observing and conditioned reinforcement. Behav Brain Sci. 1983;6:693–728. [Google Scholar]
- Dube WV, McIlvane WJ. Reinforcer frequency and restricted stimulus control. J Exp Anal Behav. 1997;68:303–316. doi: 10.1901/jeab.1997.68-303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckerman DA. Uncertainty reduction and conditioned reinforcement. Psych Record. 1973;23:39–47. [Google Scholar]
- Ehrman RN, Robbins SJ, Bromwell MA, Lankford ME, Monterosso JR, O’Brien CP. Comparing attentional bias to smoking cues in current smokers, former smokers, and non-smokers using a dot-probe task. Drug Alcohol Depend. 2002;67:185–191. doi: 10.1016/s0376-8716(02)00065-0. [DOI] [PubMed] [Google Scholar]
- Fantino E. Conditioned reinforcement: Choice and information. In: Honig WK, Staddon JER, editors. Handbook of operant behavior. Prentice-Hall; Englewood Cliffs, NJ: 1977. pp. 313–339. [Google Scholar]
- Fantino E, Freed D, Preston RA, Williams WA. Choice and conditioned reinforcement. J Exp Anal Behav. 1991;55:177–188. doi: 10.1901/jeab.1991.55-177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fantino E, Preston RA, Dunn R. Delay reduction: Current status. J Exp Anal Behav. 1993;60:159–169. doi: 10.1901/jeab.1993.60-159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fantino E, Romanowich P. The effect of conditioned reinforcement rate on choice: a review. J Exp Anal Behav. 2007;87:409–421. doi: 10.1901/jeab.2007.44-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gopher D. The skill of attention control: Acquisition and execution of attention strategies. In: Meyer DE, Kornblum S, editors. Attention and performance XIV: Synergies in experimental psychology, artificial intelligence, and cognitive neuroscience. MIT Press; Cambridge, MA: 1992. [Google Scholar]
- Grace RC. A contextual model of concurrent-chains choice. J Exp Anal Behav. 1994;61:113–129. doi: 10.1901/jeab.1994.61-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grace RC, Nevin JA. On the relation between preference and resistance to change. J Exp Anal Behav. 1997;67:43–65. doi: 10.1901/jeab.1997.67-43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimes JA, Shull RL. Response-independent milk delivery enhances persistence of pellet reinforced lever pressing by rats. J Exp Anal Behav. 2001;76:179–194. doi: 10.1901/jeab.2001.76-179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harper DN. Drug-induced changes in responding are dependent on baseline stimulus-reinforcer contingencies. Psychobiol. 1999;27:95–104. [Google Scholar]
- Hendry DP. NASA Technical Report 65–1, NASA Technical Reports Server (Document ID 19660016943) 1965. Reinforcing value of information. [Google Scholar]
- Herrnstein RJ. On the law of effect. J Exp Anal Behav. 1970;13:243–266. doi: 10.1901/jeab.1970.13-243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnsen BH, Laberg JC, Cox WM, Vaksdal A, Hugdahl K. Alcoholic subjects’ attentional bias in the processing of alcohol-related words. Psych Addict Behav. 1994;8:111–115. [Google Scholar]
- Kendall SB. Effects of two procedures for varying information transmission on observing responses. J Exp Anal Behav. 1973;20:73–83. doi: 10.1901/jeab.1973.20-73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lovaas OI, Koegel RL, Schreibman L. Stimulus overselectivity in autism: A review of research. Psych Bull. 1979;86:1236–1254. [PubMed] [Google Scholar]
- Lubman DI, Peters LA, Mogg K, Bradley BP, Deakin JFW. Attentional bias for drug cues in opiate dependence. Psych Med. 2000;30:169–175. doi: 10.1017/s0033291799001269. [DOI] [PubMed] [Google Scholar]
- Luco J. Matching, delay-reduction, and maximizing models for choice in concurrent-chains schedules. J Exp Anal Behav. 1990;54:53–67. doi: 10.1901/jeab.1990.54-53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mace FC, Lalli JS, Shea MC, Lalli EP, West BJ, Roberts M, Nevin JA. The momentum of human behavior in a natural setting. J Exp Anal Behav. 1990;54:163–172. doi: 10.1901/jeab.1990.54-163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazur JE. Preferences for and against stimuli paired with food. J Exp Anal Behav. 1999;72:21–32. doi: 10.1901/jeab.1999.72-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazur JE. Hyperbolic value addition and general models of animal choice. Psych Rev. 2001;108:96–122. doi: 10.1037/0033-295x.108.1.96. [DOI] [PubMed] [Google Scholar]
- McMicheal JS, Lanzetta JT, Driscoll JM. Infrequent reward facilitates observing responses in rats. Psychon Sci. 1967;8:23–24. [Google Scholar]
- McMillan JC. Average uncertainty as a determinant of observing behavior. J Exp Anal Behav. 22:401–408. doi: 10.1901/jeab.1974.22-401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nestor PG, O’Donnell BF. The mind adrift: Attentional dysregulation in schizophrenia. In: Parasuraman R, editor. The attentive brain. The MIT Press; Cambridge, MA: 1998. pp. 527–546. [Google Scholar]
- Nevin JA. An integrative model for the study of behavioral momentum. J Exp Anal Behav. 1992;57:301–316. doi: 10.1901/jeab.1992.57-301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA. Measuring behavioral momentum. Behav Process. 2002;57:187–198. doi: 10.1016/s0376-6357(02)00013-x. [DOI] [PubMed] [Google Scholar]
- Nevin JA, Grace RC. Behavioral momentum and the Law of Effect. Behav Brain Sci. 2000;23:73–130. doi: 10.1017/s0140525x00002405. [DOI] [PubMed] [Google Scholar]
- Nevin JA, Mandell C, Atak JR. The analysis of behavioral momentum. J Exp Anal Behav. 1983;39:49–59. doi: 10.1901/jeab.1983.39-49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nevin JA, Tota ME, Torquato RD, Shull RL. Alternative reinforcement increases resistance to change: Pavlovian or operant contingencies? J Exp Anal Behav. 1990;53:359–379. doi: 10.1901/jeab.1990.53-359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norman DA. Toward a theory of memory and attention. Psych Rev. 1968;75:522–536. [Google Scholar]
- Podlesnik CA, Shahan TA. Response-reinforcer relations and resistance to change. Behav Proc. 2008;77:109–125. doi: 10.1016/j.beproc.2007.07.002. [DOI] [PubMed] [Google Scholar]
- Schroeder SS, Holland JG. Reinforcement of eye movement with concurrent schedules. J Exp Anal Behav. 1969;12:897–903. doi: 10.1901/jeab.1969.12-897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuster RH. A functional analysis of conditioned reinforcement. In: Hendry DP, editor. Conditioned reinforcement. Homewood, IL: The Dorsey Press; 1969. pp. 192–235. [Google Scholar]
- Shahan TA. Observing Behavior: Effects of rate and magnitude of primary reinforcement. J Exp Anal Behav. 2002;78:161–178. doi: 10.1901/jeab.2002.78-161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahan TA, Burke KA. Ethanol-maintained responding of rats is more resistant to change in a context with added non-drug reinforcement. Behav Pharmacol. 2004;15:279–285. doi: 10.1097/01.fbp.0000135706.93950.1a. [DOI] [PubMed] [Google Scholar]
- Shahan TA, Magee A, Dobberstein A. The resistance to change of observing. J Exp Anal Behav. 2003;80:273–293. doi: 10.1901/jeab.2003.80-273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahan TA, Podlesnik CA. Rate of conditioned reinforcement affects observing rate but not resistance to change. J Exp Anal Behav. 2005;84:1–17. doi: 10.1901/jeab.2005.83-04. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahan TA, Podlesnik CA. Divided attention performance and the matching law. Learn Behav. 2006;34:255–261. doi: 10.3758/bf03192881. [DOI] [PubMed] [Google Scholar]
- Shahan TA, Podlesnik CA. Divided attention and the matching law: Sample duration affects sensitivity to reinforcement allocation. Learn Behav. 2007;35:141–148. doi: 10.3758/bf03193049. [DOI] [PubMed] [Google Scholar]
- Shahan TA, Podlesnik CA. J Exp Anal Behav. Conditioned reinforcement value and resistance to change. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahan TA, Podlesnik CA, Jimenez-Gomez C. Matching and conditioned reinforcement rate. J Exp Anal Behav. 2006;85:167–180. doi: 10.1901/jeab.2006.34-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Squires N, Fantino E. A model for choice in simple concurrent and concurrent-chains schedules. J Exp Anal Behav. 1971;15:27–38. doi: 10.1901/jeab.1971.15-27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Townshend JM, Duka T. Attentional bias associated with alcohol cues: Differences between heavy and occasional social drinkers. Psychopharmacology. 2001;157:67–74. doi: 10.1007/s002130100764. [DOI] [PubMed] [Google Scholar]
- Williams BA, Dunn R. Preference for conditioned reinforcement. J Exp Anal Behav. 1991;55:37–46. doi: 10.1901/jeab.1991.55-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilton RN, Clements RO. The role of information in the emission of observing responses: A test of two hypotheses. J Exp Anal Behav. 1971;16:161–166. doi: 10.1901/jeab.1971.16-161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wyckoff LB., Jr The role of observing responses in discrimination learning: Part 1. Psych Review. 1952;59:431–442. doi: 10.1037/h0053932. [DOI] [PubMed] [Google Scholar]
- Yantis S. Goal-direct and stimulus-driven determinants of attentional control. In: Monsell S, Driver J, editors. Attention and performance XVIII: Control of cognitive processes. MIT Press; Cambridge, MA: 2000. [Google Scholar]
- Zentall TR. Selective and divided attention in animals. Behav Process. 2005;69:1–15. doi: 10.1016/j.beproc.2005.01.004. [DOI] [PubMed] [Google Scholar]
- Zentall TR, Riley DA. Selective attention in animal discrimination learning. J Gen Psych. 2000;127:45–66. doi: 10.1080/00221300009598570. [DOI] [PubMed] [Google Scholar]