Filamentary microstructure and linear temperature dependence of normal state transport in optimized high temperature superconductors

Abstract

A filamentary model of “metallic” conduction in layered high temperature superconductive cuprates explains the concurrence of normal state resistivities (Hall mobilities) linear in T (T⁻²) with optimized superconductivity. The model predicts the lowest temperature T₀ for which linearity holds and it also predicts the maximum superconductive transition temperature T_c. The theory abandons the effective medium approximation that includes Fermi liquid as well as all other nonpercolative models in favor of countable smart basis states.

For a long time it has been known (1) that in high temperature cuprate superconductors not only are the normal state resistivity ρ and reciprocal Hall coefficient R_H⁻¹ anomalously linear in T, but also that this linearity is valid over the widest temperature range for exactly those compositions with the highest superconductive transition temperatures T_c. Just as the isotope effect in simple metals provided the decisive clue that identified electron-phonon interactions as the attraction responsible for a condensed superconductive Fermion state, so this coincidence demonstrates that the microscopic mechanism responsible for high temperature superconductivity (HTSC) in layered cuprates involves peculiar non-Fermi liquid features of the normal state. Theorists interested in explaining the microscopic mechanism responsible for the high T_cs of these materials could not ask for a more dramatic observation on which to base their analysis. Nevertheless, in spite of many efforts, no generally accepted explanation for either phenomenon is known, so that their concurrence with optimized superconductivity remains a mystery. The aim of the present paper is to show that a consistent model based on bridging interlayer impurities can be constructed that explains quantitatively not only this coincidence, but which also relates it to a microscopic model that explains a large number of very accurate measurements of density and temperature exponents of the metal-insulator transition (MIT) in the relatively simple case of semiconductor impurity bands where there is good reason to believe that the dopants are ideally (randomly) distributed. In this way the credentials of the cuprate impurity model are corroborated by independent simple impurity band data, which is very important because the structures of the cuprates are so complex. The ideas presented here for both problems are highly controversial and are far from being generally accepted, and the reasons for this will be discussed, as they are more important than the formal technical details of the calculations or the experiments. It should be remarked that the connection between the MIT and HTSC is not accidental, but is essential to the theory, and that there is a good deal of phenomenological evidence that supports such a relation in compositional trends of T_c (2, 3).

Linear Temperature Dependence of Normal-State Transport

The simplest explanation for the normal state linearity is that it arises solely from Fermi factors for a very narrow (width W_R) peak in the density of band states pinned to the Fermi energy E_F, where the scattering rate is band-width-limited and hence independent of T; in this model linearity is only asymptotic; it is obtained not down to T = 0, but only down to T₀ = W_R/5 (4, 36). In some materials (1) this will require values of W_R as small as 3 meV, which seems unreasonable when the calculated cuprate band widths W_B (as well as those observed by photoemission) are of order 1 eV. A way around this difficulty was proposed (5, 6) in the context of the characteristically layered structure of the cuprates, where intrinsic misfit-strain relieving domain walls in the layers are expected to suppress all intralayer conductivity, forcing currents to flow along paths that pass between layers (and around domain walls) by means of resonant tunneling (see figure 1 in ref. 7) through impurity states pinned narrowly at E_F by Coulomb forces through what was subsequently described as an “anti-Jahn-Teller effect” (8). However, this mechanism itself creates a new difficulty, just as one would expect for a phenomenon as rare as HTSC. The new difficulty is that the impurities are randomly distributed, and it is widely believed by scaling theorists (9) that there are no band (ballistic or phase-coherent smart) states associated with random impurity band conductivity. This point has become especially pivotal in the light of recent experiments on cuprates (see ref. 10, Wuyts et al. measured a series of YBCO films with variable oxygen content and defined T₀ as the maximum of dρ/dT; with increasing T_c they found, as have many others (30), a decreasing T₀ that is not much larger than T_c at the optimal composition) that have shown that defects (such as oxygen vacancies) affect normal state linearities not only very strongly but also scalably, which of course is not the case in ballistic normal metals (but then the latter do not have linearly temperature-dependent resistivities either!) and certainly not in diffusive metallic glasses, where T_c is generally very low and there are only very weak coherency effects.

Quantum Percolation Theory.

This brings us to the central point, which is the development (over a long period of time) of a new viewpoint that is in excellent agreement with experiment and that says that ballistic (or smart) basis states do exist for impurity bands in d = 3 dimensions, but that they are defined only along filamentary network that separates these smart states from localized states that coexist at the same energy (refs. 11–16 and unpublished work). Moreover even though there is no algorithm that can be used to compute in full detail such phase-coherent “random” states explicitly, their number is still countable. These existence and countability arguments have proved to be of great value in recent analyses of the characteristic exponents for the MIT as obtained in three extremely informative experiments on Si:P (17), neutron transmutation doped Ge:Ga [both uncompensated (18) and compensated (19)] and antiferromagnetic Ni(S, Se)₂ alloys (20). The details of the comparison between experiment and theory are lengthy (13–16) and will not be given here, but two important general points can be mentioned. First, in carefully prepared samples (17–20) the density exponents, which are valid in the very wide asymptotic region 0.01 < (n − n_c)/n_c < 0.4, are always observed to be integers or half integers (within the few % experimental uncertainties). This digital behavior is not observed for exponents determined from numerical simulations of conventional geometrical (bond or site) branching percolation models, nor for dynamical threshold exponents calculated, for example, by many-particle renormalization group methods (ɛ expansions) for magnetic transitions in crystals or electron-electron interactions in impurity bands, which sum selected diagrams using plane wave (effective medium) basis states. This crucial difference arises because the effective medium approximation (EMA) (ref. 16 and unpublished work) is valid in crystals but is not valid in the presence of applied fields for randomly distributed impurities near the MIT. It is just this failure of the EMA, the inadequacy of plane wave basis states for the description of quantum percolation, the extraordinarily wide asymptotic width, and the startling absence of many-electron renormalization effects, that one must find a way around, and this is done by the existence and countability theorems (10, 11) for smart ballistic states. Second, the filaments, properly speaking, are an array, not a network, as they are not allowed to interfere destructively, and so are required neither to branch nor cross (13).

Failure of the EMA

Before the discussion becomes more technical, it is convenient to elaborate further on the deficiencies of the EMA, as these have had pervasively misleading effects on theoretical discussions of both impurity band transport and the normal state transport and superconductivity in HTSC. Thus in the impurity band case the measured exponents for the density dependence are quite unexpectedly much smaller (and the transitions are much sharper) than can be explained within the EMA using scaling theory and plane wave (dirty Fermi liquid) basis states, whether or not electron-electron interactions are included. Indeed, as a last and truly desperate resort, it has recently often been suggested (9, 22) that materials like three-dimensional Si:P or two-dimensional Si MOSFETS are exhibiting superconductive behavior, which is scarcely credible. [The density of resonant phonon states (dispersion linear in q) is negligible compared with that of electronic states (dispersion quadratic in q) at large dilution.)] At the same time it is sometimes suggested that magnetic spins can promote HTSC, which goes against the fundamental idea of Cooper pairing (23). It is most probable that the EMA itself is the source of much of this confusion.

Of course, most experimental probes average over the sample, just as the EMA does, but there is no need to suppose that these averages (that may probe different local properties differently) provide an adequate description of microscopically different local properties. As a simple example, for composition x suppose that all conductive paths pass repeatedly and sequentially (ABCA… ) through two or three local environments A(x), B(x), C(x), and that these local environments are equivalent within each group, but that the groups themselves differ. Such iterated series percolative models in general cannot be described by the EMA in terms of a single effective medium D(x), and they apparently contain a plethora of adjustable parameters, but as we shall see, the values of these parameters need not be known in detail to understand the principal features of the data, including the scaling behavior. In other words, scaling behavior can transcend the EMA, and observation of scaling behavior, while compatible with the EMA, should not be taken as evidence for its validity. Moreover, schematic theoretical phase diagrams based on the EMA, such as that shown in ref. 10, may actually obscure the true microscopic nature of the mechanisms responsible for HTSC by providing the appearance, but not the substance, of a proper spatially inhomogeneous microscopic theory.

Counting Conductivity Paths in the High-T_c Cuprates

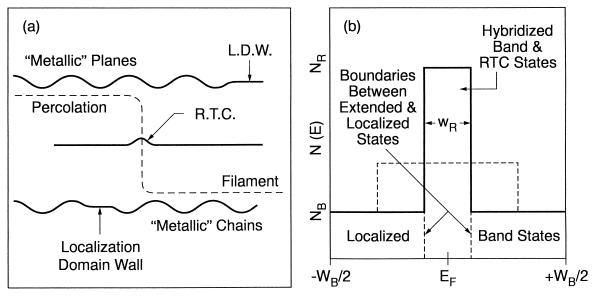
The essence of the counting model (5, 6) discussed here is illustrated in cross-section in Fig. 1. Fig. 1a is drawn for YBa₂Cu₃O_7-x but easily generalized to other cuprates with metallic CuO₂ planes and secondary metallic planes replacing the CuO_1-x chains of YBCO. In Fig. 1a, the percolative paths pass through three kinds of environments: (i), two-dimensional CuO₂ planes that are not metallic because of intraplanar domain walls; (ii), the chains, which are metallic only in short CuO segments that establish a very convenient and intrinsic length scale as they are interrupted every x⁻¹ molecules by an O vacancy, and (iii), resonant interplanar tunneling centers with an orbital pinned to E_F by the anti-Jahn-Teller effect (8), again probably an O vacancy; without the latter the material would be insulating. (The electronic structure associated with ideal CuO₂ layers may contain a logarithmic peak in its density of states associated with a two-dimensional saddle point, but the width of this peak is too great and it is essentially invariant from one cuprate to the next, so that it is highly unlikely (2) that this peak can explain either the composition dependence of the normal state or superconductive HTSC properties.) Similarly the CuO chain segments, by themselves, are not even metallic. However, if the density of resonant tunneling centers (RTC) is low enough, their width W = W_R can be only ≈10 meV or less, and thus they are potential candidates for explaining (4, 36) normal state transport linearities. A key point here is that the segments A, B, and C are connected to form filaments because the lattice relaxation associated with the anti-Jahn-Teller effect maximizes the conductivity.

Figure 1.

(a) The spatial percolative filaments, shown in cross section, follow planar locally metallic CuO₂ layers until they approach a domain wall, when they resonantly tunnel through a state associated with a defect (such as an oxygen vacancy) with an orbital pinned at E_F by the anti-Jahn-Teller effect to reach a CuO_1-x chain segment, which is also locally metallic. Note that it is only the filament (metal A)-RTC-(metal B)- sequence that is actually metallic, and the filament itself is metallic only for longitudinal wave packet motion. (b) The densities of states of the metallic band sections of the filament and the RTC near E_F, with ratios of W_R/W_B of only 4 (or 2, dashed line); a more realistic value for optimized YBCO would be 10–15. At optimized doping the total numbers of localized band states and resonant impurity states between ±W_R/2 are equal and they combine exactly, like beads on a string, to produce only pure filamentary states in this energy range, which is separated perfectly from the wider energy range where there are conventional band states localized by domain walls. In underdoped samples there are some uncombined localized band states in this range (the string is broken into sections), and in overdoped samples because of destructive interference (refs. 11–16 and unpublished work) again there are fewer independent filamentary states, which leaves behind a residue of Fermi liquid band states.

To carry the discussion further, it is necessary to understand what are the transport properties of percolative paths composed of these three elements in series. It seems that there is nothing special about the CuO₂ planes or the CuO chain segments, which are at least locally crystalline and periodic, but the randomly distributed RTC can certainly be expected to contribute anomalously (4, 36) to the normal state conductivities. It seems that the easiest way to approach these anomalies is to consider a case where only RTC are present, that is, the impurity band “random metal.” In refs. 11–16 it was rigorously shown that the explanation for the anomalously sharp impurity band MIT lies in recognizing that for d = 3 an applied electric field selects (or projectively separates) coherent extended states from incoherent localized states. Because of static and thermal disorder these states are inseparable in the absence of applied fields in the normal state, but in the presence of a steady state drift velocity v_D that is parallel to an applied electric field F the requirements of Galilean invariance can be satisfied by adding to a Ginzburg-Landau free energy a kinetic energy m(v − v_D)²/2. This term properly distinguishes localized states (v_D = 0) from extended ones (but only with respect to the component of crystal velocity parallel to F; the transverse components are still mixed by the static disorder). It represents a new kind of broken symmetry and because of this new broken symmetry one need only count the number of ballistic states and it is no longer necessary to make analogies in the normal states of either impurity bands or cuprates to superconductivity.

Calculation of the Cutoff Temperature T₀

From this analysis (13–16) we see that current can be carried coherently along filamentary paths passing from one RTC to the next. What do these coherent states look like? At the optimized composition (minimum T₀, maximum T_c), with a low concentration c of RTC and one orbital state/RTC, the fraction of localized metallic planar states with a band width W_B that can be locally and resonantly hybridized with RTC states to form extended states is cW_B/W_R. These two kinds of states alternate, which suggests equal weighting by dynamical equipartitioning (13–16), that is, at the optimal composition their numbers should be equal. (The validity of the equipartitioning principle for weighting dynamical degrees of freedom in the presence of ideal static disorder has been tested in a wide variety of classical experimental contexts and so far no exceptions to it have been found (13–16); however, here the same result is obtained by requiring that exactly one filamentary path passes through each RTC.) This means that cW_B/W_R ≈ 1 or

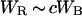1

With W_R ≈ 5T₀ (3), W_B ≈ 1 eV and c = x = 0.06 (24), corresponding to one RTC/(CuO chain segment or CuO₂ planar domain), we obtain a new result,

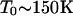2

that agrees (fortuitously) well with the experimental value T₀ ≈150K (10). Of course, the model is oversimplified, because we have neglected the effects of composition dependence of the chain and plane conductivities, but for small x these are expected to be small and merely to contribute constants to the background resistivity. Whatever the limitations of this model, it is certainly much more quantitative and specific than schematic phase diagrams based on the EMA (10).

Calculation of T_c

The next question is how one understands a filamentary superconductive phase, where each filament must be Cooper paired. Near T_c only the broad plane and chain band states resonant with the narrow band of RTC states are expected to be superconductive (see Fig. 1b), and according to Eq. 1 the total numbers of superconductive broad band and RTC narrow band states are about equal. Although the unitary transformation that constructs filamentary states exists in principle and quite a lot is known about these states in the impurity band case (refs. 11–16, unpublished work), it is not easy to transfer this knowledge to the composite layer/resonant tunneling cuprate structure filaments. As the filamentary currents are carried in series, one can guess that the transition temperature T_cf of each filament is the harmonic average of the localized T_cs of the RTC and bands separately. [In a mixed good metal-bad metal system the harmonic average often gives a good result for effective or average medium conductivities (21).] Thus

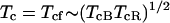3

For T_cB one can use (20–30)K, and for T_cR the Debye temperature for Cu vibrations adjacent to an O vacancy, (300–400)K. Then Eq. 3 gives T_c ≈ 100K, again in good agreement with experiment. The implications of Eq. 3 may come as a surprise. Thus T_c is high because of strong electron-phonon interactions in the CuO_1-x chain ends and RTC, not because of interactions in the CuO₂ planes, which are insulating by themselves and that function only to stabilize the lattice and connect the chain-RTC complexes.

There is a third observable to be considered, the optimal composition c = c₀. If one knew how to calculate this composition one could equivalently calculate W_R. It appears that c₀ depends not only on the intralayer domain wall spacing (which may be measurable; ref. 24), but also on the interlayer domain wall correlation length, as the latter determines the phase-space weighting for zigzag or hopscotch interlayer percolation paths (Figs. 1 and refs. 5 and 6). This is not known. However, when c < c₀ (x < 0.06 in YBCO) it appears that phase separation can occur (25), probably accompanied by layer or chain buckling. Lattice instabilities of this kind are the characteristic factor limiting T_c in metallic alloys (26).

Disjoint Densities of States

In addition to the resistivity anomaly the T⁻² dependence of the Hall mobility μ_H = R_H/ρ at the optimized composition in YBCO is also mysterious (27). It can be explained (27), however, with an extreme (and at that time apparently arbitrary) two-carrier model. Rereading this paper nearly 10 years later the author was quite surprised to find that this model is essentially identical to his (filamentary ballistic)/(localized band) model. Their high mobility, narrow band states correspond to zigzag filamentary ballistic, anti-Jahn-Teller narrowed states, and their low mobility, wide band to domain-wall localized band states. An essential feature of their two-carrier model, Fig. 1b, which represents the extra information contained in the T linearity of R_H⁻¹, is that the narrow band is not embedded in the wide one, but is totally separate from it; the latter ends abruptly just when it contacts the narrow one, which of course is pinned at E_F. This exact separation (refs. 11–16 and unpublished work) of the localized wide and extended narrow bands is an essential feature of the present model; it occurs when the equipartition condition (1) is satisfied, which defines the optimized composition. This exact separation is a peculiar feature of the layered cuprates that is made possible by the quasiperiodic nature of the intrinsic layer domain structure; it is probably absent for random impurity band metals (refs. 13–16 and unpublished work).

One of the questions that naturally arises in the zigzag filamentary model is what happens to electrons isolated in states not in the filaments. In the normal state these nonfilamentary states are diffusive in the sense that they hop incoherently either between layers or across domain walls in the CuO₂ planes (or vacancies in the CuO_1−x chains). In normal metals far from an MIT one ordinarily argues (28) that scattering by nonmagnetic impurities of extended states into extended states has little effect on Cooper pairing, apart from quenching the anisotropy of the Cooper pair amplitude Δ(k, k′). Here at the optimal composition the nonfilamentary states are insulating and localized and in a mean field approximation have negligible overlap with the extended filamentary states. As a result the phases of electrons in the small nonfilamentary islands thermally fluctuate randomly relative to adjacent filamentary Cooper pairs, so that the latter form an isolated and self-contained system that is a relatively small part of the whole and that is strongly coupled to layer buckling at CuO₂ planar domain walls. This may well be related to the many first-order structural anomalies that have been observed at the superconductive transition, for example, by ion channeling compared with neutron scattering (29).

Optimized Quantum Percolation

It may be that the present model is more informative than any based on the EMA because it goes to the heart of the mechanisms explicitly responsible for the simultaneous maximization of T_c and minimization of T₀ that were proposed long ago (4–6, 36). Current wisdom has it that the normal electronic state of the cuprates is not a Fermi liquid, but in contrast to this negative view, which is of marginal utility, the present non-EMA model of an optimized quantum percolative metal is explicit. Its central idea, the countability of ballistic states in the presence of intrinsic disorder, has already been authenticated in the context of the impurity band MIT. The discussion of the impurity band case (refs. 11–16 and unpublished work) showed that the exponents for compensated and uncompensated impurity bands are qualitatively different. The former are essentially classical because scattering from the secondary impurities destroys the phase coherence of the filaments associated with the primary impurities. Similarly here HTSC are divided into two classes that depend on whether or not the filamentary paths are all of the same type. If they are, then linear normal-state transport properties occur at the optimal composition, as in YBCO and LSCO; if not, then linearities are not observed, as in BSCCO (30).

Under- and Overdoping.

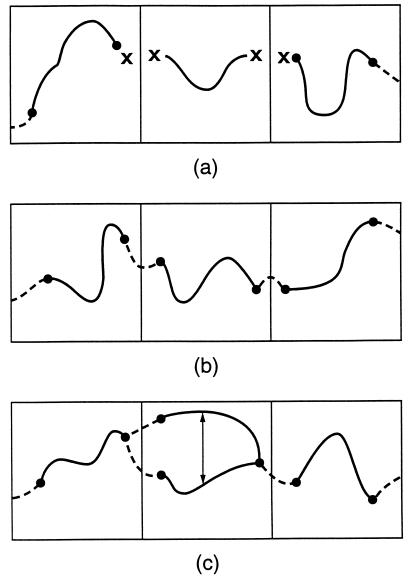
What happens in under- or overdoped samples is illustrated in the plan views (projected ab planes) in Fig. 2. For simplicity it is assumed that the CuO₂ intraplanar domain walls are eclipsed; staggered or intermediate geometries would not change the results qualitatively. In b the optimal doping geometry is illustrated, with two impurities injecting and removing carriers from each domain. In the underdoped configuration (a) there are fewer than two impurities on the average per domain, so that the conductive filaments must sometimes pass through the insulating domain walls and the network contains metal-insulator-metal junctions that localize metallic states, destroy the thermal linearities of the normal-state transport and reduce T_c. More interesting is the overdoped configuration (c). Now there are more than two impurities on average per domain and some will have three. Then there are alternative paths across a given domain, and these permit electron-electron scattering as in dirty Fermi liquids. The normal-state data for La_2-xSr_xCuO₄ (ref. 31, for example) illustrate localization on the underdoped side, but the phase transition on the overdoped side (32, 33) is generally much broader. Between x = 0.16 and x = 0.4, as x increases, T_c decreases and the resistivity temperature exponent increases from 1 to the Fermi liquid value of 2 while the material remains metallic. This suggests that dopant-dopant interactions have broadened W_R, as sketched in Fig. 1, and decreased T_cR, so that inhomogeneous electron-electron interactions, not topological filamentary disruption, are the factor that usually dominates overdoped LSCO.

Figure 2.

Schematic filamentary paths in plan view, (a) underdoped, (b) optimally doped, and (c) overdoped. The solid lines are filamentary segments in CuO₂ planes, while interplanar bridging impurities (RTC) are indicated by dots. The intraplanar domain walls are shown as straight lines. Filamentary segments in secondary metallic planes (the CuO_1-x chains in YBCO, or CuO₂ planes in LSCO) are shown as dashed lines. Shown are the effects of localization in a, where domain-wall tunneling is marked by crosses, and strong electron-electron interpath scattering in c, as indicated by the double-headed arrow. With sufficient overdoping c becomes equivalent to a dirty Fermi liquid with strong electron-electron scattering. Note that what matters is the number of filamentary segments per domain; their geometrical disposition is irrelevant.

Conclusions

In conclusion, the answer to the question of why T_c is so high in the cuprates is a simple one. The metallic CuO₂ layers have a low density of domain walls that render them metallic only in large patches. The equally low density RTC connect these patches via the secondary metallic layers to form bulk metallic paths. The band width of the RTC is very narrow because their density is low and because in a crystal with ionic bonding the usual Jahn-Teller effect is reversed by self-screening. These features, together with exact separability (11) and countability (refs. 12–16 and unpublished work) of localized and extended states at the optimal composition, explain the normal-state transport anomalies quantitatively. Wave packets moving along these metallic paths spend half the time on the RTC where they see maximal mechanically stable electron-phonon interactions, giving rise to a high T_c. The present filamentary or topological model enables us to explain why the normal-state resistivity is most linear in T (lowest T₀) in samples where T_c is maximized, and to calculate both T₀ and T_c in such optimized samples in good agreement with experiment. In spite of its schematic character and some obvious limitations (for example, why T₀ > T_c is explained for YBCO but not LSCO), the model enables us to distinguish and explain qualitative differences in the phase diagrams of YBCO, LSCO, and BSCCO. In many earlier papers (34) we have reviewed many kinds of data that show that the EMA does not describe the observed properties of superconductive cuprates, either at the superconductive or metal-insulator transitions. However, the present discussion is much more explicit in its focus on normal-state transport properties. Moreover, the model is based on, and is corroborated by, a successful quantitative analysis (refs. 10–16 and unpublished work), based on a new kind of broken symmetry, of the density, temperature and magnetic field dependences of the normal state transport properties of the much simpler, but still surprisingly analogous, semiconductor impurity bands in the asymptotic regions near their MITs. Intimations of linear transport anomalies associated with an MIT have been observed recently in quasicrystalline AlPdRe (35) and these may be explained also by quantum percolation involving narrow peaks in the electronic density of states near E_F.

ABBREVIATIONS

MIT

metal insulator transition

HTSC

high temperature superconductivity

EMA

effective medium approximation

RTC

resonant tunneling centers