Validity of Models for Predicting BRCA1 and BRCA2 Mutations

Abstract

Background

Deleterious mutations of the BRCA1 and BRCA2 genes confer susceptibility to breast and ovarian cancer. At least 7 models for estimating the probabilities of having a mutation are used widely in clinical and scientific activities; however, the merits and limitations of these models are not fully understood.

Objective

To systematically quantify the accuracy of the following publicly available models to predict mutation carrier status: BRCAPRO, family history assessment tool, Finnish, Myriad, National Cancer Institute, University of Pennsylvania, and Yale University.

Design

Cross-sectional validation study, using model predictions and BRCA1 or BRCA2 mutation status of patients different from those used to develop the models.

Setting

Multicenter study across Cancer Genetics Network participating centers.

Patients

3 population-based samples of participants in research studies and 8 samples from genetic counseling clinics.

Measurements

Discrimination between individuals testing positive for a mutation in BRCA1 or BRCA2 from those testing negative, as measured by the c-statistic, and sensitivity and specificity of model predictions.

Results

The 7 models differ in their predictions. The better-performing models have a c-statistic around 80%. BRCAPRO has the largest c-statistic overall and in all but 2 patient subgroups, although the margin over other models is narrow in many strata. Outside of high-risk populations, all models have high false-negative and false-positive rates across a range of probability thresholds used to refer for mutation testing.

Limitation

Three recently published models were not included.

Conclusions

All models identify women who probably carry a deleterious mutation of BRCA1 or BRCA2 with adequate discrimination to support individualized genetic counseling, although discrimination varies across models and populations.

Deleterious mutations of BRCA1 (MIM 113705) and BRCA2 (MIM 600185) increase the risk for breast and ovarian cancer (1–3). Whereas deleterious variants are relatively rare in the general population, they are common among families with multiple occurrences of breast or ovarian cancer (4–6). When counseling a woman facing decisions about genotyping for BRCA1 and BRCA2, it is important to accurately evaluate the probability that she carries a deleterious mutation (pretest mutation probability) and the probability that a mutation will be found if she is genotyped (which depends on the accuracy of mutation testing). Reliable, evidence-based, individualized counseling strategies can enhance informed decision making, both about whether to pursue BRCA1/BRCA2 testing and what to do with the results (7–9).

The demand for assessment of complex family histories of cancer has led to widespread use of statistical models to estimate mutation probabilities (2, 10–18). Model-based predictions are currently used in counseling about genetic testing, are included in materials distributed to women considering genetic testing (18–21), are used for determining eligibility for screening and prevention studies (22), and are factored into coverage decisions by insurers (23). More than a dozen models exist. They use different statistical methods and source populations, pedigree features, and predicted outcomes. In clinical practice, different models applied to the same person can give a wide range of probabilities that a BRCA1/BRCA2 mutation is present. This degree of variability raises concerns about whether some models are more accurate than others and calls for a careful independent comparative evaluation of the predictive performance of existing models.

We assessed the validity of commonly used models for estimating mutation probabilities of BRCA1 and BRCA2 in individuals identified through the Cancer Genetics Network. We assembled a large set of families with history of breast cancer, ovarian cancer, or both. We used standardized computational methods across contributing institutions to evaluate 7 models. Our main goal was to measure how well these models discriminated between mutation carriers and noncarriers.

METHODS

Study Overview

We conducted a cross-sectional, multicenter analysis. For each family in the study, we identified an individual (the counselee) for whom we collected genetic test results for BRCA1, BRCA2, or both; genotyping methods; pretest estimations of mutation probability using each model; and additional information about family history of cancer. We used genetic test results as the gold standard for judging the sensitivity and specificity of the various models. We evaluated all models on every counselee, except where noted.

Data Collection

Table 1 summarizes the salient data (24–32). Sources include 3 population-based studies and 8 data sets of individuals seen in clinics for women at high risk for a BRCA mutation. In the population-based studies, the participants reflected the demographic characteristics of a defined subpopulation (for example, all breast cancer cases in Orange County in the University of California, Irvine [UCI], study [31]). In contrast, patients from high-risk clinics had been referred because of a family history of cancer or were self-referred because of an interest in genetic testing (inclusion criteria varied across clinics).

Table 1.

Demographic Characteristics of Counselees and Sample Size, by Center ^*

Center	Population	Persons Tested, n	Men, %	Mean Age (SD), y	Breast Cancer, n	Ovarian Cancer, n	No Cancer, n	BRCA1 Positive, n	BRCA2 Positive, n	Reference
BCM	Ashkenazi Jewish volunteers	282	0	53.1 (11.8)	33	2	247	6	0	25
City of Hope	Counseling clinic	77	0	49.8 (13.0)	47	5	25	13	5	26
Duke University	Counseling clinic	275	0	47.8 (10.7)	237	27	22	41	18	27
FHCRC	Population-based study	583	0	45.7 (5.1)	320	6	263	22	12	28
Georgetown University	Counseling clinic	242	0	52.9 (11.4)	227	20	3	55	23	21
HCI	Counseling clinic	61	0	58.5 (15.2)	47	2	12	6	8	-
JHU	Counseling clinic	105	3	50.2 (10.3)	57	7	43	0	6	29
Penn	Counseling clinic	676	69	50.9 (13.0)	489	82	138	121	53	11, 30
UTSW	Counseling clinic	121	7	47.9 (12.8)	67	10	50	23	9	24
UCI	Population-based study	803	9	62.5 (13.6)	605	122	87	10	4	31
MDACC	Counseling clinic	117	7	51.2 (13.3)	59	8	53	25	18	32
Total	-	3342	95	52.8 (13.1)	2188	291	943	332	156	-

^*BCM = Baylor College of Medicine; FHCRC = Fred Hutchinson Cancer Research Center; HCI = Huntsman Cancer Institute; JHU = Johns Hopkins University; MDACC = M.D. Anderson Cancer Center; Penn = University of Pennsylvania; UCI = University of California, Irvine (Orange County); UTSW = University of Texas Southwestern.

Each center calculated all of the model probabilities for its own families. We designated the first genotyped person in each family as the counselee and computed predictions by using the genetic counseling software CaGene (University of Texas Southwestern Medical Center, Dallas, Texas) (24). The software version was customized and distributed to participating sites to ensure uniform procedures across all sites. Data entry and computation of model predictions were performed at the sites. This decentralized approach for data entry and probability calculations allowed site investigators to use pedigree information that models required but that centers could not export to a central site because of privacy concerns. In addition to model predictions, a subset of centers also exported the data required for the models to the National Cancer Institute’s (NCI) Cancer Genetics Network Data Coordinating Center. The study population includes 3342 families.

The institutional review boards at each participating institution approved the study protocol. All included counselees gave consent for using their data for research according to local institutional review board requirements. The Cancer Genetics Network steering committee reviewed the study design.

Genetic Testing

Appendix Table 1 (available at www.annals.org) summarizes genotyping methods by center and provides a brief description of each method. Determining whether a person carries a deleterious mutation of BRCA1 or BRCA2 is technically demanding because of the large size of these genes, the wide spectrum of mutations, and the presence of mutations whose clinical significance is unknown (33–35). Commercial testing uses sequencing to search for unknown mutations or to probe for mutations that are commonly found among Ashkenazi Jewish persons. Research settings, particularly in the time in which the study was conducted, have used less expensive and less sensitive techniques (Appendix Table 1, available at www.annals.org). Although sequencing is the most sensitive of the techniques used in our study, recent evidence highlights how it can miss certain mutations, such as large deletions or intronic mutations (3, 36). Therefore, the set of individuals carrying a mutation (the carriers) is not the same as the set of individuals who test positive for a mutation (the positive cases). Thus, Table 1 underestimates the true number of carriers; the size of the error varies according to the method of genotyping.

Models

We studied 7 models: BRCAPRO, the family history assessment tool (FHAT), Finnish, Myriad, NCI, University of Pennsylvania (Penn), and Yale University (Yale). Appendix Table 2 (available at www.annals.org) summarizes the characteristics, input variables, and output of the models. Three broad categories of models have been proposed: empirical (Finnish, Myriad, NCI, and Penn), mendelian (BRCAPRO and Yale), and expert-based (FHAT). The first step in developing an empirical model is to summarize the salient aspects of a family history in some predictor variables. The second step is to apply statistical learning techniques, such as logistic regression, to describe the relationship between these variables and the genotyping results (the dependent variable). Mendelian models represent the known modes of inheritance of deleterious genetic variants by established mathematical relationships between phenotypes (in this case, cancer status of family members) and genotypes (14, 37–41). The mendelian model inputs include cancer incidence curves (penetrance) for both carriers and noncarriers and the prevalence of deleterious variants. Expert-based models calculate scores that summarize degree of risk, using algorithms constructed on the basis of clinical judgment. For example, FHAT (16) uses a 17-question interview to produce a quantitative score (score range, 0 to 45) representing the severity of family history.

Empirical models calculate the probability of a positive test result for a mutation in the counselee (that is, the result of genetic testing), whereas mendelian models directly estimate the probability of carrying a mutation (the true mutation status of the counselee) (37). The 2 types of predictions are therefore not directly comparable, a fact often overlooked in counseling practice. Because genotyping methods are highly specific for the BRCA1 and BRCA2 genes (that is, they have a very low false-positive rate), multiplying the genotype probability by the genotyping sensitivity gives the probability of finding a mutation. Therefore, to compare an empirical model probability of a BRCA mutation with a mendelian model probability, one must know the sensitivity of the genotyping method of the study used to develop the empirical model. Expert-based scores do not have a direct probabilistic interpretation. In our analyses, we rescaled the FHAT score by dividing by its maximum value of 45.

The Penn model (11) estimates the probability of a positive BRCA1 test result in any family member. We adapted it to provide the probability of a positive test in the counselee. We assigned affected counselees the same mutation probability as the family. We assigned unaffected counselees one half the family probability if the closest affected relative of the counselee is a first-degree relative and one quarter of the family probability if the closest relative is a second-degree relative.

We used a version of the BRCAPRO (13, 14) model based on the genetic variables described by Iversen and colleagues (42).

We defined the Yale model by postulating a single gene as reflecting all highly penetrant autosomal dominant breast cancer genes and used genetic variables from a segregation analysis of the Cancer and Steroid Hormone Study (10, 43, 44).

We did not include several models. The LAMBDA model (45) and the Spanish model (46) are empirical models developed on families from Australia and Spain. The Manchester (47) model is an expert-based scoring system. These 3 models became available after the Cancer Genetics Network data collection occurred. We also did not include 2 BRCA1 prediction–only models that are precursors of models considered here (12, 13) and 2 recent mendelian models, the Breast and Ovarian Analysis of Disease Incidence and Carrier Estimation Algorithm (BOADICEA) and International Breast Cancer Intervention (IBIS) Breast Cancer Risk Evaluation Tool, for which software implementations were not readily available at the time of data collection (48, 49). This omission is a limitation of our study, although a recent study (32) concluded that the BOADICEA, BRCAPRO, and Myriad models performed similarly.

Statistical Analysis

We combined data from all centers to create a matrix in which the rows are individual counselees and the columns include estimated probability of a BRCA1 or BRCA2 mutation using each model; stratification variables, such as age, Ashkenazi ethnicity, and cancer status of the counselee, genetic test results; and genotyping methods. We defined “positive cases” as individuals who test positive for either BRCA1 or BRCA2 and “negative cases” as individuals who had negative results on both tests. We excluded counselees who tested negative for 1 gene and were not tested for the other, which limited our analysis data set to 2240 individuals. Our analytic strategy is to compare predicted testing results for each model with actual testing results for all counselees and within specific counselee strata (for example, age, Ashkenazi ethnicity, or cancer status of the counselee).

Our measurement of discrimination is the c-statistic, which is equal to the area under the receiver-operating characteristic curve. It is also the probability that a randomly chosen test-positive counselee will have a higher probability (or prediction score) of a BRCA mutation than a randomly chosen test-negative counselee (50, 51), which implies a correct rank ordering of the 2 predictions. We computed the c-statistic by using all possible pairs of counselees, one of whom is positive and the other negative. The smallest possible value of the c-statistic is 0.0, wherein all predictions are incorrectly ordered, and the largest is 1.0, wherein all predictions are correctly ordered. A c-statistic of 0.5 means that the model would correctly order half of the pairs and would incorrectly order the other half. This method is equally applicable to empirical, mendelian, and expert-based approaches.

We evaluated all models in each center. Because the NCI model is intended for use in the Ashkenazi population, we evaluated it on Ashkenazi persons only. The applicability of some models is subject to minor restrictions, such that we had to exclude some families for each model (52). We did not evaluate a model on a counselee from a family that we knew had been used to develop the model. We could not follow this rule with the Myriad model because this information was not available. As a result, we may have overestimated the performance of Myriad. However, this overlap is probably limited to individuals genotyped by gene sequencing, who make up less than 25% of all study patients.

To assess the significance of trends observed when comparing all models as a group across strata, we used a Wilcoxon rank-sum test and a 2-sided alternative.

A potential limitation of our analysis plan arises from the imperfect and differing sensitivity of genotyping methods used. Whereas the genotypes of positive counselees are accurate because the false-positive rate of genotyping is negligible (33, 35), those of negative counselees are uncertain because of possible false-negative genotyping results. This discrepancy may result in a bias in favor of empirical models, which estimate the probability of a positive mutation test, and against mendelian models, which estimate the probability of a mutation. In parallel to the analysis presented here, we developed a customized approach that allows one to evaluate the c-statistic and other measurements by comparing predictions with imputed genotypes, therefore adjusting for heterogeneous test sensitivities. Results suggest that the findings reported here penalize mendelian models. Data are not shown, but the details are available from the authors on request. Finally, a limitation of the analysis is that normalized FHAT scores do not provide probabilities, and thus the 10% threshold does not have the same interpretation for this model as it does for the others.

Role of the Funding Sources

The Cancer Genetics Network funded part of the study and is responsible for good research practices and for data storage. The Cancer Genetics Network and the other funding sources, listed under “Grant Support,” had no other role in the design, conduct, and reporting of the study.

RESULTS

Range of Predictions across Models

The models differ widely in their predictions for a given counselee. The largest range of predictions across models was 99 percentage points, reached in families with male breast cancer. On average, the range of predictions was 27 percentage points. Among all possible pairwise comparisons between the predictions of a mendelian and an empirical model for the same counselee, 12% disagreed by 50 percentage points or more.

Model Discrimination

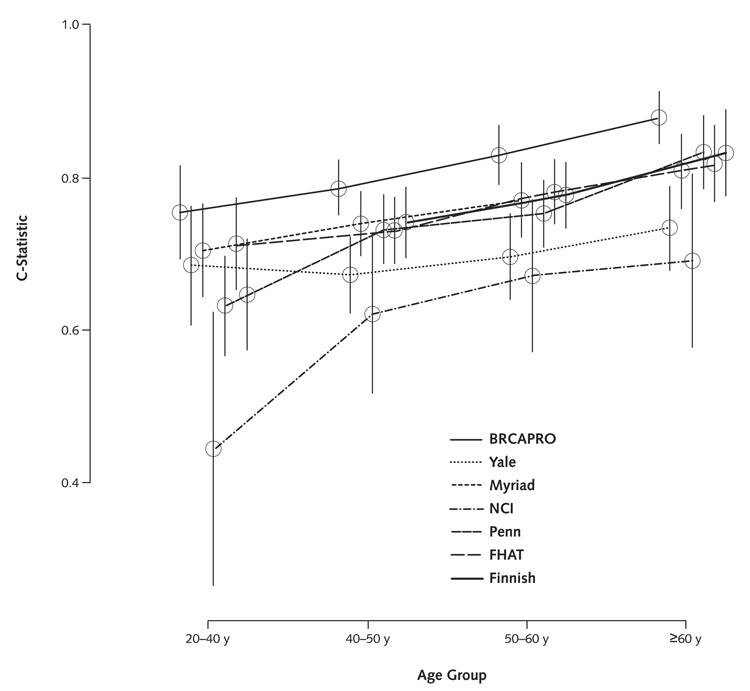
We used the c-statistic to summarize the models’ ability to distinguish individuals testing positive for either gene from those testing negative to both genes. Table 2 presents overall results, as well as results stratified by study type, ethnicity, and counselee cancer status. The Figure presents discrimination for each model, stratified by age. As seen in Table 2, in 82% of the possible comparisons between a positive and a negative counselee, BRCAPRO assigns a higher probability to the positive counselee. By comparison, the c-statistic for the Myriad model is 77%; the 95% CIs for the 2 c-statistics do not overlap.

Table 2.

C-Statistics (95% CIs) of the Models ^*

Variable	BRCAPRO	Yale	Myriad	NCI†	Penn‡	FHAT	Finnish
All persons	0.82 (0.81–0.84)	0.71 (0.68–0.74)	0.77 (0.75–0.79)	-	0.76 (0.74–0.79)	0.77 (0.75–0.8)	0.78 (0.75–0.8)
High-risk studies§	0.76 (0.73–0.79)	0.64 (0.61–0.67)	0.71 (0.68–0.74)	-	0.73 (0.7–0.76)	0.71 (0.68–0.74)	0.75 (0.73–0.78)
Population-based studies§	0.85 (0.81–0.88)	0.72 (0.65–0.79)	0.79 (0.72–0.86)	-	0.75 (0.69–0.81)	0.79 (0.73–0.85)	0.75 (0.68–0.82)
Not Ashkenazi Jewish∥	0.84 (0.82–0.86)	0.74 (0.71–0.77)	0.78 (0.75–0.81)	-	0.76 (0.74–0.79)	0.8 (0.78–0.83)	0.8 (0.78–0.82)
Ashkenazi Jewish∥	0.72 (0.67–0.77)	0.63 (0.57–0.69)	0.71 (0.66–0.76)	0.63 (0.57–0.68)	0.73 (0.68–0.79)	0.71 (0.66–0.77)	0.74 (0.68–0.8)
No cancer	0.74 (0.67–0.8)	0.62 (0.55–0.69)	0.73 (0.67–0.8)	-	0.79 (0.73–0.85)	0.68 (0.6–0.76)	0.81 (0.75–0.87)
Breast cancer only	0.84 (0.82–0.85)	0.76 (0.73–0.78)	0.76 (0.73–0.79)	-	0.74 (0.71–0.77)	0.77 (0.74–0.79)	0.74 (0.72–0.77)
Ovarian cancer only	0.88 (0.84–0.93)	0.8 (0.74–0.87)	0.87 (0.81–0.92)	-	0.68 (0.57–0.79)	0.83 (0.76–0.91)	0.82 (0.73–0.91)
Both breast and ovarian cancer	0.86 (0.78–0.94)	0.83 (0.75–0.91)	0.8 (0.7–0.91)	-	0.8 (0.71–0.89)	0.78 (0.67–0.89)	0.8 (0.72–0.89)

^*FHAT = family history assessment tool; NCI = National Cancer Institute; Penn = University of Pennsylvania; Yale = Yale University.

^†The NCI model was applied only to families of Ashkenazi ethnicity.

^‡The Penn model predicts BRCA1 mutations only. In the table, its performance in predicting mutations in either gene is evaluated to facilitate comparisons with other models and to capture a common use of the model.

^§The “population-based studies” row includes counselees from Fred Hutchinson Cancer Research Center; Baylor College of Medicine; and University of California, Irvine (Orange County). The remainder of counselees are placed in the “high-risk studies” row.

^∥The “Ashkenazi Jewish” row includes counselees of Ashkenazi ancestry from all centers. The remainder of the counselees are placed in the “not Ashkenazi Jewish” row.

Figure 1. C-statistic, by age of the counselee and model.

Points within age groups are slightly spaced horizontally for readability. Vertical bars are 95% CIs. A description of each model is given in Table 3. FHAT = family history assessment tool; NCI = National Cancer Institute; Penn = University of Pennsylvania; Yale = Yale University.

Results shown in Table 2 and the Figure identify areas of strength and weakness of individual models in specific clinical scenarios. Results differ somewhat depending on the stratum, and the 95% CIs often overlap. However, the following general trends emerge. As expected, models perform less well in individuals without breast or ovarian cancer and in younger counselees. Discrimination is generally better in the population-based studies. BRCAPRO has the largest c-statistic in all but 2 strata, although the range of c-statistics across all models is too narrow to choose a clearly superior model.

The methods used to detect mutations in BRCA1 or BRCA2 differed among the study sites, which introduces the possibility that differences among model performances reflect differences in mutation detection. In Appendix Table 3 (available at www.annals.org), we also considered separately 512 cases in which mutation screening was performed by gene sequencing. This analysis addresses the concern about confounding between centers’ characteristics and mutation testing methods, because within the gene sequencing stratum, all centers used the same method for gene sequencing and all 512 cases are from high-risk samples. The model prediction results are consistent with those obtained on all high-risk individuals across the various mutation testing methods used in different centers, suggesting that such confounding is not affecting our conclusions.

Sensitivity, Specificity, and Likelihood Ratios

To calculate sensitivity and specificity, we first specified the probability that defines the threshold between a positive model result and a negative model result. We divided the study population depending on whether each model’s prediction (probability or normalized score) exceeds a threshold of 10%. In the analysis, a mutation probability greater than 10% would be considered a positive model result. To illustrate the consequences of a referral threshold of 10%, we report the sensitivity, specificity, and likelihood ratios for the BRCAPRO model in Table 3 and for all models in Appendix Table 4 (available at www.annals.org). Comparisons across populations indicate a decrease in specificity and an increase in sensitivity as we move from population-based to high-risk studies. The ratio of the proportion of individuals above 10% among positive cases to the same proportion among negative cases is the positive likelihood ratio—the amount by which the odds of a positive test increases when a person’s estimated probability exceeds 10%.

Table 3.

Test Performance Characteristics and Posttest Probabilities for the BRCAPRO Model in 3 Populations^*

Variable	UCI Sample	FHCRC Sample	High-Risk Sample
Overall proportion of individuals testing positive	0.017	0.089	0.279
Sensitivity (95% PI)†	0.429 (0.207–0.656)	0.706 (0.547–0.834)	0.824 (0.786–0.857)
Specificity (95% PI)†	0.934 (0.913–0.950)	0.671 (0.620–0.715)	0.526 (0.499–0.551)
Positive likelihood ratio (95% PI)	6.503 (2.925–10.24)	2.148 (1.682–2.71)	1.739 (1.63–1.87)
Negative likelihood ratio (95% PI)	0.612 (0.372–0.843)	0.438 (0.242–0.669)	0.334 (0.269–0.408)
Positive predictive value (95% PI), n/n (%)‡	6/58 (10.34 [4.435–20.08])	24/139 (17.3 [11.69–24.2])	352/874 (40.3 [37.1–43.6])
Negative predictive value (95% PI), n/n (%)§	737/745 (98.9 [98.0–99.5])	235/245 (95.9 [92.9–97.9])	579/654 (88.5 [85.9–90.8])

^*95% PI = 95% posterior probability regions (obtained by using Jeffrey noninformative priors); FHCRC = Fred Hutchinson Cancer Research Center; UCI = University of California, Irvine (Orange County).

^†For a referral threshold probability of 10%.

^‡Proportion of individuals testing positive among those with probability or score >10%.

^§Proportion of individuals testing negative among those with probability or score ≤10%.

The negative likelihood ratio is the analogous ratio for proportions below or equal to the 10% threshold. According to the Bayes’ theorem, models with higher positive likelihood ratios and lower negative likelihood ratios increase the odds of testing positive more substantially when the probability exceeds 10% and decrease the odds more when the probability is below 10%, respectively. Table 3 and Appendix Table 4 (available at www.annals.org) show how these ratios vary with the model and study population. Exceeding the 10% threshold is stronger evidence for testing positive among unselected breast cancer cases (such as the UCI study [31]) than in a high-risk setting, in which more negative counselees will exceed the threshold as a result of patient selection.

Positive and Negative Predictive Values

The predictive value of a test is the probability of the target condition being present or absent corresponding to a positive or negative test result, respectively. It depends on the prevalence of the target condition in the population and the sensitivity and specificity of the test. In Table 3 and Appendix Table 5 (available at www.annals.org), we compute the proportion of test-positive individuals among those exceeding the 10% threshold (positive predictive value) and the proportion of test-negative individuals among those not exceeding the 10% threshold (negative predictive value). We perform this analysis separately for 3 subsets of the study populations, chosen because the prevalences of BRCA1 and BRCA2 mutations within 1 subset differ from those in the other 2 subsets: the UCI study, the Fred Hutchinson Cancer Research Center study (28), and all high-risk data combined. The UCI data (31) include all breast cancer cases (female and male) diagnosed in Orange County, California, during the year beginning 1 March 1994 and is therefore representative of patients with breast cancer presenting to a general oncology practice. The proportion of positive BRCA mutation tests is 1.74%. Table 4 and Appendix Table 6 (available at www.annals.org) show the consequences of referring patients with breast cancer for genetic testing and counseling if their risk exceeds 10%. For example, using the FHAT model, 4.7% of individuals with a score of 10% or greater will be positive and 99.5% of individuals with a score less than 10% will be negative. Because the predictive value of a test varies with the prevalence of the target condition, when the same referral threshold probability is applied to populations with higher prevalence, the number of test-positive cases missed by using a 10% referral threshold increases. In the high-risk population, where the proportion of positive mutation tests is 27.9%, 32% of those that exceed a 10% threshold on the FHAT score will be test-positive but only 86% of the individuals below the 10% threshold will be test-negative. A similar trend is present with the other models in Appendix Table 5 (available at www.annals.org). The Fred Hutchinson Cancer Research Center population (28) presents an intermediate case: The data are from a case–control study with a mutation prevalence of 8.85%. The cases had either early onset (age <35 years) or a first-degree family history of breast cancer and thus present an intermediate scenario between the low-risk UCI population and the high-risk population. In this population, 11.9% of those with FHAT scores that exceed a 10% threshold will be positive, and 98.2% of the individuals below the 10% threshold will be negative.

Table 4.

Number of Patients per 1000 Referred for Mutation Testing with Different Threshold Probabilities for Referral in the BRCAPRO Model ^*

Variable	Proportion Positive	Threshold	Mutation-Negative above Threshold	Mutation-Positive above Threshold	Mutation-Positive below Threshold	Mutation-Negative below Threshold	Total
UCI sample	0.017	0.05	80.9	8.7	8.7	901.6	1000
		0.1	64.8	7.5	10	917.8	1000
		0.2	47.3	5	12.5	935.2	1000
FHCRC sample	0.089	0.05	351.6	67.7	20.8	559.9	1000
		0.1	299.5	62.5	26	612	1000
		0.2	242.2	62.5	26	669.3	1000
High-risk sample	0.279	0.05	418.8	241.5	38	301.7	1000
		0.1	341.6	230.4	49.1	378.9	1000
		0.2	264.4	209.4	70	456.2	1000

^*These calculations consider the hypothetical scenario in which individuals are referred for genetic counseling whenever their predicted probability using BRCAPRO exceeds the threshold indicated in the third column. “Positive” and “negative” refer to the results of genetic testing, as described in the Methods section. Counts are rescaled to add up to 1000 for ease of comparison. See Appendix Table 4 and Appendix Table 5 (available at www.annals.org) for actual sample sizes and Appendix Table 6 (available at www.annals.org) for the similar calculations using the other models. FHCRC = Fred Hutchinson Cancer Research Center; UCI = University of California, Irvine (Orange County).

Effect of Changes in the Threshold

Table 4 illustrates the effect of increasing the threshold to 20% and lowering the threshold to 5% on the classification of patients by the BRCAPRO model. The same information for other models appears in Appendix Table 6 (available at www.annals.org). For example, in the UCI study, a threshold of 5% on the BRCAPRO model predictions leads to referral of half of the test-positive individuals in the population, while still referring less than 10% of the total number of individuals. In general, lowering the threshold will capture a larger proportion of test-positive individuals at the cost of increasing the number of referrals.

DISCUSSION

We provide a comprehensive view of the predictive performance of 7 commonly used, publicly available mutation carrier prediction models for the BRCA1 and BRCA2 genes, across a range of clinically relevant strata. As shown in Table 2, the c-statistic for the better-performing models clusters closely around 80%. Clinicians and counselors can use these results to identify the model that performs best in the strata most relevant to their activities and to weigh the differences in discrimination against practical implementation issues that are specific to their practice. BRCAPRO has the largest c-statistic overall and in all but 2 clinical strata, although the range of c-statistics across all models is too narrow to identify a clearly superior model. If used for referral outside of high-risk groups, all models have high rates of false-negative and false-positive results across a range of thresholds to refer for testing (Appendix Table 6, available at www.annals.org).

A strength of our study is the inclusion of both high-risk and population-based centers. The high-risk samples reflect genetic counseling clinics, and the population-based samples reflect the broader spectrum of patients seen in general oncology practice. The c-statistics reported for the high-risk population are similar to those of previous studies performed in similar settings (53–57). The c-statistic of models is generally greater in the population-based samples than in the high-risk samples (P = 0.036) (Table 2), which suggests that the models can be applied to more broadly representative settings than high-risk clinics. In high-risk populations, a referral threshold of 10% results in relatively high sensitivity with very low specificity. In population-based cohorts, the specificity is higher but the sensitivity is lower, and the 10% threshold misses a large proportion of test-positive cases. Likelihood ratios resulting from the 10% threshold also vary markedly across populations.

Genetic counselors used mutation probability thresholds for referral in the past, and they are still sometimes used for insurance coverage purposes (23). However, guidelines no longer recommend this practice (7). We used a threshold probability to calculate model sensitivity and specificity, which permitted us to illustrate the consequences of using the models to decide on referral for mutation testing. Results in Appendix Table 4 (available at www.annals.org) imply that using a 10% threshold for the pooled high-risk populations will, depending on the model used, exclude 10% to 20% of test-positive individuals from genetic testing. The analogous figure for unselected breast cancer cases is 1% to 8% excluded. Conversely, Table 3 and Table 4 and Appendix Table 5 (available at www.annals.org) show that the models would refer many women who do not carry mutations for testing. The low positive predictive values that we found are consistent with earlier reports (24) comparing BRCAPRO with genetic counselors’ assessments of the same family history. When models are used on unselected breast cancer cases to determine whether to refer a patient to a counseling clinic, using a 10% threshold would still miss women who would test positive, a circumstance more serious than an unnecessary referral. The estimated positive and negative predicted values (Table 3 and Appendix Table 5 [available at www.annals.org]) do not apply to healthy individuals from the general population.

We found that the estimated probability of testing positive differed widely when different models were applied to the same counselee. Genetic counselors may consider using several predictive models, as well as qualitative pedigree analysis (23), because the variation among model predictions may provide an indication of their reliability.

Limitations of our study concern the mutation testing methods used and the lack of representation of minorities. Mutation testing techniques varied across centers generally and across high-risk and population-based studies more specifically. All cases tested using gene sequencing were in high-risk centers, whereas studies of low-risk populations used less sensitive mutation testing methods. However, this potential confounding probably leads to an underestimate of the c-statistics in population-based studies; our conclusion about generalizability is therefore unlikely to be affected. Also, minority populations may be underrepresented in the populations used to develop the models, and existing models do not explicitly take into account the possibility that minority groups, such as African Americans, have a higher probability of carrying genetic variants of uncertain clinical significance, which would be missed by genetic testing. However, independent evidence suggests that BRCAPRO discriminated between carriers and noncarriers in African American (58) and Hispanic (59) families as well as it did in white families.

Genotyping for BRCA1 and BRCA2 is now widespread. Myriad Genetics Laboratories, Salt Lake City, Utah, alone tested more than 100 000 individuals by 2005 (60). Many more women are being counseled about whether to be genotyped. Model-based mutation probabilities have been a critical component of individualized counseling. Our comprehensive evaluation indicates that, overall, the concordance observed between predictions and test results is high. However, relying on model probabilities to decide about referral can cause many false-positive and false-negative referral decisions (Table 4). Decision making about genetic testing and prevention should reflect a broader range of factors, of which carrier probabilities are but one (7, 8). Other factors include the effectiveness and cost of genotyping; the available means and efficacy of measures for early detection and risk reduction; the counselee’s willingness to undergo enhanced surveillance or risk-reducing interventions; and the possible psychological, social, and ethical effects of testing. Physicians should rely on health care professionals who are experienced in cancer genetics to determine the appropriateness of genetic testing. Their evaluation may discover additional reasons for caution because of small family size, few female family members, limited or unconfirmed family history, or family histories that suggest rarer syndromes. In primary care settings for referral to further genetic counseling, setting a referral threshold probability may be a practical approach; however, we do not recommend using a strict 10% threshold, because it may miss a large proportion of clinically appropriate cases.

Appendix Tables

Appendix Table 1.

Number of Counselees, by Genotyping Method for Each Gene and Center ^*

Genotyping Method	Duke Univ.	Penn	George- town Univ.	JHU	FHCRC	BCM	MDACC	UTSW	HCI	UCI	COH
BRCA1
SSCP	1	61	170	0	583	0	0	1	0	9	0
Seq	72	127	28	68	0	0	105	105	61	0	33
ASO	0	0	0	1	0	0	0	0	0	688	0
Targeted mut screening	37	0	0	0	0	0	0	0	0	0	0
Seq for 185delAG and 5382insC	41	91	4	33	0	0	11	15	0	0	25
Seq for 185delAG only	0	0	0	0	0	282	0	0	0	106	0
CSGE	3	310	41	1	0	0	1	0	0	0	0
SSCP + ASO	0	0	18	0	0	0	0	0	0	0	0
Targeted mut screening + Seq	60	0	0	0	0	0	0	0	0	0	0
Targeted mut screening + CSGE	23	0	0	0	0	0	0	0	0	0	0
Other†	4	42	14	2	0	0	0	0	0	0	19
None‡	1	45	0	0	0	0	0	0	0	0	0
BRCA2
SSCP	0	0	171	0	384	0	0	0	0	0	0
Seq	64	242	28	66	0	0	104	101	61	0	32
CSGE	5	199	40	1	0	0	0	0	0	0	0
ASO	55	0	0	1	0	0	0	0	0	0	0
Seq for 6174delT	47	0	6	33	0	0	11	14	0	688	25
SSCP + ASO	0	0	17	0	0	0	0	0	0	0	0
Seq + ASO	24	0	0	0	0	0	0	0	0	0	0
ASO + Seq	36	0	0	0	0	0	0	0	0	0	0
Other†	0	76	13	1	0	0	0	0	0	115	19
None‡	11	159	0	3	199	282	2	6	0	0	1

^*ASO = allele-specific oligonucleotide hybridization assay (33, 61); BCM = Baylor College of Medicine; COH = City of Hope; CSGE = confirmation-sensitive gel electrophoresis (33); FHCRC = Fred Hutchinson Cancer Research Center; HCI = Huntsman Cancer Institute; JHU = Johns Hopkins University; MDACC = M.D. Anderson Cancer Center; Penn = University of Pennsylvania; Seq = full sequencing of the coding regions of the gene, as implemented by Myriad Genetics Laboratories at the time of testing (18, 61, 62); Seq for 185delAG = sequencing for Ashkenazi founder mutation 185delAG in BRCA1 (1, 63); Seq for 185delAG and 5382insC = sequencing for Ashkenazi founder mutations 185delAG and 5382insC in BRCA1 (1, 63); Seq for 6174delT = sequencing for Ashkenazi founder mutation 6174delT in BRCA1 (1, 63); SSCP = single-strand conformation polymorphism (62); targeted mut screening = sequencing for a panel of 8 known deleterious mutation in BRCA1 and 4 deleterious mutations in BRCA2 (64); UCI = University of California, Irvine (Orange County); UTSW = University of Texas Southwestern.

^†”Other” includes all genotyping methods that were used in a sample that was too small to be worth reporting in detail, as well as some cases whose genotyping method was missing.

^‡“None” indicates that individuals were tested for 1 gene and not the other, contributing to the main analysis only if they test positive. This occurs either by design or because genes are tested sequentially and the second gene is not tested after a mutation is found in the first.

Appendix Table 2.

Input Variables and Features of Each Model ^*

Variable	BRCAPRO	FHAT	Finnish	Myriad	NCI†	Penn	Yale
Model characteristics
Mendelian	•						•
Empirical			•	•	•	•
Expert-based		•
Requires a computer	•		•		•	•	•
Requires pedigree	•						•
Available in the CaGene (67) package‡	•	•	•	•	•	•	•
Trained on high-risk data	•	•	•	•		•
Size of training sample (for empirical models), n			148	238§	5318	169
Updated periodically	•			•
References: development	13, 14, 65	16	17	18, 61, 66	15	11
References: validation	24, 46, 58, 32, 53?57	16, 54	46, 55	46, 32, 53–55, 57		46, 32, 54, 55	55
Model input∥
Mendelian transmission	•						•
Exact family structure	•						•
Age of unaffected counselee	•				•		•
Age of unaffected relatives	•						•
Ashkenazi Jewish ethnicity of family	•			•	•	•	•
Breast cancer status, counselee	•	•		•	•	•	•
Breast cancer status, relatives	•	•		•	•	•	•
Breast cancer age of onset, counselee	•	•	•	•	•	•	•
Breast cancer age of onset, relatives	•	•	•	•		•	•
Ovarian cancer status, counselee	•	•	•	•	•	•
Ovarian cancer status, relatives	•	•	•	•	•	•
Ovarian cancer age of onset, counselee	•	•			•
Ovarian cancer age of onset, relatives	•	•
Male breast cancer status, counselee	•	•		•			•
Male breast cancer status, relatives	•	•		•			•
Both breast and ovarian cancer in counselee	•	•				•	•
Both breast and ovarian cancer in a single relative	•					•	•
Bilateral breast cancer status, counselee	•	•					•
Bilateral breast cancer status, relatives	•	•					•
Bilateral breast cancer, both ages of onset, counselee	•						•
Bilateral breast cancer, both ages of onset, relatives	•						•
Prostate cancer in relatives		•
Colon cancer in relatives		•
Model output
Predictions for BRCA1 and BRCA2 separately	•
Predictions for BRCA1 and BRCA2 together	•		•	•	•
Predictions for BRCA1 only						•
Probability of carrying a mutation	•						•
Probability of finding a mutation if tested			•	•	•	•
Nonprobabilistic score		•

^*FHAT = family history assessment tool; NCI = National Cancer Institute; Penn = University of Pennsylvania; Yale = Yale University.

^†Intended for use with Ashkenazi Jewish women only.

^‡CaGene manufactured by University of Texas Southwestern Medical Center, Dallas, Texas (accessed at www4.utsouthwestern.edu/breasthealth/cagene on 1 August 2007).

^§Classes were originally selected by using 238 breast cancer cases. Subsequently, chances of finding a mutation in each risk class have been updated by using empirical frequencies from additional genotyping at Myriad. We used the January 2002 version of BRCAPRO (accessed at http://astor.som.jhmi.edu/BayesMendel/brcapro.html on 1 August 2007).

^∥Models encode and utilize these in different ways

Appendix Table 3.

C-Statistics (95% CIs) of the Models, by Cancer Status of the Counselee, Study Type, Ashkenazi Ethnicity, and Overall, for Persons Tested by Gene Sequencing ^*

Model	All Persons	Not Ashkenazi Jewish	Ashkenazi Jewish	No Cancer	Breast Cancer Only	Ovarian Cancer Only	Both Breast and Ovarian Cancer
BRCAPRO	0.74 (0.69–0.79)	0.75 (0.7–0.81)	0.66 (0.49–0.83)	0.61 (0.49–0.72)	0.76 (0.71–0.81)	0.91 (0.8–1.0)	0.81 (0.63–0.99)
Yale	0.64 (0.58–0.69)	0.65 (0.59–0.71)	0.61 (0.46–0.77)	0.57 (0.46–0.67)	0.67 (0.61–0.74)	0.82 (0.68–0.95)	0.71 (0.46–0.96)
Myriad	0.67 (0.62–0.72)	0.68 (0.62–0.73)	0.66 (0.49–0.82)	0.61 (0.49–0.73)	0.65 (0.58–0.72)	0.87 (0.74–0.99)	0.67 (0.43–0.91)
NCI†	–	–	0.6 (0.45–0.75)	–	–	–	–
Penn‐	0.69 (0.63–0.75)	0.69 (0.63–0.74)	0.76 (0.61–0.92)	0.7 (0.57–0.83)	0.64 (0.57–0.71)	0.7 (0.45–0.95)	0.62 (0.38–0.86)
FHAT	0.68 (0.63–0.73)	0.69 (0.64–0.75)	0.66 (0.49–0.82)	0.58 (0.45–0.71)	0.66 (0.59–0.73)	0.84 (0.7–0.98)	0.72 (0.49–0.94)
Finnish	0.71 (0.66–0.77)	0.69 (0.64–0.75)	0.78 (0.6–0.95)	0.8 (0.69–0.91)	0.63 (0.56–0.69)	0.87 (0.69–1)	0.69 (0.47–0.91)

^*FHAT = family history assessment tool; NCI = National Cancer Institute; Penn = University of Pennsylvania; Yale = Yale University.

^†The NCI model was applied only to families of Ashkenazi ethnicity.

^‡The Penn model predicts BRCA1 mutations only. In the table, its performance in predicting mutations at either gene is evaluated to facilitate comparisons with other models and to capture a common use of the model.

Appendix Table 4.

Sensitivity, Specificity, and Likelihood Ratios of All Predictive Models ^*

Model	UCI Sample	FHCRC Sample	High-Risk Sample
Sensitivity (95% PI)†
BRCAPRO	0.429 (0.207–0.656)	0.706 (0.547–0.834)	0.824 (0.786–0.857)
Yale	0.071 (0.010–0.260)	0.765 (0.627–0.866)	0.639 (0.592–0.677)
Myriad	0.286 (0.126–0.540)	0.853 (0.734–0.936)	0.775 (0.732–0.813)
NCI	0.400 (0.102–0.775)	1.000 (0.354–1.000)	0.625 (0.522–0.697)
FHAT	0.786 (0.536–0.931)	0.941 (0.837–0.987)	0.885 (0.852–0.913)
Finnish	0.273 (0.082–0.563)	0.853 (0.712–0.931)	0.728 (0.686–0.777)
Specificity (95% PI)†
BRCAPRO	0.934 (0.913–0.950)	0.671 (0.6201–0.715)	0.526 (0.499–0.551)
Yale	0.928 (0.910–0.943)	0.597 (0.5443–0.639)	0.574 (0.543–0.605)
Myriad	0.864 (0.840–0.888)	0.683 (0.6390–0.730)	0.479 (0.449–0.512)
NCI	0.766 (0.627–0.857)	0.125 (0.0193–0.486)	0.655 (0.600–0.711)
FHAT	0.720 (0.694–0.749)	0.320 (0.2669–0.375)	0.271 (0.249–0.299)
Finnish	0.879 (0.850–0.904)	0.447 (0.3954–0.505)	0.653 (0.628–0.682)
Positive LR (95% PI)†
BRCAPRO	6.503 (2.925–10.24)	2.148 (1.682–2.71)	1.739 (1.63–1.87)
Yale	0.989 (0.125–3.67)	1.898 (1.500–2.23)	1.501 (1.37–1.65)
Myriad	2.107 (0.899–4.13)	2.689 (2.127–3.29)	1.487 (1.39–1.60)
NCI	1.709 (0.445–3.84)	1.143 (0.429–1.68)	1.813 (1.42–2.20)
FHAT	2.805 (1.981–3.45)	1.384 (1.210–1.55)	1.214 (1.16–1.27)
Finnish	2.259 (0.679–4.46)	1.543 (1.282–1.80)	2.097 (1.89–2.34)
Negative LR (95% PI)†
BRCAPRO	0.612 (0.3722–0.843)	0.438 (0.24249–0.669)	0.334 (0.269–0.408)
Yale	1.001 (0.8018–1.075)	0.394 (0.22660–0.629)	0.628 (0.548–0.708)
Myriad	0.826 (0.5284–1.018)	0.215 (0.09054–0.395)	0.47 (0.388–0.556)
NCI	0.783 (0.3129–1.229)	0 (0–9.819)	0.572 (0.454–0.750)
FHAT	0.298 (0.0957–0.632)	0.184 (0.03927–0.547)	0.424 (0.315–0.555)
Finnish	0.827 (0.5017–1.045)	0.329 (0.14274–0.637)	0.416 (0.340–0.485)

^*For each model, we divided the study population into 2 groups depending on whether the model’s prediction for a positive for either gene is >10%; crosstabulated this information with the genetic testing results; and computed the sensitivity, specificity, and LRs. The 95% PIs are 95% posterior probability regions (obtained by using Jeffrey noninformative priors). The PIs are necessary to account for skewness and small sample sizes in some cells. FHAT = family history assessment tool; FHCRC = Fred Hutchinson Cancer Research Center; LR = likelihood ratio; NCI = National Cancer Institute; UCI = University of California, Irvine (Orange County); Yale = Yale University.

^†For a referral threshold probability of 10%.

Appendix Table 5.

Predictive Performance of Models^*

Model	UCI Sample	FHCRC Sample	High-Risk Sample
Individuals testing positive among those with probability >10% [95% PI], n/n (%) †
BRCAPRO	6/58 (10.34 [4.435–20.08])	24/139 (17.3 [11.69–24.2])	352/874 (40.3 [37.1–43.6])
Yale	1/58 (1.72 [0.187–7.78])	26/167 (15.6 [10.68–21.6])	273/742 (36.8 [33.4–40.3])
Myriad	4/111 (3.60 [1.228–8.34])	29/140 (20.7 [14.64–28.0])	331/905 (36.6 [33.5–39.8])
NCI	2/13 (15.38 [3.341–40.90])	2/9 (22.2 [4.93–54.4])	75/176 (42.6 [35.5–50.0])
FHAT	11/232 (4.74 [2.545–8.06])	32/270 (11.9 [8.41–16.1])	378/1181 (32.0 [29.4–34.7])
Finnish	3/77 (3.90 [1.109–10.03])	29/218 (13.3 [9.29–18.3])	284/642 (44.2 [40.4–48.1])
Individuals testing negative among those with probability ≤10% [95% PI], n/n (%) ‡
BRCAPRO	737/745 (98.9 [98.0–99.5])	235/245 (95.9 [92.9–97.9])	579/654 (88.5 [85.9–90.8])
Yale	732/745 (98.3 [97.1–99.0])	209/217 (96.3 [93.2–98.2])	632/786 (80.4 [77.5–83.1])
Myriad	682/692 (98.6 [97.5–99.3])	239/244 (98.0 [95.6–99.2])	527/623 (84.6 [81.6–87.3])
NCI	36/39 (92.3 [80.9–97.8])	1/1 (100.0 [14.7–100.0])	192/237 (81.0 [75.7–85.6])
FHAT	568/571 (99.5 [98.6–99.9])	112/114 (98.2 [94.5–99.6])	298/347 (85.9 [81.9–89.2])
Finnish	539/547 (98.5 [97.3–99.3])	153/158 (96.8 [93.2–98.8])	673/779 (86.4 [83.9–88.7])

^*For each model, we divided the study population into 2 groups depending on whether the model’s prediction for a positive result for either gene is >10%, crosstabulated this information with the genetic testing results, and computed the positive and negative predictive values. The 95% PIs are 95% posterior probability regions (obtained by using Jeffrey noninformative priors). The PIs are necessary to account for skewness and small sample sizes in some cells. FHAT = family history assessment tool; FHCRC = Fred Hutchinson Cancer Research Center; UCI = University of California, Irvine (Orange County); Yale = Yale University.

^†Positive predictive value.

^‡Negative predictive value.

Appendix Table 6.

Number of Patients per 1000 Referred for Mutation Testing, with Different Threshold Probabilities for Referral^*

Variable	Proportion Positive	Threshold	Mutation-Negative above Threshold	Mutation-Positive above Threshold	Mutation-Positive below Threshold	Mutation-Negative below Threshold	Total
Yale
UCI sample	0.017	0.05	102.1	2.5	14.9	880.4	1000
		0.1	71	1.2	16.2	911.6	1000
		0.2	43.6	1.2	16.2	939	1000
FHCRC sample	0.089	0.05	455.7	75.5	13	455.7	1000
		0.1	367.2	67.7	20.8	544.3	1000
		0.2	291.7	59.9	28.6	619.8	1000
High-risk sample	0.279	0.05	376.3	197	82.5	344.2	1000
		0.1	306.9	178.7	100.8	413.6	1000
		0.2	234.9	158.4	121.1	485.6	1000
Myriad
UCI sample	0.017	0.05	459.5	11.2	6.2	523	1000
		0.1	133.3	5	12.5	849.3	1000
		0.2	64.8	3.7	13.7	917.8	1000
FHCRC sample	0.089	0.05	750	88.5	0	161.5	1000
		0.1	289.1	75.5	13	622.4	1000
		0.2	80.7	36.5	52.1	830.7	1000
High-risk sample	0.279	0.05	549.1	255.2	24.2	171.5	1000
		0.1	375.7	216.6	62.8	344.9	1000
		0.2	138.7	138.7	140.7	581.8	1000
NCI
UCI sample	0.096	0.05	211.5	38.5	57.7	692.3	1000
		0.1	211.5	38.5	57.7	692.3	1000
		0.2	76.9	0	96.2	826.9	1000
FHCRC sample	0.2	0.05	700	200	0	100	1000
		0.1	700	200	0	100	1000
		0.2	500	100	100	300	1000
High-risk sample	0.291	0.05	247	181.6	109	462.5	1000
		0.1	244.6	181.6	109	464.9	1000
		0.2	104.1	82.3	208.2	605.3	1000
FHAT
UCI sample	0.017	0.05	638.9	17.4	0	343.7	1000
		0.1	275.2	13.7	3.7	707.3	1000
		0.2	51.1	3.7	13.7	931.5	1000
FHCRC sample	0.089	0.05	849	88.5	0	62.5	1000
		0.1	619.8	83.3	5.2	291.7	1000
		0.2	177.1	54.7	33.9	734.4	1000
High-risk sample	0.279	0.05	678	269	10.5	42.5	1000
		0.1	525.5	247.4	32.1	195	1000
		0.2	174.7	158.4	121.1	545.8	1000
Finnish
UCI sample	0.018	0.05	216.3	9.6	8	766	1000
		0.1	118.6	4.8	12.8	863.8	1000
		0.2	60.9	4.8	12.8	921.5	1000
FHCRC sample	0.09	0.05	656.9	87.8	2.7	252.7	1000
		0.1	502.7	77.1	13.3	406.9	1000
		0.2	170.2	39.9	50.0	739.4	1000
High-risk sample	0.274	0.05	373.7	233.6	40.8	351.9	1000
		0.1	251.9	199.9	74.6	473.6	1000
		0.2	145	145.7	128.8	580.6	1000

^*Continued from Table 4. FHAT = family history assessment tool; FHCRC = Fred Hutchinson Cancer Research Center; NCI = National Cancer Institute; UCI = University of California, Irvine (Orange County); Yale = Yale University.