Calibration of estimated biting forces in domestic canids: comparison of post-mortem and in vivo measurements

Abstract

Estimates of biting forces are widely used in paleontological and comparative studies of feeding mechanics and performance, and are usually derived from lever models based on measurements made on the skull that are relevant to the mechanics of the masticatory system. Owing to assumptions and unmeasurable errors in their estimation, such values are used comparatively rather than as absolute estimates. The purpose of this paper was to provide calibration of post-mortem calculated bite force estimates by comparing them to in vivo forces derived from a sample of 20 domestic dogs (Canis familiaris) during muscle stimulation under general anaesthesia. Two lever models previously described in the literature were used to estimate post-mortem values, and regression analysis was also performed to derive best-fit equations against a number of morphometric measurements on the skull. The ranges of observed forces in vivo were 147–946 N at the canine, and 524–3417 N at the second molar. The lever models substantially underestimated these forces, giving mean values between 39% and 61% of the observed means. Predictability was considerably improved by removing the linear bias and deviation of the regression slope from unity with an adjustment equation. Best-fit statistical models developed on these animals performed considerably better (calculated means within 0.54% of observed means) and included easily measureable variables such as bodyweight, dimensions of the temporalis fossa and out-lever from the jaw joint to the biting tooth. These data should lead to more accurate absolute, rather than relative, estimates of biting forces for other extant and fossil canids, and other carnivorans by extrapolation.

Introduction

There is an ongoing interest in evaluating biting forces in relation to trophic specialization and body size in mammals (Kiltie, 1984) and other species (Erickson et al. 2003; McBrayer & Anderson, 2007). Assessment of biting forces from cranial measurements in extant carnivores has been used to estimate stress distribution in the skull (Thomason, 1991), allometric relationships of dental strength to force of biting (Christiansen & Adolfssen, 2005), and the relationship between maximal biting force and dietary specialization in carnivorans (Christiansen & Wroe, 2007). When the mammals under study are extinct, estimates of biting forces have proved useful in inferring feeding behaviour and predator–prey relationships (Wroe et al. 2005), guild structure among predators (Biknevicius & van Valkenburgh, 1996), and comparing the biomechanical performance of the feeding apparatus between extant and extinct forms (McHenry et al. 2007).

Methods of estimating maximal forces of biting for individual skulls or species in the works cited above were based on lever models of the masticatory apparatus. They included approximations of the cross-sectional area of the major jaw-adducting muscles, approximate measurements of their moment arms about the temporomandibular joint (in-levers), and moment arms of selected teeth about that joint (out-levers). Kiltie (1984) presented one such model in which the areas of the muscles were simply represented as rectangles defined by readily accessible length and width measurements of their bony attachments. Thomason (1991) presented a method in which an approximation of the total physiological cross-sectional area of the temporalis, masseter and medial pterygoid muscles was made, with in-levers based on the centroids of those areas. This latter method has been applied in several subsequent studies (Christiansen & Adolfssen, 2005; Wroe et al. 2005; Christiansen, 2007; Christiansen & Wroe, 2007), usually to derive relative forces for comparison among species rather than absolute values. The major simplifying assumptions made for these models are (1) that the true physiological cross-section of muscles, which have a complex three-dimensional architecture (Schumacher, 1961; Miller et al. 1965), can be extensively simplified, (2) that contralateral muscles are assumed to contract equally forcefully (Dessem, 1989), and (3) that sensory feedback from the dentition, which normally modulates biting force (Dessem, 1989; Lund & Kolta, 2006), can be ignored. Thus, the models are first approximations, as was recognized by the original authors. Or paleontological specimens, however, there is no means for obtaining data to support or completely obviate these assumptions.

In the case of comparative studies of extinct carnivore species, the models are defensible, in that they provide relative estimates of maximal forces of biting (which may be expected to be important in feeding performance of high-end predators), and that the forces are derived directly from the available evidence, i.e. the morphology of the skulls. Even in a recent work, in which the numerous components of the adductor musculature were represented in sophisticated computer models of the extinct saber-tooth Smilodon fatalis and the modern lion Panthera leo, the authors cautiously chose to compare the species relatively rather than using absolute values of bite force estimate (McHenry et al. 2007). Despite being able to provide some defence for the lever models, which do not accurately represent muscular anatomy, it is certainly desirable that a means of calibrating estimates of maximal biting forces made from cranial dimensions be made available. That is the objective of this paper, in which we compare measured maximal forces recorded in vivo from anaesthetized domestic dogs (Canis familiaris), with force estimates derived post-mortem from their dried skulls, applying the models of both Kiltie (1984) and Thomason (1991). Forces of biting in dogs have been previously recorded for unrestrained biting in vivo(Lindner et al. 1995), but have not been used to calibrate post-mortem methods of assessing such forces. We also take another modeling approach in which statistical equations are developed based on regression analyses to generate ‘best fit’ models of observed bite forces on morphometric measurements, to identify the variables that are most strongly related to bite force. No attempt is made to include details of muscular anatomy, as the purpose is to calibrate force estimates derived directly from the skull.

Materials and methods

Animals

Twenty domestic dogs of mixed breed were used in this study, and their data are summarized in Table 1. All dogs were in apparent good health, and spanned a wide range of size (5–40 kg bodyweight) and craniofacial form (brachycephalic to dolichocephalic). Dogs ranged in age from 10 months to 14 years (as estimated from their dentition), and were of both genders (intact, including one hermaphrodite). All animals were previously scheduled for euthanasia for reasons unrelated to the purpose of this study and were not euthanized solely for this study.

Table 1.

Descriptive data for the sample of 20 male (M) and female (F) dogs

Dog #	Bodyweight (kg)	Gender	Estimated age (years)	Estimated breed
1	15.0	F	1	Australian Shepherd-Blue Heeler cross
2	30.0	M	2	Black Labrador
3	19.0	M	3	Shar Pe cross
4	18.5	F	2	Shepherd-Collie cross
5	11.5	M	14	Spaniel cross
6	7.0	M	3	Jack Russell cross
7	21.5	M	2	Husky cross
8	15.5	F	2	Terrier-Collie cross
9	23.5	M	1.5	Shepherd cross
10	18.5	F	4.5	Collie-Hound cross
11	5.0	M	3	Dachshund
12	32.5	M	8	Shepherd cross
13	24.0	F	1.5	Pit Bull-Shepherd cross
14	30.5	F	4	Shepherd
15	26.0	M	1.5	Setter cross
16	40.0	M	8	Labrador-Shepherd cross
17	33.5	M	6	Shepherd-Husky cross
18	25.0	F	4	Shepherd
19	21.5	M	1	Labrador-Shepherd cross
20	15.0	hermaphrodite	0.8	Walker Hound

Anaesthesia and euthanasia

The following procedure was pre-approved by the University of Guelph Animal Care Committee, and adhered to Canadian federal regulations for animal use in research.

Each dog was anaesthetized with a mixture of 1 mL xylazine (100 mg mL⁻¹) and 1 mL ketamine hydrochloride (100 mg mL⁻¹), administered in the muscles of the rump. The animal was examined for depth of sedation after 10 min, and an additional 0.5–2.0 mL of the mixture was given as necessary to ensure an appropriate depth. Once that had been achieved, the forces of biting were recorded, as described in the following section, after which the animal was euthanized with an intracardiac injection of 5 mL of sodium pentobarbitol (340 mg mL⁻¹). The total time between the administration of anaesthetic and lethal injections ranged from 13 to 33 min.

Recording biting force under anaesthesia

Once under anaesthesia, each animal was weighed, and four needle electrodes were inserted into the primary jaw adducting muscles. One was placed in each of the two masseter and temporalis muscles, and stimulated in a way that caused titanic contraction of the greater part, if not all, of each muscle. These major muscles are also those represented by the lever models described below.

The electrodes were 26-gauge needles, 3 cm long, connected to 10 cm of 36-gauge, insulated copper wire such that voltage was applied to the muscle along the whole length of the hypodermic needle. The other end of the wire was soldered to a thicker lead wire, 1.5 m long, which was connected to an electrical stimulator (Grass Model SD-9, Grass Instruments, Quincy, MA, USA).

Needles were inserted in repeatable locations. Those in the temporalis muscle were inserted dorsal and slightly caudal to the coronoid process, and angled ventromedially to pass through the aponeurosis attaching to the process into the deeper parts of the muscle. Those in the masseter were inserted in the cranial third of the muscle and oriented caudomedially to pass through superficial and deep components of the muscle, throughout their lateromedial depth.

A force transducer (tuning-fork style, instrumented with strain gauges, and pre-calibrated over a range of 100–4000 N) was positioned behind the major cusps of the carnassial teeth on the left side of the animal. It therefore made contact with upper premolar 4 and molar 1, and lower molar 1 and 2 (M₁ and M₂, as shown approximately in Fig. 1). We refer to this as the M2 location.

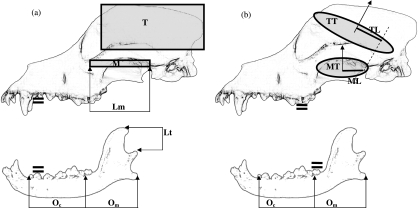
Fig. 1.

Illustration of the variables measured to calculate forces from (a) Kiltie (1984) and (b) Thomason (1991). Area measurements TT and MT were made in views parallel to the lines of action of force through their centroids (arrows), as shown in Fig. 2. The heavy solid double bars show the locations of the tines of the force transducer on upper and lower tooth rows for observed canine and molar bites. Lm is the length of the masseter origination scar on the zygomatic arch; Lt is the height of the coronoid process above the jaw condyle; M is the area of a rectangle calculated as the product of the length and width of the masseter origination scar on the zygomatic arch in ventral view, and T is the area of the temporalis origination scar calculated as the product of the length and height of the temporalis fossa in lateral view; MT is the cross-sectional area of the masseter muscle in ventral view; ML is the lever arm of the masseter about the jaw joint, TT is the cross-sectional area of the temporalis muscle in dorso-caudal view and TL is the lever arm of the temporalis about the jaw joint; O_c and O_m are the distances from the jaw joint to the canine and second molar, respectively.

The tines of the transducer were notched so that the teeth did not slide on them, with the notches asymmetrically positioned to allow for the lower teeth occluding on the lingual aspect of the upper teeth. Three electrical pulses of 60 V magnitude, at 60 Hz monopolar oscillation, were administered to the muscles for approximately half a second each, inducing full tetanic contraction of both masseter and temporalis muscles. It is likely that lateral and medial pterygoid muscles also received some stimulation. The physiological cross-section of these muscles represents approximately 15% of the total in canids (Schumacher, 1961), which gives an estimate of the maximum error in measurements of maximum biting force if these muscles received no stimulation. A period of 5–10 s was allowed to elapse between pulses. After the third pulse, the transducer was repositioned immediately behind the canine (contacting the first premolars, P¹ and P₁) and three more pulses were given. This location was strictly on the first premolars, which settled more firmly into the notches than did the canines. It was closely adjacent to the canines, the bite for which is of greater interest, and is referred to as the canine location here.

During the whole time of stimulation the transducer output was digitally recorded at 1000 Hz into a data logger (LogView, Iotech, Cleveland, OH, USA), from which the data were later downloaded into a generic personal computer for analysis. From the records for each dog, the peak magnitudes of the six bites were evaluated, and the three molar and three canine bites were averaged.

Estimation of biting force post-mortem

After euthanasia, the skull of each dog was cleaned for further study, by being defleshed in a dermestid colony, followed by degreasing, bleaching and drying. Scaled, digital photographs of the skulls were taken in lateral, ventral, dorsal, and dorsocaudal views, and the mandible was separately photographed in lateral view.

Lever models

Forces of biting at the canine (CBF) and lower molar 2 (MBF) were estimated from the scaled photographs of each skull using the equations of a pair of two-dimensional lever models from Kiltie (1984) and Thomason (1991). These models were selected because measurements could be easily extracted from images of dry skulls, and because they considered the major muscles of mastication. Each model was based on the same principle: the moments generated by the muscular forces acting about the jaw joint balance the moments of the force of biting about the jaw joint. The models differed in the method of estimating muscular forces and the lengths of their lever arms about the jaw joint.

Kiltie (1984) model:

(1a)

(1b)

Thomason (1991) model:

(2a)

(2b)

where CBF_K and CBF_T are the calculated force of biting in Newtons (N) at the canines predicted by Kiltie (1984) and Thomason (1991), respectively; MBF_K and MBF_T are the corresponding values at the second molars; FPA is the force per unit area of muscle which was taken as 300 MPa after Weijs & Hillen (1985). All equation variables are listed in Table 2 and illustrated in Fig. 1.

Table 2.

Variables used in Kiltie (1984) and Thomason (1991) equations, as well as measurements considered for inclusion in statistical models of bite force^*

Abbreviation	Definition
a	Fraction of temporalis muscle length anterior to its centroid divided by the total length
b	Caudal fraction of temporalis muscle (posterior to the centroid/total length)
BW	Bodyweight, kg
SnL	Snout length, from the caudal margin of M3 to the front of the skull, cm
SnL/SL	Snout length/skull length
Line 4	Maximum horizontal length of temporalis muscle, cm
Line 5	Maximum vertical height of temporalis muscle, cm
Line 6	Maximum vertical height of masseter, cm
Lm	Length of masseter origination scar along zygomatic arch, represents the moment arm of the masseter, cm
Lt	Height of coronoid above the jaw condyle, cm
M	Rectangular area of masseter muscle (Line 6 × Lm), cm2
MLine	Lever arm from centroid of masseter muscle about TMJ (temporomandibular joint), cm
MT	Area of masseter muscle (and medial pterygoid muscle) in ventral view, cm2
Oc, Om	Distance from jaw joint to caudal border of canine and M1, respectively, cm
SL	Skull length, cm
SW1	Skull width, behind the zygomatic arches, cm
SW2	Skull width, across the zygomatic arches, cm
SW1 or 2/SL	Ratio of skull width to skull length
T	Rectangular area of temporalis muscle (Line 4 × Line 5), cm2
TLine	Lever arm from centroid of temporalis muscle about TMJ, cm
TT	Area of temporalis muscle, cm2

^*Measurements are illustrated in Figs 1–3.

The Kiltie (1984) model estimates the size of the temporalis and masseter muscles from a lateral view of the skull, taking the area of a rectangle representing the approximate location of the muscles to be proportional to their size (Fig. 1). The Thomason (1991) model estimates the temporalis muscle size from a dorsocaudal view of the skull, and the masseter muscle size from a ventral view of the skull (Figs 1, 3). Each model determines the moment arm of the temporalis and masseter muscles differently, but the out-lever to the bite location the same (Fig. 1). For a full rationale of the structure of the lever models, one is encouraged to refer to the original publications (Kiltie, 1984; Thomason, 1991). The Kiltie (1984) model originally lacked the FPA factor, so it was added into the equation to scale the predicted force to the strength of muscle. Neither model accounted for differential contraction of the biting and balancing side musculature (Dessem, 1989), and the factor of 2 in Thomason (1991) was based on the assumption that both sides were contracting maximally. Kiltie (1984) lacked this factor, and the model was evaluated as is.

Fig. 3.

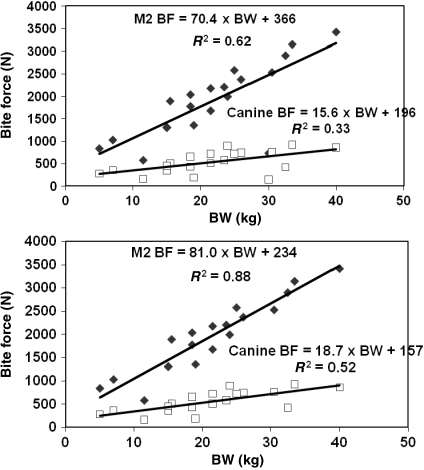
Observed bite force (BF) at M2 (solid points) and canine (hollow points) vs. observed bodyweight (BW) for the 20 dogs when dog 3 is included (Top) and excluded (Bottom). Dog 3 was statistically identified as an outlier.

Regression models

Statistical models of bite force at the canine and molar were developed from the observed bite force values of the 20 dogs. Variables considered for inclusion in the regression models are listed in Table 2 and illustrated in Fig. 2. Methods for model development are outlined below.

Fig. 2.

Measures examined for inclusion in statistical models of bite force (abbreviations listed in Table 2) from the lateral view of the skull (a), lateral lower jaw (b), dorsocaudal view (c) and ventral view (d). The dashed line indicates the dorsocaudal plane, and * indicates the centroid of the muscle. For this figure, line 4 is the maximum horizontal length of the temporalis muscle, Line 5 is the maximum vertical height of the temporalis muscle, Tline is the lever arm from the centroid of the temporalis muscle about TMJ, Line 6 is the maximum vertical height of the masseter, Lm is the length of the masseter origination scar along the zygomatic arch, Lt is the height of coronoid above the jaw condyle, O_c and O_m are the distances from jaw joint to the caudal border of the canine and M2, respectively, TT is the area of the temporalis muscle in cm², a is a fraction of the temporalis muscle length anterior to its centroid divided by the total length, b is the caudal fraction of the temporalis muscle (posterior to the centroid/total length), Mline is the lever arm from the centroid of the masseter muscle about TMJ, MT is the area of the masseter muscle (and medial pterygoid muscle) in the ventral view, SW1 and SW2 are skull width, measured across and behind the zygomatic arches, respectively, SnL is snout length, from the caudal margin of M3 to the front of the skull, and SL is skull length.

Statistical analysis

Outliers

Recorded observed bite forces were plotted against measures of body size (e.g. bodyweight and skull length) to check visually for outlying values (Fig. 3). The presence of outliers was confirmed by a Cook's distance test in PROC REG of SAS (SAS, 2000). Outliers were not included in any further analysis.

Adjustment models

It was anticipated that significant amounts of bias may exist in the predictions of Kiltie (1984) and Thomason (1991) for the domestic dog, based on previous results (Thomason et al. 1990; Thomason, 1991) and the fact that the model of Kiltie (1984) was developed for use on felids. Neither model had been scaled to canine bite forces. Two types of adjustments were attempted on the predicted bite force values from these models to correct for any bias.

Adjustment method 1 consisted of plotting observed vs. predicted bite force at the canine and molar, where the resultant regression equation provides an ‘adjustment’ equation for Kiltie (1984) and Thomason (1991). It corrects for major mismatch in scale owing to the values assumed for constants in Kiltie (1984) and Thomason (1991).

Adjustment method 2 consisted of applying the mapping function: Y₂ = b₂ + (Y₁ – b₁) ×(a₂/a₁) to the predicted BF (Y₁) (this is a function developed by Thomason, 1991), where b₁ and a₁ are the intercept and slope of the predicted vs. observed regression line, and b₂ and a₂ are the intercept and slope of the line of unity (0 and 1, respectively). This method simply maps the post-mortem values onto the in vivo ones.

Regression model development

For statistical model development, the correlation of variables (Table 2) with observed bite force (N) were determined using the PROC CORR procedure of SAS (SAS, 2000). Variables that was significantly correlated with bite force at the canine or M2 were used as inputs for a multiple regression analysis in SAS using the PROC REG MAX R procedure (SAS, 2000). This procedure selects the best-fit (1) variable model, (2) variable model, (3) variable model, etc., where variables included in the model are changed/added to maximize the R² value. Models of increasing complexity were considered until the R² did not increase significantly by the addition of another factor. Significant cranial measurements not shown in Fig. 1 are illustrated in Fig. 2. Non-significant variables from the PROC CORR procedure were not included in the regression analysis.

Model evaluation

Lever models (Kiltie, 1984; Thomason, 1991), adjusted lever models and regression models were evaluated using mean square prediction error (MSPE), calculated as:

(3)

where O_i is the observed bite force value, P_i is the predicted value and n is the number of observations. Square root of the MSPE (RMSPE), expressed as a proportion of the observed mean (%), gives an estimate of the overall prediction error. Square root of the MSPE was decomposed into random error (ED), error due to deviation of the regression slope from unity (ER), and error due to overall bias (ECT) (Bibby & Toutenburg, 1977). Equations that had the best predictive value were identified using several criteria in combination: (1) a low RMSPE, (2) having a high proportion of error from random sources, and (3) for the developed statistical equations, having only significant independent variables in the equation.

Results

Ranges of bite force recorded

Forces recorded for canine bites ranged from 147 N (± 6.9) to 926 N (± 8.1), and for M2 bites from 574 N (± 83.2) to 3417 N (± 43.1) (Table 3). There was no significant relationship between bite force value and the order of bites taken on the same dog at M2 (P = 0.3282) or the canine (P = 0.1093). Muscle fatigue after repeated stimulations did not influence the observed results. Dog 3 (30 kg) was identified as an outlier, biting significantly less at M2 than expected for its bodyweight, and was removed from further analysis of the data (Fig. 3). Removal of dog 3 from the database increased the R² of the relationship between bite force and bodyweight from 0.62 to 0.88 for the M2 bites, and from 0.33 to 0.52 for the canine bites. Forces taken at M2 for the remaining 19 dogs were significantly related to observed bodyweight (P < 0.0001), as well as forces obtained at the canine (P = 0.0086) (Fig. 3).

Table 3.

Observed bite force at the canine and M2 teeth^*

Dog #	Canine bite force (N)	SEM	M2 bite force (N)	SEM
1	354	14.3	1310	85.6
2	147	6.9	732	49.0
3	192	8.2	1353	79.1
4	433	29.9	2035	10.9
5	162	16.8	574	83.2
6	360	3.8	1025	5.1
7	722	12.5	2174	39.1
8	509	.	1890	64.1
9	580	.	2202	183.8
10	654	3.2	1774	54.3
11	281	2.4	834	27.3
12	423	13.3	2900	66.8
13	896	.	1991	85.5
14	756	.	2527	23.8
15	748	.	2371	23.0
16	859	19.3	3417	43.1
17	926	8.1	3145	53.9
18	720	24.6	2576	17.9
19	508	6.1	1675	20.6
20	453	7.9	1299	.

^*Values are the average of up to four observed bites.

Predictive equations

Lever models

The Kiltie (1984) and Thomason (1991) models were constructed to give relative estimates of bite force, and were developed on species other than dogs. Because of these differences, it was anticipated that the results of the lever models may have to be adjusted, if only in the magnitude of the results. As well, it was anticipated that the equations used for adjusting the outputs of the lever models would improve the prediction of absolute forces of biting. Adjustment equations developed are presented in Table 4 (Eqs 3–10) and predicted vs. observed results are illustrated in Fig. 4 for both the original and adjusted models.

Table 4.

Summary of (a) adjustment and (b) statistical models, where all forces of biting (BF) are in Newtons and parameters are means ± SE

Model Description/BF Location		Equation #	Equation*
(a) Adjustment Models
M2	To adjust Kiltie (1984)†	3	BF = 3.50 × BFK – 696
	To adjust Thomason (1991)†	4	BF = 2.78 × BFT – 321
Canine	To adjust Kiltie (1984)†	5	BF = 1.78 × BFK + 36.9
	To adjust Thomason (1991)†	6	BF = 1.44 × BFT + 98.1
M2	To adjust Kiltie (1984)‡	7	BF = (BFK – 323) × (1/0.223)
	To adjust Thomason (1991)‡	8	BF = (BFT – 304) × (1/0.279)
Canine	To adjust Kiltie (1984)‡	9	BF = (BFK – 145) × (1/0.279)
	To adjust Thomason (1991)‡	10	BF = (BFT – 176) × (1/0.30)
(b) Statistical models
M2		11	BF = 258 (± 172) + 80.3 (± 7.37) × BW
		12	BF = 2899 (± 1013) + 68.80 (± 7.65) × BW– 6695 (± 254) × SW/SL ratio
		13	BF = –2276 (± 450) + 1519 (± 160) × Lt
		14	BF = –1858 (± 371) + 943.4 (± 208) × Lt + 0.911 (± 0.264) × T
		15	BF = –1892 (± 331) + 15.2 (± 6.68) × BW + 910 (± 186) × Lt+ 0.761 (± 0.244) × T
		16	BF = –3802 (± 1277) + 15.4 (± 6.4) × BW + 2998 (± 1940) × SnL/SL + 28.5 (± 178) × Lt+0.733 (± 0.234) × T
		17	BF = 4263 (± 1250) + 11.3 (± 6.62) × BW + 4258 (± 2013) × SnL/SL + 794 (± 190) × Lt + 9.41 (± 5.99) × M + 0.614 (± 0.235) × T
Canine		18	BF = 157 (99.4) + 18.7 (± 4.33) × BW
		19	BF = –556 (± 238) + 88.5 (± 18.8) × Oc
		20	BF = –767 (± 269) + 60.40 (± 25.9) × Oc + 116 (± 76.8) × Line5
		21	BF = –699 (± 263) + 118 (± 49.7) × Lm + 139 (± 69.6) × Line5
		22	BF = –396 (± 324) – 265 (± 177) × tline + 194 (± 69.8) × Lm+ 158 (± 68.3) × Line5
		23	BF = –1678 (± 494) + 446 (± 201) × mline + 216 (± 151) × Lt + 266 (± 87.9) × Line5 – 2.67 (± 1.18) × TT
		24	BF = –1405 (± 443.2) + 352.4 (± 201.2) × mline + 314.5 (± 84.71) × Line5 – 3.877 (± 1.352) × TT + 1.866 (± 0.9317) × MT
		25	BF = –1563 (± 472.2) + 331.8 (± 202.6) × mline + 145.4 (± 148.7) × Lt + 301.5 (± 85.87) × Line5 – 3.920 (± 1.354) × TT+ 1.591 (± 0.9746) × MT

^*For the lever models, BF_K is BF predicted by the unadjusted Kiltie (1984) model and BF_T is BF predicted by the unadjusted  Thomason (1991) model. For the statistical models, parameters in bold are significant at P ≤ 0.05.

^†Using adjustment method 1.

^‡Using adjustment method 2.

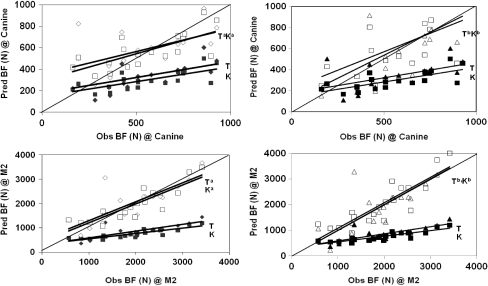
Fig. 4.

Predicted vs. observed bite force (BF) at the canine (top) and M2 (bottom) tooth, where solid dots represent unadjusted predicted BF by the Thomason (1991) model (T) or by the Kiltie (1984) model (K), and hollow points represent the equivalent predictions made by the adjusted models, where (T^a) represents models adjusted with method 1 (Eqs 3–6) and (T^b) represents models adjusted with method 2 (Eqs 7–10).

Square root of the MSPE values for the unadjusted and adjusted lever models are reported in Table 5. Unadjusted, the Kiltie (1984) model predicts bite force at M2 and canine with RMSPE values of 68.5% and 55.7%, respectively (Table 5). The unadjusted Thomason (1991) model predicts bite force at M2 and canine with RMSPE values of 63.5 and 51.4%, respectively (Table 5). For both biting locations and both lever models, the majority of MSPE error is due to ECT (Table 5). Means of the predicted M2 bite forces for the models of Kiltie (1984) and Thomason (1991) are 38.7% and 43.5% of the observed mean, respectively (Table 5); the comparable values for predicted canine bites are 54.1% and 61.3% of the observed mean (Table 5). Results indicate that the substantial levels of bias are due to underestimation of bite force for both Kiltie (1984) and Thomason (1991) models, at both the canine and M2 locations (Fig. 4).

Table 5.

Results of RMSPE analysis for lever and statistical bite force (BF) prediction models. Square roots of the mean square prediction error (RMPSE) are shown as a percentage of their respective observed means, and are decomposed into components of bias (ECT), error owing to deviation of the slope from unity (ER), and random error (ED), all expressed as percentages of RMSPE

		Predicted BF			MSPE
Location	Equation	Mean	SEM	RMSPE, %	ECT %	ER %	ED %	R2
Molar	Kiltie (1984), Eq. 1b	755	45.0	68.5	80.2	13.0	6.8	0.77
	Thomason (1991), Eq. 2b	849	62.3	63.5	79.0	8.0	13.1	0.64
	Adjusted Kiltie (1984), Eq. 3	1949	158	18.7	0.0	0.1	99.9	0.77
	Adjusted Thomason (1991), Eq. 4	2036	173	24.7	3.1	8.0	88.9	0.64
	Adjusted Kiltie (1984), Eq. 7	1951	203	21.4	0.0	24.8	80.8	0.77
	Adjusted Thomason (1991), Eq. 8	1952	223	29.3	0.0	38.5	61.5	0.64
	Eq. 11	1960	166	33.5	0.0	15.6	84.4	0.36
	Eq. 12	1958	169	35.2	0.0	19.1	80.9	0.32
	Eq. 13	1952	163	15.4	0.0	0.0	100	0.84
	Eq. 14	1951	170	11.6	0.0	0.0	100	0.91
	Eq. 15	1951	172	10.0	0.0	0.0	100	0.93
	Eq. 16	1952	173	9.27	0.0	0.0	100	0.94
	Eq. 17	1951	173	8.50	0.0	0.0	100	0.95
Canine	Kiltie (1984), Eq. 1a	300	20.7	55.7	68.0	6.3	25.7	0.52
	Thomason (1991), Eq. 2a	340	28.2	51.4	56.5	0.1	43.4	0.31
	Adjusted Kiltie (1984), Eq. 5	571	36.9	28.6	1.1	0.2	98.7	0.52
	Adjusted Thomason (1991), Eq. 6	588	40.6	35.4	2.9	5.8	91.4	0.31
	Adjusted Kiltie (1984), Eq. 9	555	74.2	39.5	0.0	50.9	49.1	0.52
	Adjusted Thomason (1991), Eq. 10	555	95.6	60.7	0.0	72.6	32.9	0.31
	Eq. 18	555	38.6	40.4	0.0	13.0	87.0	0.14
	Eq. 19	555	40.2	26.9	0.0	0.0	100	0.57
	Eq. 20	555	42.1	25.2	0.0	0.0	100	0.62
	Eq. 21	553	42.2	25.1	0.0	0.0	100	0.62
	Eq. 22	554	43.8	23.4	0.0	0.0	100	0.67
	Eq. 23	554	44.8	22.3	0.0	0.0	100	0.70
	Eq. 24	554	45.8	21.0	0.0	0.0	100	0.74
	Eq. 25	554	46.4	20.3	0.0	0.0	100	0.75

Adjustment methods 1 and 2 attempt to account and correct for the significant level of non-random error evident from decomposition of the RMSPE for the non-adjusted Kiltie (1984) and Thomason (1991) models (Table 5). Adjustment method 1 (based on regression) reduces RMSPE by an average of 55.0%, and adjustment method 2 (based on mapping) reduces RMSPE by an average of 36.0% (Table 5, Fig. 4). Adjustment method 1 succeeds in reducing the contribution of bias and deviation of the regression slope from unity to RMSPE, resulting in, for the most part, > 90% of error coming from random sources in the adjusted equations (Table 5, Fig. 4). Adjustment method 2, while significantly reducing error due to bias, does not correct error caused by deviation of the regression slope from unity (Table 5, Fig. 4). As a result of adjustment method 2 not correcting for regression slope error, the overall RMSPE values for this method are higher than for adjustment method 1, which corrects both bias and regression slope. Significant levels of random variation are, however, still evident (Table 5, Fig. 4).

Regression models

All statistical models developed are reported in Table 4, and significant equation variables are identified by bold font. Variables that appear important in predicting bite force at M2 include bodyweight (BW), height of coronoid above the jaw condyle (Lt) and the rectangular area representing the temporalis muscle (T) (Table 4), and these variables are present in Eq. 15. Of the seven M2 equations developed, Eqs 11–15 include all significant independent variables, whereas Eqs 16 and 17 also have non-significant variables. Non-significant variables indicate over-parameterization of the model, and thus these equations are not recommended despite lower MSPE values (Table 5). Increasing complexity from Eq. 11 to 15 results in lower RMSPE values and shifts the composition of the error to be entirely random (Table 5). Among these equations to consider, Eq. 15 had the lowest RMSPE value (10.0%) and 100% of error from random sources.

For the canine equations, anything above one variable started to introduce non-significant parameters into the regression equation (Table 4). Equations with non-significant variables suggest over-parameterization of the model and are not recommended despite lower MSPE values. Single variable models that came up significant included the effects of BW and the distance from jaw joint to the caudal border of canine (O_c) (Eqs 18 and 19). Other interesting variables that were introduced into the more complex equations included the length of the masseter origination scar along zygomatic arch (Lm), the maximum vertical height of the temporalis muscle (Line 5), and the area of the temporalis muscle (TT). While Eq. 18 (including the variable BW) had an RMSPE of 40.4% and 87.0% of error from random sources, Eq. 19 (including the variable O_c) performed better with an RMSPE of 26.9% and 100% of error from random sources (Table 5).

Overall, the best statistical M2 equations had lower RMSPE values and were able to explain more variability than the best statistical canine equations (Table 5). Comparing amongst the adjusted lever models and the developed statistical models, the statistical models have lower RMSPE values and more error from random sources than the adjusted lever models at both the M2 and canine bite locations (Table 5). This is, however, expected as they were developed on the same database.

Discussion

Forces recorded in vivo

Lindner et al. (1995) recorded forces ranging from 13 to 1394 N (mean = 256 N) from 22 unrestrained pet dogs (body masses 7–55 kg) biting on a bar-shaped force transducer covered in rawhide. They did not report where on the tooth row each bite was made. These values are low compared with those reported here, despite a greater range in body masses. The range of pooled canine and molar bites reported here is 147–3417 N, with a mean of 534 N at the canines and 1890 N at M2. The difference between studies is almost certainly related to the use of conscious dogs by Lindner and colleagues and anaesthetized dogs here. Sensory feedback from the teeth normally modulates forces of biting, but is inhibited by local anaesthesia (Dessem, 1989), and this certainly would be the case under the protocol used here. Other studies (e.g. Gorniak & Gans, 1980) have indicated that bite force outputs during the chewing cycle are dependent on a variety of properties, including the food itself, as well as a complex pattern of muscle recruitment (i.e. the total muscle volume is not automatically recruited all at once). This would also affect the in vivo vs. dry-skull results, and might serve to reduce the observed voluntary bite forces compared with the stimulated forces observed in this study. These facts must be borne in mind when considering forces that conscious, unrestrained dogs will generate, in comparison with the stimulated forces reported here. Stimulated forces should be regarded as maximal forces which would probably only be generated in extreme circumstances by a conscious animal owing to the possibility of tooth damage. The presence of outlying values in the recorded force data is difficult to explain. The characteristics of the dog producing those values was unremarkable, and the recording trials appeared to proceed smoothly. It is possible that one or more stimulating electrodes were incorrectly placed. This would lead to sub-maximal forces owing to lower stimulation of all or parts of each masseter and temporalis muscles. In a study in which a single masseter muscle was stimulated (Ström & Holm, 1992), forces of biting at the molars of the order of 500 N were recorded from 45-kg dogs, approximately one sixth of the peak values recorded here. This demonstrates the sensitivity of the results to the degree of muscle stimulation. Every attempt was made in this trial to place the electrodes in repeatable locations on every dog.

As might be expected, the forces retained in the analyses after outlier removal were dependent upon the bodyweight of the animal (Fig. 3). Variability in these data was presumably partly dependent on how gracile or robust the animal was, and on its cranial shape. A study by Meers (2003) also found a strong relationship between bite force and body weight in extant predators (crocodylians, carnivorans, chelonians and squamates), and stated these two variables to be the most critical for successful predation.

Lever models

Both lever models, Kiltie (1984) and Thomason (1991), underpredicted biting forces by the dogs used here. The type and number of simplifying assumptions are probably the cause, of which three are likely to be the most significant. First, the models represent a three-dimensional system in two dimensions. Secondly, they do not take into account differential forces generated on biting and balancing sides of the head (Greaves, 1983; Dessem, 1989). Thirdly, the architecture of the jaw adducting musculature – which is structurally complex in all mammals (Hiiemae & Jenkins, 1969) and important in the control and modulation of force production – is not fully represented by the models.

In the absence of calibration data of the kind reported here, most workers using lever models have accommodated the problem of under-representation by deriving relative rather than absolute values of force. Kiltie (1984) used his model to estimate relative force values for comparison among wild felids feeding on materials of different hardness. Other workers applying this type of model to compare feeding mechanics and scaling among species have similarly based the analyses on relative values (Christiansen & Adolfssen, 2005; Wroe et al. 2005).

Model performance

Lever models

Once the ‘raw’ estimates from both lever models were adjusted by regression or mapping on the observed values (Table 4), the accuracy of the predicted means improved to within 6% of the observed means (Table 5, Fig. 4). Adjustment by regression (method 1) reduced RMPSE more than adjustment by mapping (method 2), largely because it corrects error due to deviation of the regression slope from unity as well as overall bias. As a result, estimates from adjustment method 1 had less error than those from adjustment method 2.

The lever model adjustment equations suggest that use of the lever models to estimate relative forces of biting among individuals, even after adjustment, be approached with some caution. The adjustment equations not only change the magnitude of the bite force predictions, but also the slope of the relationship (adjustment method 1) between predicted and observed values. Departure of slopes from unity for the unadjusted and adjusted with method 2 equations is troublesome because it indicates that the ratio of adjusted to raw estimate varies with the magnitude of the estimate. Another general problem is that there is considerable variation in the regressions of predicted on observed data, and relationships based on the data here must be interpreted with caution, considering the limited sample size and between-animal variation. This simple, random intra-species variation is a common feature in many analyses of morphology and function. These two factors suggest, though, that errors (random or otherwise) in raw estimates of biting force may bias the relationships derived between them and other measures, such as BW.

While raw lever model estimates may correctly rank forces of biting from different animals (or species), there is a residual bias in the relative magnitude of the estimate that may or may not be removed by compensating for differences in animal size. The adjustment equations derived here help to reduce that error, effectively calibrating raw estimates from skulls of dogs, but there is no certainty that these calibrations are valid for other species. These points do not invalidate the use of lever models, particularly in paleontological applications where no other methods are available, but they do indicate the degree of caution necessary in interpreting results. The biases present in raw estimates are sufficient to skew relationships with other variables.

Regression models

All of the statistical models gave predicted means within 0.54% of the observed means of canine and M2 bite forces, but differed in RMPSE values and in the number of significant variables in the predictive equations. We suggest that Eq. 15 (Tables 4 and 5) (including the effects of BW, Lt and T) has the best predictive value for molar biting, because its value of RMPSE (10.0%) is the lowest MSPE value, almost all of this error is random, and other more complex equations contain insignificant parameters beyond this equation (Tables 4 and 5). The value of R² for this equation is 0.93, and its fit to the data is shown in Fig. 5. In comparison, the adjusted Kiltie (1984) model had an RMPSE of 18.7%, and an R² of 0.77.

Fig. 5.

Predicted bite force (BF) at M2 (top) from Eq. 15, and at the canine (bottom) from Eq. 19, vs. observed BF (N).

These data are encouraging because they indicate an acceptable degree of accuracy exists in estimating maximal forces of molar biting for domestic dogs from morphometric measurements. Body weight is readily measurable, and Lt and T can be measured roughly from radiographs or skull images. If only dry skulls are available, as when using a museum collection, adjusted (method 1) lever models provide usable results.

For canine bites, Eq. 19 was one of two with significant independent variables. It had the single variable O_c, the out-lever of the canine tooth from the jaw joint, and had an RMPSE value of 26.9%, which was 14% lower than that of Eq. 18. The R² for Eq. 19 was 0.57, somewhat lower that for Eqs 20 to 24, but these contained non-significant variables. Equation 19 appeared to be the best predictor for canine bites, and its fit to the data is shown in Fig. 4b. This equation performed only slightly better than the best adjusted lever model (Kiltie, 1984), which had an RMPSE of 28.6% and an R² of 0.52. The capability for accurately estimating maximal forces of canine biting is considerably less than for M2, but is simpler to implement in that only one variable, O_c, is necessary in the predictive equation. This is readily measured on a dry skull, and is also possible from a cooperative living animal.

We close this section with the caveat that the predictive equations developed apply most accurately to this sample of animals, and may not transfer as accurately to other samples.

Effects of cranial shape

There have been a number of studies that have examined overall skull morphology in carnivores (Radinsky, 1981a,b; Werdelin, 1983, 1987; Biknevicus & van Valkenburgh, 1996) and the allometric changes in shape with size among species (Christiansen & Adolfssen, 2005). One of the topics of discussion in this field is that of a functional linkage, or interdependence of variables that have an effect on production of force by the jaws. An analogue of cranial shape variation among carnivoran species is that among breeds of the domestic dog. Skull shape variation in dogs has been categorized as brachycephalic (short faced, e.g. Boxers and Pekinese), mesaticephalic (face of medium length, e.g. Labradors and Golden Retrievers), and dolichocephalic (long faced, e.g. Whippets and Greyhounds) (Miller et al. 1965). Although we could not do a thorough analysis of shape effects on force production, variables such as snout length/skull length (SnL/SL) and skull width/skull length (SW/SL) were included for preliminary examination. We had expected that force of biting would be inversely proportional to SnL/SL and directly to SW/SL. These variables correlated with recorded force of biting, and appeared in Eqs 11–17 for predicting M2 biting forces, but not in the most accurate equation (Eq. 15). The presence of SnL/SL was not significant in any equation (Table 4), and the coefficient for SW/SL was negative in Eq. 12, contrary to expectation.

Equation 15, including BW, which proved to have a significant relationship with M2 biting force on its own (Fig. 3), also included two cranial measurements, Lt and T, used in the Kiltie (1984) lever model. Both of these measurements carry information on cranial shape and force production by the temporalis muscle. They may suggest that dimensions of the temporalis fossa, and hence the muscle contained therein, are the most functionally relevant morphometric cranial attributes for molar biting, in conjunction with BW.

For canine biting, the inclusion of a single significant independent variable, O_c, in the most accurate equation (Eq. 19) is unexpected in that it has a positive coefficient. Based on the simple principles of levers in two dimensions, biting force would be expected to be inversely related to the length of the out-lever.

Two interpretations are possible regarding the significant variables in the two most accurate equations. The first is that cranial mechanics does not follow closely the rules of levers in two dimensions, and that the complexity of three-dimensional systems (as explored by Greaves 1983, and several other subsequent papers) make the relationship of cranial shape to force production less easy to interpret. The second is that the methods here have simply identified statistically relevant, and not mechanically relevant, variables, perhaps owing to the original choice of measurements or to the sample size.

In general this study found that: (1) models based on balancing moments acting on a two-dimensional lever systems (Kiltie, 1984; Thomason, 1991) underestimate maximal forces of biting consistently and substantially; (2) adjusting these models improves their accuracy significantly for this sample of skulls, though it is not clear whether this calibration of ‘dry skull’ estimates may be generalized beyond the set; (3) the most accurate models derived from best-fit iterative regression generally have less error than the lever models, even after adjustment [with the exception of Kiltie (1984) for M2 bites when adjusted by regression]; (4) three straightforward measurements (BW, Lt, and T) allow for accurate prediction of molar bites for this sample, and a single measurement (O_c) does the same for canine bites; (5) forces of molar biting are estimated more accurately than canine bites; and (6) caution must be used in applying these data to calibrate estimates from other domestic dogs, or to extrapolate to other canid or carnivoran species. The data we present here certainly raise more questions about cranial mechanics in canids, while meeting the original aims of comparing methods for force estimation. We intend next to challenge the predictive equations derived here, by applying them to a more detailed study of the effects of cranial shape and body size in domestic dogs (Ellis et al. 2008).