A Nonlinear Elasticity Model of Macromolecular Conformational Change Induced by Electrostatic Forces

Abstract

In this paper we propose a nonlinear elasticity model of macromolecular conformational change (deformation) induced by electrostatic forces generated by an implicit solvation model. The Poisson-Boltzmann equation for the electrostatic potential is analyzed in a domain varying with the elastic deformation of molecules, and a new continuous model of the electrostatic forces is developed to ensure solvability of the nonlinear elasticity equations. We derive the estimates of electrostatic forces corresponding to four types of perturbations to an electrostatic potential field, and establish the existance of an equilibrium configuration using a fixed-point argument, under the assumption that the change in the ionic strength and charges due to the additional molecules causing the deformation are sufficiently small. The results are valid for elastic models with arbitrarily complex dielectric interfaces and cavities, and can be generalized to large elastic deformation caused by high ionic strength, large charges, and strong external fields by using continuation methods.

1 An Electro-Elastic Model of Conformational Change

Many fundamental biological processes rely on the conformational change of biomolecules and their assemblies. For instance, proteins may change their configurations in order to undertake new functions, and molecules may not bind or optimally bind to each other to form new functional assemblies without appropriate conformational change at their interfaces or other spots away from binding sites. An understanding of mechanisms involved in biomolecular conformational changes is therefore essential to study structures, functions and their relations of macromolecules. Molecular dynamics (MD) simulations have proven to be very useful in reproducing the dynamics of atomistic scale by tracing the trajectory of each atom in the system (38). Despite the rapid progress made in the past decade mainly due the explosion of computer power and parallel computing, it remains a significant challenge for MD to study large-scale conformational changes occurring on time-scales beyond a microsecond (6). Various coarse-grained models and continuum mechanics models are developed in this perspective to complement the MD simulations and to provide computational tools that are not only able to capture characteristics of the specific system, but also able to treat large length and time scales. The prime coarse-grained approaches are the elastic network models, which describe the biomolecules to be beads, rods or domains connected by springs or hinges according to the pre-analysis of their rigidity and the connectivity. Elastic network models are usually combined with normal mode analysis (NMA) to extract the dominant modes of motions, and these modes are then used to explore the structural dynamics at reduced cost (10). Continuum models do not depend on these rigidity or connectivity analysis. On the contrary, the rigidity of the structure shall be able to be derived from the results of the continuum simulations. Typical continuum models for biomolecular simulations include the elastic deformation of lipid bilayer membranes (36) and the gating of mechanosensitive ion channels (35) induced by given external mechanical loads. It is expected that with more comprehensive continuum models we will be able to simulate the variation of the mechanical loads on the macromolecules with their conformational change, and investigate the dynamics of molecules by coupling the loads and deformation. This article takes an important step in this direction by describing and analyzing the first mathematical model for the interaction between the nonlinear elastic deformation and the electrostatic potential field of macromolecules. Such coupled nonlinear models have tremendous potential in the study of configuration changes and structural stability of large macromolecules such as nucleic acids, ribosomes or microtubules during various electrostatic interactions.

Our model is described below. Let Ω ∈ ℝ³ be a smooth open domain whose boundary is noted as ∂Ω; see Fig.(1). Let the space occupied by the flexible molecules Ω_mf be a smooth subdomain of Ω, while the space occupied by the rigid molecule(s) is denoted by Ω_mr. Let the remaining space occupied by the aqueous solvent be Ω_s. The boundaries of Ω_mf and Ω_mr are denoted by Γ_f and Γ_r, respectively. We assume that the distance between molecular surfaces and ∂Ω

$$\min \left\{\right|x-y|:x\in {\Gamma }_f\cup {\Gamma }_r,y\in \partial \Omega \}$$ (1)

is sufficiently large so that the Debye-Hückel approximation can be employed to determine a highly accurate approximate boundary condition for the Poisson-Boltzmann equation. There are charges atoms located inside Ω_mf and Ω_mr, and changed mobile ions in Ω_s. The electrostatic potential field generated by these charges induces electrostatic forces on the molecules Ω_mf and Ω_mr. These forces will in turn cause the configuration change of the molecules. We shall model this configuration rearrangement as an elastic deformation in this study. Specifically, we will investigate the elastic deformation of molecule Ω_mf (which is originally in a free state and not subject to any net external force) induced by adding molecule Ω_mr and changing mobile charge density in Ω_s. This body deformation leads to the displacement of charges in Ω_mf and the dielectric boundaries, which simultaneously lead to change of the entire electrostatic potential field. It is therefore interesting to investigate if the deformable molecule Ω_mf has a final stable configuration in response to the appearance of Ω_mr and the change of mobile charge density.

Fig. 1.

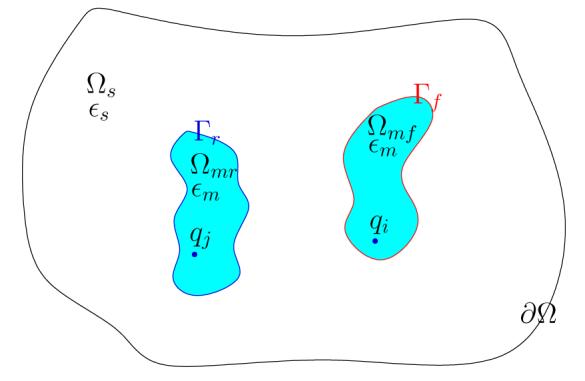
Illustration of macromolecules immersed in aqueous solvent environment.

Within the framework of an implicit solvent model which treats the aqueous solvent in Ω_s as a structure-less dielectric, the electrostatic potential field of the system is described by the Poisson-Boltzmann equation (PBE)

$$-\nabla \cdot (∊\nabla \varphi )+{\kappa }^2\sinh \left(\varphi \right)=\underset{i}{\overset{N_f+N_r}{\Sigma }}{q}_i\delta \left(x_i\right)\text{in}\Omega ,$$ (2)

where δ(x_i) is the Dirac distribution function at x_i, N_f + N_r is the number of singular charges of the system including the charges in Ω_mf (i.e.N_f) and Ω_mr (i.e., N_r). The dielectric constant ε and the modified Debye-Hückel parameter κ are piecewise constants in domains Ω_mf, Ω_mr and Ω_s. In particular, κ = 0 in Ω_mf and Ω_mr because it models the free mobile ions which appear only in the solvent region Ω_s. The dielectric constant in the molecule and that in the solvent are denoted with ε_m and ε_s, respectively. Readers are referred to (27; 28) for the importance of the Poisson-Boltzmann equation in biomolecular electrostatic interactions, and to (2; 3; 4; 5; 29; 30; 31; 32) for the mathematical analysis as well as various numerical methods for the Poisson-Boltzmann equation.

The finite(large) deformation of molecules is essential to our coupled model, but can not be described by a linear elasticity theory. We therefore describe the displacement vector field u(x) of the flexible molecule Ω_mf with a nonlinear elasticity model:

$$\begin{array}{cc}\hfill -\mathrm{div}\left(\mathbf{T}\left(\mathbf{u}\right)\right)& ={\mathbf{f}}_b\text{in}{\Omega }_{mf}^0\hfill \\ \hfill \mathbf{T}\left(\mathbf{u}\right)\cdot \mathbf{n}& ={\mathbf{f}}_s\text{on}{\Gamma }_f^0\hfill \end{array}$$ (3)

where f_b is the body force, f_s is the surface force and T(u) is the second Piola-Kirchhoff stress tensor. In this study we assume the macromolecule is a continuum medium obeying the St Venant-Kirchhoff law, and hence its stress tensor is given by the linear(Hooke's law) stress-strain relation for an isotropic homogeneous medium:

$$\mathbf{T}\left(\mathbf{u}\right)=(\mathrm{I}+\nabla \mathbf{u})[\lambda \mathrm{Tr}\left(\mathbf{E}\left(\mathbf{u}\right)\right)\mathrm{I}+2\mu \mathbf{E}\left(\mathbf{u}\right)].$$

Here λ > 0 and μ > 0 are the Lamé constants of the medium, and

$$\mathbf{E}\left(\mathbf{u}\right)=\frac{1}{2}(\nabla {\mathbf{u}}^T+\nabla \mathbf{u}+\nabla {\mathbf{u}}^T\nabla \mathbf{u})$$

is the nonlinear strain tensor. The equation (3) is nonlinear due to the Piola transformation (I + ∇u) in T(u), and the quadratic term in the nonlinear strain E(u). The third potential source of nonlinearity, namely a nonlinear stress-strain relation, is not considered here; however, our methods apply to this case as well.

It is noted that Eq.(3) is defined in the undeformed molecule body ${\Omega }_{\mathit{mf}}^0$ with undeformed boundary ${\Gamma }_f^0$, while the Poisson-Boltzmann equation (2) holds true for real deformed configurations. The deformed configuration is unknown before we solved the coupled system. We therefore define a displacement-dependent mapping Φ(u)(x) : Ω⁰ → Ω and apply this mapping to the the Poisson-Boltzmann equation such that it can also be analyzed on the undeformed molecular configuration. In ${\stackrel{-}{\Omega }}_{\mathit{mf}}$ this map Φ(u)(x) is ℐ + u where ℐ is the identity mapping. A key technical tool in our work is that this mapping is then harmonically extended to Ω to obtain the maximum smoothness. Apply this mapping, the Poisson-Boltzmann equation 2 changes to be

$$-\nabla \cdot (∊\mathbf{F}\left(\mathbf{u}\right)\nabla \varphi )+J\left(\mathbf{u}\right){\kappa }^2\sinh \left(\varphi \right)=\underset{i}{\overset{N_f+N_r}{\Sigma }}J\left(\mathbf{u}\right)q_i\delta (\Phi \left(x\right)-\Phi \left(x_i\right))\text{in}\Omega ,$$ (4)

where J(u) is the Jacobian of Φ(u) and

$$\mathbf{F}\left(\mathbf{u}\right)={(\nabla \Phi \left(\mathbf{u}\right))}^{-1}J\left(\mathbf{u}\right){(\nabla \Phi \left(\mathbf{u}\right))}^{-T}.$$ (5)

This matrix F is well defined whenever Φ(u) is a C¹-diffeomorphism (7). The functions in Eq.(4) should be interpreted as the compositions of respective functions in Eq.(2) with mapping Φ(x), i.e., ϕ (x) = ϕ(Φ(x)), ε(x) = ε(Φ(x)) and κ(x) = κ(Φ(x)).

In this paper, we shall analyze the existence of the coupled solution of the elasticity equation (3) and the transformed Poisson-Boltzmann equation (4). These two equations are coupled through displacement mapping Φ(u) in the Poisson-Boltzmann equation and the electrostatic forces to be defined later. The solution of this coupled system represents the equilibrium between the elastic stress of the biomolecule and the electrostatic forces to which the biomolecule is subjected. The existence, the uniqueness and the W^2,p-regularity of the elasticity solution have already been established by Grandmont (7) in studying the coupling of elastic deformation and the Navier-Stokes equations; thus in this work we shall focus on the solution to the transformed Poisson-Boltzmann equation and to the coupled system. We shall define a mapping S from an appropriate space X_p of displacement field u into itself, and seek the fixed-point of this map. This fixed-point, if it exists, will be the solution of the coupled system. A critical step in defining S is the harmonic extension of the Piola transformation from Ω_mf to Ω and ℝ³. The regularity of the Piola transformation determines not only the existence of the solution to the transformed Poisson-Boltzmann equation, but also the existence of the solution to the coupled system. Because most of our analysis will be carried out on the undeformed configuration we will still use Ω_mf, Ω_mr, Ω_s, Γ_f, Γ_r to denote the undeformed configurations of molecules, the solvent and the molecular interfaces, unless otherwise specified.

The paper is organized as follows. In Section 2 we review a fundamental result concerning the piecewise W^2,p-regularity of the solutions to elliptic equations in non-divergence form and with discontinuous coefficients. The nonlinear elasticity equation will be discussed in Section 3, where the major results from (7) are presented without proof. The Piola transformation will be defined, harmonically extended, and then analyzed. In Section 4 we will prove the existence and uniqueness of the solution to the Piola-transformed Poisson-Boltzmann equation, generalizing the results in (2) for the un-transformed case. Both L^∞ and W^2,p estimates will be given for the electrostatic potential in the solvent region, again generalizing results in (2). We will then define the electrostatic forces and estimate these forces by decomposing them into components corresponding to four independent perturbation steps. The estimates of these components are obtained separately and the final estimate of the surface force is assembled from these individual estimates. The coupled system will be finally considered in Section 6 where the mapping S will be defined, and the main result of the paper will be established by applying a fixed-point theorem on this map to give the existence of a solution of the coupled system.

2 Notation and Some Basic Estimates

In what follows W^k,p(𝒟) will denote the standard Sobolev space on an open domain 𝒟, where 𝒟 can be Ω,Ω_m or Ω_s. While solutions of the Poisson-Boltzmann have low global regularity in Ω, we will need to explore and exploit the optimal regularity of the solution in any subdomain of Ω. For this purpose, we define ${𝒲}^{2,p}\left(\Omega \right)=W^{2,p}\left({\Omega }_m\right)\stackrel{.}{+}{W}^{2,p}\left({\Omega }_s\right)$ where $\stackrel{.}{+}$ is the direct sum. Every function ϕ ∈ 𝒲^2,p can be written as ϕ(x) = ϕ_m(x) + ϕ_s(x) where ϕ_m(x) ∈ W^2,p(Ω_m), ϕ_s(x) ∈ W^2,p(Ω_s), and has a norm

$$\parallel \varphi {\parallel }_{{𝒲}^{2,p}}=\parallel {\varphi }_m{\parallel }_{W^{2,p}\left({\Omega }_m\right)}+\parallel {\varphi }_s{\parallel }_{W^{2,p}\left({\Omega }_s\right)}.$$ (6)

Similarly, we define a class of functions 𝒞 = 𝒞(Ω) which are continuous in either subdomain and may have finite jump on the interface, i.e., a function a ∈ 𝒞 is given by a = a_m + a_s where a_m ∈ C(Ωm), a_s ∈ C(Ω_s) are continuous functions in their respective domains. The norm in 𝒞 is defined by

$$\parallel a{\parallel }_{𝒞}=\parallel a_m{\parallel }_{C\left({\Omega }_m\right)}+\parallel a_s{\parallel }_{C\left({\Omega }_s\right)}.$$

We recall two important results. The first is a technical lemma which will be used for the estimation of the product of two W^1,p functions; this is sometimes called the Banach algebra property.

Lemma 2.1

Let 3 < p < ∞, 1 ≤ q ≤ p be two real numbers. Let Ω be a domain in ℝ³. Let u ∈ W^1,p(Ω), v ∈ W^1,q(Ω), then their product uv belongs to W^1,q, and there exists a constant C such that

$$\parallel \mathit{uv}{\parallel }_{W^{1,q}\left(\Omega \right)}\le C\parallel u{\parallel }_{W^{1,p}\left(\Omega \right)}\parallel v{\parallel }_{W^{1,q}\left(\Omega \right)}.$$

For the proof of this lemma we refer to (1). In this paper we will apply Lemma (2.1) to the case with p = q. The second result is a theorem concerning the L^p estimate of elliptic equations with discontinuous coefficients.

Theorem 2.2

Let Ω and Ω₁ ⊂⊂ Ω be bounded domains of ℝ³ with smooth boundaries ∂Ω and Γ. Let ${\stackrel{-}{\Omega }}_1=({\Omega }_1\cup \Gamma )$ and ${\Omega }_2=\Omega \setminus {\stackrel{-}{\Omega }}_1$. Let A be a second order elliptic operator such that

$$\left(\mathit{Au}\right)\left(x\right)=\{\begin{array}{cc}\left(A_{1}u\right)\left(x\right)\hfill & x\in {\Omega }_1\hfill \\ \left(A_{2}u\right)\left(x\right)\hfill & x\in {\Omega }_2\hfill \end{array}\phantom{\}},\mathit{where}{A}_i=\underset{k\le 2}{\Sigma }{a}_{\mathit{ik}}\left(x\right)D^k.$$

Then there exists a unique solution u ∈ 𝒲^2,p for the interface problem

$$\begin{array}{cc}\hfill \left(\mathit{Au}\right)\left(x\right)& =f\mathit{in}\Omega \hfill \\ \hfill \left[u\right]=u_2-u_1& =0\mathit{on}\Gamma \hfill \\ \hfill \left[{\mathit{Bu}}_n\right]=B_2\nabla u_2\cdot \mathbf{n}-B_1\nabla u_1\cdot \mathbf{n}& =h\mathit{on}\Gamma \hfill \\ \hfill u& =g\mathit{on}\partial \Omega \hfill \end{array}$$

providing that a_ik ∈ 𝒞(Ω), B_i ∈ C(Γ), f ∈ L^p(Ω), g ∈ W^2−1/p,p(∂Ω), h ∈ W^1−1/p,p(Γ), where n is the outside normal to Ω₁. Moreover, the following estimate holds true

$$\parallel u{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}\le K\left(\parallel f{\parallel }_{L^p\left(\Omega \right)}+\parallel h{\parallel }_{W^{1-1∕p,p}\left(\Gamma \right)}+\parallel g{\parallel }_{W^{2-1∕p,p}(\partial \Omega )}+\parallel u{\parallel }_{L^p\left(\Omega \right)}\right),$$ (7)

where the constant K depends only on Ω, Ω₁, Ω₂, p and the modulus of continuity of A.

Theorem (2.2) is fundamental to various results about elliptic equations with discontinuous coefficients; For example, the global H¹ regularity and H² estimates of Babüska (21), the finite element approximation of Chen et al. (22), a prior estimates for second-order elliptic interface problems (23), the solution theory and estimates for the nonlinear Poisson-Boltzmann equation (2; 3), and the continuous and discrete a priori L^∞ estimates for the Poisson-Boltzmann equation along with a quasi-optimal a priori error estimate for Galerkin methods (2) applied to the Poisson-Boltzmann equation. For the proof of Theorem (2.2) and the more general conclusions for high-order elliptic equations with high-order interface conditions we refer to (24; 25).

3 Nonlinear Elasticity and the Piola Transformation

We first state a theorem concerning the existence, uniqueness, regularity and the estimation of the solution to the nonlinear elasticity equation (7):

Theorem 3.1

Let body force f_b ∈ L^p(Ω_mf) and surface force f_s ∈ W^1−1/p,p(Γ_f), where 3 < p < ∞. There exists a neighborhood of 0 in L^p(Ω_mf) × W^1−1/p,p(Γ_f) such that if (f_b, f_s) belongs to this neighborhood then there exists a unique solution $\mathbf{u}\in W^{2,p}\left({\Omega }_{\mathit{mf}}\right)\cap W_{0,{\Gamma }_{f0}}^{1,p}\left({\Omega }_{\mathit{mf}}\right)$ of

$$\begin{array}{cc}\hfill -\mathrm{div}\left(\mathbf{T}\left(\mathbf{u}\right)\right)& ={\mathbf{f}}_b\mathit{in}{\Omega }_{\mathit{mf}},\hfill \\ \hfill \mathbf{T}\left(\mathbf{u}\right)\mathbf{n}& ={\mathbf{f}}_s\mathit{on}{\Gamma }_f\setminus {\Gamma }_{f0},\hfill \\ \hfill \mathbf{u}& =0\mathit{on}{\Gamma }_{f0},\hfill \\ \hfill {\int }_{{\Gamma }_f}(\mathrm{I}+\nabla \mathbf{u})J\left(u\right){(\mathrm{I}+\nabla \mathbf{u})}^{-T}\cdot \mathbf{n}& =3\left|{\Omega }_{\mathit{mf}}\right|,\hfill \end{array}$$ (8)

where Γ_f0 is a subset of Γ_f equipped with homogeneous Dirichlet boundary condition, I is the unit matrix. The last equation represents the incompressibility condition of the elastic deformation. Moreover, the solution can be estimated with respect to the force data:

$$\parallel u{\parallel }_{W^{2,p}\left({\Omega }_{\mathit{mf}}\right)}\le C(\parallel {\mathbf{f}}_b{\parallel }_{L^p\left({\Omega }_{\mathit{mf}}\right)}+\parallel {\mathbf{f}}_s{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}).$$ (9)

Proof

See (8).

Remark

It is noticed that $\mathbf{u}\in C^{1,1-3∕p}\left({\stackrel{-}{\Omega }}_{\mathit{mf}}\right)$ because of the continuous embedding of W^2,p(Ω_mf) in $C^{1,1-3∕p}\left({\stackrel{-}{\Omega }}_{\mathit{mf}}\right)$ for p > 3.

The displacement field u(x) solved from Eq.(8) naturally defines a mapping $\Phi \left(\mathbf{u}\right)=ℐ+\mathbf{u}\text{in}{\stackrel{-}{\Omega }}_{\mathit{mf}}$ where ℐ is the identity mapping. This mapping Φ(u)(x) has to be appropriately extended into ${ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}}$ to yield a global transformation for the Poisson-Boltzmann equation. It is critical in what follows that this extension has various favorable properties, which leads us to define a global mapping by harmonic extension:

$$\Phi \left(\mathbf{u}\right)=\{\begin{array}{cc}ℐ+\mathbf{u}\hfill & \mathbf{x}\in {\stackrel{‒}{\Omega }}_{\mathit{mf}}\hfill \\ ℐ+\mathbf{w}\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (10)

where w solves

$$\begin{array}{cc}\hfill \Delta \mathbf{w}& =0\text{in}{ℝ}^3\setminus {\stackrel{‒}{\Omega }}_{\mathit{mf}},\hfill \\ \hfill \mathbf{w}& =\mathbf{u}\mathrm{on}{\Gamma }_f.\hfill \end{array}$$ (11)

The following crucial lemma concerns the regularity of Φ(u) and the invertibility of ∇Φ(u):

Lemma 3.2

Let Φ(u) be defined in Eq.(10), we have

• (a) Φ(u) ∈ W^2,p(Ω_mf) and $\Phi \left(\mathbf{u}\right)\in C^{\infty }({ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}})$.

• (b) There exists a constant M > 0 such that for all ∥u∥_W^2,p(Ω) ≤ M, ∇Φ(u) is an invertible matrix in W^1,p(Ω_mf) and in $C^{\infty }({ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}})$.

• (c) Under condition of (b) Φ(x) is one-to-one on ℝ³, is a C¹-diffeomorphism from Ω_mf to Φ(u)(Ω_mf), and is C^∞-diffeomorphism from ${ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}}\mathit{to}\Phi \left(\mathbf{u}\right)({ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}})$.

Proof

Φ(u) ∈ W^2,p(Ω_mf) follows directly from its definition. $\Phi \left(\mathbf{u}\right)\in C^{\infty }({ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}})$ since Φ(u) = ℐ + w while w is harmonic hence analytical in $\Phi \left(\mathbf{u}\right)\in C^{\infty }({ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}})$ because it is the solution of the Laplace equation (11). For the invertibility of Φ(u) in W^1,p(Ω_mf) we refer to Lemma 2 in (7) or Theorem 5.5.1 in (8), which says that if a u ∈ Ω_mf is differentiable and

$$|\nabla \mathbf{u}\left(x\right)|<C$$

for some constant depending on Ω_mf, then $\nabla \Phi \left(\mathbf{u}\right)=\mathrm{I}+\nabla \mathbf{u}>0\forall x\in {\stackrel{-}{\Omega }}_{\mathit{mf}}$ and I + ∇u is injective on Ω_mf. The invertibility of ∇Φ(u) therefore follows from the facts that $\mathbf{u}\in C^{1,1-3∕p}\left({\stackrel{-}{\Omega }}_{\mathit{mf}}\right)$ such that for sufficiently small M

$$|\nabla \mathbf{u}|\le \parallel \mathbf{u}{\parallel }_{C^{1,1-3∕p}\left({\Omega }_{\mathit{mf}}\right)}\le C_1\parallel \mathbf{u}{\parallel }_{W^{2,p}\left({\Omega }_{\mathit{mf}}\right)}=C_{1}M\le C.$$

To prove the invertibility of $\nabla \Phi \left(\mathbf{u}\right)=\mathrm{I}+\nabla \mathbf{w}\text{in}{ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}}$ we notice the following estimate for the first derivative of the solution to Laplace equation (20):

$$|\nabla \mathbf{w}|\le \parallel \mathbf{w}{\parallel }_{C^1({ℝ}^3\setminus {\stackrel{‒}{\Omega }}_{\mathit{mf}})}\le C_2\parallel \mathbf{u}{\parallel }_{C^{1,1-3∕p}\left({\Gamma }_f\right)}\le C_{2}M\le C,$$

Therefore if M is chosen such that

$$M\le \frac{C}{\max \{C1,C2\}}$$ (12)

∇Φ(u) is an invertible matrix in ℝ³.

Remark

It follows from Lemma (3.2) that the matrix F(u) in Eq.(5) is well-defined, symmetric and positive definite. More precisely, $\mathbf{F}\left(\mathbf{u}\right)\left(x\right)\in C^{0,1-3∕p}\left({\stackrel{-}{\Omega }}_{\mathit{mf}}\right)$ and $\mathbf{F}\left(\mathbf{u}\right)\left(x\right)\in C^{\infty }({ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}})$. On the other hand, as a mapping from u ∈ W^2,p(Ω_mf) to $\mathbf{F}\left(\mathbf{u}\right)\in C^{\infty }({ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}})$, F(u) is infinitely differentiable with respect to u. In all what follows we will write F(u) and J(u) as F and J only, keeping in mind that they are u dependent.

4 Preliminary Results for the Poisson-Boltzmann Equation

4.1 The Poisson-Boltzmann equation with Piola transformation

The rigorous analysis and numerical approximation of solutions to the Poisson-Boltzmann equation (2) or its transformed version (4) are generally subject to three major difficulties: 1) the singular charge distribution, 2) the discontinuous dielectric constant on the molecular surface and 3) the strong exponential nonlinearities. However, it was recently demonstrated (2) that as far as the untransformed Poisson-Boltzmann equation (2) is concerned, some of these difficulties can be side-stepped by individually considering the singular and the regular components of the solution. Specifically, the potential solution is decomposed to be

$$\varphi =G+{\varphi }^r=G+{\varphi }^l+{\varphi }^n$$ (13)

where the singular component

$$G=\underset{i}{\Sigma }\frac{q_i}{{∊}_m|x-x_i|}$$

is the solution of the Poisson equation

$$-\nabla \cdot ({∊}_m\nabla G)={\rho }_f≔\underset{i}{\overset{N}{\Sigma }}{q}_i\delta \left(x_i\right)\text{in}{ℝ}^3;$$ (14)

while ϕ^l is the linear component of the electrostatic potential which satisfies

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\nabla {\varphi }^l)& =-\nabla \cdot ((∊-{∊}_m)\nabla G)\text{in}\Omega ,\hfill \\ \hfill {\varphi }^l& =g-G\mathrm{on}\partial \Omega ,\hfill \end{array}$$ (15)

and the nonlinear component ϕⁿ solves

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\nabla {\varphi }^n)+{\kappa }^2\sinh ({\varphi }^n+{\varphi }^l+G)& =0\text{in}\Omega ,\hfill \\ \hfill {\varphi }^n& =0\text{on}\partial \Omega ,\hfill \end{array}$$ (16)

where

$$g=\underset{i=1}{\overset{N}{\Sigma }}{q}_i\frac{e^{-\kappa |x-x_i|}}{{∊}_s|x-x_i|}$$ (17)

is the boundary condition of the complete Poisson-Boltzmann equation (2). Such a decomposition scheme removes the point charge singularity from the original Poisson-Boltzmann and it was shown in (2) that the regular component of the electrostatic potential ϕ^r = ϕ^l + ϕⁿ belongs to H¹(Ω) although the entire solution G + ϕ^r does not. The most prominent advantage of this decomposition lies in the fact that the regular component represents the reaction potential field of the system, which can be directly used to compute the solvation energy and other associated important properties of the system. It is not necessary to solve the Poisson-Boltzmann equation twice, once with uniform vacuum dielectric constant and vanishing ionic strength and the other with real physical conditions, to obtain the reaction field (30). As to be shown later on, the identification of this regular potential component as the reaction field also facilitates the analysis and the computation of the electrostatic forces.

Applying the similar decomposition to the transformed Poisson-Boltzmann equation we get an equation for the singular component G:

$$-\nabla \cdot ({∊}_m\mathbf{F}\nabla G)=J{\rho }_f\text{in}{ℝ}^3,$$ (18)

and an equation for the regular component ϕ^r:

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\mathbf{F}\nabla {\varphi }^r)+J{\kappa }^2\sinh ({\varphi }^r+G)& =\nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla G)\text{in}\Omega ,\hfill \\ \hfill {\varphi }^r& =g-G\text{on}\partial \Omega .\hfill \end{array}$$ (19)

We shall prove the existence of ϕ^r in Eq.(19) and give its L^∞ bounds by individually considering the equation for the linear component ϕ^l:

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\mathbf{F}\nabla {\varphi }^l)& =\nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla G)\text{in}\Omega ,\hfill \\ \hfill {\varphi }^l& =g-G\text{on}\partial \Omega ,\hfill \end{array}$$ (20)

and the equation for the nonlinear component ϕⁿ:

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\mathbf{F}\nabla {\varphi }^n)+J{\kappa }^2\sinh ({\varphi }^n+{\varphi }^l+G)& =0\text{in}\Omega ,\hfill \\ \hfill {\varphi }^n& =0\text{on}\partial \Omega .\hfill \end{array}$$ (21)

As mentioned above, the functions G, ϕ^l, ϕⁿ, ρ^f and κ in Eqs.(18) through (21) shall be interpreted as the compositions of the corresponding entries of these functions in untransformed equations (14) through (16) with the Piola transformation Φ(x), i.e., g = g(Φ(x)), G = G(Φ(x)), ϕ^l = ϕ^l(Φ(x)), ϕⁿ = ϕⁿ(Φ(x)), ρ^f = ρ^f(Φ(x)), κ = κ(Φ(x)).

4.2 Regularity and estimates for the singular solution component G

We first study the Eq. (18) for the singular component of electrostatic potential. We remark that the linear and nonlinear PB equations have the same singular component of the electrostatic potential. The solution of this singular component is the Green's function for the elliptic operator L defined by

$$\mathit{Lu}=-\nabla \cdot ({∊}_m\mathbf{F}\nabla u).$$ (22)

We shall use the following theorem (12) concerning the regularity and the estimate of the Green's function:

Theorem 4.1

Let Ω be an open set in ℝ³. Suppose the elliptic operator

$$\mathit{Lu}=\underset{i,j=1}{\overset{n}{\Sigma }}\frac{\partial }{\partial x_j}\left(a_{\mathit{ij}}\frac{\partial u}{\partial x_i}\right)$$

is uniformly elliptic and bounded, while the coefficients a_ij satisfying

$$|a_{\mathit{ij}}\left(x\right)-a_{\mathit{ij}\left(y\right)}|\le \omega \left(\right|x-y\left|\right)$$

for any x, y ∈ Ω, and the non-decreasing function ω(x) satisfies

$$\begin{array}{cc}\hfill \omega \left(2t\right)& \le K\omega \left(t\right)\mathit{for}\mathit{some}K>0\mathit{and}\mathit{all}\mathit{t}>0,\hfill \\ \hfill {\int }_{ℝ}\frac{\omega \left(t\right)}{t}\mathit{dt}& <\infty .\hfill \end{array}$$

Then for the corresponding Green's function G the following six inequalities are true for any x, y ∈ Ω:

• (a) G(x, y) ≤ K|x − y|⁻¹,

• (b) G(x, y) ≤ Kδ(x)|x − y|⁻².

• (b) G(x, y) ≤ Kδ(x)δ(y)|x − y|⁻³.

• (d) |∇_xG(x, y)| ≤ K|x − y|⁻².

• (e) |∇_yG(x, y)| ≤ Kδ(y)|x − y|⁻³.

• (f) |∇_x∇_yG(x, y)| ≤ K|x − y|⁻³.

where δ(y) = dist(y, ∂Ω) and the general constant K = K(a_ij, ω, Ω).

From this theorem we can derive the regularity of the Green's function of the operator (22). Indeed, by Sobolev embedding ε_m F ∈ C^0,1−3/p(ℝ³), therefore it satisfies the conditions on a_ij in this theorem provided that ω(t) = Kt^3/p. We then conclude that the singular component of the electrostatic potential G ∈ W^1,∞(Ω \ B_r(x_i)). On the other hand, from Eq. (18) we know that G(Φ(u)(x))/J(x_i) itself is the Green's function of operator (22) if F is generated by the Piola transformation according to (5) and J is the corresponding Jacobian. Thus the Green's function of differential operator (22) belongs to W^2,p(Ω\B_r(x_i)) since it is the composition of the Green's function of Laplace operator, which is of C^∞(Ω\B_r(x_i)), and the Piola transformation, which is of W^2,p(Ω). Higher regularity of G in Ω_s can be derived thanks to the harmonic extension of u to ${ℝ}^3\setminus {\stackrel{-}{\Omega }}_{\mathit{mf}}$. In particular, because all charges are located in Ω_mf and Ω_mr the Poisson equation (18) appears a Laplace equation

$$\nabla (∊\mathbf{F}\nabla G)=0\text{in}{\Omega }_s,$$

hence G(x) ∈ C^∞(Ω_s), since Ω_s is a smooth open domain and F ∈ C^∞(Ω_s).

In addition to the regularity of the Green's function, we have following estimates of G with respect to F and J.

Lemma 4.2

For any given molecule the Green's function G of operator (22) has estimates

• (a) $\parallel G{\parallel }_{L^{\infty }\left({\stackrel{-}{\Omega }}_s\right)}\le C\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}$.

• (b) $\parallel \nabla G{\parallel }_{L^{\infty }\left({\stackrel{-}{\Omega }}_s\right)}\le C\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}$.

If in addtion ∥F − I∥_W^1,p(Ω) ≤ C_f, ∥J − 1∥_W^1,p(Ω) ≤ C_J for some constant C_f and C_J, then

• (c) $\parallel G{\parallel }_{L^p(\partial \Omega )}\le C\parallel G{\parallel }_{L^{\infty }\left({\stackrel{-}{\Omega }}_s\right)}$.

• (d) ∥g ∘ Φ∥_{W^2−1/p,p(∂Ω)} ≤ C_g∥g∥_W^2,p(Ωs).

• (e) ∥g ∘ Φ − G∥_{W^2−1/p,p(∂Ω)} ≤ C_g∥g∥_W^2,p(Ωs) + C_G∥G∥_L^∞(Ωs).

• (f) $\parallel \mathbf{F}\nabla G{\parallel }_{W^{1-1∕p,p}\left(\Gamma \right)}\le C_{\Gamma }\parallel G{\parallel }_{L^{\infty }\left({\Omega }_s^{\prime }\right)}$ for some set ${\Omega }_s^{\prime }$.

Proof

This $\parallel J{\parallel }_{L^{\infty }\left({\stackrel{-}{\Omega }}_s\right)}$ is well defined since J is uniformly continuous in ${\stackrel{-}{\Omega }}_s$. To prove (a) and (b) we define q_max = max{|q_i|} and

$$\parallel {\nabla }_x{G}_i(x,x_i){\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}=\frac{K}{{\delta }^2},\parallel G_i(x,x_i){\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}=\frac{K}{\delta }$$

where δ is the smallest distance between x ∈ ∂Ω and singular charges at x_i. This smallest distance is related to the radii of atoms used in defining the molecular surface. In the sense of Connolly's molecular surface, δ is simply the smallest van der Waals radius of the atoms which have contact surface (34). We can therefore bound G and its gradient with

$$\begin{array}{cc}\hfill \parallel G{\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}& =\parallel \underset{i}{\Sigma }{\mathit{Jq}}_i{G}_i{\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}\le {\mathit{Nq}}_{\max }\parallel J{\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}\parallel G_i{\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}\hfill \\ & =\frac{\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}{\mathit{NKq}}_{\max }}{\delta },\hfill \end{array}$$ (23)

$$\begin{array}{cc}\hfill \parallel \nabla G{\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}& =\parallel \underset{i}{\Sigma }{\mathit{Jq}}_i\nabla G_i{\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}\le {\mathit{Nq}}_{\max }\parallel J{\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}\parallel {\nabla }_x{G}_i{\parallel }_{L^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)}\hfill \\ & =\frac{\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}{\mathit{NKq}}_{\max }}{{\delta }^2},\hfill \end{array}$$ (24)

where N is the total number of singular charges and $\parallel J{\parallel }_{L^{\infty }\left({\stackrel{-}{\Omega }}_s\right)}$ is the maximum Jacobian on Γ.

The statement (c) holds because ∂Ω is also a piece of boundary of Ω_s as shown in Fig.(1). To verify the statement (d), we noted that g ∘ Φ is the composition of g in Eq.(17), which is smooth in Ω_s, and the mapping Φ(x) ∈ W^2,p(Ω_s), i.e.,

$$go\Phi =\underset{i}{\Sigma }{q}_i\frac{e^{-\kappa |\Phi \left(x\right)-\Phi \left(x_i\right)|}}{{∊}_s|\Phi \left(x\right)-\Phi \left(x_i\right)|}.$$

Following the estimate of the composite function in Sobolev space (13), we have the inequality

$$\begin{array}{cc}\hfill \parallel go\Phi {\parallel }_{W^{2-1∕p,p}(\partial \Omega )}& \le \parallel g{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\hfill \\ & \le C(1+\parallel \Phi {\parallel }_{L^{\infty }\left({\Omega }_s\right)})(1+\parallel \Phi {\parallel }_{W^{2,p}\left({\Omega }_s\right)})\parallel g{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\hfill \\ & ≔C_g\parallel g{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\hfill \end{array}$$ (25)

with a constant C_g depending upon Φ(x). Here we choose to bound ∥g ∘ Φ∥_{W^2−1/p,p(∂Ω)} by ∥g ∘ Φ∥_W^2,p(Ωs) instead of ∥g ∘ Φ∥_W^2,p(Ω) since the latter is not well defined due to the singular nature of g.

The validity of inequalities (e) and (f) follows from the estimate of $\parallel G{\parallel }_{W^{2,p}\left({\Omega }_s^{\prime }\right)}$. This ${\Omega }_s^{\prime }$ is chosen such that ${\Omega }_s\subset \subset {\Omega }_s^{\prime }$. For example, we can choose ${\Omega }_s^{\prime }$ to be the union of Ω_s, Γ, ∂Ω, the domain

$${\Omega }_s^{-}=\{x\mid x\in {\Omega }_{\mathit{mf}},\text{dist}(x,\Gamma )<\frac{\delta }{2}\},$$

and the domain

$${\Omega }_s^{+}=\{x\mid x\notin \Omega ,\text{dist}(x,\partial \Omega )<\frac{\delta }{2}\}.$$

Applying the L^p estimate to Eq.(18) in Ω_s we obtain

$$\begin{array}{cc}\hfill \parallel G{\parallel }_{W^{2-1∕p,p}(\partial \Omega )}& \le C\parallel G{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\le C\left(\mathbf{F}\right)\parallel G{\parallel }_{L^p\left({\Omega }_s^{\prime }\right)}\le C\left(\mathbf{F}\right)\parallel G{\parallel }_{L^{\infty }\left({\Omega }_s^{\prime }\right)}\hfill \\ & ≔C_G\parallel G{\parallel }_{L^{\infty }\left({\Omega }_s^{\prime }\right)},\hfill \end{array}$$ (26)

where the second inequality is a consequence of the L^p estimate of the solution to −∇ ·(εF∇G) = 0 in ${\Omega }_s^{\prime }$. The coefficient C_G = C(F) depends on the ellipticity constants of F and its moduli of continuity on Ω_s, hence is bounded as long as F is bounded. By combining Eqs.(26) and (25) we get (c). For the last estimate we notice

$$\begin{array}{cc}\hfill \parallel \mathbf{F}\nabla G{\parallel }_{W^{1-1∕p,p}\left(\Gamma \right)}& \le C\parallel \left[∊\right]\mathbf{F}\nabla G{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\hfill \\ & \le C\parallel \mathbf{F}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\parallel \nabla G{\parallel }_{W^{1,p}\left({\Omega }_s\right)},(p>3)\hfill \\ & \le C\parallel \mathbf{F}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\parallel G{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\hfill \\ & \le C\left(\mathbf{F}\right)\parallel \mathbf{F}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\parallel G{\parallel }_{L^p\left({\Omega }_s^{\prime }\right)}\hfill \\ & \le C\parallel \mathbf{F}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\parallel G{\parallel }_{L^{\infty }\left({\Omega }_s^{\prime }\right)}\hfill \\ & ≔C_{\Gamma }\parallel G{\parallel }_{L^{\infty }\left({\Omega }_s^{\prime }\right)}.\hfill \end{array}$$ (27)

Remark

$\parallel G{\parallel }_{L^{\infty }\left({\Omega }_s^{\prime }\right)}$ can also be estimated by Eq.(23) if δ is replaced by δ/2 and ∥J∥_L^∞(Ω) is replaced by ∥J∥_{L^∞(Ω∪Ω⁺)}.

4.3 Regularity and estimates for the regular linearized solution component ϕ^r

We consider an elliptic interface problem modified from the Poisson-Boltzmann equation

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\mathbf{F}\nabla {\varphi }^r)+J{\kappa }^2({\varphi }^r+G)& =\nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla G)+f\text{in}\Omega \hfill \\ \hfill \left[{\varphi }^r\right]={\varphi }_s^r-{\varphi }_m^r& =0,\text{on}\Gamma \hfill \\ \hfill {\varphi }^r& =g-G\text{on}\partial \Omega ,\hfill \end{array}$$ (28)

where [ε] = ε_s − ε_m is the jump of dielectric constant and f ∈ L^p(Ω) is a given function. The equation for the regular potential solution of the linear Poisson-Boltzmann equation is a special case of (28) with f = 0. We remark that the regular component of the linear Poisson-Boltzmann equation in the absence of the Piola transformation represents a typical elliptic equation with discontinuous coefficients, for which Theorem (2.2) can be directly applied to get the existence and the estimate. In fact, the potential solution in this case is smooth in every subdomain (Proposition 1.4, (17)). When the Piola transformation is incorporated, the coefficients of the Eq. (28) are not smooth and we have to rebuild the regularity and the estimate of the regular potential solution ϕ^r, as summarized in the following theorem

Theorem 4.3

There exists a unique solution ϕ^r of (28) in H¹(Ω). Moreover, there exists a positive constant C_f such that if ∥F − I∥_W^1,p(Ω) ≤ C_f then ϕ^r belongs to 𝒲^2,p(Ω) and the following estimate holds true

$$\begin{array}{cc}\hfill \parallel {\varphi }^r{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}\le C_2(\phantom{)}\parallel & G{\parallel }_{L^p\left({\Omega }_s\right)}+\parallel f{\parallel }_{L^p\left(\Omega \right)}+\parallel g-G{\parallel }_{W^{2-1∕p,p}(\partial \Omega )}+\hfill \\ & \parallel \mathbf{F}\nabla G{\parallel }_{W^{1-1∕p,p}\left(\Gamma \right)}\phantom{(}).\hfill \end{array}$$ (29)

Before proving this 𝒲^2,p estimate, we first establish a lemma concerning the L^∞ estimate of a linear elliptic interface problem.

Lemma 4.4

Let ϕ^r solve

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\nabla {\varphi }^r)+b{\varphi }^r& =f\mathit{in}\Omega \hfill \\ \hfill \left[{\varphi }^r\right]& =0,\mathit{on}\Gamma \hfill \\ \hfill \left[∊{\varphi }_n^r\right]& =0,\mathit{on}\Gamma \hfill \\ \hfill {\varphi }^r& =g\mathit{on}\partial \Omega ,\hfill \end{array}$$

where ε is a piecewise constant as defined for problem (28) and b > 0 is a given real number, f(x) ∈ L^p(Ω), g ∈ H¹(Ω),p > 3. Then

$$\parallel {\varphi }^r{\parallel }_{L^{\infty }}\le C\left(\parallel f{\parallel }_{L^p\left(\Omega \right)}+\parallel g{\parallel }_{H^{1∕2}(\partial \Omega )}\right)$$ (30)

Proof

The existence of unique solution ϕ^r ∈ 𝒲^2,p ⊂ H¹(Ω) can be directly deduced from Theorem (2.2). We follow (2) and let ϕ^r = ϕ^l + ϕⁿ where ϕ^l solves

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\nabla {\varphi }^l)& =f\text{in}\Omega \hfill \\ \hfill \left[{\varphi }^l\right]& =0\text{on}\Gamma ,\hfill \\ \hfill \left[∊{\varphi }_n^l\right]& =0\text{on}\Gamma ,\hfill \\ \hfill {\varphi }^l& =g\text{on}\partial \Omega ,\hfill \end{array}$$

and ϕⁿ solves

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\nabla {\varphi }^n)+b({\varphi }^n+{\varphi }^l)& =0\text{in}\Omega ,\hfill \\ \hfill \left[{\varphi }^n\right]& =0\text{on}\Gamma ,\hfill \\ \hfill \left[∊{\varphi }_n^n\right]& =0\text{on}\Gamma ,\hfill \\ \hfill {\varphi }^n& =0\text{on}\partial \Omega .\hfill \end{array}$$

It is well known (21; 22) that

$$\parallel {\varphi }^l{\parallel }_{L^{\infty }}\le C\left(\parallel f{\parallel }_{L^p\left(\Omega \right)}+\parallel g{\parallel }_{H^{1∕2}(\partial \Omega )}\right),$$

while for ϕⁿ we claim that −∥ϕ^l∥_L^∞ ≤ ∥ϕⁿ∥_L^∞ ≤ ∥ϕ^l∥_L^∞. To prove this assertion we define ϕ_t = max(ϕⁿ − α, 0) where α = ∥ϕ^l∥_L^∞. Then the trace Tr(ϕ_t) = 0 hence ${\varphi }_t\in H_0^1\left(\Omega \right)$ by definition. Consider the weak formulation of the problem for ϕⁿ with test function ϕ_t

$$(∊\nabla {\varphi }^n,\nabla {\varphi }_t)+b({\varphi }^n+{\varphi }^l,{\varphi }_t)=0.$$

Since ϕ_t ≥ 0 wherever ϕⁿ ≥ α, we have

$$b({\varphi }^n+{\varphi }^l,{\varphi }_t)={\int }_{{\varphi }^n\ge \alpha }b({\varphi }^n+{\varphi }^l){\varphi }_t\mathit{dx}+{\int }_{{\varphi }^n<\alpha }b({\varphi }^n+{\varphi }^l){\varphi }_t\mathit{dx}\ge 0,$$

and

$$0\ge (∊\nabla {\varphi }^n,\nabla {\varphi }_t)=(∊\nabla ({\varphi }^n-\alpha ),\nabla {\varphi }_t)=(∊\nabla {\varphi }_t,\nabla {\varphi }_t)\ge 0.$$

Thus ∇ϕ_t = 0, and ϕ_t = 0 or ϕⁿ ≤ α in Ω follows from the Poincare inequality. By defining ϕ_t = min(ϕⁿ+α,0) and following the same procedure we can verify that ϕⁿ ≥ −α. The lemma shall be finally proved by combining the estimates of ϕ^l and ϕⁿ.

Proof: of Theorem (4.3)

Consider the general weak formulation of the elliptic equation in problem (28), i.e., find ${\varphi }^r=u\in H_0^1\left(\Omega \right)$ such that $A(u,v)=F\left(v\right),\forall v\in H_0^1\left(\Omega \right)$ where

$$\begin{array}{cc}\hfill A(u,v)& ={\int }_{\Omega }(\mathbf{F}\nabla u\nabla v+J{\kappa }^2\mathit{uv})\mathit{dx},\hfill \\ \hfill F\left(v\right)& ={\int }_{\Omega }(\nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla G)-J{\kappa }^{2}G+f)\mathit{dx}-A(g-G,v).\hfill \end{array}$$

We shall apply the Lax-Milgram theorem to obtain the existence and the uniqueness of a weak solution ϕ^r ∈ H¹ to (28). Hence we must show that F(·) is bounded, and A(·, ·) is bounded and coercive with the assumptions on the coefficient matrix F and the Jacobian J. Consider the bilinear form A(·, ·). The Piola transform matrix F is positive definite, hence F∇v · ∇v ≥ γ|∇v|² for some γ > 0. This inequality and the positiveness of Jacobian J give

$$\begin{array}{cc}\hfill A(v,v)& ={\int }_{\Omega }(\mathbf{F}\nabla v\cdot \nabla v+J{\kappa }^2{v}^2)\mathit{dx}\ge {\int }_{\Omega }\left(\gamma \right|\nabla v{|}^2+J{\kappa }^2{v}^2)\mathit{dx}\ge \lambda |u{|}_{H^1\left(\Omega \right)}^2\hfill \\ & =\gamma \left(\frac{1}{2}|v{|}_{H^1\left(\Omega \right)}^2+\frac{1}{2}|v{|}_{H^1\left(\Omega \right)}^2\right)\ge \gamma \left(\frac{1}{2{\theta }^2}\parallel v{\parallel }_{L^2\left(\Omega \right)}^2+\frac{1}{2}|v{|}_{H^1\left(\Omega \right)}^2\right)\hfill \\ & \ge m\left(\parallel v{\parallel }_{L^2\left(\Omega \right)}^2+|v{|}_{H^1\left(\Omega \right)}^2\right)=m\parallel v{\parallel }_{H^1\left(\Omega \right)}^2,\hfill \end{array}$$ (31)

where in the second inequality we applied the Poincare inequality with constant θ. Thus we verified that A(·, ·) is coercive, with coercivity constant m = min{γ/(2θ²), γ/2}.

On the other hand,

$$\begin{array}{cc}\hfill \left|A(u,v)\right|& =\left|{\int }_{\Omega }(\mathbf{F}\nabla u\cdot \nabla v\mid +J{\kappa }^2\mathit{uv})\mathit{dx}\right|\le \underset{i,j}{\Sigma }{\int }_{\Omega }\left|{\mathbf{F}}_{\mathit{ij}}{D}_i{\mathit{uD}}_{j}v\right|\mathit{dx}+{\int }_{\Omega }\left|J{\kappa }^2\mathit{uv}\right|\mathit{dx}\hfill \\ & \le \underset{i,j}{\Sigma }\parallel {\mathbf{F}}_{\mathit{ij}}{\parallel }_{L^{\infty }\left(\Omega \right)}\parallel D_i{\mathit{uD}}_{j}v{\parallel }_{L^1\left(\Omega \right)}+{\kappa }^2\parallel J{\parallel }_{L^{\infty }}\parallel \mathit{uv}{\parallel }_{L^1\left(\Omega \right)}\hfill \\ & \le \underset{i,j}{\Sigma }\parallel {\mathbf{F}}_{\mathit{ij}}{\parallel }_{L^{\infty }}\parallel u{\parallel }_{H^1\left(\Omega \right)}\parallel v{\parallel }_{H^1\left(\Omega \right)}+{\kappa }^2\parallel J{\parallel }_{L^{\infty }}\parallel u{\parallel }_{L^2\left(\Omega \right)}\parallel v{\parallel }_{L^2\Omega }\hfill \\ & \le K_1\parallel u{\parallel }_{H^1\left(\Omega \right)}\parallel v{\parallel }_{H^1\Omega }\hfill \end{array}$$ (32)

which proves that A(·, ·) is bounded with constant $K_1={\Sigma }_{i,j}\parallel {\mathbf{F}}_{\mathit{ij}}{\parallel }_{L^{\infty }}+{\kappa }^2\parallel J{\parallel }_{L^{\infty }}$.

This constant K₁ is finite because F, J belong to W^1,p(Ω) which is compactly embedded in $C^0\left(\stackrel{-}{\Omega }\right)$ for p > 3.

In order to apply the Lax-Milgram theorem it remains to show that F(v) is bounded on $H_0^1\left(\Omega \right)$. We have

$$\begin{array}{cc}\hfill \left|F\left(v\right)\right|\le |& {\int }_{\Omega }(∊-{∊}_m)\mathbf{F}\nabla \mathit{Gvdx}|+{\int }_{\Omega }|J{\kappa }^2\mathit{Gv}+\mathit{fv}|\mathit{dx}+|A(g-G,v)|\hfill \\ \hfill =& |{\int }_{{\Omega }_m}({∊}_m-{∊}_m)\mathbf{F}\nabla \mathit{Gvdx}+\hfill \\ & {\int }_{{\Omega }_s}({∊}_s-{∊}_m)\mathbf{F}\nabla \mathit{Gvdx}|+{\int }_{\Omega }|J{\kappa }^2\mathit{Gv}+\mathit{fv}|\mathit{dx}+|A(g-G,v)|\hfill \\ \hfill =& |{\int }_{{\Omega }_s}({∊}_s-{∊}_m)\mathbf{F}\nabla \mathit{Gvdx}+{\int }_{\Omega }|J{\kappa }^2\mathit{Gv}+\mathit{fv}|\mathit{dx}+|A(g-G,v)|\hfill \\ \hfill \le & {\int }_{{\Omega }_s}|({∊}_s-{∊}_m)\mathbf{F}\nabla \mathit{Gv}|\mathit{dx}+{\int }_{\Omega }|J{\kappa }^2\mathit{Gv}+\mathit{fv}|\mathit{dx}+\left|A(g-G,v)\right|\hfill \\ \hfill \le & \left[∊\right]\parallel \mathbf{F}\nabla G{\parallel }_{L^2\left(\Omega \right)}\parallel v{\parallel }_{L^2\left(\Omega \right)}+({\kappa }^2\parallel \mathit{JG}{\parallel }_{L^2\left(\Omega \right)}+\parallel f{\parallel }_{L^2\left(\Omega \right)})\parallel v{\parallel }_{L^2\left(\Omega \right)}+\hfill \\ & K_1\parallel g-G{\parallel }_{H^1\left(\Omega \right)}\parallel v{\parallel }_{H^1\left(\Omega \right)}\hfill \\ \hfill =& \left(\left[∊\right]\parallel \mathbf{F}\nabla G{\parallel }_{L^2\left(\Omega \right)}+{\kappa }^2\parallel \mathit{JG}{\parallel }_{L^2\left(\Omega \right)}+\parallel f{\parallel }_{L^2\left(\Omega \right)}+K_1\parallel g-G{\parallel }_{H^1\left(\Omega \right)}\right)\parallel v{\parallel }_{H^1\left(\Omega \right)}\hfill \\ \hfill =& K_2\parallel v{\parallel }_{H^1\left(\Omega \right)},\hfill \end{array}$$

hence F(·) is a bounded linear functional on $H_0^1\left(\Omega \right)$.

We now proceed to show the regularity result and the estimate of ϕ^r following the similar iterative technique in (7). For this purpose we introduce a sequence $\left\{{\varphi }_N^r\right\}$ generated by

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\nabla {\varphi }_N^r)+J{\kappa }^2{\varphi }_N^r& =\nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla G)-J{\kappa }^{2}G+\nabla \cdot (∊(\mathbf{F}-\mathrm{I})\nabla {\varphi }_{N-1}^r)\text{in}\Omega ,\hfill \\ \hfill \left[{\varphi }_N^r\right]& =0\text{on}\Gamma ,\hfill \\ \hfill {\varphi }_N^r& =g-G\text{on}\partial \Omega ,\hfill \end{array}$$ (33)

and prove that ${\varphi }_N^r\in {𝒲}^{2,p}\left(\Omega \right)$ and ${\varphi }_N^r$ converges to the unique solution ϕ^r of (28) in 𝒲^2,p(Ω) as N → ∞. The first term ${\varphi }_0^r$ of the sequence solves

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\nabla {\varphi }_0^r)+J{\kappa }^2{\varphi }_0^r& =\nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla G)-J{\kappa }^{2}G\text{in}\Omega \hfill \\ \hfill \left[{\varphi }_0^r\right]& =0,\text{on}\Gamma ,\hfill \\ \hfill {\varphi }_0^r& =g-G\text{on}\partial \Omega ,\hfill \end{array}$$ (34)

therefore it belongs to 𝒲^2,p(Ω) according to Theorem (2.2). Suppose now that ${\varphi }_{N-1}^r\in {𝒲}^{2,p}\left(\Omega \right)$, then $\nabla {\varphi }_{N-1}^r\in {𝒲}^{1,p}\left(\Omega \right)$ and $\nabla \cdot (∊(\mathbf{F}-\mathrm{I})\nabla {\varphi }_{N-1}^r)\in L^p\left(\Omega \right)$ following from Lemma (2.1). Thus problem (33) also has a unique solution ${\varphi }_N^r\in {𝒲}^{2,p}\left(\Omega \right)$ for all integer N according to Theorem (2.2). To prove that ${\varphi }_N^r$ converges to the unique solution ϕ^r of problem (28), we estimate $\parallel {\varphi }_N^r-{\varphi }_{N-1}^r\parallel {𝒲}^{2,p}\left(\Omega \right)$ and show it is decreasing as N → ∞. By subtracting the equations in (28) for N from those for N − 1 we obtain a problem for ${\varphi }_N^r-{\varphi }_{N-1}^r$. Applying Theorem (2.2) again we know that this problem has a unique solution in 𝒲^2,p(Ω) which has an estimate

$$\begin{array}{cc}\hfill \parallel {\varphi }_N^r-{\varphi }_{N-1}^r{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}& \le C\left(\parallel \nabla \cdot (∊(\mathbf{F}-\mathrm{I})\nabla ({\varphi }_{N-1}^r-{\varphi }_{N-2}^r)){\parallel }_{L^p\left(\Omega \right)}+\parallel {\varphi }_N^r-{\varphi }_{N-1}^r{\parallel }_{L^p\left(\Omega \right)}\right)\hfill \\ & \le C\parallel \nabla \cdot (∊(\mathbf{F}-\mathrm{I})\nabla ({\varphi }_{N-1}^r-{\varphi }_{N-2}^r)){\parallel }_{L^p\left(\Omega \right)},\hfill \\ & \le C\parallel \mathbf{F}-\mathrm{I}{\parallel }_{W^{1,p}\left(\Omega \right)}\parallel {\varphi }_{N-1}^r-{\varphi }_{N-2}^r{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)},\hfill \end{array}$$ (35)

where in the second inequality we applied Lemma (4.4) to the problem for $({\varphi }_N^r-{\varphi }_{N-1}^r)$, and the generic constant C is independent of N, F. Therefore if the constant C_f in the assumption of the theorem is chosen such that CC_f = κ < 1 then $\parallel {\varphi }_N^r-{\varphi }_{N-1}^r{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}$ is decreasing with respect to N hence the sequence ${\varphi }_n^r$ converges to a unique element $\stackrel{‒}{{\varphi }^r}$ in 𝒲^2,p(Ω). Letting N → ∞ we can observe that $\stackrel{‒}{{\varphi }^r}$ is the unique solution of problem (28), meaning $\stackrel{‒}{{\varphi }^r}={\varphi }^r$.

The estimate of ϕ^r is obtained by estimating ${\varphi }_N^r$ and passing N to ∞. We notice that ${\varphi }_N^r={\varphi }_N^r-{\varphi }_{N-1}^r+{\varphi }_{N-1}^r-{\varphi }_{N-2}^r+\cdots +{\varphi }_0^r$, hence

$$\begin{array}{cc}\hfill \parallel {\varphi }_N^r{\parallel }_{{𝒲}^{2,p}}& \le \frac{1-k^{N-1}}{1-k}\parallel {\varphi }_1^r-{\varphi }_0^r{\parallel }_{{𝒲}^{2,p}}+\parallel {\varphi }_0^r{\parallel }_{{𝒲}^{2,p}}\hfill \\ & \le C_2(\parallel G{\parallel }_{L^p\left({\Omega }_s\right)}+\parallel g-G{\parallel }_{W^{2-1∕p,p}\left(\Omega \right)}+\parallel \mathbf{F}\nabla G{\parallel }_{W^{1-1∕p,p}\left(\Gamma \right)}\text{as}N\to \infty ,\hfill \end{array}$$

where both Theorem (2.2) and Lemma (4.4) are applied to the problem of ${\varphi }_1^r-{\varphi }_0^r$ and the problem of ${\varphi }_0^r$ to get the desired bounds with respect to the 𝒲^2,p(Ω) and L^∞ norms, and C₂ absorbs κ and all the generic constants involved in these bounds.

4.4 Regularity and estimates for the regular nonlinear solution component ϕ^r

For the nonlinear Poisson-Boltzmann equation, the regular component ϕ^r of its potential solution solves

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\mathbf{F}\nabla {\varphi }^r)+J{\kappa }^2\sinh ({\varphi }^r+G)& =\nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla G)\text{in}\Omega \hfill \\ \hfill \left[{\varphi }^r\right]={\varphi }_s^r-{\varphi }_m^r& =0\text{on}\Gamma \hfill \\ \hfill {\varphi }^r& =g-G\text{on}\partial \Omega .\hfill \end{array}$$ (36)

.

The appearance of the nonlinear function sinh(x) complicates the establishment of the existence of ϕ^r. In particular, the Lax-Milgram Theorem is not applicable to problem (36). Instead we define a energy functional based on the weak formulation of (36) and show that the unique minimizer of this energy functional is the unique solution of (36). On the other hand, the establishment of the regularity and 𝒲^2,p estimate of ϕ^r for (36) is simplified thanks to Theorem (4.3).

We start with the weak formulation of (36): Find ϕ^r ∈ M ≡ {v ∈ H¹(Ω)|e^v, e^−v ∈ L²(Ω), and v = g − G on ∂Ω}, such that

$$A({\varphi }^r,v)+(B\left({\varphi }^r\right),v)+\langle f_G,v\rangle =0,\forall v\in H_o^1\left(\Omega \right),$$ (37)

where

$$\begin{array}{cc}\hfill A({\varphi }^r,v)& =(∊\mathbf{F}\nabla {\varphi }^r,\nabla v),(B\left({\varphi }^r\right),v)=(J{\kappa }^2\sinh ({\varphi }^r+G),v),\hfill \\ \hfill \langle f_G,v\rangle & ={\int }_{\Omega }(∊-{∊}_m)\mathbf{F}\nabla G\cdot \nabla v.\hfill \end{array}$$

.

We also use f_G to denote the function [ε]F(u)∇G·n on the dielectric boundary Γ, since

$$\langle f_G,v\rangle =(\left[∊\right]\mathbf{F}\nabla G\cdot \mathbf{n},v),$$ (38)

where [ε] = ε_s − ε_m is the jump in ε on Γ. Based on this weak formulation we define an energy on M:

$$E\left(w\right)={\int }_{\Omega }\frac{∊}{2}\mathbf{F}\nabla w\cdot \nabla w+J{\kappa }^2\cosh (w+G)+\langle f_G,w\rangle .$$ (39)

.

The weak solution of Eq.(19) can be characterized as the minimizer of this energy functional. This equivalence and the existence of this minimizer are due to the following four simple lemmas. For the proof of these lemmas we refer to (2); see also (3) for a different variational treatment that also develops some additional theoretical results for a more general version of the Poisson-Boltzmann equation.

Lemma 4.5

If u is the solution of the optimization problem, i.e.,

$$E\left(u\right)=\underset{w\in M}{\inf }E\left(w\right),$$

then u is the solution of (19).

Lemma 4.6

Let F (u) be a functional defined on M, if

• (1) M is weakly sequential compact, and

• (2) F is weakly lower semi-continuous on M,

then there exists u ∈ M such that

$$F\left(u\right)=\underset{w\in M}{\inf }F\left(w\right).$$

Lemma 4.7

The following results hold true

• (1) Let V be a reflective Banach space. The set M := {v ∈ V |∥v∥ ≤ r₀} is weakly sequential compact.

• (2)if $\underset{\parallel v\parallel \to \infty }{\lim }F\left(v\right)=\infty$, then $\underset{w\in V}{\inf }F\left(w\right)=\underset{w\in M}{\inf }F\left(w\right)$

Lemma 4.8

If F is a convex functional on a convex set M and F is Gâteaux differentiable, then F is w.l.s.c. on M.

The existence and the uniqueness of the weak solution to (19) can be established using these lemmas. The following lemma establishes the existence of the minimizer of the energy E(w).

Theorem 4.9

There exists a unique u ∈ M ⊂ H¹(Ω) such that

$$E\left(u\right)=\underset{w\in M}{\inf }E\left(w\right).$$

Proof

The differentiability of E(w) follows its definition. Actually we have

$$\langle DE\left(u\right),v\rangle =A(u,v)+(B\left(u\right),v)+\langle f_G,v\rangle .$$

The minimizer of E(w) exists if we can prove that

• (1) M is a convex set

• (2) E is convex on M

• (3) $\underset{\parallel w{\parallel }_{H^1\left(\Omega \right)}\to \infty }{\lim }E\left(w\right)=\infty$

It is easy to verify (1). The convexity of F∇w · ∇w follows from the fact that

$$0\le \mathbf{F}\nabla \left(\gamma w\right)\cdot \nabla \left(\gamma w\right)={\gamma }^2\mathbf{F}\nabla w\cdot \nabla w\le \gamma \mathbf{F}\nabla w\cdot \nabla w$$

for any 0 ≤ γ ≤ 1 since F is positive definite. The convexity of cosh(w + G) follows from the convexity of cosh(x) directly. Actually E(w) is strictly convex. To prove (3) we only need to show that

$$E\left(w\right)\ge C(∊,\kappa ,\mathbf{F})\parallel w{\parallel }_{H^1\left(\Omega \right)}^2+C(G,g).$$ (40)

We notice that cosh(x) ≥ 1 and

$$\begin{array}{cc}\hfill <f_G,w>& \le {∊}_s\parallel \mathbf{F}\nabla G{\parallel }_{L^2\left({\Omega }_s\right)}\parallel \nabla w{\parallel }_{L^2\left({\Omega }_s\right)}\hfill \\ & \le {∊}_s\parallel \mathbf{F}{\parallel }_{L^2\left({\Omega }_s\right)}\parallel \nabla G{\parallel }_{L^2\left({\Omega }_s\right)}\parallel \nabla w{\parallel }_{L^2\left({\Omega }_s\right)}\hfill \\ & \le \frac{{∊}_s\gamma }{2}(\parallel \nabla G{\parallel }_{L^2\left({\Omega }_s\right)}^2+\parallel \nabla w{\parallel }_{L^2\left({\Omega }_s\right)}^2),\hfill \end{array}$$

where the matrix norm

$$\gamma =\parallel \mathbf{F}{\parallel }_{L^2\left({\Omega }_s\right)}=\underset{v\in M,\parallel v{\parallel }_{L^2\left(\Omega \right)}=1}{\sup }\parallel \mathbf{F}v{\parallel }_{L^2\left({\Omega }_s\right)},$$

is finite because F is continuous. Therefore

$$\begin{array}{cc}\hfill E\left(w\right)& \ge \frac{1}{2}{\int }_{\Omega }∊\mathbf{F}\nabla w\cdot \nabla w-|<f_G,w>|\hfill \\ & \ge \frac{\gamma }{2}\left({\int }_{{\Omega }_s}{∊}_s|\nabla w{|}^2+{\int }_{{\Omega }_m}{∊}_m|\nabla w{|}^2\right)-\frac{{∊}_s\gamma }{2}(\parallel \nabla G{\parallel }_{{\Omega }_s}^2+\parallel \nabla w{\parallel }_{L^2\left({\Omega }_s\right)}^2)\hfill \\ & =\frac{\gamma }{2}{\int }_{{\Omega }_m}{∊}_m|\nabla w{|}^2-\frac{{∊}_s\gamma }{2}\parallel \nabla G{\parallel }_{L^2\left({\Omega }_s\right)}^2\hfill \\ & \ge C(∊,\gamma )\parallel \nabla w{\parallel }_{L^2\left(\Omega \right)}^2-\frac{{∊}_s\gamma }{2}\parallel \nabla G{\parallel }_{L^2\left({\Omega }_s\right)}^2.\hfill \end{array}$$

The inequality (40) follows from the equivalence of ∥∇w∥_L²(Ω) and ∥w∥_H¹(Ω) on set M. The uniqueness of the minimizer of E(w) comes from the strict convexity of E.

Theorem 4.10

There exists a unique solution ϕ^r of (28) in H¹(Ω). Moreover, there exist constants C₁, C₂ and C₃ such that ϕ^r is bounded by

$$\parallel {\varphi }^r{\parallel }_{L^{\infty }\left(\Omega \right)}\le C_1+C_2\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}+C_3\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}\parallel \mathbf{F}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}.$$ (41)

Proof

The existence of the solution ϕ^r in H¹(Ω) has been proved by theorem (4.9) and its four lemmas. It remains to verify the L^∞ bounds of ϕ^r. Let ϕ^r = ϕ^l + ϕⁿ be decomposed into a linear component ϕ^l and a nonlinear component. The linear component ϕ^l satisfies Eq.(20). The existence of a weak solution ${\varphi }^l\in H_0^1\left(\Omega \right)$ follows that ∇·((ε − ε_m)F∇G) is an operator in H⁻¹(Ω) (9). It is well known that in general

$$C_1\parallel {\varphi }^l{\parallel }_{L^{\infty }}\le \parallel {\varphi }^l{\parallel }_{H^1}\le C_2(\parallel g-G{\parallel }_{H^{1∕2}(\partial \Omega )}+\parallel f_G{\parallel }_{H^{1∕2}\left(\Gamma \right)}).$$ (42)

To estimate the nonlinear component we follow (2) and define:

$$\begin{array}{cc}\hfill {\alpha }^{\prime }& =\arg \underset{c}{\max }\{J{\kappa }^2\sinh (c+\underset{x\in {\Omega }_s}{\sup }{\varphi }^l+\underset{x\in {\Omega }_s}{\sup }G)\le 0\},\hfill \\ \hfill {\beta }^{\prime }& =\arg \underset{c}{\min }\{J{\kappa }^2\sinh (c+\underset{x\in {\Omega }_s}{\inf }{\varphi }^l+\underset{x\in {\Omega }_s}{\inf }G)\ge 0\},\hfill \\ \hfill \alpha & =\min ({\alpha }^{\prime },0),\hfill \\ \hfill \beta & =\max ({\beta }^{\prime },0).\hfill \end{array}$$

It follows from the monotonicity of sinh(x) that

$$\beta =\parallel {\varphi }^l{\parallel }_{L^{\infty }\left({\Omega }_s\right)}+\parallel G{\parallel }_{L^{\infty }\left({\Omega }_s\right)},$$ (43)

$$\alpha =-\beta .$$ (44)

We will show that α and β are the lower and upper L^∞ bounds of the nonlinear component ϕⁿ of the weak solution to (36), following the similar procedure as that used in proving Lemma (4.4).

Define

$${\varphi }_t=\max ({\varphi }^n-\beta ,0),$$

then Trϕ_t = 0 since ${\varphi }^n\in H_0^1\left(\Omega \right)$ and β > 0 by definition. Therefore ${\varphi }_t\in H_0^1\left(\Omega \right)$ and satisfies the weak formulation of Eq.(21):

$$(∊\mathbf{F}\nabla {\varphi }^n,\nabla {\varphi }_t)+\left(J{\kappa }^2\sinh ({\varphi }^n+{\varphi }^l+G),{\varphi }_t\right)=0.$$

Since ϕ_t ≥ 0 wherever ϕⁿ ≥ β, we have

$$J\left(\mathbf{u}\right){\kappa }^2\sinh ({\varphi }^n+{\varphi }^l+G)\ge J\left(\mathbf{u}\right){\kappa }^2\sinh (\beta +\underset{x\in {\Omega }_s}{\inf }{\varphi }^l+\underset{x\in {\Omega }_s}{\inf }G)\ge 0.$$

Therefore

$$0\ge (∊\mathbf{F}\nabla {\varphi }^n,\nabla {\varphi }_t)=(∊\mathbf{F}\nabla ({\varphi }^n-\beta ),\nabla {\varphi }_t)=∊\mathbf{F}\nabla {\varphi }_t\cdot \nabla {\varphi }_t\ge 0,$$

where the last inequality holds true since F is positive definite. Hence ∇ϕ_t = 0, and ϕ_t = 0 or ϕⁿ ≤ β in Ω follows from the Poincare inequality. This establishes the upper bound of ϕⁿ. By changing ϕ_t to be min(ϕⁿ + α, 0) we can also prove that α is the lower bound.

Combining the estimates for ϕ^l and ϕⁿ we finally obtain the L^∞ estimate of the regular component ϕ^r:

$$\begin{array}{cc}\hfill \parallel {\varphi }^l+{\varphi }^n{\parallel }_{L^{\infty }\left(\Omega \right)}& \le \parallel {\varphi }^l{\parallel }_{L^{\infty }\left(\Omega \right)}+\parallel {\varphi }^n{\parallel }_{L^{\infty }\left(\Omega \right)}\le \parallel {\varphi }^l{\parallel }_{L^{\infty }\left(\Omega \right)}+\parallel {\varphi }^l{\parallel }_{L^{\infty }\left({\Omega }_s\right)}+\parallel G{\parallel }_{L^{\infty }\left({\Omega }_s\right)}\hfill \\ & \le 2(C_g+C_G\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}+C_{f_G}\parallel \mathbf{F}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}+\frac{\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}{\mathit{NKq}}_{\mathit{max}}}{\delta }\hfill \\ & =C_1+C_2\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}+C_3\parallel J{\parallel }_{L^{\infty }\left(\Omega \right)}\parallel \mathbf{F}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}.\hfill \end{array}$$

We are now able to examine the regularity results and the estimate of ϕ^r in 𝒲^2,p.

Theorem 4.11

If ∥F − I∥_W^1,p(Ω) ≤ C_f then the unique solution ϕ^r of (36) belongs to 𝒲^2,p(Ω) and the following estimate holds true

$$\parallel {\varphi }^r{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}\le C\left(\parallel G{\parallel }_{L^p\left({\Omega }_s\right)}+\parallel g-G{\parallel }_{W^{2-1∕p,p}(\partial \Omega )}+\parallel \mathbf{F}\nabla G{\parallel }_{W^{1-1∕p,p}\left(\Gamma \right)}\right)$$ (45)

Proof

It is noticed that the problem (36) can be written as a form similar to its linear counterpart (28)

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\mathbf{F}\nabla {\varphi }^r)+J{\kappa }^2({\varphi }^r+G)=& \nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla G)\hfill \\ & -J{\kappa }^2(\sinh ({\varphi }^r+G)-({\varphi }^r+G))\text{in}\Omega \hfill \\ \hfill \left[{\varphi }^r\right]=& 0,\text{on}\Gamma \hfill \\ \hfill {\varphi }^r=& g-G\text{on}\partial \Omega .\hfill \end{array}$$

According to Theorem (4.3), the 𝒲^2,p regularity of ϕ^r directly follows from the facts that ∇ · ((ε − ε_m) F∇G) represents an interface condition in W^2−1/p,p(Ω) and that Jκ² (Sinh (ϕ^r + G) − (ϕ^r + G)) ∈ L^∞. In the mean time, we have an estimate

$$\parallel {\varphi }^r{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}\le C\left(\parallel G{\parallel }_{L^p\left({\Omega }_s\right)}+\parallel g-G{\parallel }_{W^{2-1∕p,p}(\partial \Omega )}+\parallel \mathbf{F}\nabla G{\parallel }_{W^{1-1∕p,p}\left(\Gamma \right)}\right).$$

5 An Electrostatic Force Model and Some Estimates

For the untransformed nonlinear Poisson-Boltzmann equation (2) the electrostatic energy of the system is defined (28; 14; 15) to be

$$E={\int }_{\Omega }[{\rho }^f\varphi -\frac{1}{2}∊{(\nabla \varphi )}^2-{\kappa }^2(\cosh \left(\varphi \right)-1)\chi ]\mathit{dx},$$ (46)

where the characteristic function χ = 1 in Ω_s and is 0 in molecules Ω_mf, Ω_mr. This energy is very similar to the energy functional defined in Eq.(39), and any potential function ϕ minimizing (39) is also the minimizer of this electrostatic energy because cosh(x) ≥ 1. The function cosh(ϕ) − 1 describes the physical fact that the total electrostatic energy is zero when ϕ is everywhere zero. The three terms in this energy represent three types of energy densities, namely, the Coulomb energy, the electrostatic stress energy and the osmotic stress energy of the mobile ions. Based on this energy function, the following density function of the force exerted on the molecule was derived (15) by using a variational derivation method:

$$\mathbf{f}={\rho }^f\mathbf{E}-\frac{1}{2}|\mathbf{E}{|}^2\nabla ∊-{\kappa }^2(\cosh \left(\varphi \right)-1)\nabla \chi ,$$ (47)

where the three terms correspond to the Coulomb force, dielectric pressure and the ionic pressure, respectively. The last two boundary forces are always in the normal direction of the molecular surface because of the gradients of ε and the characteristic function χ. The electric force defined in (47) is physically justifiable, and can be converted into a form identical to the Maxwell stress tensor(MST) (14; 33). The MST describes the volume force density in a linear dielectric, and has been widely utilized in dielectrophoretic force and electro-rotational torque calculations of colloids, macromolecules and biological cells in continuous external electric field (33). In the context of interactions between singular charges distribution and resulting singular electric field, refinements are necessary to make this force model computationally more tractable. Below we will discuss the treatments of its three components.

The first term in Eq. (47) might appear misleading because of the multiplication of two singular functions, ρ^f and E, in its expression. We therefore would emphasis that at a singular change x_i the electric potential field multiplied with ρ^f in Eq.(46) shall be interpreted as the summation of reaction potential field ϕ^r i.e., the regular component of the potential solution, and the Coulomb potential induced by all other singular charges (15):

$$\begin{array}{cc}\hfill {\rho }^f\mathbf{E}=\underset{i}{\Sigma }{q}_i\delta \left(x_i\right)\mathbf{E}≔& \underset{i}{\Sigma }{q}_i\delta \left(x_i\right)\nabla \left({\varphi }^r\left(x\right)+\underset{j\ne i}{\Sigma }{G}_j\left(x\right)\right)\hfill \\ \hfill =& \underset{i}{\Sigma }{q}_i\nabla \left({\varphi }^r\left(x_i\right)+\underset{j\ne i}{\Sigma }{G}_j\left(x_i\right)\right)\delta \left(x_i\right).\hfill \end{array}$$ (48)

This verifies that the force exerted at each charged atom is finite. The eliminated term G_i(x_i) corresponds to the self-energy of the singular charges (15).

Nevertheless, the body force density ρ^fE itself is still unbounded at the center of every charged atom where the charge density is singular, indicating that this body force density does not belongs to L^p(Ω_mf) hence does not fit the assumption on the body force in Theorem (3.1). An alternative model is therefore necessary to regularize these singular body forces to ensure the solvability of the elasticity equation. In this study, the singular the body force density is modeled by a Gaussian function

$${\mathbf{f}}_{\mathbf{b}}=\underset{i}{\Sigma }{a}_i{e}^{-{(x-x_i)}^2∕{\sigma }_i}{\mathbf{n}}_i,$$ (49)

where the unit normal vector is aligned with the corresponding gradient in Eq.(48); the decay parameter σ_i is chosen such that

$$\underset{i}{\Sigma }{a}_i{e}^{-R_i^2∕{\sigma }_i}=\delta$$ (50)

for a given sufficiently small number δ, and R_i is the van der Waals' radius of atom i. This means that the Gaussian function is essentially compact supported in its associated atom. The prefactor a_i is determined by the conservation of force in each atom:

$${\int }_{{\mathit{atom}}_i}{a}_i{e}^{-{(x-x_i)}^2∕{\sigma }_i}\mathit{dx}=q_i[{\varphi }^r\left(x_i\right)+\underset{j\ne i}{\Sigma }{G}_j\left(x_i\right)]=4\pi a_i{\int }_0^{R_i}{r}^2{e}^{-r^2∕{\sigma }_i}\mathit{dr}.$$ (51)

The body force f_b modeled by this Gaussian is uniformly continuous in Ω_mf and belongs to L^p(Ω_mf) for any p > 0. Moreover, the lemma below proves that the difference of two continuous body force densities also belongs to L^p(Ω_mf), and is small if the difference between two total body forces which they approximate is small.

Lemma 5.1

Let A₁, A₂ be two given numbers and |A₁| ≤ P, |A₂| ≤ P for some P. Let

$$f_j=a_j{e}^{-{(x-x_0)}^2∕{\sigma }_j}\mathit{such}\mathit{that}{\int }_{x-x_0\le R}{a}_j{e}^{-{(x-x_0)}^2∕{\sigma }_j}\mathit{dx}=A_j\mathit{for}j=1,2,$$

where a_j, σ_j are determined from Eqs. (51,50) for the same atom centered at x₀ and of radius R. Then if |A₁ − A₂| ≤ δ′ for some δ′ > 0, we have

$${\int }_{x-x_0\le R}|f_1-f_2{|}^p\mathit{dx}\le C{\delta }^{\prime }$$ (52)

for some constant C depending only on R and P.

Proof

The prefactor a and the decay rate σ are uniformly continuous functions of A for |A| ≤ P if

$$f={\mathit{ae}}^{-{(x-x_0)}^2∕\sigma }$$

is the approximation of A as defined by the lemma. But then there exists a constant C depending on the derivatives of a and σ with respect to A such that |f₁(x) − f₂(x)| ≤ Cδ′ if |A₁ − A₂| ≤ δ′. The conclusion of the lemma follows directly.

The last two terms in Eq.(47) represent the electrostatic surface forces on the molecule. It is worth noting that the second term is not well defined and is computationally intractable if there is no dielectric boundary smoothing, due to the discontinuous electric field E on the molecular surface indicated by the interface condition

$${∊}_m\nabla {\varphi }_m\cdot \mathbf{n}={∊}_s\nabla {\varphi }_s\cdot \mathbf{n}\text{or}{∊}_m{\mathbf{E}}_m\cdot \mathbf{n}={∊}_s{\mathbf{E}}_s\cdot \mathbf{n}.$$

To remove this ambiguity we consider a infinitesimal displacement h of the molecular surface in its out normal direction, see Fig.(2). The change of the electrostatic stress energy due to this small displacement is the work done by the dielectric pressure along this displacement:

$$\begin{array}{cc}\hfill {\int }_{{\Omega }_s^{\prime }+{\Omega }_m^{\prime }}-\frac{1}{2}∊|\mathbf{E}{|}^2\mathit{dx}-{\int }_{{\Omega }_s+{\Omega }_m}-\frac{1}{2}∊|\mathbf{E}{|}^2\mathit{dx}=& {\int }_{{\Gamma }_f\times h}-\frac{1}{2}\left({∊}_s\right|{\mathbf{E}}_s{|}^2-{∊}_m\left|{\mathbf{E}}_m{|}^2\right)\mathit{dx}\hfill \\ \hfill =& h{\int }_{{\Gamma }_f}{\mathbf{f}}_e\mathit{ds}.\hfill \end{array}$$

Fig. 2.

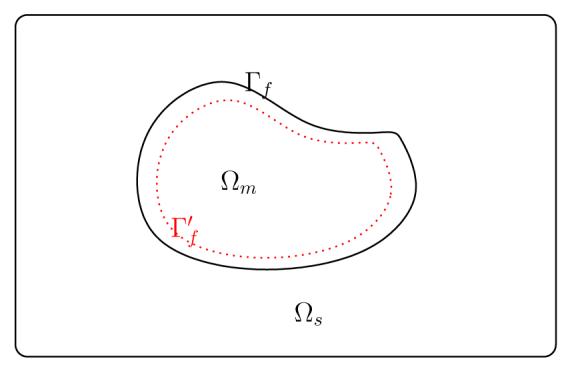
Displacement of the molecular surface Γ_f. The solid black line is the surface before displacement and the dashed red line is the surface after displacement. The new solvent region ${\Omega }_s^{\prime }$ is Ω_s plus the strip between two surfaces; The strip subtracted from Ω_m the equals the new solute region ${\Omega }_m^{\prime }$.

This suggests the dielectric force density f_e is essentially the difference between −½ε_s|E_s|² and −½ε_m|E_m|² on the dielectric interface, i.e.,

$${\mathbf{f}}_e=-\frac{1}{2}\left({∊}_s\right|{\mathbf{E}}_s{|}^2-{∊}_m\left|{\mathbf{E}}_m{|}^2\right)\mathbf{n}.$$ (53)

By combining definitions (47), (49) and (53) we would obtain a complete model of the electrostatic body force and surface force:

$${\mathbf{f}}_{\mathbf{b}}=\underset{i}{\Sigma }{a}_i{e}^{-{(x-x_i)}^2∕{\sigma }_i}{\mathbf{n}}_i,$$ (54)

$${\mathbf{f}}_{\mathbf{s}}=-\frac{1}{2}\left({∊}_s\right|{\mathbf{E}}_s{|}^2-{∊}_m\left|{\mathbf{E}}_m{|}^2\right)\mathbf{n}-{\kappa }^2(\cosh \left(\varphi \right)-1)\mathbf{n}.$$ (55)

Remark

In the sequel we will estimate ∥f_s∥_{W^1−1/p,p(Γf)}. Although ∥E_s∥_{W^1−1/p,p(Γf)} can be directly related to ∥ϕ_s∥_W^2,p(Ωs) since the latter is bounded in Ω_s, one can not estimate ∥E_m∥_{W^1−1/p,p(Γf)} similarly by relating it with ∥ϕ_m∥_W^2,p(Ωmf) because ϕ_m contains singularities and hence is unbounded in Ω_mf. Instead we follow the procedure in the proof of (e,f) in Lemma (4.2) and eventually estimate this trace norm of E in ${\Omega }_s^{-}$ which does not contain potential singularities; the details are omitted due to similarity of these two proofs.

Remark

The surface force definition presented in Eq.(55) applies only to the discontinuous dielectric model as adopted in this study. In the continuous dielectric models, which are also widely used for in the implicit solvent simulations, different surface force definition will be derived (11). However, the analysis on the electrostatic forces given in the below is also applicable to general surface force function f_s = f_s(E_s, E_m, ϕ), and might be simplified if electrical field E is continuous, i.e., ε is continuous on Γ.

The electrostatic forces defined in Eq.(54) and Eq.(55) are also subject to the Piola transformation. Moreover these forces can not be directly supplied to the elasticity equation; only the forces relative to a reference state can be supplied. This is because a molecule is in an equilibrium state and has no elastic deformation if the electrostatic potential is induced only by the molecule itself and the solvent with physiological ionic strength, in the absence of interactions with other molecules. We refer to this state as the free state and use it as the reference state. The net body force or the net surface force is therefore defined to be the difference between that for a molecule in non-free state and that for the same molecule in the free state. To abuse the notation these differences are still referred to as the body force and the surface force, and are denoted by f_b and f_s respectively:

$${\mathbf{f}}_b≔{\mathbf{f}}_b-{\mathbf{f}}_{b0}$$ (56)

$${\mathbf{f}}_s≔{\mathbf{f}}_s-{\mathbf{f}}_{s0}$$ (57)

where f_b0 and f_s0 are the body force and the surface force in the free state, and are constant vector fields for any given macromolecule.

Physically, these two forces f_b and f_s shall be vanishing if there is no change of ionic strength and no additional molecules present, and will be small for small change of ionic strength and weakly interacting additional molecules. To reflect this physical reality and to facilitate the mathematical analysis, we decompose (into four steps) the transition from the original single deformable molecule immersed in aqueous solvent with physiological ionic strength to the final system with added rigid molecules, varied ionic strength and deformed molecules. In the first step, we change only the solvent from physiological ionic strength to the target strength, and assume that the molecule Ω_mf does not have a conformational change although the net electrostatic force is not zero due to this change of ionic strength. The electrostatic potential and forces at the end of the first perturbation are denoted by ϕ₁ and f_b1, f_s1, respectively. In the second step, we alter the dielectric constant in the smooth domain Ω_mr from ε_s to ε_m. This low dielectric space represents the empty interior of the added molecules. The electrostatic potential and forces after the second step are respectively denoted by ϕ₂ and f_b2, f_s2. In the third step we place the singular charges into Ω_mr and define the electrostatic potential and forces to be ϕ₃ and f_b3, f_s3. In the last step we allow the Poisson-Boltzmann equation to couple with the elastic deformation so that the system will arrive at the final state with electrostatic potential ϕ and forces f_b, f_s. We write the net body force f_b and the net surface force as the summation of their four components

$${\mathbf{f}}_b=({\mathbf{f}}_b-{\mathbf{f}}_{b3})+({\mathbf{f}}_{b3}-{\mathbf{f}}_{b2})+({\mathbf{f}}_{b2}-{\mathbf{f}}_{b1})+({\mathbf{f}}_{b1}-{\mathbf{f}}_{b0})$$ (58)

$${\mathbf{f}}_s=({\mathbf{f}}_s-{\mathbf{f}}_{s3})+({\mathbf{f}}_{s3}-{\mathbf{f}}_{s2})+({\mathbf{f}}_{s2}-{\mathbf{f}}_{s1})+({\mathbf{f}}_{s1}-{\mathbf{f}}_{s0})$$ (59)

corresponding to the above decomposition, and estimate these components individually.

5.1 The surface force due to changing ionic strength

The electrostatic potential ϕ₀ of the system in the free state is given by

$$-\nabla \cdot (∊\nabla {\varphi }_0)+{\kappa }_0^2\sinh \left({\varphi }_0\right)=\underset{i}{\overset{N_f}{\Sigma }}{q}_i\delta (x-x_i),$$ (60)

while the electrostatic potential ϕ₁ after changing of the ionic strength satisfies

$$-\nabla \cdot (∊\nabla {\varphi }_1)+{\kappa }^2\sinh \left({\varphi }_1\right)=\underset{i}{\overset{N_f}{\Sigma }}{q}_i\delta (x-x_i).$$ (61)

By subtracting Eq.(60) from Eq.(61) we get

$$-\nabla \cdot (∊\nabla \tilde{\varphi })+({\kappa }^2-{\kappa }_0^2)\cosh \left(\xi \right)\tilde{\varphi }=({\kappa }_0^2-{\kappa }^2)\sinh \left({\varphi }_0\right)\text{in}\Omega ,$$ (62)

where $\tilde{\varphi }={\varphi }_1-{\varphi }_0$ and ξ(x) ∈ (min{ϕ₁(x), ϕ₀(x)}, max{ϕ₁(x), ϕ₀(x)}) is a function between ϕ₁ and ϕ₀ satisfying the Cauchy mean value theorem

$$\sinh \left({\varphi }_1\right)=\sinh \left({\varphi }_0\right)+\cosh \left(\xi \right)({\varphi }_1-{\varphi }_0).$$

We note that the singular charges disappear in Eq.(62), and hence $\tilde{\varphi }\in H^1\left(\Omega \right)$ and is also in C^∞ in Ω_mf and $\Omega {\stackrel{‒}{\Omega }}_{\mathit{mf}}$. Moreover, following Theorem (2.2) we have the following 𝒲^2,p estimate for ϕ:

$$\parallel \tilde{\varphi }{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}\le C\left(\parallel \tilde{\varphi }{\parallel }_{L^p\left(\Omega \right)}+\parallel ({\kappa }_0^2-{\kappa }^2)\sinh \left({\varphi }_0\right){\parallel }_{L^p\left(\Omega \right)}+\parallel \tilde{G}{\parallel }_{L^p(\partial \Omega )}\right),$$ (63)

where

$$\tilde{G}=\underset{i}{\overset{N_f}{\Sigma }}\frac{e^{-\kappa |x-x_i|}-e^{-{\kappa }_0|x-x_i|}}{{∊}_w|x-x_i|}\approx -(\kappa -{\kappa }_0)\underset{i}{\overset{N_f}{\Sigma }}\frac{e^{-\kappa |x-x_i|}}{{∊}_w}$$ (64)

is the boundary condition of $\tilde{\varphi }$ on ∂Ω, and is the difference of boundary values of ϕ₁ and ϕ₀. The approximation in Eq.(64) is well defined for small (κ − κ₀). On the other hand, Lemma (4.4) says that $\parallel \tilde{\varphi }{\parallel }_{L^p\left(\Omega \right)}$ itself can be estimate by

$$\parallel \tilde{\varphi }{\parallel }_{L^p\left(\Omega \right)}\le C\parallel \tilde{\varphi }{\parallel }_{L^{\infty }\left(\Omega \right)}\le C\left(\parallel ({\kappa }_0^2-{\kappa }^2)\sinh \left({\varphi }_0\right){\parallel }_{L^2\left(\Omega \right)}+\parallel \tilde{G}{\parallel }_{H^{1∕2}(\partial \Omega )}\right).$$ (65)

By combining Eqs. (63), (64) and (65) we get

$$\parallel {\varphi }_1-{\varphi }_0{\parallel }_{W^{2,p}\left(\Omega \right)}\le C|{\kappa }_0-\kappa |$$ (66)

We now proceed to estimate the changes of electrostatic forces f_b1−f_b0, f_s1−f_s0. The body force change

$$\parallel {\mathbf{f}}_{b1}-{\mathbf{f}}_{b0}{\parallel }_{L^p\left({\Omega }_{\mathit{mf}}\right)}\le C\underset{i}{\Sigma }\left|\tilde{\varphi }\left(x_i\right)\right|\le C|{\kappa }_0-\kappa |$$ (67)

follows from Lemma (5.1). On the other hand,

$$\begin{array}{cc}\hfill {\mathbf{f}}_{s1}-{\mathbf{f}}_{s0}=& -\frac{1}{2}{∊}_s\left(\right|\nabla {\varphi }_{1s}{|}^2-|\nabla {\varphi }_{0s}{|}^2)\mathbf{n}+\frac{1}{2}{∊}_m\left(\right|\nabla {\varphi }_{1m}{|}^2-|\nabla {\varphi }_{0m}{|}^2)\mathbf{n}\hfill \\ & -\left({\kappa }^2(\cosh \left({\varphi }_{1s}\right)-1)-{\kappa }_0^2(\cosh \left({\varphi }_{0s}\right)-1)\right)\mathbf{n}\hfill \\ \hfill =& -\frac{1}{2}{∊}_s(\nabla {\varphi }_{1s}-\nabla {\varphi }_{0s})\cdot (\nabla {\varphi }_{1s}+\nabla {\varphi }_{0s})\mathbf{n}\hfill \\ & +\frac{1}{2}{∊}_m(\nabla {\varphi }_{1m}-\nabla {\varphi }_{0m})\cdot (\nabla {\varphi }_{1m}+\nabla {\varphi }_{0m})\mathbf{n}\hfill \\ & -{\kappa }^2(\cosh \left({\varphi }_{1s}\right)-\cosh \left({\varphi }_{0s}\right))\mathbf{n}-({\kappa }^2-{\kappa }_0^2)\cosh \left({\varphi }_{0s}\right)\mathbf{n}-({\kappa }^2-{\kappa }_0^2).\hfill \end{array}$$

We note that with the mean value theorem, κ²(cosh(ϕ_1s) − κ² cosh(ϕ_0s)) can be related to the change of ionic strength as

$${\kappa }^2(\cosh \left({\varphi }_{1s}\right)-\cosh \left({\varphi }_{0s}\right))={\kappa }^2\sinh \left({\xi }^{\prime }\right)({\varphi }_{1s}-{\varphi }_{0s}).$$

Moreover, we can not bound the trace norm of |∇ϕ_1m|² − |∇ϕ_0m|² by its Sobolev norm in subdomain Ω_mf where the singularities of the potential are located. Instead we follow the remark of Eq. (55) and estimate this term in subdomain ${\Omega }_s^{-}$. Thus the surface force change in the first perturbation step can be estimated as

$$\begin{array}{cc}\hfill \parallel {\mathbf{f}}_{s1}-{\mathbf{f}}_{s0}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\le & C(\phantom{)}\parallel {\varphi }_1-{\varphi }_0{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\parallel {\varphi }_1+{\varphi }_0{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\hfill \\ & +\parallel {\varphi }_1-{\varphi }_0{\parallel }_{W^{2,p}\left({\Omega }_s^{-}\right)}\parallel {\varphi }_1+{\varphi }_0{\parallel }_{W^{2,p}\left({\Omega }_s^{-}\right)}\hfill \\ & +{\kappa }^2\left|\sinh \left({\xi }^{\prime }\right)\right|\parallel {\varphi }_1-{\varphi }_0{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\hfill \\ & +|{\kappa }^2-{\kappa }_0^2|\parallel {\varphi }_{0s}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}+|{\kappa }^2-{\kappa }_0^2|\phantom{(})\hfill \\ \hfill \le & C|\kappa -{\kappa }_0|(\phantom{)}\parallel {\varphi }_1+{\varphi }_0{\parallel }_{W^{1,p}\left({\Omega }_s\right)}+\parallel {\varphi }_1+{\varphi }_0{\parallel }_{W^{1,p}\left({\Omega }_s^{-}\right)}\hfill \\ & +{\kappa }^2\left|\sinh \left({\xi }^{\prime }\right)\right|+(\kappa +{\kappa }_0)(\parallel {\varphi }_0{\parallel }_{W^{1,p}\left({\Omega }_s\right)}+1)\phantom{(})\hfill \\ \hfill \le & C_s\left(\kappa \right)|\kappa -{\kappa }_0|,\hfill \end{array}$$ (68)

where Lemma (2.1) is applied to estimate the norm of the products of two W^1,p functions ∇ϕ₁ − ∇ϕ₀ and ∇ϕ₁ + ∇ϕ₀.

5.2 The surface force due to adding a low dielectric constant cavity

Although the variation of ionic strength will change the electrostatic potential of the system, the magnitude of potential change is usually smaller than that induced by adding molecules to the system. By adding molecules to the system we will not only have the additional singular charges but also expand a cavity of low dielectric constant in the solvent. These two effects will be considered separately, and this subsection estimates only the change of potential and forces due to the additional cavity of low dielectric constant. The effect of added charges will be analyzed in the next subsection.

The electrostatic potential ϕ₂ with an additional low dielectric cavity in the domain is described by

$$-\nabla \cdot (∊\nabla {\varphi }_2)+{\kappa }^2\sinh \left({\varphi }_2\right)=\underset{i}{\overset{N_f}{\Sigma }}{q}_i\delta (x-x_i)$$ (69)

with the same boundary conditions as Eq.(61). Here the dielectric constant ε and ionic strength κ are different from those in Eq.(61), and thus the subtraction of Eq.(61) from Eq.(69) shall be individually conducted in Ω_mf, Ω_mr and Ω_s to give the following three equations:

$$\begin{array}{cc}\hfill -\nabla \cdot ({∊}_m\nabla ({\varphi }_2-{\varphi }_1))=& 0\text{in}{\Omega }_{\mathit{mf}},\hfill \\ \hfill -\nabla \cdot ({∊}_s\nabla ({\varphi }_2-{\varphi }_1))+{\kappa }^2(\sinh \left({\varphi }_2\right)-\sinh \left({\varphi }_1\right)=& 0\text{in}{\Omega }_s,\hfill \\ \hfill -\nabla \cdot ({∊}_m\nabla {\varphi }_2)+\nabla ({∊}_s\nabla {\varphi }_1)-{\kappa }^2\sinh \left({\varphi }_1\right)=& 0\text{in}{\Omega }_{\mathit{mr}}.\hfill \end{array}$$

By assembling these three equations we get a complete equation for $\tilde{\varphi }={\varphi }_2-{\varphi }_1$ in Ω:

$$-\nabla \cdot (∊\nabla \tilde{\varphi })+{\kappa }^2(\sinh \left({\varphi }_2\right)-\sinh \left({\varphi }_1\right))=\frac{{∊}_m}{{∊}_s}{\kappa }^2\sinh \left({\varphi }_1\right),$$ (70)

where ε is the same as that in Eq.(69), and the right-hand side is vanishing in Ω_s and Ω_mf. This function (non-vanishing only in Ω_mr) is equivalent to −∇ · ((ε_s − ε_m)∇ϕ₁) + κ² sinh(ϕ₁) since

$$-\nabla \cdot ({∊}_s\nabla {\varphi }_1)+{\kappa }^2\sinh \left({\varphi }_1\right)=0\text{in}{\Omega }_{\mathit{mr}}.$$

As before we notice that κ²(sinh(ϕ₂) − sinh(ϕ₁)) can be related to cosh(ξ)ϕ̃ with a smooth function ξ bounded by ϕ₁ and ϕ₂, and therefore ϕ̃ in Eq.(70) satisies an estimate of the form

$$\begin{array}{cc}\hfill \parallel \tilde{\varphi }{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}& \le C\left(\parallel \tilde{\varphi }{\parallel }_{L^p\left(\Omega \right)}+\parallel \frac{{∊}_m}{{∊}_s}{\kappa }^2\sinh \left({\varphi }_1\right){\parallel }_{L^p\left({\Omega }_{\mathit{mr}}\right)}\right)\le C\parallel \sinh \left({\varphi }_1\right){\parallel }_{L^p\left({\Omega }_{\mathit{mr}}\right)}\hfill \\ & \le C\parallel \sinh \left({\varphi }_1\right){\parallel }_{L^{\infty }\left(\Omega \right)}\cdot V_{\mathit{mr}}\hfill \end{array}$$

which follows from Theorem (4.3) and Lemma (4.4), considering that Eq.(69) has a vanishing boundary condition. Here V_mr is the volume of Ω_mr, suggesting that ∥ϕ̃∥_𝒲^2,p(Ω) can be made arbitrarily small by reducing the volume of Ω_mr.

The change electrostatic body force induced by this additional low dielectric cavity can be estimated as

$$\parallel {\mathbf{f}}_{b2}-{\mathbf{f}}_{b1}{\parallel }_{L^p\left({\Omega }_{\mathit{mf}}\right)}\le C\underset{i}{\Sigma }\left|\tilde{\varphi }\left(x_i\right)\right|\le {\mathit{CV}}_{\mathit{mr}}.$$ (71)

The surface force change is

$$\begin{array}{cc}\hfill {\mathbf{f}}_{s2}-{\mathbf{f}}_{s1}=& -\frac{1}{2}{∊}_s\left(\right|\nabla {\varphi }_{2s}{|}^2-|\nabla {\varphi }_{1s}{|}^2)\mathbf{n}+\frac{1}{2}{∊}_m\left(\right|\nabla {\varphi }_{2m}{|}^2-|\nabla {\varphi }_{1m}{|}^2)\mathbf{n}\hfill \\ & -{\kappa }^2(\cosh \left({\varphi }_{2s}\right)-\cosh \left({\varphi }_{1s}\right)\mathbf{n}\hfill \\ \hfill =& -\frac{1}{2}{∊}_s(\nabla {\varphi }_{2s}-\nabla {\varphi }_{1s})\cdot (\nabla {\varphi }_{2s}+\nabla {\varphi }_{1s})\mathbf{n}\hfill \\ & +\frac{1}{2}{∊}_m(\nabla {\varphi }_{2m}-\nabla {\varphi }_{1m})\cdot (\nabla {\varphi }_{2m}+\nabla {\varphi }_{1m})\mathbf{n}\hfill \\ & -{\kappa }^2(\cosh \left({\varphi }_{2s}\right)-\cosh \left({\varphi }_{1s}\right))\mathbf{n},\hfill \end{array}$$

and thus can be estimated by following

$$\begin{array}{cc}\hfill \parallel {\mathbf{f}}_{s2}-{\mathbf{f}}_{s1}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\le & C(\phantom{)}\parallel {\varphi }_2-{\varphi }_1{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\parallel {\varphi }_2+{\varphi }_1{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\hfill \\ & +\parallel {\varphi }_2-{\varphi }_1{\parallel }_{W^{1,p}\left({\Omega }_s^{-}\right)}\parallel {\varphi }_2+{\varphi }_1{\parallel }_{W^{1,p}\left({\Omega }_s^{-}\right)}\hfill \\ & +{\kappa }^2\left|\sinh \left({\xi }^{\prime }\right)\right|\parallel {\varphi }_2-{\varphi }_1{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\phantom{(})\hfill \\ \hfill \le & C\parallel {\varphi }_2-{\varphi }_1{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}\le C\cdot V_{\mathit{mr}},\hfill \end{array}$$ (72)

from the similar arguments in last subsection for estimating f_s1 − f_s0.

5.3 The surface force due to additional singular charges

In this subsection we will consider the change of electrostatic potential and force caused by singular charges placed in the low dielectric space Ω_mr. The low dielectric space Ω_mr with these charges completely models the rigid molecule which is expected to interact with a flexible molecule Ω_mf. The electrostatic potential field after this third perturbation step satisfies the following equation

$$-\nabla \cdot (∊\nabla {\varphi }_3)+{\kappa }^2\sinh \left({\varphi }_3\right)=\underset{i}{\overset{N_f}{\Sigma }}{q}_i\delta \left(x_i\right)+\underset{j}{\overset{N_r}{\Sigma }}{q}_j\delta \left(x_j\right),$$ (73)

while the change of potential, ϕ̃ = ϕ₃ − ϕ₂ is the solution of the equation

$$-\nabla \cdot (∊\nabla \tilde{\varphi })+{\kappa }^2\cosh \left(\xi \right)\tilde{\varphi }=\underset{j}{\overset{N_r}{\Sigma }}{q}_j\delta \left(x_j\right),$$ (74)

which is obtained by subtracting Eq.(69) from Eq.(73). Here ξ(x) is a smooth function defined by the mean value expansion sinh(ϕ₃) = sinh(ϕ₂)+cosh(ξ)(ϕ₃−ϕ₂). To facilitate the regularity analysis of ϕ̃ we define its singular component G, which solves

$$-\nabla \cdot ({∊}_m\nabla \tilde{G})=\underset{j}{\overset{N_r}{\Sigma }}{q}_j\delta \left(x_j\right)$$ (75)

and its regular component ϕ̃^r, which is the solution of

$$-\nabla \cdot (∊\nabla {\tilde{\varphi }}^r)+{\kappa }^2\cosh \left(\xi \right){\tilde{\varphi }}^r=\nabla \cdot ((∊-{∊}_m)\nabla \tilde{G})-{\kappa }^2\cosh \left(\xi \right)\tilde{G}.$$ (76)

It shall be noted that ∇·((ε−ε_m)∇G̃) is nonzero only on the molecular surfaces Γ_f and Γ_r, and can be represented as an interface condition (ε − ε_m)∇G̃ · n on each of these two molecular surfaces similar to that in Eq.(38). We notice that

$$\tilde{G}\left(x\right)=\underset{j}{\overset{N_r}{\Sigma }}\frac{q_j}{{∊}_m|x-x_j|}$$ (77)

and is of C^∞ wherever away from any of x_j, hence of $C^{\infty }\left({\stackrel{‒}{\Omega }}_s\right)$, and thus so is −(ε − ε_m)∇G̃ · n on Γ_f and Γ_r. The 𝒲^2,p estimate of ϕ̃ in Ω_s says that

$$\begin{array}{cc}\hfill \parallel \tilde{\varphi }{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}\le & C(\phantom{)}{\kappa }^2\parallel \cosh \left(\xi \right)\tilde{G}{\parallel }_{L^p\left({\Omega }_s\right)}+\parallel ({∊}_s-{∊}_m)\nabla \tilde{G}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\hfill \\ & +\parallel ({∊}_s-{∊}_m)\nabla \tilde{G}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_r\right)}+\parallel g{\parallel }_{W^{1-1∕p,p}(\partial \Omega )}+\parallel \tilde{\varphi }{\parallel }_{L^p\left(\Omega \right)}\phantom{(})\hfill \\ \hfill \le & C\left(\parallel \tilde{G}{\parallel }_{L^p}+\parallel \tilde{G}{\parallel }_{W^{2,p}\left({\Omega }_s\right)}+\parallel g{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\right)\to 0\text{as}{q}_j\to 0\hfill \end{array}$$ (78)

where

$$g=\underset{j}{\overset{N_r}{\Sigma }}{q}_j\frac{e^{-k|x-x_j|}}{{∊}_m|x-x_j|}\text{on}\partial \Omega$$

is the boundary condition of Eq.(74), and is the difference of boundary conditions of Eq.(69) and Eq.(73).

We now analyze the change of the electrostatic forces due to the inclusion of additional singular charges. For body force we have

$$\parallel {\mathbf{f}}_{b3}-{\mathbf{f}}_{b2}{\parallel }_{L^p\left({\Omega }_{\mathit{mf}}\right)}\le C\underset{i}{\Sigma }|\tilde{\varphi }\left(x_i\right)+\underset{j\ne i}{\Sigma }{\tilde{G}}_j\left(\mathit{xi}\right)|\to 0\text{as}{q}_j\to 0,$$ (79)

and for the surface force we know

$$\begin{array}{cc}\hfill {\mathbf{f}}_{s3}-{\mathbf{f}}_{s2}=& -\frac{1}{2}{∊}_s\left(\right|\nabla {\varphi }_{3s}{|}^2-|\nabla {\varphi }_{2s}{|}^2)\mathbf{n}+\frac{1}{2}{∊}_m\left(\right|\nabla {\varphi }_{3m}{|}^2-|\nabla {\varphi }_{2m}{|}^2)\mathbf{n}\hfill \\ & -({\kappa }^2\cosh \left({\varphi }_{3s}\right)-{\kappa }^2\cosh \left({\varphi }_{2s}\right)\mathbf{n}\hfill \\ \hfill =& -\frac{1}{2}{∊}_s(\nabla {\varphi }_{3s}-\nabla {\varphi }_{2s})\cdot (\nabla {\varphi }_{3s}+\nabla {\varphi }_{2s})\mathbf{n}\hfill \\ & +\frac{1}{2}{∊}_m(\nabla {\varphi }_{3m}-\nabla {\varphi }_{2m})\cdot (\nabla {\varphi }_{3m}+\nabla {\varphi }_{2m})\mathbf{n}\hfill \\ & -{\kappa }^2(\cosh \left({\varphi }_{3s}\right)-\cosh \left({\varphi }_{2s}\right))\mathbf{n}.\hfill \end{array}$$

This surface force difference can then be estimated by

$$\begin{array}{cc}\hfill \parallel {\mathbf{f}}_{s3}-{\mathbf{f}}_{s2}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\le & C(\phantom{)}\parallel {\varphi }_{3s}-{\varphi }_{2s}{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\parallel {\varphi }_{3s}+{\varphi }_{2s}{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\hfill \\ & +\parallel {\varphi }_{3m}-{\varphi }_{2m}{\parallel }_{W^{2,p}\left({\Omega }_s^{-}\right)}\parallel {\varphi }_{3m}+{\varphi }_{2m}{\parallel }_{W^{2,p}\left({\Omega }_s^{-}\right)}\hfill \\ & +{\kappa }^2\left|\sinh \left({\xi }^{\prime }\right)\right|\parallel {\varphi }_{3s}-{\varphi }_{2s}{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\phantom{(})\hfill \\ \hfill \le & C\left(\parallel {\varphi }_3-{\varphi }_2{\parallel }_{{𝒲}^{2,p}\left({\Omega }_s\right)}+\parallel {\varphi }_3-{\varphi }_2{\parallel }_{{𝒲}^{2,p}\left({\Omega }_s^{\prime }\right)}\right)\to 0\hfill \\ & \text{as}{q}_j\to 0\hfill \end{array}$$ (80)

where the constant C depends on the 𝒲^2,p norm of ϕ₂, ϕ₃, and therefore is bounded if ϕ₂, ϕ₃, are bounded.

5.4 The surface force due to molecular conformational change

We now consider the change of electrostatic potential and surface forces induced by elastic displacement. By subtracting Eq.(73) from Eq.(4) and with a few algebraic manipulations we get the governing equation for ϕ̃ = ϕ − ϕ₃:

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\mathbf{F}\nabla \tilde{\varphi })+J{\kappa }^2\cosh \left(\xi \right)\tilde{\varphi }=& (J-1)\underset{i}{\overset{N_f+N_r}{\Sigma }}{q}_i\delta \left(x_i\right)+\nabla \cdot (∊(\mathbf{F}-\mathrm{I})\nabla {\varphi }_3)\hfill \\ & +(J-1){\kappa }^2\sinh \left({\varphi }_3\right),\hfill \end{array}$$ (81)

where the function ξ is defined by the mean value expansion sinh(ϕ) = sinh(ϕ₃)+cosh(ξ)(ϕ − ϕ₃). Unlike its counterparts in the analysis for the first two steps, this function ξ is not piecewise smooth since ϕ^r of Eq.(4) belongs to 𝒲^2,p(Ω) hence is only piecewise uniformly differentiable. The resulting mean value function ξ is therefore a piecewise uniformly continuous function. Because of the appearance of remaining singular charges in the right hand side of Eq.(81), we know that ϕ̃ is not in H¹ globally. Again we employ the decomposition ϕ̃ = G̃_f + G̃_r + ϕ̃^r to separate the singular components G̃_f, G̃_r and the regular component ϕ̃^r. The first singular component ${\tilde{G}}_f={\Sigma }_j^{N_f}{\tilde{G}}_{\mathit{fj}}$ is induced by all N_f singular charges in Ω_mf

$$-\nabla \cdot ({∊}_m\mathbf{F}\nabla {\tilde{G}}_f)=(J-1)\underset{i}{\overset{N_f}{\Sigma }}{q}_i\delta \left(x_i\right),$$ (82)

while the second singular component ${\tilde{G}}_r={\Sigma }_j^{N_r}{\tilde{G}}_{\mathit{rj}}$ is caused by all N_r singular charges in Ω_mr

$$-\nabla \cdot ({∊}_m\mathbf{F}\nabla {\tilde{G}}_r)=(J-1)\underset{j}{\overset{N_r}{\Sigma }}{q}_j\delta \left(x_j\right),$$ (83)

and both singular components have estimates similar to Eqs.(23) and (24)

$$\parallel {\tilde{G}}_f{\parallel }_{L^{\infty }\left({\Omega }_s\right)}\le \frac{\parallel J-1{\parallel }_{L^{\infty }\left(\Omega \right)}{N}_f{\mathit{Kq}}_{\mathit{max}}}{{\delta }_f}\text{in}{\stackrel{‒}{\Omega }}_s,$$ (84)

$$\parallel {\tilde{G}}_r{\parallel }_{L^{\infty }\left({\Omega }_s\right)}\le \frac{\parallel J-1{\parallel }_{L^{\infty }\left(\Omega \right)}{N}_r{\mathit{Kq}}_{\mathit{max}}}{{\delta }_r}\text{in}{\stackrel{‒}{\Omega }}_s,$$ (85)

$$\parallel \nabla {\tilde{G}}_f{\parallel }_{L^{\infty }\left({\Omega }_s\right)}\le \frac{\parallel J-1{\parallel }_{L^{\infty }\left(\Omega \right)}{N}_f{\mathit{Kq}}_{\mathit{max}}}{{\delta }_f^2}\text{in}{\stackrel{‒}{\Omega }}_s,$$ (86)

$$\parallel \nabla {\tilde{G}}_r{\parallel }_{L^{\infty }\left({\Omega }_s\right)}\le \frac{\parallel J-1{\parallel }_{L^{\infty }\left(\Omega \right)}{N}_r{\mathit{Kq}}_{\mathit{max}}}{{\delta }_r^2}\text{in}{\stackrel{‒}{\Omega }}_s.$$ (87)

By subtracting the singular components G̃_f, G̃_r from Eq.(81) we obtain an equation for the regular component

$$\begin{array}{cc}\hfill -\nabla \cdot (∊\mathbf{F}\nabla {\tilde{\varphi }}^r)+J{\kappa }^2\cosh \left(\xi \right){\tilde{\varphi }}^r=& \nabla \cdot (∊(\mathbf{F}-\mathrm{I})\nabla {\varphi }_3)+(J-1){\kappa }^2\sinh \left({\varphi }_3\right)\hfill \\ & -\nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla {\tilde{G}}_f)\hfill \\ & -\nabla \cdot ((∊-{∊}_m)\mathbf{F}\nabla {\tilde{G}}_r),\hfill \end{array}$$ (88)

where the last two items ∇ · ((ε−ε_m)F∇G̃_f) and ∇ · ((ε−ε_m)F∇G̃_r) prescribe two interface conditions on the molecular surfaces Γ_f and Γ_r:

$$f_{G_f}=({∊}_s-{∊}_m)\mathbf{F}\nabla {\tilde{G}}_f\cdot \mathbf{n},$$ (89)

$$f_{G_r}=({∊}_s-{∊}_m)\mathbf{F}\nabla {\tilde{G}}_r\cdot \mathbf{n},$$ (90)

similar to that defined in Eq.(38). For the regular component ϕ̃^r, Theorem (4.3) states that it can be estimated with respect to the 𝒲^2,p norm as follows

$$\begin{array}{cc}\hfill \parallel {\tilde{\varphi }}^r{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)}\le C& (\parallel {\tilde{\varphi }}^r{\parallel }_{L^p\left(\Omega \right)}+\parallel f_{G_f}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}+\parallel f_{G_r}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\hfill \\ & +\parallel f_{G_f}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_r\right)}+\parallel f_{G_r}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_r\right)}\hfill \\ & +\parallel (J-1){\kappa }^2\sinh \left({\varphi }_3\right){\parallel }_{L^p\left(\Omega \right)}+\parallel \nabla \cdot (∊(\mathbf{F}-\mathrm{I})\nabla {\varphi }_3){\parallel }_{L^p\left(\Omega \right)})\hfill \\ \hfill \le C& (\parallel f_{G_f}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}+\parallel f_{G_r}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\hfill \\ & +\parallel f_{G_f}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_r\right)}+\parallel f_{G_r}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_r\right)}\hfill \\ & +\parallel (J-1)\sinh \left({\varphi }_3\right){\parallel }_{L^p\left(\Omega \right)}+\parallel \mathbf{F}-\mathrm{I}{\parallel }_{W^{1,p}\left(\Omega \right)}\parallel {\varphi }_3{\parallel }_{W^{2,p}\left(\Omega \right)})\hfill \\ \hfill \le C& (\parallel J-1{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\parallel \mathbf{F}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}+\parallel J-1{\parallel }_{L^{\infty }\left(\Omega \right)}\parallel \sinh \left({\varphi }_3\right){\parallel }_{L^p\left(\Omega \right)}\hfill \\ & +\parallel \mathbf{F}-\mathrm{I}{\parallel }_{W^{1,p}\left(\Omega \right)}\parallel {\varphi }_3{\parallel }_{{𝒲}^{2,p}\left(\Omega \right)})\hfill \\ \hfill =C& (\parallel J-1{\parallel }_{W^{1,p}\left({\Omega }_s\right)}+\parallel J-1{\parallel }_{L^{\infty }\left({\Omega }_s\right)}\parallel \mathbf{F}-\mathrm{I}{\parallel }_{W^{1,p}\left(\Omega \right)}),\hfill \end{array}$$ (91)

where in the last inequality we applied the estimate in Eq.(27) for the interface conditions f_Gf and f_Gr. Finally, we estimate the change of the electrostatic forces due to the elastic deformaiton. By definition, the body force change is attributed to the variation of regular component(reaction field) ϕ̃^r and the variations of the the singular components(Coulomb potential field), and thus can be estimated as:

$$\begin{array}{cc}\hfill \parallel {\mathbf{f}}_b-{\mathbf{f}}_{b3}{\parallel }_{L^p\left({\Omega }_{\mathit{mf}}\right)}& \le C\underset{i}{\Sigma }|\tilde{\varphi }\left(x_i\right)+\underset{j\ne i}{\Sigma }{\tilde{G}}_{\mathit{fj}}\left(x_i\right)+\underset{j}{\Sigma }{\tilde{G}}_{\mathit{rj}}\left(x_i\right)|\hfill \\ & \le C(\parallel J-1{\parallel }_{W^{1,p}\left({\Omega }_s\right)}+\parallel J-1{\parallel }_{L^{\infty }\left({\Omega }_s\right)}+\parallel \mathbf{F}-\mathrm{I}{\parallel }_{W^{1,p}\left(\Omega \right)})\hfill \end{array}$$ (92)

The surface force change in this step is defined to be

$$\begin{array}{cc}\hfill {\mathbf{f}}_s-{\mathbf{f}}_{s3}=& -\frac{1}{2}{∊}_s\left(\right|\mathbf{F}\nabla {\varphi }_s{|}^2-|\nabla {\varphi }_{3s}{|}^2)\mathbf{n}+\frac{1}{2}{∊}_m\left(\right|\mathbf{F}\nabla {\varphi }_m{|}^2-|\nabla {\varphi }_{3m}{|}^2)\mathbf{n}\hfill \\ & -{\kappa }^2(\cosh \left({\varphi }_s\right)-{\kappa }^2\cosh \left({\varphi }_{3s}\right)\mathbf{n}\hfill \\ \hfill =& -\frac{1}{2}{∊}_s(\mathbf{F}\nabla {\varphi }_s-\nabla {\varphi }_{3s})\cdot (\mathbf{F}\nabla {\varphi }_s+\nabla {\varphi }_{3s})\mathbf{n}\hfill \\ & +\frac{1}{2}{∊}_m(\mathbf{F}\nabla {\varphi }_m-\nabla {\varphi }_{3m})\cdot (\mathbf{F}\nabla {\varphi }_m+\nabla {\varphi }_{3m})\mathbf{n}\hfill \\ & -{\kappa }^2\sinh \left({\xi }^{\prime }\right)({\varphi }_s-{\varphi }_{3s})\mathbf{n}.\hfill \end{array}$$ (93)

It follows that

$$\begin{array}{cc}\hfill \parallel {\mathbf{f}}_s-{\mathbf{f}}_{s3}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\le & C(\parallel \mathbf{F}\nabla \varphi -\nabla {\varphi }_3{\parallel }_{W^{1,p}\left({\Omega }_s\right)}+\parallel \mathbf{F}\nabla \varphi -\nabla {\varphi }_3{\parallel }_{W^{1,p}\left({\Omega }_s^{\prime }\right)}\hfill \\ & +\parallel \varphi -{\varphi }_3{\parallel }_{W^{1,p}\left({\Omega }_s\right)}).\hfill \end{array}$$ (94)

To relate the estimate of F∇ϕ−∇ϕ₃ to that of ϕ − ϕ₃ (the latter has already been estimated in Eq.(91)), we make use of the relation

$$\begin{array}{cc}\hfill \parallel \mathbf{F}\nabla \varphi -\nabla {\varphi }_3{\parallel }_{W^{1,p}\left({\Omega }_s\right)}=& \parallel \mathbf{F}\nabla \varphi -\mathbf{F}\nabla {\varphi }_3+\mathbf{F}\nabla {\varphi }_3-\nabla {\varphi }_3{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\hfill \\ \hfill \le & \parallel \mathbf{F}(\nabla \varphi -\nabla {\varphi }_3){\parallel }_{W^{1,p}\left({\Omega }_s\right)}+\parallel (\mathbf{F}-\mathrm{I})\nabla {\varphi }_3{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\hfill \\ \hfill \le & \parallel \mathbf{F}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\parallel (\nabla \varphi -\nabla {\varphi }_3){\parallel }_{W^{1,p}\left({\Omega }_s\right)}+\hfill \\ & \parallel (\mathbf{F}-\mathrm{I}){\parallel }_{W^{1,p}\left({\Omega }_s\right)}\parallel {\varphi }_3{\parallel }_{W^{2,p}{\Omega }_s)}\hfill \end{array}$$

and a similar relation for $\parallel \mathbf{F}\nabla \varphi -\nabla {\varphi }_3{\parallel }_{W^{1,p}\left({\Omega }_s^{\prime }\right)}$. By collecting these results together we can conclude from Eq.(94) that

$$\parallel {\mathbf{f}}_s-{\mathbf{f}}_{s3}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\le C\left(\parallel J-1{\parallel }_{W^{1,p}\left(\Omega \right)}+\parallel \mathbf{F}-\mathrm{I}{\parallel }_{W^{1,p}\left(\Omega \right)}\right),$$ (95)

which indicates the dependence and the boundedness of this electrostatic force component with respect to the elastic displacement field.

5.5 Complete estimation of the electrostatic forces

The complete estimation of the electrostatic surface force is presented this lemma:

Lemma 5.2

The electrostatic force can be made arbitrary small by reducing the variations of ionic strength, the volume of the additional low dielectric space, the added singular charge and the magnitude of the elastic deformation.

Proof

Following from its decomposition schemes (58,59), the estimation of total electrostatic body force and surface fore can be readily completed by combining their respective four components estimated in the four subsections above. The estimates for these two forces have an identical form

$$\begin{array}{cc}\hfill \parallel {\mathbf{f}}_b-{\mathbf{f}}_{b0}{\parallel }_{L^p\left({\Omega }_{\mathit{mf}}\right)}\le C(\phantom{)}|& \kappa -{\kappa }_0|+\parallel {\varphi }_2-{\varphi }_1{\parallel }_{W^{2,p}\left({\Omega }_s\right)}+\parallel {\varphi }_2-{\varphi }_1{\parallel }_{W^{2,p}\left({\Omega }_s^{\prime }\right)}\hfill \\ & +V_{\mathit{mr}}+\parallel \mathbf{F}-\mathrm{I}{\parallel }_{W^{1,p}\left(\Omega \right)}+\parallel J-1{\parallel }_{W^{1,p}\left(\Omega \right)}\phantom{(}),\hfill \end{array}$$ (96)

$$\begin{array}{cc}\hfill \parallel {\mathbf{f}}_s-{\mathbf{f}}_{s0}{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\le C(\phantom{)}|& \kappa -{\kappa }_0|+\parallel {\varphi }_2-{\varphi }_1{\parallel }_{W^{2,p}\left({\Omega }_s\right)}+\parallel {\varphi }_2-{\varphi }_1{\parallel }_{W^{2,p}\left({\Omega }_s^{\prime }\right)}\hfill \\ & +V_{\mathit{mr}}+\parallel \mathbf{F}-\mathrm{I}{\parallel }_{W^{1,p}\left(\Omega \right)}+\parallel J-1{\parallel }_{W^{1,p}\left(\Omega \right)}\phantom{(}).\hfill \end{array}$$ (97)

It is noticed in Eq.(78) that both ∥ϕ₂ − ϕ₁∥W^2,p(Ω_s) and $\parallel {\varphi }_2-{\varphi }_1{\parallel }_{W^{2,p}\left({\Omega }_s^{\prime }\right)}$ can be made arbitrarily small by adjusting the charges of added molecule Ω_mr. Moreover F(0)(x) = 0, J(0)(x) = 1 follow from their definitions and both functions are infinitely differentiable in the neighborhood of each function in

$$X_p=\{\mathbf{u}\in W^{2,p}\left({\Omega }_{\mathit{mf}}\right)\mid \parallel \mathbf{u}{\parallel }_{W^{2,p}\left({\Omega }_{\mathit{mf}}\right)}\le M\}.$$

Applying the Taylor inequality we have

$$\begin{array}{cc}\hfill \parallel \mathbf{F}-& \mathrm{I}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}\le \parallel \left|D\mathbf{F}\right|\parallel \parallel \mathbf{u}{\parallel }_{W^{2,p}\left({\Omega }_s\right)}\hfill \\ \hfill \parallel & J-1{\parallel }_{L^{\infty }}\le \parallel \left|D\mathbf{J}\right|\parallel \parallel \mathbf{u}{\parallel }_{W^{2,p}\left({\Omega }_s\right)},\hfill \end{array}$$

hence the last two items in estimates (96, 97) are also small for properly chosen X_p.

6 Main Results: Existence of Solutions to the Coupled System

We now establish the main existence result in the paper. It is noticed that for every element v ∈ X_p one can derive a Piola transformation and solve for a unique potential solution of the Poisson-Boltzmann equation with this Piola transformation. The electrostatic forces computed from this potential solution belongs to W^1−1/p,p(Γ_f) hence there is also a unique solution u to Eq.(8) corresponding to these electrostatic forces. This loop defines a map S which associates every v with a new displacement function u. Our existence result is based on the following version of the Schauder fixed-point theorem.

Theorem 6.1

Let X_p be a closed convex set in a Banach space X and let S be a continuous mapping of X_p into itself such that the image of S(X_p) is relatively compact. Then S has a fixed-point in X_p.

Proof

See (39).

The Schauder Theorem depends on establishing continuity and compactness of the map S: X_p → X_p. We notice that X_p is convex and is weakly compact in W^2,p. Therefore the mapping S has at least one fixed-point in X_p if we can verify that S is continuous in some weak topology.

Theorem 6.2

S : X_p → X_p is weakly continuous in W^2,p(Ω_mf).

Proof

This proof follows the similar arguments in (7). Let v_n be a sequence in X_p and v_n ⇀ v in W^2,p as n → ∞. With these displacement fields, we can compute the electrostatic potential ϕ_n = ϕ(v_n)( hence the electrostatic body force f_bn = f_b(v_n) and surface force f_sn = f_s(v_n)) and new displacement fields u_n = u(v_n) defining the mapping S. We know from (96), (97) and (9) that ϕ_n, f_bn, f_sn and u_n are bounded independently of n. Therefore there exists a subsequence v_nl ⊂ v_n, an electrostatic potential ϕ̅, and a displacement field ū, such that

$$\begin{array}{cc}& \varphi \left({\mathbf{v}}_{\mathit{nl}}\right)\rightharpoonup \stackrel{-}{\varphi }\text{as}l\to \infty \hfill \\ & \mathbf{u}\left({\mathbf{v}}_{\mathit{nl}}\right)\rightharpoonup \stackrel{-}{\mathbf{u}}\text{as}l\to \infty \hfill \end{array}$$

We shall prove that u(v) = ū by investigating the limit of the equations for ϕ(v_nl) and u(v_nl), and of the expression for F(v_nl), f_b(v_nl), f_s(v_nl) and J(v_nl). Since Φ(v_nl) ⇀ Φ(v) in the same weak topology as v_nl ⇀ v and W^2,p is compactly embedded in C¹, there is a subsequence of v_nk ⊂ v_nl such that

$$\begin{array}{cc}& {\mathbf{v}}_{n_k}\to \mathbf{v}\text{in}{C}^1\left(\Omega \right)\text{as}k\to \infty ,\hfill \\ \hfill \Phi \left({\mathbf{v}}_{n_k}\right)& \to \Phi \left(\mathbf{v}\right)\text{in}{C}^1\left(\Omega \right)\text{as}k\to \infty ;\hfill \end{array}$$

hence

$$J\left({\mathbf{v}}_{n_k}\right)\to J\left(\mathbf{v}\right)\text{in}{C}^0\left(\Omega \right)\text{as}k\to \infty ,$$

following the definition of J(v). The convergence of

$$\mathbf{F}\left({\mathbf{v}}_{n_k}\right)\to \mathbf{F}\left(\mathbf{v}\right)\text{in}{C}^0\left(\Omega \right)\text{as}k\to \infty ,$$

which involves the inversion of ∇Φ(v), is substantiated by continuous mapping from a n × n matrix to its inverse in C⁰(Ω), i.e.,

$$A_{n\times n}\in C^0\left(\Omega \right)\mapsto A_{n\times n}^{-1}\in C^0\left(\Omega \right)$$

in the neighborhood of each invertible matrix of C⁰(Ω), and by the invertibility of ∇Φ(v_nk) in W^1,p(Ω). Now we can pass the equations satisfied by (ϕ_nk and v_nk to the limit and deduce that

$$\begin{array}{cc}\hfill \varphi \left({\mathbf{v}}_{\mathit{nl}}\right)\rightharpoonup \varphi \left(\mathbf{v}\right)& =\stackrel{-}{\varphi },\hfill \\ \hfill {\mathbf{u}}_{\mathit{nl}}\rightharpoonup \mathbf{u}\left(\mathbf{v}\right)& =\stackrel{-}{\mathbf{u}}.\hfill \end{array}$$

This proves the continuity of mapping S in the weak topology of W^2,p.

Finally we verify that S(X_p) ⊂ X_p. By connecting the force estimates (96)-(97) and the estimate of displacement u in theorem (3.1) we observe that

$$\begin{array}{cc}\hfill \parallel \mathbf{u}{\parallel }_{W^{2,p}}& \le C\left(\parallel {\mathbf{f}}_b{\parallel }_{L^p\left({\Omega }_{\mathit{mf}}\right)}+\parallel {\mathbf{f}}_s{\parallel }_{W^{1-1∕p,p}\left({\Gamma }_f\right)}\right)\hfill \\ & \le C\left(|\kappa -{\kappa }_0|\parallel {\varphi }_2-{\varphi }_1{\parallel }_{W^{2,p}\left({\Omega }_s\right)}+\parallel \mathbf{F}-\mathrm{I}{\parallel }_{W^{1,p}\left({\Omega }_s\right)}+\parallel J-1{\parallel }_{L^{\infty }}\right)\hfill \\ & \le M\le \frac{C}{\max \{C1,C2\}}\hfill \end{array}$$ (98)

for appropriately small change in ionic strength and in the charges in the added molecules, where C, C1, C2 are the constants prescribed in inequality (12). Thus we verified that S(X_p) ⊂ X_p and Φ(u) is invertible. This gives the main result in the paper as the following theorem.

Theorem 6.3

There exists a solution to the coupled nonlinear PDE system (8) and (4) for sufficiently small κ − κ₀ and sufficiently small rigid molecule Ω_mr with sufficiently small charges.

Proof

This follows from Theorem 6.1 combined with Theorem 6.2.

7 Variational Principle for Existence and/or Uniqueness

In addition to the fixed point arguments, variational principles and quasivariational inequalities are also widely used for analyzing coupled systems of PDEs arising from multiphysics modeling. While quasivariational inequalities are exclusively used for systems with boundary conditions given by inequalities, a single energy functional for the entire system is generally required for the application of either of these two approaches, and the stationary point of this energy functional with respect to each function shall produce the corresponding differential equations and all boundary conditions. This energy functional is usually given by the total potential energy of the system, or by the sum of the potential energies of each equation if these energies are compatible. While it remains challenge to construct the total energy for our problem, we can give a coupled weak form of the entire system:

$$(\mathit{Ax},y)={({\mathbf{f}}_b,\mathbf{v})}_{L^2\left({\Omega }_{\mathit{mf}}\right)}+{({\mathbf{f}}_s,\mathbf{v})}_{L^2\left({\Gamma }_{\mathit{mf}}\right)}\forall y\in P,$$ (99)

where x = (u, ϕ), y = (v, ψ) are in the product space P of W^2,p(Ω_mf) for the displacement field u and the W^2,p(Ω) for the regular component of electrostatic potential ϕ^r, i.e., P = W^2,p(Ω_mf) × W^2,p(Ω), and the operator A is defined by

$$(\mathit{Ax},y)=(\mathbf{T}\left(\mathbf{u}\right),\mathbf{E}\left(\mathbf{v}\right))+(∊\mathbf{F}\nabla \varphi ,\nabla \varphi )+(J{\kappa }^2\sinh (\varphi +G),\psi ),$$ (100)

where the stress tensor T and the strain tensor E were given in Eq. (3).

Unlike the piezoelectric problems to which variational principles and quasivariational inequalities can be readily applied, we lack the coupling of the electrostatic potential and elastic displacement at the level of constitutive relations of the material (40; 42). Instead, our electro-elastic coupling is through the electrostatic forces. We note that variational principles have been formulated for a class of fluid-solid interaction systems (43), which resemble our problem in that the coupling is through the boundary conditions of the elasticity equation instead of the constitutive relations. This will be examined for our problem in a future work.

8 Concluding Remarks

In this paper we have proposed and carefully analyzed a nonlinear elasticity model of deformation in macromolecules induced by electrostatic forces. This was accomplished by coupling the nonlinear Poisson-Boltzmann equation for the electrostatic potential field to the nonlinear elasticity equations for elastic deformation. The electrostatic of this coupled system is desribed by an implicit solvation model, and the Piola transformation defined by the solution of the elasticity equation is introduced into the Poisson-Boltzmann equation such that both equations can be analyzed together in a undeformed configuration. A key technical tool for coupling the two models is the use of an harmonic extension of the elastic deformation field into the solvent region of the combined domain. Combining this technical tool with regularization techniques established in (2) and a standard bootstrapping technique, we showed that the Piola-transformed Poisson-Boltzmann equation is also well-defined and the regular component of its solution has a piecewise W^2,p-regularity. This regularity matches that of the elastic deformation, giving access to a Schauder fixed-point theorem-based analysis framework for rigorously establishing the existence of solutions to this coupled nonlinear PDE system for small perturbation in the ionic strength and for small added charges. The existence of large deformation for large perturbations in ionic strength and/or charges can be obtained by combining our local result with general continuation techniques for nonlinear elastic deformation (37). Our Shauder-type existence proof technique did not require that we establish a contraction property for the fixed-point mapping S; this results in losing access to a uniqueness result for the coupled system, as well losing access to a fixed error reduction property for numerical methods based on the fixed-point mapping S.

The coupling of elastic deformation to the electrostatic field is of great importance in modeling the conformational change in large macromolecules. To put this into perspective, more comprehensive and realistic continuum models for macromolecular conformational changes can be developed based on the results in this article, for example, by coupling the (stochastic) hydrodynamical forces from the Stokes or Navier-Stokes equation, or including van der Waals forces between closely positioned molecules. While mathematical models and robust numerical methods have been well studied for steady state fluid-structure interaction problems (7), the inclusion of van der Waals forces appears to be more straightforward (35). A major concern in applying these coupled models, however, is the determination of the elasticity properties of macromolecules within the continuum framework, which requires new theoretical models and quantitative comparisons between the continuum modeling and the classical molecular dynamical simulation and/or experiential measurements. In a future work we will study the development of numerical methods for this coupled system and apply this model to macromolecular systems where electrostatic forces play a dominant role.

Fig. 3.

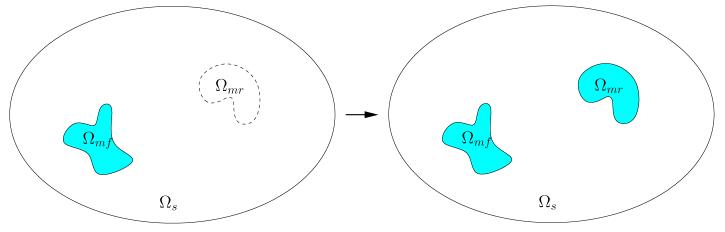
Illustration of adding rigid molecule(s). Left: Before adding rigid molecules the domain Ω_mr is occupied by solvent and hence has dielectric constant ε_s. Right: After adding molecules the domain Ω_mr has low dielectric constant ε_m.