Abstract
The electronic properties of double strands composed of trimeric LNA, PNA, DNA and RNA single strands were investigated by density-functional molecular orbital calculations. The computed hybridization energies for the double strands involving PNA or LNA are larger than those for DNA-DNA and RNA-RNA. The larger stability is attributed to the presence of a larger positive charge of the hydrogen atoms contributing to the hydrogen bonds in the PNA-DNA and LNA-DNA double-strands. These results are comparable to the experimental finding that PNA and LNA single strands display high affinity toward a complementary DNA or RNA single strand.
1. Introduction
In the recent developments of new DNA arrays, significant progress has been made toward a rapid and accurate detection of specific DNA sequences. To produce highly sensitive DNA sensors, it is essential to develop an oligomer having stronger hybridization with a complementary single-strand DNA. Many types of modifications have been introduced into native nucleic acids for developing nucleic acids with high affinity toward DNA, such as peptide nucleic acid (PNA), locked nucleic acid (LNA) and so on.
PNA was developed [1] as a new oligomer having high affinity hybridization with single-strand DNA. PNA is a nucleic acid analogue of DNA, in which the phosphate backbone of DNA is replaced with a structurally homomorphous pseudopeptide backbone. The melting temperatures for PNA-DNA and DNA-DNA double-strands with 15 base pairs into their single strands are 69°C and 54°C, respectively [2], indicating PNA-DNA is more stable than DNA-DNA. In our previous studies [3,4], the electronic properties of DNA-DNA and PNA-DNA double strands containing 3 to 6 base pairs were examined theoretically by density-functional theory (DFT)calculations to elucidate that the binding energies for PNA-DNA double strands are greater than those for the DNA-DNA. In addition, this greater stability of PNA-DNA double strands was attributed to the presence of a larger positive charge on the hydrogen atoms involved in the hydrogen bonds between PNA and DNA strands [3,4].
LNA was prepared as an ideal oligomer for recognition of RNA [5]. LNA is a nucleic acid analogue of RNA, in which the furasnose ring of the ribose sugar is chemically locked by the introduction of a methylene linkage between O2 and C4’, as shown in Fig. 1. It was experimentally found [5] that LNA displays high affinity toward both DNA and RNA single strands having a complementary base sequence to form the double-stranded LAN-DNA and LAN-RNA by hybridizing with Watson-Crick type hydrogen bonds. The melting temperatures of LNA-RNA and LNA-DNA double strands are 2–10 °C and 1–8 °C higher than those of DNA-RNA and DNA-DNA, respectively [5]. Therefore, it is expected that LNA single strand may accomplish stronger hybridization with DNA as well as RNA. However, the origin of the stronger hybridization of LNA-DNA and LNA-RNA double strands has never been elucidated theoretically.
Figure 1.
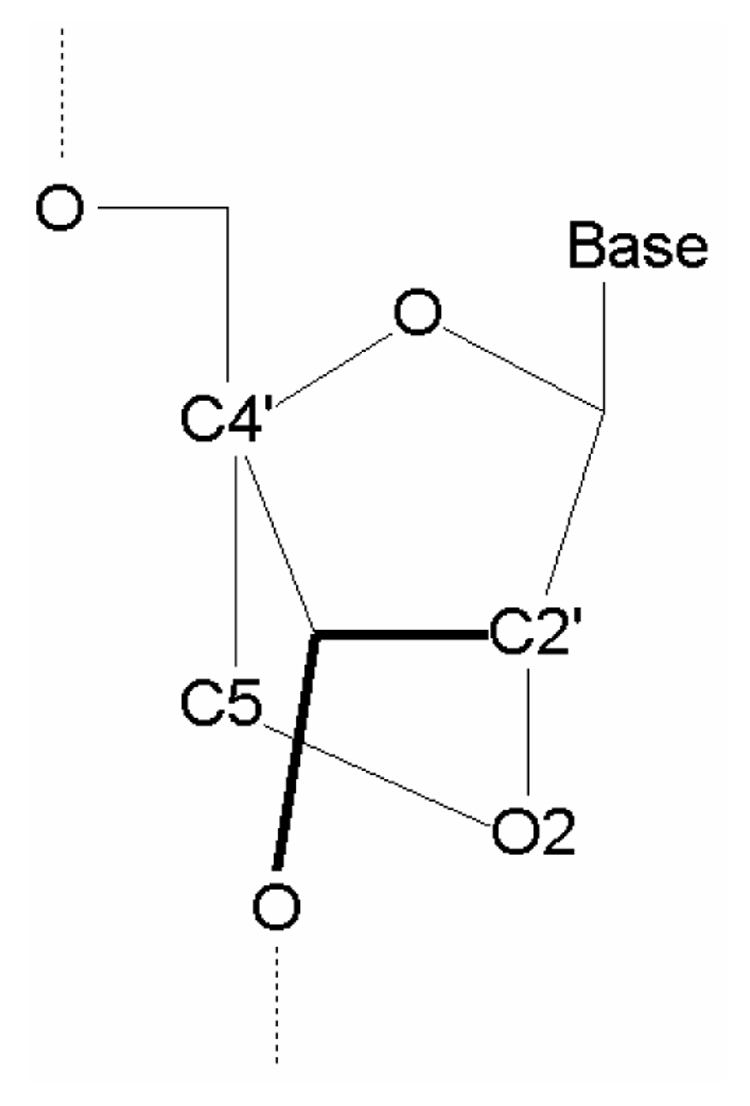
Chemical structure of the ribose sugar part of LNA and the assignment of atoms.
In the present study, we investigated the electronic properties of double-stranded nucleic acids with 3 base pairs including LNA, PNA, RNA and DNA by DFT calculations. From the comparison of the calculated results, we attempted to elucidate which nucleic acid is the most favorable for high-affinity hybridization.
2. Details of calculations
Initially, we constructed trimeric DNA-DNA, RNA-DNA and RNA-RNA double strands with the standard A-form as well as B-form conformations by using the molecular modeling software HyperChem [6]. The base sequences of these strands are d(CAG)2. The 3’ and 5’ ends of these double-strands were terminated by hydrogen atoms. To neutralize the negative charges of the PO4 parts of DNA and RNA backbones, counter ions (Na+) were added to the PO4 parts. The positions of the terminal hydrogen atoms and Na+ ions were optimized by classical molecular mechanics (MM) calculations based on AMBER [7] force field. The remaining parts of the these double-strands were fixed to the standard A- or B-form, because the classical MM optimization often causes a distorted structure for stacked base pairs in the double strands.
In constructing the PNA structure, the backbone of DNA was replaced by the corresponding PNA backbone as described in our previous studies [3,4]. The structure of the PNA backbone was partially optimized by the MM method based on AMBER force field to obtain a stable PNA backbone. The structure thus obtained was confirmed to be reliable by comparison with the experimental structure [8]. In the present study, we adopted the antiparallel conformation for PNA-DNA and PNA-RNA double strands, in which the N-terminus of the PNA strand is oriented toward the 3’ end of the complementary DNA or RNA strand.
In addition, the structures for LNA-LNA, LNA-DNA, LNA-RNA and PNA-LNA double strands were constructed by the modification of the ribose sugar part of nucleic acid as shown in Fig. 1. The structure of the modified ribose sugar part of LNA was partially optimized by the MM method.
In our previous DFT studies [3,4] for the DNA-DNA and PNA-DNA duplexes having 3 to 6 base pairs, the Perdew-Wang91 functionals (PW91) [9,10] for exchange and correlation energies and the 6-31++G**, 6-31G** and 4-31G** basis sets implemented in the ab initio molecular orbital (MO) program Gaussian03 (G03) [11] were used. In the present study, we used the PW91 functionals and the 6-31G** basis set. Because the binding energy between the two strands calculated in a finite basis set is subject to a basis set superposition error (BSSE), the binding energy was appropriately corrected by the counterpoise calculation [12, 13]. All MO calculations were performed by the G03 program package [11].
3. Results and discussion
The constructed structures of PNA-DNA and LNA-RNA double strands having 3 base pairs are shown in Fig. 2. With the structure of the base-pair parts fixed, all the other structural parameters were optimized in a vapor phase by the classical MM method based on AMBER force field. In our previous studies [3,4], we confirmed that the structures of backbones for the PNA-DNA and PNA-PNA double strands optimized by the classical MM method are comparable to those obtained by earlier MD simulations [14] as well as the experiment [15,16]. To confirm the reliability of the constructed LNA structures, we compared the bond lengths and torsion angles in the ribose sugar part of LNA for the constructed LNA-LNA, LNA-DNA, LNA-RNA and PNA-LNA with those obtained by experiment [17]. These values are listed in Table I, where the calculated values are the average over the constructed LNA-LNA, LNA-DNA, LNA-RNA and PNA-LNA. The assignment of each atom in Table I is shown in Fig. 1. The calculated values for A- and B-form conformations are almost the same with each other, and they are comparable to the experimental values, indicating that the structures of the ribose sugar part of LNA obtained by the present study are reliable.
Figure 2.
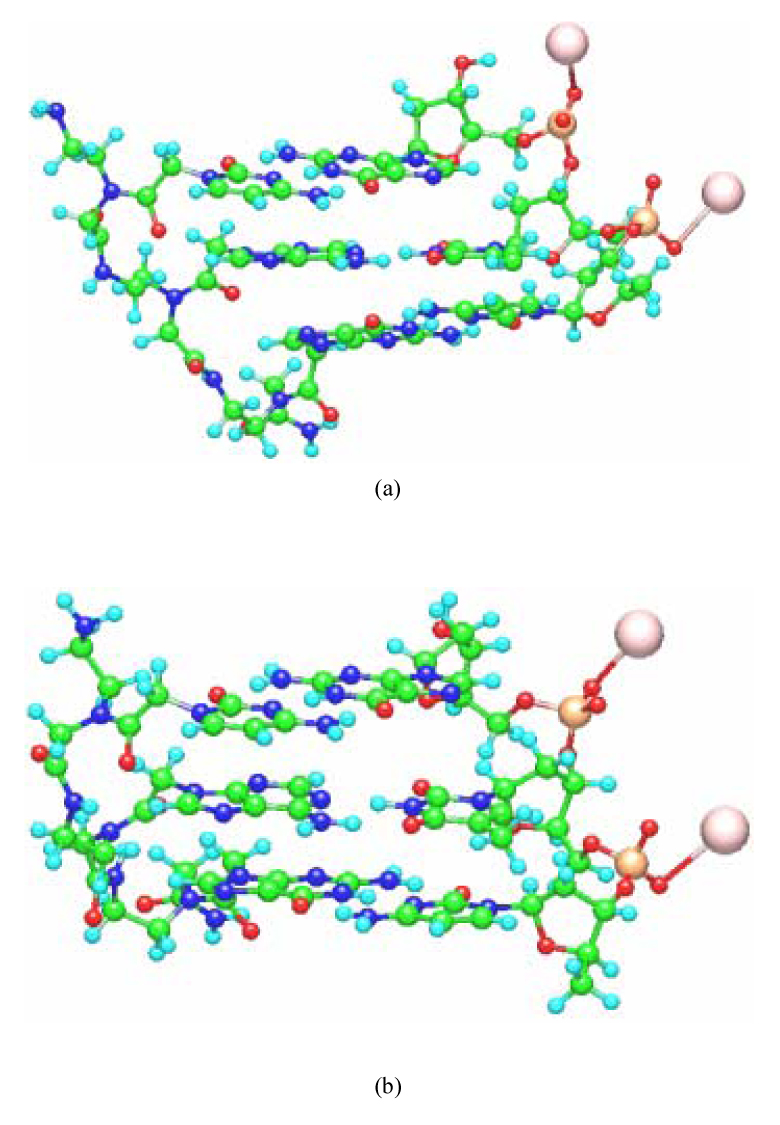
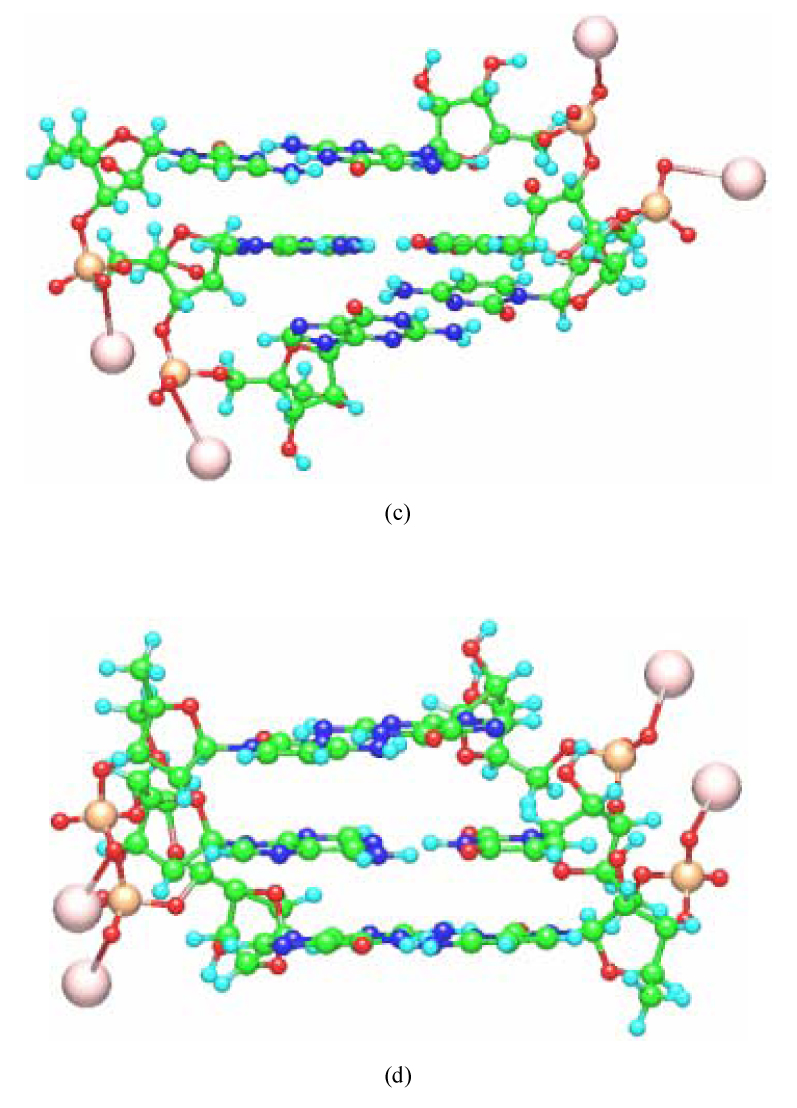
Optimized structures of (a) A-form PNA-DNA, (b) B-form PNA-DNA, (c) A-form LNA-RNA and (d) B-form LNA-RNA with the base sequence 5’-CAG-3’ obtained by the molecular mechanics calculations based on AMBER force field. Counter ions (Na+) were added to the phosphate units of the DNA, RNA and LNA backbones.
Table I.
Bond lengths (Å) and torsion angle (degree) of the ribose sugar part of LNA obtained by the experiments [17] and the present calculations for A- and B-form double-strands. The calculated values are the average over the constructed LNA-LNA, LNA-DNA, LNA-RNA and PNA-LNA. The assignment of each atom is shown in Fig. 1.
| Experimental | Calculated | ||
|---|---|---|---|
| A-form | B-form | ||
| Bond Length (Å) | |||
| C4'-C5 | 1.528 | 1.542 | 1.542 |
| C5-O2 | 1.462 | 1.444 | 1.447 |
| O2-C2' | 1.465 | 1.446 | 1.448 |
| Torsion Angel (degree) | |||
| C4'-C5-O2-C2' | 5.8 | 0.4 | 0.0 |
The computed total energies and binding energies for the B- and A-form double strands having the base sequence 5’-CAG-3’ are shown in Table II and Table III, respectively. The binding energies were appropriately corrected by the counterpoise (CP) calculations [12, 13] such as CP-RNA and PNA-CP. The double strands are listed in decreasing order of binding energy in Table II and Table III. Comparison of the binding energies for B- and A-form double strands indicates that the binding energy of B-form is greater than that of A-form for all double strands but RNA-RNA. Therefore, we employed the A-form RNA-RNA and the B-forms for all the other double strands to investigate their electronic properties.
Table II.
Total energies (Hartree) and binding energies (kcal/mol) between single-strands for the B-form double-strands having the base sequence 5’-CAG-3’. The binding energy was appropriately corrected by the counterpoise (CP) calculations [12, 13] and denoted such as CP-RNA and PNA-CP. The double-strands are listed in decreasing order of binding energy.
| Total energy | Binding energy | ||
|---|---|---|---|
| PNA-RNA | CP-RNA | PNA-CP | PNA-RNA |
| −7011.054 | −4070.382 | −2940.552 | −74.7 |
| LNA-LNA | CP-LNA | LNA-CP | LNA-LNA |
| −8461.846 | −4237.481 | −4224.248 | −73.6 |
| RNA-DNA | CP-DNA | RNA-CP | RNA-DNA |
| −8007.237 | −3884.229 | −4122.892 | −73.5 |
| LNA-DNA | CP-DNA | LNA-CP | LNA-DNA |
| −8121.823 | −3884.228 | −4237.480 | −72.2 |
| PNA-DNA | CP-DNA | PNA-CP | PNA-DNA |
| −6824.213 | −3883.616 | −2940.483 | −71.5 |
| LNA-RNA | CP-RNA | LNA-CP | LNA-RNA |
| −8307.992 | −4070.387 | −4237.492 | −70.9 |
| PNA-LNA | CP-LNA | PNA-CP | PNA-LNA |
| −7164.875 | −4224.212 | −2940.552 | −69.7 |
| PNA-PNA | CP-PNA | PNA-CP | PNA-PNA |
| −5867.590 | 2927.264 | −2940.216 | −69.1 |
| DNA-DNA | CP-DNA | DNA-CP | DNA-DNA |
| −7781.209 | −3883.613 | −3897.492 | −65.7 |
| RNA-RNA | CP-RNA | RNA-CP | RNA-RNA |
| −8193.385 | −4070.357 | −4122.933 | −59.7 |
Table III.
Total energies (Hartree) and binding energies (kcal/mol) between single-strands for the A-form double-strands having the base sequence 5’-CAG-3’. The binding energy was appropriately corrected by the counterpoise (CP) calculations [12,13] and denoted such as CP-RNA and PNA-CP. The double-strands are listed in decreasing order of binding energy.
| Total energy | Binding energy | ||
|---|---|---|---|
| LNA-RNA | CP-RNA | LNA-CP | LNA-RNA |
| −8308.312 | −4070.718 | −4237.489 | −65.9 |
| RNA-RNA | CP-RNA | RNA-CP | RNA-RNA |
| −8194.038 | −4070.679 | −4123.257 | −64.0 |
| PNA-RNA | CP-RNA | PNA-CP | PNA-RNA |
| −7010.768 | −4070.154 | −2940.520 | −59.0 |
| PNA-PNA | CP-PNA | PNA-CP | PNA-PNA |
| −5867.448 | −2926.841 | −2940.522 | −53.3 |
| PNA-DNA | CP-DNA | PNA-CP | PNA-DNA |
| −6824.110 | −3883.525 | −2940.521 | −40.2 |
| LNA-LNA | CP-LNA | LNA-CP | LNA-LNA |
| −8460.753 | −4223.200 | −4237.492 | −38.3 |
| PNA-LNA | CP-LNA | PNA-CP | PNA-LNA |
| −7163.880 | −2940.520 | −4223.301 | −37.0 |
| RNA-DNA | CP-DNA | RNA-CP | RNA-DNA |
| −8006.624 | −3883.343 | −4123.258 | −14.4 |
| LNA-DNA | CP-DNA | LNA-CP | LNA-DNA |
| −8121.056 | −3883.550 | −4237.491 | −9.4 |
| DNA-DNA | CP-DNA | DNA-CP | DNA-DNA |
| −7781.220 | −3883.540 | −3897.666 | −8.8 |
Generally, RNA double strands as well as LNA have A-form conformations. The present DFT calculations for both the A- and B-form double strands indicate that only the RNA-RNA prefers to have A-form conformation. The theoretical result is consistent with the experimental finding that RNA duplexes do not adopt any B-form geometry. On the other hand, the theoretical results for LNA-LNA and LNA-RNA are contradictory. In particular, the binding energy (38.3 kcal/mol) of A-form LNA-LNA is only half that (73.6 kcal/mol) of B-form LNA-LNA, indicating that the latter is much more stable than the former.
The binding energy of B-form PNA-RNA is the largest (74.7 kcal/mol), while that of A-form RNA-RNA is the smallest (64.0 kcal/mol). The most remarkable finding is that the replacement of DNA or RNA in the DNA-DNA or RNA-RNA double strands by the LNA or PNA single strand gives rise to greater binding energies of the double strands. Table II demonstrates that the binding energies of PNA-DNA (71.5 kcal/mol) and LNA-DNA (72.2 kcal/mol) are greater than that of DNA-DNA (65.7 kcal/mol), and that those of PNA-RNA (74.7 kcal/mol) and LNA-RNA (70.9 kcal/mol) are also greater than that of RNA-RNA (59.7 kcal/mol). These results are consistent with experiment [2,5] showing higher affinity of PNA and LNA single strands to a complementary DNA or RNA single strand.
In order to elucidate the origin of the larger binding energy for PNA-DNA compared with DNA-DNA, we investigated in our previous studies [3,4] the charge distributions around the hydrogen bonds connecting the two single strands. The computed Merz-Kollman charge distributions [18] clearly indicate that the hydrogen atoms involved in the PNA-DNA hydrogen bonds possess greater positive charges than those in DNA-DNA, leading to stronger hybridization between PNA and DNA. In the present study, we thus investigated the charge distributions for all double strands in the same way as the previous study. Table IV lists the atomic charges obtained by the PW91/6-31G** calculations. The average value means the average for all oxygen, nitrogen or hydrogen atoms contributing the hydrogen bonds between the single strands. The average charges of hydrogen atoms contributing to the hydrogen bonds for PNA-DNA and LNA-DNA are 0.52 and 0.49, respectively, which are larger than that (0.44) for DNA-DNA. In addition, the average charge of hydrogen atoms in PNA-RNA (0.49) and LNA-RNA (0.57) are greater than that for RNA-RNA (0.45). It is thus concluded from Table IV that the hydrogen atoms contributing to the hydrogen bonds between single strands for the double strands involving PNA or LNA have greater positive charges than those for the DNA-DNA or RNA-RNA double strands. This fact leads to the greater binding energies of PNA-DNA, LNA-DNA, PNA-RNA and LNA-RNA compared with the DNA-DNA and RNA-RNA.
Table IV.
Atomic charges estimated by Merz-Kollman analysis [18] of atoms contributing to the hydrogen bonds between the two single-strands for B-form double-strands. The average value means the average for all oxygen, nitrogen or hydrogen atoms contributing the hydrogen bonds between single-strands. It is noted that the results for A-form double-strand are listed for RNA-RNA, because A-form is more stable than B-form for only RNA-RNA.
| PNA-RNA | LNA-LNA | RNA-DNA | LNA-DNA | PNA-DNA | |
|---|---|---|---|---|---|
| O(C)…H-N(G) | −0.71, 0.55, −1.06 | −0.61, 0.50, −1.02 | −0.59, 0.46, −0.91 | −0.61, 0.53, −1.05 | −0.59, 0.46, −0.99 |
| N(C)…H-N(G) | −0.70, 0.42, −0.76 | −0.64, 0.38, −0.72 | −0.69, 0.37, −0.66 | −0.65, 0.43, −0.78 | −0.69, 0.47, −0.82 |
| N-H(C)…O(G) | −0.94, 0.51, −0.57 | −0.86, 0.45, −0.54 | −0.90, 0.47, −0.54 | −0.94, 0.49, −0.56 | −0.90, 0.47, −0.55 |
| N(A)…H-N(T) | −0.96, 0.51, −0.87 | −1.01, 0.42, −0.55 | −0.52, 0.31, −0.39 | −0.92, 0.56, −0.76 | −1.65, 0.93, −1.23 |
| N-H(A)…O(T) | −0.85, 0.46, −0.57 | −0.91, 0.44, −0.51 | −0.64, 0.32, −0.47 | −0.77, 0.40, −0.51 | −0.87, 0.45, −0.52 |
| N-H(G)…O(C) | −0.99, 0.47, −0.61 | −1.02, 0.50, −0.57 | −0.97, 0.47, −0.57 | −1.02, 0.48, −0.62 | −0.95, 0.43, −0.57 |
| N-H(G)…N(C) | −0.81, 0.51, −0.83 | −0.89, 0.47, −0.63 | −0.75, 0.43, −0.66 | −0.84, 0.53, −0.82 | −0.85, 0.49, −0.70 |
| O(G)…H-N(C) | −0.55, 0.49, −0.93 | −0.56, 0.45, −0.85 | −0.53, 0.41, −0.78 | −0.58, 0.49, −0.91 | −0.56, 0.45, −0.82 |
| average | −0.81, 0.49, −0.78 | −0.81, 0.45, −0.67 | −0.70, 0.41, −0.62 | −0.79, 0.49, −0.75 | −0.88, 0.52, −0.78 |
| LNA-RNA | PNA-LNA | PNA-PNA | DNA-DNA | RNA-RNA | |
| O(C)…H-N(G) | −0.61, 0.51, −1.02 | −0.69, 0.50, −1.02 | −0.61, 0.48, −0.98 | −0.54, 0.45, −0.86 | −0.58, 0.50, −1.06 |
| N(C)…H-N(G) | −0.66, 0.44, −0.81 | −0.72, 0.47, −0.80 | −0.65, 0.40, −0.74 | −0.56, 0.34, −0.59 | −0.65, 0.47, −0.92 |
| N-H(C)…O(G) | −0.91, 0.48, −0.59 | −0.88, 0.47, −0.54 | −0.93, 0.51, −0.57 | −0.83, 0.44, −0.54 | −0.96, 0.50, −0.60 |
| N(A)…H-N(T) | −1.59, 1.03, −1.31 | −0.87, 0.23, −0.30 | −1.28, 0.57, −0.64 | −0.98, 0.66, −0.55 | −1.02, 0.41, −0.33 |
| N-H(A)…O(T) | −0.94, 0.51, −0.63 | −0.93, 0.44, −0.49 | −0.82, 0.42, −0.54 | −0.49, 0.29, −0.54 | −0.43, 0.29, −0.43 |
| N-H(G)…O(C) | −1.03, 0.49, −0.60 | −1.01, 0.50, −0.66 | −1.14, 0.58, −0.67 | −0.90, 0.43, −0.55 | −1.05, 0.50, −0.56 |
| N-H(G)…N(C) | −0.92, 0.56, −0.83 | −0.81, 0.47, −0.73 | −0.97, 0.54, −0.75 | −0.72, 0.46, −0.68 | −0.76, 0.38, −0.55 |
| O(G)…H-N(C) | −0.60, 0.51, −0.94 | −0.58, 0.46, −0.87 | −0.58, 0.49, −0.90 | −0.55, 0.45, −0.85 | −0.57, 0.51, −0.95 |
| average | −0.91, 0.57, −0.84 | −0.81, 0.44, −0.68 | −0.87, 0.50, −0.72 | −0.70, 0.44, −0.65 | −0.75, 0.45, −0.68 |
The recent experimental study [19] on the deuterium isotope effect of RNA and DNA dodecamers suggested that N1-N3 hydrogen bond for A-U base pair in a RNA double strand is about 3 % stronger than that for A-T base pair in DNA double strand. Our DFT results shown in Table IV indicate that the averaged charge (0.45) of hydrogen atoms contributing to the hydrogen bonds in the A-form RNA-RNA is slightly larger than that (0.44) in the B-form DNA-DNA. In addition, the size of average atomic charges for oxygen and nitrogen atoms is also greater in RNA-RNA than that in DNA-DNA, indicating that the hydrogen bonds in RNA-RNA are stronger than those in DNA-DNA. These calculated results are qualitatively consistent with experiment.
To compare the chemical reactivity of double strands, the energy levels and the spatial distributions of the MOs lying near the highest occupied MO (HOMO) and the lowest unoccupied MO (LUMO) were examined. The energy distributions of these MOs are shown in Fig. 3, and Table V lists the energy levels and spatial distributions of HOMO-1, HOMO and LUMO. The HOMO-LUMO energy gap for PNA-DNA is the largest (0.81 eV), while that for RNA-DNA is the smallest (0.20 eV). Table V indicates that the replacement of DNA single strand of DNA-DNA by PNA or LNA causes the increase of HOMO-LUMO gap, whereas the replacement of RNA single strand in RNA-RNA by PNA or LNA makes the HOMO-LUMO gap smaller. Therefore, the replacement of DNA or RNA by PNA or LNA significantly alters the chemical reactivity of the DNA-DNA and RNA-RNA double strands.
Figure 3.
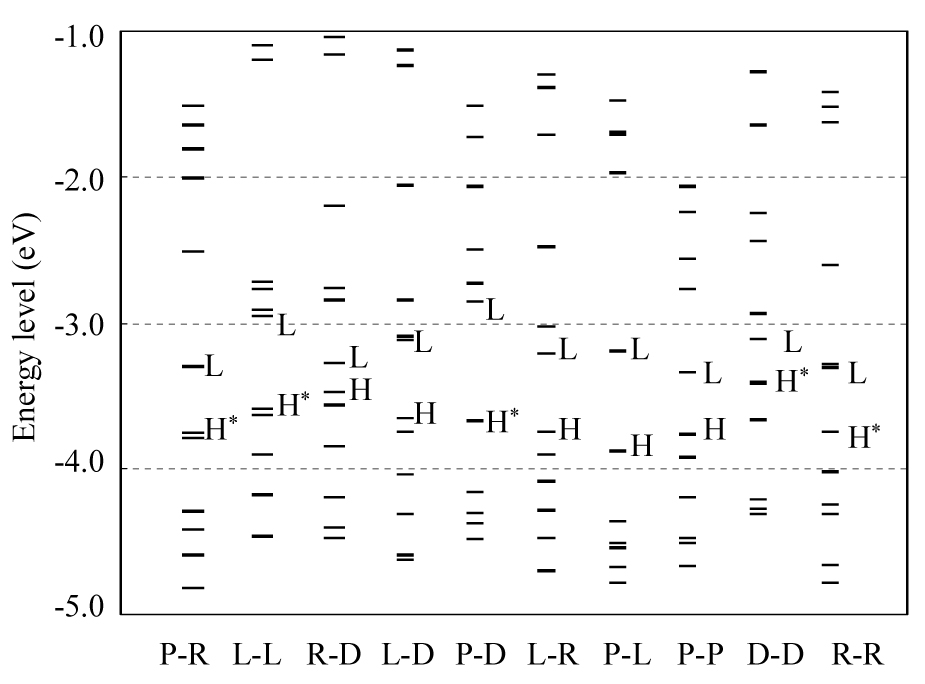
Distributions of energy levels of MOs existing near the HOMO (H) and LUMO (L) for the B-form double-strands having the base sequence 5’-CAG-3’ constructed with LNA (L), PNA (P), RNA (R) and DNA (D) single-strands. The HOMOs for PNA-RNA, LNA-LNA, PNA-DNA and DNA-DNA are doubly degenerate as shown in Table V. These HOMOs are indicated by H*. It is noted that the results for A-form double strand are listed for RNA-RNA, because A-form is more stable than B-form for only RNA-RNA.
Table V.
Energy levels (eV) and spatial distributions of HOMO-1, HOMO and LUMO for the B-form double-strands having the base sequence 5’-CAG-3’. It is noted that the results for A-form double-strand are listed for RNA-RNA, because A-form is more stable than B-form for only RNA-RNA.
| HOMO-1 | HOMO | LUMO | H-L gap | ||||
|---|---|---|---|---|---|---|---|
| Level | Distribution | Level | Distribution | Level | Distribution | ||
| PNA-RNA | −3.79 | G6 | −3.76 | G3 | −3.31 | Na of G6 | 0.45 |
| LNA-LNA | −3.63 | G6 | −3.59 | G3 | −2.95 | Na of G3 | 0.64 |
| RNA-DNA | −3.57 | G6 | −3.48 | G3 | −3.28 | Na of G6 | 0.20 |
| LNA-DNA | −3.75 | G6 | −3.66 | G3 | −3.12 | Na of G6 | 0.54 |
| PNA-DNA | −3.68 | G3 | −3.67 | G6 | −2.86 | Na of G6 | 0.81 |
| LNA-RNA | −3.91 | G3 | −3.75 | G6 | −3.21 | Na of G6 | 0.54 |
| PNA-LNA | −4.36 | G6 | −3.88 | G3 | −3.19 | Na of G6 | 0.69 |
| PNA-PNA | −3.97 | G6 | −3.77 | Backbone of G3 | −3.35 | Backbone of C4 | 0.42 |
| DNA-DNA | −3.42 | G3 | −3.41 | G6 | −3.11 | Na of G6 | 0.30 |
| RNA-RNA | −4.02 | G3 and G6 | −3.75 | G3 and G6 | −3.11 | Na of G3 | 0.44 |
-
PNA-RNA
-
Nter – C1 – A2 – G3 – Cter3’ – G6 – U5 – C4 – 5’
-
-
LNA-LNA, LNA-DNA, DNA-DNA, RNA-DNA
-
5’ – C1 – A2 – G3 – 3’3’ – G6 – T5 – C4 – 5’
-
-
PNA-DNA, PNA-LNA
-
Nter – C1 – A2 – G3 – Cter3’ – G6 – T5 – C4 – 5’
-
-
LNA-RNA, RNA-RNA
-
5’ – C1 – A2 – G3 – 3’3’ – G6 – U5 – C4 – 5’
-
-
PNA-PNA
-
Nter – C1 – A2 – G3 – CterCter – G6 – T5 – C4 – Nter
-
Since the HOMO and LUMO, respectively, mediate the hole and electron transfers through DNA, the spatial distributions of HOMO and LUMO are of crucial importance for the understanding charge-transfer pathway. As shown in Table V, the LUMOs in all double strands but for the PNA-PNA are distributed on the counter ions near the guanine base, indicating the possibility that electron transfers through the counter ions lying near the PO4 parts of the backbone with guanine base. In addition, the HOMO for PNA-PNA is distributed in the backbone of G3, whereas the HOMOs for the other double strands are localized in guanine base. These results indicate that the spatial distributions of HOMO and LUMO are significantly affected by replacing both strands of DNA-DNA by PNA, resulting in the completely different charge-transfer pathway through PNA-PNA from the other double strands.
4. Conclusions
To elucidate the difference in electronic properties between double strands involving LNA, PNA, RNA and DNA single strands, we theoretically investigated the binding energies between strands, and the distributions of charge and molecular orbitals. The computed binding energies for double strands involving PNA or LNA are greater than those for the DNA-DNA and RNA-RNA double strands. This large stability of double strands with PNA or LNA is attributed to the presence of a larger positive charge on the hydrogen atoms contributing to the hydrogen bonds between the single strands. The present DFT study suggests that PNA and LNA single strands have high affinity toward a complementary DNA or RNA single strand. The energy levels and spatial distributions of HOMO and LUMO, which play a major role in charge conduction through the double strands, are significantly modulated by the replacement of DNA by PNA.
Acknowledgements
This work was supported by the Ministry of Education, Science, Sports and Culture, Grant-in-Aid for JSPS Fellows (No. 18.282), the grants from the Kayamori Foundation of Informational Science Advancement, the Inamori Foundation, and the Japan Society for the Promotion of Science (No. 15310088). Y. I. gratefully acknowledges the support of National Institute of Health SCoRE Program-Grant No. S06GM08102.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Wang J, Nielsen PE, Jiang M, Cai X, Fernandez JR, Grant DH, Ozsoz M, Beglieter A, Mowat M. Anal. Chem. 1997;69:5200. doi: 10.1021/ac9706077. [DOI] [PubMed] [Google Scholar]
- 2.Egholm M, Buchardt O, Christensen L, Behrens C, Freier SM, Driver DA, Berg RH, Kim SK, Norden B, Nielsen PE. Nature. 1993;365:566. doi: 10.1038/365566a0. [DOI] [PubMed] [Google Scholar]
- 3.Natsume T, Ishikawa Y, Dedachi K, Kurita N. Chem. Phys. Letters. 2006;418:239. [Google Scholar]
- 4.Natsume T, Ishikawa Y, Dedachi K, Tsukamoto T, Kurita N. Intern. J. of Quantum Chem. 2006 in press. [Google Scholar]
- 5.Petersen M, Wengel J. Trends Biotechnol. 2003;21:74. doi: 10.1016/S0167-7799(02)00038-0. [DOI] [PubMed] [Google Scholar]
- 6.HyperChem 6.03. Gainesville, FL: Hyper cube Inc.; 2000. [Google Scholar]
- 7.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J. Am. Chem. Soc. 1995;117:5179. [Google Scholar]
- 8.Eriksson M, Nielsen PE. Nature Struct. Biol. 1996;3:410. doi: 10.1038/nsb0596-410. [DOI] [PubMed] [Google Scholar]
- 9.Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, Fiolhais C. Phys. Rev. B. 1992;46:6671. doi: 10.1103/physrevb.46.6671. [DOI] [PubMed] [Google Scholar]
- 10.Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, Fiolhais C. Phys. Rev. B. 1993;48:4978. doi: 10.1103/physrevb.48.4978.2. [DOI] [PubMed] [Google Scholar]
- 11.Frisch MJ, et al. Gaussian 03 (Revision B.04) Pittsburgh, PA: Gaussian, Inc.; 2003. [Google Scholar]
- 12.van Duijneveldt FB, van Duijneveldt-van de Rijdt JGCM, van Lenthe J. Chem. Rev. 1994;94:1873. [Google Scholar]
- 13.Chalasinsky G, Szczesniak MM. Chem. Rev. 1994;94:1723. [Google Scholar]
- 14.Sen S, Nilsson L. J. Am. Chem. Soc. 1998;120:619. [Google Scholar]
- 15.Eriksson M, Nielsen PE. Nature Struct. Biol. 1996;3:410. doi: 10.1038/nsb0596-410. [DOI] [PubMed] [Google Scholar]
- 16.Rasmussen H, Kastrup JS, Nielsen JN, Nielsen JM, Nielsen PE. Nature Struct. Biol. 1997;4:98. doi: 10.1038/nsb0297-98. [DOI] [PubMed] [Google Scholar]
- 17.Egli M, Minasov G, Teplova M, Kumar R, Wengel J. Chem. Commun. 2001:651. [Google Scholar]
- 18.Besler BH, Merz KM, Jr, Kollman PA. J. Comp. Chem. 1990;11:431. [Google Scholar]
- 19.Vakonakis I, LiWang AC. J. Am. Chem. Soc. 2004;126:5688. doi: 10.1021/ja048981t. [DOI] [PubMed] [Google Scholar]


