Improved Identification of Metabolites in Complex Mixtures using HSQC NMR Spectroscopy

Abstract

The automated and robust identification of metabolites in a complex biological sample remains one of the greatest challenges in metabolomics. In our experiments, HSQC carbon-proton correlation NMR data with a model that takes intensity information into account improves upon the identification of metabolites that was achieved using COSY proton-proton correlation NMR data with the binary model of [1]. In addition, using intensity information results in easier-to-interpret “grey areas” for cases where it is not clear if the compound might be present. We report on highly successful experiments that identify compounds in chemically defined mixtures as well as in biological samples, and compare our 2-dimensional HSQC analyses against quantification of metabolites in the corresponding 1-dimensional proton NMR spectra. We show that our approach successfully employs a fully automated algorithm for identifying the presence or absence of pre-defined compounds (held within a library) in biological HSQC spectra, and in addition calculates upper bounds on the compound intensities.

1. Introduction

Two dimensional (2D) NMR spectra enable improved compound identification when compared to one dimensional spectra because crowding and overlap are alleviated, and cross peaks unique to particular pairs of spin coupled nuclei are used to identify specific molecules. Sophisticated methods of quantification of metabolites using both 1D and 2D NMR are being developed (see e.g., [2–7]), but an initial analysis of one or a few representative samples to identify which metabolites are present in a particular type of biological mixture has the potential to reduce the computational burden and the potential for error by reducing the number of compounds that subsequently need to be quantified. Furthermore, the metabolite identification stage of a metabolomics study still remains a largely manual and time consuming process of cross referencing chemical shift data from, typically, 1D NMR data to library spectra. An algorithm that can robustly identify metabolites from a corresponding 2D NMR spectrum of a representative biological sample would provide considerable advantages over existing approaches.

Compound identification is made more difficult by the possibility that peaks in an NMR spectrum may be displaced due to variations in sample temperature or pH. In previous work [1] we investigated methods to identify metabolites in solution NMR spectra using binary information from 2D COSY proton-proton correlation spectroscopy. In that paper, we considered a matching of the peaks by considering the portions of the COSY spectra above the detection limit without regard to the intensity of the peaks. Heteronuclear single quantum coherence (HSQC) spectroscopy should provide increased resolution and therefore greater metabolite specificity by utilizing the greater ¹³C chemical shift dispersion on one axis of the 2D spectrum. Accordingly in this paper we improve on our previous method by considering intensity information and by using 2D HSQC proton-carbon correlation spectra, which provides carbon chemical shift information. The result is a very effective method that includes information about an upper bound on the intensities of those compounds that cannot be clearly identified as not in the sample.

An important feature of our methods is that we do not need reference spectra for all of the compounds present in the sample (although of course the upper bound on an intensity can only be reported for compounds with corresponding reference spectra). The analysis is conducted one reference compound at a time. This offers the practical advantages that the algorithm is easily parallelized and in some applications the analysis can be limited only to those compounds of interest, which requires only seconds of computational time. In the next section, we describe a formulation based on computing an upper bound on the intensity of the reference spectrum that could be present in the complex biological sample. A statistical model of the interdependence of the distortions due to pH and temperature is outlined in Appendix A. Experimental results are given in Section 3, and Section 4 offers concluding remarks.

2. Theory and Methods

In overview, the sample spectrum S is first normalized by dividing by the standard deviation of the noise and then aligned with respect to the reference spectrum R in the database. Next, possible displacements of the peaks can be enumerated (or searched) to find the one that results in an upper bound on the intensity match for the reference compound.

HSQC spectra are 2D data matrices consisting of cross peaks of protons and carbons, as shown in Figure 1. We compare the sample spectrum, denoted by S, with a series of reference spectra of known compounds, denoted by R. For each compound, the proton and carbon chemical shifts of the ith peak are denoted by p_i and c_i, respectively. These peaks may move under pH or temperature variations [8]. To match a certain compound in a sample, all possible displacements should be searched under possible experimental variations. For chemical shift of protons, we use a regression model to describe the dependency of the displacements within the molecule (Appendix A; [1]). In this case we select one proton peak as independent and regress other proton peaks with respect to this base peak. For the distortion on the carbon axis we simply search a small neighborhood around all the peaks. The target is to find the best matching of all peaks of the compound between the sample and reference spectra. We evaluate the quality of each potential displacement using a bound on the intensity described in the following section.

Figure 1.

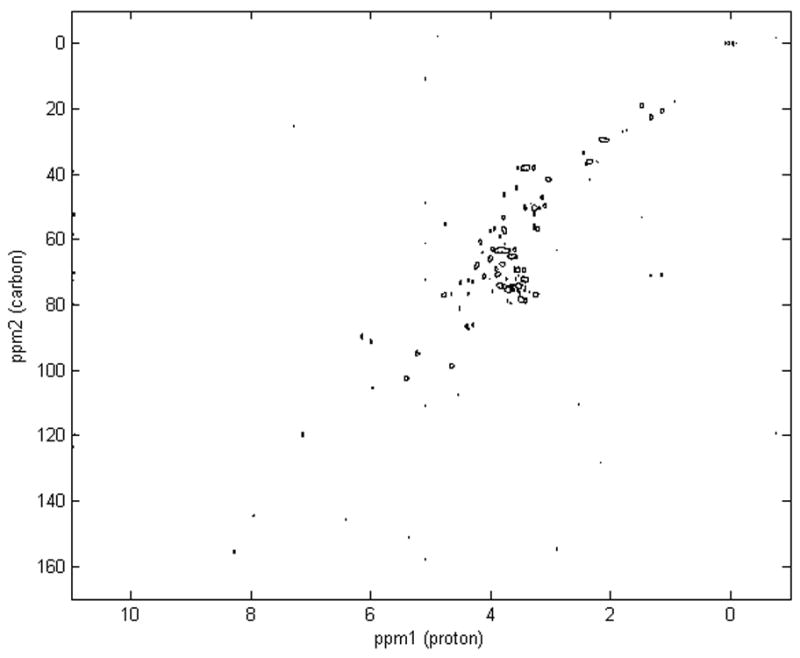
Representative 2D ¹H,¹³C HSQC NMR spectrum of a complex biological sample, the extract of fish eggs, highlighting the dispersion of peaks across the proton and carbon axes.

2.1 Intensity Bounding Function

Let R_Δ denote the shifted reference spectrum R by displacement Δ. For each peak in R_Δ, calculate the intensity ratio at the position of this peak in the sample S and shifted reference R_Δ, denoted by $r_i=\frac{\langle \mathbf{S}({\mathbf{P}}_{\mathbf{i}})\rangle }{\langle {\mathbf{R}}_{\mathbf{\Delta }}({\mathbf{P}}_{\mathbf{i}})\rangle }$, where 〈S(P_i)〉 and 〈R_Δ(P_i)〉 are the estimations of the intensities in S and R_Δ at the position of the ith peak P_i. The peak i for which the ratio is smallest, $r_{min}=\underset{i}{min}{r}_i$, bounds the intensity that could possibly be assigned to the _I reference compound. This ratio allows us to express the upper bound on the intensity as:

$$\text{O}(\mathbf{S},{\mathbf{R}}_{\mathbf{\Delta }})=\frac{1}{n}{r}_{min}\sum _j\langle {\mathbf{R}}_{\mathbf{\Delta }}({\mathbf{P}}_{\mathbf{j}})\rangle =\frac{1}{n}\underset{i}{min}\frac{\langle \mathbf{S}({\mathbf{P}}_{\mathbf{i}})\rangle }{\langle {\mathbf{R}}_{\mathbf{\Delta }}({\mathbf{P}}_{\mathbf{i}})\rangle }\sum _j\langle {\mathbf{R}}_{\mathbf{\Delta }}({\mathbf{P}}_{\mathbf{j}})\rangle$$

where n is the total number of peaks in the reference. The maximum value of this objective function represents an upper bound on the average peak intensity detected in the sample. This is illustrated in Figure 2.

Figure 2.

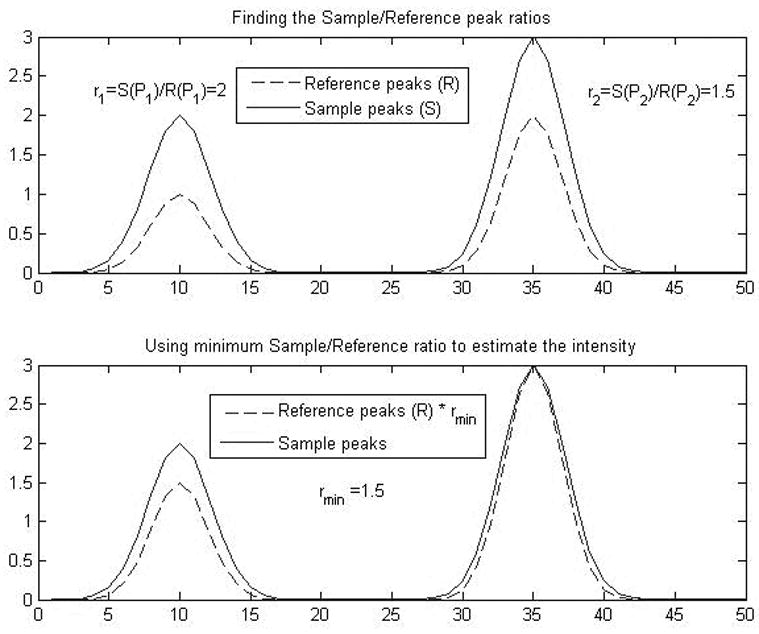
Illustration of the method used to determine the minimum Sample/Reference ratio in order to calculate the upper bound on the intensity estimation.

2.2 Intensity Estimation

Since the spectrum is represented as a data matrix on discrete grid of chemical shifts, we applied kernel density smoothing with Gaussian kernel to estimate the intensity of any arbitrary point in the spectrum. Compared with the simple moving average smoothing method, this kernel smoothing method gives more accurate estimation for noisy data, as illustrated in Figure 3.

Figure 3.

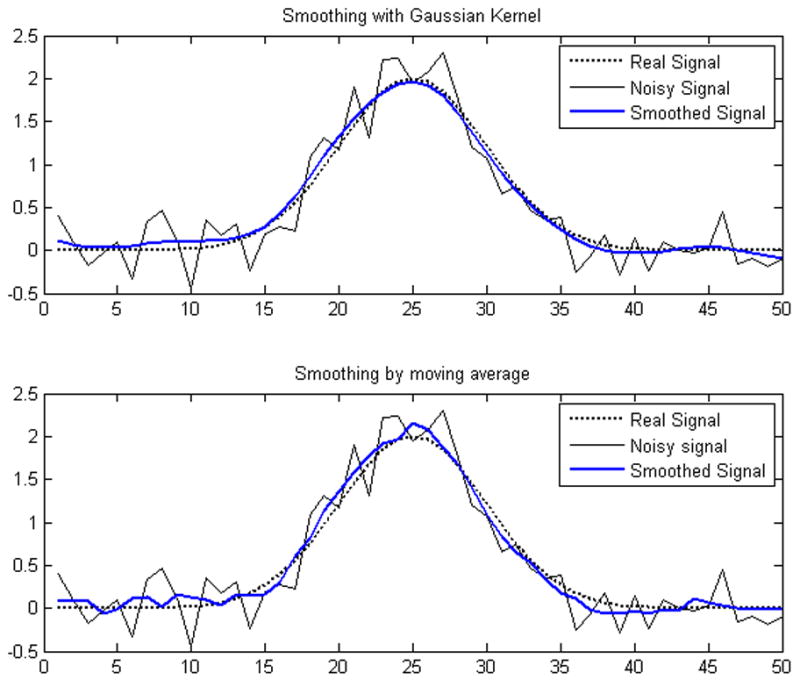
Comparison between the Gaussian kernel smoothing method and moving average smoothing method for an NMR peak.

For an arbitrary point P_i represented by the pair of proton and carbon chemical shifts, namely, p_i and c_i, the estimated intensity is

$$\langle \mathbf{S}(\mathbf{P})\rangle =\langle \mathbf{S}(p,c)\rangle =\int \int \mathbf{S}(p^{\prime },c^{\prime })G(p,c,{\sigma }_p,{\sigma }_c)d{p}^{\prime }d{c}^{\prime }$$

where G( p,c,σ_p,σ_c ) is the Gaussian Kernel centered at (p,c) with bandwidth σ_p and σ_c. Since we are dealing with 2D spectra, the kernel is bi-variate Gaussian. We choose the bandwidth to be one pixel along both the carbon and proton axes.

2.3 Maximization of the Intensity Function

The objective is to find an upper bound on the presence of the reference compound in the sample by maximizing the intensity function. We do this by searching all possible displacements of the independent proton peak p₀ within the predefined pH variation range, as well as the displacement of all carbon peaks c_i. We use δ₀ to denote the displacement of the independent peak p₀ and the vector λ to denote the displacement of carbon peaks c_i: c = {c_i | i = 1…n}. So the overall displacement Δ is represented by the combination of δ₀ and λ.

$$\underset{\mathbf{\delta },\mathbf{\lambda }}{max}[\text{O}(\mathbf{S},{\mathbf{R}}_{\mathbf{\delta },\mathbf{\lambda }})]=\underset{\mathbf{\delta },\mathbf{\lambda }}{max}\left[\frac{1}{n}\underset{i}{min}\frac{\langle \mathbf{S}(p_i,c_i)\rangle }{\langle {\mathbf{R}}_{\mathbf{\delta },\mathbf{\lambda }}(p_i,c_i)\rangle }\sum _j\langle {\mathbf{R}}_{\mathbf{\delta },\mathbf{\lambda }}(p_j,c_j)\rangle \right]$$

Subject to:

$$\begin{array}{l}{\delta }_0^{-}\le {\delta }_0\le {\delta }_0^{+}\\ {\widehat{\beta }}_i{\delta }_0-3{\widehat{\epsilon }}_i\le {\delta }_i\le {\widehat{\beta }}_i{\delta }_0+3{\widehat{\epsilon }}_i,i=1,\dots n\\ {\lambda }_i^{-}\le {\lambda }_i\le {\lambda }_i^{+}\end{array}$$

where p_i and c_i are the chemical shifts of the peaks on the proton and carbon axes respectively, ${\delta }_0^{-},{\delta }_0^{+}$ are the lower and upper bound of displacement of the independent proton peak, and ${\lambda }_i^{-},{\lambda }_i^{+}$ are the lower and upper bound of displacement of carbon peaks. β̂_i and ε̂_i are the regression coefficients and errors of the ith proton peak as described in the Appendix.

3. Experiments and Results

We tested this method using a reference database of 2D ¹H,¹³C HSQC spectra of 19 amino acids, citrate, and creatine phosphate, and a series of HSQC spectra of chemically defined synthetic samples as well as several biological samples that are described further below.

All NMR spectra were measured using an Avance DRX-500 spectrometer (Bruker, Fremont, CA) running XWINNMR software version 3.1. A 5 mm TXI probe was used for all measurements. Both 1D ¹H and 2D ¹H,¹³C HSQC were obtained for 10 mM solutions of the free amino acids, citrate, and creatine phosphate in ²H₂O, buffered with 0.2 M sodium phosphate. Spectra of all 21 standards were collected separately. Also, spectra of three mixtures of amino acids, with each amino acid present at 10 mM, were obtained (Section 3.1). The standard buffer pH was 7.4 unless noted otherwise. All data were obtained at 22°C and referenced to internal sodium 3-trimethylsilyl-2,2,3,3-d₄-propionate (TMSP; 1 mM) at 0.00 ppm chemical shift in both the proton and carbon dimensions. Gradient enhanced phase-sensitive HSQC spectra [9] were collected with 2048 points in t₂ and 256 points in t₁ over a bandwidth of 10 ppm in ¹H and 160 ppm in ¹³C with four scans per t₁ value and a recycle time of 2 sec (giving a total acquisition time of 35 minutes). The refocusing delay was 1.72 ms, based on an assumed average J_CH of 145 Hz. The resulting HSQC NMR spectra were processed in XWINNMR using standard methods, with 90 degree shifted sine-squared apodization and phase correction in both dimensions and zero filling in t₁ to yield a transformed 2D dataset of 1024 by 2048 points. The spectra are converted into ASCII format by hand written MATLAB scripts.

3.1 Defined Synthetic Samples

Mix 1, Mix 2 and Mix 3 are predefined mixtures of amino acids. The compositions of these mixtures, together with the results of our automated analyses of the HSQC spectra, are summarized in Table 1, where the intensity function values of each metabolite are listed as multiples of the standard deviation of the noise. Note that we use the words “intensity function” to refer to our computed upper bound on a function proportional to the intensity. Based upon accepted practice [10] we anticipate that an intensity function of 3 corresponds to the limit of detection of a metabolite, and an intensity function of 10 corresponds to the limit of quantification. We set a search range for the carbon chemical shift to allow possibly displacements in the carbon axis. For metabolites with less than 5 peaks, we set the search range $\mathrm{\Delta }\lambda ={\lambda }_i-{\lambda }_i^{-}={\lambda }_i^{+}-{\lambda }_i=0.8\mathit{ppm}$, and searching all possible displacements combinations could be finished in a very short amount of time. The default search ranges are user specified values intended to be beyond the distortions in chemical shift that are normally encountered in NMR spectra of biological samples (e.g., due to variation in the sample pH). For metabolites with many peaks that result in a large search space, such as isoleucine and tryptophan, we set Δλ = 0.4 ppm and Δλ = 0.2 ppm respectively to avoid excessive computation. A model for distortion on the ¹³C axis, similar to the one given in the Appendix for the ¹H axis would enable searches over larger distortion ranges with reduced computational effort.

Table 1.

Results of automated analyses of HSQC NMR spectra of defined synthetic samples. Intensity functions (listed as multiples of the standard deviation of the noise) are shown for a reference database of 19 amino acids, citrate (cit) and creatine phosphate (pcr) that were tested on ¹H, ¹³C HSQC spectra of three defined mixtures of amino acids. The compounds present in the mixtures (3 amino acids in each of Mix 1 and Mix 2, and 6 in Mix 3) are shown in bold.

Compound	Mix 1*	Mix 2*	Mix 3*
ala	322.85	0.54	297.85
arg	0.70	2.08	1.53
asn	0.76	0.63	0.32
asp	0.90	1.23	0.72
cys	0.29	1.17	1.81
gln	0.56	1.45	1.68
glu	1.48	1.57	1.97
his	0.67	761.38	917.14
ile	98.35	2.97	94.90
leu	0.54	213.76	319.59
lys	0.45	0.41	0
met	0.87	4.27	1.78
phe	0.64	3.29	4.43
pro	0.94	0.73	0.58
ser	0.58	0.09	1.82
thr	1.09	299.83	444.79
trp	0.11	0	0.57
tyr	0.65	0.82	0.93
val	476.30	3.18	448.86
cit	1.46	1.84	1.06
pcr	0.63	3.59	2.55

^*Units are normalized intensity function.

The most striking result is that a large bound on the intensity function has been calculated from the HSQC analyses for each and every amino acid that is present in the three mixtures. The largest intensity function for a false positive hit (phenylalanine in Mix 3) is 4.43, only slightly above our estimated limit of detection of 3 (and significantly lower than our estimated limit of quantification of 10). Based upon an assumption that metabolites are quantifiable if they have an upper bound on intensity greater than 10 times the standard deviation of the noise, the three amino acids in Mix 1 and Mix 2 together with the six amino acids in Mix 3 are detected with 100% sensitivity and 100% specificity. These results are a considerable improvement over our previous model that employed a binary scoring for the analysis of 2D COSY NMR spectra [1] which resulted in an average of one error per mixture.

It is important to note that the intensity functions (i.e., cross peak intensity) depend not solely on the concentration of the metabolite but are also influenced by the carbon-proton coupling (J) value and the relaxation times of the two nuclei contributing to the cross peak in relation to the recycle time of the experiment [11]. Hence some variation in the intensity function, even for different amino acids present at equal concentrations, is expected. However, as shown in Table 1, the intensities of the amino acids across the three mixtures are relatively well conserved with errors of 8.1% (Ala), 18.6% (His), 3.6% (Ile), 39.7% (Leu), 19.5% (Thr) and 5.9% (Val).

3.2 Biological Samples

To confirm the success of the automated HSQC analyses of the chemically defined mixtures we next applied the approach to HSQC spectra of biological samples (Table 2). The same search ranges for the proton and carbon chemical shifts were applied as above. HSQC spectra of three diverse biological samples were examined, including a muscle extract from a shellfish, a liver extract from a fish, and a whole egg homogenate of a second fish species, detailed below. The HSQC spectra were acquired using the same parameters as for the metabolite standards, except for the shellfish muscle we used a bandwidth of 14 ppm in ¹H and 200 ppm in ¹³C with 96 scans per t₁ value and a relaxation delay of 2 sec; for the fish liver a bandwidth of 14 ppm in ¹H and 210 ppm in ¹³C with 48 scans per t₁ value and a relaxation delay of 3.5 sec; and for the fish eggs a bandwidth of 11 ppm in ¹H and 180 ppm in ¹³C with 40 scans per t₁ value and a relaxation delay of 3 sec (giving total acquisition times in the range of 14 to 27 hrs). In order to evaluate our automated HSQC analysis we compared our results against the identification and quantification of metabolites from 1D ¹H NMR spectra of the same biological samples using the Chenomx NMR Suite metabolomics software (professional version 4.61).

Table 2.

Comparison of metabolite identification and quantification from 1D ¹H NMR spectra using Chenomx NMR Suite software with our automated analysis of 2D ¹H, ¹³C HSQC spectra of the same samples. For the 1D data all metabolites detected at 0.1 mM or greater are indicated in bold, whereas for the 2D data the limit of detection has been set at 3 times the standard deviation of the noise, above which the metabolites are in bold. The HSQC reference database contained 19 amino acids, citrate (cit) and creatine phosphate (pcr).

Compound	Abalone muscle		Medaka fish egg		Trout liver
	1D Chenomx (mM)	2D HSQC*	1D Chenomx (mM)	2D HSQC*	1D Chenomx (mM)	2D HSQC*
ala	0.30	7.21	0.83	8.49	0.62	14.44
arg	2.29	53.89	0.60	6.02	0	1.85
asn	0	1.33	0	2.25	0	1.10
asp	0.09	1.85	0.45	3.35	0	2.08
cys	0	0.98	0	0.17	0	0.68
gln	0	1.63	0.26	5.92	0.32	8.46
glu	0.66	14.67	2.46	30.10	1.18	19.25
his	0	1.00	0.16	1.96	0	2.16
ile	0.02	0.67	0.11	0.51	0.05	0.45
leu	0.04	1.23	0.27	3.37	0.07	1.60
lys	0	1.13	0.30**	7.65	0	2.50
met	0**	0.71	0.08	1.16	0	1.45
phe	0.02	1.60	0.23	7.45	0.03	1.34
pro	0	0.87	0.37	2.05	0	1.38
ser	0	1.98	0.10**	6.23	0.25**	7.95
thr	0	1.45	0.24	8.68	0.25	9.85
trp	0	0.49	0.10	0.60	0	0
tyr	0	1.09	1.06	18.11	0	1.42
val	0.05	1.21	0.21	3.32	0.08	1.41
cit	0	0.76	1.87	22.51	0	2.01
pcr	0	1.45	0.72	29.47	0.11	3.87

^*Units are normalized intensity function.

^**Metabolite concentration re-examined after inspection of corresponding 2D HSQC results. See text for details.

The first sample analysed was foot muscle from a red abalone shellfish (Haliotis rufescens) that was extracted as described previously, using perchloric acid [12,13]. The concentrations of 19 amino acids, citrate and creatine phosphate were quantified in the 1D ¹H NMR spectrum using the Chenomx NMR Suite. These results, together with the intensity function values (in terms of multiples of the standard deviation of the noise) from our automated analysis of the 2D HSQC spectrum are summarized in Table 2. Relatively few metabolites were identified by the Chenomx software. Encouragingly the 3 metabolites present at or above a concentration of 100 μM (in bold in Table 2) were all identified by our HSQC approach with intensity function values above 3, the estimated limit of detection. Furthermore, no other metabolites (of the 21 in our database that were being searched for) were detected in the HSQC spectrum, equating to a sensitivity and specificity of 100%. Of particular note is the high degree of correlation between the metabolite intensities measured in the 1D NMR spectrum with the intensity function values from the 2D HSQC spectrum (Figure 4a; r² = 0.9971).

Figure 4.

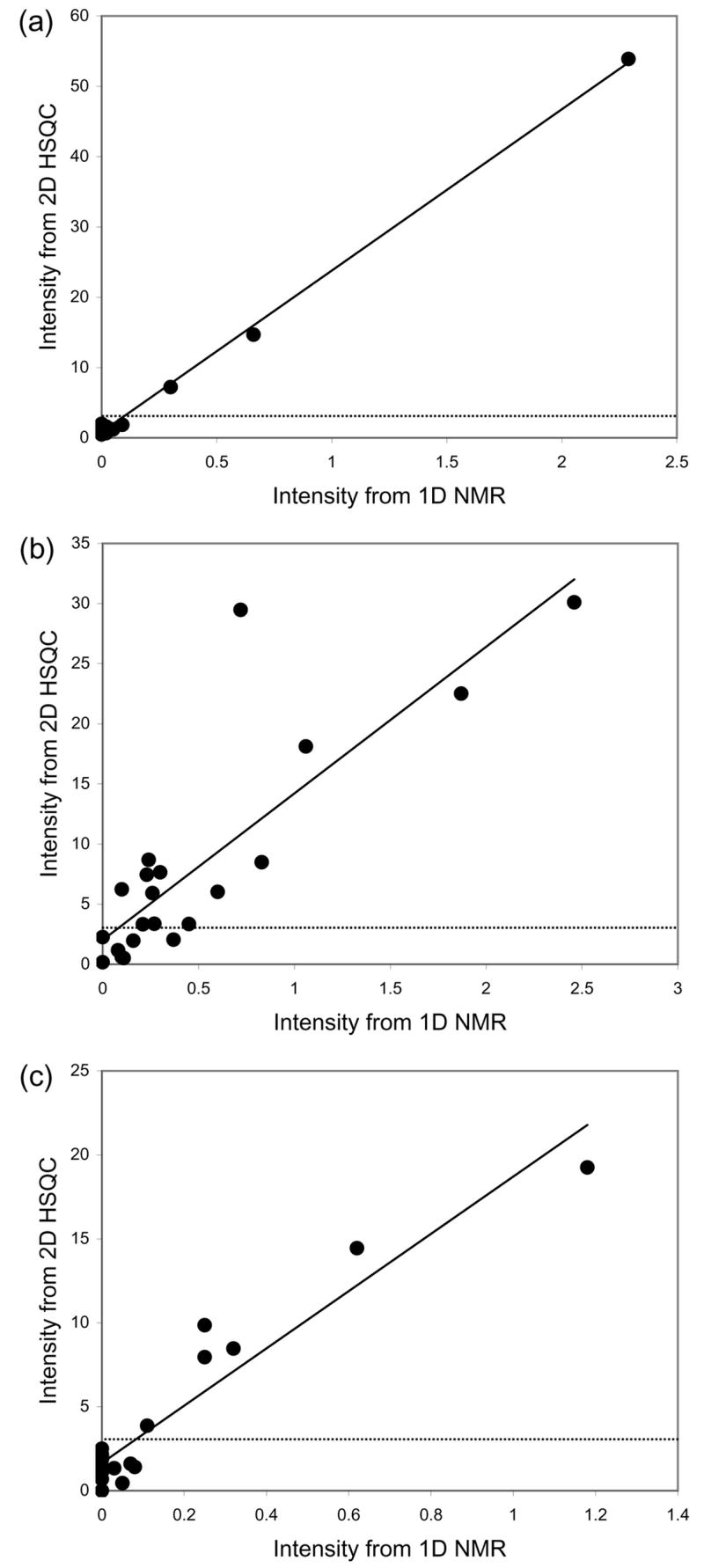
Relationship between metabolite intensities measured from 1D ¹H NMR spectra using Chenomx NMR Suite with the intensity function values derived from our automated analyses of 2D ¹H,¹³C HSQC spectra for three biological samples: (a) foot muscle extract from a shellfish, r²= 0.9971; (b) homogenate of fish eggs, r²= 0.7025; and (c) liver extract from a second fish species, r²= 0.9084. The dotted line at an HSQC intensity function value of 3 corresponds to our estimated limit of detection for the HSQC spectra.

NMR spectra of Japanese medaka (Oryzias latipes) fish eggs that were extracted using perchloric acid [14,15] yielded a considerably greater number of identifiable metabolites. Eighteen of the total of 21 standards (19 amino acids, citrate and creatine phosphate) were identified and quantified by the Chenomx software at levels greater than or equal to 100 μM (in bold in Table 2). Of these, fourteen were automatically identified from the HSQC spectrum, with the remaining 4 metabolites all present at relatively low concentrations (100, 110, 160 and 370 μM). Again, no other metabolites (of those being searched for) were detected in the HSQC spectrum. In total, ca. 45 peaks in the spectrum were identified and assigned to the metabolites in our library, while the remaining peaks (corresponding to ca. 50% of all observed peaks) remained unassigned. A relationship was again identified between the metabolite intensities measured from the 1D and 2D NMR methods (Figure 4b; r² = 0.7025). The correlation was not as good as for the abalone muscle analysis, although this was partly due to a single metabolite, creatine phosphate, which had an upper bound on the relative concentration in the 2D HSQC dataset that was higher than in the corresponding 1D spectrum.

The third dataset that was analysed comprised of metabolites extracted from steelhead trout liver using perchloric acid [16]. Again considering a cut-off of 100 μM for the unambiguous detection of metabolites in the 1D NMR spectrum and a cut-off of 3 times the standard deviation of the noise in the automated HSQC analysis, exactly the same six metabolites were identified by both approaches. This corresponds to a sensitivity and specificity of 100% for the automated analysis of the HSQC spectrum. A plot of the metabolite intensities derived from the two complementary approaches is shown in Figure 4c. The correlation between the 1D NMR peak intensities and the intensity function values from the 2D HSQC spectrum is again very good (r² = 0.9084), confirming the success of the new automated analysis of HSQC spectra.

It is important to note that the analysis of the 1D spectra using Chenomx software was conducted blind with respect to knowledge of the HSQC results. Subsequently, following an inspection of the metabolite lists derived from the 2D HSQC analyses, four inconsistencies were identified. First, in the abalone muscle 1D NMR spectrum we had incorrectly identified the presence of methionine. In fact the peak arose from O-acetylcarnitine, and methionine was not observed. For the fish egg 1D NMR spectrum, only after closer inspection were we able to detect low levels of lysine and serine, both of which were in congested areas of the spectrum precluding their accurate quantification. A similar situation occurred for serine in the 1D NMR spectrum of trout liver.

Although Figure 4 highlights the generally consistent relationship between intensities derived from the 1D and 2D HSQC spectra, this relationship is clearly not perfect. Neither method is capable of reporting highly accurate intensities, particularly for low abundance metabolites, which for the 1D spectra arises because of severe peak overlap (e.g., for serine) and for the 2D spectra because our method only reports an upper bound on the intensity. In terms of sensitivity the 2D HSQC approach, when used with a commonly accepted limit of detection [10], can identify metabolites present above ca. 100 μM. More specifically, from Table 2, the lowest concentration metabolites detected were 300, 210 and 110 μM for the muscle, egg and liver samples, respectively.

4. Conclusions

We have reported a novel method for the automated and robust identification of metabolites from 2D HSQC NMR spectra of complex biological samples. Our model takes into account the intensity information in the peaks, thereby improving upon our earlier metabolite identification method using COSY NMR data that employed a binary model [1]. In addition, the intensity information derived from the automated analyses of the 2D HSQC compares favorably with metabolite concentrations measured from the corresponding 1D NMR spectra that were analysed using a leading commercial metabolomics software package. We have thoroughly tested our approach using three chemically defined synthetic mixtures as well as three diverse biological samples, and in 5 out of these six datasets achieved 100% sensitivity and specificity. Based upon these results we propose two applications for this algorithm. First, for the metabolite identification stage of a metabolomics study that uses a 2D HSQC spectrum of a representative biological sample recorded with a long acquisition time to maximise the signal to noise. The second application stems from continuing sensitivity improvements in NMR spectroscopy, for example using microcoil probes [17] and improved data acquisition schemes facilitating fast 2D NMR experiments [18]. Recently, Markley and coworkers reported a metabolomics study in which 2D HSQC spectra were acquired in only 12 mins [19]. As such they propose that 2D HSQC is a feasible alternative to 1D NMR for metabolomics, for which the algorithm reported here could provide automated metabolite identification for all of the biological samples.

Appendix A - Displacement Dependencies

Although the peaks corresponding to many metabolites have only a small displacement response to changes in pH, temperature and matrix, in the interest of generality we develop the model for significant displacements. This was first reported in [1].

Displacements of proton peaks are related to titratable groups. We choose peaks from titratable groups to be independent, and estimate the dependency of the other functional groups.

We experimentally determine the range of the position of the peaks for independent groups. This allows us to restrict the variation of the corresponding element of b to be within values for displacements observed over reasonable variation in pH and temperature. We use regression analysis to determine the mean dependencies for other groups, which allows us to center the search for the corresponding displacements as a function of the displacement for the independent group. The regression error is used to limit the search around this value.

The regression analysis is done on 1D proton NMR spectra because all that is needed in the peak position variation. Suppose there are n 1D spectra for a particular, known, metabolite and each of them has s peaks:

$$\mathbf{P}=\left|\begin{array}{ccc}{p}_{11}& \cdot \cdot & p_{1s}\\ \cdot \cdot & \cdot \cdot & \cdot \cdot \\ p_{n1}& \cdot \cdot & p_{ns}\end{array}\right|$$

Select one spectrum {p_r1 ·· p_rs} and calculate the peak distortions of the rest of the spectra with respect to this spectrum.

$$\mathbf{\Delta }\mathbf{P}=\left|\begin{array}{ccc}\mathrm{\Delta }{p}_{11}=p_{11}-p_{r1}& \cdots & \mathrm{\Delta }{p}_{1s}=p_{1s}-p_{rs}\\ \cdots & \cdots & \cdots \\ \mathrm{\Delta }{p}_{n-1,1}=p_{n1}-p_{r1}& \cdots & \mathrm{\Delta }{p}_{n-1,s}=p_{ns}-p_{rs}\end{array}\right|$$

Take the positions of the peaks for the independent functional group $\mathbf{\Delta }{\mathbf{P}}_i=\left|\begin{array}{c}\mathrm{\Delta }{p}_{1i}\\ \cdot \cdot \\ \mathrm{\Delta }{p}_{ni}\end{array}\right|$ as independent variables and the rest ΔP_j (j ≠ i) as responses. This is a standard linear regression:

$${\mathbf{Y}}_{\mathbf{j}}=\mathbf{X}{\beta }_j+{\epsilon }_j,\mathit{where}{\mathbf{Y}}_{\mathbf{j}}=\left|\begin{array}{c}\mathrm{\Delta }{P}_{1j}\\ \cdot \cdot \\ \mathrm{\Delta }{P}_{nj}\end{array}\right|,\mathbf{X}=\left|\begin{array}{c}\mathrm{\Delta }{P}_{1i}\\ \cdot \cdot \\ \mathrm{\Delta }{P}_{ni}\end{array}\right|$$

The least square estimator of the coefficients: β̂_j = (X′X)⁻¹ X′Y_j

And the variance: ${\epsilon }_j^{\widehat{2}}=\frac{({\mathbf{Y}}_{\mathbf{j}}-\mathbf{X}{\widehat{\beta }}_j{)}^{\prime }({\mathbf{Y}}_{\mathbf{j}}-\mathbf{X}\widehat{\beta })}{n-2}$

These values are then used in the constraint that controls the search over possible distortions as follows:

$${\widehat{\beta }}_i{\delta }_0-3{\widehat{\epsilon }}_i\le {\delta }_i\le {\widehat{\beta }}_i{\delta }_0+3{\widehat{\epsilon }}_i,i=1,\dots n$$