Abstract
Oligonucleotide microarrays offer the potential to efficiently test for multiple organisms, an excellent feature for surveillance applications. Among these, resequencing microarrays are of particular interest, as they possess additional unique capabilities to track pathogens’ genetic variations and perform detailed discrimination of closely related organisms. However, this potential can only be realized if the costs of developing the detection microarray are kept at a manageable level. Selection and verification of the probes are key factors affecting microarray design costs that can be reduced through the development and use of in silico modeling. Models created for other types of microarrays do not meet all the required criteria for this type of microarray. We describe here in silico methods for designing resequencing microarrays targeted for multiple organism detection. The model development presented here has focused on accurate base-call prediction in regions that are applicable to resequencing microarrays designed for multiple organism detection, a variation from other uses of a predictive model in which perfect prediction of all hybridization events is necessary. The model will assist in simplifying the design of resequencing microarrays and in reduction of the time and costs required for their development for new applications.
INTRODUCTION
As the prevalence of oligonucleotide microarray-based detection methods increases, it becomes more important to have in silico methods to design, test and improve the analysis of assays. Microarrays have allowed for the development of new types of multiplex assays. These are potentially more efficient than multiple separate tests in terms of cost, required sample volumes, reagents and assay time. The savings of running such an assay are, however, balanced by the initial development, design and validation which become more complex, costly and time consuming. Accurate simulation models using available genetic sequence information for microorganisms can potentially minimize costs and development time for these highly multiplexed assays. Such models are used to solve in silico the global design problem that all oligonucleotide probe-based assays face: the selection of probes that are specific to an organism that will also detect all variants of that organism.
Solving this problem in silico is difficult because a variety of potential interactions between a sample sequence and a probe must be compared in order to select the optimal probes. Thus, simple predictive models are preferred for use in solving this design problem. Predictive models have been successfully developed for use in probe design for low-density oligonucleotide microarrays (1, 2) as well as PCR (3–6). These techniques use similar detection principles but require separate specifically tailored models.
Among microarray-based technologies, high-density resequencing microarrays demonstrated unique capabilities in testing for multiple pathogens, including co-infections, and in performing detailed discrimination of closely related pathogens and/or tracking genetic variations in pathogens (7, 8). Unfortunately, no simple predictive model for use in microarray design has been developed to facilitate application of high-density resequencing microarrays to detection of multiple pathogens. Design methods that exist for the original uses of resequencing microarrays are not appropriate for this application because those methods are geared for selecting large or nearly complete sequence selections from a single organism (9). Also, models developed for low-density microarrays cannot be used for designing high-density resequencing microarrays because probes are used in very different ways on the two types of array. For low-density microarray methods, the fluorescence intensity of a probe identifies the presence of a target when a specified threshold value is met. This event only ‘inferentially’ determines the identity of bases using the assumption that observing a certain level of fluorescent signal could only be the result of a target that is a perfect match of all bases of the probe (10). In contrast, a resequencing microarray uses a probe set consisting of four (or eight if antisense included) short probes to represent a portion of desired sequence and the possible base substitutions (but not deletions or insertions) of the center nucleotide position. This information, confirmed in both the sense and antisense directions, is used in a likelihood model to determine that a particular base is present. Confidence levels are determined by user-defined thresholds. The use of a large number of overlapping probe sets allows ‘direct’ determination of the identity of each base of target nucleotide sequence. The series of probe sets will resequence every base of the sequence used to generate them and allow at least partial resequencing of similar sequences thereby detecting organism variants as well.
Low-density oligonucleotide microarray design algorithms illustrate a good approach to modeling for the design problem. Sufficiently accurate predictions are achieved in these models through evaluation of the number of base matches between the target or background sequence and the probe and verification that the melting temperature calculated by GC versus AT content falls within a certain range (1, 2). The threshold number of matches and GC content needed to obtain sufficient specificity are determined empirically for a particular assay. Several other factors impacting signal intensity are sometimes incorporated into the models if the increase in calculations is not great (i.e. probe attachment to the surface, dimer formation between the fragments or loop formation resulting from the base content of the fragments). More detailed thermodynamic models have been developed that will predict the signal intensity but only at the cost of increased computation time, making them less appropriate for use in design problems (11–15).
This article describes a simple model applicable to the design of resequencing microarrays for multiple organism detection. The model predicts the base calls that will occur between one or more sequences and a group of other sequence(s) considered to be on a microarray. The design of optimal microarrays for multiple organism detection is dependent on the availability of this predictive model. It is found that the general approach employed for modeling other types of microarrays can be adapted for resequencing microarrays; however, thermodynamic information has been incorporated more explicitly to better account for variations among individual probes without adversely affecting computation speed.
METHODS
Amplification, hybridization and sequence determination
The details regarding design of the Respiratory Pathogen Microarray v.1 (RPM v.1) and experimental methods have been discussed in previous work (7, 8, 16, 17). Partial sequences from the genes containing diagnostic regions were tiled for the detection of common respiratory pathogens. The test of primers and influenza A H3N2 California-like lineage samples were evaluated using a different multiplex protocol (17). The remaining influenza samples used a random protocol (8). In this study, GCOS™ software v1.3 (Affymetrix Inc., Santa Clara, CA) was used to determine the intensities of the probes and base calls were made using GDAS v3.0.2.8 software (Affymetrix Inc., Santa Clara, CA). It should be noted that all experimental protocols used GDAS parameters setting such that, in clinical samples, only organisms that had been amplified by the multiplex mix would be present in sufficient quantities to cause base-calling events. The random protocols were applied to isolates of the particular organisms, not original clinical samples, and employed the same GDAS settings.
Model algorithm
Base calls on a resequencing microarray were modeled by assuming that, when a probe and a sample sequence have m contiguous, complementary bases including the central base, a large observable hybridization signal would occur only with the probe that matches exactly and not any of the other probes of a set. It was assumed that the bases must be contiguous in a fragment to produce a strong signal, so fragments of length m containing a mismatch were considered to produce no signal. Furthermore, any fragment that contained more than m contiguous bases was assumed to perform in the same fashion as a fragment of length m. This means the model only needed to consider fragments of length m to predict what base calls were likely to occur. This simple model predicted base calls with minimal computational requirements. Because stretches of <13 base matches were not expected to produce base-call events experimentally, time was not spent on the development of an algorithm that could test these shorter lengths. This eliminated the need to consider the nonspecific binding of segments shorter than 13 bases. Figure 1 presents an example of base-call results generated using the model with different values of m (from 23 to 13). A section of human adenovirus (Ad) serotype 4 hexon gene was used as the sequence for generating the probe sets and an Ad serotype 5 hexon sequence with deliberate base changes was used as the sample sequence. The changes were made so that specific base-call behaviors would be demonstrated in the example.
Figure 1.
A sequence used to make probe sets, reference sequence and a sample sequence are shown with an asterisk above the bases that match in prototype (generates probe sets) and sample sequences. Also shown are the reassembled model base-call results for each probe set for different values of m. Region A has 20 contiguous bases matching between sample sequence and reference sequence resulting in only N calls when m is >20. The longer region B has probe sets that make base calls up to m = 23. For each region, an increase of one or two in m results in one or two base calls at each edge to ceasing to make base calls. This occurs because it is no longer a fragment with sufficient matches. Region C has two contiguous regions of 9 and 12 bases with an SNP in between. One probe of the SNP set has 22 bases that match in the sample but no other probe in the region has more than 12 bases matching, therefore, all values of m return an N call.
The modeling algorithm consisted of generating the microarray probe sets based on a specific sequence, hereafter referred to as the prototype sequence, and then comparing potential binding fragments generated from a second ‘sample’ sequence with these probe sets. The prototype sequence was used to generate overlapping sets of four probes (i.e. for a sequence of L bases, L-24 probe sets are produced). The probes of a set were each 25-bases long and differed at the central base. One probe of each set generated exactly matched the prototype sequence. This represents what would actually be located on an experimental microarray. For a sample sequence, overlapping fragments that were m bases long were generated (i.e. for a sequence of K bases, at most K − m + 1 unique fragments could be produced). The fragments produced experimentally are normally longer than this (average of 100 bases) and in many cases have more than m bases that match a probe. It was a basic assumption of this model that this would not affect the observed call rates of a base location.
Once the microarray probes and sample fragments were generated, each probe of every probe set was tested against all the fragments from the sample sequence to determine if a perfect complement match occurs. Probes having a match were noted. More than one sample fragment could match the same probe, but this had no impact on the model results. The ability of a probe set to produce a base call was evaluated by considering the results of its probes. If only one probe of the set had a match in the sample sequence, a base call was assigned for the probe set and the next probe set was examined. An ambiguous base identity, N, was assigned when none of the sample fragments were a match to any member of the probe set. If more than one probe of a set had a match, an N was also assigned. After all probe sets were tested, the base calls (A, C, T, G or N) from each probe set were reassembled into a sequence.
Initial evaluation of the model prompted a further refinement in cases where two or more probes of a probe set hybridized with fragments of the target sequence. Each of the fragments meeting this initial criteria were lengthened by adding to the fragment the next base from the original sample sequence in the 5′–3′ direction. This lengthened fragment was then compared to the relevant probes. The lengthening process was repeated until a mismatch occurred or the end of the probe was reached. The resulting fragment lengths needed to produce a mismatch were compared and, if one was longer, then the base corresponding to that probe was assigned. Otherwise, N was still assigned.
Final model algorithm
The trend in the binding frequencies obtained experimentally indicated that the ΔG of the probe was important in determining if there would be a significant chance of producing a base call. The model was modified so that the unique fragments were generated based on ΔG rather than length. The ΔG value for each of the fragments (with m = 13) generated from the sample was calculated. Each fragment with a free energy difference below the cutoff (–14.5 kcal/mol) was used as is. For each fragment above the cutoff free energy difference, the length of the fragment was increased until its energy was below the cutoff or it reached the length of a probe (25 bases). The resulting list of fragments was then compared against every probe set as mentioned. In addition, the experimental results also suggested that fragment lengths shorter than 13 bases may produce hybridization with a reasonably high frequency if the free energy difference is above the cutoff. This was not considered for this model as it would require a significantly more time-consuming algorithm to implement and the short oligomer data used to calibrate the model contained no binding events of lengths shorter than 13 bases.
RESULTS
Initial model
An initial comparison of model predictions generated at different values of m (13 to 25) to experimental data showed that smaller values of m in the model predicted more of the bases that were observed experimentally on a microarray. The model also disagreed with experimental results in that it consistently predicted single N calls in local regions of sequence where all other bases were predicted to produce calls (data not shown). These single disagreements in regions of otherwise good agreement suggested an improvement to modeling accuracy was required. Careful examination of the model found that a large number of these cases were related to the hybridization of different target fragments to two probes within a single set. In order to consistently produce experimental base calls under these circumstances, the interaction of one fragment with the corresponding probe must be much stronger than that of the other fragment–probe pair. The algorithm was modified so that, when two probes of a set hybridized to fragments of length m from the target sequence, additional comparisons were made to provide accurate reflection of the real hybridization event. The optimal value of m to be used as a fixed threshold parameter in the model was still difficult to determine as some base calls in experimental data were due to only 13 contiguous bases matching. It was considered worthwhile to examine available data that allowed a more careful comparison based on thermodynamic parameters.
Short oligonucleotide hybridization to microarrays
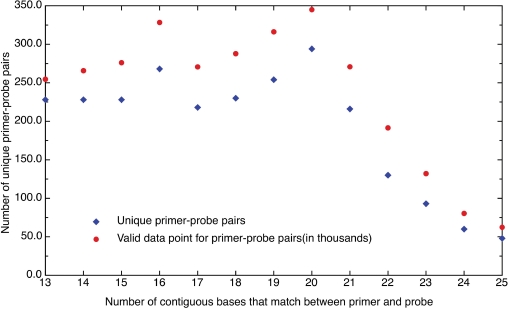
It was possible to study the hybridization and base-calling behavior of a number of fixed length oligomers (16 to 27 bases) from RPM v.1 experiments, which used a multiplex of specific primers for amplification. These primers matched portions of the sequences placed on the microarray, allowing for the study of well-characterized hybridization events in which the oligonucleotide base sequence, length and concentration were known. The data were collected from chips run with two multiplex mixtures, one containing 117 primers (777 experiments) and the other (906 experiments) consisting of 66 primers that were a subset of the 117-primer mixture. Primers that have been incorporated into amplicons were excluded from analysis as they no longer represented well-characterized hybridization events. There were 2495 distinct probe sets on the microarray having 13 to 25 contiguous bases that were a match to one of the primers. Figure 2 shows the number of unique primer-probe matches versus the number of contiguous bases involved in the match. The figure shows that the number of different pairs fell off sharply at the longer lengths and reflected the fact that few variations in base composition were represented. This impacted the averages computed at these lengths and introduced greater uncertainty in how well they represented the average performance of all potential base compositions. Figure 2 also shows the number of data points used from the experiments at each length. These matched closely but not perfectly because some segments from individual experiments were excluded from the analysis due to the incorporation of these primers into amplicons.
Figure 2.
The number of unique primer-probe pairs plotted versus the number of contiguous bases that match between primer and probe (diamond). The figure also shows the number of data points available from experiments for each length (circle). Note that the numbers of data points are in some cases less than the maximum possible due to exclusion of primers that amplified an organism for a particular experiment.
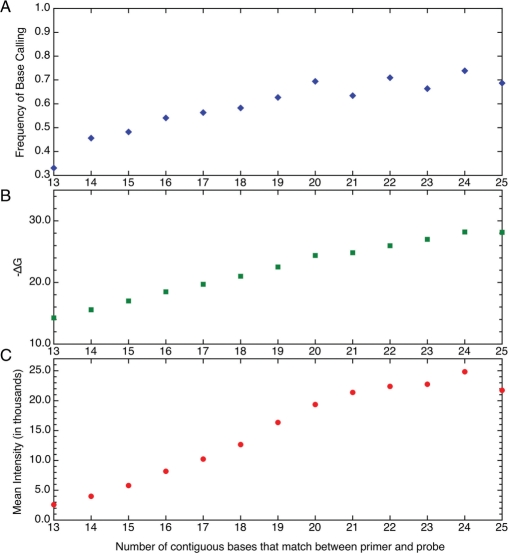
Figure 3A shows the average frequency of an unambiguous base call versus the number of contiguous bases that matched between the primer and probe. The first data point had a frequency of 33% indicating that one time in three a DNA fragment that matched 13 of the 25 bases in a probe was able to bind specifically and strongly enough to generate a unique base call. As the number of contiguous bases that matched between probe and primer increased, an increasing frequency in base calls was observed reaching 50% or more by 16. At the highest numbers of contiguous base matches, the data showed greater variability. The variations were probably due to fewer unique primer-probe matches being represented in the data at these lengths. The difference in base call frequency was largest between 13 and 14 bases. Figure 3B and C show the behavior of ΔG (as calculated by the nn model) (18, 19) and the mean fluorescence intensity versus the number of contiguous bases matching between primer and probe. The rate of increase in base-call frequency correlated much more closely with ΔG than with the mean intensity. Although the correlation with ΔG was strong, it was not perfect. This reflects the impact of other events such as dimer formation and self-looping.
Figure 3.
Shown in Panel (A) is the behavior of the average frequency of resolved base calls as related to the number of contiguous bases that match between primer and probe. The average predicted –ΔG in Panel (B) and the mean fluorescence intensity in Panel (C) are also plotted versus the number of contiguous bases that match between primer and probe.
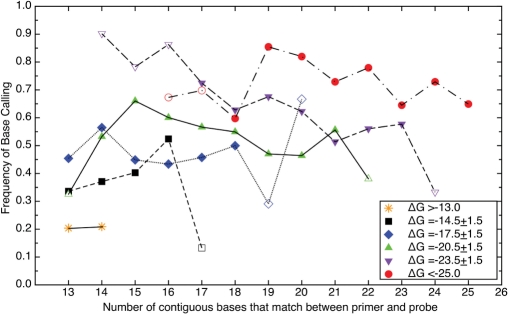
In order to provide a clear picture of the influence of primer composition, Figure 4 presents data from Figure 3A with the primer data regrouped based on ΔG (as calculated by the nn model) (18, 19). Some of these groups had very few samples and may not be representative of the average behavior of a larger sampling of primer-probe pairs (indicated by open rather than filled symbols). A trend was observed in the available data. As ΔG decreased, the frequency of base calls increased irrespective of the number of contiguous bases that matched between primer and probe. The figure also shows that a high base-call frequency was possible for many different numbers of matching contiguous bases between primer and probe (25 bases). Binning the primer-probe matches showed that the frequency of base calls on the array for lengths of 13 and 14 bases with ΔG > –13 kcal/mol was very low. There were, however, other fragments at these lengths that showed significant hybridization. Irrespective of length, primers with ΔG <–16 kcal/mol have, on average, a 50% or greater chance of hybridizing and producing a base call.
Figure 4.
The frequency of resolved base calls from primers plotted versus the number of contiguous bases that match between primer and probe. The data has been grouped based on ΔG as follows: asterisk; ΔG > –13, black square; ΔG = –14.5 ± 1.5, blue diamond; ΔG = –17.5 ± 1.5, green triangle; ΔG = –20.5 ± 1.5, inverted violet triangle; ΔG = –23.5 ± 1.5, red circle; ΔG < –25. Open symbols indicate bin with fewer than 12 000 data points.
Evaluation of the model performance
In order to evaluate the performance of the model, predictions of the model were compared to results for two different cases.
Case 1: predicting primer interference
The first test case looked at base calls in 42 microarray experiments with a blank sample (no nucleic acids added) using a new primer set designed for improved sensitivity and minimized primer interactions with the RPM.v1 microarray. Since the primers were still present, they were treated as a collection of sample sequences and evaluated using the model against every probe in place on the microarray. The model accurately predicted the base calls occurring in the experiments for primers that matched portions of the probes. While some overlap of primer sequences with probes near either the 5′ or 3′ ends of the target region was still expected, both experimental results and modeling predictions agreed on unexpected base calls within interior sequences that were not associated with a given primer. Further investigation revealed that most of these unexpected interior base calls were caused by primers designed for sequences of closely related organisms. For example, the Ad4 E1A gene sequence had 19 of 20 predicted bases called 97% of the time. This sequence was located 393 bases from the beginning of a 1200-base long target sequence (not a primer location). This region matched a primer for the Ad7 E1A gene sequence placed on the microarray. Similar agreement was seen for the other regions predicted by the model.
Case2: model predictions for long sequences
After successful demonstration of model accuracy for short fragments, predictions for entire target sequences were examined. Only samples for which conventional sequencing data and microarray results were available could be considered, as conventional sequencing data was required for model input. Modeling results were compared to microarray results for four data groupings (Table 1): influenza A/H3N2 Fujian-like lineage, influenza A/H3N2 California-like lineage, influenza B Yamagata/16/88 lineage and influenza B Victoria/2/87 lineage. Samples were grouped together based on comparison of their conventional sequencing. These groups allowed base-call frequencies to be computed from single chip experiments using clinical samples. The Fujian-like lineage samples were most similar to the sequence used to generate the probe sets on the microarray (1.3% difference). For these samples, a resolved base call on the microarray always agreed with the conventional sequencing base call. The average differences of the other groupings were larger, increasing from 1.5% in the case of the influenza A/H3N2 California-like lineage samples to 3.7% for the influenza B Yamagata/16/88 lineage samples and, finally, 9.8% for the influenza B Victoria/2/87 lineage samples. These three groups also differed from the Fujian-like lineage samples in that some base identifications made by the microarray disagreed with conventional sequencing. The influenza B samples were evaluated using the same experimental protocol as the influenza A/H3N2 Fujian-like lineage and yielded 1 (Yamagata lineage) and 4 (Victoria lineage) base-call disagreements. These base calls occurred in local regions with a large number of N calls. The model predicted N base calls for these locations.
Table 1.
Summary of average model and experimental microarray results for influenza hemagglutinin gene that could be placed in separate groups based on lineage
| Sample set | Tile | Resolved base calls | Number of SNPs | Number of N calls | |||||
|---|---|---|---|---|---|---|---|---|---|
| Influenza | Array | Model | Conv | Model | Array | Model only | Array only | Model and array | |
| A Fujian-like lineage (12)* | 770 | 85.4 ± 3.6 | 96.7 ± 0.012 | 9.8 1.3% | 9.2 1.2% | 9.2(0)a | 8.8 | 94.9 | 14.6 |
| A California-like lineage (12)* | 770 | 92.2 ± 7.8 | 95.3 ± 0.013 | 11.9 1.5% | 11.6 1.5% | 10.7(1)a | 15.3 | 38.7 | 21.5 |
| B Yamagata lineage (8)* | 660 | 77.5 ± 3.7 | 86.8 ± 0.011 | 24.5 3.7% | 17.6 2.7% | 12.2(1)a | 26.4 | 87.2 | 61 |
| B Victoria Lineage (4)* | 660 | 47.7 ± 3.9 | 51.4 ± 0.007 | 65.2 9.9% | 39.2 5.9% | 31.2(4)a | 70.2 | 94.2 | 251 |
*Numbers in parenthesis are the number of samples used for analysis.
aNumbers in parenthesis are the number of disagreements with respect to conventional results.
In the influenza A/H3N2 Fujian-like samples, the average base-call rate for the experiments was 85% while the model predictions averaged 97%. While the model predicted an average of 9.2 single nucleotide polymorphisms (SNPs) would be resolved for the Fujian-like lineage group, only 6.3 SNPs were observed on average in the experiments. On average 666.4 calls of A, C, G, T or N made in the model and microarray agreed. The discrepancies could be grouped as cases in which the experiments made base calls where the model predicted a call of N, on average 8.8 bases, or cases in which the experiments made N calls and the model made a base call, on average 94.9 bases.
In order to better understand the discrepancy in the number of experimental N calls versus those that were predicted, two types of regions were defined for a specific isolate A/Nepal/1727/2004 (Fujian-like lineage). One type of region selected was near SNPs (within 12 bases on either side) and the other was away from SNPs. This particular isolate has eight SNPs according to conventional sequencing. Base-call rates of 97.4% were obtained for the model and 88.4% for the microarray. Table 2 reports on the base calls made in the regions near SNPs. Two SNPs, location 299 and 596, were not identified on the microarray. These were located near SNPs that were identified. In total, 46 N calls were closely related with near SNP regions while 29 N calls were observed in the regions away from SNP. The later of these were distributed uniformly and were surrounded by resolved base calls. For all Fujian-like lineage samples, a similar rate of isolated base calls in region away from SNPs occurred. The locations appeared to be random and to reflect variations in assay procedure, which the model was not intended to predict. Similar behavior was observed in all of the samples in regions with a large number of base calls.
Table 2.
Location of SNP for influenza A strain compared to sequence (FluAHA3) used to generate microarray probe sets
| Location | Target base | Actual base | N calls in local region (chip) | N calls in local region (model) |
|---|---|---|---|---|
| 299a | G | A | 10 | 1 |
| 313 | G | A | 8 | 1 |
| 352 | A | C | 10 | 8 |
| 393 | A | T | 2 | 3 |
| 483 | G | A | 5 | 0 |
| 593 | G | A | 8 | 3 |
| 596a | T | C | 8 | 3 |
| 698 | C | A | 3 | 4 |
aindicates a base that was not called on the resequencing microarray.
At higher SNP rates (more differences between the sample sequence and the microarray sequence), there were three local regions that could be identified with characteristics not occurring in the Fujian-like lineage samples. Figure 5 shows a section from an influenza B sample that differed on average by 10% and contained examples of these three regions. The first region consisted of long stretches of N calls that were correctly predicted by the model. These corresponded to regions with a local SNP rate that was high enough to disrupt all base-call production. The B regions of Figure 5 represented scattered base calls in a region of predicted N calls. These areas represented local SNP rates slightly higher than one SNP per 25 bases and were also found in sample sets having 4% or more variation. The C region in Figure 5 was similar to region B except that base calls varied more widely between experiment and model. This region was only observed in samples with 10% variation from the sequence on the microarray.
Figure 5.
The sequences for the influenza B strain (FluBHA) used to generate microarray probe sets are shown. Also presented are the conventional sequencing results from an influenza B Victoria lineage sample, the results obtained using the same sample for RPM v.1 microarray analysis, and the model prediction based on the conventional sequence. Region A represents a section sequence where SNPs are very far apart or close together. In this region, the model and microarray data are in good agreement. Region B sequences have SNPs with an intermediate frequency and the agreement between model and experiment is reduced. Region C is similar to B although the number of observed base calls observed is higher.
The model prediction was not consistently accurate across the entire sequence for higher SNP rates, but this is not the measure of accuracy relevant to a predictive model used in resequencing microarray design. Our analysis program for organism identification, CIBSI V2.0, does not utilize all base calls across a sequence but rather only local regions that have a high number of base calls (9). Thus, the test of whether or not the model has adequate accuracy is to use the analysis program for organism identification. If the same correct identification of the organism occurs using experimental- or model-predicted base calls, acceptable accuracy has been obtained. We found that using the experimental results and model predictions as input into the analysis program produced the same identifications in all cases. In general, the analysis program uses the local regions of the sequence that have the fewest SNPs where the model accuracy is high. C-type regions are occasionally employed as well.
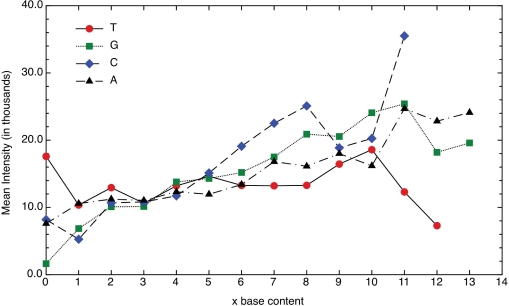
In this study, we found that base calls correlated more strongly with ΔG than with mean fluorescence intensity when probes were grouped based on nucleotide base content. This is contrary to previous work (10). The mean fluorescence intensities of the probes in this study were plotted versus the number of bases (A, G, C or T) in order to provide direct comparison to the previous work. This data confirmed the presence of a different trend for the mean fluorescence intensity versus base content (Figure 6). It was not entirely clear why this different behavior was observed and it was difficult to attribute this to a single reason when many differences exist in the assay methods. One potential cause of the differences was that the primers represent the binding behavior of short fragments (no more than 30 bases) while in real samples the average fragment is closer to 100 bases. However, when binding intensities on probes for influenza samples were examined, the trends with G content were similar to the short oligomer behavior and not that of the previous work (data not shown).
Figure 6.
The mean fluorescence intensity plotted versus the number of bases of a particular type in a primer-probe match T (circle), G (square), C (diamond) and A (triangle). These data do not account for the length of the matching sequence.
DISCUSSION
The examination of a large collection of resequencing microarray probe sets using well-defined short oligomer probes has helped define an in silico model and clearly demonstrated that fragments as short as 13 bases will produce calls when predicted ΔG is sufficiently low. The simple model for predicting hybridization patterns developed in this study shows good agreement with observed experimental results for short oligonucleotide primers. The model also shows good concordance in the overall percentage of base calls predicted versus experimental results in samples that differ from the sequence used on the microarray from 1% to 4%. It has a slightly better agreement when these differences increase to ∼10%. Using overall base-call percentage as an indicator of model performance in this way is misleading. In fact, in certain regions the inaccuracy of the model increased monotonically as the degree of variation increased. These regions are not used in the current analysis scheme and, therefore, do not impact the effectiveness of the model. The accuracy of the model in regions of low SNP rates remains good at any level of variation. The data used for development of this model demonstrates how resequencing microarrays make accurate individual base calls even as the sequence being detected diverges from the sequence used to generate the probe sets. Testing of the primers demonstrated that it is difficult to eliminate all potential cross-hybridization of primers with the probe sets placed on the microarray when considering highly multiplexed systems. Because probe-target hybridization on the microarray can be predicted, however, it is straightforward to accurately predict the cross-hybridization effects and filter out these regions from further analysis.
The shortcoming of the model is the inaccuracies that occur near SNP locations, which limits its use in other applications. This is clearly seen by separating N calls of the Fujian-like lineage sample into different regions. Further confirmation is provided by other sample sets with greater difference from the sequence placed on the microarray. The de novo sequences and base calls made by the microarray clearly suggest that fragments containing mismatches cause base calls that cannot be predicted by the current model. Unfortunately, the influenza samples neither represent a large collection of cases nor can the binding of fragments be considered well characterized. More data must be obtained before attempting to improve the model. The formation of self-loop structures within the probe lengths themselves is a potential source of N calls. This was investigated as a potential refinement to the model, but self-loops did not account for the N calls in these samples. In fact, this modification caused additional N calls to be predicted in locations that were experimentally resolved (data not shown). Self-loop formation in the actual fragments of the sample or template (average length of 100 bases) may also be a cause of inaccuracy. It was not considered in this study because properly modeling long-target interaction with large numbers of overlapping probes is a complex problem that would greatly increase computation time. More detailed thermodynamic modeling may provide insights into these issues.
Given the pathogen of interest and the probe set from a particular sequence, the current model can be used to predict whether sufficient base calls will occur to result in the organism being correctly identified by the analysis program, CIBSI V2.0 (9). This predictive model has the features required to design new multi-organism detection microarrays and to find the optimal number of sequences needed to meet the detection goals of a particular design. Because the algorithm was kept simple the solution is reached rapidly. This leads to considerable savings in the design process. An accurate predictive model is not the only consideration for the design process but, for the sake of brevity, other issues were not discussed in this article. Our current efforts focusing on a design paradigm for resequencing arrays that incorporates this model will be discussed in more detail in a separate manuscript. Also of interest is the improvement of shortcomings in the model that may lead to optimizations in the detection analysis algorithm (CIBSI V2.0). The goal here is either greater sensitivity or reduction in the number of probes required for detection of organisms.
ACKNOWLEDGEMENTS
We greatly appreciate Dr Zheng Wang's assistance in providing access to his conventional sequencing and RPM microarray results on Influenzia A and B samples. We thank Ms Anne Kusterbeck and Dr Brandy White for critically reviewing material presented in this article. The opinions and assertions contained herein are those of the authors and are not to be construed as official or reflecting the views of the Department of Defense or the U.S. Government. Funding for this research and to pay the Open Access publication charges for this article was provided by the Office of Naval Research via the Naval Research Laboratory Base program.
Conflict of interest statement. Work and initial drafts of paper were completed while work on resequencing arrays was funded by government agencies. During later revisions company licensed technologies associated with resequencing array and set of work for high with NRL for tasks concerning resequencing arrays. The work in this paper is not associated with any of that work and had already been completed.
REFERENCES
- 1.Herold KE, Rasooly A. Oligo Design: a computer program for development of probes for oligonucleotide microarrays. Biotechniques. 2003;35:1216–1221. doi: 10.2144/03356bc02. [DOI] [PubMed] [Google Scholar]
- 2.Mehlmann M, Dawson ED, Townsend MB, Smagala JA, Moore CL, Smith CB, Cox NJ, Kuchta RD, Rowlen KL. Robust sequence selection method used to develop the FluChip diagnostic microarray for influenza virus. J. Clin. Microbiol. 2006;44:2857–2862. doi: 10.1128/JCM.00135-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fitch JP, Gardner SN, Kuczmarski TA, Kurtz S, Myers R, Ott LL, Slezak TR, Vitalis EA, Zemla AT, McCready PM. Rapid development of nucleic acid diagnostics. Proc. IEEE. 2002;90:1708–1721. [Google Scholar]
- 4.Cleland CA, White PS, Deshpande A, Wolinsky M, Song J, Nolan JP. Development of rationally designed nucleic acid signatures for microbial pathogens. Expert Rev. Mol. Diagn. 2004;4:303–315. doi: 10.1586/14737159.4.3.303. [DOI] [PubMed] [Google Scholar]
- 5.Gardner SN, Lam MW, Smith JR, Torres CL, Slezak TR. Draft versus finished sequence data for DNA and protein diagnostic signature development. Nucleic Acids Res. 2005;33:5838–5850. doi: 10.1093/nar/gki896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rychlik W, Rhoads RE. A computer program for choosing optimal oligonucleotides for filter hybridization, sequencing and in vitro amplification of DNA. Nucleic Acids Res. 1989;17:8543–8551. doi: 10.1093/nar/17.21.8543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lin B, Wang Z, Vora GJ, Thornton JA, Schnur JM, Thach DC, Blaney KM, Ligler AG, Malanoski AP, Santiago J, et al. Broad-spectrum respiratory tract pathogen identification using resequencing DNA microarrays. Genome Res. 2006;16:527–535. doi: 10.1101/gr.4337206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang Z, Daum LT, Vora GJ, Metzgar D, Walter EA, Canas LC, Malanoski AP, Lin B, Stenger DA. Identifying Influenza Viruses with Resequencing Microarrays. Emerg. Infect. Dis. 2006;12:638–646. doi: 10.3201/eid1204.051441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Malanoski AP, Lin B, Wang Z, Schnur JM, Stenger DA. Automated identification of multiple micro-organisms from resequencing DNA microarrays. Nucleic Acids Res. 2006;34:5300–5311. doi: 10.1093/nar/gkl565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cutler DJ, Zwick ME, Carrasquillo MM, Yohn CT, Tobin KP, Kashuk C, Mathews DJ, Shah NA, Eichler EE, Warrington JA, et al. High-throughput variation detection and genotyping using microarrays. Genome Res. 2001;11:1913–1925. doi: 10.1101/gr.197201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Matveeva OV, Shabalina SA, Nemtsov VA, Tsodikov AD, Gesteland RF, Atkins JF. Thermodynamic calculations and statistical correlations for oligo-probes design. Nucleic Acids Res. 2003;31:4211–4217. doi: 10.1093/nar/gkg476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Held GA, Grinstein G, Tu Y. Modeling of DNA microarray data by using physical properties of hybridization. Proc. Natl Acad. Sci. USA. 2003;100:7575–7580. doi: 10.1073/pnas.0832500100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Naef F, Magnasco MO. Solving the riddle of the bright mismatches: Labeling and effective binding in oligonucleotide arrays. Phys. Rev. E. 2003;68:1–4. doi: 10.1103/PhysRevE.68.011906. [DOI] [PubMed] [Google Scholar]
- 14.Zhang L, Miles MF, Aldape KD. A model of molecular interactions on short oligonucleotide microarrays. Nat. Biotechnol. 2003;21:818–821. doi: 10.1038/nbt836. [DOI] [PubMed] [Google Scholar]
- 15.Wu C, Carta R, Zhang L. Sequence dependence of cross-hybridization on short oligo microarrays. Nucleic Acids Res. 2005;33:e84. doi: 10.1093/nar/gni082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Davignon L, Walter EA, Mueller KM, Barrozo CP, Stenger DA, Lin B. Use of resequencing oligonucleotide microarrays for identification of Streptococcus pyogenes and associated antibiotic resistance determinants. J. Clin. Microbiol. 2005;43:5690–5695. doi: 10.1128/JCM.43.11.5690-5695.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lin B, Blaney KM, Malanoski AP, Ligler AG, Schnur JM, Metzgar D, Russell KL, Stenger DA. Using resequencing microarray as a multiple respiratory pathogen detection assay. J. Clin. Microbiol. 2007;45:443–452. doi: 10.1128/JCM.01870-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.SantaLucia J., Jr A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.SantaLucia J, Jr, Hicks D. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 2004;33:415–440. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]