Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2008 Apr 14;36(10):3185–3193. doi: 10.1093/nar/gkn127

Accuracy and application of the motif expression decomposition method in dissecting transcriptional regulation

Zhihua Zhang 1, Jianzhi Zhang 1,*
PMCID: PMC2425491  PMID: 18411204

Abstract

Understanding transcriptional regulation is a major goal of molecular biology. Motif expression decomposition (MED) was recently introduced to describe the expression level of a gene as the sum of the products of the binding strengths of its cis-regulatory motifs and the activities of the corresponding trans-acting transcription factors (TFs). Here, we use computer simulation to examine the accuracy of MED. We found that although MED accurately rebuilds gene expression levels from decomposed motif binding strengths and TF activities, estimates of motif binding strengths and TF activities are unreliable. Nonetheless, MED provides accurate estimates of relative binding strengths of the same motif in different genes and relative activities of the same TF under different conditions. We found that reasonably accurate results are achievable with genome-wide expression data from only 30 conditions and that MED results are robust to the existence of unknown occurrences of known motifs, although they are less robust to the presence of unknown motifs. With these understandings, judicious use of MED will likely provide useful information about eukaryotic transcriptional regulation. As an example, MED results are used to demonstrate that motifs generally have higher binding strengths when appearing in multiple copies than appearing in one copy per promoter.

INTRODUCTION

Understanding how gene expression is regulated is a major task of molecular biology. Jacob and Monod (1) pioneered the study of transcriptional regulation at the level of interaction between cis-regulatory motifs (or elements) in a gene's promoter region and trans-acting transcription factors (TFs) in the cell. Based on their idea, one may describe the log-transformed expression level of a gene at a given cellular condition by a function of the motifs present in the gene's promoter region and the TF activities present in the condition, as given in Equation (1) in Methods section [see also (2–4)]. The availability of several high-throughput technologies such as gene-expression microarrays and chromatin immunoprecipitation on microarray chips (ChIP-chip), and rapid progress in genomics and computational biology make it possible to study patterns of transcriptional regulation at the genomic scale (5–8). For example, large architectural differences in the yeast regulatory network among different cellular conditions have been identified (7,9). Recently, Nguyen and D’Haeseleer used Jacob and Monod's model to analyze microarray gene expression data obtained from multiple conditions in order to decipher principles of transcriptional regulation (10). Their method, called motif expression decomposition (MED), decomposes a matrix (E) of gene expression levels at multiple conditions into the product of two matrices: the first (M) contains the condition-independent binding strength of each motif (in each promoter) with its corresponding TF, while the second (A) contains the activity of each TF at each condition studied. Some interesting patterns were observed from the analysis of the M matrix. For instance, the same motif with different orientations relative to the transcriptional direction may have different binding strengths, and the same motif with different physical distances from the transcriptional starting site may also have different strengths. Such findings, if correct, are invaluable for understanding the structure, function and evolution of promoters as well as those of transcriptional regulatory networks (11). Nguyen and D’Haeseleer examined the performance of MED by a cross-validation procedure, showing that the product of the decomposed M and A matrices is reasonably well correlated with the microarray gene expression levels. Although this result suggests that the method can be used to predict the expressions of some genes at a given condition when the expressions of many other genes are known at the same condition, it does not necessarily mean that the decomposed M and A matrices are accurate, as the same E may be decomposed into many different combinations of M and A (see subsequently). Because it is the M and A matrices that are of interest to most biologists, we decide to examine whether these matrices decomposed by the MED method are reliable. Because the true values of M and A matrices are unknown for any organism, here we employ a computer simulation approach. Our simulation results show that MED-derived M and A matrices are unreliable. Although this limitation of MED prohibits the direct use of M and A matrices, we find that MED accurately predicts the relative binding strengths of the same motif in different genes and relative activities of the same TF under different conditions. The performance of MED was also examined under limited expression data or partial knowledge of motifs. With improved understanding of MED, we applied MED in yeast to demonstrate at the genomic scale that motifs with >1 copy per motif have significantly higher binding strengths than the same motifs with 1 copy per motif.

METHODS

Generation of gene expression data

Based on Jacob and Monod's model of transcriptional regulation (1), the log-transformed expression level (Egc) of gene g under condition c equals the sum of the products of the binding strength of each motif and the activity of its corresponding TF. That is,

graphic file with name gkn127m1.jpg 1

Here, Ωg is the set of motifs occurring in gene g's promoter region, Mgj is the binding strength of motif j in the promoter of gene g, Ajc is the activity of TF j, which binds to motif j, under condition c. A positive M indicates an enhancer motif, whereas a negative M indicates a repressor motif. Similarly, a positive A means activation, whereas a negative A means suppression. Following Nguyen and D’Haeseleer, we write Equation (1) in a matrix format for all genes, all motifs and all conditions, as

graphic file with name gkn127m2.jpg 2

where E is a m × n matrix that gives m genes’ expression levels at n conditions, M is a m × k matrix that gives the condition-independent binding strengths of k motifs in m genes’ promoter regions and A is a k × n matrix that gives the activities of k TFs under n conditions.

We randomly generate a m × k matrix designated as MO; each element in column i of MO is a random variable drawn from the normal distribution N(bi, σ), where i = 1, 2, 3, …, k, and bi and σ are the mean and standard deviation of the normal distribution, respectively. Each bi is a random variable drawn from the normal distribution N(B, σ). We set Hg, the number of motifs in gene g, by drawing a Poisson random variable with mean equal to 3. We then randomly pick Hg of the k motifs in gene g and leave their corresponding entries in row g of MO unchanged but set zero to all other entries in row g of MO. We further make sure that each row and each column has at least one non-zero entry. If there is a row or column that contains all zeros, we randomly choose an entry and reverse the value to that in the original MO. The matrix generated after these steps is referred to as M. We randomly generate a k × n matrix designated as A. The elements in the ith row of A are random variables drawn from the normal distribution N(Ci, ϕ), where i = 1, 2, 3, …, k, and Ci is a random variable drawn from the normal distribution N(C, ϕ). We then generate gene expression data E using Equation (2). Because gene expression has stochastic variations (12) and because measurement of gene expression has errors, the observed gene expression level will differ from the above computed E. Hence, we add an error term to each expression value. For entry Eij, the error is a random variable drawn from N(0, ϵEij), where ϵ is the noise level fixed in each simulation. We have used ϵ = 0, 5, 10, 20, 30, 40, 50, and 100% in different simulations. After this step, the E matrix is referred to as the observed or true expressions. MED requires an initial M matrix designated as MI to start the decomposition. We generate MI by replacing all non-zero entries in M to 1. Unless otherwise stated, this MI is used in our simulations. As will be described later, in some occasions, we also used an MI where each non-zero entry is −1 and an MI where each non-zero entry is either 1 or −1, with equal probabilities.

Simulation

Because Nguyen and D’Haeseleer's study focused on the yeast Saccharomyces cerevisiae, we use parameters appropriate for yeast in our simulation. Using the approach outlined in the above section, we randomly generate expression data for 4500 genes under 300 conditions. The total number of TFs in the organism is set to be 100. In the dataset analyzed by Nguyen and D’Haeseleer, there were expression data from 5719 genes under 255 conditions and the total number of TFs was 62. Using the MED method (10), we decompose the expression data (matrix E) into M′ and A′ matrices and then compute E′ using E′ = M′·A′. We then compare E′ with E, M′ with M and A′ with A, as they represent the MED-derived matrices and the true matrices, respectively. At each noise level, we repeat the simulation 10 times. This number of replications is sufficient because our results are highly reproducible.

RESULTS

Performance in predicting expression levels

Using computer simulation as described in Methods section, we generated motif binding strength (M) and TF activity (A) matrices for 4500 genes under 300 conditions, including information for 100 different TFs and their corresponding motifs. We first used B = 2.5 and σ = 10 in generating the M matrix and used C = 0 and ϕ = 10 in generating A. Our B and σ values are similar to the M matrix decomposed from the yeast expression data (10). Our C and ϕ are different from the decomposed values in (10), because MED has a normalization step that artificially equalizes the average activity of each TF such that the actual TF activities cannot be seen from the decomposed A in (10). Nonetheless, even when we use C = 0 and ϕ = 0.1, similar to those observed from the decomposed A in (10), our results remain unchanged.

We then generated the gene expression matrix E by multiplying M and A matrices followed by addition of different levels of expression noise. The E matrix was decomposed into M′ and A′ matrices using the MED method. We conducted a total of 10 simulation replications. Because the results are essentially identical among the replicates, subsequently we describe our findings from the first replication.

There are three expectations if the MED method performs well. First, predicted gene expressions (E′, or the product of M′ and A′) should be close to the observed expressions (E). Second, predicted motif binding strengths (M′) should be close to their true values (M). Third, predicted TF activities (A′) should be close to their true values (A). To measure the agreement between predicted and true values of expression levels, we computed Pearson's correlation coefficient (r) between E and E′ for each gene (row), and then computed the average r value across the 4500 genes and the standard deviation of r. Similarly, to measure the agreement between predicted and true values of motif binding strengths and TF activities, we computed r between M and M′ for each motif (column) and r between A and A′ for each TF (row), and then take averages across all motifs and all TFs, respectively.

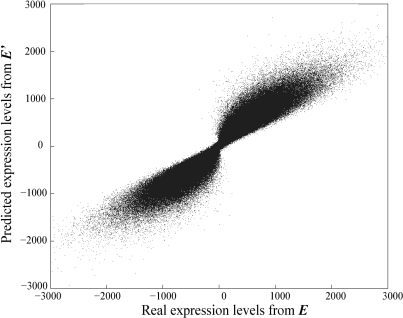
As shown in Table 1, r between E and E′ gradually declines as the noise level rises. Nonetheless, r > 0.80 even when the noise is as high as 50% of the true value and is greater than 0.90 when the noise level is <30%. These results suggest that expression levels predicted by MED are reliable. Indeed, for individual genes under individual conditions, Figure 1 shows that the predicted expression levels match the true values for the majority of genes under the majority of conditions. Figure 1 is based on the simulation results with a noise level of 30%. Qualitatively similar patterns were obtained when different levels of noise (5–100%) were introduced.

Table 1.

Pearson's correlation coefficients (± standard deviation) between the true values and MED-predicted values of expression levels (E), motif binding strengths (M) and TF activities (A)

Noise level (%) E M M ratio (within-column)a M ratio (between-column)b A A ratio (within-row)c A ratio (between-row)d
0 1.000 ± 0.000 0.120 ± 0.997 0.998 0.289 0.120 ± 0.997 0.996 −0.044
5 0.997 ± 0.001 0.179 ± 0.988 0.986 −0.028 0.179 ± 0.988 0.992 0.200
10 0.991 ± 0.005 0.119 ± 0.997 0.988 0.101 0.119 ± 0.997 0.964 0.020
20 0.962 ± 0.026 0.119 ± 0.996 0.942 0.004 0.119 ± 0.995 0.930 0.048
30 0.929 ± 0.036 0.199 ± 0.981 0.904 0.081 0.199 ± 0.981 0.862 −0.045
40 0.872 ± 0.063 0.059 ± 0.997 0.848 −0.028 0.059 ± 0.995 0.771 0.103
50 0.834 ± 0.067 0.178 ± 0.979 0.812 −0.031 0.179 ± 0.977 0.714 0.110
100 0.606 ± 0.099 0.300 ± 0.890 0.587 0.064 0.303 ± 0.893 0.435 0.170
Open in a new tab

Note: The simulated expression data are from 300 conditions.

aRelative binding strengths of the same motif in two genes.

bRelative binding strengths of two different motifs.

cRelative activities of the same TF under two different conditions.

dRelative activities of two different TFs.

Figure 1.

Figure 1.

Open in a new tab

Comparison between the true (E) and MED-predicted (E′) gene expression levels. The noise level is 30%. Note that the expression levels are log-transformed and thus can be negative.

Performance in predicting motif binding strengths and TF activities

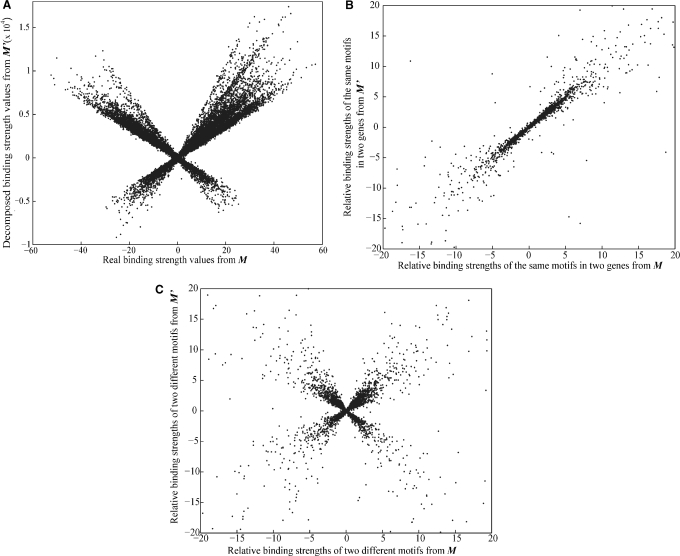
To our disappointment, however, the r values between M and M′ matrices are low (<0.3) regardless of the level of noise (Table 1). Figure 2A shows that the motif binding strength values in M and M′ are dramatically different. Similarly, the r values between A and A′ matrices are low (Table 1) and the TF activity values in A and A′ are quite different (Supplementary Figure S1A). These observations suggest that although E′ is close to E, M′ is not close to M and A′ is not close to A. It is easy to show that if M and A form one solution, multiplying column i of M′ by a and row i of A′ by 1/a (a ≠ 0) generates another solution. Because a can be 1, −1 or any non-zero number, there are infinite numbers of decomposition solutions. The original proof of the uniqueness of the MED decomposition solution was based on the arbitrary assumption that each TF has a mean activity of 1 across all conditions (i.e., the mean of each row in the A′ matrix is fixed at 1) (10). Although there is only one decomposition solution under this arbitrary assumption, the solution is not guaranteed to be the right one. In fact, our simulations showed that it is generally not the right solution. Nonetheless, our above consideration predicts that the ratio of any two entries within the same column (motif) of M′ can still be close to the corresponding ratio in M, while the ratio of any two entries from different columns of M′ should not correlate with the corresponding ratio in M. Similar predictions can be made for rows (TFs) of A and A′. These predictions were indeed confirmed in our simulations. That is, between M and M′, within-column ratios are highly correlated, whereas between-column ratios are not (Table 1; Figure 2B and C). In parallel, between A and A′, within-row ratios are highly correlated, whereas between-row ratios are not (Table 1; Supplementary Figure S1B and C). Note that in this article, we measured Pearson's correlation between true and predicted ratios by using only ratios falling in the range of [−20, 20], which account for >95% of all ratios. This treatment is preferred over the use of all ratios because of the existence of a small number of ratios with extreme values, which affects the measure of Pearson's correlation coefficient. Similar results were obtained when all ratios were considered in Spearman's rank correlation.

Figure 2.

Figure 2.

Open in a new tab

Comparison between true (M) and MED-predicted (M′) motif binding strengths. The noise level is 30%. (A) The scatter plot for true and predicted motif binding strengths. Note the difference in scale between X-axis and Y-axis. (B) True and predicted relative binding strengths of the same motifs in different genes. (C) True and predicted relative binding strengths of pairs of different motifs.

As stated earlier, if M′ and A′ form one solution, multiplying column i of M′ by a and row i of A′ by 1/a (a ≠ 0) generates another solution. Because a can be either positive or negative, it is expected that the r between a column in M and its corresponding column in M′ should be close to 1 or −1 when the noise level is low. This is indeed the case. For example, in the simulation with 30% noise, between M and M′, 60% of columns have r > 0.98, while 40% of columns have r lower than −0.98 (same for rows between A and A′). This is why we observed low average r values and high standard deviations for both motif biding strengths and TF activities (Table 1).

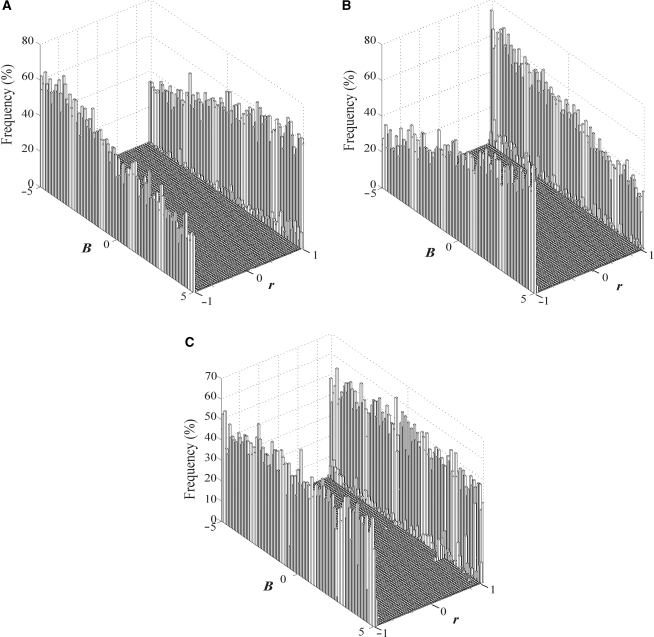
Because MED only supplies one of infinite numbers of solutions of M′ and A′, which particular solution does it provide? This question is equivalent to asking what a values MED uses. We found that the initial matrix (MI) used to start the decomposition process affects a. We conducted three sets of simulations, each containing 50 individual simulations. In the first set of 50 simulations, we started with an MI where every non-zero entry was set to be 1, as used by the original authors of MED (10). The M matrix was generated with parameter B changing from −5 to 5 in a step size of 0.2 in the 50 simulations. The A matrix was generated as usual. In the second set of 50 simulations, we started with an MI where every non-zero entry was set to be −1. In the third set of 50 simulations, we started with a MI where every non-zero entry was randomly set to be either 1 or −1, with equal probabilities. Figure 3A–C shows the distributions of Pearson's correlation coefficients between columns of M and M′ for all the simulations in the three sets, respectively. They clearly show that the entries in M′ tend to have the same sign as in MI. For example, when B is positive and most entries in M are positive, use of the MI with positive entries tends to give more positive r values (Figure 3A) than use of the MI with negative entries (Figure 3B). Similar patterns are observed in A (Supplementary Figure S2).

Figure 3.

Figure 3.

Open in a new tab

The distribution of Pearson's correlation coefficient between columns (motifs) of M and M′, when all non-zero entries in MI are (A) 1, (B) −1, and (C) randomly assigned to be either 1 or −1, with equal probabilities. B is the mean motif binding strength in M.

Combining all the simulation results, we now have a better understanding of MED. The MED algorithm is designed in such a way that only one of infinite numbers of solutions is provided and this solution depends on the initial values used in decomposition. Knowing this property, it becomes clear that the MED-decomposed binding strengths for a given motif (across genes) are not true strengths, but are expected to be true strengths multiplied by an unknown number. Furthermore, this unknown number can be different for different motifs. The relative binding strengths of the same motif in different genes can be reliably estimated by MED. However, MED cannot distinguish between enhancers and repressors, neither can it distinguish between activation and suppression TF activities. Moreover, MED-predicted binding strengths cannot be compared among different motifs, and MED-predicted TF activities cannot be compared among different TFs.

Robustness of MED

MED relies on the input of gene expression data and cis-motif information. It is important to examine the influences of these factors on the performance of MED. In the above simulations, we simulated expression data from 4500 genes at 300 conditions. A practical question is how large the expression data have to be for MED to produce reliable values of E′, M′ and A′. We do not reduce the gene number because most eukaryotes have >4500 genes. Rather, we reduce the number of conditions from 300 to 100 and 30, respectively, with the rationale that the cost for generating expression data can be significantly reduced if 100 or even 30 conditions are sufficient for predicting motif bind strengths and TF activities. Table 2 gives the results for 30 and 100 conditions, in comparison with 300 conditions. One can see that the reliability of the MED method in rebuilding E′ is not reduced when fewer conditions are used. But, for predicting relative binding strengths and TF activities, use of fewer conditions worsens the MED performance. However, if the noise level is <10%, use of 30 conditions can still provide reasonably good predictions (Table 2).

Table 2.

Pearson's correlation coefficients between true values and MED-predicted values of expression levels (E), relative motif binding strengths (M) and relative TF activities (A), when the expression data are obtained from 300, 100 and 30 conditions, respectively

Noise level (%) E M ratio (within-column)a A ratio (within-row)b
300 conditions 100 conditions 30 conditions 300 conditions 100 conditions 30 conditions 300 conditions 100 conditions 30 conditions
0 1.000 ± 0.000 0.997 ± 0.004 1.000 ± 0.000 0.998 0.993 0.976 0.996 0.998 0.996
5 0.997 ± 0.001 0.997 ± 0.001 0.998 ± 0.001 0.986 0.989 0.946 0.992 0.987 0.993
10 0.991 ± 0.005 0.990 ± 0.006 0.989 ± 0.009 0.988 0.933 0.867 0.964 0.956 0.976
20 0.962 ± 0.026 0.964 ± 0.025 0.967 ± 0.027 0.942 0.845 0.699 0.930 0.906 0.916
30 0.929 ± 0.036 0.930 ± 0.037 0.934 ± 0.049 0.904 0.840 0.586 0.862 0.873 0.818
40 0.872 ± 0.063 0.880 ± 0.061 0.887 ± 0.076 0.848 0.760 0.579 0.771 0.798 0.744
50 0.834 ± 0.067 0.833 ± 0.078 0.841 ± 0.098 0.812 0.611 0.404 0.714 0.680 0.623
100 0.606 ± 0.099 0.595 ± 0.125 0.652 ± 0.164 0.587 0.361 0.224 0.435 0.359 0.314
Open in a new tab

aRelative binding strengths of the same motif in two genes.

bRelative activities of the same TF under two different conditions.

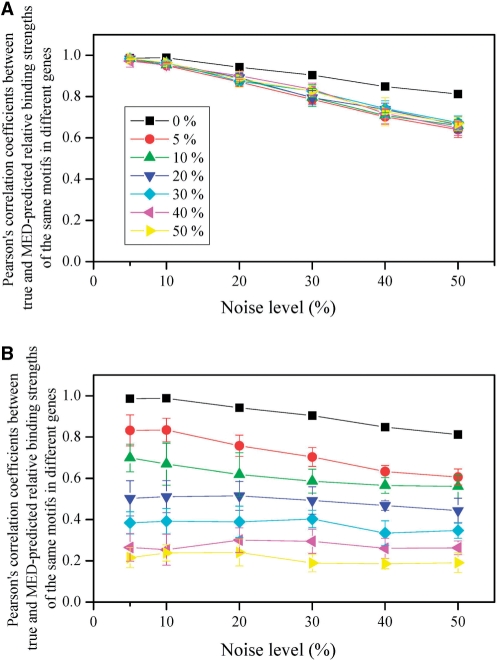
Detection of TF-binding sites is a much studied topic in the past decade (13–16). However, not all cis-regulatory motifs can be detected by current methods (13). We examined the accuracy of MED in two situations when some motifs in the genome are undetected. In the first situation, for a given TF, a fraction of its corresponding cis-motifs in the genome are assumed to be undetected. In the simulation, we fixed a random set of non-zero entries in MI at 0. We repeated the simulation 10 times, as in each replication a different set of non-zero entries from the same MI were fixed at 0. We examined r between M and M′ for relative binding strengths of the same motif in two genes. Note that presumably undetected motifs were not considered in computing r. We assumed that 0, 5, 10, 20, 30, 40 and 50% of motifs are undetected in seven sets of simulations, respectively. The results show that undetected motifs slightly worsen the performance of MED in predicting relative motif binding strengths (Figure 4A). The same is true for the relative TF activities (Supplementary Figure S3A).

Figure 4.

Figure 4.

Open in a new tab

Performance of the MED method in predicting relative motif binding strength when some motifs in the genome are undetected. The mean correlation coefficient from 10 simulations and the associated standard deviation are presented for each condition examined. In (A), a fraction of motifs (from 0% to 50%) for each TF are undetected in the genome. In (B), all motifs of a fraction of TFs (from 0% to 50%) are undetected in the genome. Different colors show different fractions.

In the second situation, we assumed that for most TFs, all of their corresponding motifs are known, while for the rest of the TFs, none of their motifs are known. In the simulation, we fixed all the entries of a random set of columns in MI at 0. We repeated the simulation 10 times, as in each replication a different set of columns from the same MI were fixed at 0. We examined r between M and M′ for relative binding strengths of the same motif in two genes. Again, presumably undetected motifs were not considered in computing r. We also assumed that 0, 5, 10, 20, 30, 40 and 50% of motifs are undetected in seven sets of simulations, respectively. The results show that this type of ignorance of motifs has a great impact on the prediction of relative motif binding strengths (Figure 4B). The same is true for the relative TF activities (Supplementary Figure S3B). Nonetheless, the predictions are not too bad (mean r > 0.65) when motifs corresponding to up to 10% of TFs are completely unknown and the noise level is not >30%.

An application of MED

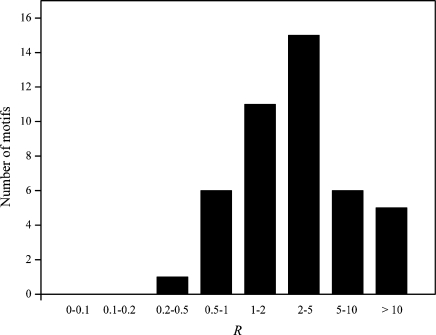
After knowing what MED can do and cannot do, we decided to use MED to address an important question in gene regulation. It is frequently observed in eukaryotic promoters that a motif appears with multiple tandem copies (6). Although it has been frequently assumed that a motif with multiple copies in a promoter has stronger binding strength than the same motif with only one copy (2,17), whether this assumption is valid at the genomic scale has not been empirically tested. This question is ideal for MED to tackle, because it only requires the mean binding strength of a given motif in one set of genes, relative to that in another set of genes. Using the same yeast dataset used by Nguyen and D’Haeseleer (10), we separated the genes into two groups for each motif. The first group includes genes that each has only one copy of this motif, whereas the second group includes genes that each has multiple copies of the motif. Of the 62 motifs that can be separated into two groups, we found 18 motifs for which the average binding strengths for the two groups have opposite signs (i.e. one is positive and other is negative). These inconsistent results are likely due to MED errors and thus are removed. For each of the remaining 44 motifs, we calculated the ratio (R) between the average binding strength of the second group and that of the first group. We then tested the null hypothesis that R = 1, against the alternative hypothesis that R > 1. We found that the average R of the 44 motifs is 4.517 ± 0.897, significantly greater than 0 (P < 10−5; t-test; Figure 5). Furthermore, 37 motifs, significantly more than half of the 44 motifs, have R > 1 (P = 3 × 10−6; binomial test; Figure 5). These results indicate that motifs with multiple copies in promoters generally have greater binding strengths than the same motifs with single copies (Figure 5).

Figure 5.

Figure 5.

Open in a new tab

Frequency distribution of the ratio (R) between the mean binding strength of a motif in promoters where it has multiple copies to the mean binding strength of the same motif in promoters where it has one copy. The distribution is from 44 different motifs in yeast.

DISCUSSION

The exponential growth of available functional genomic data opens the possibility to understand biological processes at the genomic and systems levels (6,18,19). One major advance in this endeavor is the development of methods for identifying cis-regulatory motifs in promoters of all genes in a genome. Using genome-wide microarray gene expression data and motif information, Nguyen and D’Haeseleer invented the MED method, which decomposes the gene expression data into motif binding strength data and TF activity data (10). The knowledge of binding strengths and TF activities can be used to decipher principles of transcriptional regulation. Thus, it is important to know how well MED performs. In this work, we conducted computer simulations to evaluate the MED method. Our results showed that at realistic levels of noise, which includes both expression stochasticity and microarray errors, MED-predicted gene expression levels are highly reliable. This result is not unexpected, as MED decomposes E into M′ and A′, which are then used to rebuild E′.

For both binding strengths and TF activities, however, MED cannot provide accurate predictions. Furthermore, MED cannot differentiate between enhancer and repressor motifs and cannot differentiate between activation and suppression TF activities. MED results cannot be used to compare binding strengths among different motifs and compare activities among different TFs. Nevertheless, the relative binding strengths of the same motif in different genes and the relative activities of the same TF under different conditions can be estimated with fairly high accuracy. If we have external information that a motif is an enhancer or repressor or that a TF activity under a given condition is activation or suppression (relative to the control condition), such information can be combined with MED results to provide better predictions. We note that relative binding strengths of the same motif in different genes and relative activities of the same TF under different conditions can provide much information that is valuable to our understanding of principles of transcriptional regulation. One such example is the comparison between binding strengths of the same motif when it has one copy per promoter versus multiple copies per promoter. Using MED results, we demonstrated that for the majority of motifs (84%), the binding strength is greater when a motif appears in multiple copies than when it appears in one copy. This may explain why many motifs have multiple copies in a promoter. However, we caution that this result was based on an analysis of motifs corresponding to only 62 TFs, about a third of all TFs in yeast. Because our simulation showed that MED is not robust to the ignorance of all motifs of even 10% of TFs in the genome, the validity of our result should be further examined when larger data become available.

An encouraging finding from our simulations is that at realistic levels of noise, MED requires expression data from as few as 30 conditions to provide reasonably accurate predictions of relative motif binding strengths and relative TF activities. Thus, even a small lab may be able to generate sufficient data for a genome-wide estimation of motif binding strengths in a non-model organism. Another encouraging finding is that even when some motifs (e.g. 20%) in the genome are undetected, MED can still make reasonable good predictions, as long as the majority of motifs are detected for each TF. When all motifs of some TFs are unknown, MED will have much reduced accuracy. Thus, from the perspective of MED performance, it is more important to identify most motifs for each TF than to identify all motifs for some TFs.

It should be noted, however, that the simulation results presented here were based on a number of simplified assumptions that warrant discussion. First, we assumed a simple logic of transcriptional regulation as described by Equation (1) in Methods section. If this assumption is violated, MED predictions will be less accurate. One potentially important violation is interaction between motifs or interaction between TFs, which have been observed (20,21). Second, epigenetic factors are known to affect gene expression differently for different genes under different conditions (22). Third, we assumed a relatively simple form of expression stochasticity and microarray noise. If expression errors are much larger and/or more complex, MED predictions may be less accurate. We believe that a better understanding of the molecular mechanisms of gene expression regulation will assist the development of more powerful computational tools, which in turn help further understand gene expression regulation.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

[Supplementary Data]
gkn127_index.html (950B, html)

ACKNOWLEDGEMENTS

We thank Meg Bakewell and Ben-Yang Liao for valuable comments. This work was supported by research grants from National Institutes of Health and University of Michigan Center for Computational Medicine and Biology to J.Z. Funding to pay the Open Access publication charges for this article was provided by National Institutes of Health.

Conflict of interest statement. None declared.

REFERENCES

  • 1.Jacob F, Monod J. Genetic regulatory mechanisms in the synthesis of proteins. J. Mol. Biol. 1961;3:318–356. doi: 10.1016/s0022-2836(61)80072-7. [DOI] [PubMed] [Google Scholar]
  • 2.Bussemaker HJ, Li H, Siggia ED. Regulatory element detection using correlation with expression. Nat. Genet. 2001;27:167–171. doi: 10.1038/84792. [DOI] [PubMed] [Google Scholar]
  • 3.Liao JC, Boscolo R, Yang YL, Tran LM, Sabatti C, Roychowdhury VP. Network component analysis: reconstruction of regulatory signals in biological systems. Proc. Natl Acad. Sci. USA. 2003;100:15522–15527. doi: 10.1073/pnas.2136632100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Tran LM, Brynildsen MP, Kao KC, Suen JK, Liao JC. gNCA: a framework for determining transcription factor activity based on transcriptome: identifiability and numerical implementation. Metab. Eng. 2005;7:128–141. doi: 10.1016/j.ymben.2004.12.001. [DOI] [PubMed] [Google Scholar]
  • 5.Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, et al. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002;298:799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
  • 6.Harbison CT, Gordon DB, Lee TI, Rinaldi NJ, Macisaac KD, Danford TW, Hannett NM, Tagne JB, Reynolds DB, Yoo J, et al. Transcriptional regulatory code of a eukaryotic genome. Nature. 2004;431:99–104. doi: 10.1038/nature02800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Luscombe NM, Babu MM, Yu H, Snyder M, Teichmann SA, Gerstein M. Genomic analysis of regulatory network dynamics reveals large topological changes. Nature. 2004;431:308–312. doi: 10.1038/nature02782. [DOI] [PubMed] [Google Scholar]
  • 8.MacIsaac K, Wang T, Gordon DB, Gifford D, Stormo G, Fraenkel E. An improved map of conserved regulatory sites for Saccharomyces cerevisiae. BMC Bioinformatics. 2006;7:113. doi: 10.1186/1471-2105-7-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Zhang Z, Liu C, Skogerbø G, Zhu X, Lu H, Chen L, Shi B, Zhang Y, Wang J, Wu T, et al. Dynamic changes in subgraph preference profiles of crucial transcription factors. PLoS Comput. Biol. 2006;2:e47. doi: 10.1371/journal.pcbi.0020047. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Nguyen DH, D’Haeseleer P. Deciphering principles of transcription regulation in eukaryotic genomes. Mol. Syst. Biol. 2006;2 doi: 10.1038/msb4100054. 2006.0012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Bussemaker HJ. Modeling gene expression control using Omes Law. Mol. Syst. Biol. 2006;2 doi: 10.1038/msb4100055. 2006.0013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Elowitz MB, Levine AJ, Siggia ED, Swain PS. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
  • 13.Tompa M, Li N, Bailey TL, Church GM, De Moor B, Eskin E, Favorov AV, Frith MC, Fu Y, Kent WJ, et al. Assessing computational tools for the discovery of transcription factor binding sites. Nat. Biotech. 2005;23:137–144. doi: 10.1038/nbt1053. [DOI] [PubMed] [Google Scholar]
  • 14.Elnitski L, Jin VX, Farnham PJ, Jones SJ. Locating mammalian transcription factor binding sites: a survey of computational and experimental techniques. Genome Res. 2006;16:1455–1464. doi: 10.1101/gr.4140006. [DOI] [PubMed] [Google Scholar]
  • 15.Kim SY, Kim Y. Genome-wide prediction of transcriptional regulatory elements of human promoters using gene expression and promoter analysis data. BMC Bioinformatics. 2006;7:330. doi: 10.1186/1471-2105-7-330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Maston GA, Evans SK, Green MR. Transcriptional regulatory elements in the human genome. Annu. Rev. Genomics Hum. Genet. 2006;7:29–59. doi: 10.1146/annurev.genom.7.080505.115623. [DOI] [PubMed] [Google Scholar]
  • 17.van Helden J, Andre B, Collado-Vides J. Extracting regulatory sites from the upstream region of yeast genes by computational analysis of oligonucleotide frequencies. J. Mol. Biol. 1998;281:827–842. doi: 10.1006/jmbi.1998.1947. [DOI] [PubMed] [Google Scholar]
  • 18.Ideker T, Galitski T, Hood L. A new approach to decoding life: systems biology. Annu. Rev. Genomics Hum. Genet. 2001;2:343–372. doi: 10.1146/annurev.genom.2.1.343. [DOI] [PubMed] [Google Scholar]
  • 19.Brazma A, Krestyaninova M, Sarkans U. Standards for systems biology. Nat. Rev. Genet. 2006;7:593–605. doi: 10.1038/nrg1922. [DOI] [PubMed] [Google Scholar]
  • 20.Bulyk ML, Johnson PLF, Church GM. Nucleotides of transcription factor binding sites exert interdependent effects on the binding affinities of transcription factors. Nucleic Acids Res. 2002;30:1255–1261. doi: 10.1093/nar/30.5.1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Bulyk ML, McGuire AM, Masuda N, Church GM. A motif co-occurrence approach for genome-wide prediction of transcription-factor-binding sites in Escherichia coli. Genome Res. 2004;14:201–208. doi: 10.1101/gr.1448004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Allis CD, Jenuwein T, Reinberg D. 1st edn. Cold Spring Harbor, New York: Cold Spring Harbor Laboratory Press; 2007. Epigenetics. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplementary Data]
gkn127_index.html (950B, html)
gkn127_1.pdf (155.3KB, pdf)
gkn127_nar-00054-s-2008-File007.jpg (1.1MB, jpg)
gkn127_nar-00054-s-2008-File008.jpg (1.8MB, jpg)

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES