Comparing Proteins by Their Unfolding Pattern

Abstract

Single molecule force spectroscopy has evolved into an important and extremely powerful technique for investigating the folding potentials of biomolecules. Mechanical tension is applied to individual molecules, and the subsequent, often stepwise unfolding is recorded in force extension traces. However, because the energy barriers of the folding potentials are often close to the thermal energy, both the extensions and the forces at which these barriers are overcome are subject to marked fluctuations. Therefore, force extension traces are an inadequate representation despite widespread use particularly when large populations of proteins need to be compared and analyzed. We show in this article that contour length, which is independent of fluctuations and alterable experimental parameters, is a more appropriate variable than extension. By transforming force extension traces into contour length space, histograms are obtained that directly represent the energy barriers. In contrast to force extension traces, such barrier position histograms can be averaged to investigate details of the unfolding potential. The cross-superposition of barrier position histograms allows us to detect and visualize the order of unfolding events. We show with this approach that in contrast to the sequential unfolding of bacteriorhodopsin, two main steps in the unfolding of the enzyme titin kinase are independent of each other. The potential of this new method for accurate and automated analysis of force spectroscopy data and for novel automated screening techniques is shown with bacteriorhodopsin and with protein constructs containing GFP and titin kinase.

INTRODUCTION

Biomolecules like DNA, RNA, or proteins are polymers that self-assemble into a more or less compact form. The function of these molecules is determined by their structure and dynamics. Because the folding potential determines both structure and dynamics, it is a central research goal to investigate the energy landscape of biomolecules to understand their function. However, biomolecules are individuals. Different populations and states cannot be distinguished by ensemble experiments. The resulting average makes detailed insight into the underlying mechanisms difficult. Therefore, it is essential to investigate biomolecules on a single molecule level.

Molecular processes of biological relevance are adapted to energies close to the thermal energy kT. Thermal excitations drive the dynamics of processes and cause fluctuations. Therefore, it is a common goal to compare experimental data from individual biomolecules, which are subjected to large fluctuations. In this article, we describe a solution for single molecule force spectroscopy.

In mechanical single molecule experiments, the barriers of the energy landscape are determined by means of force extension traces. The force extension traces are obtained by measuring the force and the distance of a probe, which contacts the biomolecule and is retracted during one cycle of an experiment. Realizations of this technique are the atomic force microscope (AFM) (1) and optical (2,3), or magnetic tweezers (4). In the beginning of a retraction cycle, the unfolded part of the molecule is stretched. As illustrated in Fig. 1, its elastic response causes a rise in force with increasing extension. Many models have been developed to describe this force extension behavior. The most prominent ones are the worm-like chain (WLC), the freely jointed chain (FJC), the freely rotating chain (FRC), and modifications that take into account the backbone elasticity at high forces.

FIGURE 1.

Transformation of force spectroscopy data from extension space into contour length space. The left side illustrates an AFM experiment. During retraction of the cantilever, the force and the extension are recorded. In the beginning, the unfolded part of the molecule is stretched and the force increases until the energy barrier is overcome by thermal fluctuations. Further stretching results again in a rise of force (dark gray). The rupture force and position differs from trace to trace due to fluctuations and may change on altered experimental conditions. The transformation of each data point from extension to contour length space and the accumulation in a histogram is shown on the right side. The representation with respect to this molecular coordinate does not exhibit the variances of the extension, but directly characterizes the energy barriers of the folding potential. Details that are lost by fitting, are still conserved with this approach.

Several models were developed that describe how the energy barriers of the folding potential are overcome under an external force. For our purposes here we can stick to the simplest picture: because the force increases continuously with increasing extension, the energy landscape gets tilted more and more until the barrier is overcome by thermal fluctuations. Both the force and extension at which this occurs are therefore subject to fluctuations and depend on the timescale of the experiment, and specifically, on the loading rate (5,6). This is illustrated by means of the distributions on the left side of Fig. 1. The new folding state of the molecule is associated with a sudden increase in the contour length. As a consequence, the force drops and the elastic response of the completely unfolded part of the molecule is observed on further extension (Fig. 1, dark gray).

Because the rupture forces can be determined directly from force extension traces, we focus on the positions of energy barriers. Until now, the positions were determined by fitting such force extension traces with models for polymer elasticity. However, extension is an inappropriate variable for the characterization of molecular energy landscapes as it depends on fluctuations, external experimental parameters such as the loading rate, as temperature (7), properties of the solution and other changes that result in a different bond strength (8,9). Therefore, we perform a variable transformation from extension to contour length. The contour length is an appropriate variable, because it is independent of fluctuations and mutable external parameters and directly reflects the folding state of the molecule (right side of Fig. 1). With known monomer length, this new coordinate can be scaled to the number of polymer units to localize the energy barriers.

Besides its physical meaning, this new representation of force spectroscopy data has other advantages, as well. Although contour length histograms directly reflect energy barriers, they are also independent of fluctuations and external experimental parameters. Their height fluctuations and all of the details along the unfolding pathway are preserved with high resolution. This allows the comparison of different traces, the automated recognition of a specific molecular pattern, and a reasonable averaging of traces.

MATERIALS AND METHODS

Sample preparation and AFM measurements

All measurements, except the ones concerning bacteriorhodopsin (BR), were carried out with a home built AFM and with Olympus biolevers B (Bio-lever, Olympus, Tokyo, Japan), which have a spring constant ranging from 5 to 6 pN/nm. In the first example, we show unfolding traces of an Ig-GFP protein construct. It consists of four Ig-domains at the N-terminus of GFP (Ig27–Ig30) and four other Ig-domains at its C-terminus (Ig31–34) as well as a mutant of O⁶-alkylguanine-DNA-alkyltransferase (hAGT):

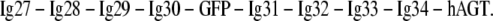hAGT can be used for the covalent immobilization of benzylguanine. However, the data shown in this article is recorded with unspecifically adsorbed proteins. Therefore, the unfolding of hAGT might be observed in some traces. A detailed description of the protein construct can be found in reference (10). The protein solution was incubated for 20 min on a glass substrate with freshly evaporated gold surface at a concentration of ∼1 mg/ml. After washing with PBS, the cantilevers were calibrated using the equipartition theorem (11), and the automated recording of force extension traces was started with a pulling speed of 1 μm/s.

The unfolding of the enzyme titin kinase was studied through a protein construct that was expressed in Escherichia coli and that consists of two Ig-domains and one fibronectin domain on the N-terminus of the titin kinase followed by two Ig domains at its C-terminus (kindly provided by Gereon Franzen and Mathias Gautel, King's College London):

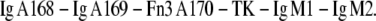The protein solution was incubated for 20 min on a glass substrate with freshly evaporated gold surface and washed with PBS.

As shown in Rief et al. (12), the mechanical properties of Fn domains are very similar to the ones of Ig-domains. Because the Fn domains serve only as spacer that provide a characteristic fingerprint, these domains will not be distinguished from Ig-domains.

The third data set shows the unfolding of BR. The sample preparation, data recording, and the interpretation of force extension traces are published elsewhere (13). Membranes of purple bacteria were immobilized on mica and imaged with a multimode AFM (Nanoscope IIIa, Digital Instruments, Santa Barbara, CA) and a cantilever with a spring constant of 90 pN/nm (OMCL TR400PS,Olympus). After identification of the membrane orientation, individual BR proteins were unfolded from the cytoplasmic side of the membrane.

Models for polymer elasticity and their transformation functions

Several models have been developed to describe the elastic response of unfolded biopolymers in force extension traces. Solving these relations for contour length, the transformation function is obtained with which the transformation from the extension space to the contour length space is carried out. In the following, we explain this principle more mathematically and give examples of models, where the transformation functions were deduced.

The function describing the force extension behavior is denoted F(x,L,..). The force F depends on the extension x, on the contour length L and on other parameters that are fixed. The aim of our new method is to transform each data point from extension space [F_i,x_i] into contour length space [F_i,L_i]. Using the correct restrictions L,x,F > 0, x < L, all models for polymer elasticity are one-to-one mappings. This means that only one defined force value F_i exists for a given point [x_i,L_i]. Therefore the model can be solved for the desired parameter L. With the obtained function L(F,x,..) each data point can be transformed into contour length space: [F_i,x_i] → [F_i,L_i(F_i,x_i)].

One of the most common models is the worm-like chain model (WLC) introduced by Bustamante et al. (14)

(1)

In a first approximation, the persistence length p is fixed. Solving this model for the contour length L results in the transformation function L_WLC(F,x).

However, it has been shown that the persistence length has to be adjusted to different force regimes (12). Therefore, modifications to this model like the QM-WLC (15) have been developed that account for the backbone elasticity of the polymer and allow for a more accurate fit in the high force regime. The result of the quantum mechanical ab initio calculation was approximated by the polynomial representation (2)

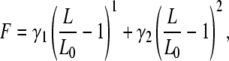(2)

and the elastic parameters of this expansion were determined. For peptides it was found that γ₁ = 27.4 nN and γ₂ = 109.8 nN. To take into account the force dependency of the contour length, the transformation is done in two steps. First, the data is transformed with the WLC model, L_WLC(F,x). In the second step, the force-independent contour length at zero force is determined by solving the expansion (2) for L₀ and inserting L_WLC and F: L₀ = L₀(L_WLC, F) .

Finally, the freely rotating chain model (FRC) considers bonds of length b, which are connected by fixed angles γ. However, the torsional angles are not restricted. A detailed discussion of the stretching behavior is given in (16), which can be summarized as follows.

In the infinite-chain limit, the Kuhn length a is given by 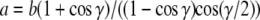and the persistence length p of the FRC equals The force extension behavior exhibits three different scaling ranges and is given by

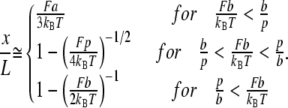(3)

Again, the transformation function is obtained by solving for L.

Once a force-extension trace is transformed into a force-contour length trace, all points above the noise level are accumulated in an area-normalized contour length histogram referred to as barrier position histogram.

RESULTS AND DISCUSSION

In this section, we apply the transformation method to several proteins. Although not all examples have a mechanical function in nature, the identification of energy barriers in the contour length histograms allows for conclusions about the energy landscape. The pathway through the folding potential (i.e., the order of unfolding events) can be determined and visualized by means of the cross-superposition of contour length histograms.

The positions of energy barriers in the contour length histograms are independent of fluctuations and external experimental parameters. Therefore, contour length histograms can be averaged, which is not the case for force extension traces. In addition, this approach makes it possible to detect characteristic unfolding patterns. The implementation in a pattern recognition algorithm could enable new force spectroscopy screening techniques.

Transformation of Ig-GFP unfolding traces with the WLC model

In the first example, we analyze the unfolding of an Ig-GFP protein construct by means of its contour length histogram. A typical force extension trace is shown in Fig. 2 a. The regular saw-tooth pattern at high extensions is caused by Ig-domains (marked in dark gray) and serves as a fingerprint for the selection of relevant traces. Because the protein construct consists of four Ig-domains on the N-terminus of the GFP and four on its C-terminus, each unfolding trace that shows more than four Ig-domains must contain the unfolding of GFP (Fig. 2 a). The initial peak is presumably due to the unfolding of hAGT.

FIGURE 2.

Transformation of force spectroscopy data into barrier position histograms. (a) Force extension trace of the Ig-GFP protein construct. Cleary visible is the sawtooth pattern caused by unfolding of hAGT, GFP, and IG-domains. (b) Transformed trace. The transformation of each point was done with the WLC model and a persistence length of 0.4 nm. (c) Barrier position histogram. All points above the noise level of 10 pN were accumulated in a area-normalized histogram with a bin width of 1 nm. The coordinate of this representation is independent of fluctuations, and the energy barriers can be directly determined.

Fig. 2 b shows the transformation of the force extension trace with the WLC model using a persistence length of 0.4 nm. At low forces, the thermal excitation of the cantilever causes significant noise in the contour length space. Therefore, only points with forces above a threshold of 10 pN were collected in the contour length histogram (Fig. 2 c). The contour length coordinate does not depend on fluctuations or variable experimental parameters, but it directly reflects the molecular folding states and its energy barriers. This histogram in which the barrier position is measured along the unfolded part of the protein, will therefore be referred to as the barrier position histogram.

The first two barriers in Fig. 2 c presumably correspond to the unfolding of hAGT. Once the rupture of the first GFP β-sheet occurs, the protein is no longer stable, and the unfolded portion contributes to the total contour length (the intermediate steps reported in Dietz et al. (17) were not resolved in this study). Therefore, all points recorded after bond rupture appear at a new contour length position that is characteristic for the new folding state of the protein. The same holds true for the unfolding of the Ig-domains. After each rupture, the protein construct is in a new folding state and each point appears at the corresponding contour length. For the GFP unfolding, we measure a peak-to-peak distance of 77 ± 0.5 nm that agrees with the finding of a contour length increment of 76.6 nm in reference (17). Each Ig-domain unfolding shows an increase in contour length of 29 ± 0.5 nm, which is again in agreement with other studies (18).

Comparison of different models: WLC, QM-WLC, and FRC

We now compare different models for polymer elasticity with respect to the quality of barrier position histograms. The standard WLC-model does not account for backbone elasticity at high forces. Therefore, an ab initio based modification (QM-WLC) was introduced in Hugel et al. (15), which describes the elasticity above 200 pN better. As a third model, we use the FRC model that treats molecules as bonds of fixed length b, which are connected by fixed angles γ but at arbitrary torsional angles (16).

These three models are compared in Fig. 3. The part of a force extension trace in Fig. 3 a is transformed, and it is shown in Fig. 3 b that the peaks of the QM-WLC model are higher and slightly narrower than the ones obtained by the standard WLC (p = 0.4 nm in both cases). This indicates that the QM-WLC describes the data more accurately. However, the best result is achieved with the FRC model (γ = 22°, b = 0.4 nm). The full width at half maximum (FWHM) of the different models is compared in Table 1. Fig. 3 c shows the section of a trace with forces up to 600 pN. At these high forces, the WLC model is no longer able to resolve small intermediate steps. In contrast, both the QM-WLC and the FRC models resolve the two folding states, which are separated by 5 nm.

FIGURE 3.

Comparison of different models for polymer elasticity. (a) Fraction of a force extension trace. (b) Three energy barrier histograms obtained by transforming trace (a) with the WLC model (p = 0.4 nm), the QM-WLC model and the FRC model (γ = 22°, b = 0.4 nm). The best result is achieved with the FRC, which produces the highest and sharpest peaks (compare Table 1). (c) Fraction of a force extension trace showing a small step at high forces. (d) Three energy barrier histograms of trace (c) with the same parameters as in (b). In contrast to the WLC, the QM-WLC and FRC models are able to resolve the small substep of 5 nm at 500 pN.

TABLE 1.

Comparison of different transformation models

Peak number	1	2
FWHM: WLC	4.7 nm	4.0 nm
FWHM: QM-WLC	3.8 nm	3.2 nm
FWHM: FRC	2.3 nm	2.4 nm

These results show that sharp peaks and a high resolution are achieved in barrier position histograms using an appropriate model and suitable parameters for the transformation.

Averaging in contour length space preserves information

Small energy barriers of the unfolding potential are not resolved in each trace. To extract these details, several traces are necessary. However, the dependency of the rupture position on fluctuations prevents reasonable averaging of force extension traces. Therefore, traces were in the past usually superpositioned.

In the following, we show that barrier position histograms can be averaged due to the independence of fluctuations. The matter under investigation is the well-studied membrane protein BR. Because the data has already been published (13), it represents a suitable model system. In Fig. 4 a, 13 traces of BR, unfolded from the cytoplasmic side of the membrane, are superpositioned. As mentioned above, averaging is not possible in this representation because the coordinate is subjected to fluctuations.

FIGURE 4.

Averaging of barrier position histograms. (a) Superposition of 13 BR force extension traces. (b) The transformation into contour length space was accomplished with the WLC model and a persistence length of 0.4 nm. (c) The averaged barrier position histogram is obtained by averaging each peak of the 13 barrier position histograms. The threshold force was set to 60 pN and the bin width amounts to 0.36 nm.

The transformation into contour length space was done with the WLC model and a persistence length of 0.4 nm (Fig. 4 b). Because of the high spring constant of the cantilevers (90 pN/nm), the force threshold for the barrier position histograms was set to 60 pN. The averaged barrier position histogram shown in Fig. 4 c was obtained by averaging each corresponding peak of the 13 barrier position histograms. By using a Gaussian fit, the precise positions of energy barriers were determined. A comparison of these values to those obtained by the force extension traces fit with the WLC model is shown in Table 2. The mean deviation equals 0.3 nm, and the maximum deviation of 1 nm is still within the error of the WLC fit.

TABLE 2.

Barrier positions in the unfolding potential of BR determined by barrier position histograms and WLC fits to force extension traces

Histogram (±1 nm)	16.2	20.6	33.6	36.3	39.4	41.3	54.7	59.2	62.9	63.5	78.7	81.3	84.9
WLC fit (±1 nm)	16.2	20.0	33.6	36.1	39.4	40.7	54.9	59.0	62.6	64.5	79.2	81.6	85.1

Other averaging methods or ensemble experiments are susceptible to fluctuations, which would obscure information about the unfolding potential. Averaging in contour length space by contrast preserves the details of the energy landscape due to the fluctuation independence of the individual traces in this representation.

Comparing unfolding pathways of bacteriorhodopsin and titin kinase

Barrier position histograms show the barriers of the molecular energy landscape. Because of its high dimensionality, several pathways between two given states may exist, which allow for conclusions about the architecture of a protein.

The experimental determination and visualization of unfolding pathways can be achieved by means of the cross-superposition of 2D barrier position histograms. First, the n entries h1_i, i = 1…n, of the first histogram h1 are assigned to the n columns of each row of a n × n matrix M1: M1_ki = h1_i, k,i = 1…n. Graphically represented, the energy barriers appear as stripes. The second n × n matrix M2 is created by assigning the n entries h2_i of the second histogram h2 to the n rows of each column of M2: M2_ki = h2_k, k,i = 1…n. In the graphical representation the stripes are rotated by 90°. Addition of the two matrices results in the n × n superposition matrix S, S = M1 + M2. In this pattern, each part of the first histogram interferes with each part of the second one. The reason why we use the sum of the matrices, reflecting the probability of occurrence of either of two events, in contrast to multiplication, reflecting the occurrence of both events, is ascribed to the clearer signal. As shown by the examples below, matching squares, corresponding to matching unfolding events, can be directly identified. Graphically represented, multiplication would result in points from which the same information could be reconstructed, however, it cannot be as easily seen as in the case of summation.

Fig. 5 shows two cross-superpositions of four different histograms that are obtained from BR force extension traces. The way to read the pattern is the following: first the smallest squares, formed by matching contour length increments, are determined. If subsequent squares are aligned in the diagonal with positive slope, they occur in the same order in both traces. If the diagonal has negative slope, the order is permutated. This is also the case for squares that consist of multiple small squares. In the cross-superposition of Fig. 5 a, the matching parts of the two histograms are colored. For a better overview, several of the smaller substeps are combined. Those unfolding events with squares that are aligned along the diagonal with positive slope occur in the same order. If not all energy barriers are resolved in each trace, the cross-superposition pattern cannot be filled with smallest squares. This case is shown in Fig. 5 b. The unfolding steps, which are marked in blue, fit and have the same size and sequence as in Fig. 5 a. But because there is a step, which is not visible in histogram 4, the two corresponding steps of histogram 3 must be combined to obtain the smallest square that fits. The smallest square is marked in green and is again aligned along the diagonal with positive slope.

FIGURE 5.

Cross-superposition of four BR barrier position histograms. (a) Both histograms show the same energy barriers. The smallest squares are aligned along the diagonal with positive slope indicating that the order of unfolding events is identical. The same holds true for b. However, histogram 4 lacks one energy barrier. Therefore the squares that are marked in green must be combined to determine the smallest matching steps.

The 13 traces indicate that BR always unfolds along the same pathway. This observation supports the common notion that during the unfolding process one helix after the other is pulled out of the membrane (13,19,20).

The unfolding behavior of the Ig-titin kinase protein construct (Ig-TK) is different from that of BR. To corroborate the notion that the enzyme titin kinase acts as a force sensor in muscles (21,22), it is essential to study its mechanical properties. However, we will not give a detailed interpretation of the unfolding traces here, and an explanation of their physiological meaning would go beyond the scope of this article, as well. The unfolding traces from the protein construct shall only serve as an example for protein unfolding, which does not always occur in the same sequence. Because the titin kinase is flanked by three spacer domains on the N-terminus and two domains on the C-terminus, each trace showing the unfolding of more than three domains contains the unfolding of the titin kinase.

Fig. 6 shows the cross-superpositions of barrier position histograms that are obtained by transforming the force extension traces with the QM-WLC model (p = 0.6 nm). The four even increments of ∼29 nm, which are marked in yellow, are due to the unfolding of four Ig/Fn-domains. Because the folded protein construct is contacted at random positions, the initial part of a histogram may exhibit the rupture of Ig-domain fragments in addition to unspecific interactions. This part can be separated from the TK unfolding by choosing the rupture of the first Ig-domain as the point of reference. A search backward for matching increments results in the colored squares that have a contour length of 124 ± 2 nm in total. In Fig. 6 a, the squares corresponding to the different unfolded segments of the titin kinase are marked in violet, red, green, and blue. Again, small substeps are combined for clarity. Because these squares are aligned along the diagonal with positive slope, the enzyme chose the same unfolding pathway in both traces. The cross-superposition of Fig. 6 b shows the same increments between the titin kinase energy barriers. However, the green and red squares are aligned along the diagonal with negative slope, indicating that their order is switched. Although this is a rare case, it shows that these two unfolding events do not depend on each other completely and that different unfolding pathways exit. The combination of these two states into a larger square shows the same sequence as in Fig. 6 a. As this is the case in all traces, the last energy barrier depends strongly on the proceeding ones.

FIGURE 6.

Cross-superposition of Ig-TK barrier position histograms. The even increments of ∼29 nm, which are located in the upper right corner, are due to Ig/Fn domain unfolding (yellow). Segments between the major barriers of the titin kinase are marked in blue, green, and red. In a the segments are aligned along the diagonal with positive slope. This indicates that the order of unfolding events is the same in both traces. The titin kinase in contrast takes two different unfolding pathways in b. Because the two segments, marked in green and red, are aligned along the diagonal with negative slope, their order is changed.

These examples show that by means of the cross-superposition of barrier position histograms, unfolding pathways can be determined and visualized. The special dependencies among the different energy barriers provide new and otherwise unobtainable insight into the architecture of a molecule.

In the last part of this article, we describe how the transformation into barrier position histograms can be implemented in a powerful pattern recognition algorithm.

Pattern recognition with barrier position histograms

Single molecule force spectroscopy experiments pose the challenge of discriminating between impurities or nonspecific interactions and selecting only those traces that exclusively stem from the molecule under investigation. Although the concentration of adsorbed molecules must be low enough to observe individual molecules, each approach of the cantilever to the surface will not results in contact with the molecule of interest. This is especially true in the case where molecules are unspecifically attached to the surface and tip: the rate of yield can be in the 1/1000 range. In addition, force extension traces showing adsorption of other molecules (e.g., impurities) must be filtered out. The use of protein constructs, fusion proteins and protein polymers makes the selection easier, because their regular unfolding pattern results in better contrast. However, the automatic detection of these patterns (23,24) is difficult because both the extension and the force of an unfolding pattern differ from trace to trace due to fluctuations. Variances of experimental parameters such as pulling speed, temperature, solution properties, or changes that result in different bond strengths have even greater impact. This is not the case if the force extension traces are transformed into the contour length space with the transformation method introduced in this article. As the contour length is a molecular coordinate, which is independent of force and only reflects the folding state of the molecule, the barrier position histograms of different traces can be directly compared, even if experimental parameters are altered.

We developed force spectroscopy data analysis software (IgorPro 5.0, Wavemetrics, Lake Oswego, OR) that includes a pattern recognition algorithm based on barrier position histograms. The currently implemented models for polymer elasticity, with which the transformation is carried out, are the WLC, QM-WLC, two-state FJC, and FRC models. The software can be used to identify and filter traces showing a particular pattern. In these traces, energy barriers are automatically detected and the relevant parameters of peaks such as contour length, rupture force and loading rate can be determined and stored. It can also be used to screen traces for a specific molecule in a multi component sample.

We show the performance of this method by applying it to a data set of 1000 force extension traces of the Ig-GFP construct. In this case, the regular pattern caused by Ig-domain unfolding is detected by means of the autocorrelation function of the barrier position histogram (Fig. 7 a). Our algorithm attributes to each trace an evaluation value that considers the level of the autocorrelation function at a certain contour length as well as the sharpness of a possible peak at this position. To prefer traces with several Ig-domains, the process is repeated for the double contour length. We chose 29 nm for this parameter, but it can be adjusted for each regular pattern. The trace shown in Fig. 7 a exhibits seven contour length increments of ∼29 nm and high, sharp peaks in its autocorrelation (Fig. 7 b). Using the formula given in the Appendix, it is evaluated with a quality factor of +8.7. In contrast to this, the trace in Fig. 7 e, which shows the unfolding of BR, does not exhibit increments of 29 nm and therefore it has a low autocorrelation at this value (quality factor −1.1). In this way, the algorithm can identify traces with special properties and select the relevant traces for further analysis.

FIGURE 7.

Pattern recognition and screening for different single molecule compounds based on barrier position histograms. (a) Barrier position histogram of Ig-GFP. The even 29 nm spacings of the Ig-domain unfolding cause peaks in the autocorrelation function (b) at 29 nm and at integer multiples. The evaluation procedure of a trace takes into account the correlation at 29 nm and 58 nm as well as the sharpness of the peaks and yields a value of +8.7 (for details see Appendix). In this manner, a set of data can be filtered for relevant traces. To compare two different traces, the cross correlation of the corresponding barrier position histograms can be calculated. The result with the Ig-TK trace (c) and another Ig-TK trace (not shown) is diagramed in d and exhibits a correlation of 87%. In contrast, the correlation function in f of the traces of the two different molecules Ig-TK (c) and BR (e) only shows a correlation of 37%. In this way, traces of a multi-component sample could be classified and attributed to the corresponding molecules.

Besides this very useful application, the transformation of force extension traces into barrier position histograms also allows for the comparison of different traces. By calculating the correlation function of two histograms, the maximum degree of correlation can be determined. If the two traces correspond to the same molecule, then their barrier position histograms exhibit a similar pattern, which results in a high degree of correlation. This is shown in Fig. 7 d by means of two Ig-TK traces. The maximum degree of correlation from these two traces is 87%. In the other case, where two traces correspond to different molecules, the correlation is expected to be lower, as shown in Fig. 7 f. The maximum degree of correlation between the histogram of BR and of the Ig-tk construct equals 37%.

In this manner, a data set containing different types of traces can be classified. It is even imaginable to screen a sample with unknown composition with respect to a known molecular unfolding pattern.

CONCLUSIONS

In this article, we introduced a new method for representing and analyzing force spectroscopy data. By transforming force extension traces into contour length space, histograms can be created that reflect the folding barriers of a molecule. The new molecular coordinate is independent of fluctuations and varying external parameters. Energy barriers can be directly determined, and details along the unfolding pathway are conserved. Different unfolding pathways can be determined and visualized from the cross-superposition barrier position histograms. In contrast to BR, which is known to always exhibit the same order of unfolding events, we found that sequences of unfolding steps in titin kinase follow a more complex pattern.

The implementation of this method in a pattern recognition algorithm enables the automated identification of traces with characteristic features. Different traces can be compared and classified allowing for the examination of a multi component sample or a sample with unknown composition. This technique may become a very useful tool for research and enable new approaches for screening techniques.

APPENDIX: EVALUATION OF ENERGY BARRIER HISTOGRAMS

The aim is to filter contour length histograms that exhibit several peaks with even spacing l_max. First, the evaluation algorithm finds the maximum in the autocorrelation function a(l) in the interval [l_max − w/2, l_max + w/2] with width w. In the second step, the relative height of the maximum is determined by averaging on both sides of the maximum l_max in the interval [l_max − 3/2w, l_max − 1/2w] and [l_max + 1/2w, l_max + 3/2w] respectively:

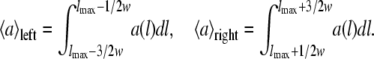The evaluation value v is obtained by the following equation:

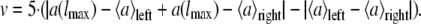This procedure is done for l and 2l and the obtained values are added.