Lateral Pressure Dependence of the Phospholipid Transmembrane Diffusion Rate in Planar-Supported Lipid Bilayers

Abstract

The dependence of 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) flip-flop kinetics on the lateral membrane pressure in a phospholipid bilayer was investigated by sum-frequency vibrational spectroscopy. Planar-supported lipid bilayers were prepared on fused silica supports using the Langmuir-Blodgett/Langmuir-Schaeffer technique, which allows precise control over the lateral surface pressure and packing density of the membrane. The lipid bilayer deposition pressure was varied from 28 to 42 mN/m. The kinetics of lipid flip-flop in these membranes was measured by sum-frequency vibrational spectroscopy at 37°C. An order-of-magnitude difference in the rate constant for lipid translocation (10.9 × 10⁻⁴ s⁻¹ to 1.03 × 10⁻⁴ s⁻¹) was measured for membranes prepared at 28 mN/m and 42 mN/m, respectively. This change in rate results from only a 7.4% change in the packing density of the lipids in the bilayer. From the observed kinetics, the area of activation for native phospholipid flip-flop in a protein-free DPPC planar-supported lipid bilayer was determined to be 73 ± 12 Ų/molecule at 37°C. Significance of the observed activation area and potential future applications of the technique to the study of phospholipid flip-flop are discussed.

INTRODUCTION

The study of phospholipid membrane dynamics is central to the understanding of cellular function and regulation. In particular, the process of transmembrane migration of lipids, also referred to as flip-flop, is critical to the functioning of the cell. For instance, the flip-flop of phospholipids has been implicated with cell apoptosis, and the externalization of certain phospholipids via transmembrane migration is a known mechanism of intercellular signaling (1,2). Perhaps more importantly, it is known that phospholipid flip-flop must occur within cellular membranes to support uniform growth, as phospholipid synthesis is known to occur only on the cytosolic side of the membrane (3). Additionally, flip-flop is essential for the maintenance of phospholipid asymmetry in cellular membranes (4,5).

In recent years, there have been a plethora of studies aimed at measuring phospholipid flip-flop kinetics and thermodynamics by fluorescence, electron-spin resonance (ESR), nuclear magnetic resonance, and lipid extraction studies (3–12), yet there has been little progress toward developing an understanding of the mechanistic pathways for the transbilayer migration of lipid species. Most studies have assumed a protein-dependent flipping mechanism, and relatively few studies have focused on the intrinsic flip-flop of pure phospholipids since the pioneering study by Kornberg and McConnell (6). Additionally, the bulk of these studies have made use of chemically modified lipids, which have been shown to exhibit altered kinetics and thermodynamics relative to native lipid species (6–8,13). A more complete thermodynamic analysis of native lipid translocation is an important step toward the elucidation of the mechanism for lipid flip-flop. Our work aims to address some of the fundamental questions regarding the transbilayer migration of lipids in membranes (3,15). In this article, we present an investigation of the lateral pressure-dependent kinetics and thermodynamics of native lipid flip-flop using sum-frequency vibrational spectroscopy (SFVS), which allows for the direct study of membrane lipid asymmetry using only the native lipid species without the need for exogenous fluorescent or spin-labeled probes.

An examination of available literature regarding phospholipid flip-flop yields numerous examples of temperature-dependent kinetic studies, with occasional thermodynamic analysis following Arrhenius activation theory (6,13,16). At present, only one of these studies provides Arrhenius parameters for unlabeled lipid species (13). The vast majority of lipid flip-flop kinetics studies have employed solution phase vesicles as the model membrane system (4,6–11). To our knowledge, there has been no data presented to date which addresses the lateral pressure dependence of the flip-flop process. This is due, in part, to the difficulty of controlling lateral surface pressure when using vesicles as model membranes. In vesicles, the final pressure or packing density of the film cannot be controlled during sample preparation. In fact, spherical membranes in solution are in a tension free state due to their geometry, and the effective internal lateral pressure cannot be directly measured (17,18). The inability to control the lateral pressure in vesicles has limited the study of lateral pressure-dependent flip-flop kinetics in model membrane systems. This is in contrast to monolayer systems or bilayers prepared by the Langmuir-Blodgett (LB), or Langmuir-Schaefer (LS) deposition methods, where the lateral pressure can be precisely controlled (17,18). Studies of the effects of lateral pressure and packing density on the dynamics of LB/LS membrane models make possible a more meaningful comparison between the various model systems and in vivo biological membranes (19,20). The combined use of SFVS and planar-supported lipid bilayer (PSLB) membranes, prepared by the LB and LS methods, allows for the first direct study of flip-flop kinetics in PSLBs as a function of lateral surface pressure.

THEORY

Langmuir-Blodgett/Langmuir-Schaeffer deposition

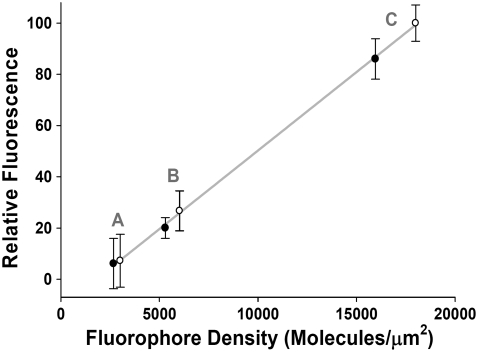
PSLBs have been chosen as a model for the study of membrane asymmetry and lipid flip-flop. In contrast to liposomal models, PSLBs have the advantage that there is (in effect) an infinite radius of curvature, which reduces the forces experienced in liposomal assays and represents more closely in vivo cellular membranes. It should be noted that large unilamellar vesicles also satisfy this requirement; however, there are no methods for creating asymmetric distribution of native lipid species in these systems. One concern often raised when using PSLBs in membrane studies is the influence of the substrate on membrane properties. Fluorescence recovery after photobleaching and fluorescent correlation studies have shown that membrane fluidity in the upper and lower leaflets of PSLBs on a silica surface are identical, within error (21,22), suggesting that there is no strong coupling of the bilayer to the substrate. In addition, the efficacy of these model membrane systems has been well established by a number of researchers (23–33). PSLBs are typically prepared by two distinct methods, either by the Langmuir-Blodgett (LB)/Langmuir-Schaeffer (LS) technique(23,32,34,35) or vesicle spreading (33,35–38). Vesicle spreading utilizes solution-phase liposomes which are fused to a solid support, typically a glass or fused silica substrate, forming a uniform bilayer-coated surface. Vesicle fusion, by itself, does not allow for control over the composition of the bilayer with regard to lipid packing density or the composition of lipids in the two leaflets of the bilayer. In contrast to vesicle fusion, LB methods can be used to prepare bilayer assemblies with a great amount of control over the lipid composition and structural arrangement of the bilayer. This deposition method involves spreading a monolayer of lipid at the air-water interface of a LB trough and compressing the film to the desired surface pressure. A substrate is then slowly withdrawn from the water subphase through the air/water interface, transferring a monolayer of lipids onto the substrate (LB deposition). Throughout the deposition process, the surface pressure is maintained via feedback between a Wilhelmy plate film balance and the trough barriers. An example of the control afforded by the LB method is illustrated in Fig. 1, where 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) monolayers containing either 0.12, 0.23, or 0.69 mol % of 1-palmitoyl-2-[12-[(7-nitro-2-1,3-benzoxadiazol-4-yl)amino]dodecanoyl]-sn-glycero-3-phosphocholine (NBD-DPPC) were prepared at lateral surface pressures of 20 and 40 mN/m. The fluorescence intensity for each sample was obtained using a model No. BX4 microscope (Olympus, Melville, NY) with a 10× objective using epi-illumination and collection. Fig. 1 shows the measured fluorescence intensity for the six samples examined. A linear correlation between the surface density of the NBD-DPPC probe, as measured from the LB trough, and the measured fluorescence intensity is observed for all concentrations of NBD-DPPC prepared at both 20 mN/m and 40 mN/m. These results indicate that the surface density of lipids at the air/water interface is conserved upon transfer to the solid support. Fig. 1 also nicely demonstrates the precise control of film packing density and lipid composition which is afforded by the LB method. Our findings are in agreement with previous quantitative radiolabeling measurements which established that the amount of material deposited on the substrate was equal to the surface coverage at the air-water interface before LB transfer (39). The control of lipid-packing density is not possible by any current liposomal bilayer preparation techniques.

FIGURE 1.

Relative fluorescence intensity for DPPC monolayers containing either 0.12 (A), 0.23 (B), or 0.69 mol % (C) of an NBD labeled analog. For each concentration, samples were prepared at 20 mN/m (solid circles) and 40 mN/m (open circles), with the observed intensities shown as a function of calculated fluorophore surface density (see Fig. 3 for surface density/pressure data).

To measure the kinetics of flip-flop as a function of lateral pressure, the combined LB/LS method of bilayer preparation is used (40). An LB monolayer is prepared as described above, after which a second monolayer of different composition can then be prepared at the air/water interface and transferred to the substrate by pushing the substrate into the subphase in a horizontal orientation (LS deposition). This method of bilayer preparation has the distinct advantage of directly controlling the lateral surface pressure and packing density of the lipid film throughout the formation of the lipid bilayer, as illustrated above. The composition of each leaflet of the bilayer is also readily manipulated by employing the LB/LS method of bilayer formation. Vesicle fusion methods require either chemical or physical modification of the lipid population in the two leaflets of the membrane after bilayer formation to produce an asymmetric distribution of lipids in the bilayer. The LB/LS method may be used to directly form asymmetric bilayers without the requirement of chemical or physical modification. Such planar bilayers with asymmetric composition are readily investigated by SFVS (13,41).

Sum-frequency vibrational spectroscopy

SFVS was used in this study to investigate the kinetics of phospholipid flip-flop in model membrane films. SFVS is a coherent second-order nonlinear optical spectroscopy, with the chemical selectivity of infrared (IR) and Raman spectroscopy and is inherently surface-specific in nature (42). Because of its inherent surface specificity, SFVS provides a means of investigating the composition of the membrane without the requirement of using soluble probe molecules or chemically modified lipids. A number of excellent sources are available for a detailed review of SFVS theory (42,43). Briefly, SFVS involves spatially and temporally overlapping a visible laser source with a tunable infrared laser source at the sample of interest, yielding photons at the sum of the two input frequencies (Eq. 1),

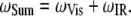(1)

The SFVS intensity depends on the square of the geometric Fresnel coefficients for the sum-frequency 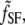and input visible and IR beams f_vis and f_IR, respectively, which describe the local electric field intensities at the interface, and the second-order nonlinear susceptibility tensor χ(2), which describes the response of the system to the input electric fields:

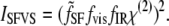(2)

The nonlinear susceptibility has both a resonant and a nonresonant contribution, 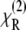and 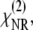respectively,

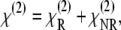(3)

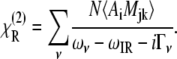(4)

The resonant contribution (Eq. 4) describes the interaction of the tunable input IR field with the molecules that comprise the interface, and clearly shows the dependence of the SFVS process on both the IR (A_i) and Raman transition probabilities (M_jk), where N is the number of molecules, ω_v is the frequency of the vibrational transition, ω_IR is the input IR frequency, and Γ_v is the linewidth for the transition. The bra and ket notation in Eq. 4 denote the ensemble average over all possible orientations. A SFVS spectrum is obtained by scanning the input IR frequency ω_IR. An increase in SFVS signal will be observed for the resonant vibrational frequencies (ω_ν) of the molecules comprising the interface.

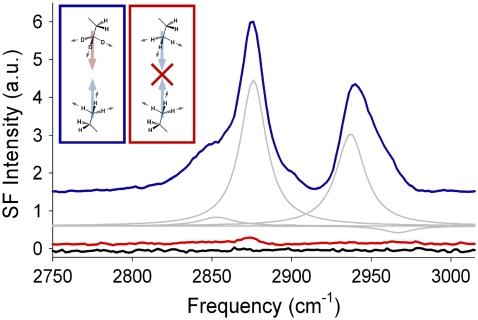
One interesting aspect of SFVS that makes it well suited for studying interfacial phenomena is the coherent nature of the process. The coherence of the sum-frequency output makes it sensitive to the relative orientation of the transition dipole moments being probed. Isotropic systems which have a random distribution of transition dipoles will have little or no net signal as a result of destructive interference between transitions with opposing orientations. This aspect of SFVS is what gives rise to the well-known surface specificity of the technique for systems where the bulk material is isotropic. The break in local symmetry at the interface between two isotropic materials allows for the generation of coherent SFVS emission. The symmetry constraints on χ(2) also have important consequences for well-ordered systems such as lipid bilayer membranes. For instance, it has been demonstrated that the terminal methyl symmetric stretch (CH₃ ν_s) at 2876 cm⁻¹ may be used as an intrinsic probe of membrane asymmetry (13,41). This is due to the fact that the transition dipole moments of the terminal methyl groups of the lipid alkyl chains are oriented perpendicular to the interface (44). Methyl groups in opposite leaflets of a bilayer have opposing transition dipole moments, leading to destructive interference in SFVS and no net signal will be observed (inset, Fig. 2). If the membrane system is prepared such that an asymmetric distribution of lipids is found across the leaflets of the bilayer, complete destructive interference is not possible and considerable SFVS signal is observed (13). The interference of opposing methyl groups can easily be observed by selectively measuring the normal component of the vibrations, using an s-polarized sum-frequency, s-polarized visible, and p-polarized IR polarization combination. This is illustrated in the SFVS spectrum of an asymmetric bilayer of DPPC and 1,2-dipalmitoyl-D62-sn-glycero-3-phosphocholine (DPPC-d₆₂), shown in Fig. 2. The bilayer in question was prepared by sequential deposition of a monolayer consisting of a proteated lipid species, and an opposing monolayer of its deuterated analog. A SFVS spectrum of a symmetric bilayer consisting of the same lipid species is shown for comparison. This bilayer was prepared with an equimolar mixture of proteated and deuterated lipids in each leaflet. Destructive interference between the two leaflets is clearly demonstrated for this sample. The cancellation effect demonstrated in Fig. 2 is the basis by which membrane asymmetry may be measured using SFVS, and will be discussed in further detail below.

FIGURE 2.

A SFVS spectrum of an asymmetric bilayer of DPPC (proximal layer) and DPPC-d₆₂ (distal layer) at 23°C is shown in blue. Individual peaks corresponding to the CH₂ ν_s (2850 cm⁻¹), CH₃ ν_s (2876 cm⁻¹), CH₂ Fermi resonance (2900 cm⁻¹), CH₃ Fermi resonance (2937 cm⁻¹), and CH₃ asymmetric stretch (ν_as) (2967 cm⁻¹) are shown in gray, determined by fitting the spectrum to Eq. 4 (44). A SFVS spectrum of the same bilayer after heating to 50°C for several minutes and subsequently cooling to 23°C (red). For comparison, the SFVS spectrum of a symmetric bilayer consisting of 1:1 DPPC/DPPC-d₆₂ recorded at 23°C (black) is also shown. Spectra are offset for clarity. (Inset) Illustration of dipole cancellation for opposed methyl groups in a symmetric lipid bilayer and the absence of dipole cancellation for an asymmetric bilayer in which one leaflet is deuterated.

For the lipid membrane systems investigated, the nonresonant contribution to the SFVS signal has been found to be negligible, allowing to be dropped from Eq. 3. For the case of a phospholipid bilayer system, the two leaflets will have a relatively narrow distribution of orientations, and the orientational average may be expressed in terms of two populations representing the proximal and distal leaflets of the bilayer, respectively. The susceptibility χ(2) may then be expressed in terms of the molecular hyperpolarizability (β) and the orientation averages for the CH₃ v_s vibrational modes in the distal and proximal leaflets of the bilayer,

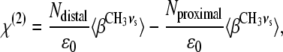(5)

where ɛ₀ is the vacuum permittivity constant, N_distal is the number of molecules in the distal leaflet, and N_proximal is the number of molecules in the proximal leaflet (45).

Eq. 5 shows the dependence of the nonlinear susceptibility on the two populations of lipids in the film (distal and proximal), where the negative sign describes the destructive interference that occurs as a consequence of the opposing orientation of the two populations. It can be clearly seen from Eq. 5 that an equal population of molecules in each leaflet will lead to complete destructive interference. However, by deuterating the lipids in one leaflet of the bilayer, a nonzero susceptibility will result as the CH₃ v_s and CD₃ v_s have different resonant frequencies and will therefore not interfere with each other (13,41).

The interference of the CH₃ ν_s may also be exploited to examine the time-dependent asymmetry of a lipid bilayer (41). By preparing a phospholipid bilayer which contains one leaflet of native phospholipids opposite to a leaflet which has a deuterated analog of the same phospholipids, the decrease in the CH₃ v_s intensity over time can be measured as the two leaflets mix, giving rise to a symmetric system where destructive interference is observed between the oppositely oriented dipoles. This principle is illustrated in Fig. 2, where the SFVS spectrum of an initially asymmetric bilayer is compared to the spectrum of the same bilayer after complete lipid translocation has occurred. The relationship between the time-dependent asymmetry of the bilayer and the observed SFVS intensity is given by

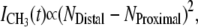(6)

where the asymmetry of the bilayer is expressed as the lipid population difference in the distal (N_Distal) and proximal (N_Proximal) leaflets of the bilayer. The kinetics of lipid translocation can be determined directly from the time evolution of the SFVS CH₃ v_s intensity using (13,41),

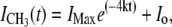(7)

where I_Max is the maximum CH₃ v_s intensity, k is the rate constant for flip-flop, t is time in seconds, and I_o represents the baseline offset due to data acquisition equipment (41). By monitoring the SFVS signal over time and fitting the response to Eq. 7, the rate constant for phospholipid flip-flop is readily obtained.

MATERIALS AND METHODS

1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) and 1,2-dipalmitoyl-D62-sn-glycero-3-phosphocholine (DPPC-d₆₂) (Avanti Polar Lipids, Alabaster, AL) were purchased and dissolved to 1 mg/mL in CHCl₃ (Malinkrodt Baker Bioscience, Phillipsburg, NJ). Hemicylindrical fused silica prisms (Almatz Optics, Marlton, NJ) were used as the substrate for the supported bilayer samples. These prisms were cleaned overnight in a solution of 70% sulfuric acid and 30% hydrogen peroxide before thorough rinsing and a final plasma cleaning step where the substrates were exposed to an argon plasma for ∼3 min (Harrick Plasma, Ithaca, NY). Bilayer samples were prepared on a Minitrough (KSV Instruments, Helsinki, Finland), at the desired surface pressure. The sample deposition method has been discussed in detail elsewhere (13). SFVS experiments were conducted using a custom OPO/OPA system (LaserVision, Bellevue, WA) pumped by a 7-ns Surelite 1 NdYAG laser (Continuum, Santa Clara, CA) at 10 Hz repetition rate. Details of the laser system and data acquisition have also been detailed elsewhere (13).

RESULTS AND DISCUSSION

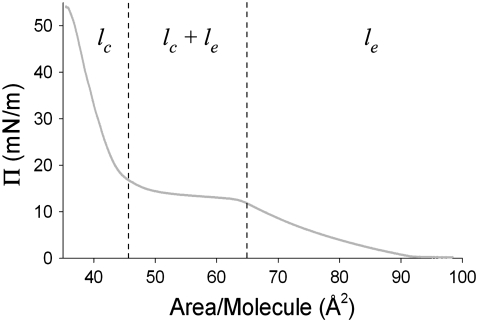
Model bilayers were prepared by sequential deposition of DPPC and DPPC-d₆₂ on a hemicylindrical fused silica prism using the LB/LS method. A surface-pressure/area isotherm for DPPC at 23°C is shown in Fig. 3. The liquid-condensed (l_c) and liquid-expanded (l_e) phase regions are clearly seen in Fig. 3, as well as the (l_c + l_e) phase coexistence region (46). All samples used in this study were prepared in the l_c phase, with pressures ranging from 28 to 42 mN/m. These surface pressures correspond to packing densities of 41.1 ± 0.1 and 38.3 ± 0.1 Ų/molecule.

FIGURE 3.

A surface pressure/area isotherm for DPPC at 23°C. The liquid-expanded phase (l_e), liquid-condensed phase (l_c), and phase-coexistence regions are highlighted. All samples used in this study were prepared in the l_c phase.

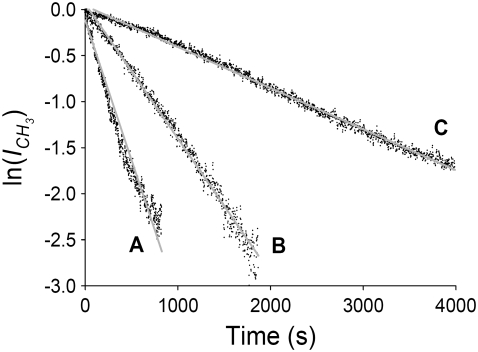
Once the bilayers were prepared they were then mounted in a Teflon flow cell which was subsequently purged with D₂O before collecting any SFVS data to avoid spectral interference between the phospholipid CH₃ stretching vibrational mode and the H₂O vibrational modes. The spectrometer was then tuned to the terminal methyl symmetric stretching mode (I_CH3 v_s) of the DPPC lipids in the bilayer. The temperature of the cell was elevated to 37°C and maintained at that temperature using a thermoelectric heating plate which was incorporated into the cell. The terminal methyl (CH₃ v_s) SFVS intensity (at 2876 cm⁻¹) was monitored versus time after the temperature had reached a stable reading of 37°C (Fig. 4). The time to reach a stable temperature reading was typically 300–500 s. Data collected during this time was not used for determination of the rate constant. After reaching a stable temperature, the SFVS CH₃ v_s intensity decayed exponentially to a limiting value. The intensity decays were then fit using Eq. 7 to determine the rate of lipid translocation. Decay rates and half-lives as a function of deposition pressure are summarized in Table 1, where the half-life for flip-flop is given by t_1/2 = ln(2)/2k. For comparison, the measured rate of DPPC flip-flop at 37°C at the extremes of surface pressure examined, 28 mN/m and 42 mN/m, are 10.9 × 10⁻⁴ s⁻¹ and 1.03 × 10⁻⁴ s⁻¹ respectively. The corresponding half-lives are 5.3 min and 56 min, respectively. It is noted that the rates of flip-flop measured by SFVS, such as those presented above, are much faster than the rates measured by ESR (13). The difference in measured rates has been attributed to the modified headgroup used in the ESR study (13).

FIGURE 4.

Sample pressure-dependent SFVS CH₃ v_s intensity decays measured at 2876 cm⁻¹ for asymmetric DPPC/DPPC-d₆₂ bilayers recorded at 37°C. Raw data is shown as black points, with the fit to the data shown in a shaded line for samples prepared at deposition pressures of 28 mN/m (A), 37 mN/m (B), and 40 mN/m (C).

TABLE 1.

Summary of DPPC flip-flop kinetics as a function of lateral surface pressure (Π) measured at 37°C for all samples studied

Π (mN/m)	k (s−1) × 104	ln(k)	t1/2 (min)
28	10.93 ± 0.12	−6.82 ± 0.07	5.28 ± 0.06
31	5.61 ± 0.07	−7.49 ± 0.09	10.3 ± 1.3
34	7.47 ± 0.06	−7.20 ± 0.06	7.73 ± 0.06
36	2.02 ± 0.01	−8.51 ± 0.04	28.7 ± 0.6
37	3.22 ± 0.02	−8.04 ± 0.05	17.9 ± 0.1
40	1.31 ± 0.01	−8.94 ± 0.07	44.1 ± 0.3
42	1.03 ± 0.01	−9.18 ± 0.09	56.0 ± 0.5

The error is reported to two standard deviations and was generated from the fit to the SFVS intensity decays. The error in the lateral surface pressure is ∼ ±0.2 mN/m.

What is most notable about the lateral pressure-dependent data obtained is the strong dependence of the rate of flip-flop on the lateral surface pressure of the film. A 7.4% change in packing density is accompanied by an order-of-magnitude change in the rate of transbilayer migration at 37°C. It would be quite interesting to relate the lateral pressure dependence of the flip-flop rate directly to variations in the internal lateral pressure in biological cells or even to vesicle systems. Unfortunately, direct measurement of the effective lateral surface pressure is not possible in vesicles or in biological cells in vivo (47). However, recent work by Marsh provides an estimate of the correspondence between monolayer lateral surface pressures and the equivalent effective lateral pressure in vesicle bilayer systems (17). This work estimates that the best correspondence between a lipid monolayer at the air-water interface and bilayer systems (vesicles) in solution occurs for lipid monolayers in the relatively narrow surface pressure range of 30–35 mN/m (17). Interpolation of our kinetic data yields t_(1/2) values from 7 min to 16 min for this range, with slightly greater than a twofold increase in the flip-flop rate constant between the limits of 30–35 mN/m proposed by Marsh (17). This shows a surprising degree of variability within this relatively narrow range of lateral pressures.

While there are still a large number of obstacles preventing a direct comparison of lateral pressure-dependent flip-flop kinetics to the effects of lateral pressure in vivo, our data does provide a unique opportunity to measure pressure-dependent activation thermodynamics in bilayer systems. Presently, the body of thermodynamic data relating to phospholipid flip-flop is considerably smaller than the body of kinetic data available, and much more data is needed to better describe flip-flop thermodynamics (6,13). Expanding our understanding of the thermodynamics of flip-flop is essential to an understanding of the mechanism and energetics of flip-flop, and how they relate to membrane asymmetry, growth of the cell, etc.

Area of activation for DPPC flip-flop

From the kinetic data obtained, the pressure-dependent thermodynamics of activation may be determined by applying the concepts of transition state theory (TST) to the process of flip-flop. This represents the first presentation of lateral pressure-dependent activation thermodynamics in model membrane systems, and is an important step toward understanding of the flip-flop transition state and possible mechanisms for flip-flop.

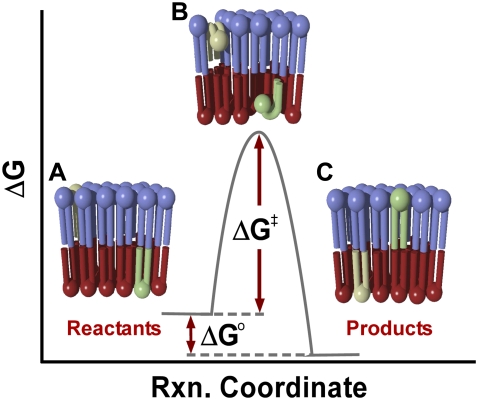
Transition state theory (TST) provides a useful tool for the thermodynamic analysis of phospholipid flip-flop. In general, a chemical reaction can be viewed according to TST as proceeding along a reaction coordinate from reactants to products (Fig. 5). For the reaction to proceed, the reactants must acquire sufficient energy to overcome the energetic barrier to conversion, known as the activation barrier. For the case of phospholipid flip-flop in a PSLB, lipid molecules on the proximal leaflet of the bilayer may be thought of as ground-state reactants which must cross an energetic barrier via a flip-flop transition state to reach the distal leaflet (analogous to conversion to products), illustrated in Fig. 5. Viewed in this fashion, the transition state for the process of phospholipid flip-flop would most likely represent the phospholipid molecule with its polar headgroup located within the hydrophobic core, as this unfavorable interaction represents the greatest energy barrier to flip-flop (Fig. 5). The generality of TST means that it is very well suited to modeling this transition across the membrane despite the fact that there is no breaking or forming of covalent bonds in this process, as would typically be found for a chemical reaction modeled by TST. Using this approach, an expression for the area of activation for phospholipid flip-flop in PSLBs may be derived.

FIGURE 5.

A general reaction coordinate diagram illustrating free energy as a function of reaction progress. Also shown are a series of illustrations depicting the translocation of a lipid starting with the initial state (A), followed by the transition state for phospholipid flip-flop (B), and ending in the final state after exchange (C). For the case of phospholipid flip-flop, ΔG⁰ = ΔH⁰ −TΔS⁰ will reduce to ΔG⁰ = −TΔS⁰, as there is no enthalpic driving force for mixing of the phospholipid components. This depiction is not meant to suggest cooperativity across the leaflets.

It is well known that investigation of the pressure dependence of a reaction rate allows one to measure an activation volume (ΔV^‡) for a reaction according to Eq. 8, where ΔV^‡ represents the difference in volume occupied by the reactants in their ground state and at the transition state, k is the rate constant for the reaction, T is temperature, P is pressure, and R is the gas constant (48):

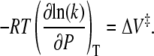(8)

This approach is used in the current study to determine an activation area for the process of phospholipid flip-flop. As the bilayer film is best thought of as a two-dimensional gas, the relevant pressure measurement of such a system is the lateral surface pressure (Π) with dimensions of mN/m. For such a two-dimensional film, the rate dependence on lateral surface pressure (two-dimensional) rather than pressure (three-dimensional) yields an activation area (Δa^‡), rather than an activation volume (Eq. 9).

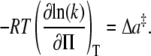(9)

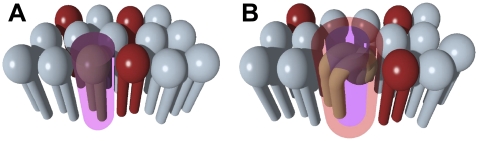
The activation area for phospholipid flip-flop represents the difference in area for a lipid at the transition state, relative to the reactant ground state. This concept is illustrated in Fig. 6, for flip-flop of a single lipid molecule. Measurement of the rate of flip-flop (k) as a function of the lateral surface pressure (Π) can be used to determine the activation area for phospholipid flip-flop.

FIGURE 6.

An illustration of the activation area for flip-flop according to one possible transition-state geometry. The area occupied in the ground state is shown in purple (A), with the net area at the transition state shown in pink (B). The difference between the two areas represents the activation area for phospholipid flip-flop.

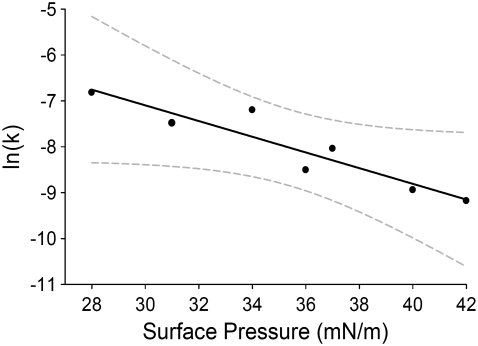
The activation area for DPPC flip-flop at 37°C in a planar-supported lipid bilayer was determined using the data shown in Table 1. A plot of ln(k) versus surface pressure was prepared and fit to Eq. 9 using a linear least-squares regression (Fig. 7). From the slope of the resulting line, the activation area for flip-flop of DPPC at 37°C in a PSLB is calculated to be 73 ± 12 Ų/molecule. This represents an increase in the area occupied by a DPPC lipid molecule of 73 Ų/molecule from an initial equilibrium area of ∼40 Ų/molecule. At the transition state, the area occupied by the DPPC molecule has more than doubled to 113 ± 12 Ų/molecule. It should be noted that the calculation of the activation area depends only on the relative change in lateral membrane pressure and not the absolute pressure (see Eq. 9). It could be argued that the pressure of the lipid film measured at the air/water interface is not equal to the pressure of the film upon transfer to the substrate. However, we have shown in Fig. 1 that there is a direct correlation between both the concentration of the fluorescent lipid NBD-DPPC and the packing density at 20 and 40 mN/m. It is true that the pressure in the deposited film may not be the same as that on the substrate, but the relative change in packing density (pressure) is conserved (see Fig. 1). Therefore, changes in the packing density of the lipid film upon transfer to the solid support will not affect the calculated activation area. Thus the calculated value for Δa^‡ will not be affected by any minor error in the absolute area per molecule which may exist, and any error in the absolute area per molecule stated will only appear as a shift in the total area at the transition state (a^‡ = a_initial + Δa^‡), where a^‡ is the total area per molecule at the transition state and a_initial is the initial area in the ground state. As a final note, the previously mentioned radionuclide study was able to demonstrate that the absolute area per molecule of an LB monolayer deposited onto a silica substrate was nearly identical to the area density of at the interface before deposition (39). This would suggest that any discrepancy between the monolayer area density before, and after, deposition is quite small.

FIGURE 7.

A plot of ln(k) versus surface pressure (Π) for DPPC/DPPC-d₆₂ bilayers at 37°C. Also shown is the linear least-squares fit to the data (solid line) and confidence bounds at 95% (shaded dashed line).

The value for the activation area calculated above can be compared to theoretical upper and lower bounds to better understand its significance. A lower bound for the activation area can be calculated with the assumptions that transfer across the membrane follows a unimolecular process, and that the geometry of the lipid molecule can be treated as a cylinder whose area is equal to the equilibrium area per molecule of the lipid in the membrane and height of the cylinder equal to half the bilayer thickness (∼22 Å) (49). If the system is idealized as a hexagonal close-packed structure in the ground state, with an area per molecule of 40 Ų, the area occupied by a lipid molecule bent along itself would occupy an area equivalent to at least two neighboring sites plus the excluded space between them. For the system described above, this would be a value of 84 Ų/molecule. Alternatively, if the cylinder were to turn completely orthogonal to the lipids comprising the membrane, the occupied area would instead be ∼158 Ų/molecule. The net area at the transition state determined by SFVS falls within the range of 84–158 Ų/molecule, suggesting that the transition state possesses a geometry intermediate to the two extreme cases presented above. This is expected, as the lower bound is not likely to be accomplished due to the large torsional angle the lipid alkyl chain would have to adopt, and the upper bound creates a larger packing disturbance and exposes more of the hydrophobic tail to the bulk aqueous environment. Intuitively the transition state should be a compromise of these two energetically unfavorable cases.

It should be noted that Δa^‡ is determined from ensemble kinetic measurements, although reported on a per molecule basis, and is not indicative of the specific mechanism of flip-flop with regard to the number of molecules involved in the transition or the cooperativity across the leaflets of the bilayer. Additionally, the treatment of the lipid bilayer as a hexagonal close-packed structure is an idealization intended for illustrative purposes. While the data does not provide details as to the absolute geometry of the transition state, it does provide useful information about the dependence of lipid flip-flop on the packing in the bilayer and the expansion of the neighboring molecules that must occur to accommodate transmembrane movement of phospholipids, be this spread over one lipid molecule or many.

To our knowledge, this is the first report of an activation area for phospholipid flip-flop. SFVS, in combination with the LB/LS method of bilayer preparation, shows promise for the study of lateral pressure-dependent kinetics and thermodynamics in a wide number of model lipid systems. More complex membrane models which incorporate multiple phospholipid species, integral membrane proteins, or small molecules such as cholesterol are being studied to further expand our knowledge of flip-flop thermodynamics. The results presented here open the way for a complete thermodynamic description of the transition state for flip-flop in planar-supported membranes. By extending this treatment to additional lipid species and membrane compositions, it is our hope that a general thermodynamic description of phospholipid flip-flop may be achieved.