Insights into the Mechanism of ADP Action on Flagellar Motility Derived from Studies on Bull Sperm

Abstract

Adenosine diphosphate (ADP) is known to have interesting effects on flagellar motility. Permeabilized and reactivated bull sperm exhibit a marked reduction in beating frequency and a greatly increased beat amplitude in the presence of 1–4 mM ADP. In this study we examined the force production of sperm reactivated with 0.1 mM ATP with and without 1 mM ADP and found that there is little or no resulting change in the stalling force produced by a bull sperm flagella in response to ADP. Because bull sperm bend to a higher curvature after ADP treatment we explored the possibility that ADP-treated sperm flagella are more flexible. We measured the stiffness of 50 μM sodium vanadate treated bull sperm in the presence of 4 mM ADP, but found no change in the passive flagellar stiffness. When we analyzed the torque that develops in ADP-treated sperm at the point of beat reversal we found that the torque developed by the flagellum is significantly increased. Our torque estimates also allow us to calculate the transverse force (t-force) acting on the flagellum at the point of beat direction reversal. We find that the t-force at the switch-point of the beat is increased significantly in the ADP treated condition, averaging 0.7 ± 0.29 nN/μm in 0.1 mM ATP and increasing to 2.9 ± 1.2 nN/μm in 0.1 mM ATP plus 4 mM ADP. This suggests that ADP is exerting its effect on the beat by increasing the tenacity of dynein attachment at the B-subtubule. This could be a direct result of a regulatory effect of ADP on the binding affinity of dynein for the B-subtubule of the outer doublets. This result could also help to explain a number of previous experimental observations, as discussed.

INTRODUCTION

It is known that ADP has interesting effects on the motility of flagella. Dissected fragments of bull sperm flagella that are treated with 1 mM Mg-ATP show a jittering, uncoordinated motion. The same isolated segments can be converted to rhythmic beating by the inclusion of ADP (1). ADP will also stabilize the motility of Triton X-100 extracted ATP-reactivated bull sperm models (2). The effects of ADP on sea urchin sperm motility are well documented (3). There is a reduction in beating frequency and an increase in the bend angle of the propagating waves as the ADP concentration is increased. These changes are attributed to a competition of ADP, especially the Mg-ADP form, with the normal Mg-ATP substrate, with the effect similar to reducing MgATP concentration (3). However, it has also been reported that demembranated models produced from certain immotile mutants of Chlamydomonas will initiate spontaneous beating in the presence of ADP (4,5). ADP has also been reported to facilitate beating of sea urchin flagella at very low ATP concentrations that would not normally support motility (6). It would almost seem that ADP is a tonic to restore functionality to dysfunctional flagella, which seems to go beyond its action as a competitive inhibitor of motility.

What do we know about the action of ADP? Intact axonemes can be made to disintegrate by microtubule extrusion by the action of ATP and proteolytic digestion. If ADP is also included the velocity of microtubule extrusion is greatly reduced (7). These results suggest that the reduced beating frequency in ADP-treated sperm could be explained by a reduction in the velocity of microtubule sliding in ADP-treated flagella. Paradoxically, Yagi (8) reported that inner arm dyneins actually improve their ability to translocate microtubules in the presence of ADP as compared to ATP alone. In line with this it has also been reported that the completeness of the disintegration is actually increased in the presence of ADP (9). This seems, at least superficially, to counter the slowing action of ADP on intact doublet sliding rates, and suggests a mechanism by which a selective effect on the inner arms could actually have a strengthening effect on beating amplitude and a positive effect on coordinated beating.

It was suggested that perhaps the action of ADP could be explained if dynein has a nucleotide binding site that is regulatory in nature (9). It is well established that the four AAA domains of the dynein heavy chain have functional P-loop nucleotide binding sites (for review see 10). It is also established that it is the ATP hydrolysis at AAA1 that drives motor function (11). However, both AAA1 and AAA3 domains are reported to be functional ATPase sites (12,13). It was suggested that the nucleotide binding site of the P-loop of AAA3 is associated with the affinity of microtubule (MT) binding at the stalk (14,15). In line with this idea it was proposed that a shift in the positioning of the two alpha helices of the dynein stalk relays the influence of the bound nucleotide to the MT binding site at the tip of the stalk (16). In flagella, it is the binding of the stalk to the B-subtubule that mediates force transmission between the outer doublets. Therefore, there is a possibility that this nucleotide binding site regulates the affinity of the dynein head attachment to the adjacent doublet during the dynein power stroke, and the subsequent release and relocation of the stalk to a new binding site.

A variation on this regulatory scheme was proposed recently by Inoue and Shingyoji (17). They speculate that one of the four AAA binding sites, possibly AAA2, is a long-residence noncatalytic binding site specific for ADP. They hypothesize that when that site is occupied by ADP it facilitates motor activity and when ATP is substituted at that site motor activity is inhibited. They propose that ADP occupancy at one of the noncatalytic binding sites provides the link for coordination of the binding at the stalk and the principal ATP hydrolysis site at AAA1. The specific AAA domain that serves this function is not determined. The available experimental evidence for the functions of the specific nucleotide binding domains does support the idea that one or more of the domains AAA2, 3, or 4 is a high affinity ADP binding site with a regulatory function (15,18,19).

Results from kinetic studies of the dynein cross-bridge cycle suggest that release of bound ADP is the rate limiting step in the dynein cross-bridge cycle (20). The ADP bound state corresponds to the step in the cycle where the dynein head is tightly bound to the adjacent doublet MT and is a critical force generating intermediate (21). Free ADP should therefore lengthen the high MT affinity step in the duty cycle. This would be accomplished by increasing the occupancy time of bound ADP in the nucleotide binding pocket of a regulatory nucleotide binding site on the dynein head.

In this study, we provide some mechanical and biophysical evidence that such a regulatory arrangement could be altering the strength of adhesion of the dynein heads to their binding sites on the B-subtubule. We suggest that an increase in the duration of the tightly bound phase of the dynein cross-bridge cycle is the mechanism responsible for the observed effects on flagellar beating.

MATERIALS AND METHODS

Sperm preparation

Ejaculated Holstein bull sperm obtained from Genex CRI (Tiffin, OH) were shipped cold via overnight carrier in a milk-based extender. Cells were stored as received at 0–5°C for a maximum of 3 days before use. To prepare the sperm stock solution, cells were washed from the milk-based extender by diluting 4 ml of the semen solution with 6 ml of sodium citrate buffer (0.097 M sodium citrate, 2 mM fructose, and 5 mM magnesium sulfate, pH 7.4). This mixture was then centrifuged at 1000 × g for 10 min, and the supernatant decanted. The remaining pellet was resuspended in 10 ml of sodium citrate, centrifuged, decanted, and repeated once more. After the third wash, the pellet of cells was brought up to a final volume of 4 ml with sodium citrate and used within 4 h.

Reactivations

For each reactivation, 10 μl of stock sperm solution was added to 3 ml of a reactivation mixture in a petri dish (Falcon 35-1007, Becton Dickinson Labware, Franklin Lakes, NJ). The reactivation mixture (pH 7.8) was composed of 0.024 M potassium glutamate, 0.132 M sucrose, 0.02 M Tris-HCl, 1 mM dithiothreitol (DTT), 0.1% Triton X-100 (Pierce, Rockford, IL), 0.5 mM EGTA, and 0.003 mM cAMP. This is a standard reactivation protocol (22), which was modified as necessary to carry out this study. First, the ATP concentration was reduced to 0.1 mM. Second, ADP was added to some reactivations at various concentrations. When altering the nucleotide concentrations we altered the MgSO₄ concentration in the reactivations to 0.6 mM for 0.1 mM ATP only, 1 mM for 0.5 mM ADP, 2 mM for 1 mM ADP, 2.5 mM for 2 mM ADP, and 5 mM for 4 mM ADP. This was done to ensure sufficient Mg⁺² was present to complex with ATP and ADP. We also ran some trials to determine the t-force at 4 mM ADP with 1 mM Mg⁺², rather than 5 mM, to ensure that the Mg⁺² concentration was not responsible for our result at high ADP concentration. All reactivated sperm were placed in a shallow glass slide chamber accessible to micromanipulation with a Sutter Instrument (Novato, CA) MP-285 when placed on a Nikon TE2000U microscope (Melville, NY). Cells were allowed to settle and adhere by their head to the glass. Only those that were attached to the glass with their flagellum free to beat were analyzed.

Beat frequency and curvature

For each cell analyzed, 3–10 beat frequencies were obtained from the digital image sequences of reactivated sperm and averaged. All radius of curvature measurements were obtained by matching computer-generated circles of known radius to the curve of the flagellum between 5 μm and 10 μm using Matrox Imaging's Inspector 8.0 software (Dorval, Quebec, Canada).

Shear angle

To determine the shear angle, a line was drawn through the midline of the sperm head on a tracing or digital image of a beating flagellum and was marked every 5 μm from the head/tail junction to the end of the flagellum. At each 5 μm mark, a line tangent to the flagellum was drawn. The preceding and subsequent 5 μm marks were used as guides to mark the tangent lines in the correct angle and direction of the beat. The angle created by the intersection of the tangent line and the midline of the sperm head is the shear angle. As a matter of convention, angles were given a positive sign if they were on the principal side of the beat and a negative sign if they were on the reverse side of the beat. Every fourth frame of one complete beat cycle was plotted as a function of flagellar position.

Microprobe production and calibration

For this study two main types of borosilicate glass microprobes were made using a Sutter Instrument Company P-87 pipette puller. For measuring force and stiffness, 1 mm solid rod was pulled to a taper length of ∼8–9 mm and tip diameter of ∼1 μm and force-calibrated following the polystyrene bead method as detailed previously (22). The mean probe stiffness value from a number of individual calibration points was extrapolated to the probe tip by regression analysis from the individual calibrations as detailed in that same study. For cutting the reactivated flagellum, 1 mm OD/0.50 mm ID capillary tubing was pulled to a tip size of ∼3–8 μm with a taper length of ∼7 mm. These microprobes were used like a knife to cut off distal portions of the flagellum of a beating sperm cell until the flagellum ceased to beat. All glass was purchased from Sutter.

Stall force measurement

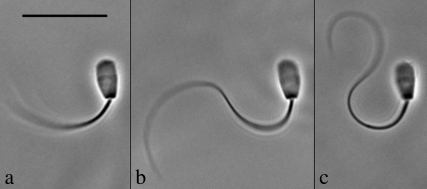
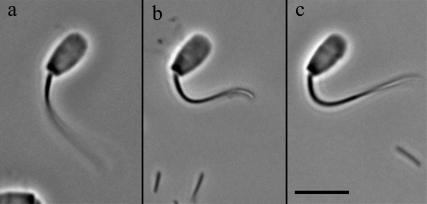
The stall force was measured following the methods described previously in Schmitz et al. (22). Mechanical stalls of the flagellum against the probe were conducted in 0.1 mM ATP and in 0.1 mM ATP + 1 mM ADP. Attempts to measure the stall force of 4 mM ADP-treated cells proved unsatisfactory for analysis. The peculiar shape that the flagellum exhibits after 4 mM ADP treatment, as can be seen in Fig. 1, made it extremely difficult to obtain stalls that were stable and still met our strict criteria for vector analysis of the force experienced by the probe.

FIGURE 1.

The effect of ADP on the principal bend at the switch-point of the beat in bull sperm. All three images show a single frame that corresponds to the time point of greatest curvature development of the principal bend in Triton X-100 extracted cells reactivated to motility with 0.1 mM ATP. The ADP concentration is 0 mM in a, 1 mM in b, and 4 mM in c. All three cells are securely stuck to the slide surface with the flagellum beating freely. In every case, the next frame from the one shown had a reduced principal bend curvature in the region 5–10 μm from the head-tail junction and a portion of the flagellum was reversing the direction of the beat. This indicates that the selected frame is close to the switch-point of beat reversal. Bar = 20 μm.

Passive stiffness

We followed the methods detailed in Schmitz-Lesich and Lindemann for measuring the passive stiffness (23). Briefly, this method required three separate, unique solutions. The first solution contained 0.45 M sodium acetate, 2.5 mM magnesium acetate, 0.5 mM EDTA, 50 μM NaVO₃, and 10 mM HEPES in a total volume of 3 ml. The second solution combined 0.5 ml of the first mixture with 0.6 μl of 10% Triton X-100 and 100 μl of the stock sperm solution added. The third solution was the same as the first mixture except that 0.1 mM ATP and 60 μl of the second solution were added. The NaVO₃ solution was always made fresh on the day of the experiment to prevent the possibility of oxidation.

t-Force analysis (whole and cut cells)

The measurement of the active moment at the switch point of the beat and the estimation of the t-force from the active moment was accomplished by recording the motion of actively beating reactivated sperm that had their head stuck to the glass surface of the microscope slide with their flagellum free to beat. Under these conditions, a bull sperm flagellum develops a principal bend during each beat cycle that reaches a maximum curvature at a position ∼7 μm (5–10 μm) from the flagellar base. Images of cells in this condition are shown in Fig. 1. It is the point at which the flagellum switches from bending in one direction and begins to bend back in the opposite direction. This condition is easily identified from the digital image recordings of beating sperm. The sequence files (.avi files) are advanced one frame at a time to find the image where the flagellum exhibits the maximum extension in the principal bend direction and the frame immediately after this image shows a reduction in curvature of the flagellum and a change in the direction of the beat. We used the same criteria to select frames for t-force analysis of the cut flagella.

All chemical reagents used in this study were of the highest purity available from Sigma Chemical Co. (St. Louis, MO) unless stated otherwise.

RESULTS

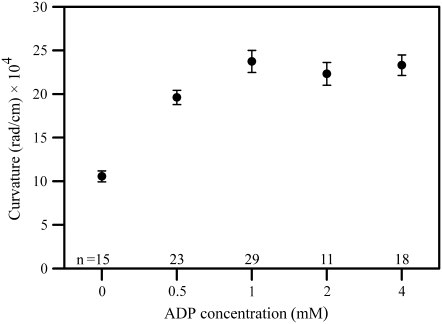
ADP has a pronounced and characteristic effect on the motility of bull sperm that are demembranated with Triton X-100 and reactivated with ATP. The flagellar beat becomes slower and the amplitude of the beat becomes larger in the presence of ADP as compared to sperm reactivated with ATP alone. Video sequences of beating sperm cells are presented for both the 0.1 mM ATP only (Supplementary Material, Movie S1) and the 0.1 mM ATP + 4 mM ADP (Movie S2) reactivations. The increased amplitude of the beat is the result of a greatly increased curvature of the bends that are produced in the flagellum. Fig. 2 shows the effect of increasing concentrations of ADP on the curvature of the principal bend at a position ∼7 μm from the base of the flagellum. It can be seen that the effect of ADP on the curvature is fully developed at 1 mM and is sustained at higher concentrations. Table 1 presents a summary of the beat frequencies and maximum principal bend curvatures measured from bull sperm reactivated with 0.1 mM ATP, with and without ADP present. The beating frequency is approximately half of the ATP-only control value when either 1 mM or 4 mM ADP is present in the sample, a difference that is highly significant. The higher values for curvature of the principal bend are significant to the p < 0.0001 level.

FIGURE 2.

The effect of ADP on curvature development in reactivated bull sperm. The mean (±SE) maximum curvature development of bull sperm flagella is plotted as a function of ADP concentration. Curvatures were measured between 5–10 μm from the head-tail junction on images where the flagellum was exhibiting the greatest curvature development of the principal bend in 0.1 mM ATP-reactivated sperm cells. The next frame showed a portion of the flagellum reversing the direction of the beat. As ADP content is increased from 0 to 1 mM, a significant increase in maximum curvature generation occurs (p < 0.0001; t-test). At all concentrations >1 mM ADP there is significant increased maximum curvature development (p < 0.0001) compared to cells without ADP present. There is no benefit to maximum curvature development using ADP concentrations >1 mM.

TABLE 1.

Beat frequency and maximum curvature of bull sperm flagella

	Number of cells analyzed*	Beat frequency (Hz)	Number of cells analyzed	Max P bend curvature (×105 radians)
0.1 mM ATP	22	2.07 ± 0.46	15	1.1 ± 0.2
0.1 mM ATP and 1.0 mM ADP	10	1.07 ± 0.19†	29	2.4 ± 0.7†
0.1 mM ATP and 4.0 mM ADP	15	1.05 ± 0.35†	18	2.3 ± 0.5†

Data are mean ± SD.

^*For each cell analyzed 3–10 frequencies were measured and averaged.

^†p < 0.0001.

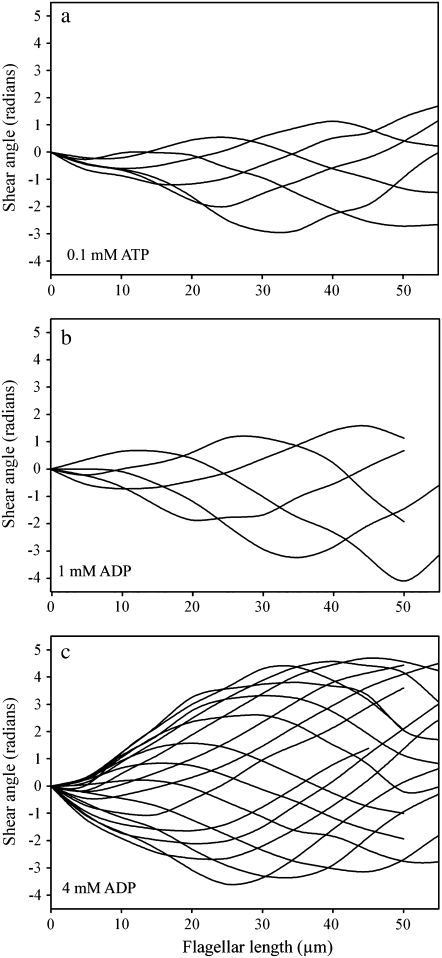
Fig. 1 provides a visual sense of the difference in the principal bend in side by side comparison of a video image showing the principal bend at the end point of the beat for a cell reactivated with 0.1 mM ATP in a and similar frames of a cell in 0.1 mM ATP + 1 mM ADP in b and + 4 mM ADP in c. Greater curvature development during the beat cycle is also reflected in greater development of shear during the beat. Fig. 3 shows plots of the shear angle versus the position along the flagellum for one complete beat cycle of a cell reactivated in 0.1 mM ATP only (Fig. 3 a), and 1 mM (Fig. 3 b) and 4 mM ADP (Fig. 3 c). The changes in the beating pattern induced by ADP are clearly marked by a greater extent of interdoublet sliding and a greater development of bending before the beat reversing direction. As seen in Fig. 3, the effect of ADP on shear angle, and thus interdoublet sliding, is most pronounced for 4 mM ADP.

FIGURE 3.

Shear angle plots for reactivated bull sperm as ADP content is varied. Each of the three plots presents the shear angle data for approximately one full beat cycle with every fourth frame plotted. All are produced from images of Triton X-100 extracted bull sperm reactivated with 0.1 mM ATP. The ADP concentration is 0 mM in a, 1 mM in b, and 4 mM in c. All of the cells were in the head stuck configuration. Note that the shear angle excursion over the course of the beat becomes progressively larger as ADP concentration increases, especially within the first 10 μm of a beating flagellum. Shear angle is the local tangent angle at a point along the flagellum minus the angle at the flagellar base. Shear angle measurements are proportional to the amount of interdoublet sliding within the axoneme.

To address the underlying mechanism of action of ADP on the flagellum we first asked the question: is the increased bending during the beat cycle a consequence of a change in the force produced by the dynein motors? In a previous report we directly measured the stalling force and the torque that reactivated bull sperm produce when opposed by a calibrated glass microprobe that acts as an obstacle to completion of the beat (22). We used the same technique to examine the stalling force and the torque produced by reactivated bull sperm with 0.1 mM ATP alone and supplemented with 1 mM ADP, which we have shown gives a significant ADP effect.

Table 2 presents the result of these experiments. There was a very small (nonsignificant) increase in the torque produced by stalled bull sperm in 1 mM ADP (4.1 × 10⁻¹⁵ N · m) as compared to the no ADP controls (3.6 × 10⁻¹⁵ N · m) but this was largely the result of the average lever arm at the probe position being somewhat larger for that data set. We think the longer average lever arm was more due to the altered geometry of the flagellar beat in the ADP-treated cells than to any real change in the dynein force. There was only a small and nonsignificant difference in the raw force generated by the cells with or without ADP (2.1 vs. 1.9 × 10⁻¹⁰ N) and only a small, but significant, decrease in force between 0.1 mM ATP and the previously reported value of 2.5 × 10⁻¹⁰ N for 1 mM ATP. We used the same method as used in the earlier report (22) to find the approximate force per dynein head in the stalled condition. The 0.1 mM ATP-only data yields a force per dynein head of 4.2 pN, and the 0.1 mM ATP + 1 mM ADP data yields a force per dynein head of 3.8 pN. These values are much too close to suggest a systematic change in the dynein stalling force. Consequently, the stalling force of the dynein motor does not seem to be the explanation for the increase in bending with ADP, at least not in terms of increasing the active torque available for bending.

TABLE 2.

Measurement of force from bull sperm flagella during an isometric stall

	Isometric stalls (n)	Frames of stall (n)	Force (×10−10 N)	Lever arm (μm)	Torque (×10−15 N × m)
1.0 mM ATP*	48	40 ± 66	2.52 ± 0.68	15.3 ± 3.8	3.89 ± 1.58
0.1 mM ATP	16	129 ± 223†	2.08 ± 0.79†	16.8 ± 4.1	3.56 ± 1.83
0.1 mM ATP and 1.0 mM ADP	14	71 ± 56	1.94 ± 0.35‡	21.5 ± 2.6§	4.11 ± 0.53

Data are mean + SD.

^*Previously published data (20).

^†p < 0.05.

^‡p < 0.005.

^§p < 0.0001.

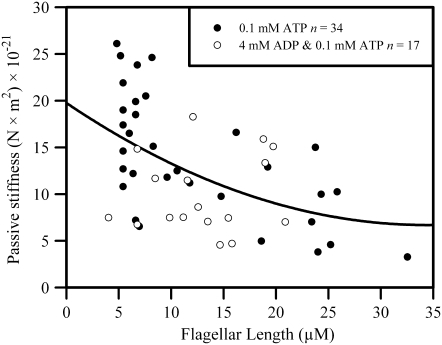
Greater bending in the presence of ADP could conceivably also result from a greater flexibility of the flagellum. We used a method devised in an earlier study (23) to directly measure the stiffness of the passive flagellum when the dynein motors are rendered nonfunctional with 50 μM sodium metavanadate (NaVO₃). The results of these experiments are shown in Fig. 4. We found that the stiffness of the basic flagellar structure is not noticeably influenced by the presence of 4 mM ADP. Because 4 mM ADP was the maximum concentration used in this report it is unlikely that the changes in waveform we see are an action of ADP on the stiffness of the structural components of the axoneme. Although the large cell-to-cell scatter in the stiffness values obtained from our determinations is unfortunate, it is noteworthy that the scatter is very similar with or without ADP.

FIGURE 4.

Passive flagellar stiffness of bull sperm flagella with and without ADP. A scatter plot is shown of the accumulated determinations of flagellar stiffness on detergent extracted bull sperm that were rendered passive by 50 μM NaVO₃ in the presence of 0.1 mM ATP. The flagella were bent with a force-calibrated glass microprobe. The resistance to bending was found from the force that the flagellum exerts against the calibrated microprobe when bent at various positions along the flagellar length. The stiffness, found by dividing the measured bending torque by the curvature of the induced bend, is plotted against the position of the imposed bend along the flagellum. The open circles are from measurements where 4 mM ADP was included in the solution.

Analysis of the t-force

The equation of motion of a flagellum in a viscous medium is a Newtonian balance where the active moment (or torque) that drives the motility is at all times opposed by the sum of the torque due to viscous drag and the torque due to elastic deformation. As given previously (24), it can be written as:

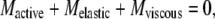(1)

where M denotes the moment (or torque) acting at each position along the flagellum.

Under the conditions that prevail in most rapidly beating cilia and flagella, the viscous moment is quite large and therefore, it is very difficult to accurately solve for the active torque produced in the flagellum without recourse to complex hydrodynamic modeling. The motility conditions that we used in this study present an opportunity for simplification.

We selected for analysis reactivated cells that had their heads stuck to the glass slide and exhibited a regular flagellar beat. We reactivated motility with 0.1 mM ATP, which produces a slow but well coordinated beat. Reactivated bull sperm under these conditions exhibit a beat that is quite cilia-like with a sweeping beat that has an effective stroke-like phase during the development of the principal bend and a recovery stroke-like phase in the reverse bend direction. This simplifies the beat considerably as compared to the free swimming condition, in that for the most part the flagellum sweeps back and forth between two extremes of excursion as the P and R bends reach full development in the midpiece region of the flagellum. At the end of each stroke of the beat cycle the flagellum as a whole reverses direction as the next stroke begins. These points of beat direction reversal we refer to as the switch point of the beat and they present the best opportunity for biophysical analysis.

The drag torque can be estimated for a bull sperm beating with its head attached to the glass surface using the drag coefficient determined by Rikmenspoel (25) and the Geometric Clutch computer model for a bull sperm (26). The bull sperm model was run under conditions that simulate a bull sperm beating with the head stuck to the slide. The drag torque was output from the model and examined over the course of a full beat cycle. The modeled result suggests that the drag torque acting on the basal 10 μm of the flagellum reaches a value very close to zero when the P-bend reaches its maximum curvature just before switching of the dyneins occurs and the beat reverses direction. This finding can be understood intuitively. In the head-stuck condition, bull sperm show a cilia-like beat with an effective stroke phase that culminates in the formation of the principal bend in the midpiece region. The flagellar bending in the midpiece reaches its maximum extent just before the beat reverses direction. At that point in time, the overall movement of the distal 75% of the flagellum undergoes a net reversal of direction. When the net direction of motion of the flagellum reverses, the drag torque acting on the basal portion of the flagellum is reduced to near zero. Consequently, for these head-immobilized bull sperm at the beat reversal point the torque balance equation can be simplified to:

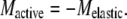(2)

This simpler relationship can be made more specific in that the elastic moment can be specified in terms of the curvature of the flagellum and the stiffness of the flagellum, such that:

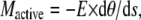(3)

where E is the local elastic modulus or stiffness and dθ/ds is the local curvature at the point of interest along the flagellum. The active moment (M_active) is a torque acting at the same position along the flagellum and is derived from the linear tension and compression on the outer doublets of the flagellum acting across the spatial separation of the doublets carrying the tension. The dynein motors that are actively bending the flagellum generate the effective tension and compression as a force couplet applied to the doublets that they span. When a series of doublets is spanned by active dynein motors, the resultant tension and compression is transferred to the first and last element of the active series. Consequently, the bending torque that acts on an intact flagellum due to the action of the dynein motors will tend to accumulate on doublet elements 1 and 5-6 of the 9 + 2 axonemal ring. A more extensive analysis of this and an illustration to help the reader visualize this relationship can be found in an earlier report (26).

The bending torque that results from the action of the dynein motors is a consequence of the force couple acting between the terminal elements of the active group of dyneins (in most cases doublets 1 and 5-6), multiplied by the spacing (or lever arm) between these same elements. Because the linear tension and the compression present on the terminal doublets of the active sequence are the accumulation of oppositely directed force contributions from the same group of active dyneins, the linear tension on one terminal element will be equal and opposite to the compression on the other terminal element. The magnitude of the bending torque that is M_active will be a product of the tension multiplied by the separation of the terminal elements. If all the dyneins on one side of the axoneme act in concert to bend the flagellum in one direction then the effective spacing that constitutes the lever arm will be the axoneme diameter.

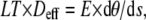(4)

where LT is the linear tension and D_eff is the effective separation based on the axoneme diameter.

In mammalian sperm, the axoneme is modified from the simple 9 + 2 arrangement that is found in most other cilia and flagella. The outer nine doublets do not form a connection to the basal body, but instead are connected along much of their length to the outer dense fibers (ODFs). These auxiliary structures are a persistent feature in the sperm of mammals and they anchor at the base of the flagellum to a structure called the connecting piece (27). Consequently, the linear tension developed by the dyneins, and deposited on the doublets, is secondarily transmitted to the basal anchor by the ODFs. The ODFs have a somewhat larger spatial separation than the doublets themselves and as a result they increase the effective diameter across the axoneme, especially in the basal portion of the flagellum. A table of the effective diameters (D_eff) across a bull sperm axoneme was published previously (26) and was used in the current analysis. Therefore, the linear tension on the outermost elements of the bull sperm axoneme can be found using the formula:

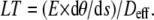(5)

In the case of bull sperm reactivated at 0.1 mM ATP with their heads stuck and with their flagella near the point of beat direction reversal, the linear tension acting across the axoneme may be found by this simple relationship. The stiffness at the point of consideration needs to be specified and the curvature must be obtained from measurement.

The linear tension can also be used to find the magnitude of the transverse force acting across the axoneme. The largest component of the transverse force acting across the axoneme can be found by the relationship:

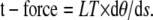(6)

This component of the total t-force is typically more than 10 times larger than the component resulting locally from the interdoublet linkages (28,29) and therefore may be considered the main compnent of distorting force acting on the axoneme at the time of dynein bridge switching.

We used Eq. 3 to calculate the active moment and Eqs. 5 and 6 to calculate the t-force acting on the bull sperm flagellum at the switch point of the beat. Fig. 5 shows schematically the procedure used for the data acquisition and the subsequent calculation of the t-force for an example cell. Once the frame that most closely represented the switch point of the beat was identified, a circle was fitted to the flagellum at the point of maximum curvature. We consistently found this to be at 7–8 μm from the head-tail junction. The measured curvature at this position, and a stiffness of 1.4 × 10⁻²⁰ N × m² for the bull sperm flagellum at the same location (estimated from the regression line of Fig. 4), was used to find the active moment by applying Eq. 3. The linear tension on the outer elements of the axoneme was then found using Eq. 5 and an effective diameter of 2.7 × 10⁻⁷ m for this flagellar position from the appended table in Lindemann (26). This linear tension acting across the axoneme was then used in Eq. 6 to determine the t-force. The image and example calculation shown in Fig. 5 is for one cell from the 4 mM ADP data set.

FIGURE 5.

Calculation of the t-force from the principal bend image of a bull sperm at the switch-point of the beat. The method we used to analyze the magnitude of the t-force, with and without ADP, is illustrated for one of the cells included in the data set. The sperm cell is reactivated with 0.1 mM ATP and is stuck to the slide by its head with the flagellum beating freely. The selected frame is the one that exhibits the greatest curvature in the region 5–10 μm from the head-tail junction (i.e., the next captured image showed less curvature and a switch in direction of beating in that same segment). The curvature is measured and the radius of curvature, r, is recorded. The radius of curvature, stiffness, and effective diameter are used in the formula shown to find the tension on the outermost axonemal component that is inducing the bend (see text for details). The tension on the axoneme multiplied by the curvature of the bend yields the global component of the t-force acting across the axoneme. The actual calculation for the specific cell shown is given as an example. This cell was treated with 4 mM ADP and yielded a t-force of 2.5 nN/μm.

Table 3 presents the accumulated t-force values for reactivated bull sperm with 0.1 mM ATP only (control) and supplemented with 1 mM or 4 mM ADP. There is a highly significant difference (p < 0.0001) in the t-force values between the control and the cells at both ADP concentrations. Although not included in the table, the effect of 4 mM ADP on the t-force was also significant (p = 0.0002) when only 1 mM MgSO₄ was present (1.9 ± 1.1 nN/μm, n = 7). The difference is sufficiently large that it is well beyond the potential error in estimating curvatures by our method, which we have found to be approximately ±10%. We naturally have some concern about the validity of the stiffness value because the scatter in our accumulated stiffness data is so large. The scatter is not something we have been able to eliminate by improvements in our measurement techniques, but seems to be a real cell-to-cell variation inherent in mammalian sperm. Repeated stiffness measurements on a single cell do not show as much disparity. Much finer measurements carried out on sea urchin flagella using the same technique also do not show the same degree of scatter. This leads us to the conclusion that there is a large cell-to-cell variation in the stiffness of bull sperm and other mammalian sperm, as we have comparable data on rat (23) and mouse (K. Lesich and C. Lindemann, unpublished).

TABLE 3.

t-Force analysis of bull sperm flagella

Flagellum	0.1 mM ATP	0.1 mM ATP and 1.0 mM ADP	0.1 mM ATP and 4 mM ADP
Intact
t-force (nN/μm)	0.7 ± 0.29	3.2 ± 1.7*	2.9 ± 1.2*
n	17	28	19
Cut
Flagellar length range (μm)	18–35	14–29	22–39
Flagellar length mean (μm)	25	22	29†
Precut t-force (nN/μm)	1.1 ± 1.0	3.5 ± 1.4‡	3.2 ± 1.1‡
Postcut t-force (nN/μm)	1.0 ± 0.8	2.3 ± 1.5§	4.0 ± 1.4*
n cut cells	7	6	9
Total n cuts	9	17	17

Data are mean ± SD.

^*p < 0.0001.

^†p < 0.05 compared to 1 mM ADP.

^‡p < 0.005.

^§p < 0.05.

Our stiffness results presented in Fig. 4 indicate that the range of stiffness is not influenced by the presence of ADP under the conditions of our stiffness measurement protocol. Therefore, it is unlikely that a systematic lowering of the stiffness can account for the large increase in curvature that is raising the estimated t-force.

We also devised a second method of estimating the active moment and the t-force in a bull sperm to validate our findings from the analysis of the data from beating cells. We have shown previously that when reactivated bull sperm are shortened by microdissection, the beat will arrest when a critical minimal length is reached. For ATP only conditions this length is ∼15 μm (30). When flagella are a shortened by dissection to a length of 16–25 μm, beating is intermittent with periodic stalls at the switch point where maximum curvature is reached. We used this method to look at the curvature, and hence the torque and t-force, of transiently stalled, clipped flagella to determine the effect of ADP on the active moment and the t-force generated in these cells. In a transient arrest the drag term of the moment balance equation can be safely set to zero, as motion has stopped.

We confirmed that there is a similar increase in the curvature and therefore, an increase in the active moment and the t-force of transiently arrested bull sperm flagella when ADP is present. Our accumulated data from the clipping study is also shown in Table 3 for comparison with the results from intact flagella. Both approaches, the t-force estimates from the intact beating cells and the results from clipped cells, have some potential deficiencies. The uncertainty concerning the validity of the zero drag assumption is a drawback of the intact cell data. The potential for introduced damage to the axonemal integrity of the clipped cells due to rolling, pulling or crushing the flagellum is inherently a problem with the clipped study. Together, the two approaches compliment each other and give a greater certainty to our t-force result.

As seen in Table 3, there was a reasonably good agreement between the postcut and precut t-force values for the same cohort of cells, with the exception that at the 1 mM ADP concentration the arrests at lengths shorter than 22 μm showed a substantial decline from the precut values. This is the underlying cause of the drop from 3.5 to 2.3 nN/μm in the t-force. A similar drop was not noted for the shorter clipped flagella at 4 mM ADP and several of the longer clipped flagella actually showed a substantial increase in the curvature and t-force. This accounts for the somewhat increased mean value after clipping. Neither the decrease at 1 mM nor the increase at 4.0 mM was statistically significant. The other observation of interest was that the 4 mM ADP-treated cells showed complete arrest of the beat at a longer average length, as compared to the ATP only controls, 24 μm (n = 4) vs. 15 μm (30), respectively.

The results from clipped cells confirm the validity of the assumption of zero drag torque used in the dynamic analysis of beating reactivated cells. Removal of the distal 30 μm of the flagellum renders the shape of the flagellum monotonic in curvature, as seen in Fig. 6, and movement of the flagellum becomes uniform in direction, in that the recurrent R-bend on the distal flagellum is eliminated. Therefore, when the P-bend reaches maximum curvature there is no residual movement of the flagellum through the surrounding fluid at all. Under these conditions the t-force at the switch point of the beat is still maintained at approximately the same levels as in the intact beating flagella. This provides an independent supporting estimate of the increase in t-force produced by ADP and at a similar confidence level as in the intact cells. The fact that at least a majority of the clipped cells still generate a similar curvature and t-force after cutting to lengths near the arrest length also confirms our assertion that the t-force at the switch point of the beat is a relatively conserved feature.

FIGURE 6.

The beat switch-point in bull sperm flagella shortened by microdissection. The cells shown were reactivated with 0.1 mM ATP and shortened by microdissection with a glass microprobe. The frames displayed are the images exhibiting the greatest curvature in the beat. The reactivation medium included 0 mM ADP (a), 1 mM ADP (b), and 4 mM ADP (c), respectively. Note that the curvature of the most strongly bent part of the flagellum is similar to the principal bends of the intact cells shown in Fig. 1. The same analysis as illustrated in Fig. 5 was used to estimate the t-force on cut flagella and the results are summarized in Table 3. The shortened sperm have only one bend present along the entire length of flagellum. Because of this, the entire flagellum is transiently stationary at the end point of principal bend formation and consequently has zero velocity relative to the surrounding fluid. The data from the clipped sperm show that the assumption of zero viscous drag in the analysis of t-force on the intact cells was justified and gives an additional validation of the effect of ADP on the t-force. Bar = 10 μm.

An ancillary observation also tends to support the conclusion that the presence of ADP markedly increases the transverse tension on the beating axoneme. Triton X-100 extracted bull sperm lack a plasma membrane but still retain a substantial sheath of protein in both the midpiece and principal piece (2). We do not see spontaneous splitting of the axoneme and extrusion of internal microtubules in ATP-reactivated bull sperm models during the first 20 min of reactivation. In contrast, we have observed and recorded at least eight events in the course of this study where reactivated sperm in the presence of 4 mM ADP have undergone structural failure in the midpiece region with consequent extrusion of internal axonemal elements. When observed, this always occurs in the same region (7–12 μm from the head-tail junction) where the curvature, and hence the t-force, is greatly elevated. This leads us to the conclusion that there is a significantly greater stress on the axoneme and supporting structures in the presence of ADP, especially in the region where the principal bend develops its maximum curvature.

DISCUSSION

The results reported here provide a new way to view the seemingly paradoxical effects of ADP on flagellar motility in a unified conceptual framework. We found that in the presence of 1 mM and 4 mM ADP the curvature, active bending torque, and the t-force are elevated at the switch point of the flagellar beat. We have also determined that ADP does not cause these effects by changing the stiffness of the flagellum nor does it seem to alter significantly the stalling force that the dyneins can generate. Under these circumstances there must be a significant change in the level of t-force at the switch point of the beat. This tells us something important about how ADP acts on dynein. It implies that dynein can remain engaged in the force producing state under greater amounts of interdoublet stress when ADP is present.

This suggests an explanation for the increased bend angles and increased wavelength that are observed in the presence of ADP (3). The largest component of t-force is a product of curvature and longitudinal force acting on the doublets. Development of a greater t-force therefore requires a greater curvature to develop, or a greater longitudinal force on the doublets, or both. Increased bend angles result when flagellar bends have a greater curvature. Increased wavelength correlates with an increase in the interbend distance, which in turn correlates with an increase in the number of dyneins involved in the process of bend formation, and a greater longitudinal force on the doublets. The increase we observe in the arrest length of the cut flagella in the presence of 4 mM ADP seems to suggest that more dynein are also required to reach the switch point when ADP is present. Therefore, it seems that in bull sperm an increase in both the number of participating dynein and the maximum curvature contributes to achieving a greater t-force at the crest of each bend.

The primary concept that emerges from this study is that in the presence of ADP more t-force is developed at the switch point that terminates the action of the dynein bridges. In the context of the Geometric Clutch hypothesis, outwardly directed (negative) t-force is required to overcome the adhesion that the active dyneins generate when they pull on the adjacent doublets. The origin of this adhesive force is the component of tension on the dynein stalk that is orthogonal to the axis of the doublets (29). Essentially, a large outwardly directed t-force is necessary to pry the doublets apart and bring about release of the dyneins from their binding sites. ADP apparently makes the dynein attachment more resistive, therefore making it harder to pry the doublets apart and terminate the action of the dynein. In the Geometric Clutch computer model this property of the dynein equates to the concept of bridge “adhesion” (28), and in the computed model is controlled by the parameter called the adhesion scaling factor, which determines how much of the dynein force generated by each dynein resists the t-force.

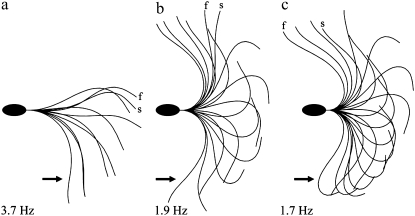
A version of the Geometric Clutch specifically adapted to model a bull sperm flagellum was published (26). This model successfully predicted and replicated observed behaviors of real bull sperm (30). Fig. 7 shows the output of the computer model for one beat cycle of the flagellum in the head stuck configuration. Fig. 7, a–c shows the way the beat changes when the adhesion scaling factor values are increased. In Fig. 7 a the adhesion scaling coefficients are set at 2.4 and 2.5 for the P and R bend dyneins, respectively. They are raised by 15% in Fig. 7 b and by 20% in Fig. 7 c, with all other modeling parameters held constant. As shown, the beat amplitude increases from image a to image c, whereas the beat frequency drops to ∼50% of the original. Most importantly, the curvature of the principle bend at the switch point of beat reversal shows a striking increase. All of these changes are consistent with our experimental results on the reactivated sperm models when ADP concentration is increased. The modeled iteration that most closely represents the position of the real cells we have used for our analysis is indicated with an arrow for comparison to the images in Fig. 1 and Fig. 6.

FIGURE 7.

The effect of varying dynein adhesion in the Geometric Clutch computer model. The version of the Geometric Clutch model specifically developed to simulate a bull sperm flagellum (24) was used to explore the effect of dynein adhesion on the simulated beat. Three panels show the result of executing the model program, in the head stuck configuration, while varying only the scaling factor for dynein adhesion. The scaling factor was increased by 15% between a and b and by an additional 5% between b and c. The scaling factor determines what fraction of the dynein force in the model is used to reduce the probability of detachment of the dynein bridges. An increase of this single parameter of the model, while holding all other modeling parameters constant, produces some of the same changes that are actually seen in reactivated bull sperm when the ADP concentration is increased. There is a strong increase in the curvature of the principal bend at the switch-point frame (arrows). There is also an increase in the amplitude of the beat and a similar reduction in the beat frequency, as exhibited by the real sperm. In the context of the Geometric Clutch mechanism, this indicates that ADP may be exerting its action on the beat cycle by making the dynein motors more difficult to detach from their binding sites on the adjacent doublet.

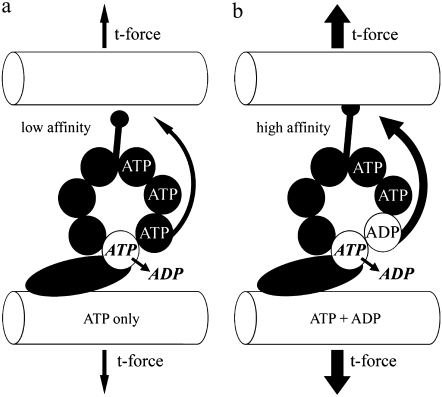
We propose the following mechanism of action of ADP, which is consistent with our results and also with the results of the other investigations we have noted. ADP delays the release rate for bound ADP, resulting in a higher number of dynein heads in the high affinity MT-bound step of the cross-bridge cycle. This may be accomplished by a specific regulatory site as first proposed by Omoto and her collaborators (4,5,9). Fig. 8, which is based on a regulatory scheme recently elaborated by Inoue and Shingyoji (17), illustrates how such a nucleotide regulation could result in a change in the t-force threshold for dynein disengagement. If such a relationship is validated, it would establish an important touchstone linking much of the experimental work on dynein with the theoretical framework provided by the Geometric Clutch hypothesis.

FIGURE 8.

A hypothetical mechanism relating ADP, dynein, and t-force. This illustration is based on the proposal put forth by Inoue and Shingyoji (17), and supported by our results presented in this study. The binding of ADP to a long residency regulatory site on the globular domain of the dynein head increases the force transfer to the neighboring doublet by enhancing the affinity of tubulin binding at the tip of the dynein stalk. This may be accomplished by enhanced transfer of a coordinating signal through the multiple p-loops of the AAA domain and/or an enhanced stability of the complete 3-D structure. The ultimate consequence, as relates to our work, is that the t-force that can be held and transferred through the stalk-tubule binding site is also affected, and therefore the release point to switch the dynein “off” is greatly increased. This results in the modification of the beat cycle to a higher t-force threshold for switching, consistent with what we see experimentally.

If the dynein spend a longer proportion of the cross-bridge cycle in the high affinity state when ADP is bound to a regulatory site, this would in turn slow down the cross-bridge cycle time. This ultimately reduces the free sliding rate at a given ATP concentration and hence, the experimentally observed reduction of the disintegration rate of axonemes in the presence of ADP (7). On the other hand, it would also explain why ADP gives rise to a more extensive activation of sliding in fragmented axonemes (8,9). This is because the dyneins spend a longer time in the high-affinity MT-bound state. This is the state that contributes to the adhesion between the doublets. It is also the property of the dynein that initiates a cascade of attachment between the outer doublets. Adhesion is the specific property that gives the computed version of the Geometric Clutch its ability to spontaneously start up beating (28). It is noteworthy that real flagella that are unable to beat spontaneously can in many instances be started by providing ADP (4,5). Therefore, our theoretical interpretation is in good concordance with several experimental observations.

It was noted that several of the effects of ADP are similar, or identical, to the effects of reducing Mg-ATP concentration (3). This issue also warrants some consideration. ATP binding to the dynein head is known to be the trigger for the release of the dynein from its binding site on the MT (31–33). When ATP concentration is very low, this necessitates more of the dynein remaining in the high affinity bound state. In this regard, very low ATP can bring about an increase in the adhesion between doublets in much the same way that ADP can. This is seen in the conversion of outer arm dynein to a processive motor when ATP concentration is reduced sufficiently (34). At the extreme, if ATP concentration is low enough then nearly all of the dyneins are in the bound high affinity state and rigor is the result. As the axoneme approaches the rigor state the capacity for spontaneous motility is lost. At the opposite extreme, when ATP concentration is very high many types of cilia and flagella also tend to lose their ability to sustain spontaneous beating, especially if ADP is kept low. Bull sperm preparations subjected to concentration of ATP 5 mM or higher will be completely immotile or exhibit only slight jittering motion (35). Including ADP in the mixture can convert the sperm to vigorous motility. Relaxation of the flagellum at high ATP may be a result of a greatly reduced affinity of the binding site on the dynein head; in essence, too little adhesion develops to support a cascade of dynein attachment and spontaneous beating is lost. ADP can sometimes restore beating under these conditions.

Under the same conditions that ADP can restore beating to quiescent flagella, mechanical bending of the flagellum was shown to facilitate a restoration of a beat cycle (6,36,37). In an intact flagellum, imposing a bend creates a positive t-force that forces the doublets closer together (28). This can apparently act as a stimulus to dynein-bridge formation and aid in a cascade of dynein activation when the inherent adhesive properties of the dynein are insufficient to produce a spontaneous cascade.

This viewpoint is supported experimentally by the findings that the isolated outer arms become more processive as ATP concentration is reduced (34) and inner arms become more efficient at translocation as ADP levels are increased (38). Processive motors by definition have the ability to hang on to the cargo. In isolated preparations of motor proteins, processive behavior is the most closely related property to the adhesion concept in the Geometric Clutch hypothesis, because both terms relate to the ability of the motors to hold on to their cargo.

In conclusion, it seems that ADP exerts an action on flagellar motility by increasing the threshold of t-force required to terminate an episode of bend formation. A strong case can be made that this action is a result of ADP increasing the population of dynein molecules that reside in the high MT binding affinity state. The beauty of this simple interpretation is that it can provide a uniform and consistent basis to explain the effects seen at high and low ATP concentrations, as well as the mysterious effects of ADP on spontaneous beat generation in immotile flagella.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.