Are Current Molecular Dynamics Force Fields too Helical?

Abstract

Accurate force fields are essential for the success of molecular dynamics simulations. In apparent contrast to the conformational preferences of most force fields, recent NMR experiments suggest that short polyalanine peptides in water populate the polyproline II structure almost exclusively. To investigate this apparent contradiction, with its ramifications for the assessment of molecular force fields and the structure of unfolded proteins, we performed extensive simulations of Ala₅ in water (∼5 μs total time), using twelve different force fields and three different peptide terminal groups. Using either empirical or density-functional-based Karplus relations for the J-couplings, we find that most current force fields do overpopulate the α-region, with quantitative results depending on the choice of Karplus relation and on the peptide termini. Even after reweighting to match experiment, we find that Ala₅ retains significant α- and β-populations. In fact, several force fields match the experimental data well before reweighting and have a significant helical population. We conclude that radical changes to the best current force fields are not necessary, based on the NMR data. Nevertheless, experiments on short peptides open the way toward the systematic improvement of current simulation models.

All-atom molecular dynamics (MD) simulations are a powerful tool for the exploration and mechanistic interpretation of biological phenomena at a molecular scale (1). Nonetheless, longer simulation times and interest in the unfolded states of proteins (2–4) and in natively unstructured peptides (5,6) are uncovering deficiencies in the commonly used energy functions, or “force fields” (7), stimulating recent refinements of peptide backbone potentials (8–11). Conventional force field development relies heavily on gas-phase quantum chemical calculations and spectroscopic and thermodynamic data for small molecules (7). Experimental data for short peptides in solution would be a valuable addition (12), even if those data are usually averaged over heterogeneous equilibrium ensembles of structures (13,14).

Polyalanine is a well-established model for studies of peptide conformation and helix formation (2,4,11,15–18). An elegant recent study by Graf et al. (19) used scalar couplings measured by NMR in a series of polyalanine peptides (Ala₃ to Ala₇) to probe the distributions of backbone (φ,ψ) angles. Scalar couplings calculated from MD simulations were in only modest agreement with experiment. However, the simulation data could be reweighted by adjusting the relative populations of the α-, β-, and polyproline-II (ppII) regions of the Ramachandran map, with the implicit assumption that the simulations give a reasonably accurate sampling within each state. Remarkably, the reweighted populations indicated that Ala₃ to Ala₇ almost exclusively populate the ppII region of Ramachandran space with a small population of the β-region and negligible α-population.

In view of the importance of this conclusion for future force field development and structure in unfolded proteins (2,4), we have revisited it, employing a large set of MD simulation trajectories of polyalanine in explicit solvent at 300 K (4.9 μs total) (20,21). Details of the simulations are available in Supplementary Material, Data S1.

Remarkably, the 12 force field variants employed differ widely in their sampling of the Ramachandran space. Based on the scalar coupling data, most force fields indeed have too large a helical propensity. However, the quantitative results are sensitive to i), the choice of Karplus relation; ii), the protonation state; and iii), terminal blocking. Overall, we conclude that the NMR data are consistent with force fields that give a small helical population for Ala₅, and do not require exclusive formation of ppII structure.

We classified (φ,ψ) space into “α” (–160 < φ < −20 and −120 < ψ < 50), “β” (–180° < φ < −90° and 50° < ψ < 240°; or 160° < φ < 180° and 110° < ψ < 180°), “ppII” (–90° < φ < −20° and 50° < ψ < 240°), and “other” regions, based on a set of φ,ψ frequencies recently derived from the Protein Data Bank (see Fig. S1 in Data S1). The more restrictive definition of Graf et al. (19) truncates the α-region in particular (see Fig. S1 in Data S1). The fraction of residues in the “other” category was always <0.5% except for the Gromos force fields (∼3%) and was combined with ppII in the subsequent analysis (note that omitting it altogether has a negligible effect on the results).

We quantified the agreement between experimental J-couplings and those calculated from unweighted simulation trajectories via Karplus relations (22) using

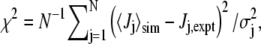where is the average of coupling j from the simulation. The set of N experimental couplings (19) J_j,expt includes ³J_HNHα, ³J_HNC', ³J_HαC', ³J_CC', ³J_HNCβ (probing φ), ¹J_NCα, ²J_NCα (probing ψ), and ³J_HNCα (probing both φ and ψ) for each of the five residues. σ_j is the estimated systematic error in the couplings determined from the Karplus equation, arising mainly from the neglect of substituent effects (23) in the Karplus equation parameters (values and sources for σ_j given in Table S4 in Data S1). Sampling errors in 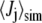and experimental errors in J_i,expt are relatively small and so were not added to σ_j. We used the Karplus parameters of the original article (19), and two additional sets, with parameters determined from DFT calculations (24) on Ace-Ala-NMe (DFT1) and Ala-Ala-NH₂ (DFT2). These may be more relevant to alanine, with its small side chain, than parameters fitted after pooling data from different residue types.

The α-helical content for different force fields varies between 13 and 98%, with high α-content resulting in poor agreement with experiment (Fig. 1, Table 1, and Table S5 in Data S1). However, a range of force fields with 10–30% α-content give a low χ² ≤ 2; with the χ² definition used here, this means the deviation from experiment is comparable to the error σ_j. In general, simulations of zwitterionic peptides or those with protonated C-termini resulted in lower χ² than those for blocked peptides (see below).

FIGURE 1.

Secondary structure populations. Ternary diagrams on the left (A, C, and E) and right (B, D, and F) show the relative populations before and after reweighting for (A and B) the original Karplus parameters (19), (C and D) DFT1, and (E and F) DFT2 (24), respectively. Symbol areas are proportional to 1/χ²: (blue) blocked termini, (red) zwitterionic, (yellow) protonated C-terminus without ions, (green) protonated C-terminus with ions. Arrows indicate the direction in which each axis should be read, and colors indicate the corresponding scale and isolines.

TABLE 1.

Ramachandran populations for Ala₅, before and after reweighting, for some representative force-fields (a full list is available in Data S1)

		Unweighted					Reweighted
	Time (ns)	χ2			Populations		DFT1			DFT2			Orig
FORCE-FIELD		DFT1	DFT2	ORIG	% α	% β	χ2	% α	% β	χ2	% α	% β	χ2	% α	% β
Amber03*	120	1.8	1.5	1.6	33.0	30.7	1.4	11.0	39.9	0.8	8.0	24.5	0.3	6.6	5.3
Amber99SB	120	4.2	4.9	4.2	19.7	55.5	1.7	14.4	31.0	1.0	11.7	18.3	0.6	7.3	6.9
AmberGS	80	5.2	2.8	1.9	45.8	9.8	1.5	3.2	47.5	1.0	4.2	32.6	0.7	3.7	14.8
CHARMM27/cmap*	80	2.0	2.0	2.2	41.5	25.3	1.3	14.0	32.1	1.0	14.1	18.7	0.9	11.4	7.1
OPLS-aa/L*	80	1.8	2.0	2.0	30.9	33.5	1.5	10.0	42.0	1.1	7.7	22.3	0.4	5.2	3.9
Gromos53a6	80	1.8	2.3	2.3	13.5	50.2	1.4	3.4	41.6	1.0	3.1	21.3	0.6	2.5	5.3
Gromos43a1*	80	1.4	1.4	1.6	14.0	41.2	1.2	2.4	40.8	0.7	2.3	23.7	0.5	2.6	8.6

In these simulations, the peptides were protonated at both termini (net charge +1).

^*Force fields with χ² ≤ 2.25 before reweighting, corresponding to deviations from experiment up to 1.5 σ_j on average.

To determine the secondary structure populations that give the closest match with experiment, we adopt the procedure of Graf et al. (19). Each trajectory frame of a simulation was reweighted by a factor proportional to exp[−(n_αɛ_α+n_βɛ_β)], where n_α and n_β are the number of residues in the α-and β-regions in that frame, and ɛ_α and ɛ_β are corresponding energy corrections (in k_BT units relative to ppII), which are chosen to minimize χ². The secondary structure content after reweighting is shown in Fig. 1 B, D, and F (optimal ɛ_α and ɛ_β are given in Table S6 in Data S1). Using the Karplus parameters of Graf et al. (19), we also find almost exclusively ppII structure (Fig. 1 B). However, with the DFT1 and DFT2 parameter sets (24), there is a balance between β and ppII structure, with a small α-population (Fig. 1 D and F). Table 1 summarizes the Ramachandran populations before and after reweighting for a representative subset of the force fields.

Terminal effects on helical propensity are significant for short peptides (12), one reason being that the terminal charges at neutral pH oppose the helix dipole. We have quantified this effect by using pairs of simulations: one of a blocked peptide and the other of a C-terminally protonated peptide, both using the same force field. We optimize ɛ_α and ɛ_β for the protonated molecule, which corresponds to experiment, and reweight the blocked molecule with the same values. The results (Fig. 2) show that blocking tends to favor α-structure over ppII; part of the reason for the low helicity reported by the NMR data is likely the use of uncapped peptides with protonated C-termini.

FIGURE 2.

Secondary structure populations for C-terminally protonated (blue) and blocked (red) peptides after re-weighting using (A) the original Karplus equation (19), (B) DFT1, and (C) DFT2 (24). Axes are as in Fig. 1.

The widely varying secondary structure propensities of polyalanine in different force fields (17) (Fig. 1) demonstrate the need for ongoing force field development. Although we find that, in general, current force fields overestimate α-structure, those that best match the experimental J-couplings have a significant α-helical fraction. For force fields for which χ² ≤ 2 before reweighting (Table 1), the helical fraction varies between 14% and 33% (unweighted) and 2% and 11% (reweighted). We also find that terminal blocking significantly increases the α-content of Ala₅. With the same weight factors as for the unblocked peptide, the helical population of blocked peptides is between 12% and 23%. Lastly, the choice of Karplus equation parameters affects the results. Residue-specific parameters for Karplus equations should improve the accuracy of structural information obtained from scalar couplings (24), which would make them useful in force field refinement.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.