Cooperativity and Specificity in Enzyme Kinetics: A Single-Molecule Time-Based Perspective

Abstract

An alternative theoretical approach to enzyme kinetics that is particularly applicable to single-molecule enzymology is presented. The theory, originated by Van Slyke and Cullen in 1914, develops enzyme kinetics from a “time perspective” rather than the traditional “rate perspective” and emphasizes the nonequilibrium steady-state nature of enzymatic reactions and the significance of small copy numbers of enzyme molecules in living cells. Sigmoidal cooperative substrate binding to slowly fluctuating, monomeric enzymes is shown to arise from association pathways with very small probability but extremely long passage time, which would be disregarded in the traditional rate perspective: A single enzyme stochastically takes alternative pathways in serial order rather than different pathways in parallel. The theory unifies dynamic cooperativity and Hopfield-Ninio's kinetic proofreading mechanism for specificity amplification.

There is a resurgence of interest in the theory of enzyme kinetics due to several recent developments in biochemical research: Foremost is the systems approach to cell biology which demands quantitative characterizations of cellular enzymatic reactions in terms of Michaelis-Menten (MM)-like kinetics (1–3). Second, recent advances in single molecule enzymology have generated exquisite information on protein dynamics in connection to enzyme catalysis (4). And third, the theoretical advance of our understanding of biochemical reaction networks in terms of the thermodynamics of open-system, nonequilibrium steady state (often nowadays abbreviated as NESS) (5–7). Single-molecule enzymology and enzymatic reactions inside cells have shown the necessity of modeling enzyme reactions in terms of stochastic mathematics (8–13).

The above-mentioned developments have led us to reexamine the concept(s) of cooperativity in the context of enzyme kinetics. Protein conformational changes, especially those induced by ligand bindings and/or covalent modifications, are one of the cornerstones of molecular biology that connect macromolecular physics with cellular biological functions. Beside allosterism, cooperativity has been studied in monomeric enzymes with only a single substrate binding site; this has led to the important concepts of hysteretic behavior and mnemonic enzymes (reviewed in (14–17)). It is understood that such cooperativity is a NESS phenomenon. Therefore, it is fitting to call it dynamic cooperativity (18) in contrast to equilibrium allosterism. Kinetic cooperative is another term used in the literature. This work, however, focuses on nonequilibrium cooperative behavior in steady states rather than on transient kinetics. A nonequilibrium steady state (NESS) has constant chemical fluxes in the system, while an equilibrium state has zero flux in each and every reaction (19).

The early experimental evidence for fluctuating protein dynamics was provided by Linderstrøm-Lang and his amide proton hydrogen-deuterium exchange method (20). Dynamic cooperativity can occurs in enzymes with slow fluctuating conformational substates within the unbound (E) form. Such slow fluctuations, also called dynamic disorder, are precisely what has been firmly established in recent single-molecule experiments (4,11,13).

On the theory side, an alternative to the MM approach that is particularly applicable to single-molecule enzyme kinetics has also emerged. This theory, originated by Van Slyke and Cullen in 1914 (21), develops enzyme kinetics from a time perspective rather than the traditional rate perspective. As we shall show, the time approach, while it is equivalent in principle to that of MM, provides a much more intuitive understanding of the nature of dynamic cooperativity.

This article is organized as follows. We first establish a single-molecule perspective for enzyme kinetics in terms of state probabilities, cycle fluxes, and most importantly, mean first passage times: This is a new kinetic language that differs from the traditional one. Using this distinct approach, we present some of the results well-known in textbooks, specifically the double reciprocal relation for irreversible enzymes and the Briggs-Haldane result on reversible enzymes. Stochastic enzyme kinetics with more than one, but still a small number of copies of an enzyme, is studied in the section Single Enzyme to Small Copy Numbers Inside Cells. This is a realistic situation for many regulatory reactions inside cells. Small biochemical reaction systems are now routinely modeled by the chemical master equation (22). We present a novel relationship between the theory of single molecules and the quasi-steady-state analysis of the chemical master equation of enzyme kinetics recently developed by Rao and Arkin (23). The section Fluctuating Enzymes and Dynamic Cooperativity introduces dynamic cooperativity, which appears as sigmoidal behavior, as it emerges in monomeric, single-site enzymes with conformational fluctuations in the unbound state. Two necessary conditions for such behavior are established, namely, slow conformational fluctuations and a NESS driven by the substrate turnover reaction. The Cooperativity and Specificity section discusses cooperativity and specificity, e.g., sensitivity to substrate concentration and to affinity, as two manifestations of a single theory. Both dynamics cooperativity and the Hopfield-Ninio's kinetic proofreading mechanism for specificity amplification (24,25) exhibit a square-law effect. A summary and a brief outlook are provided in the last section.

MICHAELIS-MENTEN-BRIGGS-HALDANE KINETICS REVISITED

The year 2002 marked the 100th anniversary of V. Henri's original theory of enzyme kinetics (26), which was rediscovered some 11 years later, in 1913, by Michaelis and Menten (27) in Germany; their names are now permanently associated with one of the most celebrated mathematical equations in biochemistry. Enzyme kinetic theory, together with concepts such as “rapid equilibrium” and “quasi-steady-state,” are taught in almost every biochemistry class. What is less known is the work of van Slyke and Cullen (21) that appeared in 1914 in the U.S. and which contains an approach based on enzyme cycle time rather than reaction flux. (The article contains a discussion of Henri's work. This approach had been in the literature, but to my knowledge it was only fully developed in 1987 by Ninio (28).) The latter approach is particularly apt for analyzing stochastic data from studies of single enzyme molecules one at a time.

This alternative formulation differs significantly from that of the classic MM kinetic theory. What has been discovered is that the classic results can be derived in a much more natural and fundamental way through a single-molecule perspective. It provides the necessary bridge between the study of the rich dynamics of single enzyme molecule, both in vitro and in situ, and the classic kinetic parameters such as the Michaelis constants and maximal velocities.

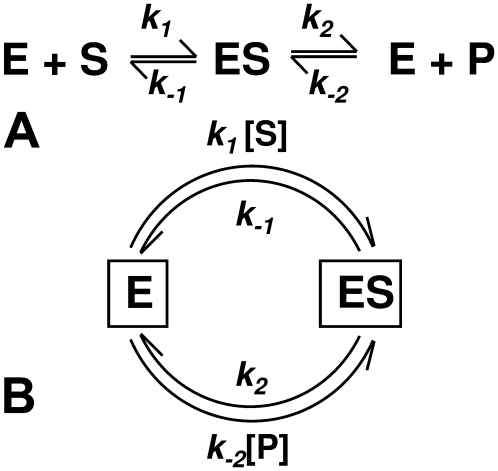
The simplest enzyme kinetic model assumes one enzyme-substrate complex, ES, as the intermediate state in the transition from the substrate S to product P (Fig. 1 A). The traditional language for enzyme kinetics is based on concentrations and rates. Studying enzyme kinetics in terms of single enzyme molecules, however, requires a different way to think about the problem and to look at the data. One no longer deals with deterministic concentrations of a substrate [S](t) or a product [P](t), but rather with the stochastic numbers of molecules N_S(t) or N_P(t). While the stochastic observations N_S(t) and N_P(t) are not themselves reproducible in repeated measurements, their statistical behavior is. Hence, instead of asking “what is the concentration of the product at time t,” we shall now ask “what is the probability of having number n of product molecules at time t,” that is, P_P(n, t) = Pr {N_P(t) = n} where n takes positive integer values and P_P(n, t) is between zero and unity.

FIGURE 1.

The simple, classic enzyme kinetic scheme in panel A corresponds to a cyclic reaction of a single enzyme in panel B. It is easy to obtain the steady-state probability for E and ES, namely, p_E = (k_–1 + k₂)/(k₁[S] + k_–1 + k₂ + k_–2[P]) and p_ES = (k₁[S] + k_–2[P])/(k₁[S] + k_–1 + k₂ + k_–2[P]), and the steady-state cycle flux = k₁[S]p_E – k_–1p_ES = k₂p_ES – k_–2[P]p_E. If [P] = 0, we have Eq. 1.

It turns out that the probability of “having a number n of the product molecules at time t” is precisely the probability that “the n^th product molecule arrives before time t and the (n + 1)^th arrives after time t,” i.e., Pr {N_P(t) = n} = Pr {T_n ≤ t, T_n+1 > t} where T_n is the arrival time of the n^th product molecule, that is, the time for the enzyme to complete n cycles. Since the enzyme returns to its unbound state after each catalytic cycle, the difference (T_n+1 – T_n) is the waiting-time for the n^th individual turnover; note that it is statistically identical to and independent of (T_n – T_n–1). Therefore, single-molecule enzymology for irreversible enzymes focuses on the statistical distribution of individual enzyme cycle times (4). (For reversible enzymes, the argument is more complex, see below.)

If the substrate-to-product transition has one single rate-limiting step, then N_P(t) and T_n are known to be Poisson processes (29). Most enzymatic reactions are multistep reactions, however. Hence the study of the Poisson process has to be generalized to what is known as renewal processes in the theory of probability (30). Simply put: the repeated irreversible enzyme cycles with random duration can be modeled as one might for the repeated changing of light bulbs. If the enzyme reaction is reversible, then one needs to consider both the waiting-time distributions for forward and backward cycles. I first carried out such analysis for single-enzyme kinetics in the context of single motor proteins (ATPase) and MM kinetics (8,31). More extensive recent development can be found in the literature (32–34).

Lineweaver-Burk double reciprocal relation: a single-molecule derivation

As we have discussed, from the perspective of the single enzyme the substrate turnover kinetics in Fig. 1 A are intimately related to the cycle kinetics of the enzyme as shown in Fig. 1 B. Thus, one naturally seeks to compute the steady-state cycle flux. The steady state is sustained by a constant provision of the substrate and removal of the product. For a laboratory system with a single molecule, this requires either a regenerating system or substrate/product in excess. The steady-state probabilities for a single enzyme are found to be

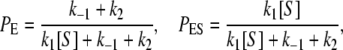(1)

while the steady-state cycle flux, i.e., the velocity of the enzymatic reaction, is

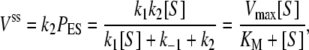(2)

where the MM constant and maximal velocity are K_M = (k₂ + k_–1)/k₁, V_max = k₂.

The mean waiting time, or mean first passage time, 〈T〉, can also be obtained as well. Decomposing the overall reaction of converting one S to one P, there is first, the binding step taking mean time 1/(k₁[S]); then there is the dwell time in the state ES, 1/(k_–1 + k₂); and finally the S molecule either becomes a P or returns back to S, which means arrival or an additional time 〈T〉 with corresponding probabilities k₂/(k_–1 + k₂) and k_–1/(k_–1 + k₂). Hence, in total, we find (21,28):

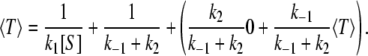(3)

By rearranging we see that the equation for 〈T〉 can be written as α₁〈T〉 = 1/(k₁[S]) + α₂ in which α₁ and α₂ are independent of [S]; indeed, by solving Eq. 3 for 〈T〉 explicitly, we obtain

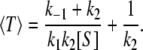(4)

On comparing this with Eq. 2, we see that 1/〈T〉 = V^ss: the flux per enzyme is precisely the inverse of the mean time per turnover.

One immediate insight from the above derivation is that no matter how complex the enzymatic reaction mechanism is, including protein dynamic disorder, as long as there is only one unbound form of the enzyme, E, the mean waiting time always has a term associated with the time for binding (∝ 1/(k₁[S])) and a term independent of [S]: This implies a straight line in the Lineweaver-Burk double-reciprocal plot (2,3), an alternative way of saying, MM hyperbolic kinetics.

The probability distribution for the waiting time T can also be calculated (4); the result is

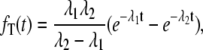(5)

where 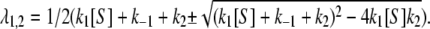It is easy to verify, through a little calculation, that the mean waiting time, 〈T〉 = (λ₁ + λ₂)/(λ₁λ₂), which agrees with Eq. 4. The distribution is not exponential but rather peaks at t* = 1/(λ₁ – λ₂) ln(λ₁/λ₂). For an experimentalist who measures f_T(t), its shape thus contains valuable information regarding enzymatic mechanism.

Reversible reactions, nonequilibrium steady state, and the Haldane relation

We now turn to the simplest reversible enzyme mechanism for a single enzyme, namely the Michaelis-Menten-Briggs-Haldane (35) reactions, shown in Fig. 1. One can again obtain the steady-state cycle flux as above. (Details are available in Fig. S1 in Supplementary Materials, Data S1, Sec. 1.) One can also analyze the reversible enzymatic reaction in terms of the cycle times of transforming one S into a P and turning one P to an S. To do that, we redraw the kinetic scheme in Fig. 1 A as

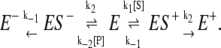(6)

To compute the waiting-time distributions for individual forward and backward cycles, we suppose that the enzyme starts in the central E state, and can either bind a substrate and go forward or a product and go backward. A cycle is completed when the system reaches either the E⁺ state or the E⁻ state. The mean cycle time is then

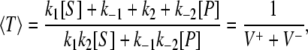(7)

where V⁺ and V⁻ are forward and backward fluxes with V⁺ – V⁻ = V^ss. (see Eq. S3 in Data S1) The difference between the forward flux and backward flux is not because a difference in cycle times; instead, it arises because the probabilities of cycling forward and backward are different, namely,

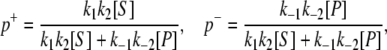(8)

respectively. Hence, in the steady state we have V^ss = V⁺ – V⁻ = p⁺/〈T〉 – p⁻/〈T〉, while the chemical driving force of the biochemical reaction is ΔG_PS = RT ln([S]K_eq/[P]) = RT ln(V⁺/V⁻). This relation between the ratio of V⁺/V⁻ and K_eq is known as the Haldane equation (3). Note that V^ss × ΔG is the amount of heat dissipated from the biochemical reaction per unit time when the reaction is in a nonequilibrium steady state. The fact V^ss × ΔG_PS is never negative is a consequence of the Second Law of Thermodynamics (2,3). It is analogous to the equation in electrical circuit theory: current × voltage = power dissipated.

One can also compute the distributions for the forward and backward cycle times separately. It comes as a surprise that the two distributions are identical (see Sec. 2 in Data S1). However, a more careful study shows that this equality is a generalization of the Haldane relation (36). Furthermore, the Haldane relation and its generalization are consequences of the principle of detailed balance in enzyme kinetics (34,37–39).

FROM SINGLE ENZYME TO SMALL COPY NUMBERS INSIDE CELLS

When there are not just one but rather a few copies of an enzyme, as inside a cell (40), the kinetics needs to take into account the stochastic numbers of enzymes in the states E and ES, etc. The mathematical model for this type of kinetic system the chemical master equation which embodies the so-called Gillespie algorithm (22). (See (2) for an introductory account of the stochastic, chemical master equation modeling.) When the number of substrate molecules is much greater than the number, m, of the enzyme molecules, the stochastic, quasi-steady-state approximation developed by Rao and Arkin (23) applies and shows that the arrivals of the product of an irreversible enzymatic reaction follow a Poisson process with an exponential waiting time distribution. Specifically, one has the distribution 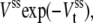where V^ss is the traditional steady-state velocity V_max(n + 1)/(K_M + n + 1), in which n is the number of substrate molecules while V_max is proportional to the total number of enzyme molecules, m.

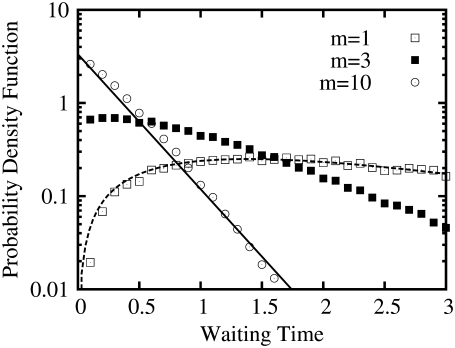
How does this result relate to Eq. 5 for a single enzyme, where, as seen, the waiting time distribution is not a simple exponential when m = 1? Fig. 2 shows the waiting-time distribution for product arrival with a single enzyme molecule (m = 1), as well as with m = 3 and 10 enzyme molecules. Evidently with increasing m, the distribution approaches a simple exponential, as depicted by the straight line in the semilog plot. This agrees with the predictions of Rao and Arkin (23). (Also see Sec. 3 in Data S1 for a proof.) Clearly, the more detailed kinetic information contained in the waiting-time distribution of a single enzyme is rapidly averaged-out with increasing m.

FIGURE 2.

Waiting time probability distributions for product arrivals as functions of the number of enzyme molecules, m. For an irreversible enzyme reaction with a single enzyme (m = 1), k₁[S] = 0.667, k_–1 = 0.083, and k₂ = 0.75, the expected waiting time distribution is shown by the open squares (simulation) and dashed line: (e^−t/2 – e^−t) (Eq. 5 with λ₁ = 1, λ₂ = 0.5). It has a mean waiting time 〈T〉 = 3 (Eq. 4). The solid squares and open circles are the waiting time distributions, from simulations, for three (m = 3) and ten (m = 10) enzyme molecules, respectively. For large m, the waiting time distribution becomes exponential with a mean time 〈T〉/m (30,41); the solid line represents 3.33e^−(10/3)t.

FLUCTUATING ENZYMES AND DYNAMIC COOPERATIVITY

The cycle time approach to MM kinetics has clearly shown that if an enzyme has a single well-defined unbound state E, then no matter how complex is the ES state, the MM hyperbolic kinetics results. The recent single-molecule measurements, however, show convincingly that many enzymes have slow conformational dynamics in their bound, as well as unbound, states (4). One therefore naturally seeks the behavioral and functional consequences of such dynamic characters of enzymes.

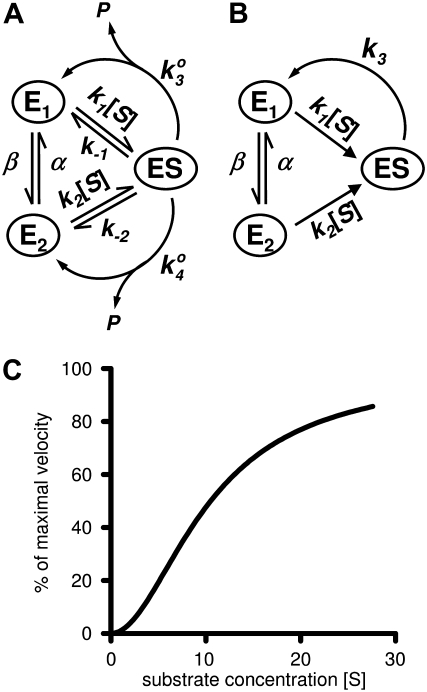
The simplest kinetic model, beyond that in Fig. 1, which considers conformational fluctuations in E is presented in Fig. 3 A. A model similar to this was first studied by Wong and Hanes in 1962 (42). Enzymes with slow dynamics have long been suggested to possess cellular regulatory functions. Frieden, in fact, had introduced the concept of hysteretic enzyme as early as 1970 (43), and since then a very sizable literature on such enzyme behavior has grown. Yet, the true roles of hysteretic enzymes in cellular regulations has been elusive. Ricard and Cornish-Bowden (16) and Cornish-Bowden and Cárdenas (17), following the lead of Rabin (44) and Ainslie et al. (45), have championed the concept of mnemonic enzymes. As we shall show, while both hysteretic and mnemonic enzymes are consequences of slow conformational disorder, they are in fact saying something different: One concept emphasizes transient kinetics and the other relates to a driven NESS.

FIGURE 3.

(A) The simplest kinetic model with two unbound enzyme states that exhibits dynamic cooperativity. One can simplify the notation by taking (B) Assuming k₄ ≪ k₃ in panel A, and under the condition k₁[S] ≫ β ≫ k₂[S] ≫ α, the steady-state probability of ES, p_ES, is proportional to [S]². (C) The steady-state velocity for the enzymatic reaction in panel B, with k₁ = 100, k₂ = 0.01, α = 0, β = 1, and k₃ = 100, shows a sigmoidal shape. Note that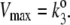

Steady-state cycle flux of a fluctuating enzyme: rapid exchange and quasistatics

The kinetic scheme in Fig. 3 A, although look formidable, can be simplified: Let us first put 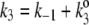and 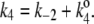Then the steady-state probabilities and cycle flux of the reaction triangle can be obtained by either the method of King-Altman (2), or by using Mathematica (Wolfram Research, Champaign, IL). One finds:

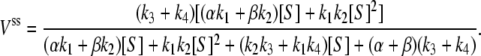(9)

We shall first discuss two limiting cases that are particularly instructive:

1. Rapid exchange equilibrium between E₁ and E₂. In this case, the overall rate of E → ES is r⁺ = (αk₁ + βk₂)[S]/(α + β), while the overall rate of ES → E is r⁻ = k₃ + k₄. Therefore, the steady-state probability for the ES is

   (10)

   while the overall velocity is V^ss = (k₃ + k₄)p_ES. One can verify these results by working with Eq. 9, and letting α and β both become much greater than any other terms. Therefore, under rapid equilibrium, E₁ and E₂ are really a single kinetic state and MM behavior is expected.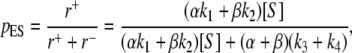
2. Quasistatic, nonexchanging E₁ and E₂, i.e., α = β = 0. In this case, instead of computing the rates of the turnovers, we compute the average time for each turnover. The time needed for ES → E is t⁻ = 1/(k₃ + k₄), while the time for E → ES is the average of, first, 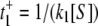for E₁ → ES and, second, 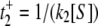for E₂ → ES, with corresponding probabilities p₁ = k₃/(k₃ + k₄) and p₂ = k₄/(k₃ + k₄); overall we thus obtain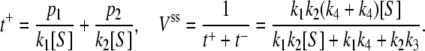

   (11)

Again, one can check this easily from Eq. 9 with α = β = 0.

An insight from the above two analyses is that sometimes thinking in terms of rates is simpler, while other occasions considering times is simpler. The difference depends on whether the kinetic processes are in parallel or in serial. In the former, one sums the rates, while for the latter, one sums the times. The two approaches are, of course, equivalent. In fact, one can derive Eq. 9 using exactly the methods developed in Michaelis-Menten-Briggs-Haldane Kinetics Revisited, above. With nonzero α and β, the mean first passage times to ES, starting at E₁ and E₂, are

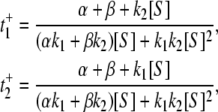(12)

respectively. Again, since the probabilities of E₁ and E₂ are p₁ and p₂ as given above, we have 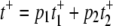while V^ss in Eq. 9 becomes 1/(t⁺ + t⁻).

Enzyme-substrate binding in equilibrium

The square-law dependence on [S] in the denominators of Eq. 12 for 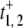is interesting because it indicates the possibility of positively cooperative, sigmoidal behavior in the enzyme substrate binding. To explore this, we first note that if k₃/k₄ = k₁α/(k₂β), there will be no steady-state flux between E₁ and E₂. (See Secs. 4 and 5 in Data S1.) In this case, one can verify that t⁺ = (α + β)/{(k₁α + k₂β)[S]} = 1/r⁺ so that the quadratic dependence on [S] disappeared. Therefore, having a nonequilibrium steady-state flux between E₁ and E₂ is a necessary condition for dynamic cooperativity. Such a flux is present when an enzyme is operating inside a cell, with sustained substrate and product concentrations.

Sigmoidal behavior and positive cooperativity

Knowing that a NESS flux between E₁ and E₂ is necessary, we now study the particular model shown in Fig. 3 B, with k₄ ≪ k₃. Fig. 3 C shows one example of the behavior. In fact, the general condition to observe a sigmoidal curve is that k₄ ≪ k₃, and k₁[S] ≫ β ≫ k₂[S] ≫ α. We see that the conditions β ≪ k₁[S] and α ≪ k₁[S] mean that conformational fluctuations between E₁ and E₂ are much slower than the rates of substrate binding.

What is the origin of the [S]² dependence? We can answer this question by considering 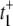as given in Eq. 12a. Since k₄ has been set to zero, p₂ = 0 and t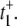⁺ = Under the condition k₁[S] ≫ β ≫ k₂[S] ≫ α, we get 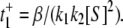The value of 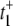arises from two pathways: E₁ → ES (Path I) and E₁ → E₂ →ES (Path II). The time for Path I is 1/(k₁[S]), while for Path II is 1/β + 1/(k₂[S]) ≈ 1/(k₂[S]). The probability of taking Path II, however, is very small: β/(β + k₁[S]) ≈ β/(k₁[S]). Therefore we see that 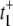is determined by the very low probability Path II which has an extremely long mean transit time! The time for Path I, 1/(k₁[S]), is negligible in comparison.

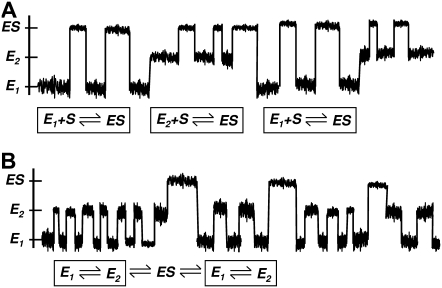
How can the very small probability Path II be dominant? This seems to be counterintuitive. The answer resides in the conventional thinking about kinetics in terms of flux. When applied to multiple pathways in parallel, clearly the small probability, low flux pathways are negligible. However, the nature of the slow conformational fluctuations between E₁ and E₂ indicates that such an enzyme goes through several catalytic cycles via Path I, before taking the Path II occasionally. The overall time should, thus, be determined by the average time, which is dominated by Path II. This difference is illustrated in Fig. 4.

FIGURE 4.

Schematic plots illustrating the dynamical difference between slow and rapid fluctuating states E. In the former, the enzyme substrate associations occur in serial order (A), while in the latter, they are in parallel. The overall association is determined by the average time in panel A but average rate in panel B.

To understand dynamic cooperativity in terms of molecular interactions, the most illuminating way is again to consider only one enzyme. In this case, the cooperativity is not in the occupation of one enzyme by its substrate influencing the occupation of another enzyme: that would be the allosteric cooperativity. Rather, more substrate molecules will increase the probability of Path I, as well as decrease the time for Path II. Hence the origin of substrate-substrate interaction is through competitions for the sites and paths of enzyme molecules (46).

COOPERATIVITY AND SPECIFICITY

Square-law effect in dynamic cooperativity and specificity amplification

As we have shown, dynamic cooperativity arises from the [S]² dependence of p_ES and V^ss in a monomeric single-site enzyme. Now, imagine that we have two competing substrates S and S′ at equal concentration. Substrate S, however, has a higher affinity for the enzyme via its on-rate, k₁/k′₁ = k_–2/k′_–2 = θ > 1, where the k values are the corresponding association rate constants for S′. All the other rate constants are the same for S and S′. Then the same dynamic cooperativity mechanism leads to the of enzyme-substrate complex probability ratio

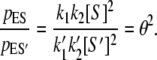(13)

In other words, the specificity of the enzyme E for its substrates is amplified in the NESS kinetics.

If the different affinities between S and S′ arise from their off-rates rather than from the on-rates, i.e., k_–1/k′_–1 = 1/θ, then specificity amplification can be accomplished if there is a slow isomerization in the ES state. With the same algebra, one can show that the binding affinity ratio θ is amplified to θ² (6). (See Sec. 6 in Data S1.) This last result is in fact the celebrated Hopfield-Ninio kinetic proofreading mechanism for high fidelity in protein biosynthesis and DNA replications (24,25). An important element of the Hopfield-Ninio mechanism is that the kinetics have to be coupled to driven cofactors so that the enzyme is operating under a NESS. In protein biosynthesis the coupled reaction is GTP hydrolysis; in DNA replication, the coupled reaction is the dNTP hydrolysis carried out by 3′-5′ exonuclease.

It is satisfying to see that the quadratic term in sigmoidal dynamic cooperativity is in fact intimately related to the square-law effect of kinetic proofreading. As we have stated, the cooperative binding with respect to substrate S represents, in fact, the same mechanism for specificity amplification residing in the on-rates. It has been shown that the square-law effect is only a limitation of single kinetic cycle. For multiple kinetics cycles, i.e., multiple 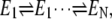the cooperativity (and specificity amplification) can be much greater (47).

Mnemonic and hysteretic enzymes

The term “mnemonic” has been used to represent dynamic cooperativity (16,17). Hysteretic behavior, on the other hand, is usually represented by bursts and lags in the transient enzyme kinetics (14). Neet and Ainslie have carefully discussed the distinctions between these two aspects of slow conformational fluctuations (15). In the context of single-molecule enzyme kinetics, the enzyme reaction time is represented by the arriving time distribution f_T(t) for E + S → E + P. The lags (and bursts) are a feature of f_T(t) near t = 0, and dynamic cooperativity is related to a long-tail of f_T(t) for large t (small probability with very long time). Both bias f_T(t) toward larger time; i.e., slower dynamics, but they emphasize different aspects of f_T(t).

In this review, we focused completely on the steady state of a driven enzyme with slow conformational fluctuations. We believe that one has to understand the nonequilibrium steady state of a biochemical reaction system before one can truly understand its dynamics in terms of its hysteretic behavior.

SUMMARY

The classic Michaelis-Menten (MM) theory can be reformulated in terms of single enzyme cycle kinetics. With sustained substrate and product concentrations, the steady-state cycle flux precisely equals the reciprocal of the mean cycle time, which agrees with the canonical MM velocity, i.e., a linear relation in the Lineweaver-Burk double reciprocal plot. The MM theory can be reformulated in terms of a time perspective rather than the customary rate perspective: Instead of computing the rates, one calculates the mean passage times.

In single-molecule enzymology, the kinetics of the canonical reversible enzyme mechanism 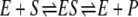is completely characterized in terms of two quantities: the cycle-time distribution f_T(t) and the probability p₊ of a forward cycle.

The single-enzyme cycle time f_T(t) has been measured in the laboratory (4). In general it is not a single exponential. However, if there are several enzyme molecules at work (say >10), then the time interval between product arrivals quickly approaches an exponential distribution.

The time perspective provides a better understanding for the cooperativity in monomeric enzymes that exhibit sigmoidal substrate dependence. It is shown that the [S]² dependence arises from pathways for catalysis with very small probabilities but extreme long passage times; hence, the mean passage time is dominated by the path of low probability. Furthermore, dynamic cooperativity occurs only when the enzyme conformational fluctuations are slow compared to catalysis.

Finally, we have demonstrated that dynamic cooperativity in monomeric enzymes, which is characterized by [S]² dependence on substrate concentration, shares the same molecular mechanism as kinetic proofreading, first proposed by Hopfield and Ninio (24,28) for explaining the high fidelity of protein biosynthesis and DNA replication. The kinetic proofreading mechanism is capable of amplifying specificity in nonequilibrium steady state (NESS) (7,47).

Enzyme cooperativity is one of the significant paradigms in molecular biology (48). Its importance in biochemical processes is derived from its nonlinear behavior and its connection to decision-making in cellular biology. In the past, the theory of enzyme cooperativity has been dominated by equilibrium, allosteric regulation in multisubunit enzyme complexes. This theory shows that, in a living biochemical system, enzyme cooperativity can also occur in monomeric enzymes. Such enzymes, however, have to be coupled to a substrate catalytic cycle. Indeed, cellular signal transduction has to have an energy cost (7). Although we know that cellular energy drives biosynthesis and cell motility, and sustains biochemical gradients, we do not currently know how much energy is utilized in cellular information processing.

There is a growing interest in extending the static view of proteins which holds that the three-dimensional structures are the sole molecular basis to protein dynamics. But what is protein dynamics? Recent single-molecule experiments have shown that many proteins are dynamically fluctuating, with a range and a rate. In the past, the function of enzyme fluctuations was mainly discussed in the context of “the role of the protein matrix as a local solvent for the bound chemical subsystem of the enzyme-catalyzed reaction” (49). For example, an entire volume (49) has been devoted to this line of inquiry. Such studies focus only on isolated enzymes and their catalysis (50).

Dynamic cooperativity as discussed in this review is a consequence of slow conformational fluctuations. But it transcends individual macromolecules and enters the realm of protein substrate reaction networks in NESS. We would like to borrow a statement that cogently describes central tasks ahead (49): “Enzymes are biological entities first, and isolated object of physiochemical analysis second…. The natural habitat of many enzymes in the living cell is far different from that in bulk aqueous solution in vitro.”

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.